Hybrid Nanofluid Flow over a Permeable Shrinking Sheet Embedded in a Porous Medium with Radiation and Slip Impacts
Abstract
1. Introduction
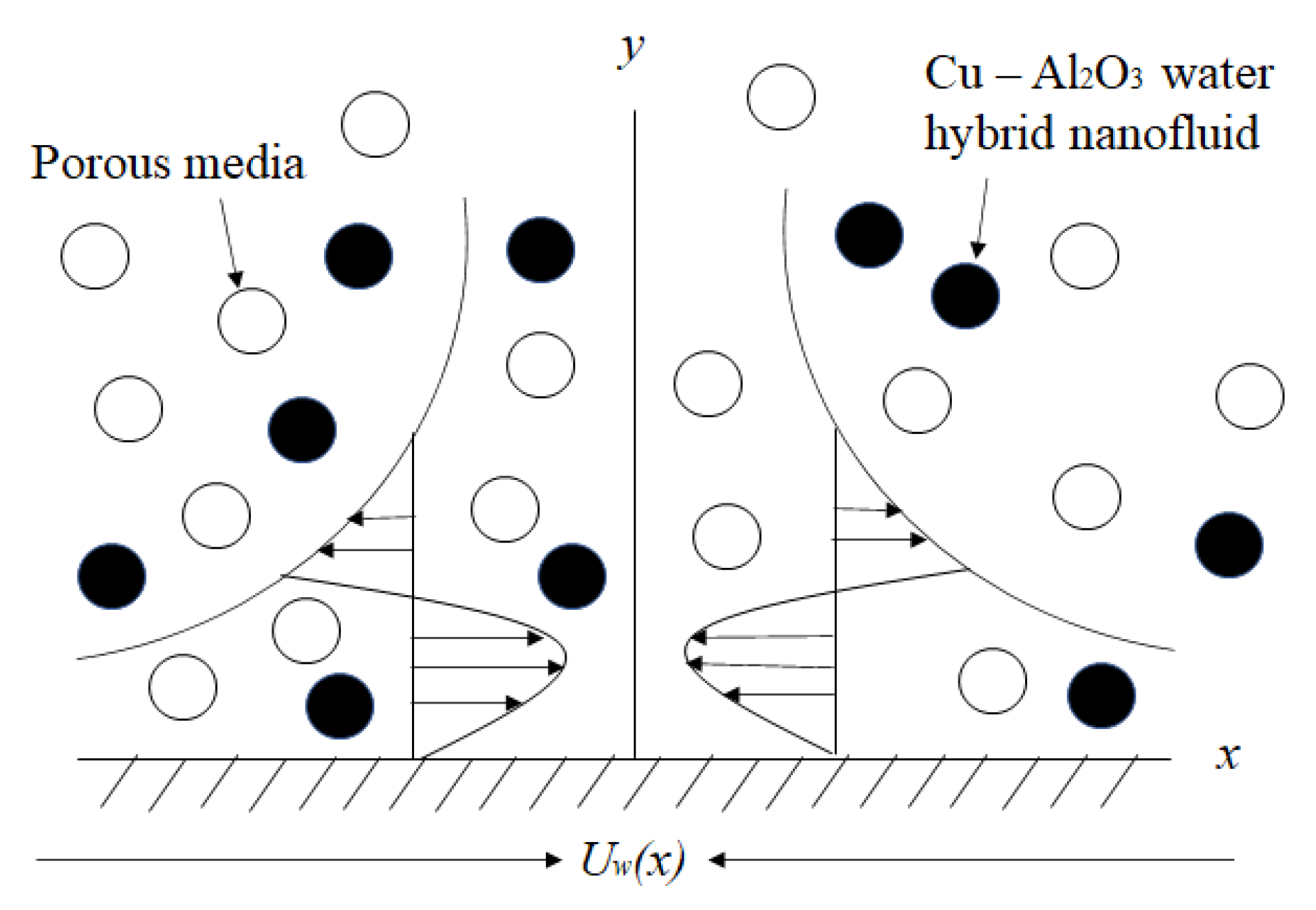
2. Problem Formulation
3. Numerical Soluion
4. Stability Analysis
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| Al2O3 | Aluminium Oxide |
| bvp4c | Boundary value problem – fourth-order method |
| Cu | Copper |
| CuO | Copper Oxide |
| KKL | Koo–Kleinstreuer–Li approach |
| MHD | Magnetohydrodynamics |
| ODE | Ordinary differential equations |
| PDE | Partial differential equations |
References
- Choi, S.U.; Eastman, J.A. Enhancing thermal conductivity of fluids with nanoparticles. In Proceedings of the 1995 International Mechanical Engineering Congress and Exhibition, San Francisco, CA, USA, 12–17 November 1995. [Google Scholar]
- Saidur, R.; Leong, K.Y.; Mohammed, H.A. A review on applications and challenges of nanofluids. Renew. Sustain. Energy Rev. 2011, 15, 1646–1668. [Google Scholar] [CrossRef]
- Moghadasi, R.; Rostami, A.; Hemmati–Sarapardeh, A. Application of nanofluids for treating fines migration during hydraulic fracturing: Experimental study and mechanistic understanding. Adv. Geo-Energy Res. 2019, 3, 198–206. [Google Scholar] [CrossRef]
- Motsumi, T.G.; Makinde, O.D. Effects of thermal radiation and viscous dissipation on boundary layer flow of nanofluids over a permeable moving flat plate. Phys. Scr. 2012, 86, 045003. [Google Scholar] [CrossRef]
- Sheikholeslami, M. Effect of uniform suction on nanofluid flow and heat transfer over a cylinder. J. Braz. Soc. Mech. Sci. Eng. 2015, 37, 1623–1633. [Google Scholar] [CrossRef]
- Naramgari, S.; Sulochana, C. MHD flow over a permeable stretching/shrinking sheet of a nanofluid with suction/injection. Alex. Eng. J. 2016, 55, 819–827. [Google Scholar] [CrossRef]
- Daniel, Y.S.; Aziz, Z.A.; Ismail, Z.; Salah, F. Effects of thermal radiation, viscous and Joule heating on electrical MHD nanofluid with double stratification. Chin. J. Phys. 2017, 55, 630–651. [Google Scholar] [CrossRef]
- Kumar, N.; Sonawane, S.S.; Sonawane, S.H. Experimental study of thermal conductivity, heat transfer and friction factor of Al2O3 based nanofluid. Int. J. Commun. Heat. Mass Transf. 2018, 90, 1–10. [Google Scholar] [CrossRef]
- Upreti, H.; Pandey, A.K.; Kumar, M. MHD flow of Ag-water nanofluid over a flat porous plate with viscous-Ohmic dissipation, suction/injection and heat generation/absorption. Alex. Eng. J. 2018, 57, 1839–1847. [Google Scholar] [CrossRef]
- Bakar, S.A.; Arifin, N.M.; Ali, F.M.; Bachok, N. The effects of soret and dufour on mixed convection boundary layer flow of a porous media along a permeable surface filled with a nanofluid and radiation. J. Adv. Res. Fluid Mech. Therm. Sci. 2019, 53, 35–46. [Google Scholar]
- Jamaludin, A.; Nazar, R.; Pop, I. Mixed convection stagnation-point flow of a nanofluid past a permeable stretching/shrinking sheet in the presence of thermal radiation and heat source/sink. Energies 2019, 12, 788. [Google Scholar] [CrossRef]
- Khashi’ie, S.N.; Arifin, N.M.; Hafidzuddin, E.H.; Wahi, N. Dual stratified nanofluid flow past a permeable shrinking/stretching sheet using a non-Fourier energy model. Appl. Sci. 2019, 9, 2124. [Google Scholar] [CrossRef]
- Maleki, H.; Safaei, M.R.; Alrashed, A.A.; Kasaeian, A. Flow and heat transfer in non-Newtonian nanofluids over porous surfaces. J. Therm. Anal. Cal. 2019, 135, 1656–1666. [Google Scholar] [CrossRef]
- Chaudhary, S.; Kanika, K.M. Heat generation/absorption and radiation effects on hydromagnetic stagnation point flow of nanofluids towards a heated porous stretching/shrinking sheet with suction/injection. J. Porous Media 2020, 23. [Google Scholar] [CrossRef]
- Shuaib, M.; Ali, A.; Khan, M.A.; Ali, A. Numerical investigation of an unsteady nanofluid flow with magnetic and suction effects to the moving upper plate. Adv. Mech. Eng. 2020, 12, 1687814020903588. [Google Scholar] [CrossRef]
- Ahmad, S.; Pop, I. Mixed convection boundary layer flow from a vertical flat plate embedded in a porous medium filled with nanofluids. Int. Commun. Heat Mass Transf. 2010, 8, 483. [Google Scholar] [CrossRef]
- Sheikholeslami, M.; Ziabakhsh, Z.; Ganji, D.D. Transport of Magnetohydrodynamic nanofluid in a porous media. Coll. Surf. A Phys. Eng. Asp. 2017, 520, 201–212. [Google Scholar] [CrossRef]
- Bakar, S.A.; Arifin, N.M.; Ali, F.M.; Bachok, N.; Nazar, R.; Pop, I. A stability analysis on mixed convection boundary layer flow along a permeable vertical cylinder in a porous medium filled with a nanofluid and thermal radiation. Appl. Sci. 2018, 8, 483. [Google Scholar] [CrossRef]
- Rashad, A.M.; Khan, W.A.; El-Kabeir, S.M.; El-Hakiem, A. Mixed convective flow of micropolar nanofluid across a horizontal cylinder in saturated porous medium. Appl. Sci. 2019, 17, 5241. [Google Scholar] [CrossRef]
- Dogonchi, A.S.; Seyyedi, S.M.; Hashemi-Tilehnoee, M.; Chamkha, A.J.; Ganji, D.D. Investigation of natural convection of magnetic nanofluid in an enclosure with a porous medium considering Brownian motion. Case Stud. Therm. Eng. 2019, 14, 100502. [Google Scholar] [CrossRef]
- Haq, R.U.; Raza, A.; Algehyne, E.A.; Tlili, I. Dual nature study of convective heat transfer of nanofluid flow over a shrinking surface in a porous medium. Int. J. Commun. Heat. Mass Transf. 2020, 114, 104583. [Google Scholar] [CrossRef]
- Hayat, T.; Haider, F.; Alsaedi, A.; Ahmad, B. Unsteady flow of nanofluid through porous medium with variable characteristics. Int. J. Commun. Heat. Mass Transf. 2020, 119, 104904. [Google Scholar] [CrossRef]
- Ghadikolaei, S.S.; Yassari, M.; Sadeghi, H.; Hosseinzadeh, K.; Ganji, D.D. Investigation on thermophysical properties of TiO2–Cu/H2O hybrid nanofluid transport dependent on shape factor in MHD stagnation point flow. Powder Technol. 2017, 322, 428–438. [Google Scholar] [CrossRef]
- Sundar, L.S.; Sharma, K.V.; Singh, M.K.; Sousa, A.C.M. Hybrid nanofluids preparation, thermal properties, heat transfer and friction factor—A review. Renew. Sustain. Energy Rev. 2017, 68, 185–198. [Google Scholar] [CrossRef]
- Jamaludin, A.; Naganthran, K.; Nazar, R.; Pop, I. MHD mixed convection stagnation-point flow of Cu-Al2O3/water hybrid nanofluid over a permeable stretching/shrinking surface with heat source/sink. Eur. J. Mech. B Fluids 2020, 84, 71–80. [Google Scholar] [CrossRef]
- Khashi’ie, N.S.; Arifin, N.M.; Pop, I. Mixed convective stagnation point flow towards a vertical riga plate in hybrid Cu-Al2O3/water nanofluid. Mathematics 2020, 8, 912. [Google Scholar] [CrossRef]
- Waini, I.; Ishak, A.; Pop, I. Flow and heat transfer of a hybrid nanofluid past a permeable moving surface. Chin. J. Phys. 2020, 66, 606–619. [Google Scholar] [CrossRef]
- Wahid, N.S.; Arifin, N.M.; Turkyilmazoglu, M.; Hafidzuddin, M.E.H.; Abd Rahmin, N.A. MHD Hybrid Cu-Al2O3/Water Nanofluid Flow with Thermal Radiation and Partial Slip Past a Permeable Stretching Surface: Analytical Solution. J. Nano Res. 2020, 64, 75–91. [Google Scholar] [CrossRef]
- Wahid, N.S.; Arifin, N.M.; Khashi’ie, N.S.; Pop, I. Hybrid Nanofluid Slip Flow over an Exponentially Stretching/Shrinking Permeable Sheet with Heat Generation. Mathematics 2021, 9, 30. [Google Scholar] [CrossRef]
- Khashi’ie, N.S.; Arifin, N.M.; Pop, I. Non-Darcy mixed convection of hybrid nanofluid with thermal dispersion along a vertical plate embedded in a porous medium. Int. Commun. Heat. Mass Transf. 2020, 118, 104866. [Google Scholar] [CrossRef]
- Ghadikolaei, S.S.; Hosseinzadeh, K.; Hatami, M.; Ganji, D.D. MHD boundary layer analysis for micropolar dusty fluid containing Hybrid nanoparticles (Cu Al2O3) over a porous medium. J. Mol. Liq. 2018, 268, 813–823. [Google Scholar] [CrossRef]
- Nadeem, S.; Abbas, N. Effects of MHD on modified nanofluid model with variable viscosity in a porous medium. In Nanofluid Flow in Porous Media; IntechOpen: London, UK, 2019. [Google Scholar]
- Subhani, M.; Nadeem, S. Numerical investigation into unsteady magnetohydrodynamics flow of micropolar hybrid nanofluid in porous medium. Phys. Scr. 2019, 94, 105220. [Google Scholar] [CrossRef]
- Aminian, E.; Moghadasi, H.; Saffari, H. Magnetic field effects on forced convection flow of a hybrid nanofluid in a cylinder filled with porous media: A numerical study. J. Ther. Anal. Calori. 2020, 141, 2019–2031. [Google Scholar] [CrossRef]
- Waini, I.; Ishak, A.; Grosan, T.; Pop, I. Mixed convection of a hybrid nanofluid flow along a vertical surface embedded in a porous medium. Int. Commun. Heat. Mass Transf. 2020, 114, 185–198. [Google Scholar] [CrossRef]
- Devi, S.A.; Devi, S.S.U. Numerical investigation of hydromagnetic hybrid Cu–Al2O3/water nanofluid flow over a permeable stretching sheet with suction. Int. J. Nonlinear Sci. Numer. Simul. 2016, 17, 249–257. [Google Scholar] [CrossRef]
- Rajagopal, K.R. On a hierarchy of approximate models for flows of incompressible fluids through porous solids. Math. Model. Methods Appl. Sci. 2007, 17, 215–252. [Google Scholar] [CrossRef]
- Nield, D.A.; Bejan, A. Convection in Porous Media; Springer: New York, NY, USA, 2006. [Google Scholar]
- Rosseland, S. On the transmission of radiation through an absorbing medium in motion, with applications to the theory of sun-spots and solar rotation. Astro J. 1926, 63, 342. [Google Scholar] [CrossRef]
- Shampine, L.F.; Kierzenka, J.; Reichelt, M.W. Solving boundary value problems for ordinary differential equations in MATLAB with bvp4c. Tutor. Notes 2003, 2000, 1–27. [Google Scholar]
- Zainal, N.A.; Nazar, R.; Naganthran, K.; Pop, I. MHD flow and heat transfer of hybrid nanofluid over a permeable moving surface in the presence of thermal radiation. Int. J. Numer. Methods Heat Fluid Flow 2020, 31, 858–879. [Google Scholar] [CrossRef]
- Wang, C.Y. Stagnation flow towards a shrinking sheet. Int. J. Non-Linear Mech. 2008, 43, 377–382. [Google Scholar] [CrossRef]
- Bhattacharyya, K.; Mukhopadhyay, S.; Layek, G.C. Steady boundary layer slip flow and heat transfer over a flat porous plate embedded in a porous media. J. Pet. Sci. Eng. 2011, 78, 304–309. [Google Scholar] [CrossRef]
- Merkin, J.H. Mixed convection boundary layer flow on a vertical surface in a saturated porous medium. J. Eng. Math. 1980, 14, 301–313. [Google Scholar] [CrossRef]
- Merrill, K.; Beauchesne, M.; Previet, J.; Paullet, J.; Weidman, P. Final steady flow near a stagnation point on a vertical surface in a porous medium. Int. J. Heat. Mass Transf. 2006, 49, 4681–4686. [Google Scholar] [CrossRef]
- Merkin, J.H. On dual solutions occurring in mixed convection in a porous medium. J. Eng. Math. 1986, 20, 171–179. [Google Scholar] [CrossRef]
- Weidman, P.D.; Kubitschek, D.G.; Davis, A.M.J. The effect of transpiration on self-similar boundary layer flow over moving surfaces. Int. J. Eng. Sci. 2006, 44, 730–737. [Google Scholar] [CrossRef]
- Harris, S.D.; Ingham, D.B.; Pop, I. Mixed convection boundary-layer flow near the stagnation point on a vertical surface in a porous medium: Brinkman model with slip. Transp. Porous Media 2009, 77, 267–285. [Google Scholar] [CrossRef]

| Properties | Nanofluid | Hybrid Nanofluid |
|---|---|---|
| Density | ||
| Heat capacity | ||
| Dynamic viscosity | ||
| Thermal conductivity | ||
| where | ||
| Physical Characteristics | Water (f) | Al2O3 (s1) | Cu (s2) |
|---|---|---|---|
| Density, (kg/m) | 997.0 | 3970 | 8933 |
| Thermal expansion, (K) | |||
| Thermal conductivity, k (W/m K) | 0.6071 | 40 | 400 |
| Thermal capacity, (J/kg K) | 4180 | 765 | 385 |
| Present Study | Bhattacharyya et al. [43] | Wang [42] | |
|---|---|---|---|
| −0.50 | 1.49566 | 1.49655 | 1.49567 |
| −0.625 | 1.52071 | 1.50715 | – |
| −0.75 | 1.48929 | 1.48929 | 1.48930 |
| −1.00 | 1.32882 (0) | 1.32881 (0) | 1.32282 (0) |
| −1.15 | 1.08223 (0.11670) | 1.08223 (0.11670) | 1.08223 (0.11670) |
| −1.20 | 0.93247 (0.23364) | 0.93247 (0.23364) | – |
| Upper Solution | Lower Solution | ||
|---|---|---|---|
| 0.2 | −1.6 | 0.87412 | −0.56313 |
| −1.7 | 0.90673 | −0.56422 | |
| −1.8 | 0.94051 | −0.56540 | |
| 0.3 | −1.6 | 0.91186 | −0.59207 |
| −1.7 | 0.93004 | −0.61358 | |
| −1.8 | 0.96728 | −0.63776 |
| Upper Solution | Lower Solution | ||
|---|---|---|---|
| 0.1 | −1.6 | 0.51620 | −0.47993 |
| −1.7 | 0.55783 | −0.48015 | |
| −1.8 | 0.59022 | −0.48154 | |
| 0.2 | −1.6 | 0.73326 | −0.52197 |
| −1.7 | 0.74748 | −0.52244 | |
| −1.8 | 0.81905 | −0.52293 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abu Bakar, S.; Md Arifin, N.; Khashi’ie, N.S.; Bachok, N. Hybrid Nanofluid Flow over a Permeable Shrinking Sheet Embedded in a Porous Medium with Radiation and Slip Impacts. Mathematics 2021, 9, 878. https://doi.org/10.3390/math9080878
Abu Bakar S, Md Arifin N, Khashi’ie NS, Bachok N. Hybrid Nanofluid Flow over a Permeable Shrinking Sheet Embedded in a Porous Medium with Radiation and Slip Impacts. Mathematics. 2021; 9(8):878. https://doi.org/10.3390/math9080878
Chicago/Turabian StyleAbu Bakar, Shahirah, Norihan Md Arifin, Najiyah Safwa Khashi’ie, and Norfifah Bachok. 2021. "Hybrid Nanofluid Flow over a Permeable Shrinking Sheet Embedded in a Porous Medium with Radiation and Slip Impacts" Mathematics 9, no. 8: 878. https://doi.org/10.3390/math9080878
APA StyleAbu Bakar, S., Md Arifin, N., Khashi’ie, N. S., & Bachok, N. (2021). Hybrid Nanofluid Flow over a Permeable Shrinking Sheet Embedded in a Porous Medium with Radiation and Slip Impacts. Mathematics, 9(8), 878. https://doi.org/10.3390/math9080878







