Wall Shear Stress Topological Skeleton Analysis in Cardiovascular Flows: Methods and Applications
Abstract
1. Introduction
2. Topological Skeleton of a Vector Field
3. Lagrangian Approach
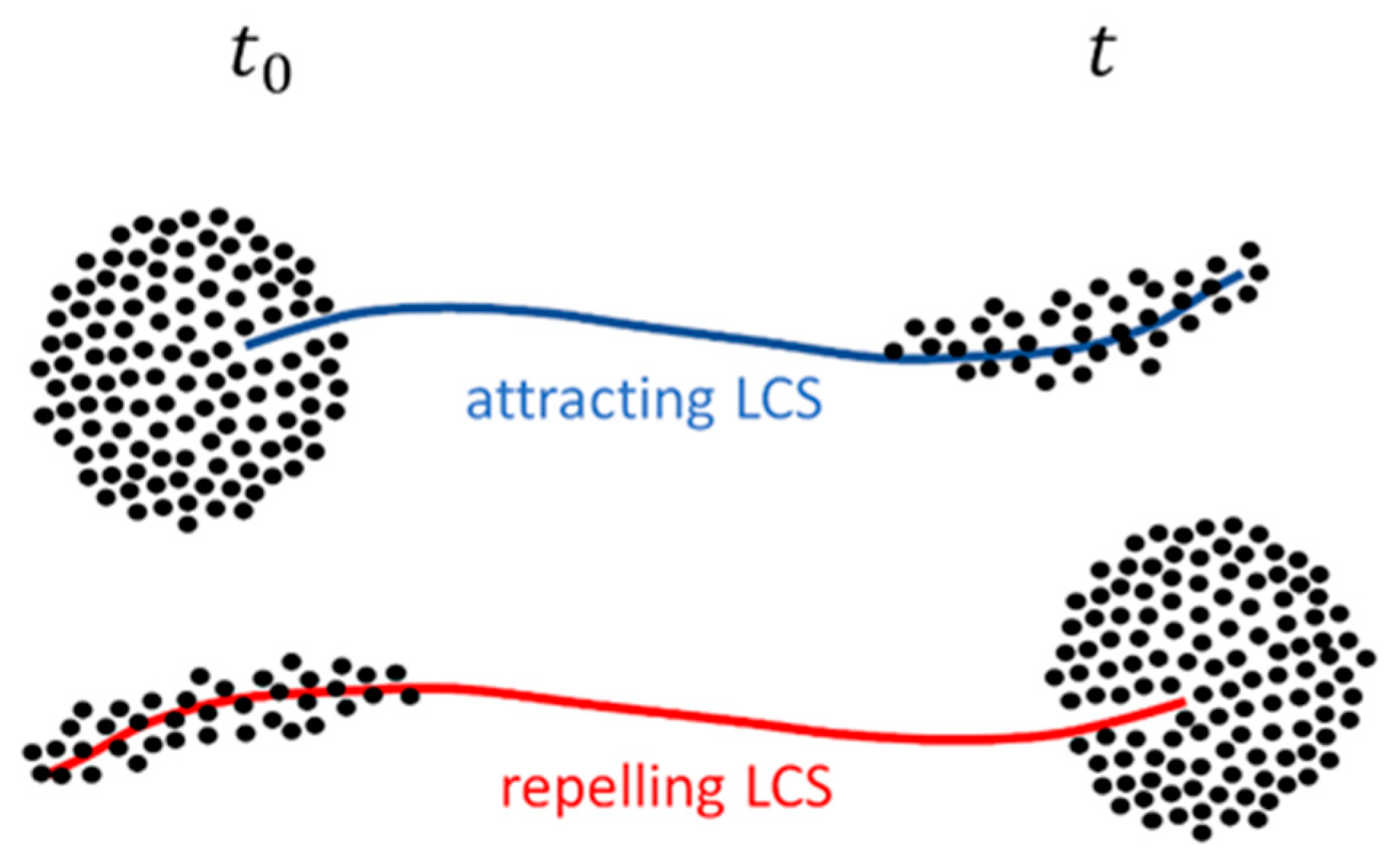
3.1. Lagrangian Coherent Structures
3.2. LCS Application to Intravascular Flows
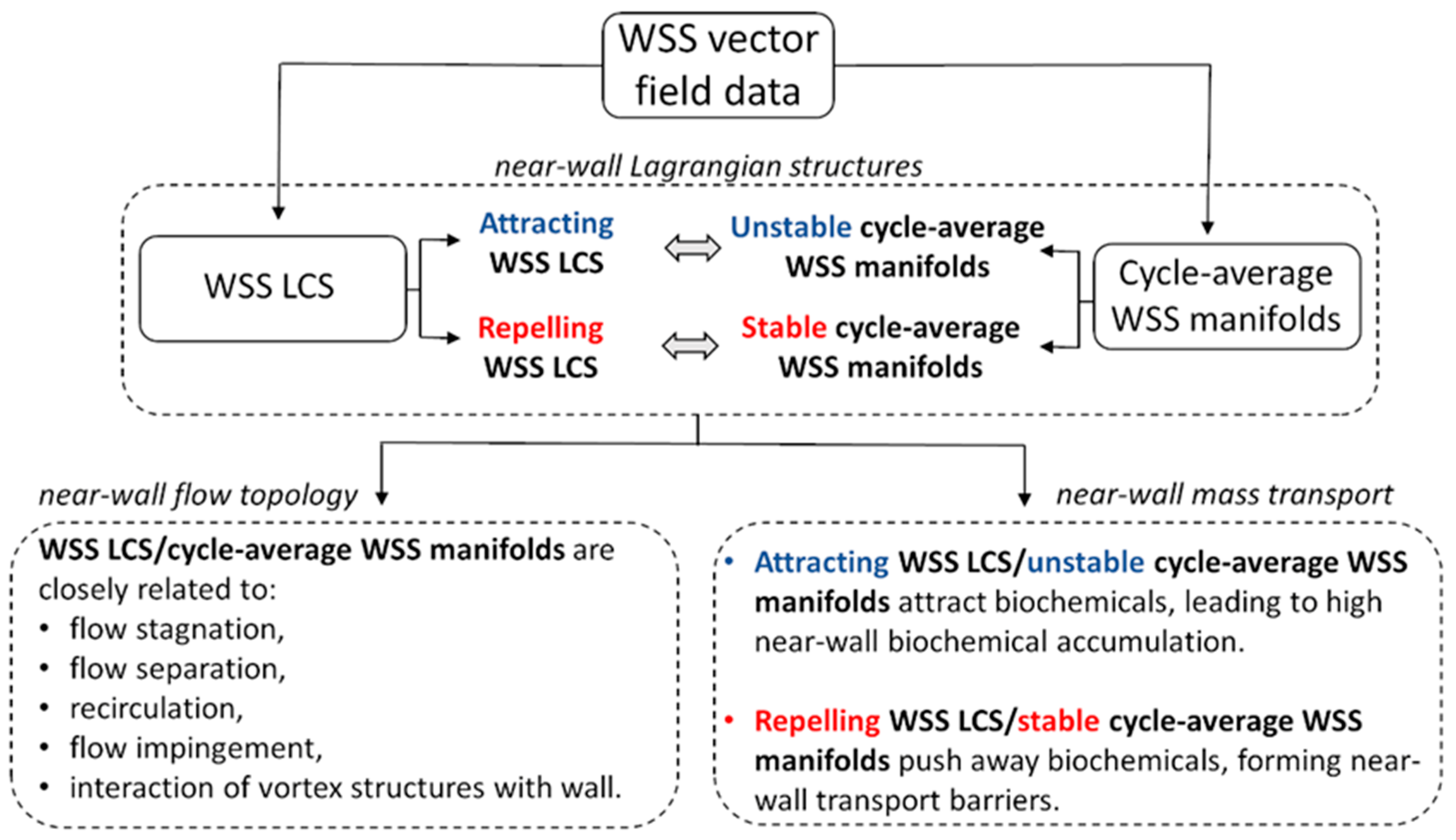
3.3. LCS Application to Near-Wall Flow Features
4. Eulerian Approach
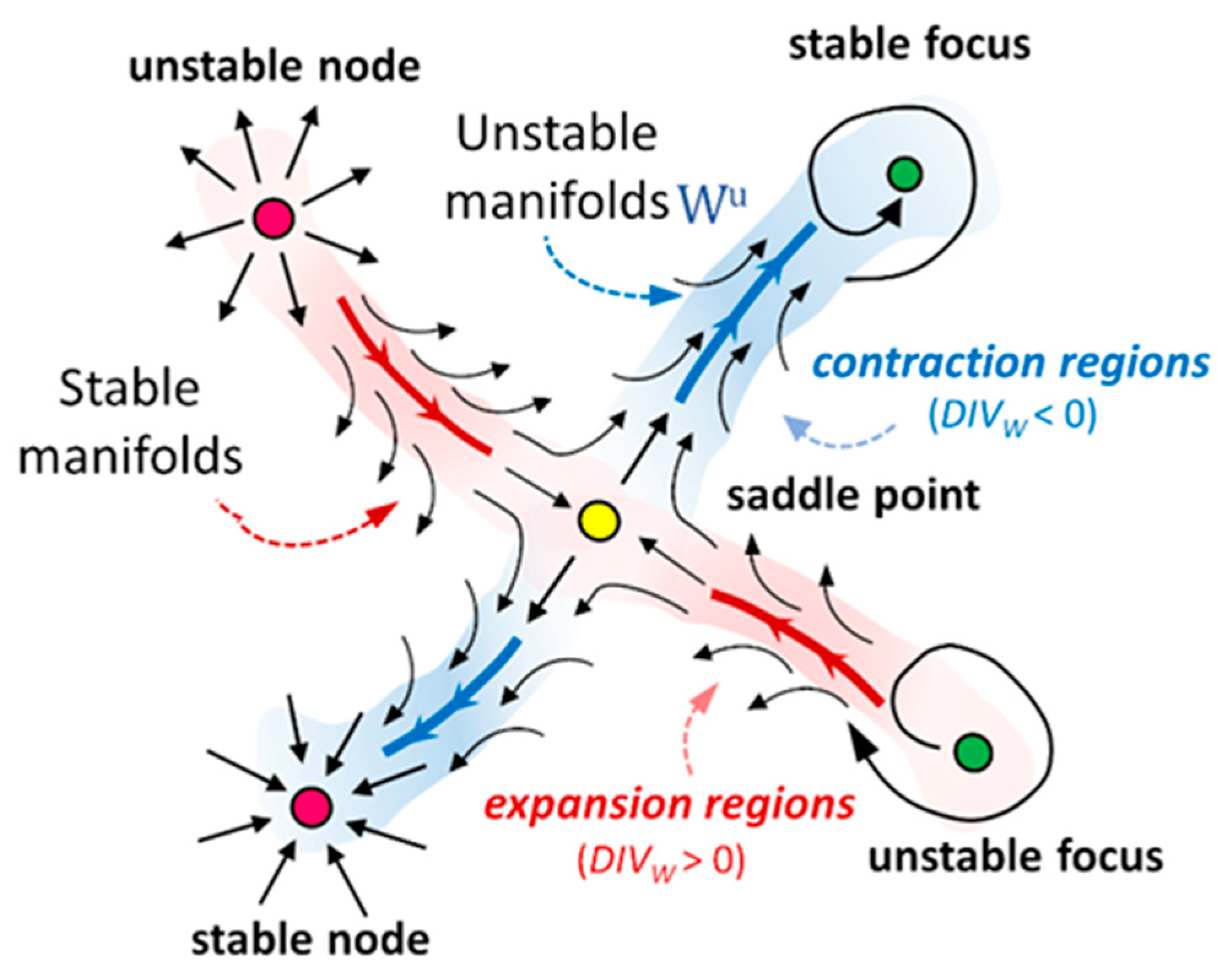
4.1. Volume Contraction Theory
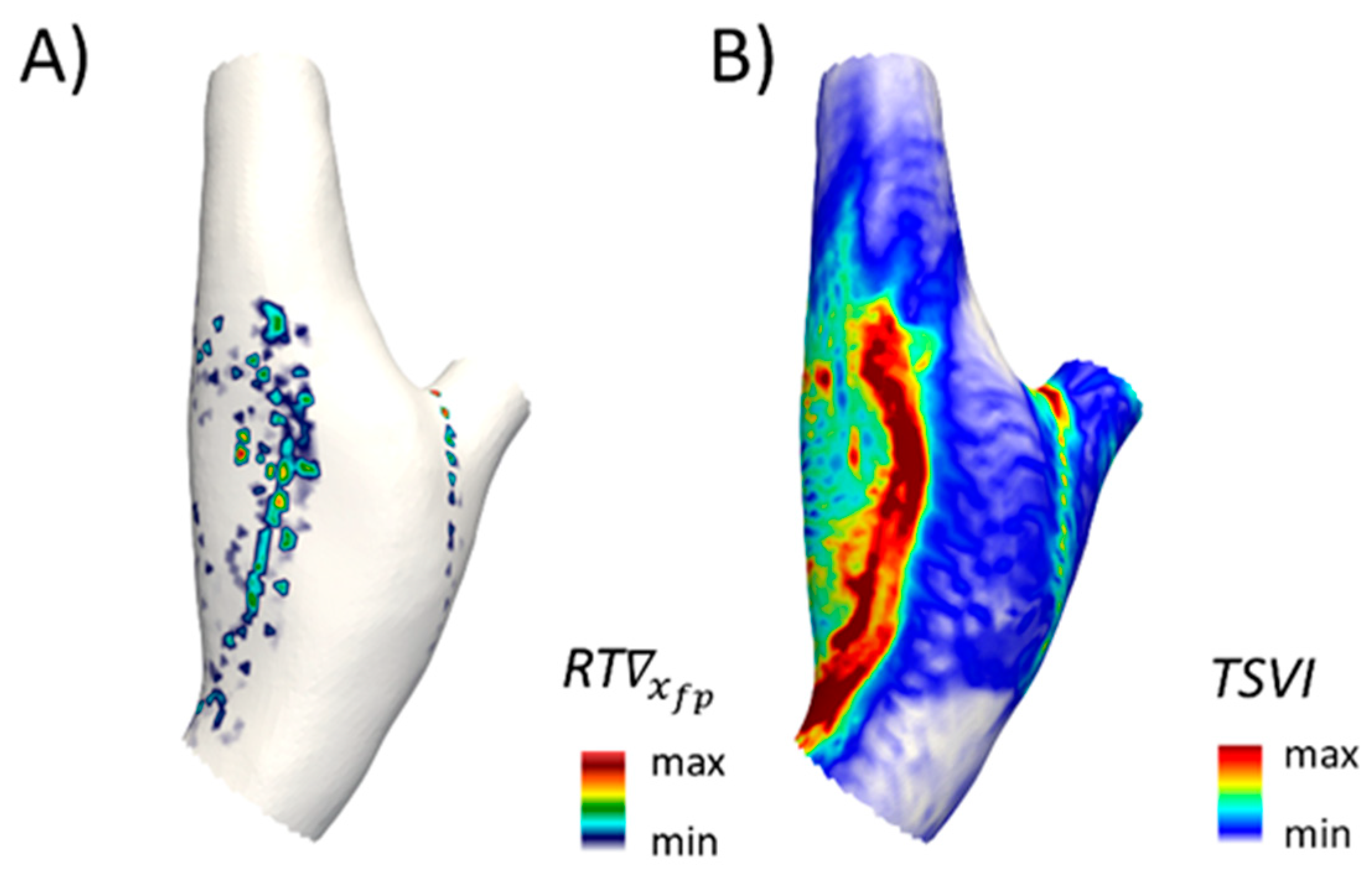
4.2. Eulerian-Based Approach for WSS Topological Skeleton Identification
- a local positive value of the divergence of the WSS field at the luminal surface means that locally shear forces exert an expansion action on the endothelium;
- a local negative value of the divergence of the WSS field at the luminal surface means that locally shear forces exert a contraction action on the endothelium.
4.3. Application of the Eulerian-Based Method for WSS Topological Skeleton Analysis to Cardiovascular Flows
5. Future Directions
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Kwak, B.R.; Bäck, M.; Bochaton-Piallat, M.-L.; Caligiuri, G.; Daemen, M.J.A.P.; Davies, P.F.; Hoefer, I.E.; Holvoet, P.; Jo, H.; Krams, R.; et al. Biomechanical factors in atherosclerosis: Mechanisms and clinical implications. Eur. Heart J. 2014, 35, 3013–3020. [Google Scholar] [CrossRef] [PubMed]
- Morbiducci, U.; Kok, A.M.; Kwak, B.R.; Stone, P.H.; Steinman, D.A.; Wentzel, J.J. Atherosclerosis at arterial bifurcations: Evidence for the role of haemodynamics and geometry. Thromb. Haemost. 2016, 115, 484–492. [Google Scholar] [CrossRef]
- Malek, A.M.; Alper, S.L.; Izumo, S. Hemodynamic shear stress and its role in atherosclerosis. J. Am. Med. Assoc. 1999, 282, 2035–2042. [Google Scholar] [CrossRef]
- Zarins, C.K.; Giddens, D.P.; Bharadvaj, B.K.; Sottiurai, V.S.; Mabon, R.F.; Glagov, S. Carotid bifurcation atherosclerosis. Quantitative correlation of plaque localization with flow velocity profiles and wall shear stress. Circ. Res. 1983, 53, 502–514. [Google Scholar] [CrossRef]
- Caro, C.G.; Fitz-Gerald, J.M.; Schroter, R.C. Atheroma and arterial wall shear. Observation, correlation and proposal of a shear dependent mass transfer mechanism for atherogenesis. Proc. R. Soc. Lond. Ser. B Biol. Sci. 1971, 177, 109–159. [Google Scholar] [CrossRef]
- Ku, D.N.; Giddens, D.P.; Zarins, C.K.; Glagov, S. Pulsatile flow and atherosclerosis in the human carotid bifurcation. Positive correlation between plaque location and low oscillating shear stress. Arteriosclerosis 1985, 5, 293–302. [Google Scholar] [CrossRef]
- Wang, C.; Baker, B.M.; Chen, C.S.; Schwartz, M.A. Endothelial cell sensing of flow direction. Arterioscler. Thromb. Vasc. Biol. 2013, 33, 2130–2136. [Google Scholar] [CrossRef]
- Peiffer, V.; Sherwin, S.J.; Weinberg, P.D. Does low and oscillatory wall shear stress correlate spatially with early atherosclerosis? A systematic review. Cardiovasc. Res. 2013, 99, 242–250. [Google Scholar] [CrossRef]
- Gallo, D.; Bijari, P.B.; Morbiducci, U.; Qiao, Y.; Xie, Y.J.; Etesami, M.; Habets, D.; Lakatta, E.G.; Wasserman, B.A.; Steinman, D.A. Segment-specific associations between local haemodynamic and imaging markers of early atherosclerosis at the carotid artery: An in vivo human study. J. R. Soc. Interface 2018, 15. [Google Scholar] [CrossRef]
- Hoogendoorn, A.; Kok, A.M.; Hartman, E.M.J.; de Nisco, G.; Casadonte, L.; Chiastra, C.; Coenen, A.; Korteland, S.A.; Van der Heiden, K.; Gijsen, F.J.H.; et al. Multidirectional wall shear stress promotes advanced coronary plaque development: Comparing five shear stress metrics. Cardiovasc. Res. 2020, 116, 1136–1146. [Google Scholar] [CrossRef]
- Kok, A.M.; Molony, D.S.; Timmins, L.H.; Ko, Y.-A.; Boersma, E.; Eshtehardi, P.; Wentzel, J.J.; Samady, H. The influence of multidirectional shear stress on plaque progression and composition changes in human coronary arteries. EuroIntervention 2019, 15, 692–699. [Google Scholar] [CrossRef]
- Timmins, L.H.; Molony, D.S.; Eshtehardi, P.; McDaniel, M.C.; Oshinski, J.N.; Giddens, D.P.; Samady, H. Oscillatory wall shear stress is a dominant flow characteristic affecting lesion progression patterns and plaque vulnerability in patients with coronary artery disease. J. R. Soc. Interface 2017, 14. [Google Scholar] [CrossRef] [PubMed]
- Colombo, M.; He, Y.; Corti, A.; Gallo, D.; Casarin, S.; Rozowsky, J.M.; Migliavacca, F.; Berceli, S.; Chiastra, C. Baseline local hemodynamics as predictor of lumen remodeling at 1-year follow-up in stented superficial femoral arteries. Sci. Rep. 2021, 11, 1613. [Google Scholar] [CrossRef]
- Gallo, D.; Steinman, D.A.; Morbiducci, U. Insights into the co-localization of magnitude-based versus direction-based indicators of disturbed shear at the carotid bifurcation. J. Biomech. 2016, 49, 2413–2419. [Google Scholar] [CrossRef]
- Arzani, A.; Gambaruto, A.M.; Chen, G.; Shadden, S.C. Lagrangian wall shear stress structures and near-wall transport in high-Schmidt-number aneurysmal flows. J. Fluid Mech. 2016, 790, 158–172. [Google Scholar] [CrossRef]
- Farghadan, A.; Arzani, A. The combined effect of wall shear stress topology and magnitude on cardiovascular mass transport. Int. J. Heat Mass Transf. 2019, 131, 252–260. [Google Scholar] [CrossRef]
- Arzani, A.; Shadden, S.C. Wall shear stress fixed points in cardiovascular fluid mechanics. J. Biomech. 2018, 73, 145–152. [Google Scholar] [CrossRef]
- Arzani, A.; Gambaruto, A.M.; Chen, G.; Shadden, S.C. Wall shear stress exposure time: A Lagrangian measure of near-wall stagnation and concentration in cardiovascular flows. Biomech. Model. Mechanobiol. 2017, 16, 787–803. [Google Scholar] [CrossRef]
- Mazzi, V.; Gallo, D.; Calò, K.; Najafi, M.; Khan, M.O.; De Nisco, G.; Steinman, D.A.; Morbiducci, U. A Eulerian method to analyze wall shear stress fixed points and manifolds in cardiovascular flows. Biomech. Model. Mechanobiol. 2020, 19, 1403–1423. [Google Scholar] [CrossRef]
- Morbiducci, U.; Mazzi, V.; Domanin, M.; De Nisco, G.; Vergara, C.; Steinman, D.A.; Gallo, D. Wall Shear Stress Topological Skeleton Independently Predicts Long-Term Restenosis After Carotid Bifurcation Endarterectomy. Ann. Biomed. Eng. 2020, 48, 2936–2949. [Google Scholar] [CrossRef]
- Mahmoudi, M.; Farghadan, A.; McConnell, D.; Barker, A.J.; Wentzel, J.J.; Budoff, M.J.; Arzani, A. The Story of Wall Shear Stress in Coronary Artery Atherosclerosis: Biochemical Transport and Mechanotransduction. J. Biomech. Eng. 2020. [Google Scholar] [CrossRef] [PubMed]
- Ethier, C.R. Computational modeling of mass transfer and links to atherosclerosis. Ann. Biomed. Eng. 2002, 30, 461–471. [Google Scholar] [CrossRef]
- Tarbell, J.M. Mass transport in arteries and the localization of atherosclerosis. Annu. Rev. Biomed. Eng. 2003, 5, 79–118. [Google Scholar] [CrossRef]
- De Nisco, G.; Tasso, P.; Calò, K.; Mazzi, V.; Gallo, D.; Condemi, F.; Farzaneh, S.; Avril, S.; Morbiducci, U. Deciphering ascending thoracic aortic aneurysm hemodynamics in relation to biomechanical properties. Med. Eng. Phys. 2020, 82, 119–129. [Google Scholar] [CrossRef]
- Garth, C.; Tricoche, X.; Scheuermann, G. Tracking of vector field singularities in unstructured 3D time-dependent datasets. In Proceedings of the IEEE Visualization 2004, Austin, TX, USA, 10–15 October 2004; pp. 329–336. [Google Scholar]
- Shadden, S.C.; Lekien, F.; Marsden, J.E. Definition and properties of Lagrangian coherent structures from finite-time Lyapunov exponents in two-dimensional aperiodic flows. Phys. D Nonlinear Phenom. 2005, 212, 271–304. [Google Scholar] [CrossRef]
- Haller, G. Distinguished material surfaces and coherent structures in three-dimensional fluid flows. Phys. D Nonlinear Phenom. 2001, 149, 248–277. [Google Scholar] [CrossRef]
- Haller, G. Lagrangian coherent structures. Annu. Rev. Fluid Mech. 2015, 47, 137–162. [Google Scholar] [CrossRef]
- Nolan, P.J.; Serra, M.; Ross, S.D. Finite-time Lyapunov exponents in the instantaneous limit and material transport. Nonlinear Dyn. 2020, 100, 3825–3852. [Google Scholar] [CrossRef]
- Lekien, F.; Shadden, S.C.; Marsden, J.E. Lagrangian coherent structures in n-dimensional systems. J. Math. Phys. 2007, 48, 1–19. [Google Scholar] [CrossRef]
- Shadden, S.C.; Arzani, A. Lagrangian postprocessing of computational hemodynamics. Ann. Biomed. Eng. 2015, 43, 41–58. [Google Scholar] [CrossRef] [PubMed]
- Shadden, S.C.; Taylor, C.A. Characterization of coherent structures in the cardiovascular system. Ann. Biomed. Eng. 2008, 36, 1152–1162. [Google Scholar] [CrossRef]
- Arzani, A.; Shadden, S.C. Characterization of the transport topology in patient-specific abdominal aortic aneurysm models. Phys. Fluids (1994). 2012, 24, 81901. [Google Scholar] [CrossRef]
- Green, M.A.; Rowley, C.W.; Haller, G. Detection of Lagrangian coherent structures in three-dimensional turbulence. J. Fluid Mech. 2007, 572, 111–120. [Google Scholar] [CrossRef]
- Peacock, T.; Haller, G. Lagrangian coherent structures: The hidden skeleton of fluid flows. Phys. Today 2013, 66, 41–47. [Google Scholar] [CrossRef]
- Ehrlich, L.W.; Friedman, M.H. Particle paths and stasis in unsteady flow through a bifurcation. J. Biomech. 1977, 10, 561–568. [Google Scholar] [CrossRef]
- Perktold, K. On the paths of fluid particles in an axisymmetrical aneurysm. J. Biomech. 1987, 20, 311–317. [Google Scholar] [CrossRef]
- Perktold, K.; Peter, R.; Resch, M. Pulsatile non-Newtonian blood flow simulation through a bifurcation with an aneurysm. Biorheology 1989, 26, 1011–1030. [Google Scholar] [CrossRef] [PubMed]
- Perktold, K.; Hilbert, D. Numerical simulation of pulsatile flow in a carotid bifurcation model. J. Biomed. Eng. 1986, 8, 193–199. [Google Scholar] [CrossRef]
- Steinman, D.A. Simulated pathline visualization of computed periodic blood flow patterns. J. Biomech. 2000, 33, 623–628. [Google Scholar] [CrossRef]
- Tambasco, M.; Steinman, D.A. On assessing the quality of particle tracking through computational fluid dynamic models. J. Biomech. Eng. 2002, 124, 166–175. [Google Scholar] [CrossRef]
- Tambasco, M.; Steinman, D.A. Path-dependent hemodynamics of the stenosed carotid bifurcation. Ann. Biomed. Eng. 2003, 31, 1054–1065. [Google Scholar] [CrossRef]
- Yang, W.; Feinstein, J.A.; Shadden, S.C.; Vignon-Clementel, I.E.; Marsden, A.L. Optimization of a Y-graft design for improved hepatic flow distribution in the fontan circulation. J. Biomech. Eng. 2013, 135, 11002. [Google Scholar] [CrossRef]
- Yang, W.; Vignon-Clementel, I.E.; Troianowski, G.; Reddy, V.M.; Feinstein, J.A.; Marsden, A.L. Hepatic blood flow distribution and performance in conventional and novel Y-graft Fontan geometries: A case series computational fluid dynamics study. J. Thorac. Cardiovasc. Surg. 2012, 143, 1086–1097. [Google Scholar] [CrossRef]
- Amili, O.; MacIver, R.; Coletti, F. Magnetic Resonance Imaging Based Flow Field and Lagrangian Particle Tracking From a Left Ventricular Assist Device. J. Biomech. Eng. 2019, 142. [Google Scholar] [CrossRef] [PubMed]
- Mukherjee, D.; Padilla, J.; Shadden, S.C. Numerical investigation of fluid–particle interactions for embolic stroke. Theor. Comput. Fluid Dyn. 2016, 30, 23–39. [Google Scholar] [CrossRef]
- Morbiducci, U.; Ponzini, R.; Rizzo, G.; Cadioli, M.; Esposito, A.; De Cobelli, F.; Del Maschio, A.; Montevecchi, F.M.; Redaelli, A. In vivo quantification of helical blood flow in human aorta by time-resolved three-dimensional cine phase contrast magnetic resonance imaging. Ann. Biomed. Eng. 2009, 37, 516–531. [Google Scholar] [CrossRef]
- Morbiducci, U.; Ponzini, R.; Rizzo, G.; Cadioli, M.; Esposito, A.; Montevecchi, F.M.; Redaelli, A. Mechanistic insight into the physiological relevance of helical blood flow in the human aorta: An in vivo study. Biomech. Model. Mechanobiol. 2011, 10, 339–355. [Google Scholar] [CrossRef] [PubMed]
- Arzani, A.; Les, A.S.; Dalman, R.L.; Shadden, S.C. Effect of exercise on patient specific abdominal aortic aneurysm flow topology and mixing. Int. J. Numer. Method Biomed. Eng. 2014, 30, 280–295. [Google Scholar] [CrossRef]
- Gharib, M.; Rambod, E.; Kheradvar, A.; Sahn, D.J.; Dabiri, J.O. Optimal vortex formation as an index of cardiac health. Proc. Natl. Acad. Sci. USA 2006, 103, 6305–6308. [Google Scholar] [CrossRef] [PubMed]
- Charonko, J.J.; Kumar, R.; Stewart, K.; Little, W.C.; Vlachos, P.P. Vortices formed on the mitral valve tips aid normal left ventricular filling. Ann. Biomed. Eng. 2013, 41, 1049–1061. [Google Scholar] [CrossRef]
- Töger, J.; Kanski, M.; Carlsson, M.; Kovács, S.J.; Söderlind, G.; Arheden, H.; Heiberg, E. Vortex ring formation in the left ventricle of the heart: Analysis by 4D flow MRI and Lagrangian coherent structures. Ann. Biomed. Eng. 2012, 40, 2652–2662. [Google Scholar] [CrossRef]
- Hendabadi, S.; Bermejo, J.; Benito, Y.; Yotti, R.; Fernández-Avilés, F.; del Álamo, J.C.; Shadden, S.C. Topology of blood transport in the human left ventricle by novel processing of Doppler echocardiography. Ann. Biomed. Eng. 2013, 41, 2603–2616. [Google Scholar] [CrossRef]
- Astorino, M.; Hamers, J.; Shadden, S.C.; Gerbeau, J.-F. A robust and efficient valve model based on resistive immersed surfaces. Int. J. Numer. Method Biomed. Eng. 2012, 28, 937–959. [Google Scholar] [CrossRef]
- Shadden, S.C.; Astorino, M.; Gerbeau, J.-F. Computational analysis of an aortic valve jet with Lagrangian coherent structures. Chaos 2010, 20, 17512. [Google Scholar] [CrossRef]
- Sadrabadi, M.S.; Hedayat, M.; Borazjani, I.; Arzani, A. Fluid-structure coupled biotransport processes in aortic valve disease. J. Biomech. 2021, 110239. [Google Scholar] [CrossRef]
- Xu, Z.; Chen, N.; Shadden, S.; Marsden, J.; Kamocka, M.; Rosen, E.; Alber, M.S. Study of blood flow impact on growth of thrombi using a multiscale model. Soft Matter 2009, 5, 769–779. [Google Scholar] [CrossRef]
- Mutlu, O.; Olcay, A.B.; Bilgin, C.; Hakyemez, B. Evaluating the Effectiveness of 2 Different Flow Diverter Stents Based on the Stagnation Region Formation in an Aneurysm Sac Using Lagrangian Coherent Structure. World Neurosurg. 2019, 127, e727–e737. [Google Scholar] [CrossRef]
- Mutlu, O.; Olcay, A.B.; Bilgin, C.; Hakyemez, B. Evaluating the Effect of the Number of Wire of Flow Diverter Stents on the Nonstagnated Region Formation in an Aneurysm Sac Using Lagrangian Coherent Structure and Hyperbolic Time Analysis. World Neurosurg. 2020, 133, e666–e682. [Google Scholar] [CrossRef]
- Gambaruto, A.M.; Doorly, D.J.; Yamaguchi, T. Wall shear stress and near-wall convective transport: Comparisons with vascular remodelling in a peripheral graft anastomosis. J. Comput. Phys. 2010, 229, 5339–5356. [Google Scholar] [CrossRef]
- Gambaruto, A.M.; João, A.J. Computers & Fluids Flow structures in cerebral aneurysms. Comput. Fluids 2012, 65, 56–65. [Google Scholar] [CrossRef]
- Goodarzi Ardakani, V.; Tu, X.; Gambaruto, A.M.; Velho, I.; Tiago, J.; Sequeira, A.; Pereira, R. Near-Wall Flow in Cerebral Aneurysms. Fluids 2019, 4, 89. [Google Scholar] [CrossRef]
- Calò, K.; Gallo, D.; Steinman, D.A.; Mazzi, V.; Scarsoglio, S.; Ridolfi, L.; Morbiducci, U. Spatiotemporal Hemodynamic Complexity in Carotid Arteries: An Integrated Computational Hemodynamics and Complex Networks-Based Approach. IEEE Trans. Biomed. Eng. 2020, 67, 1841–1853. [Google Scholar] [CrossRef]
- Tada, S. Numerical study of oxygen transport in a carotid bifurcation. Phys. Med. Biol. 2010, 55, 3993–4010. [Google Scholar] [CrossRef] [PubMed]
- De Nisco, G.; Zhang, P.; Calò, K.; Liu, X.; Ponzini, R.; Bignardi, C.; Rizzo, G.; Deng, X.; Gallo, D.; Morbiducci, U. What is needed to make low-density lipoprotein transport in human aorta computational models suitable to explore links to atherosclerosis? Impact of initial and inflow boundary conditions. J. Biomech. 2018, 68, 33–42. [Google Scholar] [CrossRef] [PubMed]
- Chiu, J.J.; Chien, S. Effects of disturbed flow on vascular endothelium: Pathophysiological basis and clinical perspectives. Physiol. Rev. 2011, 91, 327–387. [Google Scholar] [CrossRef]
- Morris, P.D.; Narracott, A.; von Tengg-Kobligk, H.; Silva Soto, D.A.; Hsiao, S.; Lungu, A.; Evans, P.; Bressloff, N.W.; Lawford, P.V.; Hose, D.R.; et al. Computational fluid dynamics modelling in cardiovascular medicine. Heart 2016, 102, 18–28. [Google Scholar] [CrossRef] [PubMed]
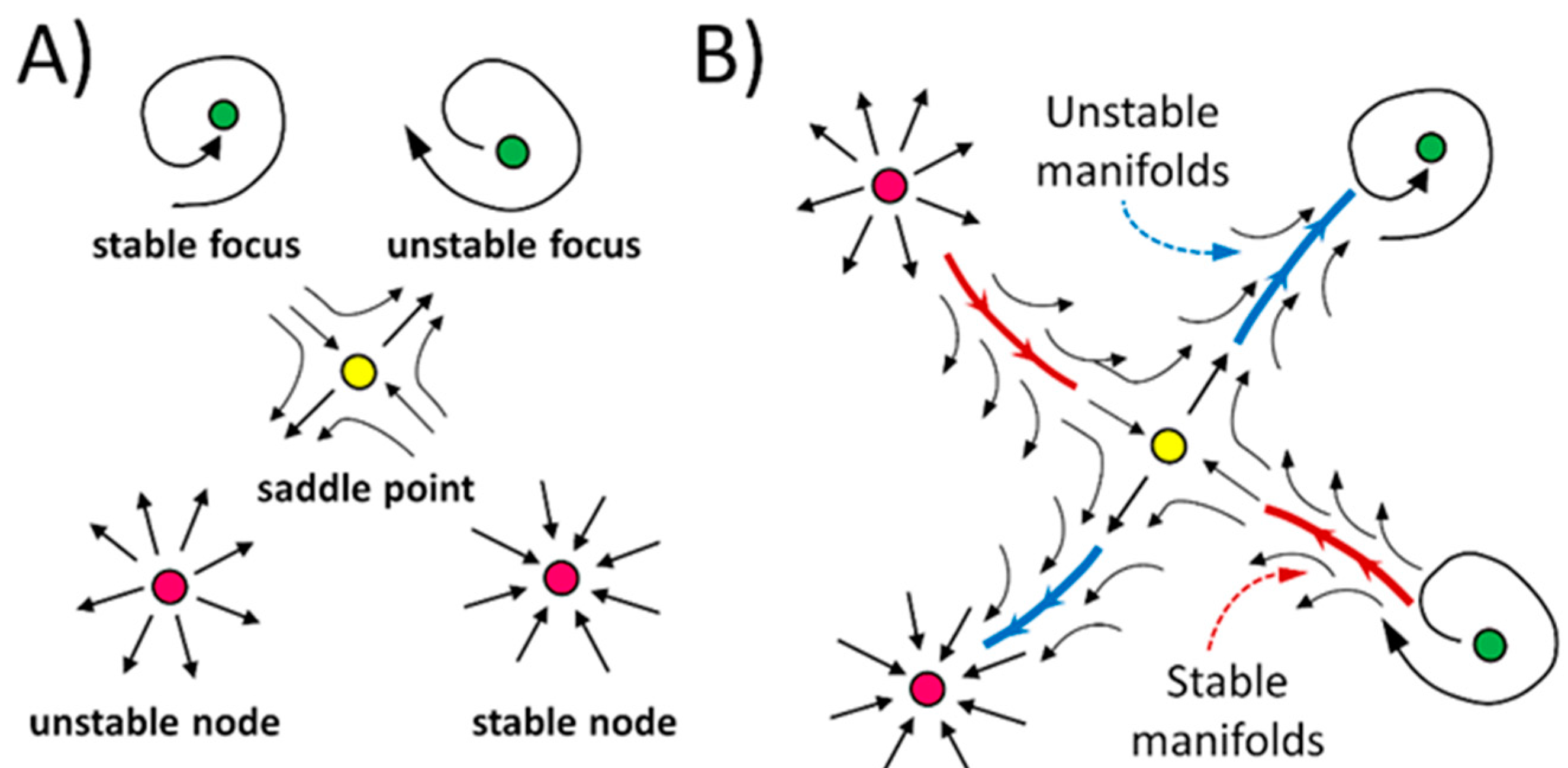






| λ | Fixed Point |
|---|---|
| Saddle point | |
| Unstable node | |
| Stable node | |
| Unstable focus | |
| Stable focus |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mazzi, V.; Morbiducci, U.; Calò, K.; De Nisco, G.; Lodi Rizzini, M.; Torta, E.; Caridi, G.C.A.; Chiastra, C.; Gallo, D. Wall Shear Stress Topological Skeleton Analysis in Cardiovascular Flows: Methods and Applications. Mathematics 2021, 9, 720. https://doi.org/10.3390/math9070720
Mazzi V, Morbiducci U, Calò K, De Nisco G, Lodi Rizzini M, Torta E, Caridi GCA, Chiastra C, Gallo D. Wall Shear Stress Topological Skeleton Analysis in Cardiovascular Flows: Methods and Applications. Mathematics. 2021; 9(7):720. https://doi.org/10.3390/math9070720
Chicago/Turabian StyleMazzi, Valentina, Umberto Morbiducci, Karol Calò, Giuseppe De Nisco, Maurizio Lodi Rizzini, Elena Torta, Giuseppe Carlo Alp Caridi, Claudio Chiastra, and Diego Gallo. 2021. "Wall Shear Stress Topological Skeleton Analysis in Cardiovascular Flows: Methods and Applications" Mathematics 9, no. 7: 720. https://doi.org/10.3390/math9070720
APA StyleMazzi, V., Morbiducci, U., Calò, K., De Nisco, G., Lodi Rizzini, M., Torta, E., Caridi, G. C. A., Chiastra, C., & Gallo, D. (2021). Wall Shear Stress Topological Skeleton Analysis in Cardiovascular Flows: Methods and Applications. Mathematics, 9(7), 720. https://doi.org/10.3390/math9070720









