Abstract
In this paper, daily confirmed cases of COVID-19 in different countries are modelled using different mathematical regression models. The curve fitting is used as a prediction tool for modeling both past and upcoming coronavirus waves. According to virus spreading and average annual temperatures, countries under study are classified into three main categories. First category, the first wave of the coronavirus takes about two-year seasons (about 180 days) to complete a viral cycle. Second category, the first wave of the coronavirus takes about one-year season (about 90 days) to complete the first viral cycle with higher virus spreading rate. These countries take stopping periods with low virus spreading rate. Third category, countries that take the highest virus spreading rate and the viral cycle complete without stopping periods. Finally, predictions of different upcoming scenarios are made and compared with actual current smoothed daily confirmed cases in these countries.
1. Introduction
The epidemic coronavirus disease (COVID-19) was first detected in December 2019 in Wuhan city, China. Then it started to transmit to countries all over the world till the WHO declared it as a pandemic disease [1] on 11 March 2020. The new virus has different characteristics than the family it came from (coronaviruses). It has higher infection rates and average incubation period of 5.1 days. The maximum incubation period for the virus is 14 days [2]. The epidemic infection occurs through physical contacts with individuals or contaminated surfaces. New public safety steps have been associated to mitigate the impact of this pandemic disease like cancellation of public events, assuring online education, closing clubs and other places opened for social gatherings like concerts and sporting events. The total number of confirmed cases worldwide reached 62,844 million on 1 December 2020 with 1465 million deaths [3]. The main challenge during studying epidemics is how to predict the disease behavior, how many people will be infected in the future, determining the pandemic peak, second wave of the disease time of action, and the total deaths after the pandemic ends. Different researchers from different majors such as applied mathematics, data science, and epidemiology have been working on studying these trends of predictions. Based on this analysis, governments can take proper actions to limit the human and economic losses. Coronavirus not only represents a health crisis but also represents an economic crisis where people are losing their jobs without knowing when normality will return. The International Labor Organization estimates that 25 million people could lose their jobs [4]. The prediction of the peak date from one country to another and simulation of the variations could depend on the behaviors of people toward social distancing, hygiene measures, temperature, relative humidity, and wind speed.
It is known that the human immune system suffers from depression during the winter season, as the cold, dry air works to dry out the mucus in our noses, which acts as a first line of defense, to prevent viruses. Studies have proven that if the temperature increases, the infected person will spread the COVID-19 to fewer people. Some studies also indicate that the virus cannot survive at 86° Fahrenheit (F) so in this paper, the countries are categorized into three main categories and these will have a reflection on human cells infections. The first category of countries, with low transmission rates, have an average annual temperature between (60 and 100.4) °F. The second category of countries, with medium transmission rates, have an average annual temperature between (37 and 89) °F and finally the third category of countries, with the highest transmission rates, have an average annual temperature between (36.14 and 66.3) °F. The higher the spread rates, the higher the rates of infection of human cells and also their exposure to the virus will be higher, and thus the possibility of human cells to sustain the virus will depend on the location of the country and also in which category it belongs.
There are a few published papers, studying the analysis of COVID-19. In [5], authors used numerical approaches and logistic modelling technique to make a complete analysis for COVID-19. In [6], authors made a fractional-order-modified SEIR model of pandemic diseases and applied it on COVID-19 to predict the virus spreading behavior in Pakistan and Malaysia. In [7], authors made predictions about coronavirus transmission dynamics in the African countries. The model parameters (protection rate, infection rate, average incubation time, average quarantined time, cure rate, and mortality rate) are selected using Metropolis-Hasting (MH) parameter optimization method [8]. Authors modelled COVID-19 daily confirmed cases in Egypt and Iraq by using Gaussian fitting model and logistic model [9,10,11]. The virus dynamic behavior is modelled with a new SEIR model. One of the important quantities should be calculated during modelling virus dynamics is the basic reproduction number. This value helps eliminate the disease and expected number of secondary infections produced by an infected individual in a population when all individuals are susceptible to infection. In [12], authors made a multi-strain-modified SEIR epidemic model for COVID-19 and wrote a complete analysis on how to control the value of the reproduction number to control the next upcoming virus peaks.
In this paper as a way to predict the upcoming coronavirus waves, a new state-of-art of regression models are used to model daily confirmed cases in different countries. In this study, countries are classified based on the time of the full viral wave and the average annual temperatures, where if time of the viral wave is lower, the virus transmission rate is higher. Fourier model and sum of sine-waves model are used to fit the daily confirmed data and predict the upcoming wave peaks for these countries. In this paper, the actual data from [3,13] are used for generating the predictive regression models without making any statistical modifications on them. The mathematical regression models fit the data from 1 March 2020 (day 0) to 15 November 2020 (day 260) and hence, the models can predict different scenarios for each country in the period from 16 November 2020 (day 261) to 10 April 2021 (day 400). The real smoothed data from [14] was used to verify the accuracy of the prediction models. All used datasets used in this paper have been attached with a separate supplementary material file. The countries under study are categorized into three main categories:
- -
- First category: countries in which coronavirus wave takes low transmission about two-year seasons (about 180 days) to make a complete virus cycle: (case study of Saudi Arabia and Egypt).
- -
- Second category: countries with higher transmission rates with one-year season (about 90 days) to make complete virus cycle. These countries take offline periods with low spreading rate before entering the next wave cycle: (case study of United Kingdom, Germany and Italy).
- -
- The third category: countries with the highest transmission rates with one-year season (about 90 days) to make complete cycle and without offline periods (consecutive waves): (case study of United States of America and Russia).
The remainder of this paper is organized as follows: Section 2 describes the mathematical background of the proposed predictive modelling. Section 3 elaborates the used optimization algorithm to fit the data. Section 4 includes the results of applying the predictive models on the available data of the three category countries. In the end the conclusions are given.
2. Predictive Mathematical Modelling
Mathematical curve fitting is a key for getting a mathematical relation between measured values and their dependent input parameters named as regression models [15] like Polynomial Model, Exponential Model, Power Model, and Fourier Model [16,17,18]. Choosing the suitable model to represent coronavirus data can be measured by the mean of determination coefficient () which takes values from 0 to 1. Higher value of means higher model accuracy [18]. can be calculated from Equation (1) with N data points.
where is the average value of measured data, is the measured data value at time and is the corresponding value using the fitting model equation.
The used mathematical curve fitting techniques here for modeling daily confirmed cases of COVID-19 and predict upcoming scenarios are Fourier fitting models and sum of sine-waves fitting models.
2.1. Fourier Fitting Models
Fourier models are used to model periodic functions with three main parts which are constant term, cosine-wave terms and sine-wave terms. As coronavirus is spreading like a wave and has a possibility of repetitions so this leads to near periodic wave assumptions. So, modelling using Fourier fitting model here is a good choice of fitting. Fourier fitting model equation with n-terms is presented in Equation (2) [19] and w is the fundamental frequency of sine and cosine terms.
() are unknown coefficients and selected using numerical optimization techniques to satisfy the least square regression criteria between data and fitting model.
2.2. Sum of Sine-Waves Fitting Models
Sine-waves are always used to model periodic functions. Using the sum of sine waves with different frequencies can be used to model near periodic functions. These models are used here to fit data of coronavirus daily confirmed cases in the countries under study. Also modelling by this kind of mathematical equations can result in predicting next upcoming coronavirus waves in the countries under study. Equation (3) represents the sum of sine-waves equation with n-terms.
() are unknown coefficients and optimized using numerical optimization techniques to minimize the error between model and measured daily confirmed cases.
The used optimization algorithm for optimal selections of each model coefficients is invasive weed optimization algorithm (IWO) [20]. The optimization process leads to increasing model accuracy and decreasing root mean square of errors (RMSE) between actual number (N) of data points and the fitting model. The objective function will be minimized using the optimization algorithm when modelling data by Fourier model with n-terms is as indicated in Equation (4). Similarly, the objective function used when modelling with the sum of sine-waves is as indicated in Equation (5).
Minimize:
Subject to:
Minimize:
Subject to:
3. Invasive Weed Optimization Algorithm
Invasive weed optimization algorithm will be used to select the optimal values of each fitting model coefficients. Steps of invasive weed optimization technique [20]:
- -
- Populations Initialization: populations (seeds) with finite numbers are being scattered over d-dimensional searching space at random positions. The variable d is the number of the optimization process variables.
- -
- Seeds Reproduction: seeds grow to form plants and produce newer number of seeds.
- -
- Spatial Dispersal: The new seeds are being randomly scattered over the search space using standard normal distribution functions with variable variance. The standard deviation () of the normal random functions will be produced with initial value () and final value () in all steps. During simulation, a nonlinear alteration- modulation index () is selected to reach certain satisfactory performance. Standard deviation () at each iteration () is calculated, where is the maximum number of iterations.
- -
- Competitive Exclusion: In this process and after maximum number of plants is reached, only the plants with lower fitness can pull out and produce seeds, others are being tossed out. The process continues in each iteration till maximum iterations is reached. Flow chart of the algorithm is as indicated in Figure 1.
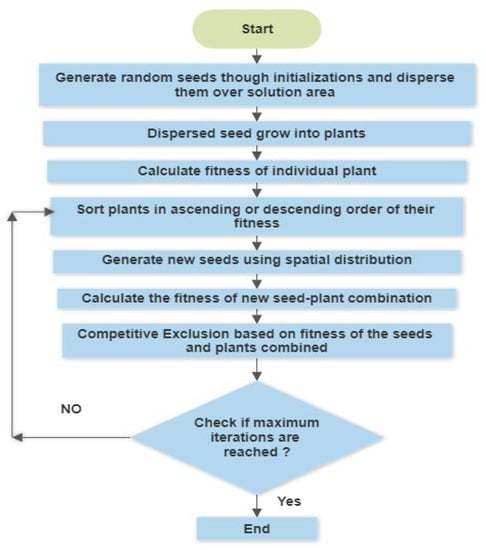 Figure 1. Invasive weed optimization (IWO) algorithm flow chart.
Figure 1. Invasive weed optimization (IWO) algorithm flow chart.
Before starting the optimization process to get each fitting model coefficients and reach the different scenarios for each country, the following mathematical assumptions are made and taken into consideration during the optimization process:
- First category countries: these countries have low virus transmission rates and large wave time period, so the next upcoming wave peak will not exceed the first wave peak.
- Second category countries: these countries have medium transmission rates and will have two consecutive waves and with peaks multiples of the first wave peak but not out of control.
- Third category: these countries have the high transmission rates, so the next wave will have increased consecutive peaks and virus spread will be out of control without any limitations.
4. Results and Discussion
Results in this part are segmented according to the three main categories (first category countries, second category countries, and third category countries). Each country modelled with three fitting models to fit coronavirus data from 1 March 2020 (day 0) to 15 November 2020 (day 260) with least square error regression and predict different next upcoming wave scenarios. Optimization process is handled with 100 iterations for each model. Finally, all predictions of the models are compared with the real smoothed current data of daily confirmed cases in these countries [14].
4.1. First Category Countries
The two countries under study here are Egypt and Saudi Arabia. Starting with Egypt, coronavirus daily confirmed cases are modelled using sum of sine-waves model with number of terms equals four, seven, and eight. The accuracy of modelling with these models is described with model determination coefficient , sum square of error (SSE), and root mean square of errors (RMSE). Table 1 shows the accuracy of each model. Optimized coefficients of each model reached by the optimization technique is also presented. According accuracy of fitting the three models have very near accuracy of fitting (). In case of next upcoming wave peak in Egypt, the three models give different scenarios. As shown in Figure 2a, Model one scenario for Egypt has a peak of daily confirmed cases of 1535 person in day 310 (4 January 2021). Model two predicts the wave peak in day 317 (11 January 2021) with daily confirmed cases 1481. Model three predicts the best scenario of Egypt with the peak of daily confirmed cases of 952 person in day 307 (1 January 2021). Also, these three models predict how will be the daily confirmed cases numbers after the wave peak till day 360 (23 February 2021).

Table 1.
Used mathematical fitting models for Egypt data with optimized coefficients.
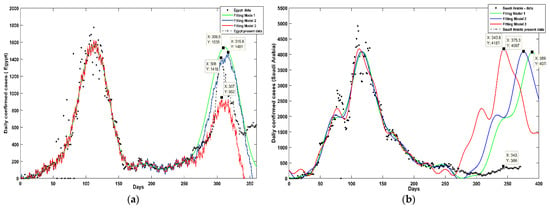
Figure 2.
Curve fitting models for daily confirmed cases for first category countries: (a) curve fitting models for Egypt data; (b) curve fitting models for Saudi Arabia data.
Saudi Arabia daily confirmed cases data are modelled using Fourier model with number of terms equals six, seven, and eight. Each model optimized coefficients are as indicated in Table 2. The accuracy of each model is described through , SSE and RMSE. From Figure 2b, Saudi Arabia takes higher time about 200 days to complete the first virus wave cycle while Egypt takes only 150 days. This means that the next wave peak of Saudi Arabia will be delayed than Egypt. Model one predicts that next peak of Saudi Arabia will be in day 389 (29 March 2021) with daily confirmed cases 4078 person. In case of the model number two, the wave peak will be in day 376 (16 March 2021) with daily confirmed cases of 4097 person. Model three predicts that next peak will be in day 344 (16 February 2021) with daily confirmed cases 4181 person. The different scenarios of Saudi Arabia have near peak values but with a shift in time of action. For all scenarios the second wave cycle will not end before day 400 (10 April 2021).

Table 2.
Used mathematical fitting models for Saudi Arabia data with optimized coefficients.
The accuracy of the proposed models of each country is measured through sketching current real smoothed data for Egypt and Saudi Arabia [14] on same sketch with their predictive models as indicated in Figure 2. In case of Egypt, the actual current smoothed data are very near in shape with the forecasting models. The most accurate model of predictions is model three with peak value equals 1481 people in day 317 (11 January 2021) in comparison with the actual second virus peak which equals 1418 people in day 306 (31 December 2021). In case of Saudi Arabia, model one is the most accurate model to make predictions till day 307 (1 January 2021). After that date, Saudi Arabia starts to vaccinate its population which results in over damping the second virus wave with peak equals 386 people in day 343 (15 February 2021). The actual vaccinated people in both Egypt and Saudi Arabia are as indicated in Table 3. Egypt starts to vaccinate thousands of people from its population after 24 February 2021 (day 352). This vaccination could damp the next wave of Egypt based on the number of actual vaccinated people per cumulative cases.

Table 3.
Actual vaccinated people in first category countries [14].
4.2. Second Category Countries
Countries under study in this category are United Kingdom, Italy, and Germany. These three countries first virus wave cycle takes only one-year season (within 90 days) which means that second wave started in these countries before the first category countries. Starting with United Kingdom, daily confirmed cases are modelled using the sum of sine-waves model with number of terms four, five, and six. The optimized coefficients of each model using IWO algorithm are as indicated in Table 4. Accuracy of each model can also be shown through SSE, and RMSE. All models predict that countries in this category will be exposed to consecutive waves. As shown Figure 3a, Model one predicts the best-case scenario and indicating that United Kingdom reached the peak of second wave and will have next peak in day 357 (26 February 2021) with peak value equals 13,180 persons which is lower than the current peak. Model two predicts that next wave peak will be with daily confirmed cases equals 32,910 persons in day 311 (11 January 2021). Model three predicts that next peak will reach 37,110 daily confirmed cases in day 316 (17 January 2021).

Table 4.
Used mathematical fitting models for United Kingdom data with optimized coefficients.
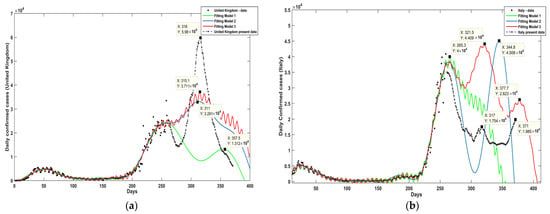
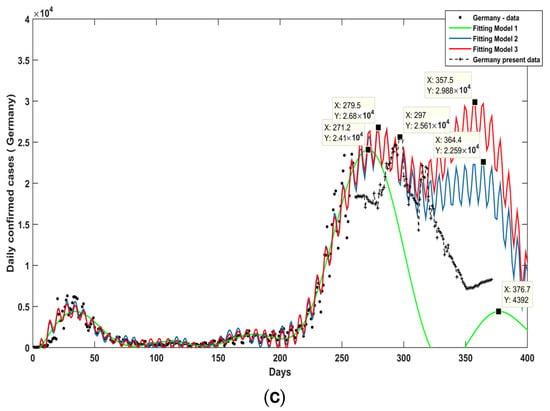
Figure 3.
Curve fitting models for daily confirmed cases for second category countries: (a) curve fitting models for United Kingdom data; (b) curve fitting models for Italy data; (c) curve fitting models for Germany data.
Italy daily confirmed cases are modelled using the sum of sine-waves model with five, six, and seven terms. Each model accuracy of fitting and optimized coefficients is as described in Table 5. Model one makes the best scenario as it predicts that Italy has reached the peak of the second wave in day 265 (20 November 2020) with daily confirmed cases equals 40,000 and it will not have a third wave before day 400 (10 April 2021). Model two same as model one shows that Italy reached second wave peak and will have the next wave peak on day 345 (14 February 2021) with number of daily confirmed cases equals 45,080. Model three predicts that Italy will have two next upcoming peaks (third and fourth peak). The third peak will be in day 322(22 January 2021) with daily confirmed cases equals 40,900 and fourth peak will be in day 378 (18 March 2021). The reached results of the three models are as sketched in Figure 3b.

Table 5.
Used mathematical fitting models for Italy data with optimized coefficients.
Germany daily confirmed coronavirus data are modelled using Fourier model with four terms and sum of sine-waves model with number of terms equals seven and eight. Each model fitting accuracy and optimized results is as indicated in Table 6. The accuracy is also compared here through R2, SSE, and RMSE indices. As indicated in Figure 3c, the first model describes the best scenario for Germany with reached second wave peak in day 272 (27 November 2020) and the value equals 24,100 persons then daily confirmed cases starts to decrease again. The third wave of the virus will have a peak in day 377 (17 March 2021) but with smaller value than second wave peak where it only equals 4392 cases. Second and third fitting models admitted the same scenario about the second wave peak with same daily confirmed cases and in same day. Both models predict that it will be in day 279 (3 December 2021) with daily confirmed cases equals 26,800 persons. The third wave predicted peak time of action is different when comparing model two and model three. Model two predicts that it will be in day 365 (5 March 2021) with daily confirmed cases equals 22,590 persons.

Table 6.
Used mathematical fitting models for Germany data with optimized coefficients.
Forecasting accuracy of the predictive models of each country is made through sketching current real smoothed data for United Kingdom, Italy, and Germany [14] on same sketch with their proposed predictive models as indicated in Figure 3. The predictive models are helpful tools for forecasting virus behavior till day 307 (1 January 2021) as they give curves very near in shape with actual current smoothed data. All countries in this category started to vaccinate their population to limit the virus spreading and each country’s actual vaccinated people per actual confirmed cases is as indicated in Table 7. In case of United Kingdom, government starts to vaccinate its population with high rate to control virus transmission and damp the next virus waves. However, United Kingdom has the highest virus wave peak among countries in this category with peak equals 59,810 in day 316 (10 January 2021) but using vaccination with high rate results in over damping the virus next wave and makes daily today confirmed cases lower than both Italy and Germany. The actual vaccinated people per actual confirmed cases for United Kingdom reached 5.06 as indicated in Table 7. In case of Italy, the actual vaccinated people per actual confirmed cases is still low with value equals 1.179, so virus daily confirmed cases started to increase again as indicated in Figure 3b. From indicated results, Italian government should increase the number of actual vaccinated people per cumulative cases to more control virus behavior. In case of Germany, the actual number of vaccinated people per cumulative cases has an intermediate value. As, indicated in Figure 3c, today daily confirmed cases of Germany start to increase again with a lower rate so, number of actual vaccinated people per cumulative cases should slightly increase.

Table 7.
Actual vaccinated people in second category countries [14].
4.3. Third Category Countries
Case studies in this category are United States of America (U.S.A) and Russia. These countries have the highest transmission rates of virus spread and suffer from consecutive virus waves without offline periods and increasing virus peak wave value. U.S.A. daily confirmed cases data are modelled using sum of sine-waves model with five, six, and seven terms. Accuracy of each model is as described in Table 8. As in Figure 4a, first model represents the best-case scenario where it expects that next upcoming wave peak will be in day 350 (19 February 2021) with daily confirmed cases equals 405,900 persons. Model two expects the intermediate scenario with peak daily confirmed cases equals 529,800 in day 365 (6 March 2021). Model three is the worst-case scenario with the highest peak value as it expects that it will be 830,400 cases in day 365 (6 March 2021).

Table 8.
Used mathematical fitting models for U.S.A. data with optimized coefficients.
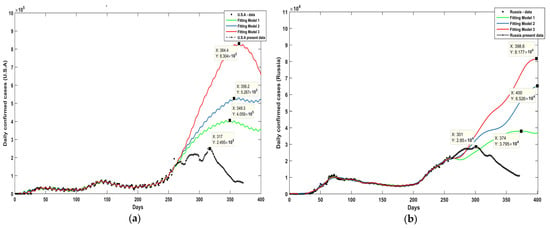
Figure 4.
Curve fitting models for daily confirmed cases for third category countries: (a) Curve fitting models for U.S.A. data; (b) Curve fitting models for Russia data.
Daily confirmed cases data for Russia are modelled using five, seven, and eight terms of sum of sine-waves model. Each model optimized coefficients, satisfying least square regression criteria, is as indicated in Table 9. All models have accuracy of fitting and low SSE. In case of models’ predictions, model one predicts the best-case scenario with the next upcoming wave peak which equals 37,950 in day 374 (15 March 2021). Model two predicts the intermediate scenario with next wave peak to be in day 400 (10 April 2021) with 65,260 daily confirmed cases. Model three expects the next peak in day 397 (7 March 2021) with daily confirmed cases equals 81,770 persons, so it represents the worst case with the highest value of peak daily confirmed cases.

Table 9.
Used mathematical fitting models for Russia data with optimized coefficients.
Current real smoothed data for U.S.A. and Russia [14] are sketched with the predictive modelling curves as in Figure 4. In case of U.S.A, forecasting models give good predictions when compared with current data till day 307 (1 January 2021). After that date, U.S.A. began to vaccinate its population so virus transmission rate starts to decrease and next virus wave is damped. The actual number of vaccinated people in U.S.A. till 5 March 2021 is as indicated in Table 10. In case of Russia, all predictive models give very accurate predictions till day 310 (4 January 2021). After that date, Russia began to vaccinate its population. Vaccination makes the next virus wave over damped. The actual vaccinated people per cumulative confirmed cases for both U.S.A. and Russia are as indicated in Table 10. As this value is higher, the vaccination effect will be stronger and virus transmission rate will be lower and virus break out is more controlled.

Table 10.
Actual vaccinated people in third category countries [14].
5. Conclusions
In this article, both Fourier models and sums of sine-waves models are used to predict the upcoming coronavirus peaks in the countries under study. In the first category countries (Egypt and Saudi Arabia), the models used gave different scenarios for each country in a form of three different scenarios with different wave peak and action time. From obtained results, Egypt and Saudi Arabia will be only exposed to a second wave till 10 April 2021. In case of second category countries (United Kingdom, Italy, and Germany), the models used gave different three scenarios of upcoming coronavirus wave peak. Most of the used models predict that these countries will suffer from two consecutive wave peaks and will suffer a third virus wave before 10 April 2021. In these countries, the spread of the virus will be controlled because the time for the second wave is limited and the daily confirmed cases decrease after the second wave reaches its peak. In the third category countries (The United States and Russia), the used models expect that these countries will reach the peak of the third wave of coronavirus before 10 April 2021, and these countries will suffer from consecutive increasing peaks. Finally, all predictive models for countries under study are compared to their current smoothed current data of daily confirmed cases to check their prediction accuracy. In the case of Egypt, the only country without vaccination effect, predictive models give very near curve shapes to the actual smoothed current data. For the remaining countries, with different values of actual vaccinated people per cumulative cases, the predictive models are helpful tools of forecasting virus behavior till day 307 (1 January 2021). After that date, the vaccination effect starts to limit the virus transmission rate and the next wave is damped in these countries. In our future work, we will make developments on the current predictive models considering how vaccination affects the virus spread rate.
Author Contributions
The authors declare that the study was realized in collaboration with the same responsibility. All authors have read and agreed to the published version of the manuscript.
Funding
RUDN University Strategic Academic Leadership Program: RUDN University Strategic Academic Leadership Program.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Informed consent was obtained from all subjects involved in the study.
Data Availability Statement
All used data in this paper are valid online on WHO coronavirus (COVID-19) dashboard. DOI: https://covid19.who.int/ (accessed on 15 November 2020) and Worldometers. Coronavirus Cases. 2020. DOI: https://www.worldometers.info/Coronavirus/Coronavirus-cases (accessed on 15 November 2020).
Acknowledgments
The research is partially supported by the Community University Research Engagement Centre (CUrE) and the RUDN University Program 5-100.
Conflicts of Interest
The authors declare that they have no conflict of interest.
References
- World Health Organization. Available online: https://www.who.int/emergencies/diseases/novel-coronavirus2019 (accessed on 15 November 2020).
- Lauer, S.; Grantz, K.; Bi, Q.; Jones, F.; Zheng, Q.; Meredith, H.; Azman, A.; Reich, N.; Lessler, J. The Incubation Period of Coronavirus Disease 2019 (COVID-19) From Publicly Reported Confirmed Cases: Estimation and Application. Ann. Intern. Med. 2020, 172, 577–582. [Google Scholar] [CrossRef]
- World Health Organization. WHO Coronavirus (COVID-19) Dashboard. Available online: https://covid19.who.int/ (accessed on 15 November 2020).
- Barua, S. Understanding Coronanomics: The economic implications of the Coronavirus (COVID-19) pandemic. SSRN Electron. J. 2020. [Google Scholar] [CrossRef]
- Ahmed, A.; Salam, B.; Mohammad, M.; Ali, A.; Sarbaz, A.; Khoshnaw, S. Analysis Coronavirus disease (COVID-19) model using numerical approaches & logistic model. Int. Open Access J. Aims Bioeng. 2020, 7, 130–146. [Google Scholar]
- Alrabaiah, H.; Arfan, M.; Shah, K.; Mahariq, I.; Ullah, A. A comparative study of spreading of novel Coronavirus disease by using fractional order modified SEIR model. Alex. Eng. J. 2020. [Google Scholar] [CrossRef]
- Zhao, Z.; Li, X.; Liu, F.; Zhu, G.; Ma, C.; Wang, L. Prediction of the COVID-19 spread in African countries and implications for prevention and control: A case study in South Africa, Egypt, Algeria, Nigeria, Senegal and Kenya. Sci. Total Environ. 2020, 729, 138959. [Google Scholar] [CrossRef]
- Zhu, G.; Li, X.; Su, Y.; Zhang, K.; Bai, Y.; Ma, J.; Li, C.; Hu, X.; He, J. Simultaneous parameterization of the two-source evapotranspiration model by Bayesian approach: Application to spring maize in an arid region of northwest China. Geosci. Model Dev. 2014, 7, 741–775. [Google Scholar] [CrossRef]
- Amar, L.; Taha, A.; Mohamed, M. Prediction of the final size for COVID-19 epidemic using machine learning: A case study of Egypt. Infect. Dis. Model. 2020, 5, 622–634. [Google Scholar] [CrossRef] [PubMed]
- Schüttler, J.; Schlickeiser, R.; Schlickeiser, F.; KrSchöttlerger, M. COVID–19 Predictions Using a Gauss Model, Based on Data from April 2. Physics 2020, 2, 197–212. [Google Scholar] [CrossRef]
- Bacaër, N. Verhulst and the logistic equation (1838). In A Short History of Mathematical Population Dynamics; Springer Ltd.: London, UK, 2011; pp. 35–39. [Google Scholar]
- Khyar, O.; Allali, K. Global dynamics of a multi-strain SEIR epidemic model with general incidence rates: Application to COVID-19 pandemic. Nonlinear Dyn. 2020, 102, 489–509. [Google Scholar] [CrossRef] [PubMed]
- Worldometers. Coronavirus Cases. 2020. Available online: https://www.worldometers.info/Coronavirus/Coronavirus-cases (accessed on 15 November 2020).
- Our World in Data. Available online: https://ourworldindata.org/grapher/daily-cases-covid-region (accessed on 6 March 2021).
- Chapra, S.C.; Canale, R.P. Numerical Methods for Engineers; McGraw-Hill, Inc.: New York, NY, USA, 1988. [Google Scholar]
- Süli, E.; Mayers, D.F. An Introduction to Numerical Analysis; Cambridge University Press: Cambridge, UK, 2003. [Google Scholar]
- Guest, P.G.; Guest, P.G. Numerical Methods of Curve Fitting; Cambridge University Press: Cambridge, UK, 2012. [Google Scholar]
- Abuelma’atti, M. A simple algorithm for fitting measured data to Fourier-series models. Int. J. Math. Educ. Sci. Technol. 2006. [Google Scholar] [CrossRef]
- Wang, F.; Zhang, K. The theoretical analysis and algorithm on a class of optimal curve fitting problems. Appl. Math. Comput. 2006, 183, 622–633. [Google Scholar] [CrossRef]
- Mehrabian, A.; Lucas, C. A novel numerical optimization algorithm inspired from weed colonization. Ecol. Inform. 2006, 1, 355–366. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).