Abstract
Use of a case-control design to compare the accuracy of two binary diagnostic tests is frequent in clinical practice. This design consists of applying the two diagnostic tests to all of the individuals in a sample of those who have the disease and in another sample of those who do not have the disease. This manuscript studies the comparison of the predictive values of two diagnostic tests subject to a case-control design. A global hypothesis test, based on the chi-square distribution, is proposed to compare the predictive values simultaneously, as well as other alternative methods. The hypothesis tests studied require knowing the prevalence of the disease. Simulation experiments were carried out to study the type I errors and the powers of the hypothesis tests proposed, as well as to study the effect of a misspecification of the prevalence on the asymptotic behavior of the hypothesis tests and on the estimators of the predictive values. The proposed global hypothesis test was extended to the situation in which there are more than two diagnostic tests. The results have been applied to the diagnosis of coronary disease.
1. Introduction
The main parameters to assess and compare the accuracy of binary diagnostic tests (BDTs) are sensitivity and specificity. The sensitivity (Se) is the probability of the result of the BDT being positive when the individual has the disease, and the specificity (Sp) is the probability of the result of the BDT being negative when the individual does not have the disease. Other parameters that are used to assess and compare two BDTs are the predictive values (PVs). The positive predictive value (PPV) is the probability of an individual having the disease when the result of the BDT is positive, and the negative predictive value (NPV) is the probability of an individual not having the disease when the result of the BDT is negative. The PVs represent the accuracy of the diagnostic test when it is applied to a cohort of individuals, and they are measures of the clinical accuracy of the BDT. The PVs depend on Se, Sp and on the disease prevalence (p), and are easily calculated applying Bayes Theorem, i.e.,
whereas the Se and the Sp quantify how well the BDT reflects the true disease status (present or absent), the PVs quantify the clinical value of the BDT, since both the individual and the clinician are more interested in knowing how probable it is to have the disease given a BDT result.
The comparison of the performance of two binary diagnostic tests is a topic of special importance in the study of statistical methods for the diagnosis of diseases. This comparison is made through a paired-design or through a case-control design. The paired design consists of applying the two BDTs and the gold standard to all of the individuals in a single sample. The case-control design consists of applying the two BDTs to all of the individuals in two samples, one made up of individuals who have the disease (case sample) and another made up of individuals who do not have the disease (control sample). The advantages and disadvantages of the case-control design over the paired design can be seen in the book by Pepe [1]. Summarizing, the case-control design has some advantages over the paired design: (a) the case-control design is more efficient in terms of sample size requirements, (b) case-control studies allow for the exploration of subject-related characteristics of the test. Nevertheless, the case-control design has the disadvantage is that by using it we cannot estimate the prevalence of the disease.
In paired designs, the comparison of PVs has been the subject of several studies. Bennett [2,3], Leisenring et al. [4], Wang et al. [5] and Kosinski [6] studied hypothesis tests to independently compare the PPVs and the NPVs of two BDTs. Moskowitz and Pepe [7] studied the estimation of the PVs through a confidence region. Roldán-Nofuentes et al. [8] studied the joint comparison of the PPVs and NPVs of two BDTs, and proposed a global hypothesis test based on the chi-square distribution to simultaneously compare the PVs of two BDTs.
In a case-control design, Mercaldo et al. [9] have studied the estimation of the PVs of a BDT, assuming that the prevalence of the disease (p) is known. The prevalence can be known from other studies, such as population studies of health services, cohort studies, etc. Mercado et al. have verified through simulation experiments that the confidence interval with the best asymptotic behavior is the logit interval, whose equations are:
and
where and are the estimators of the PVs calculated from Equation (1), is the percentile of the normal standard distribution, and the variances are:
where and are the estimators of sensitivity and specificity, is the size of the case sample and is the size of the control sample.
In this article, we extended the study of Mercaldo et al. [9] to the case of two BDTs, studying different hypothesis tests to compare the PVs of the two BDTs subject to a case-control design. Subject to a case-control design, the two BDTs are applied to all of the individual in two samples, one of individuals who have the disease (case sample) and another with individuals who do not have the disease (control sample). In this design, the sample sizes and are set by the researcher. The sample of individuals that have the disease is extracted from a population of individuals that have the disease (e.g., registers of diseases), and the control sample is extracted from a population of individuals who are known not to have the disease. As the PVs depend on the disease prevalence and subject to a case-control design the quotient is not an estimator of the prevalence, in order to estimate and compare the PVs subject to this design it is necessary to know the value of the prevalence of the disease. This value can be obtained from health surveys or from previous studies. Consequently, the methods of comparison of the PVs subject to a paired design cannot be applied when there is a case-control design. In Section 2, we study hypothesis tests to simultaneously compare the PVs of two BDTs subject to a case-control design. A global hypothesis test is studied to simultaneously compare the PVs of the two BDTs, i.e.,
and simultaneous comparison is also studied from individual hypothesis tests, i.e.,
each of them to the error and also applying multiple comparison methods. In Section 3, simulation experiments are carried out to study the type I errors and the powers of the hypothesis tests proposed in Section 2, and we study the effect of the misspecification of the prevalence on the asymptotic behavior of the hypothesis tests proposed in Section 2 and on the estimators of the PVs. In Section 4, the results are applied to a real example on the diagnosis of coronary heart disease. In Section 5, the model proposed in Section 2 was extended to the situation in which we compare the PVs of more than two BDTs, and in Section 6 the results are discussed.
2. Global Hypothesis Test
Let us consider two BDTs, Test 1 and Test 2, which are applied to all of the individuals in two samples, one of individuals who have the disease (case sample) and another of individuals who do not have it (control sample). Let and be two binary variables that model the results of each BDT, in such a way that when the result of the corresponding BDT is positive and when it is negative. In Table 1, we can see the probabilities associated to the application of both BDTs to both types of individuals (cases and controls), as well as the frequencies observed.

Table 1.
Probabilities and observed frequencies subject to case-control design.
Using the conditional dependence model of Vacek [10], the probabilities given in the table are written as:
and
with . The parameter () is the covariance between the two BDTs in cases (controls), where if and if , and it is verified that and . If then the two BDTs are conditionally independent on the disease status. In practice, the assumption of the conditional independence is not realistic, and therefore and/or . In terms of the probabilities , the sensitivities are written as:
and the specificities are written as:
The estimators of sensitivities are and , and the estimators of specificities are and . The estimators of their variances are , , and . Therefore, the sensitivities and the specificities are estimated as proportions of marginal totals. In this way, in the case sample we are interested in the marginal frequencies and , and therefore these frequencies are the product of a type I bivariate binomial distribution [11]. In an analogous way, from the control sample, the marginal frequencies and are the product of a type I bivariate binomial distribution. In the individuals with the disease, the type I bivariate binomial distribution is characterized [11] by , and the correlation coefficient () between and . In an analogous way, in the individuals who do not have the disease, the type I bivariate binomial distribution is characterized by , and the correlation coefficient () between and . Therefore, the proposed model is a parametric model based on the distribution of the marginal frequencies in each table. In the individuals with the disease (cases), the correlation coefficient between the two BDTs is:
and in the individuals who do not have the disease (controls), the correlation coefficient between the two BDTs is:
It is easy to show that , , and . All of the other covariances are zero, since the two samples are independent. The estimators of and are and . Assuming that the disease prevalence p is known, the estimators of the predictive values are:
for Test 1, and
for Test 2, where . Let the variance-covariance matrixes be defined as:
and
Let be a vector whose components are the sensitivities and the specificities, and let be a vector whose components are the PVs. The variance-covariance matrix of is:
where is the Kronecker product. Applying the delta method, the matrix of variances- covariances of is:
Expressions of the variances-covariances of the PVs can be seen in Appendix A. The PVs of each BDT depend on the same parameters, the sensitivity and the specificity of the test and disease prevalence, and therefore they are related parameters. Consequently, the PVs of the two BDTs can be compared simultaneously. The global hypothesis test to simultaneously compare the PVs of the two BDTs is:
which is equivalent to the hypothesis test:
where is a complete range matrix sized whose elements are known constants, i.e.:
As the vector is distributed asymptotically according to a multivariate normal distribution, i.e., , then the test statistic for the global hypothesis test (4) is:
which is distributed asymptotically according to Hotelling’s T-squared distribution with a dimension 2 and degrees of freedom, where 2 is the dimension of the vector When is large, the statistic is approximately distributed according to a central chi-square distribution with 2 degrees of freedom when the null hypothesis is true.
On the other hand, the individual comparison of the positive (negative) predictive values is solved with the hypothesis test:
where PV is PPV or NPV. Based on the asymptotic normality of the estimators, the test statistic for this hypothesis test is:
which is distributed asymptotically according to a normal standard distribution, and where the variances-covariances are obtained from the Equation (3) (see Appendix A).
The global hypothesis test simultaneously compares the PPVs and the NPVs of the two BDTs. Some alternative methods to this global hypothesis test, based on the individual hypothesis tests, are: (1) testing the hypotheses and (Equation (6)) each one to an error; (2) testing the hypotheses and (Equation (6)) and applying a multiple comparison method such as the Bonferroni method [12] or the Holm method [13], which are methods that are very easy to apply based on the p-values. Bonferroni method [12] consists of solving each individual hypothesis test to an error equal to . The Holm method is a step-down method which is based on Bonferroni method but is more conservative. In Appendix B, the Holm method [13] is summarized.
3. Simulation Experiments
Simulation experiments were carried out to study the type I errors and the powers of the four methods proposed to simultaneously compare the predictive values: the global hypothesis test based on the chi-square distribution (Equation (5)), the individual hypothesis tests each one to an error (Equation (6)), the individual hypothesis tests (Equation (6)) applying the Bonferroni method and the individual hypothesis tests (Equation (6)) applying the Holm method. We have also studied the effect of a misspecification of the prevalence on the asymptotic behavior of these methods and on the estimators of the PVs.
The experiments were designed setting the values of the PVs. For each BDT, we took as PVs the values 0.60, 0.65, …, 0.90, 0.95, and as disease prevalence we took the values 10%, 25% and 50%. Based on the PVs and the prevalence, Se and Sp of each BDT were calculated from the Equation (1), only considering those cases in which the solutions are between 0 and 1. As values of the correlation coefficients and we took low values (25% of the maximum value), intermediate (50% of the maximum value) and high (75% of the maximum value), where the maximum value of each correlation coefficient is: and respectively. As sample sizes, we took the values . The simulation experiments were carried out with R [14], using the “bindata” package [15] to generate the samples of each type I bivariate binomial distribution.
Regarding the random samples, these were generated in the following way. Firstly, once the values of the PVs and of the prevalence were set, we calculated the sensitivities, the specificities and the maximum values of the coefficients and . We then generated 10,000 random samples from a type I bivariate binomial distribution with a sample size , probabilities and , and correlation coefficient . Similarly, we generated another 10,000 random samples from a type I bivariate binomial distribution with a sample size , probabilities and , and correlation coefficient . In this way, we obtained the marginal frequencies and ( and ) of each one of the 10,000 case (control) samples. The rest of the marginal frequencies were easily calculated: , , and . In order to construct the table of each case sample, we generated a random value from a doubly truncated binomial distribution of parameters and , with . This is necessary so that the sum of the frequencies leads to the marginal totals randomly generated through the type I bivariate binomial distribution. In the same way, in order to construct the table of each control sample, we generated a random value from a doubly truncated binomial distribution of parameters and , with . For each one of the 10,000 case (control) samples, once we have generated the values , and (, and ) it is easy to construct the complete table. Thus, , and for the case samples, and , and for the control samples. For the experiments was set. Moreover, all of the samples were generated in such a way that in all of them the parameters and the variances-covariances can be estimated. If in a random sample it is obtained that , with , then and , and therefore the test statistic cannot be calculated since is a non-singular matrix. This problem occurs mainly when the sample size is small or moderate. In this situation, the sample has been discarded and another is generated in its place until the 10,000 samples are obtained.
3.1. Type I Errors and Powers
In Table 2 and Table 3, we can see some results obtained for the type I errors of the global test and of the alternative methods proposed in Section 2. In these tables, we can only see the results for the global test, the individual comparisons with and with the Bonferroni method. The results obtained with the Holm method are not shown as they are practically the same as those obtained with the Bonferroni method. From the results obtained we can draw the following conclusions. In general terms, the type I error of the global hypothesis test fluctuates around the nominal error, especially in the case of samples sized , depending on the prevalence and the correlations between the two BDTs. For samples with smaller sizes , the type I error of the global test is lower than . The correlations between the two BDTs have an important effect on the type I error of the global test, with a decrease in the type I error when there is an increase in the correlation coefficients.

Table 2.
Type I errors for and .

Table 3.
Type I errors for and .
Regarding the method based on the individual hypothesis tests and to an error each one of them, the type I error may clearly overwhelm the nominal error (a situation that we have considered when the type I error is greater than 7%), especially when the correlations are not high. Consequently, this method may lead to erroneous results (false significances) and, therefore, should not be used. As for solving the global test from the individual tests applying the Bonferroni (Holm) method, the type I error has a very similar behavior to that of the global hypothesis test.
Regarding the powers of the hypothesis tests, in Table 4 and Table 5 we can see some of the results obtained for the global test and other alternative methods. The results obtained with the Holm method are not shown as they are practically the same as those obtained with the Bonferroni method. The power of the global hypothesis test is calculated as the proportion of samples in which it is accepted that or (being true that or ). From the results, the following conclusions are obtained. The disease prevalence has an important effect on the power of each one of the methods to solve the global test, and the power increases with an increase in the prevalence. Regarding the correlations and , these do not have a clear effect on the power, and the power increases sometimes and decreases other times when the correlations increase. In general terms, when the prevalence is small we need large samples so that the power of the global hypothesis test is greater than 80%; for a prevalence of 25% with sample sizes we obtain a power greater than 80%; and for a very large prevalence with sample sizes we obtain a very higher power, greater than 80%–90%, depending on the difference between the PVs.

Table 4.
Powers for , , and .

Table 5.
Powers for , and .
The power of the method based on the individual hypothesis tests to an error is greater than that of the global test based on the chi-square distribution due to the fact that its type I error is also greater. Regarding the hypothesis test based on the individual tests with the Bonferroni method, in general terms, its power is very similar to that of the global test when the sample sizes are large. When the sample sizes are small or moderate, in general terms and depending on prevalence and correlations, the power of the global test is slightly greater than that of the individual tests with the Bonferroni method. The same conclusions are obtained when the Holm method is applied (whose results are almost identical to those of the Bonferroni method).
The graphs in Figure 1 show the powers of the three methods when , , and , for different sample sizes , and values intermediate of the correlation coefficients. These graphs show that when varies and the rest of the PVs are constant, the powers decrease when the prevalence increases. Similarly, the graphs in Figure 2 show the powers of the three methods when , , and , for different sample sizes , and values intermediate of the correlation coefficients. These graphs show that when the varies and the rest of the PVs are constant, the power of each method increases when the prevalence increases.
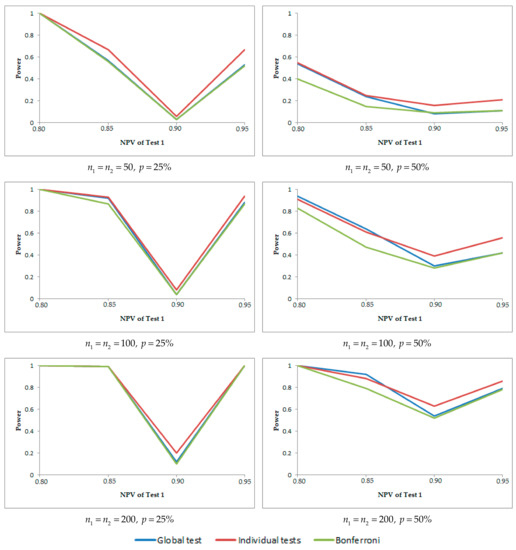
Figure 1.
Powers of the three methods when the negative predictive value (NPV) of a binary diagnostic test varies and the rest of the PVs are constant.
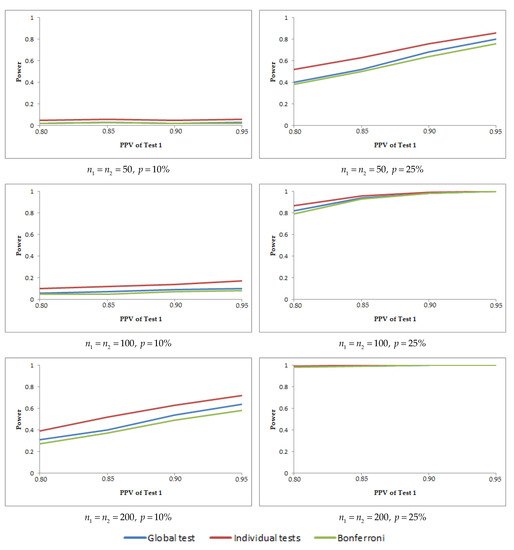
Figure 2.
Powers of the three methods when the positive predictive value (PPV) of a binary diagnostic test varies and the rest of the PVs are constant.
As conclusions of the results obtained in the simulation experiments, the global hypothesis test based on the chi-square distribution behaves well in terms of the type I error (it does not overwhelm the nominal error of 5%), the same as the individual tests along with the Bonferroni (Holm) method. The method based on the individual tests to a global error should not be used as it may clearly overwhelm the nominal error.
In the simulation experiments, the proportion of times that and that are correctly concluded has also been studied. This issue is of special interest when the alternative hypothesis of the global test is true, as it can be a valid method to investigate the causes of significance. The study was carried out by applying the individual hypothesis tests together with the Bonferroni (Holm) method. Individual tests to an error have not been considered as they have a type I error that can exceed the nominal error. If it is verified that , then this study is equivalent to studying the power of the individual test to an error (since the Bonferroni method has been applied), where is or . If it is verified that then this study is equivalent to studying the type I error of the individual test to an error. In the scenarios considered in Table 4 and Table 5 it is verified that and that . Therefore, for these two scenarios, the power of the test and the type I error of the test have been studied, each with an error equal to . Table 6 and Table 7 show the results obtained applying the Bonferroni method. The results obtained with the Holm method are not shown as they are practically the same as those obtained with the Bonferroni method.

Table 6.
Power of the test and type I error of the test when , , and .

Table 7.
Power of the test and type I error of the test , , and .
In general terms, the hypothesis test has a high power when the sample sizes are moderate or high, depending on the prevalence and the correlation coefficients. Its behavior is very similar to that of the global hypothesis test. With respect to the test , its type I error fluctuates around the nominal error (2.5%) when the sample sizes are moderate or large, depending on the prevalence of the correlation coefficients. In general terms, the hypothesis tests and have a good asymptotic behavior, both in terms of power and type I error.
From the results obtained in the simulation experiments, we propose the following method to compare the PVs of two BDTs subject to a case-control design: (1) Applying the global hypothesis test based on the chi-square distribution (Equation (5)) to an error; (2) If the global hypothesis test is not significant, the equality hypothesis of the PVs is not rejected; if the global hypothesis test is significant to an error, the investigation of the causes of the significance is made by testing the individual tests (Equation (6)) and applying the Bonferroni method or the Holm method to an error. Therefore, if the global test is significant, the investigation of the significance consists in solving the individual hypothesis tests and , each of them to an error (Bonferroni method) or applying Holm method.
This method to simultaneously compare the PVs is very similar to other methods used in other statistical models, such as the analysis of variance: first the global test is resolved to an error, and if it is significant then the causes of significance are investigated from pairwise comparisons and the application of a multiple comparison method.
3.2. Effect of the Prevalence
The estimation and comparison of the PVs of two BDTs subject to a case-control design requires knowledge of the disease prevalence. To study the effect of a misspecification of the prevalence on the comparison of the PVs and on the estimators of the PVs, we carried out simulation experiments similar to those made to study the type I errors and the powers. For this purpose, we took as the prevalence for the inference a misspecification equal to 10% and to 20% of the value of the prevalence set, and we have studied the type I errors and the powers of the global test and of the Bonferroni and Holm methods, and the relative root mean square error (RRMSE) of the estimator of each PVs. Thus, for each estimator we calculated the relative root mean square error (RRMSE), i.e.,
where is the PPV or the NPV of the ith BDT and is its estimator calculated from the kth sample , and . For the values of the parameters we took as prevalence respectively, and to estimate the PVs we took as prevalence with . A value can be considered as a small (moderate) value of the relative deviation.
Table 8 shows some of the results obtained for the type I errors and the powers of the global test and the Bonferroni method (the results of the Holms method are not shown as they are practically identically to those obtained with the Bonferroni method). In this Table we show the results when there is no misspecification of the prevalence and when there is a misspecification of the prevalence ( or ). From the results of these experiments, it is verified that the type I errors of the methods studied do not overwhelm the nominal error (). In general terms there are no important differences between the type I errors when there is a misspecification of the prevalence and when there is not. Regarding the powers, the conclusions are also very similar, there are no important differences between the powers when there is a misspecification of the prevalence and when there is not.

Table 8.
Effect of a misspecification of the prevalence.
Regarding the estimators, Table 8 shows some of the results obtained for the RRMSEs (in %) of the estimators of the PVs of Test 1 (the results for Test 2 are identical). In general terms, the difference between the RRMSEs is small (around 5% or less, in absolute value) when the two sample sizes are moderate or large and the relative deviation is small (10%) or moderate (20%). Therefore, a small or moderate misspecification of the prevalence ( or ) does not have an important effect on the estimators of the PVs when the samples are moderate or large. Additionally, there is not an important difference between the RRMSEs when the sample sizes are small and the relative deviation is small. However, the difference between the RRMSEs is larger when the sample sizes are small and the relative deviation is moderate. In this situation, a misspecification of the prevalence has an important effect on the estimators of the PVs.
4. Example
The results obtained have been applied to the diagnosis of coronary heart disease, using an electrocardiogram and an echocardiography as diagnostic tests. Both tests have been applied to a sample of 105 older men with coronary heart disease (case sample) and to another sample of 120 older men without this disease (control sample). In Table 9 we can see the frequencies obtained, where the random variable models the result of the electrocardiogram and the variable models the result of the echocardiography. In order to illustrate the method proposed, we are going to consider that the prevalence of the disease in older men is 5%. The objective is to compare the clinical accuracy (PVs) of both BDTs in the population whose prevalence of coronary heart disease is 5%. The comparison of the PVs will be made with .

Table 9.
Diagnosis of coronary heart disease.
From the case sample, the estimates of the two sensitivities (and their standard errors, SE) and of the correlation coefficient between them are , and . From the control sample, the estimates of the two specificities and of the correlation coefficient between them are , and . Assuming that the prevalence of coronary heart disease is 5%, the estimates of the PVs are:
and
Applying the delta method (Equation (3)), the estimated variance-covariance matrix of the estimators of the PVs is:
Applying Equation (5), the value of the test statistic for the global test:
is and the p-value is 0.023, and therefore the null hypothesis of the global test is rejected. Testing the individual hypothesis tests it is found that the value of the test statistic for is equal to 2.552 (two sided p-value is 0.011) and that the value of the test statistic for is equal to 1.469 (two sided p-value is 0.142). Applying the Bonferroni (or Holm) method, the hypothesis of equality of the positive predictive values is rejected and the hypothesis of equality of the negative predictive values is not rejected. Therefore, in a population in which the prevalence of coronary heart disease is 5%, the positive predictive value of electrocardiogram is significantly greater than that of the echocardiography (95% confidence interval for the difference: 0.056 to 0.422), while there are no significant differences between the two negative predictive values.
5. More Than Two BDTs
Let us consider that J BDTs are applied to all of the individuals in the case sample and the control sample. For each BDT we define the random variable in a similar way to how this was done in Section 2. Let and be the sensitivity and the specificity of the jth BDT, with . Let be the number of individuals with the disease for whom ,…, , with when the result of the jth BDT is positive and when it is negative. In a similar way, is the number of without the disease for whom ,…, . Let us consider the probabilities , with . Thus, for example for three BDTs, using the dependence model of Torrance–Rynard and Walter [16], these probabilities are:
and
with , and , and where () is the covariance between the jth BDT and the kth BDT for individuals with the disease (without the disease). The estimators of these probabilities are , with . The sensitivity and the specificity of the jth BDT are:
and its estimators are:
The estimators of the variances-covariances of these estimators are , , and , and the rest of the covariances are equal to zero. The estimators of the PVs of the jth BDT are:
and
where p is the disease prevalence and .
Let be the vector whose components are the sensitivities and the specificities, and let be the vector whose components are the PVs. The variance-covariance matrix of the vector , with a dimension , is similar to that given in Equation (2), where and are matrixes with a dimension . Applying the delta method, the variance-covariance matrix of , with a dimension , has an expression similar to that given in Equation (3). The PVs of each one of the J BDTs depend on the same parameters (the sensitivity and the specificity of the jth diagnostic test) and, therefore, these parameters can be compared simultaneously. The global hypothesis test to simultaneously compare the PVs of the J BDTs is:
which is equivalent to the hypothesis test:
where is a matrix with a dimension , i.e.,
is a matrix with a dimension whose elements are all equal to 0, and is a matrix with a dimension where each component is equal to 1, each element is equal to for , and the rest of the elements in this matrix are equal to 0. Applying the multivariate central limit theorem it is verified that . Then, the statistic is distributed according to Hotelling’s T-squared distribution with a dimension and degrees of freedom, where is the dimension of the vector . When is large, the statistic is distributed according to a central chi-squared distribution with degrees of freedom when the null hypothesis is true, i.e.,
Finally, the method to compare the PVs of the J BDTs would consist of the following steps: (1) Solve the global hypothesis test to an error calculating the statistic based on the chi-squared distribution; (2) if the global test is not significant to an error then we do not reject the homogeneity of the J PVs, but if the hypothesis test is significant then the causes of significance are investigated comparing the PPVs (NPVs) in pairs (Equation (6)) and applying a multiple comparison method (e.g., Bonferroni or Holm).
6. Discussion
The comparison of the positive and negative predictive values of two binary diagnostic tests is an important topic in the study of statistical methods in diagnostic medicine. Subject to a paired design, this topic has been subject to different studies. In this article we studied the simultaneous comparison of the predictive values of two diagnostic tests subject to a case-control design, analyzing and comparing several methods. These methods consisted of a global test based on the chi-square distribution, a method based on the individual comparisons each one to an error, and other two methods based on individual comparisons along with a multiple comparison method. The multiple comparison methods that were used were the Bonferroni method and the Holm method, which are methods based on the p-values of the individual hypothesis tests and are very easy to apply. The methods studied to compare the predictive values require knowing the prevalence of the disease. The prevalence can be known from other studies, such as population studies of health services, cohort studies, etc. If the researcher has a great uncertainty about the value of the prevalence, the problem can be solved by using several values for the prevalence and then analyzing and comparing the results obtained.
Simulation experiments were carried out to study the type I errors and the powers of the four methods proposed. These experiments were based on the generation of random samples with type I bivariate binomial distributions, which are the distributions that are inherent to case-control design, since proportions of marginal totals are estimated from these samples. The results have shown that the global hypothesis test based on the chi-square distribution behaves well in terms of type I error, and does not overwhelm the nominal error. Regarding its power, in general this strongly depends on the disease prevalence, and it is necessary to have very large samples when the prevalence is small and relatively small sample sizes when the prevalence is high, so that the power will be high.
Based on the results of the simulation experiments, a method has been proposed to compare the predictive values of two diagnostic tests subject to a case-control design. This method, which is similar to that proposed by Roldán-Nofuentes et al. [8], consists of the following steps: (1) Simultaneously comparing the predictive values applying the global hypothesis test based on the chi-square distribution to an error; (2) if the global hypothesis test is not significant, then the equality hypothesis of the PVs is not rejected. If the global hypothesis test is significant to an error, then the causes of the significance are studied solving the individual hypothesis tests and applying the Bonferroni method or the Holm method to an error. This procedure that we propose is similar to the analysis of variance: firstly, the global test is solved and, if this is significant, then the causes of the significance are studied starting with paired comparisons along with some multiple comparison method.
Simulation experiments were carried out to study the effect of a misspecification of the prevalence in the asymptotic behavior of the global hypothesis test based on the chi-square distribution and on the methods based on multiple comparisons. In general terms, we can conclude that a small or moderate misspecification of the prevalence do not have an important effect on the behavior of these hypothesis tests, especially when the sample sizes are moderate or large.
The global hypothesis test was extended to the situation in which we simultaneously compare the PVs of more than two BDTs, and for this we propose a method which is similar to that proposed for two BDTs. To be able to calculate the global test statistic it is necessary that to be non-singular. For two BDTs, this matrix is non-singular when it is verified that , with . If then the method proposed to compare the PVs cannot be applied A solution to this problem consists in adding the value 0.5 to all the observed frequencies (the sample size increases by two units), a very frequent solution in the analysis of tables. Simulation experiments have been carried out to study the type I errors and the powers of the hypothesis tests proposed in Section 2, using this solution when in a sample it is verified that . These experiments have been designed in a similar way to those performed in Section 3. Table 10 shows some results (type I errors and powers) for some of the scenarios considered in Section 3, as well as the average proportions (of the three correlation scenarios) of case (control) samples in which the value 0.5 has been added. Obviously, the proportion of samples in which the value 0.5 has been added is greater when the sample size is small. In general terms, the conclusions are the same as those obtained in the simulation experiments presented in Section 3, although the powers of all hypothesis tests are slightly lower when the sample sizes are small. Therefore, adding 0.5 to all the observed frequencies of a sample in which is an adequate solution to be able to apply the PVs comparison method.

Table 10.
Type I errors and powers when 0.5 is added to the samples in which .
Author Contributions
The two authors have collaborated equally in the realization of this work. Both authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by the Spanish Ministry of Economy, Grant Number MTM2016-76938-P, and by the University of Nouakchott Alaasriya.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
We thank the three referees for their helpful comments that improved the quality of this manuscript. We thank Professor Cheikh Saad Bouh Camara, the president of the University of Nouakchott, for his help to finance the publication of this manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
Performing algebraic operations in Equation (3) it is found that:
and
and where and .
Appendix B
Let us assume that we are going to solve K hypothesis test vs. with . Let be the p-values obtained ordered from the lowest to the highest, and therefore is the p-value that corresponds to the hypothesis test vs. . The Holm method [13] consists of the following steps:
Step 1. If then hypothesis is rejected and we go to the next step; if then no null hypothesis is rejected and the process finishes.
Step 2. If then is rejected and we go to the next step; if we do not reject the null hypotheses with and the process finishes….
Step K. If then is rejected and the process finishes; and if then is not rejected and the process finishes.
References
- Pepe, M.S. The Statistical Evaluation of Medical Tests for Classification and Prediction; Oxford University Press: New York, NY, USA, 2003. [Google Scholar]
- Bennett, B.M. On comparison of sensitivity, specificity and predictive value of a number of diagnostic procedures. Biometrics 1972, 28, 793–800. [Google Scholar] [CrossRef] [PubMed]
- Bennett, B.M. On tests for equality of predictive values for t diagnostic procedures. Stat. Med. 1985, 4, 535–539. [Google Scholar] [CrossRef] [PubMed]
- Leisenring, W.; Alonzo, T.; Pepe, M.S. Comparisons of predictive values of binary medical diagnostic tests for paired designs. Biometrics 2000, 56, 345–351. [Google Scholar] [CrossRef] [PubMed]
- Wang, W.; Davis, C.S.; Soong, S.J. Comparison of predictive values of two diagnostic tests from the same sample of subjects using weighted least squares. Stat. Med. 2006, 25, 2215–2229. [Google Scholar] [CrossRef] [PubMed]
- Kosinski, A.S. A weighted generalized score statistic for comparison of predictive values of diagnostic tests. Stat. Med. 2013, 32, 964–977. [Google Scholar] [CrossRef] [PubMed]
- Moskowitz, C.S.; Pepe, M.S. Comparing the predictive values of diagnostic tests: Sample size and analysis for paired study designs. Clin. Trials 2006, 3, 272–279. [Google Scholar] [CrossRef] [PubMed]
- Roldán-Nofuentes, J.A.; Luna del Castillo, J.D.; Montero-Alonso, M.A. Global hypothesis test to simultaneously compare the predictive values of two binary diagnostic tests. Comput. Stat. Data Anal. 2012, 56, 1161–1173. [Google Scholar] [CrossRef]
- Mercaldo, N.D.; Kit, F.L.; Zhou, X.H. Confidence intervals for predictive values with an emphasis to case-control studies. Stat. Med. 2007, 26, 2170–2183. [Google Scholar] [CrossRef] [PubMed]
- Vacek, P.M. The effect of conditional dependence on the evaluation of diagnostic tests. Biometrics 1985, 41, 959–968. [Google Scholar] [CrossRef] [PubMed]
- Kocherlakota, S.; Kocherlakota, K. Bivariate Discrete Distributions; Marcel Dekker INC: New York, NY, USA, 1992. [Google Scholar]
- Bonferroni, C.E. Teoria statistica delle classi e calcolo delle probabilità. Pubblicazioni del R Istituto Superiore di Scienze Economiche e Commerciali di Firenze 1936, 8, 3–62. [Google Scholar]
- Holm, S. A simple sequential rejective multiple testing procedure. Scand. J. Stat. 1979, 6, 65–70. [Google Scholar]
- RC Team. R: A Language and Environment for Statistical Computing; RC Team: Vienna, Austria, 2016; Available online: https://www.R-project.org/ (accessed on 17 March 2021).
- Leisch, F.; Weingessel, A.; Hornik, K. Bindata Package. Available online: https://cran.r-project.org/web/packages/bindata/ (accessed on 17 March 2021).
- Torrance-Rynard, V.L.; Walter, S.D. Effects of dependent errors in the assessment of diagnostic test performance. Stat. Med. 1997, 16, 2157–2175. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).