RiskLogitboost Regression for Rare Events in Binary Response: An Econometric Approach

Abstract

A boosting-based machine learning algorithm is presented to model a binary response with large imbalance, i.e., a rare event. The new method (i) reduces the prediction error of the rare class, and (ii) approximates an econometric model that allows interpretability. RiskLogitboost regression includes a weighting mechanism that oversamples or undersamples observations according to their misclassification likelihood and a generalized least squares bias correction strategy to reduce the prediction error. An illustration using a real French third-party liability motor insurance data set is presented. The results show that RiskLogitboost regression improves the rate of detection of rare events compared to some boosting-based and tree-based algorithms and some existing methods designed to treat imbalanced responses.

1. Introduction

Research on rare events is steadily increasing in real-world applications of risk management. Examples include fraud detection [1], credit default prediction [2], bankruptcy prediction [3], emerging markets anomalies [4], customer churn predictions [5], and accident occurrence for insurance studies [6]. We address the rare event modeling problem with a purposefully designed method to identify rare potential hazards in advance and facilitate an understanding of their causes.

Rare events are extremely uncommon patterns whose atypical behavior is difficult to predict and detect. A broad consensus [7,8,9,10] favors the definition of rare events data as binary variables with much fewer events (ones) than non-events (zeros). In other words, the degree of imbalance is more extreme in rare events than it is in class imbalanced data, such that rare events are characterized by the number of ones being hundreds to thousands of times smaller than the number of zeros.

Imbalanced data and rare events have been studied mostly as statistical problems with potential application in diverse fields of biology, political science, engineering, and medicine. To name a few, ref. [11] develop a computational method for evaluating the extreme probabilities from random initialization of nonlinear dynamical systems. Ref. [12] proposes a solution for the rare events problem with fuzzy sets. Ref. [13] proposes a resampling strategy via gamma distribution for imbalanced data in medical diagnostics. Ref. [14] proposes a penalized maximum likelihood fixed effects estimator for binary time-series-cross-sectional data for political science applications. Ref. [15] proposes a learning-based stochastic optimization model using rare event data on U.S. federal government agencies. Ref. [16] introduces dynamic models for rare events and time-inhomogeneity in fluctuating currency markets.

The insurance literature draws heavily on discrete probability distributions, where the occurrence of few or non-events are considered as rare or extreme. For instance, authors like [17,18] use generalized linear models to predict insurance fraud. Ref. [19] develops an extension of the Poisson approximation of binomial distributions for rare events. Another work revolves around solutions reached by rare-event simulations [20]. Refs. [21,22,23] employ non-parametric methods for heavy tailed distributions. Ref. [24] employs transaction aggregation to detect credit card fraud when the occurrence of ones in the dependent variable is much less than zeros. However, very few papers in this field have been devoted to studying rare events in binary response such as [25,26,27], and even fewer that go beyond econometric methods, such as [9], which employs advanced machine learning methods.

In fact, developing algorithms that can handle rare events powered by the latest machine learning advances faces two important challenges:

(i)

Some models exhibit bias towards the majority class or underestimate the minority class. Some classifiers are suitable for balanced data [28,29] or treat the minority class as noise [30]. Moreover, some popular tree-based and boosting-based algorithms have been shown to have a high predictive performance measured only with evaluation metrics that consider all observations equally important [31].

(ii)

Unlike econometric methods, several machine learning methods are considered as black boxes in terms of interpretation. They are frequently interpreted using single metrics such as classification accuracy as unique descriptions of complex tasks [32], and they are not able to provide robust explanations for high-risk environments.

In this paper we address these two challenges in an attempt to predict and explain rare events, which will be referred to as dependent or target variables. We propose a RiskLogitboost regression, which is a Logitboost-based algorithm that leads to the convergence of coefficient estimates after some iterations, as occurs when using Iteratively Re-Weighted procedures. Moreover, bias and weighting corrections are incorporated to improve the predictive capacity of the events (ones).

More specifically, our prediction strategy consists of: (i) increasing the accuracy of minority class prediction, and (ii) building an interpretable model similar to classical econometric models. After the introduction, this paper is organized as follows. Section 2 presents the background to the three main approaches used in this research: boosting methods for imbalanced data sets, penalized regression models, and interpretable machine learning. Section 3 describes in detail the proposed RiskLogitboost regression in the rare event problem framework. Section 4 shows the illustrative data used to prove the RiskLogitboost regression. Section 5 discusses the results obtained in terms of predictive capacity and interpretability. Finally, Section 6 presents the conclusions of the paper.

2. Background

To formally define the novel RiskLogitboost regression as a supervised machine learning method, this section first addresses three important notions which are the basis of our strategy. A rigorous description of boosting-based algorithms is presented since it is the core procedure of our method. We will obtain certain key expressions from penalized linear models to approximate RiskLogitboost as an econometric method. Finally, two widely recognized interpretable machine learning techniques are briefly described to gain an overview of how traditional machine learning has been interpreted so far.

Supervised machine learning methods are used to predict a response variable denoted as $Y_i$, i = 1, …, n. The data consist of a sample of n observations of the response, and the prediction is established by a set of covariates denoted as $X_{ip}$, p = 1, …, P with P predictor variables. The model is trained by a base learner $F\left(X_{ip};u\right)$, which is a function of covariates $X_{ip}$ and the parameters represented by u. The predicted response is denoted as ${\widehat{Y}}_i$.

The purpose of supervised machine learning is to minimize the learning error measured by a loss function φ using an optimization strategy like gradient descent. The loss function is the distance between the observed $Y_i$ and the predicted response ${\widehat{Y}}_i$ which is denoted as φ($Y_i$, ${\widehat{Y}}_i$).

2.1. Boosting Methods

Boosting methods for additive functions are developed within an iterative process through a numerical optimization technique called gradient descent. Each function minimizes a specified loss function φ. Ref. [33] applied the boosting strategy to some loss criteria for classification and regression problems (we use the term “classification problem” if $Y_i$ is qualitative, whereas if $Y_i$ is quantitative, we use the term “regression problem”. The latter does not refer to regression models studied in econometrics; it refers to a predictive model) such as: least-squares ${\left(Y_i-{\widehat{Y}}_i\right)}^2$ for the least-squares regression; least absolute-deviation $\left|Y_i-{\widehat{Y}}_i\right|$ for the least-absolute-deviation regression; Huber for M-Regression $0.5{\left(Y_i-{\widehat{Y}}_i\right)}^2$ if $\left|Y_i-{\widehat{Y}}_i\right|\le \delta$ or $\delta \left|Y_i-{\widehat{Y}}_i\right|-\delta /2$ otherwise; and the Logistic binomial log-likelihood log$\left(e^{-2Y_i{\widehat{Y}}_i}\right)$ for two-class Logistic classification.

The Gradient Boosting Machine shown in Algorithm 1 is the base proposal of [33]. The algorithm initializes with a prediction guess of ${\widehat{Y}}_i{}^0$. Then a boosting process of D iterations is carried out in four stages: the first transforms the new response denoted as ${\tilde{r}}_i{}^d$ computed as the negative gradient of $\phi \left(Y_i,{\widehat{Y}}_i{}^d\right)$ at iteration d. The second stage fits a least squares regression with the recently computed ${\tilde{r}}_i{}^d$ as the response. The third stage minimizes the loss function between the observed $Y_i$ and ${\widehat{Y}}_i{}^d$ + γ$F\left(X_{ip};u^d\right)$ and the result is delivered in γ. Finally, the last stage updates the prediction ${\widehat{Y}}_i{}^d$ by summing ${\widehat{Y}}_i{}^{d-1}$ and $\gamma F\left(X_{ip};u^d\right)$.

Algorithm 1.Gradient Boosting Machine

1. $\mathrm{Initial}\hspace{1em}\mathrm{values}:\hspace{1em}{\widehat{Y}}_i{}^0=\hspace{1em}argmi{n}_{\rho }{\sum }_{i=1}^n\phi \left(Y_i,\rho \right).$

2. For d = 1 to D do:

2.1 $\mathrm{Transformation}:\hspace{1em}{\left.{\tilde{r}}_i{}^d=-\frac{\partial \phi \left(Y_i,{\widehat{Y}}_i{}^d\right)}{\partial {\widehat{Y}}_i{}^d}\right|}_{Y_i={\widehat{Y}}_i{}^{d-1}}^{}.$

2.2 $\mathrm{Fitting}:\hspace{1em}{u}^d=\hspace{1em}argmi{n}_{u,\varpi }{\sum }_{i=1}^n{\left[{\tilde{r}}_i{}^d-\varpi F\left(X_{ip};u\right)\right]}^2.\hspace{1em}$

2.3. $\mathrm{Minimizing}:\hspace{1em}{\gamma }^d=\hspace{1em}argmi{n}_{\gamma }{\sum }_{i=1}^n\phi \left[Y_{i,}{\widehat{Y}}_i{}^d+\gamma F\left(X_{ip};u^d\right)\right]$.

2.4 $\mathrm{Updating}:\hspace{1em}{\widehat{Y}}_i{}^d=\hspace{1em}{\widehat{Y}}_i{}^{d-1}+{\gamma }^{d}F\left(X_{ip};u^d\right)$.

3. End for

Adaboost was one of the first boosting-based prediction algorithms [34,35]. It trains the base learner in a reweighted version by allocating more weight to misclassified observations. Many other boosting techniques have since been derived, such as RealBoost [33], which allows a probability estimate instead of a binary outcome. Logitboost [33] can be used for two-class prediction problems by optimizing an exponential criterion. Gentle Adaboost [33] builds on Real Adaboost and uses probability estimates to update functions. Madaboost [36] modifies the weighting system of Adaboost. Brownboost [37] is based on finding solutions to Brownian differential equations. Delta Boosting [38] uses a delta basis instead of the negative gradient as transformed response.

In the context of rare event and imbalanced prediction problems, various boosting-based methods have been proposed in the literature, including but not limited to RareBoost [39], which calibrates the weights depending on the accuracy of each iteration. Asymmetric Adaboost [40] is a variant of Adaboost and incorporates a cascade classifier. SMOTEBoost [41] incorporates SMOTE (synthetic minority over-sampling techniques) in a boosting procedure. DataBoost-IM [42] treats outliers and extreme observations in a separate procedure to generate synthetic examples of majority and minority classes. RUSBoost [43] trains using skewed data. MSMOTEBoost [44] rebalances the minority class and eliminates noise observations. Additional cost-sensitive methods [45,46,47,48,49,50] have been developed by introducing cost items in the boosting procedure.

Other boosting extensions include the tree boosting-based methods, which have been considered a great success, due to their predictive capacity, in the machine learning community. The tree gradient boost [51] varies from the original gradient boost in the initial value of the first prediction ${\widehat{Y}}_i{}^0$, and the use of a Logistic loss function and a tree base learner.

A tree gradient boost as shown in Algorithm 2 consists of six stages. The first states the values for the initial prediction, ${\widehat{Y}}_i{}^0$. The second stage obtains the new transformed response with the negative gradient of a Logistic loss function. The third maps the observations onto J leaves of the tree at iteration d. The tree learner is ${\sum }_{j=1}^J{u}_{j}1(X_{ip}ϵR_j)$ with J terminal nodes known as leaves, and $R_j$ classification rules (regions), j = 1, …, J. Parameter u corresponds to the score of each leaf, which is the proportion of cases classified as events given covariates $X_{ip}$. Gini and entropy are two metrics for choosing how to split a tree. Gini is a measurement of the likelihood of an incorrect classification of a new observation if it were randomly classified according to the distribution of class labels of the covariates. Entropy measures how much information there is in a node.

Algorithm 2. Tree Gradient Boost

1. $\mathrm{Initial}\hspace{1em}\mathrm{values}:\hspace{1em}{\widehat{Y}}_i{}^0=\frac{1}{2}log\frac{1+\overline{Y}}{1-\overline{Y}}$, where $\overline{Y}$ is the mean of $Y_i$.

2. For d = 1 to D do:

2.1 $\mathrm{Transformation}:\hspace{1em}{\tilde{r}}_i{}^d=\hspace{1em}\frac{2Y_i}{1+exp\left(2Y_i{\widehat{Y}}_i{}^{d-1}\right)}$

2.2 $\mathrm{Mapping}:\hspace{1em}{R}_{jd}$$\hspace{1em}=\hspace{1em}\mathrm{j}-\mathrm{leaf}\mathrm{scores}\hspace{1em}({\tilde{r}}_i$$,\hspace{0.17em}{X}_1^n$)

2.3 $\mathrm{Minimizing}:\hspace{1em}{\mathsf{\gamma }}_j^d\hspace{1em}=\hspace{1em}argmi{n}_{\mathsf{\gamma }}\frac{{\sum }_{X_iϵR_{jd}}{\tilde{r}}_i}{{\sum }_{X_iϵR_{jd}}\left|{\tilde{r}}_i\left(2-\left|{\tilde{r}}_i\right|\right)\right|}$.

2.4 $\mathrm{Updating}:\hspace{1em}{\widehat{Y}}_i{}^d\hspace{1em}=\hspace{1em}{\widehat{Y}}_i{}^{d-1}\hspace{1em}+\hspace{1em}{\sum }_{j=1}^J{\mathsf{\gamma }}_j^d\hspace{1em}1(X_iϵR_{jd})$

3. End for

The fourth stage requires minimizing a Logistic loss function: $argmi{n}_{\mathsf{\gamma }}{\sum }_{X_iϵR_{jd}}^{n}log\left[1+exp\left(-2Y_i\left({\widehat{Y}}_i{}^{d-1}+{\mathsf{\gamma }}^d\right)\right)\right]$ delivered in ${\gamma }_j^d$. However, since there is no closed form for ${\gamma }_j^d$, a Newton-Raphson approximation is computed. Finally, the sixth stage updates the final ${\widehat{Y}}_i{}^d$.

Tree gradient boosting techniques tend to overfit especially when data are complex or highly imbalanced [31]. Regularization is a popular strategy to penalize the complexity of the tree and allow out-of-sample reproducibility. This involves adding a shrinkage penalty or regularization term to the loss function φ($Y_i$,${\widehat{Y}}_i$) so that the leaf scores shrink: ${\sum }_{i=1}^n\phi \left(Y_i,{\widehat{Y}}_i\right)+{\sum }_{d=1}^D\mathsf{ή}\left({\widehat{Y}}^d\right)$ ($\mathsf{ή}$ = $\mathsf{\lambda }\Vert \dot{\mathrm{u}}\Vert$, where $\mathsf{\lambda }$ is a regularization parameter associated with L1-norm or L2-norm of the scores vector). Moreover, ref. [52] introduced cost-complexity pruning that penalizes the number of terminal nodes J according to the following expression: ${\sum }_{i=1}^n\phi \left(Y_i,{\widehat{Y}}_i\right)+{\sum }_{d=1}^D\lambda J.$ As a consequence, these strategies seem quite risky for analysts who want to keep the effect of the covariates even when this effect is small or not significant, because after applying regularization or pruning the score of the leaf is arbitrarily shrunk and the correspondingly less important characteristics disappear.

2.2. Penalized Regression Methods

In the econometric setting, regression models have commonly been used to describe the relationship between a response $Y_i$ and a set of covariates $X_{ip}$. Regression models are used to predict a target variable ${\widehat{Y}}_i$, and allow interpretability of the coefficients by measuring the effect of the covariates on the expected response.

Logistic regression models are used to model the binary variable $Y_i$. $Y_i$ follows a Bernoulli distribution, where ${\pi }_i$ is the probability that $Y_i$ equals 1, expressed as follows:

$${\pi }_i=\frac{exp\left(X_i\mathit{\beta }\right)}{1+exp\left(X_i\mathit{\beta }\right)}.$$

(1)

Note that $X_i\mathit{\beta }$ is the matrix notation of ${\beta }_o+{\sum }_{p=1}^P{X}_{ip}{\beta }_p$, where $\mathit{\beta }$ is the parameter vector. $1-{\pi }_i$ is the probability that $Y_i$ equals 0:

$${\pi }_i=\frac{1}{1+exp\left(X_i\mathit{\beta }\right)}.$$

(2)

The Logistic regression uses a logit function as the linear predictor defined as:

$${\eta }_i=log\left(\frac{{\pi }_i}{1-{\pi }_i}\right)={\beta }_o+{\sum }_{p=1}^P{X}_{ip}{\beta }_p.$$

(3)

Then, the classical likelihood function is the joint Bernoulli probability distribution of observed values of $Y_i$ as follows:

$$l\left({\beta }_o,\dots ,{\beta }_P;X_i\right)={\prod }_{i=1}^n\left[{\pi }_i{}^{Y_i}{\left(1-{\pi }_i\right)}^{1-Y_i}\right].$$

(4)

Taking logarithms of (4), and replacing with Expressions (1) and (2) we obtain:

$$l\left({\beta }_o,\dots ,{\beta }_P;X_i\right)={\sum }_{i=1}^n\left[Y_i\left(X_i\mathit{\beta }\right)-log\left(1+exp\left(X_i\mathit{\beta }\right)\right)\right].$$

(5)

Then Logistic regression estimates can be found by maximizing the log likelihood from (5) or minimizing the negative log likelihood function, which can be seen as a loss function to be minimized. Maximization is achieved by deriving $l\left({\beta }_o,\dots ,{\beta }_P;X_i\right)$ by all the P + 1 parameters, obtaining a vector of P + 1 partial derivate equation known as the score and denoted as $\stackrel{=}{\mathrm{l}}\left({\beta }_o,\dots ,{\beta }_P;X_i\right)$ (We denote $\prime$ to transpose vectors and matrices).

$$\stackrel{=}{\mathrm{l}}\left({\beta }_o,\dots ,{\beta }_P;X_i\right)=\left[\begin{array}{ccc}\frac{\partial l}{\partial {\beta }_o},& \dots & ,\frac{\partial l}{\partial {\beta }_P}\end{array}\right]\prime$$

(6)

However, when fitting a simple model like a Logistic regression, it is sometimes the case that many variables are not strongly associated with the response $Y_i,$ which lowers the classification accuracy of the model. That this problem can be improved with alternative fitting procedures such as constraining or shrinking (also known as regularization) before considering non-linear models was recognized by [53]. The idea is that complex models are sometimes built with irrelevant variables, but by shrinking coefficient estimates we manage to reduce variance, and thus the prediction error.

However, when complex models arise, the machine learning literature suggests imposing some degree of penalty on the Logistic regression so that the variables that contribute less are shrunk through a regularization procedure.

Ridge Logistic regression, shown in Algorithm 3, follows the dynamics of the Logistic regression, but the term $\mathsf{\lambda }{\left[{\sum }_{\mathrm{p}=1}^{\mathrm{P}}{\mathsf{\beta }}_{\mathrm{p}}\right]}^2$ known as the regularization penalty is added to the negative likelihood function, as in (4). Thus, covariates with a minor contribution are forced to be close to zero.

Algorithm 3. Ridge Logistic Regression.

1.  Minimizing the negative likelihood function: $L=-{\prod }_{i=1}^n{\pi }_i{}^{Y_i}{\left(1-{\pi }_i\right)}^{1-Y_i}$

2.  Penalizing: $L^{\ast }=-{\prod }_{i=1}^n{\pi }_i{}^{Y_i}{\left(1-{\pi }_i\right)}^{1-Y_i}$ +$\lambda {\left[{\sum }_{p=1}^P{\beta }_p\right]}^2.$

On the other hand, Lasso Logistic regression, shown in Algorithm 4, follows the dynamics of the Logistic regression, but a regularization penalty $\mathsf{\lambda }\left|{\sum }_{\mathrm{p}=1}^{\mathrm{P}}{\mathsf{\beta }}_{\mathrm{p}}\right|$ is added to the negative likelihood function. In this case, less contributive covariates are forced to be exactly zero. In both cases, $\mathsf{\lambda }$ is a shrinkage parameter, so the larger it is, the smaller the magnitude of the coefficient estimates [53].

Algorithm 4. Lasso Logistic Regression.

1.  Minimizing the negative likelihood function: $L=-{\prod }_{i=1}^n{\pi }_i{}^{Y_i}{\left(1-{\pi }_i\right)}^{1-Y_i}$

2.  Penalizing: $L^{\ast }=\hspace{1em}-{\prod }_{i=1}^n{\pi }_i{}^{Y_i}{\left(1-{\pi }_i\right)}^{1-Y_i}$ + $\lambda \left|{\sum }_{p=1}^P{\beta }_p\right|$.

2.3. Interpretable Machine Learning

Unlike statistical models in econometrics, machine learning algorithms are generally not self-explanatory. For example, generalized linear models provide coefficient estimates and their standard errors give information about the effect of covariates, whereas machine learning requires alternative methods to make the models understandable. Two popular approaches are described below.

Variable importance (VI), as proposed by [52], measures the influence of inputs on the variation of ${\widehat{Y}}_i$. We obtain the importance in a decision tree by summing the improvements in the loss function over all splits on a specific covariate $X_p$; in other words, variable importance is calculated by the node impurity weighted by the node probability (The node probability is calculated by the number of observations contained in that node of the tree divided by total number of observations). For ensemble techniques, the VI of all the trees that composed the ensemble is averaged.

Partial Dependence Plots (PDP) proposed by [51] show the marginal effect of a covariate $X_p$ on the prediction. The predicted function $\widehat{Y}$ is evaluated in certain values of the specific covariate $X_p$ while averaging over a range of values of all the other covariates.

3. The Rare Event Problem with RiskLogitboost Regression

The RiskLogitboost regression is an extension of Logitboost [33] that modifies the weighting procedure to improve the classification of rare events. It also adapts a bias correction from [54] in the boosting procedure, which is also applied to regression models such as those in [7,8,10].

To formally define the RiskLogitboost regression, we first describe briefly the Logitboost shown in Algorithm 5. It first initializes with ${\widehat{Y}}_i{}^0$= 0 and ${\pi }^0\left(X_i\right)=0.5$. Then the boosting procedure continues with four stages. The first one transforms the response. Logitboost also uses the exponential loss function $e^{Y_i{\widehat{Y}}_i}$ which is a quadratic approximation of ${\mathbf{\chi }}^{\mathbf{2}}$ and $z_i$ (transformed response) (see further details in Appendix A). The second stage involves calculating the weights by computing the variance of the transformed response $Var[z_i|X]$ (see further details in Appendix B). The third stage fits a least squares regression with response $z_i$. Finally, the fourth stage updates the prediction ${\widehat{Y}}_i{}^d$ and $\pi \left(X_i\right)$ by computing F$\left(X_{ip};u^d\right)$ as $X_i\mathit{\beta }$ for this particular case.

Algorithm 5. Logitboost

1. $\mathrm{Initial}\hspace{1em}\mathrm{values}:\hspace{1em}{\widehat{Y}}_i{}^0=0$,

$\hspace{1em}{\pi }^0\left(X_i\right)=0.5$$,\hspace{1em}\mathrm{where}\hspace{1em}\pi \left(X_i\right)$ are the probability estimates.

2. For d= 1 to D do:

2.1 $\mathrm{Transformation}:\hspace{1em}{z}_i^d=\frac{Y_i{}^{d-1}-\pi {\left(X_i\right)}^{d-1}}{\pi {\left(X_i\right)}^{d-1}\left(1-\pi {\left(X_i\right)}^{d-1}\right)}$

2.2 $\mathrm{Weighting}:\hspace{1em}{w}_i{}^d\hspace{1em}=\pi {\left(X_{i\hspace{1em}}\right)}^{d-1}\hspace{1em}\left(1-\pi {\left(X_i\right)}^{d-1}\right)$

2.3 $\mathrm{Minimizing}:\hspace{1em}{\beta }^d$$\hspace{1em}=\hspace{1em}argmi{n}_{\beta }{\sum }_{i=1}^n{w}_i{}^d{\left[z_i^d-\left({\beta }_o+{\sum }_{p=1}^P{X}_{ip}{\beta }_p\right)\right]}^2$

2.4 $\mathrm{Updating}:\hspace{1em}{\widehat{Y}}_i{}^d={\widehat{Y}}_i{}^{d-1}+\frac{1}{2}$ $F\left(X_{ip};u^d\right),$ and

$\pi {\left(X_i\right)}^d$ = $\frac{exp\left({\widehat{Y}}_i{}^{d-1}\right)}{exp\left({\widehat{Y}}_i{}^{d-1}\right)+exp\left(-{\widehat{Y}}_i{}^{d-1}\right)}$

3. End for

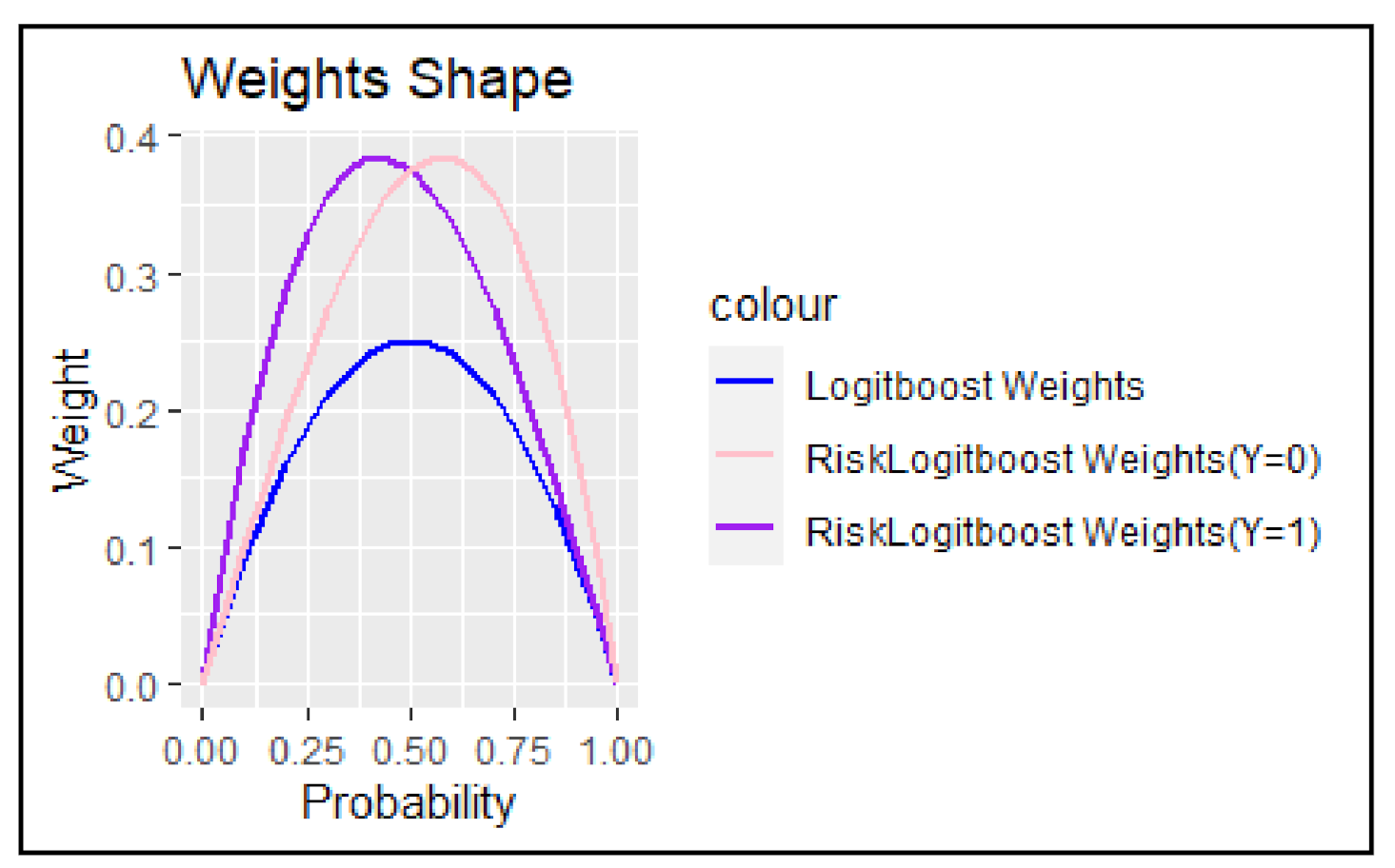
3.1. RiskLogitboost Regression Weighting Mechanism to Improve Rare-Class Learning

We propose a weighting mechanism that might be considered as a mixed case of oversampling and undersampling. The main idea is to overweight observations whose estimated probability $\pi \left(X_i\right)$ is further from the observed value $Y_i$, in other words, observations that are more likely to be misclassified. The new majority class observations are interpolated through a threshold that determines the calibration of weights. The proposed weighting mechanism takes the following form:

$$w_i^{\ast }\hspace{1em}=\hspace{1em}\left\{\begin{array}{c}[\pi \left(X_i\right)\left(1-\pi \left(X_i\right)\right]\left(1+\left|Y_i-\pi \left(X_i\right)\right|\right);\hspace{1em}if\hspace{1em}\left|Y_i-\pi \left(X_i\right)\right|>\overline{Y}\\ [\pi \left(X_i\right)\left(1-\pi \left(X_i\right)\right]\left(1-\left|Y_i-\pi \left(X_i\right)\right|\right);\hspace{1em}if\left|Y_i-\pi \left(X_i\right)\right|\le \overline{Y}\hfill \end{array}\right.$$

The original weights $w_i$ of the Logitboost are now multiplied by a factor $\left(1\pm \left|Y_i-\pi \left(X_i\right)\right|\right)$ that is related to the distance between $Y_i$ and $\pi \left(X_i\right)$.

Figure 1 shows the relationship between weights according to the estimated probabilities of the Logitboost and the RiskLogitboost regression. Logitboost overweights observations whose estimated probability is around 0.5 and then decreases gradually and symmetrically on either side. The result of the weighting mechanism in the RiskLogitboost regression shows that low estimated probabilities are overweighted when $Y_i$ = 1 while high estimated probabilities are underweighted when $Y_i$ = 0. In Figure 1 we show that, once the weighting mechanism is transformed, we maintain the u–inverted shape for Y = 1 and Y = 0.

Refs. [9,26,55,56] proposed weighting mechanisms for parametric and non-parametric models to improve the predictive performance of imbalanced and rare data.

3.2. Bias Correction with Weights

Bias correction will lead to a lower root mean square error. Ref. [54] proposed a bias correction method and showed that the bias of the coefficient estimators for any generalized model can be computed as ${\left(X^{\prime }WX\right)}^{-1}{X}^{\prime }W\mathsf{\aleph }$, where $W$ is the diagonal matrix of $w_i$. However, we propose replacing $w_i$ by $w_i^{\ast }$ since the behaviour, and therefore the bias, for the RiskLogitboost is computed as ${\left(X^{\prime }{W}^{\ast }X\right)}^{-1}X\prime W^{\ast }\mathsf{\aleph }$.

The factor $\mathsf{\aleph }$ equals $Q_{ii}\left({\pi }^D\left(X_i\right)-0.5\right)$, where $Q_{ii}$ is the diagonal elements of the Fisher information matrix denoted as Q. The matrix Q measures the amount of information that matrix $X$ carries about the parameters; in other words, it is the variance of the gradient of the log-likelihood function with respect to the parameter vector known as the score.

$Q_{rk}$ is the Fisher information matrix for two arbitrary generic parameters: ${\beta }_k$ and ${\beta }_r$.

$$Q_{rk}=-E\left(\frac{{\partial }^{2}lnl\left({\beta }_o,\dots ,{\beta }_k,\dots ,{\beta }_r,\dots ,{\beta }_P;X_i\right)}{\partial {\beta }_r{\beta }_k}\right).$$

(7)

Now let us take the partial derivative of $l\left({\beta }_o,\dots ,{\beta }_P;X_i\right)$ in (5) with respect to ${\beta }_k$.

$$\frac{\partial l}{\partial {\beta }_k}={\sum }_{i=1}^n{Y}_i\frac{\partial l}{\partial {\beta }_k}\left(X\mathit{\beta }\right)-\frac{\partial l}{\partial {\beta }_k}log\left(1+exp\left(X\mathit{\beta }\right)\right),$$

(8)

where

$$\frac{\partial l}{\partial {\beta }_k}\left(X_i\mathit{\beta }=X_{ik}\right)$$

(9)

and

$$\frac{\partial l}{\partial {\beta }_k}log\left(1+exp\left(X_i\mathit{\beta }\right)\right)=\frac{exp\left(X\mathit{\beta }\right)}{1+exp\left(X\mathit{\beta }\right)}\frac{\partial l}{\partial {\beta }_k}\left(X_i\mathit{\beta }\right)$$

$$\frac{\partial l}{\partial {\beta }_k}log\left(1+exp\left(X\mathit{\beta }\right)\right)={\pi }_i{X}_{ik}.$$

(10)

Considering (9) and (10), we obtain:

$$\frac{\partial l}{\partial {\beta }_k}={\sum }_{i=1}^n{Y}_i{X}_{ik}-{\pi }_i{X}_{ik}.\hspace{1em}$$

(11)

Now, let us compute the second derivative of (8) with respect to ${\beta }_r$.

$$\frac{{\partial }^{2}l}{\partial {\beta }_k{\beta }_r}=\frac{\partial }{\partial {\beta }_r}\frac{\partial l}{\partial {\beta }_k}$$

$$\frac{{\partial }^{2}l}{\partial {\beta }_k{\beta }_r}={\sum }_{i=1}^n{X}_{ik}\left(Y_i-\frac{\partial }{\partial {\beta }_r}\left({\pi }_i\right)\right)$$

(12)

And,

$$\frac{\partial }{\partial {\beta }_r}\left({\pi }_i\right)=\frac{exp\left(X_i\mathit{\beta }\right)\frac{\partial }{\partial {\beta }_r}\left(X_i\mathit{\beta }\right)\left(1+exp(X_i\mathit{\beta })\right)-exp\left(X_i\mathit{\beta }\right)exp\left(X_i\mathit{\beta }\right)\frac{\partial }{\partial {\beta }_r}\left(X_i\mathit{\beta }\right)\hspace{1em}}{{\left(1+exp(X_i\mathit{\beta })\right)}^2}$$

$$\frac{\partial }{\partial {\beta }_r}\left({\pi }_i\right)={\pi }_i{X}_{ir}\left(1-{\pi }_i\right).$$

(13)

Plugging (13) into (12):

$$\frac{{\partial }^{2}l}{\partial {\beta }_k{\beta }_r}=-{\sum }_{i=1}^n{X}_{ik}{X}_{ir}{\pi }_i\left(1-{\pi }_i\right)$$

(14)

Recall that Var ($Y_i$) = ${\pi }_i(1-{\pi }_i$), since $Y_i$ follows a Bernoulli distribution and coincides with vector $w_i$ (second stage of Algorithm 5). However, the new RiskLogitboost replaces $w_i$ with $w_i^{\ast }$ again in Equation (14).

If we generalize expression (14) for all P parameters, we obtain:

$$\frac{{\partial }^{P}l}{\partial {\beta }_{1,\dots ,}{\beta }_P}=X^{\prime }{W}^{\ast }X,$$

(15)

where $W^{\ast }$ is the diagonal matrix of $w_i^{\ast }$. Equation (15) is a variance-covariance matrix. Thus, Q is expressed as an n_xn symmetric matrix:

$$Q=X{\left(X^{\prime }{W}^{\ast }X\right)}^{-1}{X}^{\prime }.$$

(16)

Finally, each transformed parameter is computed as ${\beta }_{RiskLogitboost}$ = ${\beta }^D$–${\left(X^{\prime }WX\right)}^{-1}{X}^{\prime }W\mathsf{\aleph }$.

3.3. RiskLogitboost Regression

The RiskLogitboost regression (Algorithm 6) modifies the original version of Logitboost to improve the classification of the rare events (ones). This algorithm comprises 11 stages. The first states the initial values of the prediction ${\widehat{Y}}_i$ and probability $\pi \left(X_i\right)$.

The second obtains the transformed answer as explained in Algorithm 5. In the third stage we compute ${\widehat{Y}}_i{}^d=\frac{1}{2}log\frac{\pi {\left(X_i\right)}^{d-1}}{\left(1-\pi {\left(X_i\right)}^{d-1}\right)}$, which is the value that minimizes a negative binomial log-likelihood loss function: $log\left(1+exp\left(-2Y_i{\widehat{Y}}_i\right)\right)$ used for two-class classification and regression problems. However, ${\widehat{Y}}_i$ also minimize the exponential loss function $e^{-Y_i{\widehat{Y}}_i}$ used in Logitboost [33]. Therefore, the exponential loss function approximates the log-likelihood denoted as transformed answer $z_i,$ as explained in Algorithm 5.

The fourth stage computes the weights that were explained in detail in Section 3.1. The fifth stage normalizes the weights of the previous stage so as to convert them into a distribution that must add up to 1.

The fifth stage consists of fitting a weighted linear regression to $z_i^d$ and obtaining the P + 1 parameters $\beta$. Perhaps the constant ${\beta }_0$ is computed by setting $X_p$ to a vector of ones. As proposed in the original Logitboost, the sixth stage updates the final prediction ${\widehat{Y}}_i{}^d$ to fit the model by maximum likelihood using Newton steps as follows:

We update the prediction ${\widehat{Y}}_i$ + $F\left(X_{ip};u^d\right)$, where $u$ corresponds to parameters $\mathit{\beta }$. The outcome of $F\left(X_{ip};u^d\right)$ would be $X_i\mathit{\beta }$ in a logistic regression with ${\pi }_i$ expressed in (1), which is $exp\left(2F\left(X_{ip};u^d\right)\right)$, as follows:

$${\pi }_i=\frac{exp\left(2F\left(X_{ip};u^d\right)\right)}{1+exp\left(2F\left(X_{ip};u^d\right)\right)}$$

$${\pi }_i=\frac{exp\left(2X_i\mathit{\beta }\right)}{1+exp\left(2X_i\mathit{\beta }\right)}.$$

(17)

Recalling $l\left({\beta }_o,\dots ,{\beta }_P;X_i\right)$ from (5), we compute the expected log-likelihood of ${\widehat{Y}}_i$ + $F\left(X_{ip};u^d\right)$.

$$E\left[l\left({\widehat{Y}}_i+F\left(X_{ip};u^d\right)\right)\right]={\sum }_{i=1}^{n}2Y_i\left({\widehat{Y}}_i+F\left(X_{ip};u^d\right)\right)-log\left(1+2exp\left({\widehat{Y}}_i+F\left(X_{ip};u^d\right)\right)\right).$$

(18)

The Newton method for minimizing a strictly convex function requires the first and second derivatives. Let g be the first derivative and H be the second derivative, also known as the Hessian matrix.

$$g=\frac{\partial E\left[l\left({\widehat{Y}}_i+F\left(X_{ip};u^d\right)\right)\right]}{\partial F\left(X_{ip};u^d\right)}$$

$$g=2E(Y_i-{\pi }_i)$$

(19)

$$H=\frac{{\partial }^{2}E\left[l\left({\widehat{Y}}_i+F\left(X_{ip};u^d\right)\right)\right]}{\partial F{\left(X_{ip};u^d\right)}^2}$$

$$=-4E({\pi }_i\left(1-{\pi }_i\right)$$

(20)

Hence,

$${\widehat{Y}}_i={\widehat{Y}}_i-H^{-1}g$$

$${\widehat{Y}}_i\hspace{1em}=\hspace{1em}{\widehat{Y}}_i+\frac{1}{2}E\left(\frac{Y_i-{\pi }_i}{{\pi }_i\left(1-{\pi }_i\right)}\right)$$

(21)

This result is a very close approximation of the iteratively reweighted least squares method (Appendix A, Equation (A2)) to the likelihood shown in (5). The key difference is the factor ½ that multiplies the expected value. The seventh stage consists of checking that probabilities are bounded between 0 and 1, since adding a $\delta$ might lead to a number larger than 1.

The eighth stage consists of inverting $\frac{1}{2}log\frac{\pi {\left(X_i\right)}^{d-1}}{\left(1-\pi {\left(X_i\right)}^{d-1}\right)}$ (explained in the third stage), which yields the probability estimates. Once the iterative process is finished, we obtain the coefficient estimates of iteration D in stage nine through the expression suggested by [57,58]. Last but not least, we obtain $\beta$* by subtracting ${\beta }^D$–bias.

Algorithm 6. RiskLogitboost regression

1. $\mathrm{Initial} \mathrm{values}: {\widehat{Y}}_i{}^0$ = 0,

${\pi }^0\left(X_{i }\right)= 0.5$$, \mathrm{where} \pi \left(X_{i }\right)$ are the probability estimates.

2. For d = 1 to D do:

2.1 $\mathrm{Transformation}: z_i^d= \frac{Y_i{}^{d-1} -\pi {\left(X_{i }\right)}^{d-1}}{\pi {\left(X_{i }\right)}^{d-1}\left(1-\pi {\left(X_{i }\right)}^{d-1}\right)+\delta }$$, \mathrm{where} \delta =0.0001$

2.2 $\mathrm{Population} \mathrm{Minimizer}: {\widehat{Y}}_i{}^d= \frac{1}{2}log\frac{\pi {\left(X_{i }\right)}^{d-1}}{\left(1-\pi {\left(X_{i }\right)}^{d-1}\right)}$

2.3 $\mathrm{Weighting}: w_i{}^{\ast d}=\left\{\begin{array}{c}[\pi \left(X_{i }\right)\left(1-\pi \left(X_{i }\right)\right]\left(1+\left|Y_i-\pi \left(X_{i }\right)\right|\right) ;if \left|Y_i-\pi \left(X_{i }\right)\right|>\overline{Y}\\ \left[\pi \left(X_{i }\right)\left(1-\pi \left(X_{i }\right)\right]\right[1-\pi \left(X_{i }\right)] ;if \left|Y_i-\pi \left(X_{i }\right)\right|\le \overline{Y}\hfill \end{array}\right.$

2.4 $\mathrm{Normalizing}: w_i{}^d=\frac{w_i{}^{\ast d}}{{\sum }_{i=1}^n{w}_i{}^{\ast d}}$

2.5 $\mathrm{Minimizing}: {\beta }^d$$= argmi{n}_{\beta }{\sum }_{i=1}^n{w}_i{}^d {\left[z_i^d- \left({\beta }_o+{\sum }_{p=1}^P{X}_{ip}{\beta }_p\right)\right]}^2$

2.6 $\mathrm{Updating} \mathrm{prediction}: {\widehat{Y}}_i{}^d= {\widehat{Y}}_i{}^{d-1}+ \frac{1}{2}$$F\left(X_{ip} ;u^d\right)$.

2.7 $\mathrm{Checking} \mathrm{probabilities}: \pi {\left(X_{i }\right)}^d=\min \left\{\frac{1}{1+exp \left(-2{\widehat{Y}}_i{}^{d-1}\right) }+ \delta , 1\right\}$

3. End For

4. $\mathrm{Converting}: {\pi }^d(Y_{i }=1|X_{ })= \frac{1}{1+exp \left(-2{\widehat{Y}}_i{}^{d-1}\right) }$

${\pi }^d(Y_{i }=0|X_{ })= \frac{1}{1+exp \left(2{\widehat{Y}}_i{}^{d-1}\right) }$

5. $\mathrm{Obtaining} \mathrm{the} P \mathrm{Parameters}: {\beta }_p^D= \frac{{\sum }_{i=1}^n\left(X_p{}^D{z}_i^D\right)}{{\sum }_{i=1}^n{\left(X_p{}^D\right)}^2}$$, \forall$ p = 1, …, P.

6. Correcting Bias: $\beta \ast = {\beta }^D$$- {\left(X_i^{\prime }{w}_i{X}_{i }\right)}^{-1}{X}_i^{\prime }{w}_i{\mathsf{\aleph }}_i$.

4. Illustrative Data

The illustrative data set used for testing classical and alternative machine learning algorithms is a French third-party liability motor insurance data set available from [59] through publicly available data sets in the library CASdatasets in R. It contains 413,169 observations that were recorded mostly in one year about risk factors for third-party liability motor policies.

This data set contains the following information about vehicle characteristics: The power of the car ordered by category (Power); the car brand divided into seven categories (Brand); the fuel type, either diesel or regular (Gas). This data set also includes information about the policy holder’s characteristics such as: the policy region in France based on the 1970–2015 classification (Region); the number of inhabitants per km² in the city in which the driver resides (Density). More information is included about the policy holders’ characteristics: the car age measured in years (Car age); and the driver’s age (Driver Age). Finally, the occurrence of accident claims $Y_i$ is coded as 1 if the policy holder had suffered at least one accident, and otherwise coded as 0. A total of 3.75% of policy holders had reported at least one accident (rare event ratio).

5. Discussion of Results

This section first presents the predictive performance of some machine learning algorithms jointly with the RiskLogitboost regression when Y = 1 in the extreme observations; secondly, this section shows that the model is interpretable through the coefficient estimates.

5.1. Predictive Performance of Extremes

Table 1. Root Mean Square Error (RMSE) for observations with Y = 1.

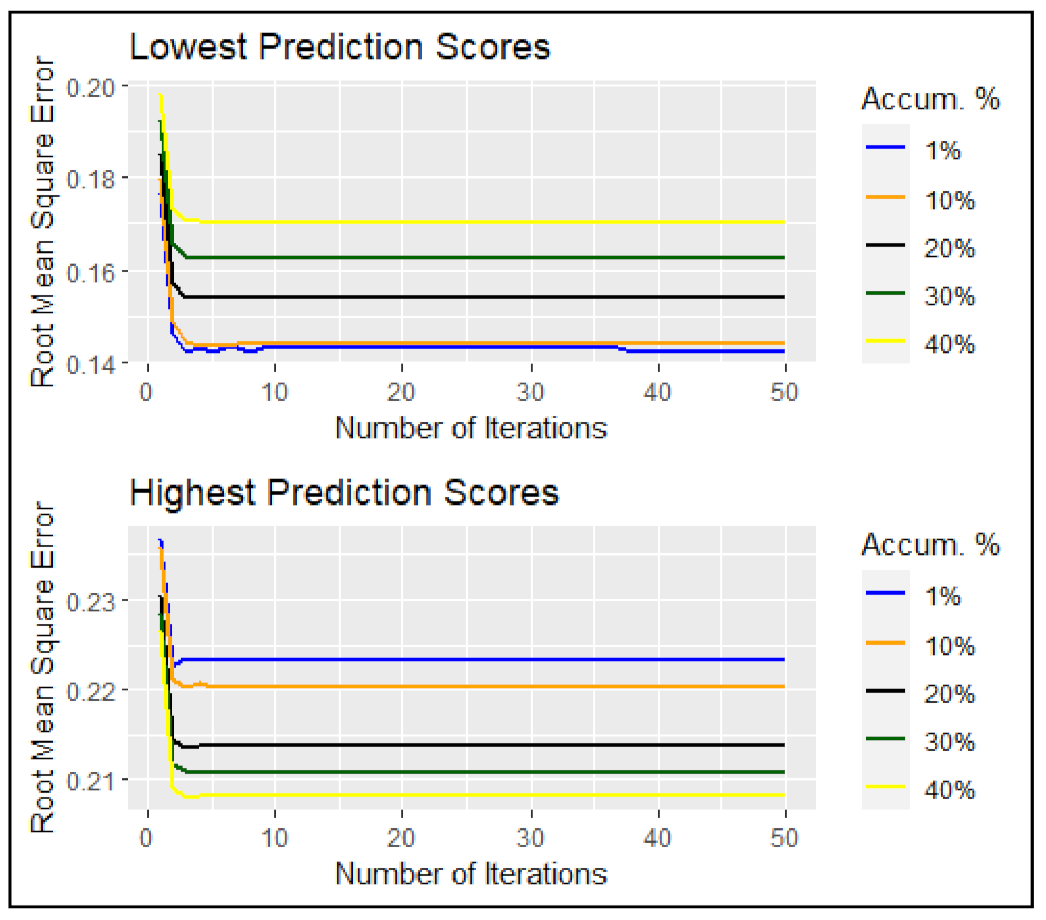
Training Data Set (RMSE Y = 1)
	Lower Extreme						Upper Extreme
	0.01	0.05	0.10	0.20	0.3	0.4	0.01	0.05	0.10	0.20	0.3	0.4
RiskLogitboost regression	0.2454	0.1825	0.1496	0.1132	0.0927	0.0803	0.0000	0.0000	0.0000	0.0000	0.0000	0.0000
Ridge Logistic	0.9629	0.9629	0.9629	0.9629	0.9628	0.9628	0.9627	0.9627	0.9627	0.9627	0.9627	0.9627
Lasso Logistic	0.9628	0.9628	0.9628	0.9628	0.9628	0.9628	0.9628	0.9628	0.9628	0.9628	0.9628	0.9628
Boosting Tree	0.9787	0.9747	0.9727	0.9700	0.9679	0.9665	0.9162	0.9293	0.9417	0.9495	0.9522	0.9539
Logitboost	0.9829	0.9799	0.9781	0.9736	0.9707	0.9688	0.9416	0.9479	0.9505	0.9530	0.9545	0.9557
SMOTEBoost	0.6963	0.6901	0.6852	0.6800	0.6761	0.6725	0.6046	0.6090	0.6117	0.6178	0.6222	0.6264
RUSBoost	0.5811	0.5742	0.562	0.5517	0.5447	0.5391	0.4466	0.4727	0.4853	0.4931	0.4970	0.5001
WLR	0.9992	0.9982	0.9973	0.9961	0.9950	0.9939	0.4788	0.7092	0.7961	0.8676	0.8996	0.9183
PLR (PSWa)	0.9992	0.9982	0.9973	0.9961	0.9950	0.9939	0.4788	0.7092	0.7961	0.8676	0.8996	0.9183
PLR (PSWb)	0.9820	0.9790	0.9771	0.9725	0.9697	0.9678	0.9407	0.9470	0.9496	0.9520	0.9536	0.9547
SyntheticPL	0.9830	0.9803	0.9783	0.9736	0.9708	0.9689	0.9380	0.9467	0.9497	0.9523	0.9540	0.9552
WeiLogRFL	0.3696	0.2860	0.2386	0.1826	0.1498	0.1297	0.0000	0.0000	0.0000	0.0000	0.0000	0.0000
Testing Data Set (RMSE Y = 1)
	Lower Extreme						Upper Extreme
	0.01	0.05	0.10	0.20	0.3	0.4	0.01	0.05	0.10	0.20	0.3	0.4
RiskLogitboost regression	0.4690	0.3725	0.3133	0.2421	0.1991	0.1724	0.0000	0.0000	0.0000	0.0000	0.0000	0.0000
Ridge Logistic	0.9629	0.9629	0.9629	0.9629	0.9628	0.9628	0.9627	0.9627	0.9627	0.9627	0.9627	0.9627
Lasso Logistic	0.9628	0.9628	0.9628	0.9628	0.9628	0.9628	0.9628	0.9628	0.9628	0.9628	0.9628	0.9628
Boosting Tree	0.9788	0.9750	0.9731	0.9705	0.9683	0.9669	0.9156	0.9297	0.9424	0.9498	0.9525	0.9542
Logitboost	0.8745	0.8723	0.8710	0.8688	0.8674	0.8665	0.8558	0.8577	0.8586	0.8595	0.8601	0.8606
SMOTEBoost	0.6959	0.6901	0.6854	0.6801	0.6762	0.6727	0.6042	0.6088	0.6116	0.6180	0.6226	0.6270
RUSBoost	0.5781	0.5600	0.5515	0.5425	0.5358	0.5312	0.4434	0.4539	0.4727	0.4858	0.4913	0.4948
WLR	0.9993	0.9982	0.9973	0.9961	0.9950	0.9938	0.4523	0.7057	0.7959	0.8664	0.8989	0.9178
PLR (PSWa)	0.9993	0.9982	0.9973	0.9961	0.9950	0.9938	0.4523	0.7057	0.7959	0.8664	0.8989	0.9178
PLR (PSWb)	0.9822	0.9792	0.9773	0.9729	0.9700	0.9681	0.9409	0.9471	0.9497	0.9522	0.9537	0.9549
SyntheticPL	0.8745	0.8721	0.8708	0.8686	0.8673	0.8664	0.8559	0.8577	0.8587	0.8596	0.8602	0.8607
WeiLogRFL	0.4690	0.3725	0.3133	0.2421	0.1991	0.1724	0.0000	0.0000	0.0000	0.0000	0.0000	0.0000

The results are presented for observations that correspond to policy holders who suffered an accident (Y = 1). All results were analyzed by groups of prediction scores, also known as predicted probabilities. Each RMSE for 1%, 5%, 10%, 20%, 30% and 40% of the lowest accumulated prediction scores is shown on the left-hand side of the table under “Lower Extreme”, and each RMSE for 1%, 5%, 10%, 20%, 30% and 40% of the highest accumulated prediction scores is shown on the right-hand side of the table under “Upper Extreme”. Abbreviations: WLR (Weighted Logistic Regression) [26], PLR (Penalized Logistic regression for complex surveys), with two weighting mechanisms PSWa and PSWb [9]. SyntheticPL (Synthetic Penalized Logitboost) [56], WeiLogRFL (Weighted Logistic) of [10].

and

Table 2. Root Mean Square Error (RMSE) for observations with Y = 0.

Training Data Set (RMSE Y = 0)
	Lower Extreme						Upper Extreme
	0.01	0.05	0.10	0.20	0.3	0.4	0.01	0.05	0.10	0.20	0.3	0.4
RiskLogitboost regression	0.7508	0.8219	0.8605	0.9062	0.9352	0.9514	1.0000	1.0000	1.0000	1.0000	1.0000	1.0000
Ridge Logistic	0.0371	0.0371	0.0371	0.0371	0.0371	0.0372	0.0373	0.0373	0.0373	0.0373	0.0373	0.0373
Lasso Logistic	0.0372	0.0372	0.0372	0.0372	0.0372	0.0372	0.0372	0.0372	0.0372	0.0372	0.0372	0.0372
Boosting Tree	0.0197	0.0221	0.0247	0.0273	0.0294	0.0313	0.0773	0.0583	0.0513	0.0470	0.0451	0.0436
Logitboost	0.0157	0.0188	0.0202	0.0227	0.0264	0.0289	0.0574	0.0510	0.0485	0.0460	0.0445	0.0434
SMOTEBoost	0.2978	0.3070	0.3116	0.3171	0.3206	0.3240	0.3958	0.3909	0.3865	0.3797	0.3752	0.3704
RUSBoost	0.4219	0.4403	0.4488	0.4579	0.4646	0.4692	0.5566	0.5463	0.5281	0.5149	0.5094	0.5058
WLR	0.0008	0.0020	0.0029	0.0043	0.0055	0.0067	0.5230	0.3106	0.2356	0.1733	0.1433	0.1250
PLR (PSWa)	0.0008	0.0020	0.0029	0.0043	0.0055	0.0067	0.5230	0.3106	0.2356	0.1733	0.1433	0.1250
PLR (PSWb)	0.0166	0.0198	0.0212	0.0237	0.0274	0.0299	0.0582	0.0519	0.0495	0.0470	0.0455	0.0444
SyntheticPL	0.0157	0.0183	0.0198	0.0225	0.0262	0.0287	0.0601	0.0521	0.0493	0.0466	0.0450	0.0439
WeiLogRFL	0.6258	0.7202	0.7758	0.8467	0.8945	0.9212	1.0000	1.0000	1.0000	1.0000	1.0000	1.0000
Testing Data Set (RMSE Y = 0)
	Lower Extreme						Upper Extreme
	0.01	0.05	0.10	0.20	0.3	0.4	0.01	0.05	0.10	0.20	0.3	0.4
RiskLogitboost regression	0.5446	0.6488	0.7134	0.7988	0.8598	0.8957	1.0000	1.0000	1.0000	1.0000	1.0000	1.0000
Ridge Logistic	0.0374	0.0374	0.0374	0.0374	0.0374	0.0374	0.0374	0.0374	0.0374	0.0374	0.0374	0.0374
Lasso Logistic	0.0372	0.0372	0.0372	0.0372	0.0372	0.0372	0.0372	0.0372	0.0372	0.0372	0.0372	0.0372
Boosting Tree	0.0197	0.0220	0.0246	0.0272	0.0293	0.0312	0.0774	0.0583	0.0512	0.0470	0.0451	0.0436
Logitboost	0.1247	0.1269	0.1279	0.1295	0.1311	0.1322	0.1440	0.1420	0.1411	0.1401	0.1395	0.1390
SMOTEBoost	0.2976	0.3069	0.3116	0.3171	0.3206	0.3240	0.3959	0.3909	0.3865	0.379	0.375	0.3705
RUSBoost	0.4189	0.4259	0.4383	0.4487	0.4558	0.4614	0.5534	0.5280	0.5154	0.5074	0.5034	0.5003
WLR	0.0009	0.0020	0.0029	0.0043	0.0055	0.0067	0.5294	0.3119	0.2364	0.1738	0.1438	0.1254
PLR (PSWa)	0.0008	0.0020	0.0029	0.0043	0.0055	0.0067	0.5230	0.3106	0.2356	0.1733	0.1433	0.1250
PLR (PSWb)	0.0167	0.0198	0.0212	0.0236	0.0273	0.0298	0.0582	0.0519	0.0495	0.0470	0.0455	0.0444
SyntheticPL	0.1247	0.1271	0.1283	0.1298	0.1313	0.1323	0.1438	0.1418	0.1409	0.1400	0.1394	0.1389
WeiLogRFL	0.5446	0.6488	0.7134	0.7988	0.8598	0.8957	1.0000	1.0000	1.0000	1.0000	1.0000	1.0000

The results are presented for observations that correspond to policy holders who did not suffer an accident (Y = 0). All results were analyzed by groups of prediction scores also known as predicted probabilities. So, eEach RMSE for 1%, 5%, 10%, 20%, 30% and 40% of the lowest accumulated prediction scores is shown on the left-hand side of the table under “Lower Extreme”, and each RMSE for 1%, 5%, 10%, 20%, 30% and 40% of the highest accumulated prediction scores is shown on the right-hand side of the table under “Upper Extreme”. Abbreviations: WLR (Weighted Logistic Regression) [26], PLR (Penalized Logistic regression for complex surveys), with two weighting mechanisms PSWa and PSWb [9]. SyntheticPL (Synthetic Penalized Logitboost) [56]. WeiLogRFL (Weighted Logistic) of [10].

show the Root Mean Square Error (RMSE) for observations when Y = 1 and Y = 0, respectively. Even though the Boosting Tree has optimized hyperparameters, it produced a larger error than all other methods when Y = 1 (The Boosting Tree is built with 10-fold cross validation and has optimized hyperparameters through grid search which correspond to the number of trees (50), the maximum depth of variable interactions (1), the minimum number of observations in the terminal nodes of the trees (10), and shrinkage (0.1) with the caret package in R; the Lasso and Ridge Logistic models had the lowest deviance among several trials with shrinkage values). This can be attributed to the fact that high predictive performance algorithms such as tree-based methods reduce the global error, which is mainly influenced by the majority class (usually coded as 0) when data are imbalanced. Thus, observations modelled using this type of method show high levels of error when Y = 1. This means that the riskiest observations (with misclassifications costs) are poorly detected, and observations whose probability is not high enough are more likely to be misclassified.

The RiskLogitboost regression had the lowest error for observations whose estimated probability was in the lower extremes. This is an important result since the proportion of cases for this set of observations usually tends to be underestimated by traditional predictive modeling techniques. Moreover, the RiskLogitboost regression perfectly predicted observations whose estimated probability was in the highest extremes, suggesting that observations that are more likely to belong to the rare event (Y = 1) will never be misclassified. From a risk analysis perspective, this is a valuable achievement since it reduces misclassification costs for this group.

Observations classified with SMOTEBoost and RUSBoost outperform Logitboost, Ridge Logistic, Lasso Logistic, and Boosting Tree; however, their predictive performance is still below that of the RiskLogitboost regression. Even though the SMOTEBoost and RUBoost are designed to handle imbalance data sets, RiskLogitboost seems to be more efficient at detecting rare events.

Similar performance is obtained between the Weighted Logistic Regression (WLR) [26], Penalized Logistic regression for complex surveys (PLR), with the two weighting mechanisms PSWa and PSWb [9], and SyntheticPL (Synthetic Penalized Logitboost) [56]. Both WLR and PLR with PSWa provide exactly the same result because the PLR incorporates the sampling design, as well as a resampling correction. The sampling correction of both methods coincide when data are simple random samples. RiskLogitboost still outperforms these modern methods for imbalanced and rare event data. The Weighted Logistic for rare events (WeiLogRFL) [10] might be considered as the second best. In contrast, when Y = 0 the Boosting Tree, Ridge Logistic regression and Lasso Logistic had a lower RMSE than the RiskLogitboost regression. These three methods classify the non-events (Y = 0) accurately whereas the RiskLogitboost regression tends to underestimate their occurrence. The results obtained by the RiskLogitboost are quite close to the WeiLogRFL. Moreover, WLR, RLR and boosting tree obtained the lowest RMSE of highest and lowest prediction scores. SyntheticPL outperforms RUSBoost and SMOTEBoost, even though its purpose improves the predictive performance of imbalanced data.

The results when Y = 1 also showed that Logitboost was superior, in predictive capacity terms, to the Ridge Logistic regression, Lasso Logistic regression and Boosting Tree in the testing data set. In this particular case, the Ridge Logistic regression and Lasso Logistic performed similarly in the training data set.

Figure 2 shows the highest and lowest prediction scores for all observed response Y. The RiskLogitboost regression started with higher levels of RMSE in the first iterations, after which they decreased until becoming stable. The RMSE did not vary from the fortieth iteration onwards. As a result, we were able to maintain the convergence process since the proposed transformation for the weighting procedure (Section 3.1) achieved identical stability to that of the original Logitboost.

5.2. Interpretable RiskLogitboost Regression

Table 3. Coefficient Estimates, Standard Error and Confidence Intervals provided by the RiskLogitboost regression.

Variables	Categories	RiskLogitboost Regression	RiskLogitboost Regression (Standard Error)	RiskLogitboost Regression (Confidence Intervals)
	* Intercept	20.874	7.4130	(6.3445; 35.4035)
Power	e	−0.6527	3.5641	(−7.6383; 6.3329)
	f	−1.3379	3.4769	(−8.1526; 5.4768)
	g	−0.8003	3.4506	(−7.5635; 5.9629)
	h	4.9061	4.9344	(−4.7653; 14.578)
	i	7.8770	5.4611	(−2.8268; 18.5808)
	j	8.0675	5.5682	(−2.8462; 18.9812)
	* k	18.1880	7.1178	(4.2371; 32.1389)
	* l	45.3320	1.0540	(43.2662; 47.3978)
	* m	99.6840	1.5136	(96.7173; 102.6507)
	* n	144.1900	1.7590	(140.7424; 147.6376)
	* o	145.8000	17.6033	(111.2975; 180.3025)
Brand	Japanese (except Nissan) or Korean	−7.6774	5.7732	(−18.9929; 3.6381)
	Mercedes, Chrysler or BMW	−2.0130	6.7667	(−15.2757; 11.2497)
	Opel, General Motors or Ford	−6.5298	5.7170	(−17.7351; 4.6755)
	other	8.2048	7.9329	(−7.3437; 23.7533)
	* Renault, Nissan or Citroen	−10.3760	4.9954	(−20.1669; −0.5850)
	Volkswagen, Audi, Skoda or Seat	−5.5055	5.8621	(−16.9952; 5.9842)
Region	Basse-Normandie	10.279	7.1850	(−3.8036; 24.3616)
	Bretagne	−3.4953	4.9434	(−13.1844; 6.1938)
	Centre	−6.5749	4.2924	(−14.9880; 1.8382)
	* Haute-Normandie	27.6060	9.3055	(9.3672; 45.8448)
	Ile-de-France	−4.1033	5.12264	(−14.1437; 5.9371)
	* Limousin	34.5520	10.0028	(14.9465; 54.1575)
	Nord-Pas-de-Calais	0.0897	5.7443	(−11.1691; 11.3485)
	Pays-de-la-Loire	−2.7310	5.0910	(−12.7094; 7.2474)
	Poitou-Charentes	2.4523	5.9926	(−9.2932; 14.1978)
	Density	0.0003	0.00025	(−0.0003; 0.0009)
	Gas Regular	0.0187	2.1895	(−4.2727; 4.3101)
	Car Age	0.1053	0.1969	(−0.2806; 0.4912)
	Driver Age	0.0217	0.0712	(−0.1179; 0.1613)

The base category is other for the covariates Power, Brand and Region, and diesel for the covariate Gas. * Indicates that the coefficient is significant at the 95% confidence level. The standard error (se) root square of the diagonal of the variance-covariance matrix was computed as ${\left(X_i^{\prime }{w}_i{}^D{X}_i\right)}^{-1}$. We built a 95% confidence interval for β as [β − 1.96 se; β + 1.96 se].

presents the coefficient estimates, standard errors and confidence intervals obtained by the RiskLogitboost regression. Due to the design and the way of fitting the RiskLogitboost regression, similar to generalized linear models (i.e., logistic regression) as fully explained in Section 3, we may obtain the odds ratio by exponentiating the estimated coefficient estimates.

The results provided by the RiskLogitboost regression suggest that the likelihood of a policy holder having an accident increased if they had e, k, l, m, n, o type Power vehicle; in particular, drivers with o–type Power were the most likely to have an accident among all types of Power.

The policy holder was more likely to have an accident if they drove in the Regions of Haute-Normandie and Limousin, whereas driving in the Regions of Bretagne, Centre, Haute Normandie, Ile de France, Pays de la Loire, Basse Normandie, Nord Pas de Calais and Poitou Charentes did not influence the likelihood of a person having an accident.

Policy holders driving Renault, Nissan or Citroen cars were less likely to have an accident than those driving other brands of car.

As expected, the Lasso Logistic regression shrunk all coefficients to zero except the one corresponding to the intercept; in this sense, this method is not informative and is actually disadvantageous for analyzing the effects. The Ridge Logistic Regression provided a very small magnitude of the coefficient estimates, and overall the covariates in the Ridge Logistic regression seemed to have a small effect on the final prediction, which makes sense because 96.25% of the cases had not reported an accident. However, this model risks underestimating the probability of having an accident.

All in all, the coefficients obtained by the RiskLogitboost regression are much bigger than those obtained by the other regressions since this type of algorithm tends to overestimate the probability of occurrence of the target variable to avoid classifying risky observations as ${\widehat{Y}}_i$ = 1 instead of ${\widehat{Y}}_i$ = 0.

Table 4. Variable importance of the six most relevant covariates according to RiskLogitboost, Boosting Tree, Ridge Logistic regression and Logitboost.

Order	RiskLogitboost	Boosting Tree	Ridge Logistic	Logitboost
First	Power o	Driver Age	Brand Japanese (except Nissan) or Korean	Region Limousin
Second	Power n	Brand Japanese (except Nissan) or Korean	Region Haute-Normandie	Power m
Third	Power m	Car Age	Brand Opel, General Motors or Ford	Power l
Fourth	Power l	Density	Brand Volkswagen, Audi, Skoda or Seat	Power n
Fifth	Region Limousin	Brand Opel, General Motors or Ford	Region Nord-Pas-de-Calais	Region Haute-Normandie
Sixth	Region Haute-Normandie	Region Haute-Normandie	Brand Mercedes, Chrysler or BMW	Power k

The Lasso Logistic regression has no significant coefficient estimates with which to compute the variable importance technique.

shows the variable importance of the six most relevant covariates according to RiskLogitboost, Boosting Tree, Ridge Logistic and Logitboost regressions. The results show no consensus between the methods; however, the Boosting Tree and Ridge Logistic regression have certain categories of Brand and Region as the most important covariates, while certain categories of Power and Region seem to be the most relevant according to Logitboost and RiskLogitboost.

As a consequence, it seems that there is no consensus in the results provided by the variable importance technique, which is risky in terms of interpretation. Analysts should consider that the results of a Boosting Tree, Ridge Logistic or Lasso Logistic regression can generate misleading inferences because they underestimate the occurrence of rare events; the covariates that appear to be most contributive will be those with more effect on non-events (Y = 0). By contrast, the variable importance technique suggests that RiskLogitboost better identifies the covariates that are the most influential in the occurrence of rare events (Y = 1).

Figure 3 shows the partial dependence plot (PDP) obtained from a Boosting Tree. Each plot shows an average model prediction for each value of the covariate of interest. The intuitive interpretation of this plot is that the magnitude on the y axis shows more or less likelihood of the occurrence of the event (Y = 1). In this particular case, drivers with m–type Power were more likely to have an accident than drivers with d–type Power. Newer vehicles were less likely to be involved in an accident than older ones. Drivers aged between approximately 30 and 80 were less likely to have an accident than very old or very young drivers. Moreover, policy holders who drove in the region of Limousin were the least likely to have an accident in comparison with other regions of France. Last but not least, it seems that Japanese (except Nissan) or Korean vehicles were more likely to be involved in an accident than other brands.

6. Conclusions

On balance, RiskLogitboost brings a key advantage to the prediction of rare events, principally when the detection of the minority class is fundamental or extremely important in the case study, and the impact of false negatives is irrelevant or barely important. The treatment and the interpretation of rare events is more accurate when using the RiskLogitboost, and it may contribute to the prevention of events whose occurrence would be disastrous, and whose cost policy holders are not willing to accept or able to afford.

The RiskLogitboost regression is a boosting-based machine learning algorithm shown to improve the prediction of rare events compared to certain well-known tree-based and boosting-based algorithms. It will be of most value where the failure to predict the occurrence of the rare event and when it will occur is high. RiskLogitboost regression implements a weighting mechanism and a bias correction that lower prediction error to better predict such rare events by overestimating their probabilities. The results presented here show that the lowest RMSE in the upper and lower extremes occurs when Y = 1. This comes at a cost. The RiskLogitboost regression RMSE tended to increase when Y = 0 in the extreme observations due to the fact that the algorithm adjusts misclassified observations, which, in the context of rare events with a binary response, are coded as Y = 1. This cost is low, when the cost of false negatives is much smaller than the cost of false positives.

While regularization procedures can be incorporated in econometric methods such as logistic regression, they have two main drawbacks. First, the resulting models may not be adequately interpretable because the shrinkage from such procedures depends on the penalty term, causing loss of the real effect of the covariates on the final prediction. Second, such procedures cannot classify rare events efficiently.

The Tree Boosting regression had the lowest RMSE in the majority class observations (Y = 0) but showed poor performance in the minority class observations. It is also more in the nature of a black box in terms of interpretability, requiring more reliance on the variable importance method and PDP. The PDP from the Tree Boosting regression is relatively informative, but all covariates are treated as significant or relevant for the final prediction, which is sometimes inconsistent with an econometric model like a regression. Moreover, while a PDP is easy to implement when there are only a few variables, with more variables interpretation is more difficult. It is often desirable to achieve both high predictive performance for rare events and interpretability. Tree-based and boosting-based methods may be unsuitable in such situations because they underestimate the probability that the rare event will occur while also underestimating the effect of the covariates that are most important to predicting the rare event rather than the majority class. RiskLogitboost delivers high predictive performance while also facilitating interpretation by identifying the covariates most important to prediction of the rare event.

The RiskLogitboost has still limitations when decreasing the false negative rate since it focuses on reducing efficiently the error of observations $Y_i$ = 1. However, for those case studies whose cost of false negative rate tends to be high, the proposed method could be redesigned so as to improve the detection of observations $Y_i$ = 0. This would be a proposal for further research.