The Analysis of a Model–Task Dyad in Two Settings: Zaplify and Pencil and Paper

Abstract

This paper examines the added value of a digital tool that constitutes a new model to introduce students to multiplication. Drawing on the theory of semiotic mediation, the semiotic potential of this new model is analysed with respect to the same task that can be solved in two different settings (the digital tool and pencil and paper). The analysis shows that the task solutions undergo significant changes depending on to the technological settings. Even though the end product of the model–task dyads might look the same in both settings, the product emerges from the different processes that would mediate quite different meanings for multiplication. This suggests that while designing tasks that involve mathematical models, rather than focusing only on the end product, considering the whole process would reveal the extensive potential meanings the model–task dyad can mediate.

1. Introduction

The repeated addition model is pervasively used in schools around the world to teach multiplication although it cannot fully capture the essence of multiplicative situations (see below for more detail). Students might be able to come up with the right answer to multiplication equations by using this model, yet this does not guarantee an understanding of multiplicative relationships [1]. Additive thinking still overweighs the multiplicative thinking, when students in the upper grades interpret the situations that are open to both ways of thinking [2].

This has in part driven the growth of research around the use of different models [3,4,5] These models represent multiplicative situations by illustrating a number of pre-given objects that are spatially organized different from that of the repeated addition model. However, this static approach to depict multiplication excludes the processes that are involved in multiplying. This paper describes a new model—henceforth called Zaplify—that draws on but is not identical to existing models. Like the others, Zaplify is spatially organized in order to highlight multiplicative relationships. Unlike the other models, it has been developed by using multi-touch technology affordances so that the model also requires physical multiplicative actions. Zaplify does not draw on game design elements such as time constraint, embedded tasks and level. Instead, it offers an open exploratory environment for students to bodily experience multiplicative structures.

Given existing models, it is reasonable to ask why a new one is necessary and, furthermore, to consider what exactly it can contribute to the teaching and learning of mathematics. This is the basic question that I pursue in this paper (This is an expanded version of the conference paper written by Güneş [6]). However, instead of focusing just on the model, I examine how a given task changes according to the models and the technological environments (dynamic or static) in which it is situated. Therefore, I follow the theory of semiotic mediation in analysing the model–task dyad by looking at how the same task might be solved with different models that are enacted in different environments, as a way of understanding how the model might give rise to different solutions and different ways of reasoning about those solutions. Thus, this paper attempts to answer the question Watson and Ohtani [7] posed to further the research in task design: “How different design principles reflect or generate different perceptions of mathematical concepts” (p. 14).

2. The Theory of Semiotic Mediation

Drawing on Vygotsky’s theoretical construct of semiotic mediation, Maria Giuseppina Bartolini Bussi and Maria Alessandra Mariotti developed the Theory of Semiotic Mediation (hereafter, TSM) to explain mathematics learning through collective use of mathematical artefacts. There are four assumptions underlying this theory [8]. First, forming scientific concepts is among the main objectives of the teaching-learning process that involves both acting on artefacts to accomplish some tasks and building mathematical meanings out of these actions. Creating signs within an intricate interplay constitutes the origin of this semiotic process. Second, these scientific concepts cannot be formed without conscious awareness. Individuals create personal meanings by interacting with the artefact. Semiotic processes bring these personal meanings into consciousness and enable individuals to formulate scientific concepts out of these personal meanings. Third, “mathematical meanings are culturally and historically established” and they “can be crystallized and embed into certain artefacts and signs” [8] (p. 22). Unlike most learners, the teacher, as an expert in the field, can identify such embedded mathematical meanings. Lastly, TSM assumes that intensive human mediation is necessary for learners to form mathematical meanings by using such artefacts.

Based on these assumptions, TSM hypothesizes that “meanings are rooted in the phenomenological experience, but their evolution is achieved by means of social construction in the classroom, under the guidance of the teacher” [9] (p. 225) and accounts for this evolution with a theoretical construct called didactic cycle [10]. As the aim of this paper is to analyse the potential link between artefacts and mathematical meanings, rather than a teacher’s exploitation of this link, I will only explain TSM’s constructs of “artefact”, “signs” and “the semiotic potential of an artefact”.

2.1. Artefact and Signs

Bartolini Bussi and Mariotti [10] defined an artefact as any object that was made by human beings: “Sounds and gestures; utensils and implements; oral and written forms of natural language; texts and books; musical instruments; scientific instruments; tools of the information and communication technologies” are examples of various types of artefacts (p. 746). The TSM’s use of the term “sign” is aligned with Pierce’s description: “something which stands to somebody for something in some respect or capacity” [11] (p. 118). The sign functions both to represent something, and to create meaning through their intricate interplay [11]. As the teaching/learning process is based on meaning making, signs play an important role in this process. In their seminal work, Bartolini Bussi and Mariotti [10] referred to Vygotsky’s list of signs that includes “language; various systems for counting; mnemonic techniques; algebraic symbol systems; works of art; writing; schemes, diagrams, maps, and mechanical drawings; all sorts of conventional signs; etc.” (p. 751).

Even though Bartolini Bussi and Mariotti [10] defined artefacts and signs separately and listed several examples for each construct, it might be difficult to distinguish them in some cases because some of the above-mentioned examples are given both as an artefact and as a sign (e.g., gesture, language). This prompted me to consider artefacts and signs not as disjoint materials but as phenomenological entities. At this point, Bartolini Bussi and Mariotti’s [10] reference to Vygotsky’s analogy between tools and signs together with Wartowsky’s categorization of artefacts is helpful in explaining how TSM distinguishes the artefact from the sign.

In the Vygotskian account, the analogy between the “tool” and the “sign” might reflect the distinction between TSM’s constructs of artefact and sign:

The invention and use of signs as auxiliary means of solving a given psychological problem (to remember, compare something, report, choose, and so on) is analogous to the invention and use of tools in one psychological respect. The sign acts as an instrument of psychological activity in a manner analogous to the role of a tool in labour.

(Vygotsky, 1978, as cited in [10] p. 753)

This analogy reflects two distinctions between the sign and the tool. First, the nature of the activity differs. Artefacts are used to conduct physical activity, whereas signs play a role in psychological activities. Second, their mediating functions are different. While the tool functions as externally oriented, it exerts human influence on the object of physical activity; the sign functions as internally oriented, it does not change anything in the object of a psychological activity. It is an internal activity aimed at mastering oneself [12] (p. 55). In other words, we change the world via tools, we master ourselves via signs.

Wartowsky (1979, as cited in [10]) separated the artefacts into three types, according to the user’s phenomenological experience. A primary artefact is used to navigate one’s environment. A secondary artefact is used to preserve and to transmit skills, which is necessary for the use of primary artefacts. Finally, tertiary artefacts do not have a practical goal in the sense of primary artefacts, yet they “constitute an autonomous ‘world’, in which the rules, conventions and outcomes no longer appear directly practical” (1979, as cited in [10] p. 779).

For example, if I move the handle of a door, I can open the door physically. Here, the handle, a human made object, is the primary artefact which helps me to open the door. If I then move my hand in the air, as if grabbing the handle and rotating my fist downwards, this gesture becomes a secondary artefact because it helps me remember how to open the door or to communicate to others how to open the door. In other words, the gesture stands (in part, at least) for the act of opening the door, the same way Pierce characterized signs: “Something which stands to somebody for something in some respect or capacity” (Pierce, 1932, as cited in [11] p. 118). The rotation of the handle might then be modelled as an angle, which is a geometrical construct that conforms to certain geometrical rules. In this case, the notation of angle constitutes a tertiary artefact. Within this categorization, the primary artefacts might correspond to the TSM’s notion of artefact. The secondary artefacts can be associated with what the TSM refers to as signs.

2.2. The semiotic Potential of an Artefact

Wartowsky’s categorization of artefacts might present them as mutually exclusive entities. However, the same object might be used both as an artefact and as a sign according to the phenomenological experience of the user [13]. For example, for a novice learner, an abacus might be interpreted as a tool to record the counting activity, whereas for an expert, such as a teacher, the abacus might represent place-value. Thus, the same artefact has the potential to mediate two different but related meanings. Bartolini Bussi and Mariotti [10] described this as the semiotic potential of an artefact.

The artefacts that have semiotic potential can be used to help its users enact mathematical relationships that are novel to them. According to the TSM, whenever individuals use an artefact to achieve a mathematical task in a social context, they will be using the artefact in a certain way and will be creating certain signs both to achieve the given task and to create shared meanings. The TSM categorizes these signs according to their relationship to the artefact and to the mathematical culture. The artefact sign plays a role in expressing the relationship between the task and the artefact. It is associated with the operations conducted to achieve the task. The mathematical sign expresses the relationship between the artefact use and mathematical knowledge, and it is aligned with the existing mathematical culture. The pivot sign “may refer both to the activity with the artifact; in particular [it] may refer to specific instrumented actions, but also to natural language, and to the mathematical domain” [10] (p. 757). It plays an important role in the evolution of artefact signs into mathematical signs.

The evolution of artefact signs into mathematical signs is the aim of mathematics education and this is achieved by the semiotic mediation of the artefacts and the cultural mediation of the teacher [10]. At this point, Mariotti [14] considered the analysis of an artefact’s semiotic potential as an a priori phase in designing a successful teaching sequence, because the specific utilisation schemes (Verillon and Rabardel [15] defined the utilization schemes in the Piagetian tradition as “the structured set of the generalizable characteristics of artifact utilization activities” (p. 86).) can be predicted from examining the tasks in relation to the artefact. In this paper, by comparing the semiotic potentials of Zaplify and pencil and paper with respect to the same task, I aim to identify the added value of Zaplify in evoking various meanings of multiplication. The comparison is not meant to argue that one is better than the other; it simply brings to the foreground the particular value of Zaplify that may be difficult to appreciate when it is assumed that paper-and-pencil is the presumed technology of learning multiplication.

3. Repeated Addition Versus Multiplication

The repeated addition model (RAM) of multiplication, equates a multiplication sentence to an addition sentence. For example, 4 × 3 is arithmetically represented as the repeated sum of 3 taken 4 times. The visual representation of this repeated addition involves 4 groups of 3 objects as in Figure 1:

RAM depicts multiplication as the collection of equal groups. Therefore, it may suggest that multiplication involves a spatial organization of pre-existing objects. Even though this model represents objects in groups, the quantity of the groups is not as visible in the mathematical expression as the size of the groups (which is represented by the total number of purple apples in a group, as in Figure 1). Therefore, RAM emphasizes only a one-unit count which is represented by purple apples. The groups are spatially separated, and this separation might portray each addend as independent of the others. The RAM might therefore suggest that changing the size of one group would not require a change in the sizes of the other groups.

RAM is widely evoked in mathematics curricula as a bridge between addition and multiplication (e.g., Turkish mathematics curriculum, British Columbia mathematics curriculum). However, multiplication is explicitly distinguished from repeated addition by several researchers. Their definitions of multiplication emphasize both its static and dynamic aspects by pointing to the relationships between the quantities involved in multiplication and to the underlying actions taken in multiplicative situations.

Schwartz [16] situated the meaning of multiplication within mathematical modelling activity. He claimed that the identification of quantities and referents (the attributes to be measured) is the basis for such an activity. He distinguished two types of quantities: extensive and intensive. Extensive quantities are the ones that are directly counted or measured like weight, height or amount. Intensive quantities cannot be quantified directly but must be calculated through other quantities such as speed (the travelled distance per unit time).

Schwartz [16] separated mathematical operations into two groups: referent preserving and referent transforming operations. The former produces a third like quantity out of two like quantities. Addition and subtraction are such operations. Referent transforming operations produce a quantity with a different referent. Multiplication enters this second category, and Schwartz [16] described it as a mapping from “a quantity in one space to another quantity in another space” (p. 50). Thus, all multiplicative situations require the identification of three referents and three relationships between them. For example, the multiplication that reveals the number of points in a 3 × 4 array (Figure 2) can be represented as:

{3, the number of rows} × {4, the number of points per row} = {12, the number of points}

In this situation there are three relationships between the number of rows (R), of points (P), and of points per row (PpR): R = P/PpR, PpR = P/R, P = R × PpR.

Vergnaud [17], like Schwartz, proposed that identifying the relationships between the variables was essential for multiplication. However, he identified two variables and four values attached to them.

In Figure 3, Vergnaud [17] distinguished two relationships: scalar and functional. The scalar relationship is the ratio between two values of a variable: for example, the ratio between the number of cars is five to one and this is the same for the number of tires. On the other hand, the functional relationship is the ratio between two values of two distinct variables. For example, the functional relationship between the number of cars and the number of tires is four. This is similar to Schwartz’s [16] intensive quantity that builds a many-to-one correspondence between the number of cars and tires. One car corresponds to four tires and this correspondence holds for each car.

Drawing on Piaget, Clark and Kamii [18] pointed to two important difference between multiplication and repeated addition. First, multiplication involves two units each of which quantifies two distinct entities. There is a many-to-one correspondence between these units. This correspondence may be associated with Vergnaud’s [17] functional relationship, for example between the number of cars and the number of tires: one car corresponds to four tires. The car represents a composite unit that is made up of four units. Whereas addition emphasizes only one unit that quantifies the size of the groups (as in the above-mentioned case of purple apples). Equal groupings might recall composite units. However, they are not quantified in the addition: the amount of groups is not assigned a numerical value, unlike the size of the groups.

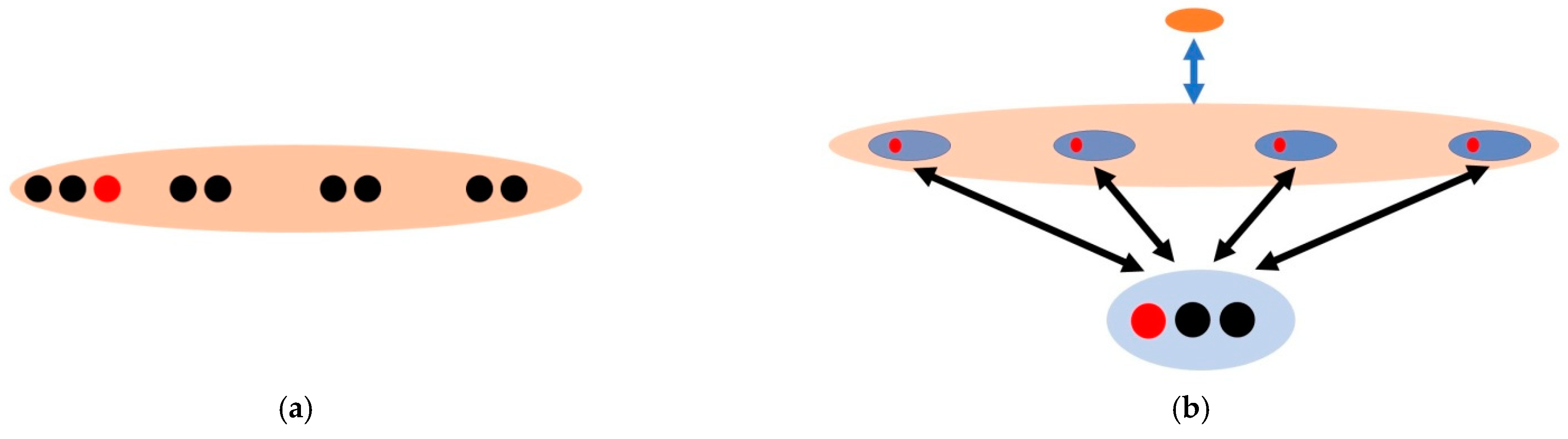
Based on this difference, inclusion relationships between the units of addition and multiplication also have different natures. Since there is only one unit in repeated addition, they are included in one level among themselves as in Figure 4a. When we add “2”s, we act on the units that quantify the size of the groups. Thus, these units (they are represented by the individual black discs in Figure 4a) construct a collection of multiple individual units. Moreover, each addend acts independently from the others. Therefore, let us say in 2 + 2 + 2 + 2, increasing the size of the first group from two to three (this is represented by the red dot added next to the first two black dots in Figure 4a), does not have to change the size of the rest of the groups. Therefore, the groups that are depicted in repeated addition do not necessitate a many-to-one correspondence that holds for each group. Whereas in multiplication, the single units (represented by black discs in Figure 4b) that take part in the body of the composite unit create a single multitude (represented by the blue ellipses in Figure 4b). As these single units are included among themselves, they are also included in each multitude simultaneously because of the many-to-one correspondence between the composite and the single units (represented by the arrows in Figure 4b). Thus, any change in the size of one multitude, let us say from two to three (as represented by the red dot added next to two black discs in Figure 4b), is mirrored on the size of the other multitudes (as represented by the red discs added into four blue ellipsis in Figure 4b). Therefore, increasing the first factor of the multiplication 2 × 4 = 8 by one unit increases the product by four units.

Confrey [19] took a dynamic approach and described multiplication with respect to creating a numerical quantity. She described multiplication as, “an action of creating simultaneously multiple versions of an original” and named this action as “splitting” (p. 292). The notion of an original in this definition might recall the single unit of repeated addition. Fortunately, Confrey [19] explicitly stated the main difference between splitting and repeated addition: they differ based on how the change occurs. In repeated addition, identifying a unit and counting instances of that unit consecutively brings the change. Whereas in splitting, change occurs through a simultaneous one-to-many splitting-action. Moreover, Confrey [19] defined the unit as “the invariant relationship between a successor and its predecessor; it is the repeated action” (p. 312) and distinguishes between additive unit in a repeated addition and a multiplicative unit in splitting. Thus, she considered the unit of the operations in relation to the action. Counting the results of splitting action might also be associated with the model of repeated addition. However, Confrey [19] warned that, “the cognitive act of recognizing a situation as multiplicative and displaying it appropriately occurs prior to this counting action” (p. 311).

Davydov [20] explained multiplication with respect to the operations involved in the quantifying activities. He defined such activities as “assigning a numerical value of some magnitude in relation to a given unit” (p. 11). Such activities become cumbersome when the given unit-count is too small. Davydov [20] described multiplication as a practical tool to quantify magnitudes by transferring the unit count from a smaller to a larger one “for which a relationship to another, smaller unit, is already established” (p. 12). Davydov’s conceptualization of multiplication emphasized both a multiplicative action (transfer of the unit count) and multiplicative relationships between the quantities.

For example, let us say a grocery shop employee needs to make an inventory for the amount of honey in stock. Honey is sold in individual jars and they come in boxes of 8. The employee can assign a numerical value to the amount of honey either in relation to a jar or in relation to a box. In this case, the jar and the box are the two distinct unit-counts for quantifying activity, and they have an established relationship because of packaging: each box corresponds to 8 jars. If the employee wants to assign a numerical value to the amount of honey with respect to jars, they can directly count the jars one by one. Alternatively, the employee can indirectly quantify it with respect to jars by counting the boxes and transferring the unit-count from the jars (the smaller unit-count) to the boxes (larger unit-count) thanks to the established relationship between them. If there are 14 boxes of honey jars, the operations that are involved in indirect measurement are represented as “8 × 14 = 112”. In this equation, 8 represents the established relationship between the smaller (the jar) and the larger (the box) unit-counts. This is similar to Schwartz’s [16] intensive quantity and Vergnaud’s [17] functional relationship. 14 represents the numerical value of the magnitude (the amount of honey) in relation to the larger unit-count (the box); 112 represents the numerical value of the magnitude (the amount of honey) in relation to the smaller unit-count (the jar).

As shown in the above models of multiplication, the researchers conceptualized multiplication by focusing either on the relationship between the quantities, or on the action underlying the multiplicative situations, or both.

Table 1. The various meanings of multiplication.

The Researcher	Key Concepts of Multiplication
Schwartz [16]	Multiplication is a mapping from “a quantity in one space to another quantity in another space” (p. 50). All multiplicative situations require the identification of three referents and three relationships between them.
Vergnaud [17]	Multiplicative situations include two variables and a functional relationship (many-to-one correspondence) between them.
Clark and Kamii [18]	Multiplication has two units which have inclusion relationships in two levels.
Confrey [19]	Multiplication is “an action of creating simultaneously multiple versions of an original” and named this action as “splitting” (p. 292).
Davydov [20]	Multiplication is a practical tool to quantify magnitudes by transferring the unit count from a smaller to a larger one “for which a relationship to another, smaller unit, is already established” (p. 12).

summarizes these approaches.

4. Touch Times

TT [21] is an iPad application designed to enhance multiplicative thinking as different from repeated addition. The design of TT draws both on Davydov’s [20] notion of change in unit-counts and on Vergnaud’s [17] notion of functional relationship. TT consists of two worlds called Grasplify and Zaplify. Both worlds are designed to convey the multiplicative ideas brought by Davydov and Vergnaud, yet they embedded these ideas in distinct models that prompt learners to embody them in different ways. This paper will focus only on the Zaplify world, which can be described as a dynamic array model.

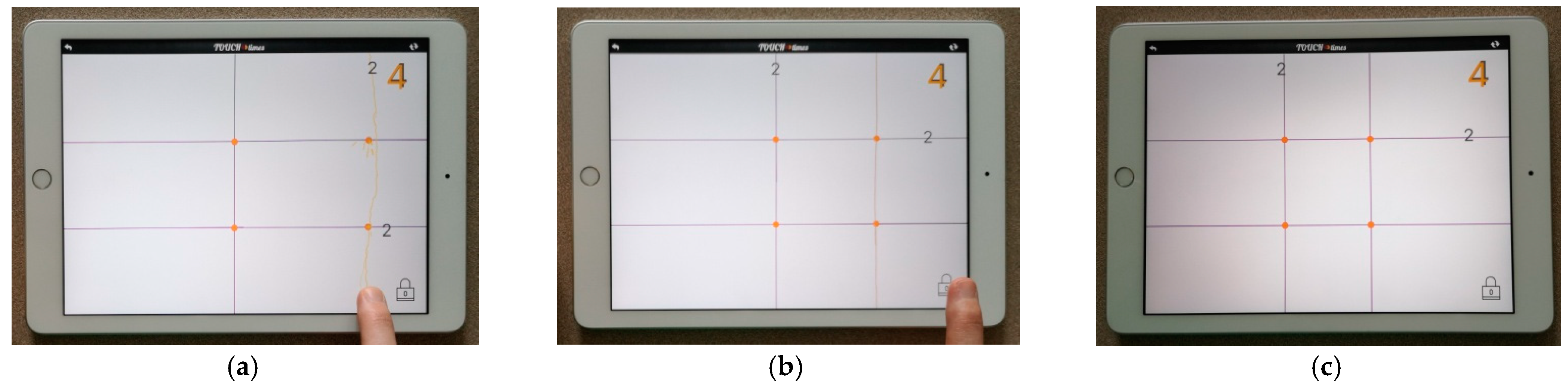
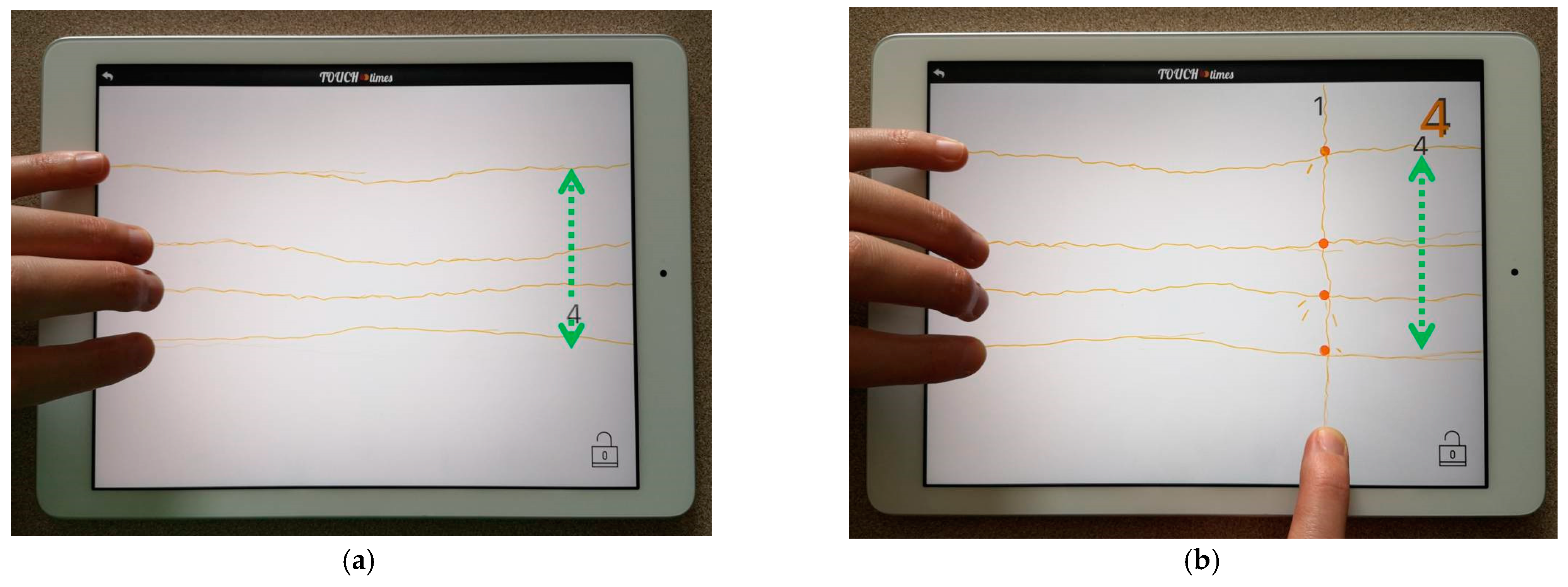
Zaplify starts with an empty screen. When the tablet is placed horizontally on a surface, four fingerprints appear just above the lower edge of the tablet, and three fingerprints appear on the left edge of the tablet (Figure 5a). Then, a diagonal appears on the screen as the fingerprints gradually fade away (Figure 5b). These fingerprints and the diagonal line are introduced automatically by the app to guide users to place their fingers both horizontally and vertically in the designated areas (upper and lower triangular areas) which are formed by the diagonal. While the fingerprints completely disappear in a few seconds, the diagonal line stays on the screen until the user touches on the screen (Figure 5c). Users can create two types of Zaplify objects: lightening rods and lightening balls (these will be explained in detail below).

Zaplify can be used in two modes: unlocked and locked. The user can change the screen mode by touching the lock icon at the lower right corner of the screen. This icon becomes visible once the user touches on the screen and creates a Zaplify object (Figure 6). In unlocked mode, the Zaplify object(s) stay(s) on the screen as long as the user maintains the finger contact. In locked mode, the Zaplify objects stay on the screen even after the user lifts their finger-created the object/s. It is possible to shift from unlocked to locked mode any time. When the screen mode changes, the visual characteristics of the Zaplify objects slightly alter.

When a user places a finger on the screen in unlocked mode, a yellow object that looks like a “lightening rod” (referred to as “lines” henceforth) appears. The lines extend from one edge of the screen to the opposite edge. These lines are not static objects, rather they continuously tremble like lightning strikes. The lines seem to be passing through the point where the user’s fingertip contacts the screen. If the user touches the lower triangular area, Zaplify produces vertical lines (Figure 6a), while touches in the upper triangular area produce horizontal lines (Figure 6b). Screen contact can be made with one finger at a time or with multiple fingers simultaneously. Multiple fingers can create either only vertical lines (Figure 6a), only horizontal lines (Figure 6b) or both (Figure 6c), according to the position of the fingers.

The number of vertical and horizontal lines are indexed separately by two black numerals. The numeral at the top of the screen represents the number of vertical line(s) (Figure 6a) and it continuously moves from left to right on a horizontal path, repeatedly passing over all vertical lines. The numeral at the right edge of the screen represents the number of horizontal lines (Figure 6b) and it follows a vertical path up and down spanning all horizontal lines.

Whenever a horizontal line intersects with a vertical line, a lightening ball (referred to as “points” henceforth) gradually appears at the close vicinity of the intersection point. Like the lines, the points are not static objects. They vibrate like sizzling sparks. The total number of points is represented by an orange numeral that appears at the upper right corner of the screen (Figure 6c). No orange numeral appears at the upper right corner unless there is an intersection (Figure 6a,b).

When a user lifts a finger, the line that is created by that finger and the points that vibrate on it disappear all together. This change is immediately mirrored in the numerals that represent the numbers of lines and the product. The orange numeral that represents the number of points (the ones before the finger is lifted) moves down until the bottom edge of the screen and then disappears. Meanwhile, a new orange numeral that represents the number of points (the ones that are left after the finger is lifted) appears on the upper right corner of the screen.

The Zaplify objects are created according to the same principles in locked mode: (1) Users create line objects when they touch the screen; (2) The location of touch designates the orientation (vertical/horizontal) of the lines; (3) The circular object(s) appear at the intersection(s) of perpendicular lines. In locked mode, the Zaplify objects stay on the screen once they are created. Therefore, they do not disappear, even though the line-making fingers are lifted. The Zaplify objects are also dynamic in this mode, yet they do not vibrate as dramatically as they do in unlocked mode.

Let us say a user first creates two horizontal and one vertical lines in locked mode. When the user touches the screen, a new yellow vertical line appears, and it vibrates as in the unlocked mode (Figure 7a). Once the user lifts that finger, the amplitude of the vibration reduces and the colour of the line changes to a darker hue (Figure 7b); all the lines that are parallel to it (vertical lines in this example) gradually slide (to the left in this example) until the grid becomes symmetrical (Figure 7c).

5. Method

According to TSM, an artefact that is used to solve a task has a semiotic potential if it mediates two meanings: (1) with respect to the achievement of the task; (2) with respect to the mathematical culture [10]. Therefore, the semiotic potential of the artefact cannot be identified without considering the specific task. I have analysed the semiotic potential of pencil and paper and Zaplify based on the task called “Making 198 with various M-ples”. M-ple is a specific Zaplify term that refers to a line that has exactly M (any positive integer) points on it, as in Figure 8. For example, three-ple is a line that has only three points on it. In this analysis, I assume that students are already comfortable with this term.

The task consists of the following questions:

(1)

Make the product 198 by counting up with two-ples?

(2)

Make the product 198 by counting up with three-ples?

(3)

Make the product 198 by counting up with four-ples?

(4)

Make the product 198 by counting up with five-ples?

(5)

Make the product 198 by counting up with nine-ples?

5.1. The Underlying Task Design Principles

I chose this task because it followed many task design principles proposed in [22]. I draw particularly on the two following principles: (1) providing students with tasks that would involve a variety of examples (e.g., [23,24]) and (2) providing students with tasks that lead to conflicting situations (e.g., [25,26,27]). Keeping certain aspects of the examples intact and changing others prompt discernment and awareness by enabling students to separate “certain aspects of something from other aspects”, to contrast their experiences, to make generalizations [25] (p. 248). Conflicting situations “creat[e] learning opportunities for students … to re-evaluate and refine their mathematical and proof-related knowledge” [27] (p. 217).

This Zaplify task achieves the first principle by prompting students to count up by various M-ples. Both the act of counting up and the target product stay invariant, unlike the M-ples. Moreover, the product is chosen to be a big number so that students will be counting up for an extended time period and creating several products until they reach 198. This is designed to help students focus on the structure rather than on computation [28]. Repeating the process for a while would create new examples in which the structures they discern hold true. Therefore, this repetition could enable students to make a generalization out of their experiences, thus crystalizing the multiplicative meanings that emerge. This task would also lead to a conflict: the third and the fourth subtasks do not have a solution in Zaplify. Although students first have to create an M-ple and then tap one finger repetitively until they create the target product in each case, this strategy would not work for making 198 with four-ples and five-ples. This task also follows the sequence suggested by Bokhove [25]: “first appropriate pre-crisis items, then the item that intends to intentionally cause a crisis (for some students), and then some post-crisis items” (p. 242). The task starts with counting up by two-ple and three-ple. These are pre-crisis items that would build students’ confidence because it is very easy to reach 198 by repeating taps. Then, the crisis items (counting up with four-ples and five-ples to make 198) follow. They would possibly pose frustration in students’ bodies yet prompt them to ask “why”, which is an important question for learning. Finally, the last subtask includes a post-crisis item that students can solve without having difficulty.

Another design principle highlighted in [22] was that of feedback. The feedback in Zaplify has the “trivial sense in which the appearance and behavior of objects that are constructed is feedback” (Finzer, as cited in [23], p. 66). For example, students are not given any message saying whether they achieve the task or not. The numeral that represents the product in Zaplify is the feedback for students to judge if they succeed because this type of feedback “offers immediate information, which is directly related to one’s actions, and which can guide further actions, especially if a goal has not been reached” [29] (p. 190). Moreover, the feedback is “constrained by the mathematics underlying the environment… In this way unexpected implications of the mathematics may be revealed” (Laborde, as cited in [23], p. 62). For example, in Zaplify the M-ples are all connected to each other in the array form. It is impossible to create various types of M-ples at the same time. This multiplicative relationship that underlies Zaplify would reveal that some numbers cannot be reached by counting up with any M-ples as happens in the above-mentioned crisis items.

This task is designed specifically for Zaplify. Therefore, it is not a task that teachers would ask their students to solve it with pencil and paper. I analyzed the semiotic potential of pencil and paper with respect to this task to understand the unique contribution of Zaplify to students’ meanings for multiplication.

5.2. Data Analysis

Mariotti [14] suggested that Rabardel’s theoretical notion of utilization schemes that are associated with specific tasks were important tools to analyze the semiotic potential of an artefact. Verillon and Rabardel [15] defined the utilization schemes in the Piagetian tradition as “the structured set of the generalizable characteristics of artifact utilization activities” (p. 86). Borrowing a theoretical construct from cognitivist approaches might seem to be contradictory for TSM, which draws on a social constructivist approach (primarily through Vygotsky). However, rather than a scheme that was defined as an entity existing in the mind of the person independent from the social context, Mariotti [14] seemed to be interested in the person’s real actions that can be observed by another individual. In the same article in which she promoted the utilization schemes as a tool for analysis of the semiotic potential of an artefact, she wrote:

Thus, the artefact and the modes of its use may appear as key elements in the emergence of mathematical knowledge in the school context. They become a unit of analysis that can guide the design of teaching and learning activities.

(p. 26)

Parallel to Mariotti’s [14] account, I have focused on the real actions (modes of use) conducted around/with artefact in my analysis rather than the schemes that are believed to exist in the mind. However, I decided that the unit of analysis should be the potential signs emerging from the user’s potential modes of use. Since the meanings are created through the interplay of signs [10], identifying the signs with respect to this intricate interplay would reveal the potential meanings. These signs may include the potential gestures, potential words to describe both artefact and the interactions with/around the artefact. In order to capture these potential signs, I video recorded an iPad screen as I solved the given Zaplify task and verbally described the steps I took. An M-ple can be created in many ways that might be associated with:

I analyzed the third case that was aligned with Davydov’s [20] argument about the direction of the transfer of unit-counts (from the smaller unit-count to the larger unit-count, not vice versa). Students might create the M-ples in any of these ways. However, a teacher’s role is to select the most appropriate signs that emerge from the artefact use and highlight them in the classroom activities to exploit the semiotic potential of the artefact [30]. Therefore, I chose to illustrate the most appropriate mode of Zaplify use that would be associated with the targeted meanings of multiplication.

I organized the transcription of the video recording in a table format that included three parts: the written record of my verbal accounts, written descriptions of my bodily actions and Zaplify objects (Figure 9). I highlighted the transcription with specific colours to match the signs that were simultaneously created in different modalities. For example, the parts highlighted in yellow happened at the same time: as I was saying “then”, I was pressing my four fingers on the iPad screen and Zaplify created four horizontal lines. I have compartmentalized the video recording into ten-second-intervals to systemize the transcription. Surprisingly, this artificial separation did not create a semantic break between the cells except for one incident in which my verbal account “I am going to press my four fingers, at once, on the upper triangular” was in two separate cells. In this case, I moved the first part of the sentence down to the following cell together with the corresponding records of the bodily actions and the screen configurations. In my analysis, I identified the signs that would be associated with various meanings of multiplication and examined the relationship between them.

6. Semiotic Potential of Pencil and Paper

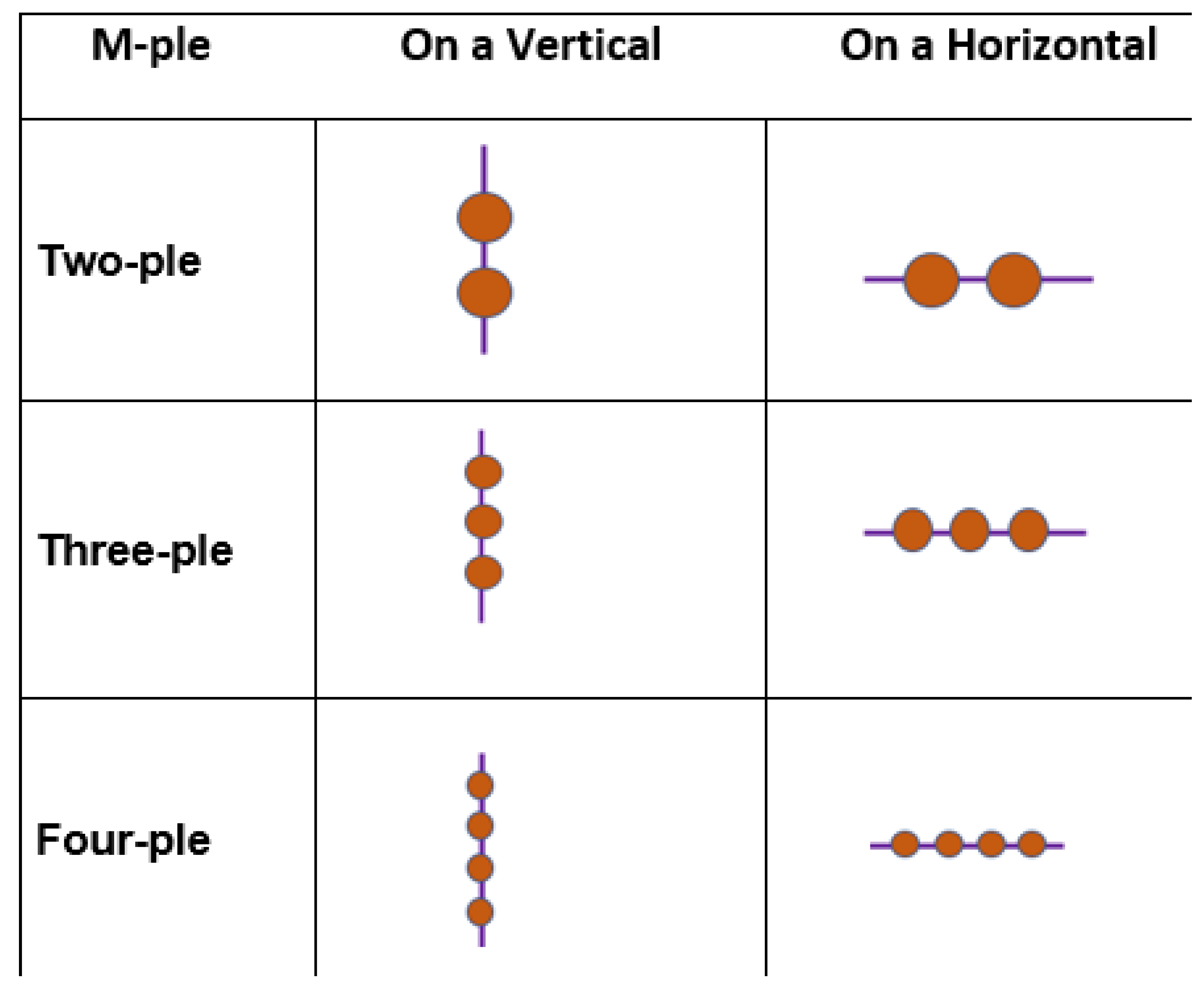
In order to create an M-ple that is aligned with the multiplication expression M × 1, students must first draw as many parallel lines as the number of points that should be on the M-ple. Then, they must draw one perpendicular line that intersects with these parallel lines. After students finish drawing the perpendicular line, they must draw individual points at the intersections. Pencil and paper allows students to draw each line and point one at a time (Figure 10a,c). Similarly, as they draw the perpendicular line, the intersections of the lines would appear one by one, sequentially (Figure 10b). Students can also start by drawing as many points as there would be on a given M-ple and then draw the lines that would pass through these points.

Drawing perpendicular lines would create visual and haptic distinction in students’ experiences due to the orientations of lines. Students most probably start drawing the horizontal lines from the left to the right and vertical lines from the top to the bottom. This spatial and orientational separations might be described by two distinct signs (e.g., “vertical” and “horizontal”; tracing gestures from left to right for horizontal lines and top to bottom for vertical lines) that might be associated with two distinct unit-counts of multiplication.

While students draw the vertical line, the trace of the pencil passes over the existing traces of the parallel lines (Figure 10b). This physical interaction between the traces of perpendicular lines might evoke for students the relationship between the multiplicative factors: one factor spreads over the other factor. Moreover, physical contact with the points that are drawn at the intersections might help students identify inclusion relationships in two levels (as per Clark and Kamii [18]): a point at the intersection is included both in the horizontal and in the vertical line simultaneously.

Drawing points at the intersections of lines might evoke the idea of double unitizing (as per Davydov [20]). While each horizontal line corresponds to one point, the vertical line corresponds to M points and thus constitutes an M-ple. Therefore, the former might be associated with the smaller unit-count, while the latter might evoke the larger unit-count. The number of points on an M-ple might be associated with the functional relationship between the sizes of unit-counts. As the referent of the intensive quantity is different from the ones that create it [16], the points are the objects that are different from the lines that create them. They refer neither to the number of horizontal lines, nor to the number of vertical lines but to the horizontal lines per vertical lines.

Creating points one by one at the intersections of lines might emphasize a sequential nature for unitizing action. Therefore, drawing an M-ple might evoke for students the idea of combining multiple single units instead of creating a single multitude as Confrey [19] suggested.

In order to count up with the given M-ple, students must repeatedly draw M-ples and add up the points on them until they reach the given product. This might associate multiplication with a counting activity as opposed to Confrey’s [19] warning that, “the cognitive act of recognizing a situation as multiplicative and displaying it appropriately occurs prior to this counting action” (p. 311).

Every time students draw a new M-ple, the number of intersections on the new M-ple must be the same as the previous M-ples. However, the free nature of the pencil and paper might prompt students to draw as many points as they want on a line. Therefore, while they have M points on the previous M-ples, they might draw fewer points on the following vertical line to reach the given product. This allows students to reach 198 irrespective of the M-ples they draw. For example, they can create four-ples to reach 198. In this case, after they make the product 196 by drawing the 49th four-ple, they may not completely draw the 50th four-ple. After they create two points on the 50th vertical line and reach 198, they might simply stop drawing (Figure 11). This gradual increase in the number of points might also be associated with the conception of product as the combination of single units rather than the combination of multitudes. Moreover, this potential inconsistency of the number of points on each M-ple might evoke for students a functional relationship that is not spread equally across each larger unit-count.

7. Semiotic Potential of Zaplify

This task must be solved in locked mode, because the target number is very large and creating it by keeping the fingers on the screen is not feasible. When Zaplify is in locked mode, the lines stay on the screen even though the user lifts the finger(s) that create(s) them. When the user holds a line in locked mode, it is yellow and very vibrant. It looks as if it passes below the user’s fingertip. As soon as the contact between the line making-finger and the screen diminishes, the line becomes purple and less vibrant. All lines slightly glide across the screen until they become equidistant.

The task starts with an empty screen that is divided by a diagonal (Figure 5c). Before touching the screen, I say, “In order to make, in order to count up, by four-ples until one hundred-ninety-eight”. Starting to “Make … one hundred-ninety-eight” on an empty screen might be associated with a meaning for multiplication that refers to creating a quantity from scratch, rather than structuring a given quantity as represented by the static repeated addition model. This dynamism is aligned with Confrey’s [19] description of multiplication as “creating multiple versions of an original” (p. 292).

The first step of counting by four-ples in Zaplify might be associated with the concept of composite unit.

00:10: C: I am going to press, my four fingers (stretching four left hand fingers on the edge of the screen), at once (pressing four fingers down simultaneously), on the upper triangular, this is going to make, four horizontal lightning rods.

During this episode, I first see an empty screen divided by a diagonal (Figure 5c); then four horizontal lines and the black numeral “4” appear on the screen (Figure 12a), and then the lines vibrate, and the numeral continuously moves up and down.

In this episode, the quantity is represented in three modalities: through (1) the utterance of “four fingers”, (2) stretching and pressing four fingers; (3) the appearance of four lines on the screen. While the verbal and the bodily account quantify the fingers, the Zaplify account quantifies the lines. The location of the lines creates a relationship between the lines and the fingers: The lines pass through my fingertips creating a correspondence between the lines and the fingers. This correspondence transfers the quantity of the fingers to the quantity of the lines. This transfer and the appearance of the black numeral “4” on the screen might evoke the mathematical meaning of “fourness” as a composite unit. Moreover, pressing four fingers simultaneously while uttering the word “four” might strengthen this idea of a composite unit.

The third step of the task creates a four-ple. Creating an M-ple in Zaplify can be associated with the concepts of factors, product, transfer of unit counts and the functional relationship.

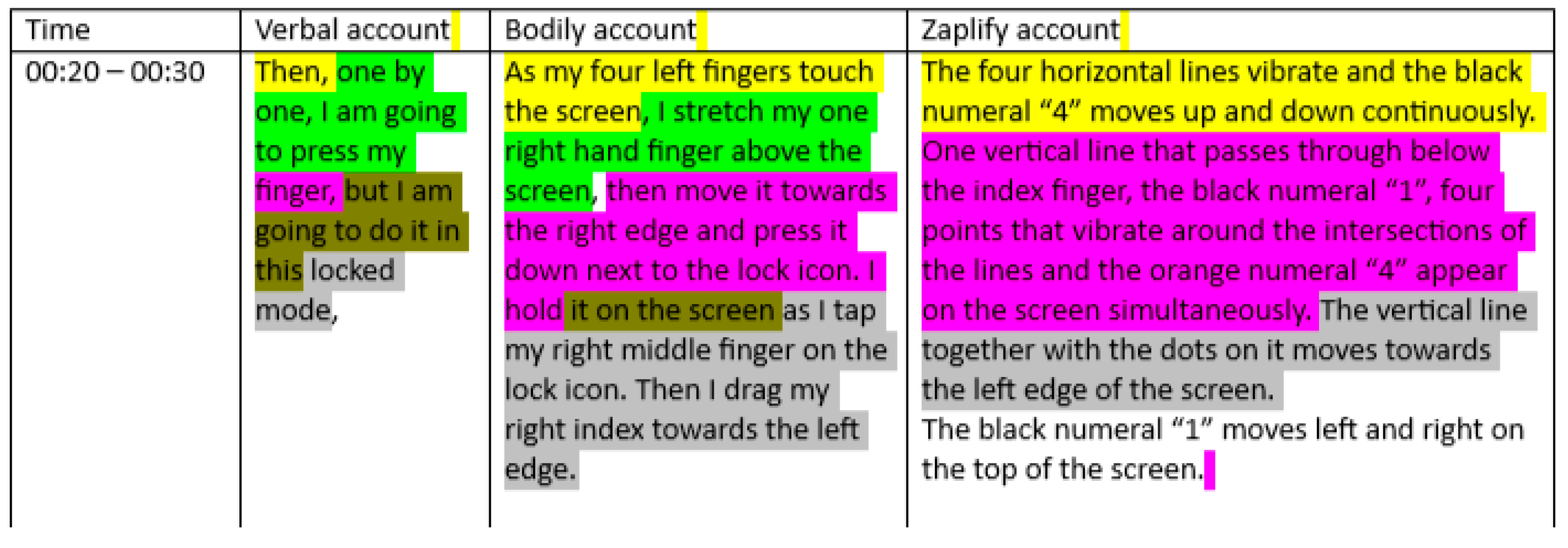
00:20: C: Then (holding four left fingers on the screen), one by one, I am going to press my (stretching right index finger above the screen) finger (moving the index finger to the right edge and pressing it down).

During this episode, the four horizontal lines vibrate and the black numeral “4” moves up and down continuously. One vertical line appears as if it passes below the index finger. The black numeral “1”, four points that vibrate around the intersections of the perpendicular lines and the orange numeral “4” appear on the screen simultaneously (Figure 12b). The vertical line together with the points on it moves towards the left edge of the screen. The black numeral “1” follows the vertical until it is stabilized (Figure 13a).

In this episode, certain signs that are created in each modality reveal contrasting relationships. For example, using right and left hand creates a bodily contrast; the orientation of horizontal and vertical lightning rods, the vertical and horizontal routes of the black numerals create a visual contrast. In addition to these contrasts, placing fingers on two different sides of the diagonal creates a spatial separation between the line-making fingers and the lines they create. These contrasting signs might be related to two distinct quantities that have distinct referents (as per Vergnaud [17] and Schwartz [16]). The two numerals that represent these quantities might be associated with two distinct unit-counts of multiplication (as per Davydov [20]). While one four-ple (the vertical line that has four points on it) might be associated with the larger unit-count, four one-ples (the horizontal lines with one point) might be associated with the smaller unit-count.

As soon as the vertical line intersects the parallel lines, this creates as many points as the number of parallel lines. Creating multiple points with one finger might be associated with the transfer of unit-counts in multiplication (as per Davydov [20]). Moreover, as happens in the solution of the task by using pencil and paper, the number of points on a four-ple might be associated with the functional relationship between the sizes of the unit counts (as per Vergnaud [17]). In addition to the functional relationship, four points on the vertical line can also be associated with the product in this episode.

The idiosyncratic character of the Zaplify objects might mediate the difference between the factors and the product. While the lines can be related to the factors of multiplication, points can be related to the product. The difference between the colours and the movement of the numerals contributes to this separation as well: while the moving numerals that represent the number of lines are black, the static numeral that represents the number of points is orange. Thus, it might evoke for students a meaning for multiplication different from repeated addition in which both addends and the sum are represented with the same type of objects. However, the factors and the product do not act as independent entities. As the vertical line moves to the left, the points on it move to the left with the same pace. This might be associated with the co-varying relationship between the product and the factors.

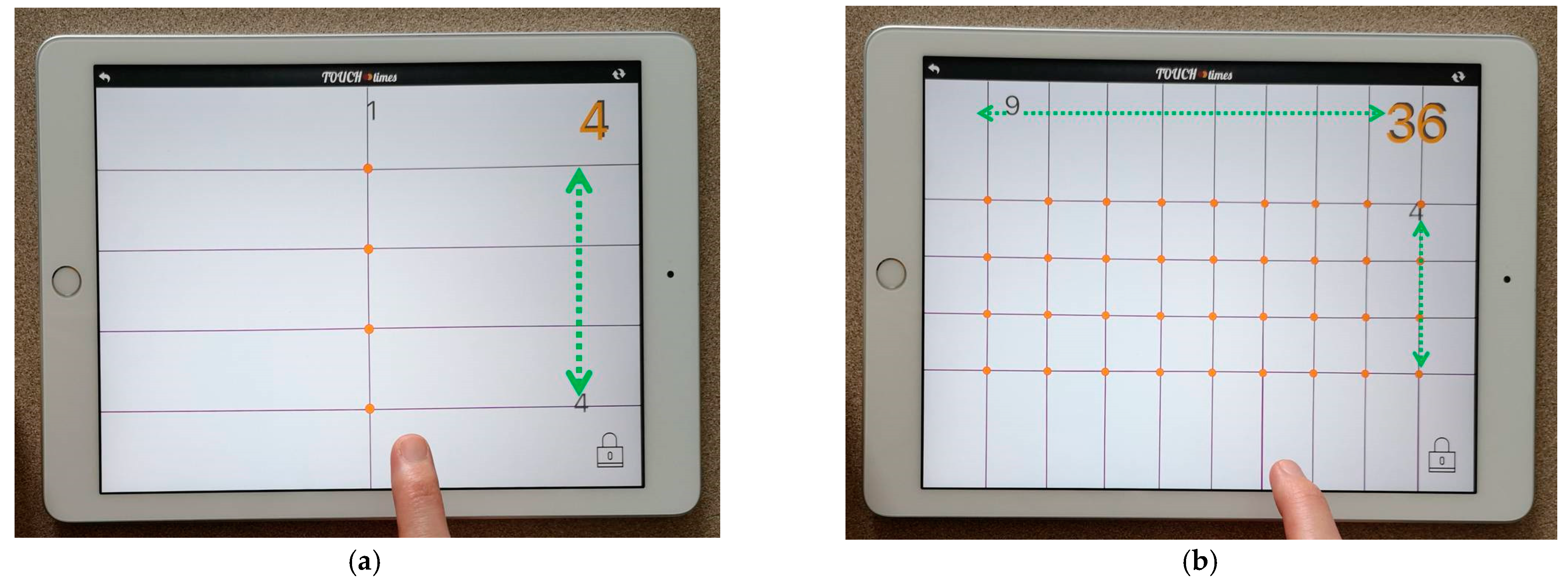
In a later episode, I start to increase the product by repeatedly tapping my right index finger along the bottom of the screen as I say, “I press my one finger”. This mode of use might be related to various meanings of multiplication. During this episode, the four-ple and the black numeral “1” stay at the centre of the screen and the black numeral “4” moves up and down continuously on the right edge of the screen (Figure 13a). A new vertical appears on the screen with each tap. Each vertical line passes below the right index finger and slides (either to the right or to the left) when the finger is lifted. Every time a new vertical is created, four new points appear where the vertical line intersects four horizontals. At the end of this episode, there are nine verticals on the screen (Figure 13b). During this episode, the black numeral increases by one starting from “1” until “9”, it moves left and right at the top of the screen (Figure 13a,b). The orange numeral increases by four starting from “4” until “36” (Figure 13a,b).

The repetition of unitizing action creates the same signs again and again that might result in a generalization about multiplication. Every time I place a new finger below the diagonal, a new four-ple (a line with four points) appears. The number of points on each four-ple is the same as the number of horizontal lines. Thus, this repeating four-ples might evoke for the students the functional relationship between the units as a constant entity that is spread across each larger unit count (as per Vergnaud [17]).

The simultaneous actions may create connections between the Zaplify objects. Both the black numeral that represents the factor and the orange numeral that represents the product simultaneously change with each tap. Thus, the synchronized haptic and visual experiences might create a connection between the factors and the product. However, the amount of change in the numerals is not the same. While the black numeral that represents the number of vertical lines increases by one, the orange numeral increases by four, which corresponds to the number of horizontal lines. Therefore, the horizontal lines might be perceived as playing a role in this connection between the verticals and the orange points. This imbricative connection might be associated with the covariation of product with respect to both factors.

In the above analysis, I illustrate the solution of the third subtask. The rest of the subtasks can be solved in a similar way by creating different M-ples and repeatedly tapping one finger only on one triangular area until reaching the given product. However, among these five M-ples only the two-ples, three-ples, and nine-ples would allow students to create exactly the given target product 198. Working with different M-ples, students would not reach the given product in each case. For example, when they create four-ples to reach 198. In this case, after they make the product 196 by pressing the 49^th four-ple, pressing one finger on the screen would create the 50th four-ple. Since the orange numeral would abruptly change from 196 to 200 with the 50th four-ple, the students cannot see 198 on the screen contrary to their expectation (Figure 14a,b). This unexpected change in the product might prompt students to explore the covarying relationship between the factors and the product.

8. Discussion

As a researcher who works on educational technologies, one of the questions I have been repeatedly asked is “what can this technology do that pencil-and-paper cannot do?”. In this paper, I answer this question by analysing the semiotic potential of both pencil and paper and Zaplify. However, the unbreakable link between the task and the semiotic potential of an artefact problematizes this question. As the tasks are created based on their artefacts (e.g., dragging task in a dynamic geometry environment (DGE) is a task specific to DGE), different artefacts prompt distinct modes of use to solve the task (e.g., drawing lines with pencil and paper versus pressing fingers on the iPad screen). The different modes of use have potential to create different personal meanings, which can in turn evoke different mathematical meanings. Therefore, rather than asking “what does Zaplify adds to the pencil-and-paper?”, the question should be “what is the unique contribution of each artefact to students’ meanings?”. However, this does not imply that those meanings are always mutually exclusive.

The analysis of the semiotic potentials of Zaplify and pencil and paper show that each artifact has the potential to mediate meanings that could help students distinguish multiplication from repeated addition. Both artefacts can mediate multiplication as a binary operation in which each quantity has a distinct referent. While the horizontals quantify one factor as the smaller unit count, the verticals quantify the other factor as the larger unit count [20]. The points on the M-ples represent the functional relationship (as per Vergnaud [17]) between the smaller and the larger units. In each artefact, the referent of the product is different from the factors.

The binary nature of multiplication can be mediated based on the contrasting signs. Each artefact has the potential to mediate such signs. However, Zaplify can provide students with more means to create contrasting signs. For example, the diagonal in Zaplify that visually divides the screen into two separate areas might also be related to the difference between the referents of two multiplicative factors. Moreover, the numerals in Zaplify quantify two different types of lines. Therefore, they might also be related to the distinction between the referents of the factors. Students may also add numerals on their drawings. However, these signs would be static on paper. Whereas in Zaplify, numerals move in two different directions that might give students another opportunity to discuss the difference between the referents of the factors.

Solving a task in Zaplify results in simultaneous actions. This simultaneity presents another unique contribution of Zaplify in mediating various meanings for multiplication. When using Zaplify, a student can use both of her hands, each spatially separated, at the same time. This has the potential to provide a haptic experience that can differentiate the factors. While drawing, students can also experience a spatial haptic difference because of the orientation of tracing gesture. However, these separations would also be temporally apart, lessening the contrast between the haptic experiences.

The simultaneous actions conducted in Zaplify also support the idea of the transfer of unit counts (as per Davydoy [20]). In Zaplify, one finger brings M point(s) as soon as the M-ple-making finger touches the screen. This transfer is not simultaneous when using pencil and paper. Every point must be drawn sequentially, so the correspondence between the unit counts is revealed after students complete their drawing and count the total number of points on the line. Therefore, this temporal separation between the points might hinder the emphasis on the simultaneous unitizing action of multiplication.

Pencil and paper can also contribute to students’ meaning making process in a unique way. The intersections between the perpendicular lines and the points in Zaplify appear without users’ direct manipulation: students interact with these signs only through visual experience. Whereas when students draw the intersections and the points with pencil and paper, they create these signs both with visual and haptic experiences. Therefore, drawing an array with pencil and paper might provide more means to mediate the relationship between the factors and the product.

Each artefact has a unique contribution to the mediation of multiplication as different from repeated addition. Therefore, instead of choosing one artefact over the other, combining these similar but unique artefacts in the learning process would enrich students’ meaning-making process as Maschietto and Soury-Lavergne [31] suggested. They conceptualized the combined use of a physical pedagogical artefact and its digital counterpart as duo of artefact and showed that the use of technology added value to the use of physical objects as classroom teaching equipment because different artefacts triggered different signs, and different signs lead to different cognitions.

The analysis of the semiotic potential of the artefacts revealed two types of interplay between the signs: the contrasting play and the parallel play. In a contrasting play, signs are situated as opposed to each other or the signs that signify differences become salient. Whereas in the parallel play, signs that signify a commonality between the entities are related to each other with linguistic, visual, or haptic connections. Even though in each episode the interplay between visual and haptic signs carries the contrasting and the parallel meanings simultaneously, prompting certain linguistic signs might highlight the targeted interplay between the signs. For example, in each episode, while the vertical and horizontal lines present a contrast between the Zaplify objects, the repetition and the simultaneity of actions present a similarity between the objects. Therefore, the users would simultaneously experience these interplays. When a question prompts students to create additional linguistic signs within a parallel interplay, these signs would highlight the experiences related to similarity over contrast for that session.

The semiotic analysis of artefacts based on TSM is conducted with respect to a pre-given task. However, this analysis can also give educators insights about how to design new tasks. Starting the analysis with the targeted mathematical meanings and relating them to the specific modes of artefact use provide educators with a framework to progress in their designs. The task designer first decides which mathematical meanings to evoke and then they consider which mode of artefact use might be related to these meanings, as illustrated in [32]. The compartmentalization of the video recording into ten-seconds intervals shows that the main task (making 198 in Zaplify) consists of many sub tasks that require different modes of artefact use. For example, creating an M-ple, increasing the number of M-ples, making a specific product are three subtasks embedded in this main task. Each of these subtasks requires a certain mode of artefact use that would mediate specific personal and mathematical meanings. Therefore, the identification of appropriate subtasks and the integration of them in a specific way would evoke the desired mathematical meanings.

Since the meanings emerge from the interplay of the signs [8], examining the relationships between the signs that participate in the targeted mathematical meanings might help the task designer to prompt an appropriate mode of use for the artefact. Let us take Confrey’s [19] description of multiplication: “creating versions of an original” (p. 292). This expression consists of the interplay between three main signs: “creating”, “version”, and “original”. Here, original refers to the first example of its species. Therefore, the question of “what counts as the original in Zaplify” would be the catalyzer for the designer to choose a specific subtask. However, the separate analysis of these signs would reduce the overall meaning of multiplication. For example, analyzing the sign “original” without considering the sign “version” would be incomplete. It is important to ask, “how are the original and the version related to each other?”. This relationship can be associated with a common notion of multiplication that is emphasized by many researchers, yet with different names: functional relationship (as per Vergnaud [17]), intensive quantity (as per Schwartz [16]), many-to-one correspondence (as per Clark and Kamii [18]). Therefore, the original and its version should be prompted according to the specific relationship between them. For example, if one point is considered as the original, then making an M-ple would be considered as the version of an original. If an M-ple is taken as an original, making multiple M-ples would be a version of it.

9. Conclusions

Task design, most of the time, does not explicitly designate a specific technology. However, the paper-and-pencil is generally the implied technology especially when the task prompts students to use static mathematical models. However, with digital technology-specific tasks, we also do not often think about what the task might offer in other technological settings. In this paper, I have analysed the model–task dyad in two distinct settings through the theory of semiotic mediation to examine the affordances of the Zaplify model in mediating multiplication as different from repeated addition. This is similar to identifying the potential of a duo of artefacts in mediating mathematical meanings in the sense that the analysis requires close examination of two similar artefacts. However, unlike a duo of artefact, the analysis of the model–task dyad allows researchers to imagine the possibility of two artefact by considering how a single task might be interesting and relevant to each.

The analysis of the semiotic potential of two artefacts with respect to the same task illustrates how the tasks can undergo some changes when attempted in two different environments. These changes seem to be minor if the focus is directed at the end product, which is the array. However, the processes that result in the array in both environments include many actions that can mediate quite different meanings for multiplication. This analysis suggests that while designing a task, the focus should not be only on the end product; instead, designers should also consider the bodily actions involved in the task solution.

As the term suggests, this analysis identified the potential of these artefacts to mediate various meanings of multiplication. The next step will be to study how these potentials do/not unfold in a real classroom when students attempt to solve the task with each of these artefacts.