Multivariate Classes of GB2 Distributions with Applications
Abstract
1. Introduction
2. The GB2 Distribution
2.1. Representations of the GB2 Distribution
2.2. Previous Work about Multivariate GB2 Distributions
3. Multivariate Distributions with GB2 Marginals
3.1. Multivariate GB2 Income Distributions with p Fixed
3.2. Multivariate GB2 Distributions with q Fixed
3.3. More Multivariate Distributions
4. A General Multivariate GB2 Distribution
4.1. The Model
4.2. The Bivariate Case
5. Multivariate GB2 Distribution with Support above the Diagonal
Marginal and Conditional Distributions
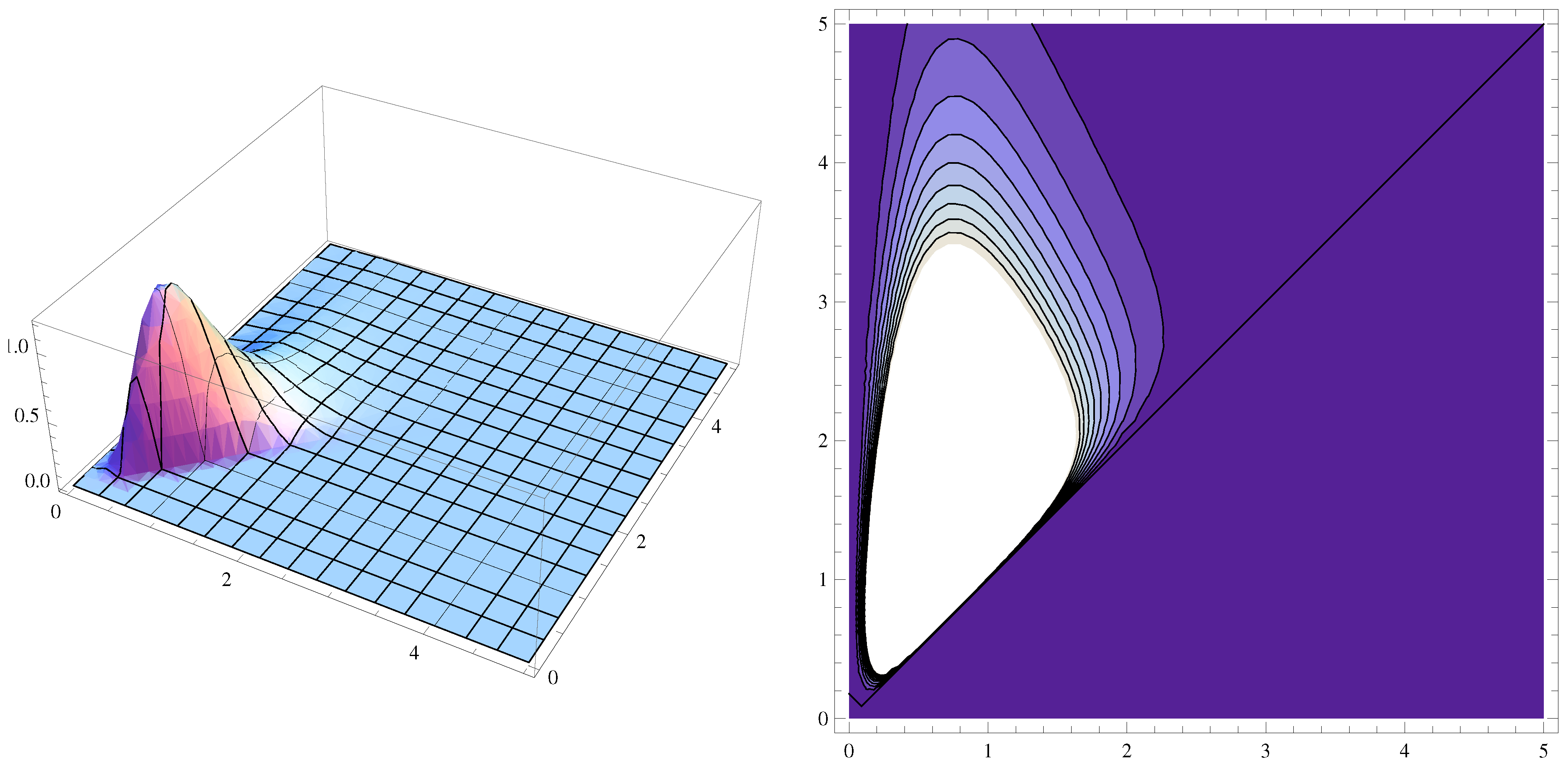
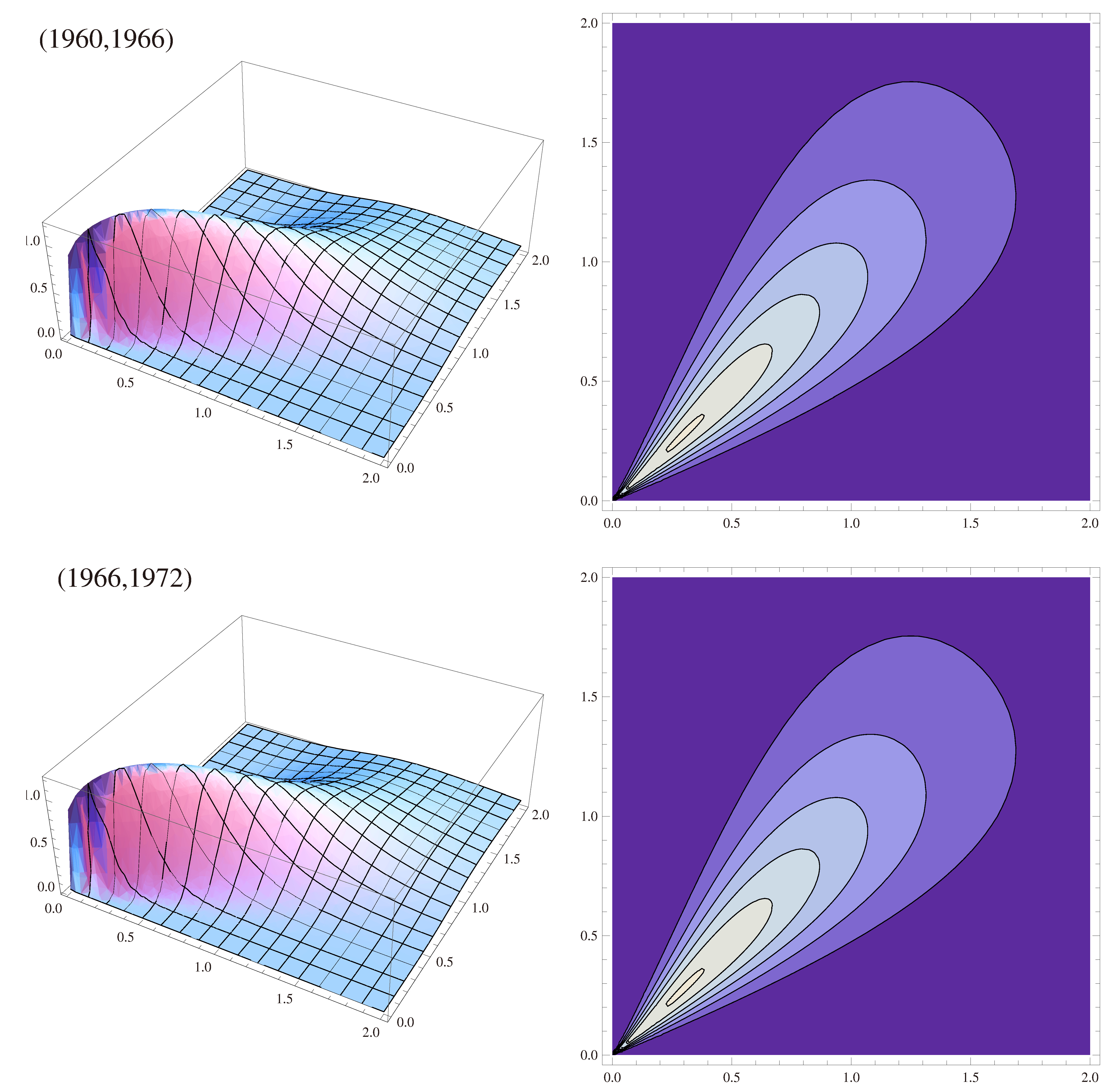
6. Applications
6.1. Modeling Bivariate Income Distributions
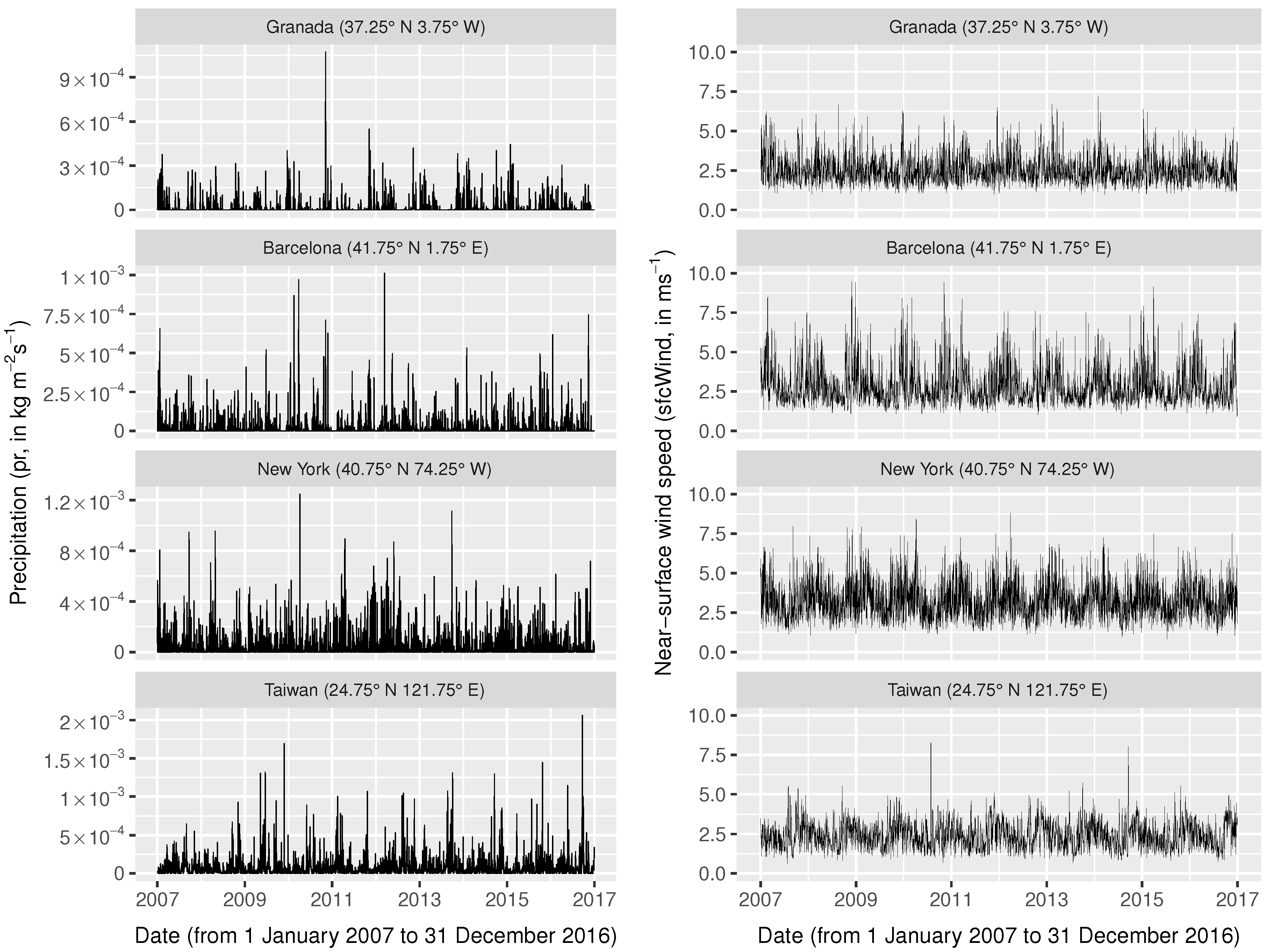
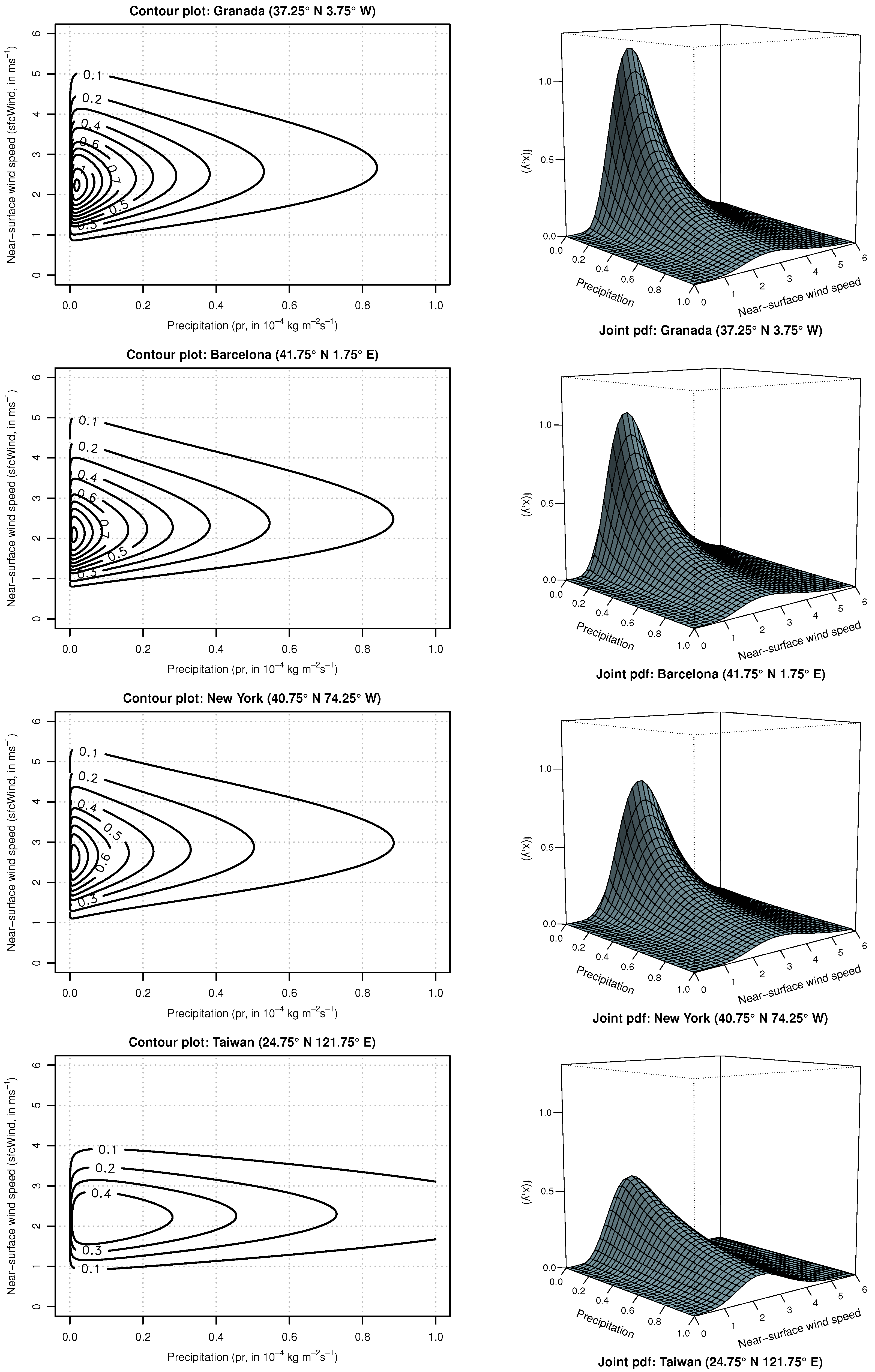
6.2. Modeling Compound Precipitation and Wind Events
6.2.1. Data
6.2.2. Methods
6.2.3. Results
7. Conclusions and Future Research
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Some Results about Whittaker’s and Hypergeometric Functions
References
- Cowell, F.A. Measurement of Inequality. In Handbook of Income Distribution; Atkinson, A.B., Bourguignon, F., Eds.; Elsevier: Amsterdam, The Netherlands, 2000; Volume 1, pp. 87–166. [Google Scholar]
- Slottje, D.J. Using grouped data for constructing inequality indices: Parametric vs. non-parametric methods. Econ. Lett. 1990, 32, 193–197. [Google Scholar] [CrossRef]
- Parker, S.C. The generalized beta as a model for the distribution of earnings. Econ. Lett. 1999, 62, 197–200. [Google Scholar] [CrossRef]
- McDonald, J.B. Some generalized functions for the size distribution of income. Econometrica 1984, 52, 647–663. [Google Scholar] [CrossRef]
- Butler, R.J.; McDonald, J.B. Using incomplete moments to measure inequality. J. Econom. 1989, 42, 109–119. [Google Scholar] [CrossRef]
- Majumder, A.; Chakravarty, S.R. Distribution of Personal Income: Development of a New Model and Its Application to U.S. Income Data. J. Appl. Econom. 1990, 5, 189–196. [Google Scholar] [CrossRef]
- McDonald, J.B.; Xu, Y.J. A generalization of the beta distribution with applications. J. Econom. 1995, 66, 133–152. [Google Scholar] [CrossRef]
- Chotikapanich, D.; Prasada Rao, D.S.; Tang, K.K. Estimating Income Inequality in China Using Grouped Data and the Generalized Beta Distribution. Rev. Income Wealth 2007, 53, 127–147. [Google Scholar] [CrossRef]
- Kleiber, C. On the Lorenz order within parametric families of income distributions. Sankhya B 1999, 61, 514–517. [Google Scholar]
- Sarabia, J.M.; Castillo, E.; Slottje, D.J. Lorenz ordering between McDonald’s generalized functions of the income size distribution. Econ. Lett. 2002, 75, 265–270. [Google Scholar] [CrossRef]
- McDonald, J.B.; Butler, R.J. Some generalized mixture distributions with an application to unemployment duration. In The Review of Economics and Statistics; MIT Press: Cambridge, MA, USA, 1987; pp. 232–240. [Google Scholar]
- McDonald, J.B.; Butler, R.J. Regression models for positive random variables. J. Econom. 1990, 43, 227–251. [Google Scholar] [CrossRef]
- Cummins, J.D.; Dionne, G.; McDonald, J.B.; Pritchett, B.M. Applications of the GB2 family of distributions in modeling insurance loss processes. Insur. Math. Econ. 1990, 9, 257–272. [Google Scholar] [CrossRef]
- Dutta, K.K.; Babbel, D.F. Extracting Probabilistic Information from the Prices of Interest Rate Options: Tests of Distributional Assumptions. J. Bus. 2005, 78, 841–870. [Google Scholar] [CrossRef]
- Kmietowicz, Z.W. The Bivariate Lognormal Model for the Distribution of Household Size and Income. Manch. Sch. Econ. Soc. Stud. 1984, 52, 196–210. [Google Scholar] [CrossRef]
- Nalbach-Leniewska, A. Measures of Dependence of the Multivariate Lognormal Distribution. Math. Oper.-Ser. Stat. 1979, 10, 381–387. [Google Scholar] [CrossRef]
- Mardia, K.V. Multivariate Pareto distributions. Ann. Math. Stat. 1962, 33, 1008–1015. [Google Scholar] [CrossRef]
- Arnold, B.C. Pareto Distributions; International Cooperative Publishing House: Fairland, MD, USA, 1983. [Google Scholar]
- Chiragiev, A.; Landsman, Z. Multivariate flexible Pareto model: Dependency structure, properties and characterizations. Stat. Probab. Lett. 2009, 79, 1733–1743. [Google Scholar] [CrossRef]
- Asimit, A.V.; Furman, E.; Vernic, R. On a multivariate Pareto distribution. Insur. Math. Econ. 2010, 46, 308–316. [Google Scholar] [CrossRef]
- Slottje, D.J. A measure of income inequality based upon the beta distribution of the second kind. Econ. Lett. 1984, 15, 369–375. [Google Scholar] [CrossRef]
- Slottje, D.J. Relative price changes and inequality in the size distribution of various components of income. J. Bus. Econ. Stat. 1987, 5, 19–26. [Google Scholar] [CrossRef]
- Arnold, B.C.; Castillo, E.; Sarabia, J.M. Conditional Specification of Statistical Models; Springer: New York, NY, USA, 1998. [Google Scholar]
- Arnold, B.C.; Castillo, E.; Sarabia, J.M. Conditionally specified distributions: An introduction (with discussion). Stat. Sci. 2001, 16, 249–274. [Google Scholar]
- Arnold, B.C. Bivariate distributions with Pareto conditionals. Stat. Probab. Lett. 1987, 5, 263–266. [Google Scholar] [CrossRef]
- Arnold, B.C.; Castillo, E.; Sarabia, J.M. Multivariate distributions with generalized Pareto conditionals. Stat. Probab. Lett. 1993, 17, 361–368. [Google Scholar] [CrossRef]
- Sarabia, J.M.; Castillo, E.; Pascual, M.; Sarabia, M. Bivariate income distributions with lognormal conditionals. J. Econ. Inequal. 2007, 5, 371–383. [Google Scholar] [CrossRef]
- Sarabia, J.M. Multivariate GB2 Distributions. In Proceedings of the 6th St. Petersburg Workshop on Simulation, St. Petersburg, Russia, 28 June–4 July 2009; pp. 237–241. [Google Scholar]
- Singh, S.K.; Maddala, G.S. A function for the size distribution of incomes. Econometrica 1976, 44, 963–970. [Google Scholar] [CrossRef]
- Dagum, C. A new model of personal income distribution: Specification and estimation. Econ. Appl. 1977, 30, 413–437. [Google Scholar]
- Kleiber, C.; Kotz, S. Statistical Size Distributions in Economics and Actuarial Sciences; John Wiley: New York, NY, USA, 2003. [Google Scholar]
- Arnold, B.C.; Sarabia, J.M. Majorization and the Lorenz Order with Applications in Applied Mathematics and Economics; Springer: Berlin/Heidelberg, Germany, 2018. [Google Scholar]
- Chotikapanich, D.; Griffiths, W.E.; Hajargasht, G.; Karunarathne, W.; Prasada Rao, D.S. Using the GB2 Income Distribution. Econometrics 2018, 6, 21. [Google Scholar] [CrossRef]
- Jones, M.C. Families of distributions arising from distributions of order statistics (with discussion). Test 2004, 13, 1–43. [Google Scholar] [CrossRef]
- Rada-Mora, E.A.; Nagar, D. Multivariate generalized beta distribution. Random Oper. Stoch. Equ. 2007, 15, 163–180. [Google Scholar] [CrossRef]
- Yang, X.; Frees, E.W.; Zhang, Z. A generalized beta copula with applications in modeling multivariate long-tailed data. Insur. Math. Econ. 2011, 49, 265–284. [Google Scholar] [CrossRef]
- Sarabia, J.M.; Prieto, F.; Jorda, V. Bivariate beta-generated distributions with applications to well-being data. J. Stat. Distrib. Appl. 2014, 1, 15. [Google Scholar] [CrossRef]
- Cockriel, W.M.; McDonald, J.B. Two multivariate generalized beta families. Commun. Stat.-Theory Methods 2018, 47, 5688–5701. [Google Scholar] [CrossRef]
- Balakrishnan, N.; Lai, C.D. Continuous Bivariate Distributions, 2nd ed.; Springer: New York, NY, USA, 2009. [Google Scholar]
- Olkin, I.; Liu, R. A bivariate beta distribution. Stat. Probab. Lett. 2003, 62, 407–412. [Google Scholar] [CrossRef]
- Fang, K.T.; Kotz, S.; Ng, K.W. Symmetric Multivariate and Related Distributions; Chapman and Hall: London, UK, 1990. [Google Scholar]
- Jones, M.C. A dependent bivariate t distribution with marginals on different degrees of freedom. Stat. Probab. Lett. 2002, 56, 163–170. [Google Scholar] [CrossRef]
- Sarhan, A.M.; Balakrishnan, N. A new class of bivariate distributions and its mixture. J. Multivar. Anal. 2007, 98, 1508–1527. [Google Scholar] [CrossRef][Green Version]
- El-Bassiouny, A.H.; Jones, M.C. A bivariate F distribution with marginals on arbitrary numerator and denominator degrees of freedom, and related bivariate beta and t distributions. Stat. Methods Appl. 2009, 18, 465–481. [Google Scholar] [CrossRef][Green Version]
- Sarabia, J.M.; Gómez-Déniz, E. Construction of multivariate distributions: A review of some recent results (with discussion). Stat. Oper. Res. Trans. 2008, 32, 3–36. [Google Scholar]
- Esary, J.D.; Proschan, F.; Walkup, D.W. Association of random variables, with applications. Ann. Math. Stat. 1967, 38, 1466–1474. [Google Scholar] [CrossRef]
- Guillén, M.; Sarabia, J.M.; Prieto, F. Simple risk measure calculations for sums of positive random variables. Insur. Math. Econ. 2013, 51, 273–280. [Google Scholar] [CrossRef]
- Kleiber, C. Dagum vs. Singh-Maddala income distributions. Econ. Lett. 1996, 53, 265–268. [Google Scholar] [CrossRef]
- Jones, M.C.; Larsen, P.V. Multivariate distributions with support above the diagonal. Biometrika 2004, 91, 975–986. [Google Scholar] [CrossRef]
- Vinh, A.; Griffiths, W.E.; Chotikapanich, D. Bivariate income distributions for assessing inequality and poverty under dependent samples. Econ. Model. 2010, 27, 1473–1483. [Google Scholar] [CrossRef]
- Takahasi, K. Note on the Multivariate Burr’s Distribution. Ann. Inst. Stat. Math. 1965, 17, 257–260. [Google Scholar] [CrossRef]
- Björklund, A.; Jäntti, M. Intergenerational Income Mobility in Sweden Compared to the United States. Am. Econ. Rev. 1997, 87, 1009–1018. [Google Scholar]
- Chetty, R.; Hendren, N.; Kline, P.; Saez, E.; Turner, N. Is the United States still a land of opportunity? Recent trends in intergenerational mobility. Am. Econ. Rev. 2014, 104, 141–147. [Google Scholar] [CrossRef]
- Greenwood, J.; Guner, N.; Kocharkov, G.; Santos, C. Marry your like: Assortative mating and income inequality. Am. Econ. Rev. 2014, 104, 348–353. [Google Scholar] [CrossRef]
- Maasoumi, E.; Wang, L. The gender gap between earnings distributions. J. Political Econ. 2019, 127, 2438–2504. [Google Scholar] [CrossRef]
- Jäntti, M.; Sierminska, E.M.; Van Kerm, P. Modeling the Joint Distribution of Income and Wealth. Res. Econ. Inequal. 2015, 23, 301–327. [Google Scholar]
- Chetty, R.; Hendren, N. The impacts of neighborhoods on intergenerational mobility I: Childhood exposure effects. Q. J. Econ. 2018, 133, 1107–1162. [Google Scholar] [CrossRef]
- Martius, O.; Pfahl, S.; Chevalier, C. A global quantification of compound precipitation and wind extremes. Geophys. Res. Lett. 2016, 43, 7709–7717. [Google Scholar] [CrossRef]
- Cugerone, K.; De Michele, C.; Ghezzi, A.; Gianelle, V. Aerosol removal due to precipitation and wind forcings in Milan urban area. J. Hydrol. 2018, 556, 1256–1262. [Google Scholar] [CrossRef]
- Frieler, K.; Lange, S.; Piontek, F.; Reyer, C.P.; Schewe, J.; Warszawski, L.; Zhao, F.; Chini, L.; Denvil, S.; Emanuel, K.; et al. Assessing the impacts of 1.5 °C global warming-simulation protocol of the Inter-Sectoral Impact Model Intercomparison Project (ISIMIP2b). In Geoscientific Model Development; Copernicus Publications: Argentina, Germany, 2017. [Google Scholar]
- Lange, S. Bias correction of surface downwelling longwave and shortwave radiation for the EWEMBI dataset. Earth Syst. Dyn. 2018, 9, 627–645. [Google Scholar] [CrossRef]
- Lange, S. EartH2Observe, WFDEI and ERA-Interim Data Merged and Bias-Corrected for ISIMIP (EWEMBI). V. 1.1. GFZ Data Services. 2019. Available online: https://doi.org/10.5880/pik.2019.004 (accessed on 23 October 2020).
- Lange, S. Trend-preserving bias adjustment and statistical downscaling with ISIMIP3BASD (v1. 0). In Geoscientific Model Development; Copernicus Publications: Argentina, Germany, 2019; Volume 2. [Google Scholar]
- Akaike, H. A new look at the statistical model identification. IEEE Trans. Autom. Control 1974, 19, 716–723. [Google Scholar] [CrossRef]
- Guillén, M.; Sarabia, J.M.; Belles-Sampera, J.; Prieto, F. Distortion risk measures for nonnegative multivariate risks. J. Oper. Risk 2018, 13, 35–57. [Google Scholar] [CrossRef]
- Roozegar, R.; Balakrishnan, N.; Jamalizadeh, A. On moments of doubly truncated multivariate normal mean-variance mixture distributions with application to multivariate tail conditional expectation. J. Multivar. Anal. 2020, 177, 104586. [Google Scholar] [CrossRef]
- Sarabia, J.M.; Guillén, M.; Chuliá, H.; Prieto, F. Tail risk measures using flexible parametric distributions. Stat. Oper. Res. Trans. 2019, 53, 223–236. [Google Scholar]
- Gradshteyn, I.S.; Ryzhik, I.M. Table of Integrals, Series, and Products, 5th ed.; Jeffrey, A., Ed.; Academic Press: San Diego, CA, USA, 1994. [Google Scholar]
| Location | Coordinates | Grid Point | Probability of |
|---|---|---|---|
| Coordinates | Compound Event | ||
| Alhambra, Granada, Spain | N W | N W | 0.2935 |
| Sagrada Familia, Barcelona, Spain | N E | N E | 0.3452 |
| Statue of Liberty, New York City, USA | N W | N W | 0.4610 |
| Taipei World Financial Center, Taiwan | N E | N E | 0.8555 |
| Location | ||||||||
|---|---|---|---|---|---|---|---|---|
| Granada | 16.3187 | 3.0369 | 7.9799 | 0.4702 | 1.1355 | 12.1607 | 5.3893 | −3992.44 |
| ( N W) | (2.8526) | (1.0185) | (2.4878) | (0.0783) | (0.1419) | (4.0787) | (1.2403) | |
| Barcelona | 16.6511 | 2.0810 | 11.7500 | 0.5627 | 0.9280 | 16.4814 | 3.9937 | −5004.23 |
| ( N E) | (2.1999) | (0.4537) | (3.1215) | (0.0626) | (0.0878) | (4.0430) | (0.9927) | |
| New York | 13.8062 | 2.5009 | 6.7216 | 0.4862 | 1.3179 | 16.5038 | 5.6226 | −7793.07 |
| ( N W) | (1.8616) | (0.5979) | (1.3626) | (0.0587) | (0.1096) | (4.0350) | (0.8037) | |
| Taiwan | 11.0710 | 2.1498 | 2.3624 | 0.6120 | 2.0889 | 11.1861 | 5.4784 | −14,855.81 |
| ( N E) | (2.3232) | (0.3306) | (0.4214) | (0.0542) | (0.2086) | (3.9155) | (0.5138) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sarabia, J.M.; Jordá, V.; Prieto, F.; Guillén, M. Multivariate Classes of GB2 Distributions with Applications. Mathematics 2021, 9, 72. https://doi.org/10.3390/math9010072
Sarabia JM, Jordá V, Prieto F, Guillén M. Multivariate Classes of GB2 Distributions with Applications. Mathematics. 2021; 9(1):72. https://doi.org/10.3390/math9010072
Chicago/Turabian StyleSarabia, José María, Vanesa Jordá, Faustino Prieto, and Montserrat Guillén. 2021. "Multivariate Classes of GB2 Distributions with Applications" Mathematics 9, no. 1: 72. https://doi.org/10.3390/math9010072
APA StyleSarabia, J. M., Jordá, V., Prieto, F., & Guillén, M. (2021). Multivariate Classes of GB2 Distributions with Applications. Mathematics, 9(1), 72. https://doi.org/10.3390/math9010072








