Neutrosophic Completion Technique for Incomplete Higher-Order AHP Comparison Matrices
Abstract
1. Introduction
2. Materials and Methods
2.1. Preliminaries on Classical AHP Method
2.2. Analytic Hierarchy Process in a Neutrosophic Environment
2.2.1. Neutrosophic Logic Fundamentals
2.2.2. On the Construction of the Neutrosophic AHP Comparison Matrix
2.2.3. Derivation of Weights from a Neutrosophic Comparison Matrix
2.2.4. Deneutrosophication Process
2.3. Completion Method for Neutrosophic AHP Comparison Matrices
2.3.1. The Classical DEMATEL Technique
2.3.2. Completion Method for Neutrosophic AHP Matrices
3. Problem Definition
4. Results
4.1. Scalar Weights Derived from the Baseline Complete Comparison Matrix
4.2. Completion Results
4.3. Comparison of the Results Considering a Different Expert
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
| C1 | C2 | C3 | C4 | C5 | C6 | C7 | C8 | C9 | |
|---|---|---|---|---|---|---|---|---|---|
| C1 | 1 | 1/3 | 1/6 | 1/6 | 1/6 | 1/3 | 1/4 | 1/4 | 1/4 |
| C2 | 3 | 1 | 1/2 | 1/5 | 1/4 | 1/2 | 3 | 1/2 | 1/2 |
| C3 | 6 | 2 | 1 | 1 | 1/2 | 3 | 7 | 6 | 6 |
| C4 | 6 | 5 | 1 | 1 | 1/2 | 3 | 7 | 6 | 6 |
| C5 | 6 | 4 | 2 | 2 | 1 | 2 | 6 | 5 | 5 |
| C6 | 3 | 2 | 1/3 | 1/3 | 1/2 | 1 | 2 | 1/2 | 1/2 |
| C7 | 4 | 1/3 | 1/7 | 1/7 | 1/6 | 1/2 | 1 | 1/2 | 1/2 |
| C8 | 4 | 2 | 1/6 | 1/6 | 1/5 | 2 | 2 | 1 | 1 |
| C9 | 4 | 2 | 1/6 | 1/6 | 1/5 | 2 | 2 | 1 | 1 |
| C1 | C2 | C3 | C4 | C5 | C6 | C7 | C8 | C9 | |
|---|---|---|---|---|---|---|---|---|---|
| C1 | 1 | 0.8 | 0.5 | 0.7 | 0.9 | 0.8 | 0.8 | 0.6 | 0.2 |
| C2 | 0.8 | 1 | 0.7 | 0.8 | 0.6 | 0.6 | 0.4 | 0.7 | 0.7 |
| C3 | 1/2 | 2/3 | 1 | 0.8 | 0.8 | 0.7 | 0.8 | 0.7 | 0.6 |
| C4 | 0.7 | 0.8 | 0.8 | 1 | 0.8 | 0.3 | 0.4 | 0.5 | 0.6 |
| C5 | 0.9 | 0.6 | 0.8 | 0.8 | 1 | 0.2 | 0.7 | 0.6 | 0.4 |
| C6 | 0.8 | 0.6 | 0.7 | 0.3 | 0.2 | 1 | 0.8 | 0.8 | 0.4 |
| C7 | 0.8 | 0.4 | 0.8 | 0.4 | 0.7 | 0.8 | 1 | 0.5 | 0.5 |
| C8 | 0.6 | 0.7 | 0.7 | 0.5 | 0.6 | 0.8 | 0.5 | 1 | 0.4 |
| C9 | 0.2 | 0.7 | 0.6 | 0.6 | 0.4 | 0.4 | 0.5 | 0.4 | 1 |
| Expert’s Profile Defining Parameters | Value |
|---|---|
| Knowledge degree in design of infrastructures | 0.60 |
| Expertise in economic assessments | 0.60 |
| Expertise in environmental assessments | 1.00 |
| Expertise in social life-cycle assessments | 0.80 |
| Expert’s credibility. Truth membership parameter t | 0.80 |
| Expressed mean self confidence | 0.66 |
| Expert’s certainty. Indeterminacy membership parameter i | 0.34 |
| Consistency ratio of the comparison matrix | 0.07 |
| Expert’s inconsistency. Falsehood membership parameter f | 0.72 |
| Scenario | C1 | C2 | C3 | C4 | C5 | C6 | C7 | C8 | C9 |
|---|---|---|---|---|---|---|---|---|---|
| Expert 1 | 0.049 | 0.019 | 0.179 | 0.262 | 0.168 | 0.024 | 0.046 | 0.152 | 0.101 |
| Expert 2 | 0.027 | 0.060 | 0.204 | 0.214 | 0.237 | 0.076 | 0.048 | 0.074 | 0.061 |
References
- Worrell, E.; Price, L.; Martin, N.; Hendriks, C.; Ozawa, L. Carbon dioxide emissions from the global cement industry. Annu. Rev. Energ. Environ. 2001, 26, 303–329. [Google Scholar] [CrossRef]
- García, J.; Yepes, V.; Martí, J.V. A hybrid k-means cuckoo search algorithm applied to the counterfort retaining walls problem. Mathematics 2020, 8, 555. [Google Scholar] [CrossRef]
- Penadés-Plà, V.; García-Segura, T.; Yepes, V. Robust design optimization for low-cost concrete box-girder bridge. Mathematics 2020, 8, 398. [Google Scholar] [CrossRef]
- Kim, S.; Frangopol, D.M. Multi-objective probabilistic optimum monitoring planning considering fatigue damage detection, maintenance, reliability, service life and cost. Struct. Multidisc. Optim. 2018, 57, 39–54. [Google Scholar] [CrossRef]
- García-Segura, T.; Yepes, V.; Frangopol, D.M. Multi-objective design of post-tensioned concrete road bridges using artificial neural networks. Struct. Multidiscip. Optim. 2017, 56, 139–150. [Google Scholar] [CrossRef]
- Van den Heede, P.; De Belie, N. A service life based global warming potential for high-volume fly ash concrete exposed to carbonation. Constr. Build. Mater. 2014, 55, 183–193. [Google Scholar] [CrossRef]
- García, J.; Martí, J.V.; Yepes, V. The Buttressed walls problem: An application of a hybrid clustering particle swarm optimization algorithm. Mathematics 2020, 8, 862. [Google Scholar] [CrossRef]
- García-Segura, T.; Penadés-Plà, V.; Yepes, V. Sustainable bridge design by metamodel-assisted multi-objective optimization and decision-making under uncertainty. J. Clean. Prod. 2018, 202, 904–915. [Google Scholar] [CrossRef]
- Gursel, A.P.; Ostertag, C. Comparative life-cycle impact assessment of concrete manufacturing in Singapore. Int. J. Life Cycle Assess. 2017, 22, 237–255. [Google Scholar] [CrossRef]
- Penadés-Plà, V.; Martí, J.V.; García-Segura, T.; Yepes, V. Life-cycle assessment: A comparison between two optimal post-tensioned concrete box-girder road bridges. Sustainability 2017, 9, 1864. [Google Scholar] [CrossRef]
- Navarro, I.J.; Yepes, V.; Martí, J.V. Social life cycle assessment of concrete bridge decks exposed to aggressive environments. Environ. Impact Assess. 2018, 72, 50–63. [Google Scholar] [CrossRef]
- Sierra, L.A.; Pellicer, E.; Yepes, V. Method for estimating the social sustainability of infrastructure projects. Environ. Impact Assess. 2017, 65, 41–53. [Google Scholar] [CrossRef]
- Navarro, I.J.; Yepes, V.; Martí, J.V. Sustainability assessment of concrete bridge deck designs in coastal environments using neutrosophic criteria weights. Struct. Infrastruct. Eng. 2020, 16, 949–967. [Google Scholar] [CrossRef]
- Saaty, T.L. The Analytic Hierarchy Process; McGraw-Hill: New York, NY, USA, 1980. [Google Scholar]
- Tavana, M.; Shaabani, A.; Javier Santos-Arteaga, F.; Raeesi Vanani, I. A review of uncertain decision-making methods in energy management using text mining and data analytics. Energies 2020, 13, 3947. [Google Scholar] [CrossRef]
- Yannis, G.; Kopsacheili, A.; Dragomanovits, A.; Petraki, V. State-of-the-art review on multi-criteria decision-making in the transport sector. J. Traffic Transp. Eng. 2020, 7, 413–431. [Google Scholar] [CrossRef]
- Navarro, I.J.; Penadés-Plà, V.; Martínez-Muñoz, D.; Rempling, R.; Yepes, V. Life cycle sustainability assessment for multi-criteria decision making in bridge design: A review. J. Civ. Eng. Manag. 2020, 26, 690–704. [Google Scholar] [CrossRef]
- Radwan, N.; Senousy, M.; Riad, A. Neutrosophic AHP multi-criteria decision making method applied on the selection of learning management system. Int. J. Adv. Comp. Technol. 2016, 8, 95–105. [Google Scholar]
- Hedelin, B. Complexity is no excuse. Sustain. Sci. 2019, 14, 733–749. [Google Scholar] [CrossRef]
- Zadeh, L. Outline of a new approach to the analysis of complex systems and decision processes. IEEE Trans. Sys. Man. Cyb. 1973, 3, 28–44. [Google Scholar] [CrossRef]
- Zadeh, L. Fuzzy sets. Inform. Control 1965, 8, 338–353. [Google Scholar] [CrossRef]
- Milošević, D.M.; Milošević, M.R.; Simjanović, D.J. Implementation of adjusted fuzzy AHP method in the assessment for reuse of industrial buildings. Mathematics 2020, 8, 1697. [Google Scholar] [CrossRef]
- Lin, C.-N. A fuzzy analytic hierarchy process-based analysis of the dynamic sustainable management index in leisure agriculture. Sustainability 2020, 12, 5395. [Google Scholar] [CrossRef]
- Salehi, S.; Ghazizadeh, M.J.; Tabesh, M.; Valadi, S.; Nia, S.P. A risk component-based model to determine pipes renewal strategies in water distribution networks. Struct. Infrastruct. Eng. 2019. [Google Scholar] [CrossRef]
- Smarandache, F. A Unifying Field in Logics, Neutrosophy: Neutrosophic Probability, Set and Logic; American Research Press: Rehoboth, DE, USA, 1999. [Google Scholar]
- Liu, P.; Liu, X. The neutrosophic number generalized weighted power averaging operator and its application in multiple attribute group decision making. Int. J. Mach. Learn. Cyb. 2018, 9, 347–358. [Google Scholar] [CrossRef]
- Peng, J.J.; Wang, J.; Yang, W. A multi-valued neutrosophic qualitative flexible approach based on likelihood for multi-criteria decision-making problems. Int. J. Syst. Sci. 2017, 48, 425–435. [Google Scholar] [CrossRef]
- Saaty, T.; Ozdemir, M. Why the magic number seven plus or minus two. Math. Comput. Model. 2003, 38, 233–244. [Google Scholar] [CrossRef]
- Harker, P.T. Incomplete pairwise comparisons in the analytic hierarchy process. Math. Mod. 1987, 9, 837–848. [Google Scholar] [CrossRef]
- Chen, K.; Kou, G.; Tarn, J.M.; Song, Y. Bridging the gap between missing and inconsistent values in eliciting preference from pairwise comparison matrices. Ann. Oper. Res. 2015, 235, 155–175. [Google Scholar] [CrossRef]
- Bozóki, S.; Fülöp, J.; Rónyai, L. On optimal completion of incomplete pairwise comparison matrices. Math. Comput. Model. 2010, 52, 318–333. [Google Scholar] [CrossRef]
- Dong, M.; Li, S.; Zhang, H. Approaches to group decision making with incomplete information based on power geometric operators and triangular fuzzy AHP. Expert Syst. Appl. 2015, 42, 7846–7857. [Google Scholar] [CrossRef]
- Zhou, X.; Hu, Y.; Deng, Y.; Deng, Y.; Chan, F.T.; Ishizaka, A. A DEMATEL-based completion method for incomplete pairwise comparison matrix in AHP. Ann. Oper. Res. 2018, 271, 1045–1066. [Google Scholar] [CrossRef]
- Sumathi, I.R.; Antony Crispin Sweety, C. New approach on differential equation via trapezoidal neutrosophic number. Complex Intell. Syst. 2019, 5, 417–424. [Google Scholar] [CrossRef]
- Deli, I.; Subas, Y. A ranking method of single valued neutrosophic numbers and its applications to multi-attribute decision making problems. Int. J. Mach. Learn. Cyb. 2017, 8, 1309–1322. [Google Scholar] [CrossRef]
- Ye, J. Subtraction and Division Operations of simplified neutrosophic sets. Information 2017, 8, 51. [Google Scholar] [CrossRef]
- Liang, R.; Wang, J.; Zhang, H. A multi-criteria decision-making method based on single-valued trapezoidal neutrosophic preference relations with complete weight information. Neural Comput. App. 2018, 30, 3383–3398. [Google Scholar] [CrossRef]
- Sodenkamp, M.A.; Tavana, M.; Di Caprio, D. An aggregation method for solving group multi-criteria decision-making problems with single-valued neutrosophic sets. Appl. Soft Comput. 2018, 71, 715–727. [Google Scholar] [CrossRef]
- Sierra, L.A.; Pellicer, E.; Yepes, V. Social sustainability in the life cycle of Chilean public infrastructure. J. Constr. Eng. Manag. 2016, 142, 05015020. [Google Scholar] [CrossRef]
- Abdel-Basset, M.; Manogaran, G.; Mohamed, M.; Chilamkurti, N. Three-way decisions based on neutrosophic sets and AHP-QFD framework for supplier selection problem. Future Gener. Comput. Syst. 2018, 89, 19–30. [Google Scholar] [CrossRef]
- Dubois, D. The role of fuzzy sets in decision sciences: Old techniques and new directions. Fuzzy Set. Syst. 2011, 184, 3–28. [Google Scholar] [CrossRef]
- Buckley, J.J. Fuzzy hierarchical analysis. Fuzzy Set. Syst. 1985, 17, 233–247. [Google Scholar] [CrossRef]
- Wang, Y.M.; Elhag, T.M. On the normalization of interval and fuzzy weights. Fuzzy Set. Syst. 2006, 157, 2456–2471. [Google Scholar] [CrossRef]
- Enea, M.; Piazza, T. Project selection by constrained fuzzy AHP. Fuzzy Optim. Decis. Mak. 2004, 3, 39–62. [Google Scholar] [CrossRef]
- Chu, T.; Tao, C. Ranking fuzzy numbers with an area between the centroid point and original point. Comput. Math. Appl. 2002, 43, 111–117. [Google Scholar] [CrossRef]
- Gabus, A.; Fontela, E. World Problems, an Invitation to Further Tought within the Framework of Dematel; Battelle Geneva Research Centre: Geneva, Switzerland, 1972. [Google Scholar]
- Goedkoop, M.; Heijungs, R.; Huijbregts, M.; De Schryver, A.; Struijs, J.; Van Zelm, R. ReCiPe 2008: A Life Cycle Impact Assessment Method Which Comprises Harmonised Category Indicators at the Midpoint and the Endpoint Level; Ministerie van Volkshuisvesting: The Hague, The Netherlands, 2009. [Google Scholar]
- UNEP/SETAC. Guidelines for Social Life Cycle Assessment of Products; UNEP/SETAC Life-Cycle Initiative: Paris, France, 2009. [Google Scholar]
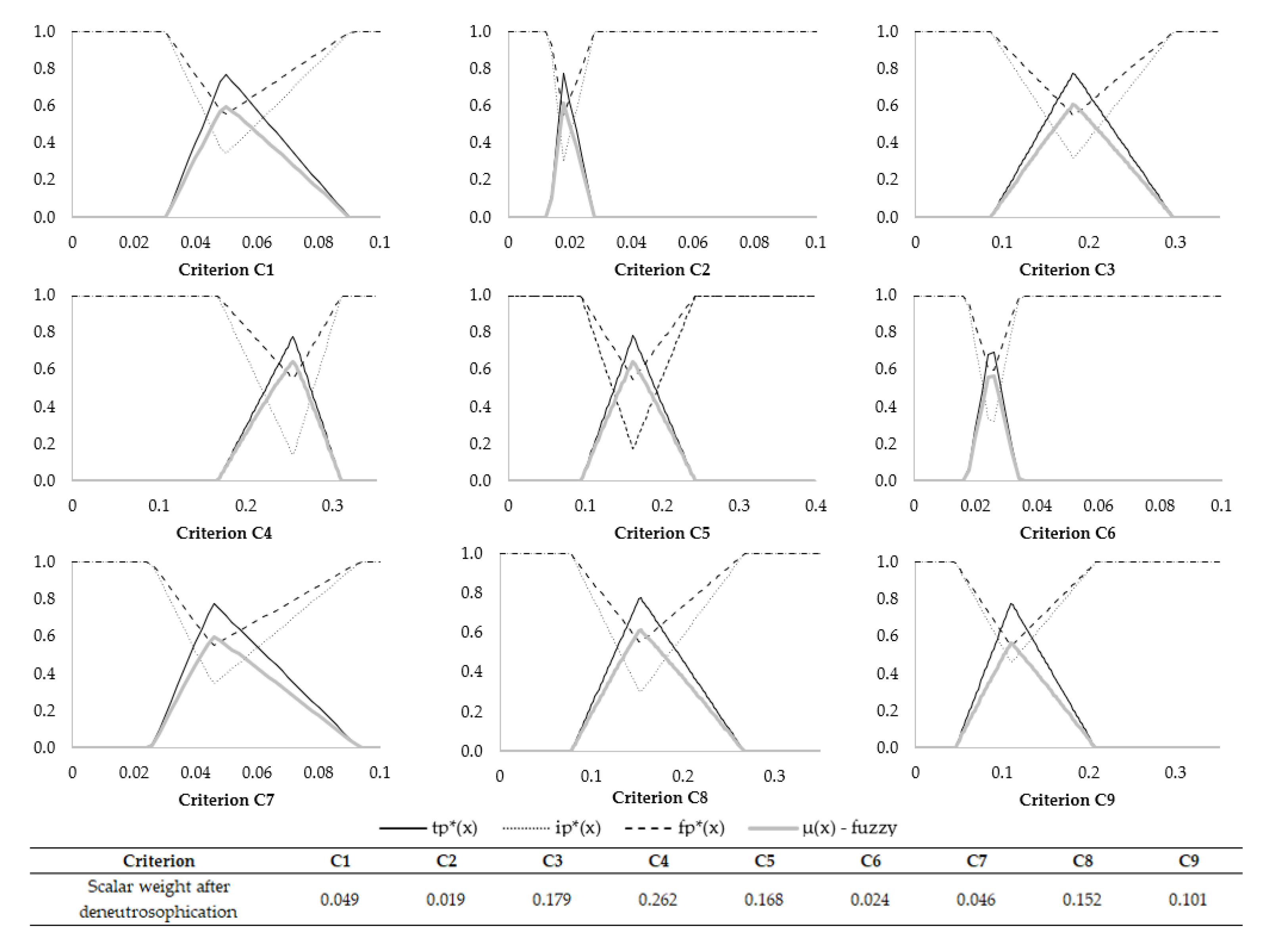
| Certainty cij | Steps ∆(cij) on Saaty’s Extended Scale |
|---|---|
| cij = 1 | 0 |
| 0.8 ≤ cij < 1 | 1 |
| 0.6 ≤ cij < 0.8 | 2 |
| 0.4 ≤ cij < 0.6 | 3 |
| 0.2 ≤ cij < 0.4 | 4 |
| 0 ≤ cij < 0.2 | 5 |
| cij = 0 | 6 |
| Number of criteria n | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| Random Index RI | 0.58 | 0.90 | 1.12 | 1.24 | 1.32 | 1.41 | 1.45 |
| Sustainability Dimension | Criterion | Comments |
|---|---|---|
| Economy | C1—Construction costs | Costs associated to materials production and installation, machinery, and workers |
| C2—Maintenance and demolition costs | Costs associated to materials production and installation, machinery, and workers involved in maintenance activities | |
| Environment | C3—Damage on human health | Emission of pollutants causing respiratory diseases, carcinogenics |
| C4—Damage on ecosystems | Land occupation, emission of pollutants | |
| C5—Resource depletion | Depletion of natural resources resulting from extraction activities | |
| Society | C6—Employment generation | Accounts for gender equity, unemployment, safety, and fair salary |
| C7—Development of local economies | Economic investments derived from material production activities and machinery rental | |
| C8—Impacts on infrastructure users | Accessibility and drivers’ safety | |
| C9—Impacts on local communities | Public opinion considering aesthetics and disturbances |
| C1 | C2 | C3 | C4 | C5 | C6 | C7 | C8 | C9 | |
|---|---|---|---|---|---|---|---|---|---|
| C1 | 1 | 6 | 1/5 | 1/6 | 1/5 | 4 | 1 | 1/4 | 1/3 |
| C2 | 1/6 | 1 | 1/7 | 1/7 | 1/6 | 1/3 | 1/3 | 1/6 | 1/7 |
| C3 | 5 | 7 | 1 | 1/2 | 1 | 5 | 5 | 2 | 2 |
| C4 | 6 | 7 | 2 | 1 | 1 | 7 | 6 | 2 | 5 |
| C5 | 5 | 6 | 1 | 1 | 1 | 5 | 4 | 1 | 1 |
| C6 | 1/4 | 3 | 1/5 | 1/7 | 1/5 | 1 | 1/4 | 1/6 | 1/6 |
| C7 | 1 | 3 | 1/5 | 1/6 | 1/4 | 4 | 1 | 1/5 | 1/3 |
| C8 | 4 | 6 | 1/2 | 1/2 | 1 | 6 | 5 | 1 | 2 |
| C9 | 3 | 7 | 1/2 | 1/5 | 1 | 6 | 3 | 1/2 | 1 |
| C1 | C2 | C3 | C4 | C5 | C6 | C7 | C8 | C9 | |
|---|---|---|---|---|---|---|---|---|---|
| C1 | 1 | 0.80 | 0.80 | 0.90 | 0.90 | 0.60 | 0.60 | 0.70 | 0.20 |
| C2 | 0.8 | 1 | 0.80 | 0.90 | 0.90 | 0.70 | 0.70 | 0.80 | 0.20 |
| C3 | 0.8 | 0.8 | 1 | 0.70 | 0.80 | 0.70 | 0.50 | 0.50 | 0.50 |
| C4 | 0.9 | 0.9 | 0.7 | 1 | 0.90 | 0.80 | 0.80 | 0.90 | 0.90 |
| C5 | 0.9 | 0.9 | 0.8 | 0.9 | 1 | 0.70 | 0.70 | 0.70 | 0.90 |
| C6 | 0.6 | 0.7 | 0.7 | 0.8 | 0.7 | 1 | 0.80 | 0.80 | 0.80 |
| C7 | 0.6 | 0.7 | 0.5 | 0.8 | 0.7 | 0.8 | 1 | 0.50 | 0.50 |
| C8 | 0.7 | 0.8 | 0.5 | 0.9 | 0.7 | 0.8 | 0.5 | 1 | 0.60 |
| C9 | 0.2 | 0.2 | 0.5 | 0.9 | 0.9 | 0.8 | 0.5 | 0.6 | 1 |
| Expert’s Profile Defining Parameters | Value |
|---|---|
| Knowledge degree in design of infrastructures | 1.00 |
| Expertise in economic assessments | 0.60 |
| Expertise in environmental assessments | 0.80 |
| Expertise in social life-cycle assessments | 0.40 |
| Expert’s credibility. Truth membership parameter t | 0.76 |
| Expressed mean self confidence | 0.74 |
| Expert’s certainty. Indeterminacy membership parameter i | 0.26 |
| Consistency ratio of the comparison matrix | 0.06 |
| Expert’s inconsistency. Falsehood membership parameter f | 0.59 |
| Scenario | C1 | C2 | C3 | C4 | C5 | C6 | C7 | C8 | C9 |
|---|---|---|---|---|---|---|---|---|---|
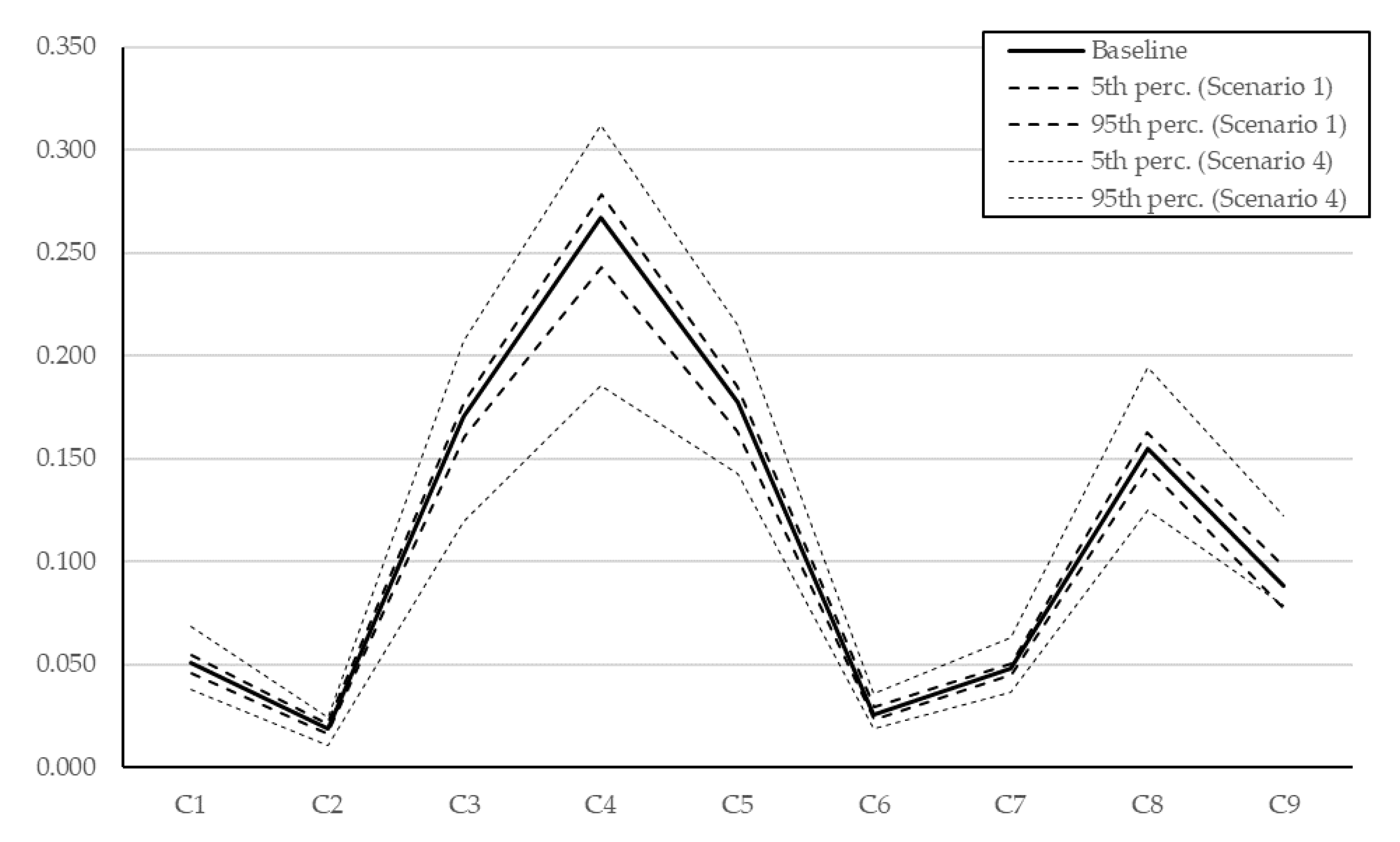
| Baseline | 0.049 | 0.019 | 0.179 | 0.262 | 0.168 | 0.024 | 0.046 | 0.152 | 0.101 |
| 3 missing | 0.051 | 0.019 | 0.170 | 0.267 | 0.177 | 0.026 | 0.048 | 0.155 | 0.088 |
| 5 missing | 0.052 | 0.019 | 0.169 | 0.263 | 0.178 | 0.026 | 0.048 | 0.155 | 0.091 |
| 8 missing | 0.053 | 0.018 | 0.168 | 0.257 | 0.178 | 0.026 | 0.049 | 0.156 | 0.096 |
| 12 missing | 0.053 | 0.018 | 0.164 | 0.249 | 0.178 | 0.027 | 0.051 | 0.159 | 0.101 |
| Max. deviation from baseline | 8.4% | 8.7% | 8.1% | 4.9% | 6.3% | 10.2% | 10.5% | 4.5% | 0.1% |
| Scenario | C1 | C2 | C3 | C4 | C5 | C6 | C7 | C8 | C9 |
|---|---|---|---|---|---|---|---|---|---|
| 3 missing | 5.25% | 7.41% | 3.26% | 4.22% | 3.76% | 6.62% | 3.29% | 3.22% | 6.75% |
| 5 missing | 7.11% | 9.92% | 5.58% | 6.64% | 5.26% | 8.54% | 5.31% | 4.88% | 8.29% |
| 8 missing | 10.45% | 14.63% | 9.39% | 9.89% | 7.93% | 13.14% | 8.63% | 8.23% | 9.07% |
| 12 missing | 17.22% | 23.00% | 15.83% | 15.57% | 12.60% | 19.44% | 15.81% | 12.95% | 13.87% |
| Scenario | C1 | C2 | C3 | C4 | C5 | C6 | C7 | C8 | C9 |
|---|---|---|---|---|---|---|---|---|---|
| Baseline | 0.027 | 0.060 | 0.204 | 0.214 | 0.237 | 0.076 | 0.048 | 0.074 | 0.061 |
| 3 missing | 0.025 | 0.071 | 0.225 | 0.210 | 0.230 | 0.074 | 0.043 | 0.070 | 0.052 |
| 5 missing | 0.025 | 0.070 | 0.220 | 0.209 | 0.233 | 0.074 | 0.043 | 0.071 | 0.055 |
| 8 missing | 0.025 | 0.068 | 0.214 | 0.206 | 0.238 | 0.074 | 0.043 | 0.072 | 0.059 |
| 12 missing | 0.024 | 0.065 | 0.209 | 0.202 | 0.242 | 0.073 | 0.045 | 0.076 | 0.065 |
| Max. deviation from baseline | 10.1% | 6.9% | 2.6% | 5.8% | 2.3% | 3.1% | 6.6% | 2.6% | 6.4% |
| Max. deviation observed for expert 1 | 8.4% | 8.7% | 8.1% | 4.9% | 6.3% | 10.2% | 10.5% | 4.5% | 0.1% |
| Scenario | C1 | C2 | C3 | C4 | C5 | C6 | C7 | C8 | C9 |
|---|---|---|---|---|---|---|---|---|---|
| 3 missing | 7.34% | 7.08% | 5.86% | 5.43% | 6.61% | 5.34% | 6.35% | 6.90% | 9.06% |
| 5 missing | 9.55% | 9.49% | 8.14% | 7.53% | 8.26% | 8.07% | 8.73% | 8.35% | 10.21% |
| 8 missing | 13.56% | 13.85% | 11.85% | 10.86% | 10.31% | 12.67% | 12.88% | 11.07% | 11.48% |
| 12 missing | 21.73% | 22.79% | 17.63% | 17.54% | 14.69% | 21.64% | 19.19% | 15.62% | 15.21% |
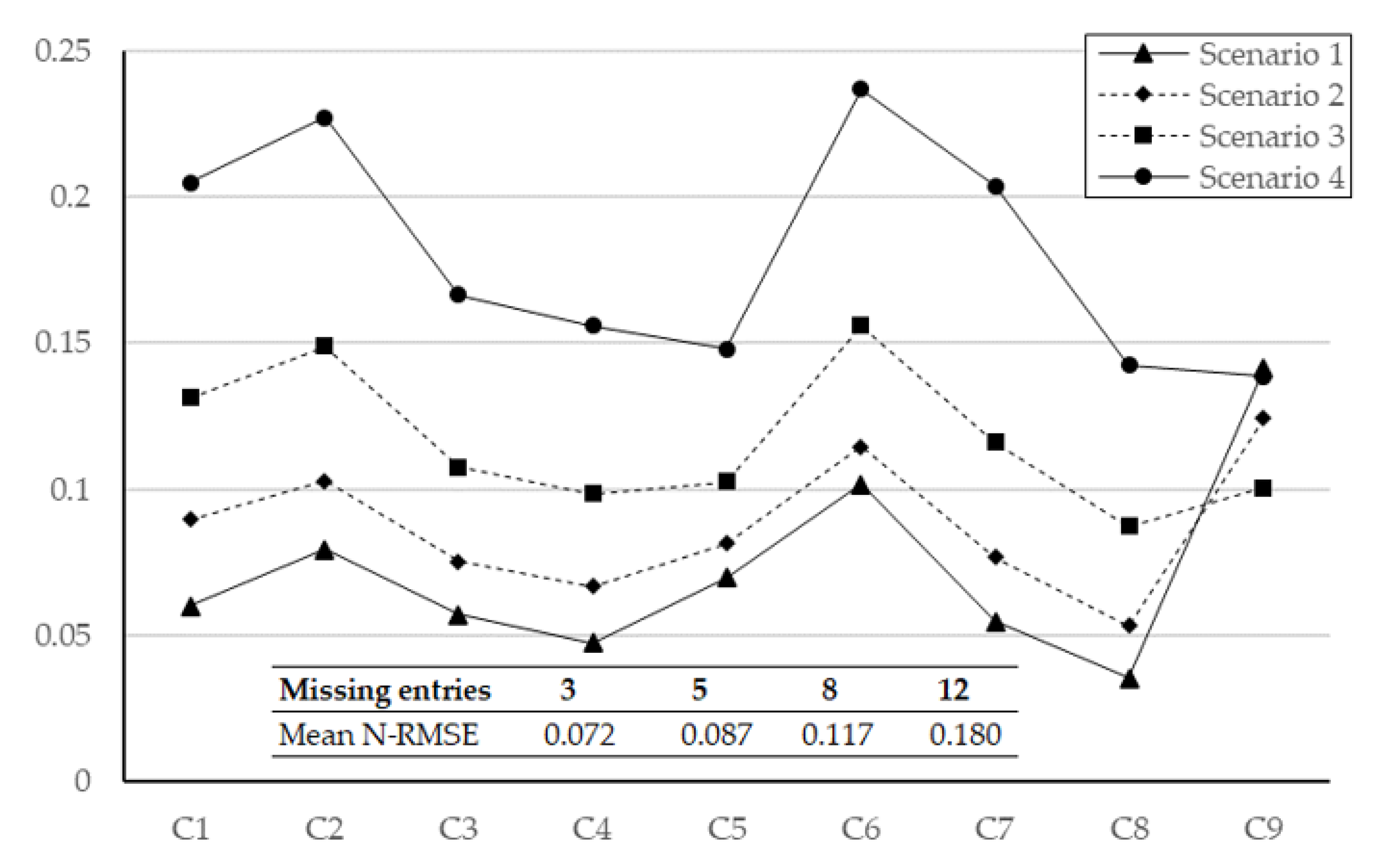
| Scenario | 3 | 5 | 8 | 12 |
|---|---|---|---|---|
| Expert 1 | 0.072 | 0.087 | 0.117 | 0.180 |
| Expert 2 | 0.105 | 0.112 | 0.133 | 0.191 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Navarro, I.J.; Martí, J.V.; Yepes, V. Neutrosophic Completion Technique for Incomplete Higher-Order AHP Comparison Matrices. Mathematics 2021, 9, 496. https://doi.org/10.3390/math9050496
Navarro IJ, Martí JV, Yepes V. Neutrosophic Completion Technique for Incomplete Higher-Order AHP Comparison Matrices. Mathematics. 2021; 9(5):496. https://doi.org/10.3390/math9050496
Chicago/Turabian StyleNavarro, Ignacio J., José V. Martí, and Víctor Yepes. 2021. "Neutrosophic Completion Technique for Incomplete Higher-Order AHP Comparison Matrices" Mathematics 9, no. 5: 496. https://doi.org/10.3390/math9050496
APA StyleNavarro, I. J., Martí, J. V., & Yepes, V. (2021). Neutrosophic Completion Technique for Incomplete Higher-Order AHP Comparison Matrices. Mathematics, 9(5), 496. https://doi.org/10.3390/math9050496







