Discontinuous Galerkin Isogeometric Analysis of Convection Problem on Surface
Abstract
1. Introduction
2. Model Problem and Discretization
2.1. Differential Operators on Surfaces
2.2. Isogeometric Analysis
2.3. DG-IgA Discretization
3. Numerical Experiments
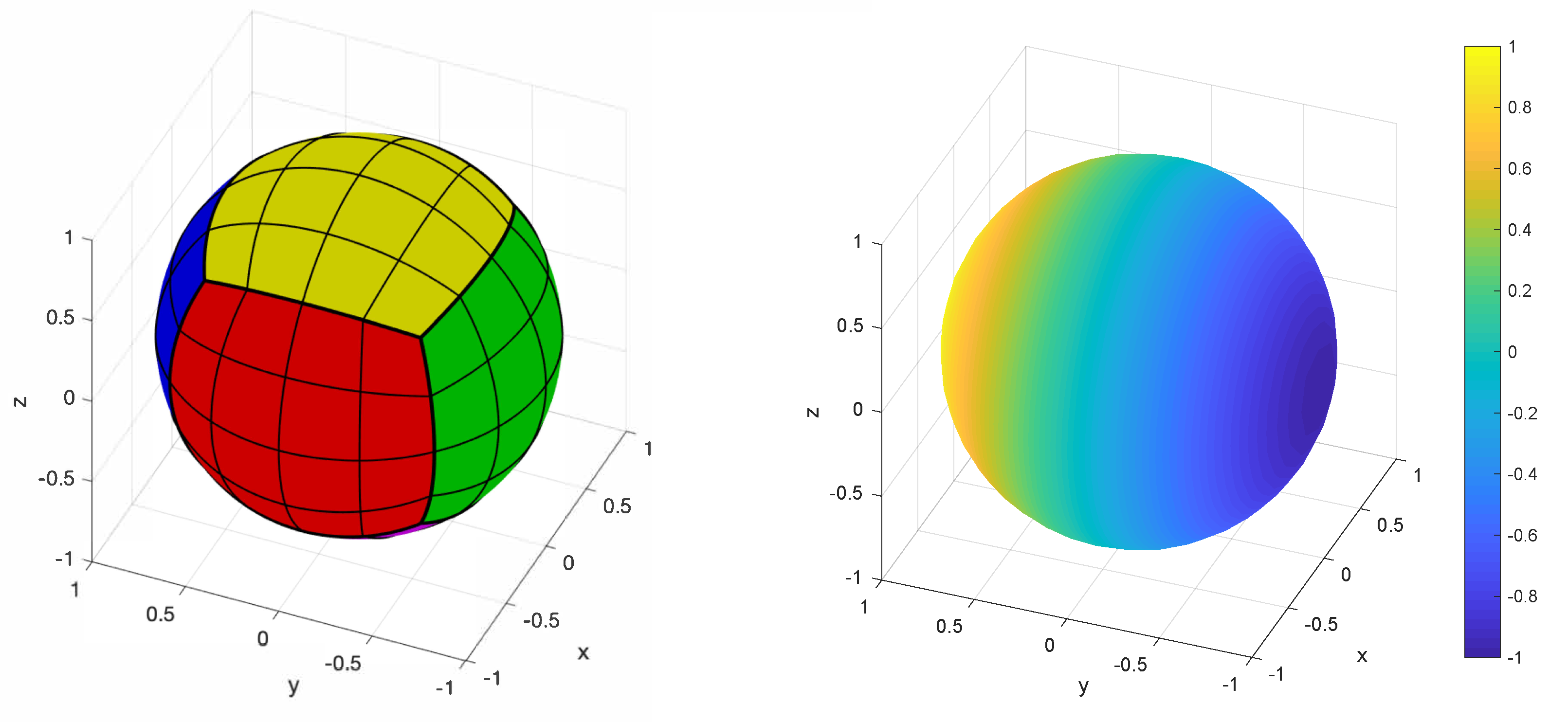
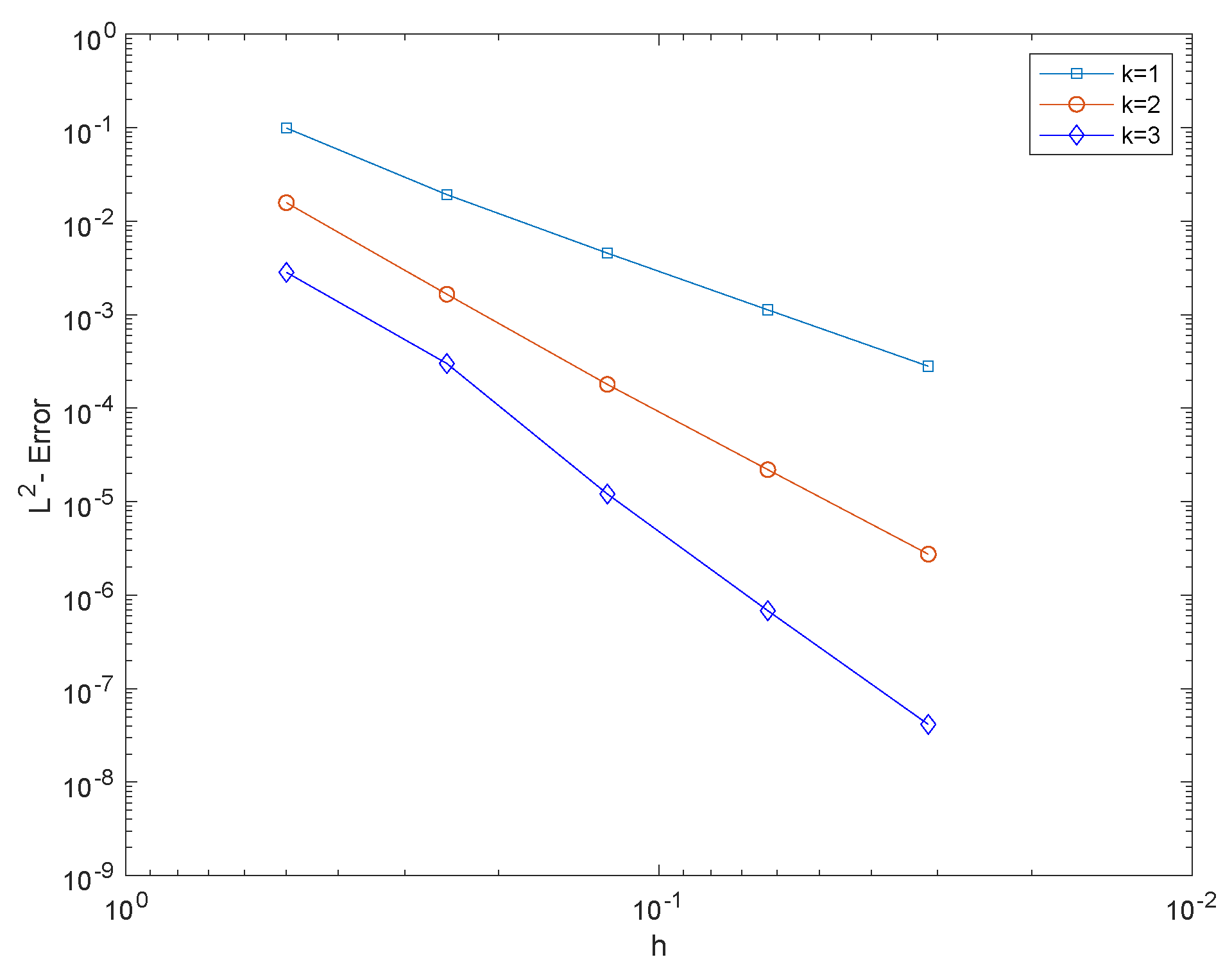
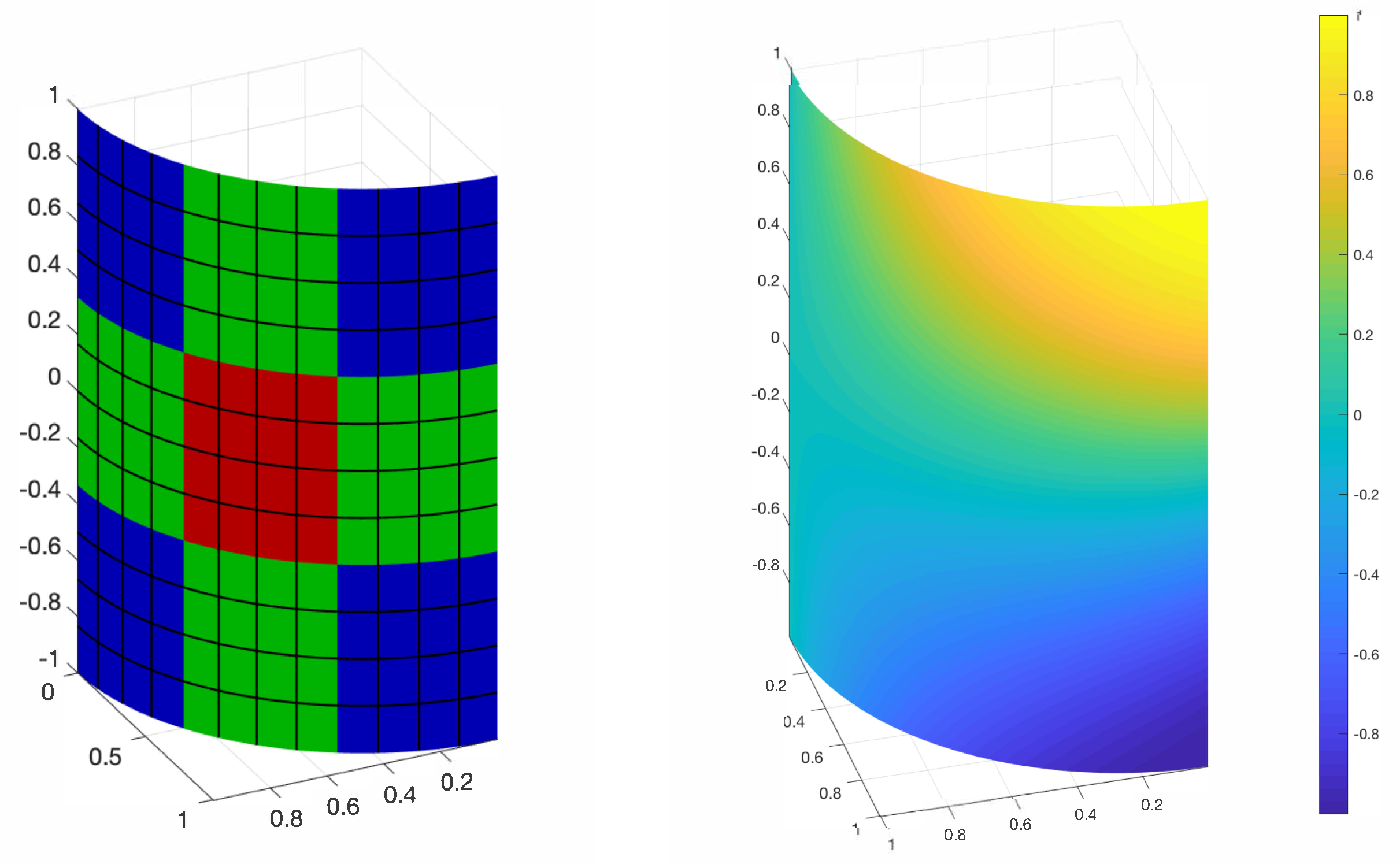
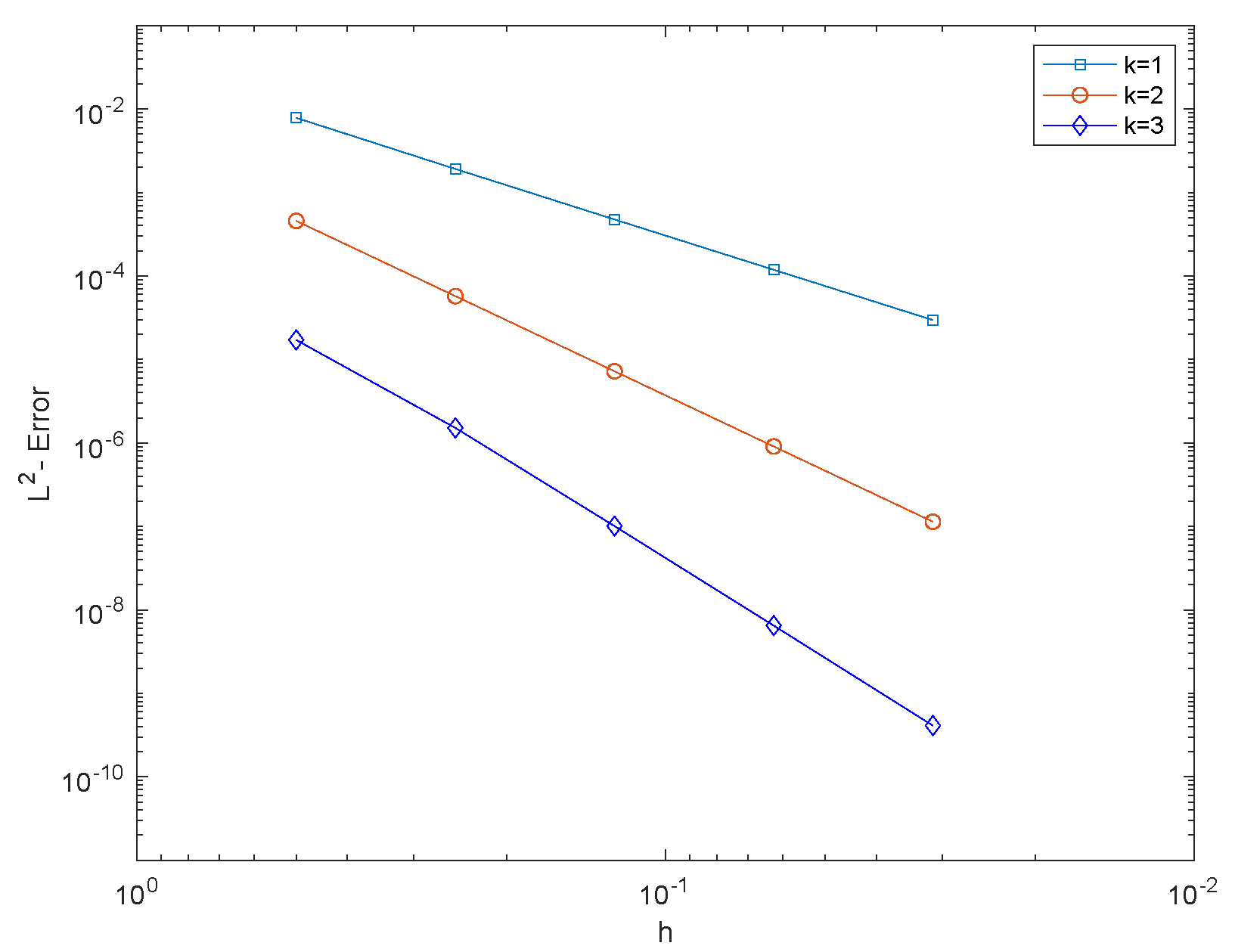
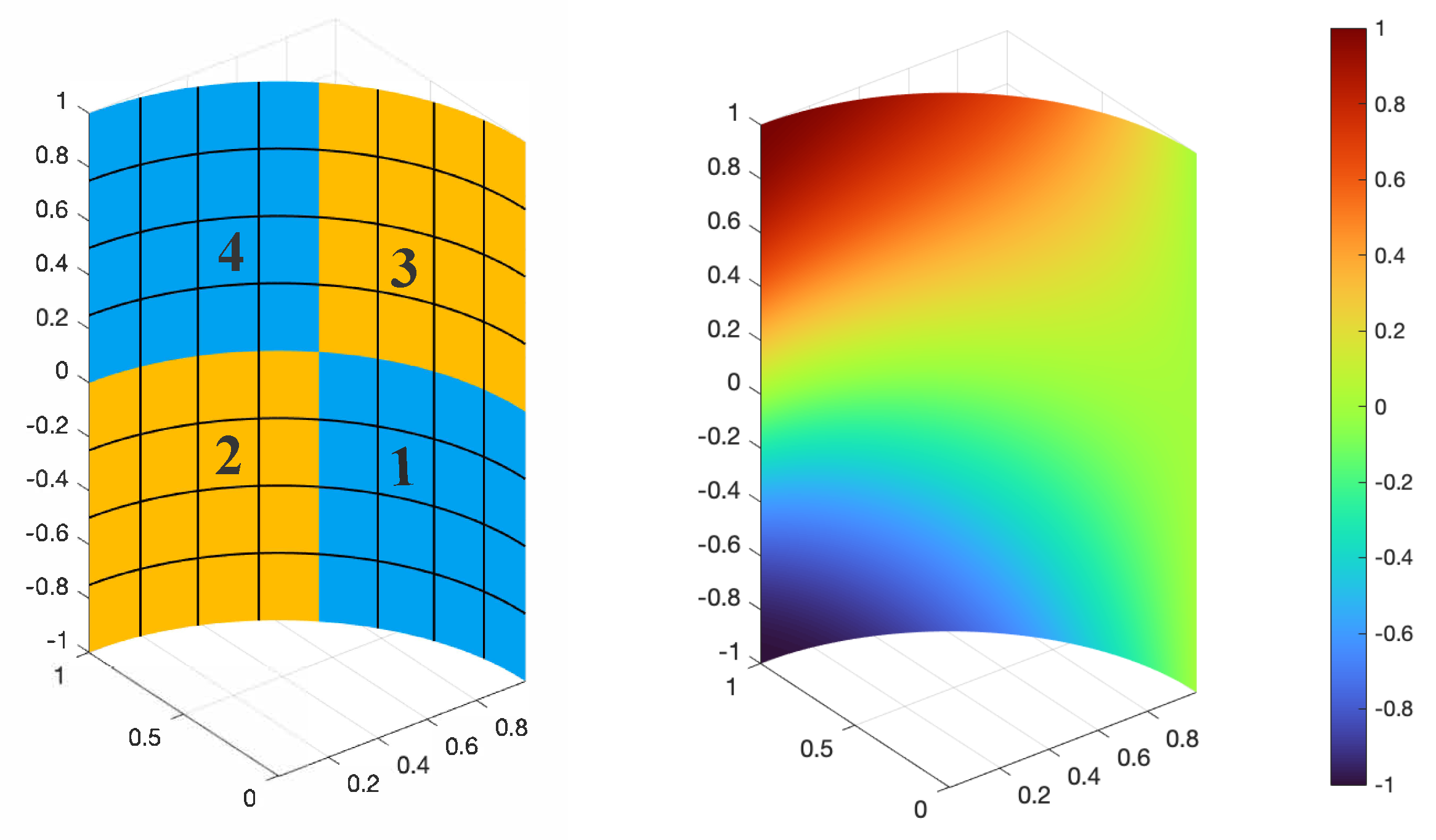
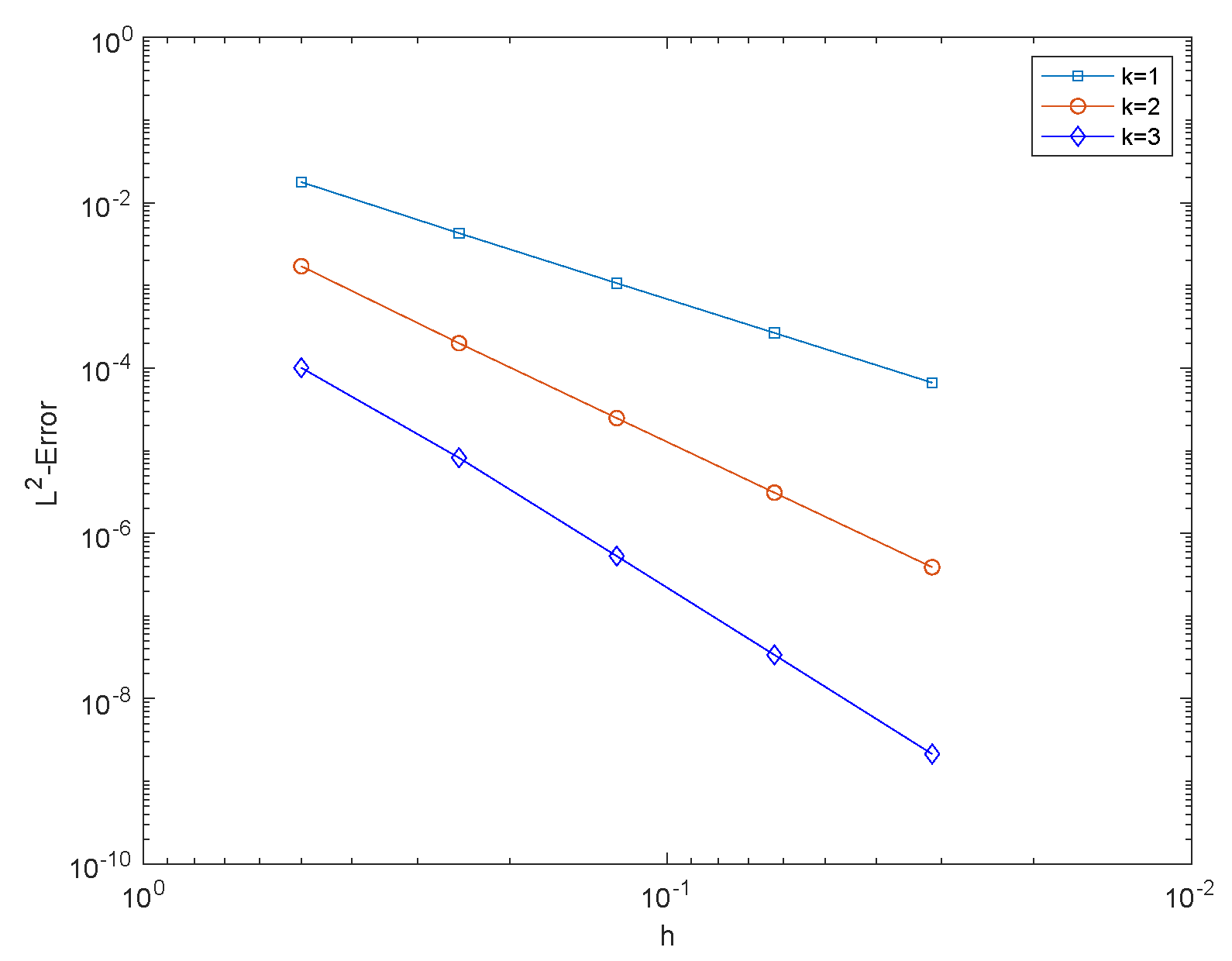
3.1. Numerical Experiment 1
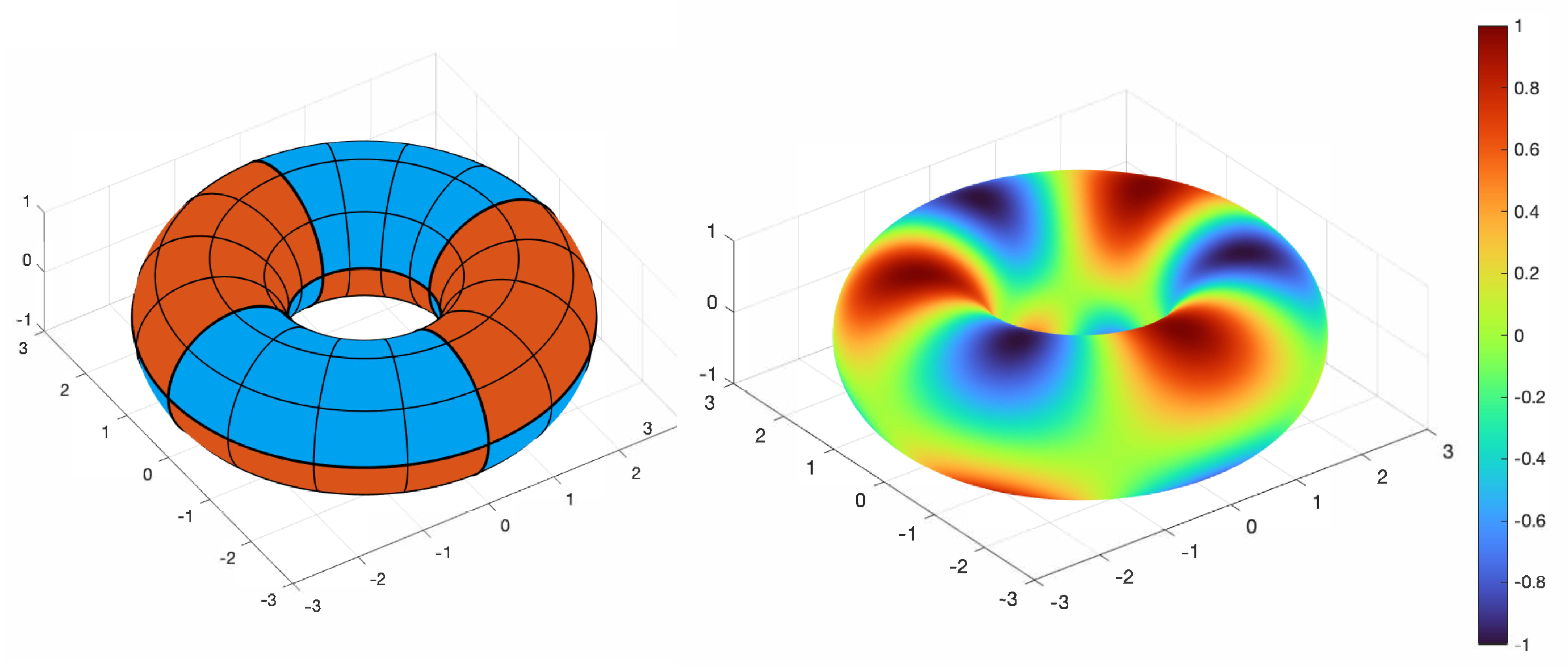
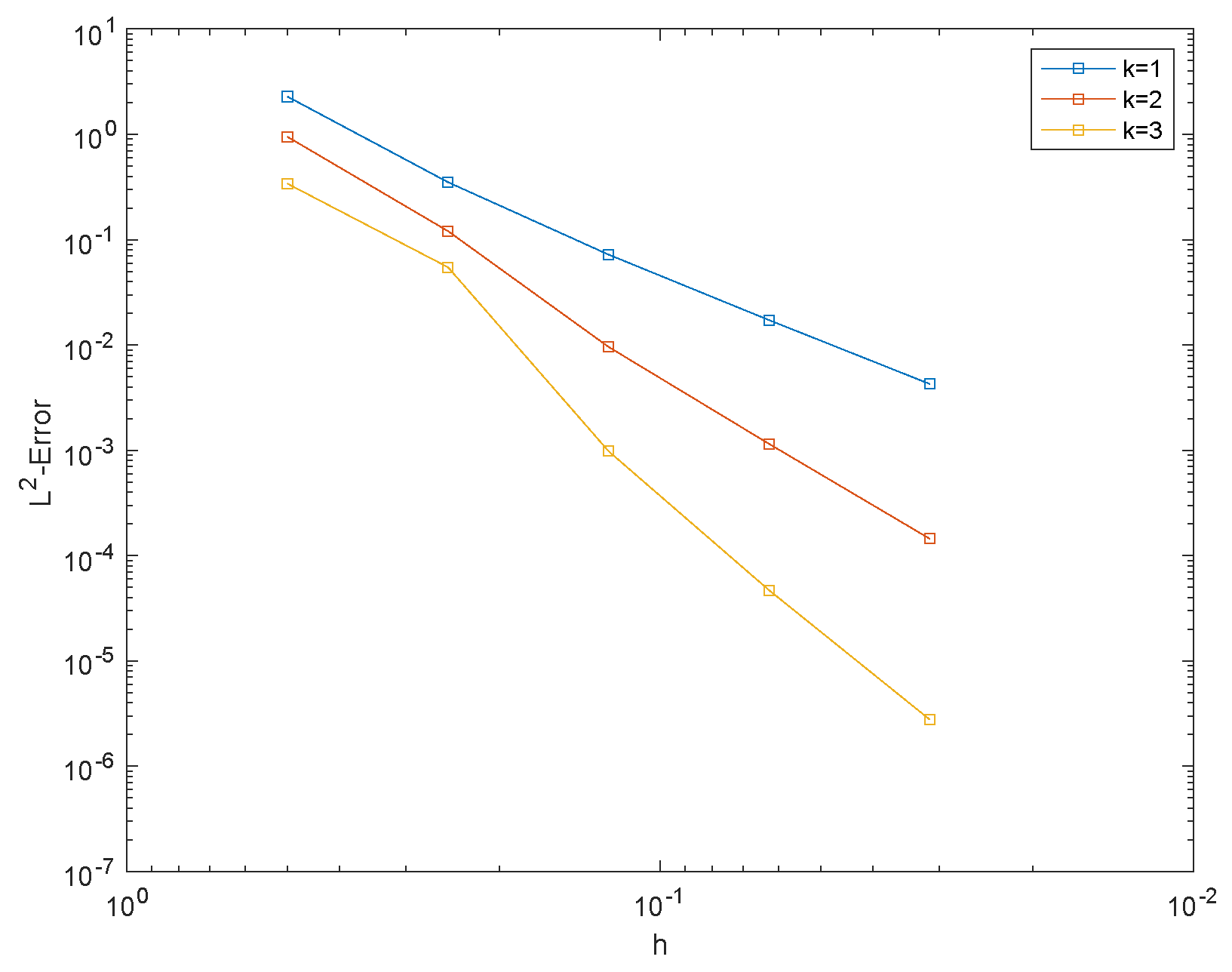
3.2. Numerical Experiment 2
3.3. Numerical Experiment 3
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Milliken, W.J.; Stone, H.A.; Leal, L.G. The effect of surfactant on transient motion of newtonian drops. Phys. Fluids A 1993, 5, 69–79. [Google Scholar] [CrossRef]
- Elliott, C.M.; Stinner, B. Modeling and computation of two phase geometric biomembranes using surface finite elements. J. Comput. Phys. 2010, 229, 6585–6612. [Google Scholar] [CrossRef]
- Dziuk, G. Finite elements for the Beltrami operator on arbitrary surfaces. Partial differential equations and calculus of variations. Lect. Notes Math. 1988, 1357, 142–155. [Google Scholar]
- Bonito, A.; Pasciak, J.E. Convergence analysis of variational and non-variational multi-grid algorithms for the Laplace-Beltrami operator. Math. Comp. 2012, 81, 1263–1288. [Google Scholar] [CrossRef]
- Houston, P.; Schwab, C.; Süli, E. Discontinuous hp-finite element methods for advection-diffusion-reaction problems. SIAM J. Numer. Anal. 2002, 39, 2133–2163. [Google Scholar] [CrossRef]
- Xiong, C.; Li, Y. Error analysis for optimal control problem governed by convection diffusion equations: DG method. J. Comput. Appl. Math. 2011, 235, 3163–3177. [Google Scholar] [CrossRef][Green Version]
- Xiong, C.; Luo, F.; Ma, X.; Li, Y. A priori error analysis for optimal distributed control problem governed by the first order linear hyperbolic equation: hp-streamline diffusion discontinuous galerkin method. J. Numer. Math. 2016, 24, 125–134. [Google Scholar] [CrossRef]
- Xiong, C.; Li, Y. A posteriori error estimators for optimal distributed control governed by the first-order linear hyperbolic equation: DG method. NMPDEs 2011, 27, 491–506. [Google Scholar] [CrossRef]
- Xiong, C.; Becker, R.; Luo, F.; Ma, X. A priori and a posteriori error analysis for the mixed discontinuous Galerkin finite element approximations of the biharmonic problems. NMPDEs 2017, 33, 318–353. [Google Scholar] [CrossRef]
- Wang, L.; Xiong, C.; Wu, H.; Luo, F. A priori and a posteriori error analysis for discontinuous Galerkin finite element approximations of biharmonic eigenvalue problems. Adv. Comput. Math. 2013, 45, 2623–2646. [Google Scholar] [CrossRef]
- Dedner, A.; Madhavan, P. Discontinuous Galerkin Methods for Hyperbolic and Advection-Dominated Problems on Surfaces. 2015. Available online: https://arxiv.org/pdf/1505.06752.pdf (accessed on 20 December 2020).
- Hughes, T.J.R.; Cottrell, J.A.; Bazilevs, T. Isogeometric analysis: CAD, finite elements, NURBS, exact geometry and mesh refinement. Comput. Methods Appl. Mech. Engrg. 2005, 194, 4135–4195. [Google Scholar] [CrossRef]
- Langer, U.; Toulopoulos, I. Analysis of multipatch discontinuous Galerkin IgA approximations to elliptic boundary value problems. Comput. Vis. Sci. 2015, 17, 217–233. [Google Scholar] [CrossRef]
- Zhang, F.; Xu, Y.; Chen, F. Discontinuous Galerkin methods for isogeometric analysis for elliptic equations on surfaces. Commun. Math. Stat. 2014, 2, 431–461. [Google Scholar] [CrossRef][Green Version]
- Hofer, C.; Langer, U.; Toulopoulos, I. Discontinuous Galerkin Isogeometric Analysis of Elliptic Diffusion Problems on Segmentations with Gaps. Comput. Math. Appl. 2015, 72, 1811–1827. [Google Scholar] [CrossRef]
- Bazilevs, Y.; Hughes, T.J.R. NURBS-based isogeometric analysis for the computation of flows about rotating components. Comput. Mech. 2008, 43, 143–150. [Google Scholar] [CrossRef]
- Elfverson, D.; Larson, M.G.; Larsso, K. A new least squares stabilized Nitsche method for cut isogeometric analysis. Comput. Methods Appl. Mech. Eng. 2019, 349, 1–16. [Google Scholar] [CrossRef]
- Schumaker, L.L. Spline Functions: Basic Theory, 3rd ed.; Cambridge University Press: Cambridge, UK, 2007. [Google Scholar]
- Brezzi, F.; Marini, L.D.; Süli, E. Discontinuous Galerkin methods for first-order hyperbolic problems. Math. Model. Methods Appl. Sci. 2004, 14, 1893–1903. [Google Scholar] [CrossRef]
| Degree k | Mesh Size h | Error | Convergence Order |
|---|---|---|---|
| 1 | 1/2 | 9.934 × 10 | — |
| 1/4 | 1.926 × 10 | 2.366 | |
| 1/8 | 4.561 × 10 | 2.078 | |
| 1/16 | 1.128 × 10 | 2.016 | |
| 1/32 | 2.813 × 10 | 2.004 | |
| 2 | 1/2 | 1.580 × 10 | — |
| 1/4 | 1.656 × 10 | 3.255 | |
| 1/8 | 1.799 × 10 | 3.202 | |
| 1/16 | 2.202 × 10 | 3.031 | |
| 1/32 | 2.748 × 10 | 3.002 | |
| 3 | 1/2 | 2.840 × 10 | — |
| 1/4 | 3.006 × 10 | 3.240 | |
| 1/8 | 1.210 × 10 | 4.635 | |
| 1/16 | 6.826 × 10 | 4.148 | |
| 1/32 | 4.150 × 10 | 4.040 |
| Degree k | Mesh Size h | Error | Convergence Order |
|---|---|---|---|
| 1 | 1/2 | 2.2825 × 10 | — |
| 1/4 | 3.5096 × 10 | 2.7013 | |
| 1/8 | 7.2088 × 10 | 2.2835 | |
| 1/16 | 1.7199 × 10 | 2.0674 | |
| 1/32 | 4.2620 × 10 | 2.0127 | |
| 2 | 1/2 | 9.4780 × 10 | — |
| 1/4 | 1.2046 × 10 | 2.9760 | |
| 1/8 | 9.5761 × 10 | 3.6530 | |
| 1/16 | 1.1486 × 10 | 3.0595 | |
| 1/32 | 1.4448 × 10 | 2.9910 | |
| 3 | 1/2 | 0.3400 × 10 | — |
| 1/4 | 5.4673 × 10 | 2.6368 | |
| 1/8 | 9.7914 × 10 | 5.8032 | |
| 1/16 | 4.6835 × 10 | 4.3859 | |
| 1/32 | 2.7729 × 10 | 4.0781 |
| Degree k | Mesh Size h | Error | Convergence Order |
|---|---|---|---|
| 1 | 1/2 | 7.832 × 10 | — |
| 1/4 | 1.912 × 10 | 2.0344 | |
| 1/8 | 4.748 × 10 | 2.0097 | |
| 1/16 | 1.185 × 10 | 2.0023 | |
| 1/32 | 2.962 × 10 | 2.0004 | |
| 2 | 1/2 | 4.5649 × 10 | — |
| 1/4 | 5.7310 × 10 | 2.9937 | |
| 1/8 | 7.2113 × 10 | 2.9905 | |
| 1/16 | 9.0619 × 10 | 2.9924 | |
| 1/32 | 1.1364 × 10 | 2.9954 | |
| 3 | 1/2 | 1.7089 × 10 | — |
| 1/4 | 1.5120 × 10 | 3.4986 | |
| 1/8 | 1.0073 × 10 | 3.9079 | |
| 1/16 | 6.4755 × 10 | 3.9594 | |
| 1/32 | 4.1048 × 10 | 3.9796 |
| Degree k | Mesh Size h | Error | Convergence Order |
|---|---|---|---|
| 1 | 1/2 | 1.774 × 10 | — |
| 1/4 | 4.277 × 10 | 2.0531 | |
| 1/8 | 1.063 × 10 | 2.0085 | |
| 1/16 | 2.656 × 10 | 2.0006 | |
| 1/32 | 6.640 × 10 | 2.0002 | |
| 2 | 1/2 | 1.7036 × 10 | — |
| 1/4 | 1.9959 × 10 | 3.0935 | |
| 1/8 | 2.4770 × 10 | 3.0104 | |
| 1/16 | 3.1024 × 10 | 2.9971 | |
| 1/32 | 3.8885 × 10 | 2.9961 | |
| 3 | 1/2 | 1.0065 × 10 | — |
| 1/4 | 8.1947 × 10 | 3.6186 | |
| 1/8 | 5.3064 × 10 | 3.9489 | |
| 1/16 | 3.3827 × 10 | 3.9715 | |
| 1/32 | 2.1381 × 10 | 3.9838 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, L.; Xiong, C.; Yuan, X.; Wu, H. Discontinuous Galerkin Isogeometric Analysis of Convection Problem on Surface. Mathematics 2021, 9, 497. https://doi.org/10.3390/math9050497
Wang L, Xiong C, Yuan X, Wu H. Discontinuous Galerkin Isogeometric Analysis of Convection Problem on Surface. Mathematics. 2021; 9(5):497. https://doi.org/10.3390/math9050497
Chicago/Turabian StyleWang, Liang, Chunguang Xiong, Xinpeng Yuan, and Huibin Wu. 2021. "Discontinuous Galerkin Isogeometric Analysis of Convection Problem on Surface" Mathematics 9, no. 5: 497. https://doi.org/10.3390/math9050497
APA StyleWang, L., Xiong, C., Yuan, X., & Wu, H. (2021). Discontinuous Galerkin Isogeometric Analysis of Convection Problem on Surface. Mathematics, 9(5), 497. https://doi.org/10.3390/math9050497






