Abstract
Choosing a supplier is a complex decision-making process that can reduce the total cost of production inputs and increase profits without increasing the price or sacrificing product quality. However, supplier selection processes usually involve multiple quantitative and qualitative criteria which increase the complexity of the problem and may decrease the accuracy and effectiveness of the process. Such complex decision-making problems can be supported by using multicriteria decision-making (MCDM) models. While there have been multiple MCDM models to support supplier selection processes in different industries and sectors, only a few are developed to support the supplier selection processes in the garment industry, especially under uncertain decision-making environment. This paper presents an integrated mathematical model under a fuzzy environment and applies it to the supplier selection process in the garment industry. In this research, the authors utilize the Buckley extension based fuzzy Analytical Hierarchical Process (FAHP) method in combination with linear normalization based fuzzy Grey Relational Analysis (F-GRA) method to develop a MCDM approach to the supplier selection process under a fuzzy environment. As a result, supplier 08 (SA08) is the optimal supplier. The contribution of this work is to propose an MCDM model for ranking potential suppliers in the garment industry under a fuzzy environment. The proposed approach can also be applied to support complex decision-making processes under a fuzzy environment in different industries.
1. Introduction
Vietnam’s garment industry is in the top 5 most exporting countries in the world textile industry. Many Indian companies have invested in Vietnam’s garment sector. In contrast, Vietnam’s garment enterprises can develop investment in manufacturing ready-to-wear garments in India to supply the country’s 1.3 billion people market [1]. The bottleneck of Vietnam’s textile and garment industry is raw materials. Every year, textile day imports 100% cotton, imports 900,000 tons of yarn and fabric over 11 billion USD, while India’s strengths are cotton, fiber, and yarn [1]. Therefore, the two sides can complement each other for mutual development. The current challenge for the garment industry is to find raw material, towards higher quality and larger scope, rapidly changing world market, the rapid development of science and technology.
The dependence on imported raw materials and lack of high-quality human resources for the textile and dyeing stages are challenges for the sustainable development of Vietnam’s textile and garment industry when joining the global textile value chain. Supply chain management (SCM) has become an important issue, affecting the productivity and efficiency of businesses around the world. A supply chain includes all businesses and processes that involve, directly or indirectly, in meeting customer demand. A typical supply chain includes not only manufacturers and suppliers but also transport companies, logistics activities, retailers, and end customers [2]. Supply chain management covers all production and business activities of a company. Effective supply chain management will provide businesses with competitive advantages, help them gain a foothold in the market, and expand the strategy of the business [2]. Selecting a supplier is a complex decision-making problem that involves different quantitative and qualitative criteria. However, such complexity of the problem may decrease the accuracy and effectiveness of the process and reduce the overall supply chain performance. These decision-making problems can be supported by using multicriteria decision making (MCDM) models. There are many multicriteria decision-making methods identified such as the Analytical Hierarchical Process (AHP), Analytic Network Process (ANP), Fuzzy Analytic Network Process (FANP), Artificial Neural Network (ANN), Data Envelopment Analysis (DEA), etc. that can be employed to solve similar decision-making problems [3].
The AHP model is a commonly quantitative approach used for supplier selection in many industries [3,4,5,6,7,8,9,10,11,12,13]. ANP models are also applied to solve the same type of problem on SCM as AHP model [14,15,16], which is a network analysis method that considers hierarchy and interactions. This approach considers the interplay between the elements to give the result of the priority rating among the criteria and combining with fuzzy numbers will help solve the complex problem.
While there have been multiple MCDM models to support supplier selection processes in different industries and sectors, only a few are developed to support the supplier selection processes in the garment industry, especially under uncertain decision-making environment. The aim of this paper is to propose a fuzzy MCDM method utilizing the Buckley extension based fuzzy Analytical Hierarchical Process (FAHP) method in combination with linear normalization based fuzzy Grey Relational Analysis (F-GRA) method. In this process, a FAHP model is applied to calculate the weight of the related criteria. Then, Fuzzy-GRA is applied for ranking all potential suppliers.
2. Literature Review
2.1. MCDM Methods and Applications
MCDM models are frequently developed to support decision-makers in solving complex multicriteria decision-making problems in different industries and sectors. These decision-making problems include location selection [17,18,19], material selection [20,21], and asset allocation [22]. Among these, many MCDM models have been developed to solve supplier evaluation and selection problems of different supply chains in various industries.
2.2. Application of MCDM Methods in Supplier Selection Processes
Multicriteria Decision-Making (MCDM) models for supplier selection problems developed with a focus on improvements to the performance of suppliers or on the method used to rank and select suppliers. In Biswas’s study [23] multiple decision-making methods are compared and applied to develop an integrated multi-criteria decision-making (MCDM) framework to perform a comparative analysis of Indian health care supply chains’ performances. Most MCDM models are based on a set of supplier performance criteria [24]. These models differ from each other by having different criteria or utilizing different MDCM methods. Timmerman proposed a single-objective weighted linear model in which suppliers are assessed based on related criteria, these evaluations are then combined into a single score which is used to rank the suppliers [25]. Petrovic et al. [26] performed a comparative study where three different MCDM approaches are applied in order to help decision-makers to identify the most suitable method for the supplier selection process.
There have been many researches that applied linear programming for supplier selection processes [27,28,29]. Chaundry et al. introduced linear and mixed binary integer programming models that support the vendor performance evaluation process [30]. Rosenthal et al. proposed a mixed-integer linear programming model to solve the vendor selection problem [31]. Ghodsypour et al. [32] proposed a mixed-integer non-linear programming model to support solving a multiple sourcing problem; Weber et al. [33] presented a decision support system approach by using Multi-objective Programming for the supplier selection process. Gao et al. [34] proposed a multi-objective model for purchasing materials. Kannan et al. [35] introduced a Fuzzy MCDM model for supplier selection and order allocation while incorporating green criteria. Karpak et al. [36] discussed visual interactive goal programming (VIG) for supplier evaluation and selection problems. Chang et al. [37] proposed an integrated model based on multi-choice goal programming and multi-segment goal programming to support the supplier selection process. Kuo et al. [38] created a hybrid MCDM model based on the ANP and DEA methodologies for supporting the supplier selection process.
Chakraborty et al. [39] utilized D numbers-based Measurement Alternatives and Ranking according to the COmpromise Solution (MARCOS) method to developed a MCDM model to solve the supplier selection problem in the iron and steel industry. Ramakrishnan and Chakraborty [40] developed a cloud The Technique for Order of Preference by Similarity to Ideal Solution (TOPSIS) model for the green supplier selection process in the automobile industry. Ho et al. [41] concluded that the most common criteria of supplier selection decision-making processes were quality, cost, management, technology, and flexibility. Kuo-Ping Lin et al. [42] built a supplier selection process based on six main criteria. Peng Jia et al. [43] have pointed out in the literature review that the framework has developed including economic, environmental, and social sustainability criteria. José Roberto et al. [44] also suggested the criteria for selecting and evaluating suppliers based on traditional measurements such as cost, quality, JIT, and continuous improvement capability.
While there have been many MCDM models developed to solve the supplier selection problem in various sectors and industries, few try to solve the problem of garment supply chains that are heavily supplier dependent, especially under uncertain decision-making environments. Therefore, this research aims to develop a fuzzy multicriteria decision-making model method based on Buckley extension based Fuzzy AHP and linear normalization based Fuzzy GRA to support the supplier selection process in the garment industry.
3. Research Process
Among many areas where MCDM techniques are frequently applied, supplier selection involves not only quantitative criteria, such as price and lead time, but also qualitative ones such as reputation and communication easiness. Therefore, it is important that Fuzzy theory is integrated into supplier selection MCDM models to better present the uncertain nature of the decision-making environment. In this paper, Buckley extension-based fuzzy Analytical Hierarchical Process (FAHP) and linear normalization based fuzzy Grey Relational Analysis are chosen to develop the MCDM model. While there are several methods that can be applied to calculate the criteria weights; such as Best-Worst Method, Level Based Weight Assessment (LBWA) method, the FUll COnsistency Method (FUCOM), and A Step-wise Weight Assessment Ratio Analysis (SWARA); FAHP is chosen to develop this model due to its easy-to-compute and its availability in decision-making software, which allow the proposed model to be easier to be applied.
The development process includes three main stages and is shown in Figure 1:
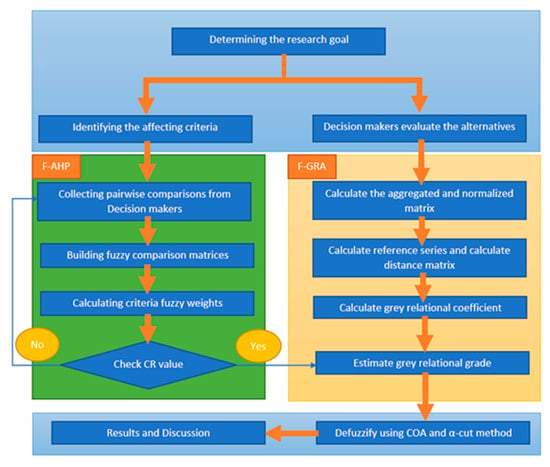
Figure 1.
Research process.
Stage 1: Analyzing and evaluate the current supplier selection practice of the company, then identify the main problem of the process. Identifying critical criteria of the supplier selection process through literatures and experts’ interview.
Stage 2: Applying Buckley extension-based fuzzy Analytical Hierarchical Process (Fuzzy-AHP) to calculate fuzzy weights of the criteria. Then, using the calculated weight as the input for linear normalization based fuzzy Grey Relational Analysis (Fuzzy-GRA) in order to calculate the fuzzy grey relational grades of the potential suppliers.
Stage 3: Defuzzifying the fuzzy grey relational grades using two common methods: the Center of Area method and α-cut method. Then, rank the potential suppliers according to their crisp grey relational grade. The results are then used to perform a sensitivity analysis to verify that the proposed method is reliable across common defuzzification techniques and different resolving coefficient values.
4. Theoretical Framework
4.1. A Triangular Fuzzy Number (TFN)
A Triangular Fuzzy Number (TFN) can be defined as and are parameters that specify the smallest likely value, the promising value, and the largest possible value of the TFN. A typical TFN is shown in Figure 2 and can be described as:
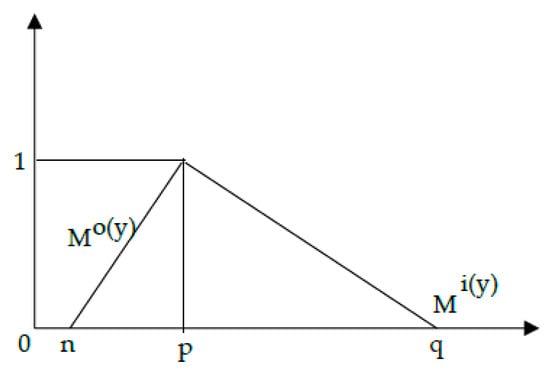
Figure 2.
Triangular fuzzy number.
A fuzzy number is given as:
with represent the two sides of the fuzzy number, respectively.
4.2. Buckley Extension Based Fuzzy-AHP Algorithm
The Analytic hierarchy process (AHP) is known as an effective method to support solving multi-criteria decision-making problems developed by Saaty [45]. While the method is commonly used in different MCDM models, AHP has certain limitations due to its inability to combine the uncertainty and inaccuracy inherent in the mapping between decision-makers’ perceptions and judgments into crisp numbers used in the method. There are several ways to overcome these limitations, one of them is the integration of fuzzy set theory into the AHP method to create Fuzzy-AHP models.
Fuzzy-AHP is a popular MCDM technique that is frequently employed to deal with the uncertainty and vague nature of human’s decision-making processes as the technique can represent these elements better than the classic AHP method due to the incorporation of the fuzzy set theory [46,47].
In this research, Buckley’s Fuzzy-AHP method is utilized to calculate the criteria weights as it can be extended to solve decision-making problems in fuzzy environments and its approach is simpler compared to other Fuzzy-AHP methods. The steps of Buckley’s Fuzzy-AHP are as follows [48]:
Step 1: Build pairwise comparison matrices of all the related criteria as:
where:
criterion has relative importance to criterion
criterion has relative importance to criterion
Step 2: Examine the consistency of the calculated fuzzy pairwise comparison matrices.
Step 3: Apply the geometric mean technique to calculate the fuzzy geometric mean as Equation (5):
where is the fuzzy comparison value of criterion i to criterion n; thus is the geometric mean of fuzzy comparison value of criterion i to each criterion.
Step 4: The fuzzy weights of each criterion is calculated as follows:
with as the fuzzy weight of the criterion which can be shown as where , , and are the lower, middle, and upper values of , respectively.
4.3. Linear Normalization-Based Fuzzy GRA Method
A typical Fuzzy-GRA algorithm includes eight steps as follows [49,50]:
Step 1: Firstly, a panel of k decision-makers ( is consulted. Each decision-maker will rank each criterion ( in increasing order:
with .
Step 2: The normalized decision matrix R are calculated as:
with
Step 3: Calculate the reference series as:
Step 4: Determine the distance matrix where the distance between each comparison value to the reference value is calculated as:
Step 5: The fuzzy grey relational coefficient () is defined as:
with , , and is the resolving coefficient .
Step 6: The fuzzy grey relational grade () is calculated as:
where the weight of the criterion is with .
Step 7: Apply Center of Area (COA) or α-cut method to defuzzify the grey relational grade of each alternative.
- (a)
- Center-of-Area method
The COA method can be applied to calculate the priorities and overall scores of the alternative by transforming fuzzy grey relational grade into crisp numbers [51]. A crisp number corresponding to the convex fuzzy number can be estimated as:
- (b)
- Alpha-cut method
The α-cut method is applied in this research to validate the results and performance of the proposed model. The α-cut method can be used to compare two fuzzy number in terms of their α-cut values [51,52].
The α-cut method can be utilized to convert the total weighted performance matrices into interval performance matrices which show the αleft and αright value of each alternative:
With:
The calculated interval performance matrices can then be converted into real numbers by applying the function and values, with as follow:
where
Step 8: Rank the alternatives using the defuzzified values with better alternatives having higher values.
5. Numerical Application
Currently, the textile and garment industry plays an increasingly important role in the Vietnamese economy, in particular one of the industries with the highest export turnover in the country in recent years and especially exports to the USA market. On the other hand, it is also one of the industries in which Vietnam has a competitive advantage and exploits it effectively. In fact, Vietnam’s garment export products in recent years have continuously increased in terms of both quantity, product categories, and value of export turnover, becoming one of the main export products of Vietnam.
However, 2019 is a difficult year for the Vietnam Textile and Garment industry when faced with many unpredictable fluctuations from the market. According to the Vietnam Textile and Apparel Association, the textile industry is facing huge development opportunities from the recently signed Free Trade Agreements (FTAs). In order to enjoy the incentives brought by FTAs, the domestic textile and garment industry has hardly taken advantage of it because it has to strictly meet the rules of origin from fabric, yarn onwards. Meanwhile, in Vietnam, there is a shortage of factories producing raw materials, weaving, dyeing unable to actively source raw materials.
In a closed garment production chain, the role of raw material suppliers always plays an important role in sustainable industry development. In this research, we applied MCDM model for ranking all potential suppliers in the garment industry.
First, the criteria are selected from related literature and industrial expert reviews. Then, the 10 potential suppliers are identified. The information of criteria and supplier are shown in Table 1 and Table 2.

Table 1.
Criteria and sub-criteria.

Table 2.
Potential supplier list.
Next, five industrial experts, including experienced procurement managers and supply chain managers, are requested to compare the criteria with the aim of selecting the best supplier. In this stage, a linguistic scale for relative importance (Table 3) is employed.

Table 3.
Linguistic terms and corresponding fuzzy numbers.
The Buckley Extension Based Fuzzy-AHP Algorithm method is applied to calculate the weight of all criteria, some data are shown in Appendix A. These weights are shown in Table 4 and Table 5.

Table 4.
Results from Buckley extension based fuzzy-analytic hierarchy process (AHP) method.

Table 5.
Fuzzy weight from fuzzy AHP (FAHP) model.
In the next step, Linear Normalization Based Fuzzy GRA Method (Fuzzy-GRA) is employed for ranking all potential suppliers. The results of the Fuzzy-GRA model are shown in Table 6 and Table 7 and Figure 3.

Table 6.
Results from center-of-area defuzzification.

Table 7.
Results from α-cut method.
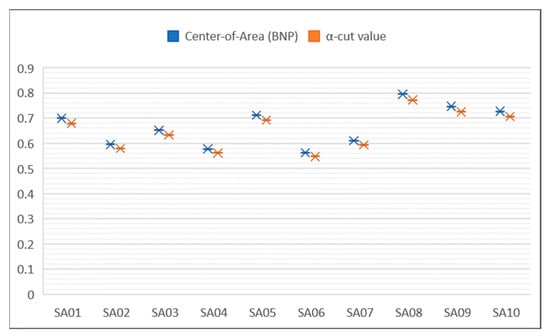
Figure 3.
Ranking score from Center of Area (BNP) and α-cut method.
6. Results and Discussion
In this section, the proposed model’s rationality and stability are verified using the concept of sensitivity analysis. In this case, the resolving coefficient values (ζ) are used to test the reliability of the proposed approach between ζ = 0.1 and ζ = 1. From Figure 4 and Figure 5, it can be seen that, with changing values of ζ, the ranking results are the same with both defuzzification methods. Therefore, the ranking results of the proposed model are robust and reliable.
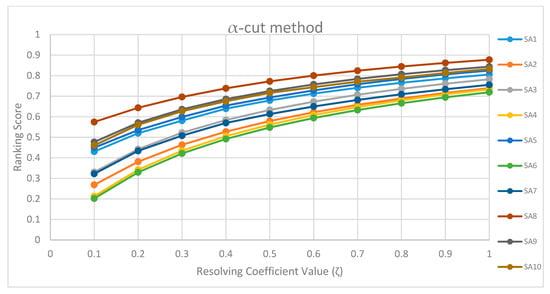
Figure 4.
Variation analysis of ζ values of each alternative for α-cut method.
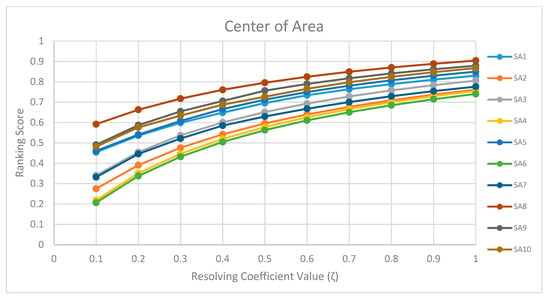
Figure 5.
Variation analysis of ζ values of each alternative for center-of-area method.
In the global value chain, the stages that bring the highest value are designing samples, supplying raw materials, and trading. However, the Vietnamese garment industry is currently engaged in the production of low-value end products. Besides, businesses are mainly subcontractors for firms in the region, unable to design and build their own brands. In order to rise, there is no other way to eliminate the imbalance in the special chain that needs to find the right material supplier. Choosing a supplier is a complex decision that can reduce the total cost of production inputs and increase profits without increasing the price or sacrificing product quality. This is expected as high flexibility suppliers can provide many benefits to the garment supply chain where demand uncertainty has become an important issue since the Trade War between the US and China began and the appearance of the Covid-19 pandemic.
In this research, the authors propose a fuzzy multicriteria decision-making model method including Buckley extension based fuzzy Analytical Hierarchical Process (Fuzzy-AHP) and linear normalization based fuzzy Grey Relational Analysis (Fuzzy-GRA) combined Multi-Criteria Decision-Making (MCDM) methodology. In this process, a FAHP model is applied to calculate the weight of the related criteria. Then, the Center-of-Area method and α-cut method are applied for ranking all potential suppliers. From the results in Figure 3, both defuzzification methods give identical results, with Supplier 8 (SA08) as the optimal supplier. This means the proposed method is robust to different deffuzify methods. Therefore, it is confirmed that the results of the supplier ranking are reliable.
The research has successfully created a hybrid MCDM model using Fuzzy AHP and Fuzzy GRA to assist the supplier evaluation and selection process in the garment industry. Results from the case study show that the model is feasible and reliable.
7. Conclusions
Traditionally, garment materials mainly come from China. However, with the impact of the ongoing US-China trade war, the textile manufacturer is looking at other markets such as Vietnam, Bangladesh, and Mexico to limit the uncertainty introduced by the trade war. As the decision to choose a supplier in a constantly changing competitive environment is crucial for a company to succeed, it is important that companies in the garment industry have a robust and effective sourcing strategy. As such, supplier selection is an important process for any company in the industry.
There have been multiple literatures about the development of MCDM models and their applications in various fields of science and engineering. While there have also been many applications of MCDM models in supplier selection problems, not many literatures have focused on solving these multicriteria decision-making problems in a fuzzy environment, especially in the garment industry. Therefore, hybrid AHP with fuzzy logic and Fuzzy GRA is utilized in this study to support the supplier selection process in the garment industry.
Initially, a Fuzzy Analytic Hierarchy Process (FAHP) model is employed to calculate the fuzzy weights of the criteria of the supplier selection processes. Then, a Fuzzy grey relational analysis (FGRA) process is applied to rank all potential suppliers. The FGRA model proposed can be applied to other multiple criteria decision-making problems since it shows good results in the research. As a result, supplier 08 (SA08) is the optimal supplier.
The contribution of this work is to propose a multicriteria decision-making model (MCDM) for ranking potential suppliers in the garment industry under a fuzzy environment. However, the proposed approach still has certain limitations. Although there already exist many upper-level theories and domain-specific theories regarding the decision-making process under fuzzy environment, few express the attributes of alternatives as numerous types of fuzzy numbers. Thus, future works can focus on solving this limitation so as to reduce the difficulties of putting the proposed approach into practice.
Author Contributions
Conceptualization, J.-F.C., C.-J.L., C.-N.W., M.-H.H. and V.T.N.; data curation, J.-F.C., C.-J.L., C.-N.W. and V.T.N.; formal analysis, M.-H.H. and V.T.N.; funding acquisition, J.-F.C., C.-N.W., M.-H.H. and V.T.N.; investigation, J.-F.C. and V.T.N.; methodology, J.-F.C., C.-J.L. and V.T.N.; project administration, C.-J.L., C.-N.W., M.-H.H. and V.T.N.; resources, J.-F.C. and C.-N.W.; software, C.-N.W. and V.T.N.; supervision, V.T.N.; visualization, M.-H.H.; writing—original draft, C.-J.L. and C.-N.W.; writing—review and editing, J.-F.C. and C.-N.W. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A

Table A1.
Integrated matrix.
Table A1.
Integrated matrix.
| X1 | X2 | X3 | X4 | X5 | X6 | X7 | X8 | X9 | X10 | X11 | X12 | X13 | X14 | X15 | |||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| A1 | 4.4 | 5.4 | 6.4 | 4.0 | 5.0 | 6.0 | 2.8 | 3.8 | 4.8 | 4.6 | 5.6 | 6.6 | 4.6 | 5.6 | 6.6 | 2.8 | 3.8 | 4.8 | 5.0 | 6.0 | 7.0 | 5.4 | 6.4 | 7.4 | 4.2 | 5.2 | 6.2 | 2.8 | 3.8 | 4.8 | 4.8 | 5.8 | 6.8 | 4.6 | 5.6 | 6.6 | 6.0 | 7.0 | 8.0 | 5.8 | 6.8 | 7.8 | 5.8 | 6.8 | 7.8 |
| A2 | 2.8 | 3.8 | 4.8 | 3.4 | 4.4 | 5.4 | 4.6 | 5.6 | 6.6 | 4.2 | 5.2 | 6.2 | 4.8 | 5.8 | 6.8 | 2.8 | 3.8 | 4.8 | 4.8 | 5.8 | 6.8 | 5.0 | 6.0 | 7.0 | 4.4 | 5.4 | 6.4 | 4.4 | 5.4 | 6.4 | 4.0 | 5.0 | 6.0 | 4.2 | 5.2 | 6.2 | 4.4 | 5.4 | 6.4 | 5.0 | 6.0 | 7.0 | 4.4 | 5.4 | 6.4 |
| A3 | 2.8 | 3.8 | 4.8 | 3.2 | 4.2 | 5.2 | 4.4 | 5.4 | 6.4 | 5.0 | 6.0 | 7.0 | 5.0 | 6.0 | 7.0 | 4.6 | 5.6 | 6.6 | 5.0 | 6.0 | 7.0 | 4.4 | 5.4 | 6.4 | 6.2 | 7.2 | 8.2 | 4.4 | 5.4 | 6.4 | 4.4 | 5.4 | 6.4 | 4.0 | 5.0 | 6.0 | 4.6 | 5.6 | 6.6 | 4.6 | 5.6 | 6.6 | 5.0 | 6.0 | 7.0 |
| A4 | 2.8 | 3.8 | 4.8 | 3.2 | 4.2 | 5.2 | 4.4 | 5.4 | 6.4 | 4.6 | 5.6 | 6.6 | 5.2 | 6.2 | 7.2 | 3.0 | 4.0 | 5.0 | 5.4 | 6.4 | 7.4 | 4.6 | 5.6 | 6.6 | 5.8 | 6.8 | 7.8 | 4.4 | 5.4 | 6.4 | 4.0 | 5.0 | 6.0 | 4.0 | 5.0 | 6.0 | 4.6 | 5.6 | 6.6 | 5.0 | 6.0 | 7.0 | 4.6 | 5.6 | 6.6 |
| A5 | 4.4 | 5.4 | 6.4 | 4.0 | 5.0 | 6.0 | 4.4 | 5.4 | 6.4 | 5.0 | 6.0 | 7.0 | 4.4 | 5.4 | 6.4 | 4.4 | 5.4 | 6.4 | 4.8 | 5.8 | 6.8 | 4.4 | 5.4 | 6.4 | 5.0 | 6.0 | 7.0 | 3.0 | 4.0 | 5.0 | 4.8 | 5.8 | 6.8 | 4.4 | 5.4 | 6.4 | 4.4 | 5.4 | 6.4 | 4.4 | 5.4 | 6.4 | 4.8 | 5.8 | 6.8 |
| A6 | 3.2 | 4.2 | 5.2 | 3.4 | 4.4 | 5.4 | 4.2 | 5.2 | 6.2 | 4.8 | 5.8 | 6.8 | 4.4 | 5.4 | 6.4 | 4.6 | 5.6 | 6.6 | 5.0 | 6.0 | 7.0 | 4.6 | 5.6 | 6.6 | 5.0 | 6.0 | 7.0 | 4.4 | 5.4 | 6.4 | 4.4 | 5.4 | 6.4 | 3.8 | 4.8 | 5.8 | 3.2 | 4.2 | 5.2 | 3.4 | 4.4 | 5.4 | 3.2 | 4.2 | 5.2 |
| A7 | 2.4 | 3.4 | 4.4 | 4.2 | 5.2 | 6.2 | 4.6 | 5.6 | 6.6 | 5.0 | 6.0 | 7.0 | 4.6 | 5.6 | 6.6 | 5.4 | 6.6 | 7.8 | 5.8 | 6.8 | 7.8 | 5.8 | 6.8 | 7.8 | 5.4 | 6.4 | 7.4 | 4.2 | 5.2 | 6.2 | 4.2 | 5.2 | 6.2 | 3.4 | 4.4 | 5.4 | 3.2 | 4.2 | 5.2 | 3.4 | 4.4 | 5.4 | 2.8 | 3.8 | 4.8 |
| A8 | 4.4 | 5.4 | 6.4 | 4.6 | 5.6 | 6.6 | 4.6 | 5.6 | 6.6 | 4.6 | 5.6 | 6.6 | 5.8 | 6.8 | 7.8 | 4.4 | 5.4 | 6.4 | 4.4 | 5.4 | 6.4 | 4.4 | 5.4 | 6.4 | 6.2 | 7.2 | 8.2 | 4.4 | 5.4 | 6.4 | 4.4 | 5.4 | 6.4 | 4.4 | 5.4 | 6.4 | 4.4 | 5.4 | 6.4 | 4.4 | 5.4 | 6.4 | 4.4 | 5.4 | 6.4 |
| A9 | 3.0 | 4.0 | 5.0 | 2.8 | 3.8 | 4.8 | 2.8 | 3.8 | 4.8 | 4.6 | 5.6 | 6.6 | 5.8 | 6.8 | 7.8 | 3.8 | 4.8 | 5.8 | 4.6 | 5.6 | 6.6 | 4.8 | 5.8 | 6.8 | 6.2 | 7.2 | 8.2 | 6.2 | 7.2 | 8.2 | 6.6 | 7.6 | 8.6 | 6.0 | 7.0 | 8.0 | 5.6 | 6.6 | 7.6 | 5.2 | 6.2 | 7.2 | 4.6 | 5.6 | 6.6 |
| A10 | 4.2 | 5.2 | 6.2 | 4.4 | 5.4 | 6.4 | 4.2 | 5.2 | 6.2 | 4.4 | 5.4 | 6.4 | 5.0 | 6.0 | 7.0 | 4.4 | 5.4 | 6.4 | 6.2 | 7.2 | 8.2 | 5.4 | 6.4 | 7.4 | 5.8 | 6.8 | 7.8 | 5.2 | 6.2 | 7.2 | 5.2 | 6.2 | 7.2 | 5.4 | 6.4 | 7.4 | 6.0 | 7.0 | 8.0 | 5.6 | 6.6 | 7.6 | 5.8 | 6.8 | 7.8 |

Table A2.
Normalized matrix.
Table A2.
Normalized matrix.
| X1 | X2 | X3 | X4 | X5 | X6 | X7 | X8 | X9 | X10 | X11 | X12 | X13 | X14 | X15 | |||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| A1 | 0.69 | 0.84 | 1.00 | 0.61 | 0.76 | 0.91 | 0.42 | 0.58 | 0.73 | 0.66 | 0.80 | 0.94 | 0.59 | 0.72 | 0.85 | 0.36 | 0.49 | 0.62 | 0.63 | 0.73 | 0.88 | 0.59 | 0.69 | 0.81 | 0.68 | 0.81 | 1.00 | 0.34 | 0.46 | 0.59 | 0.56 | 0.67 | 0.79 | 0.58 | 0.70 | 0.83 | 0.75 | 0.88 | 1.00 | 0.74 | 0.87 | 1.00 | 0.74 | 0.87 | 1.00 |
| A2 | 0.44 | 0.59 | 0.75 | 0.52 | 0.67 | 0.82 | 0.70 | 0.85 | 1.00 | 0.60 | 0.74 | 0.89 | 0.62 | 0.74 | 0.87 | 0.36 | 0.49 | 0.62 | 0.65 | 0.76 | 0.92 | 0.63 | 0.73 | 0.88 | 0.66 | 0.78 | 0.95 | 0.54 | 0.66 | 0.78 | 0.47 | 0.58 | 0.70 | 0.53 | 0.65 | 0.78 | 0.55 | 0.68 | 0.80 | 0.64 | 0.77 | 0.90 | 0.56 | 0.69 | 0.82 |
| A3 | 0.44 | 0.59 | 0.75 | 0.48 | 0.64 | 0.79 | 0.67 | 0.82 | 0.97 | 0.71 | 0.86 | 1.00 | 0.64 | 0.77 | 0.90 | 0.59 | 0.72 | 0.85 | 0.63 | 0.73 | 0.88 | 0.69 | 0.81 | 1.00 | 0.51 | 0.58 | 0.68 | 0.54 | 0.66 | 0.78 | 0.51 | 0.63 | 0.74 | 0.50 | 0.63 | 0.75 | 0.58 | 0.70 | 0.83 | 0.59 | 0.72 | 0.85 | 0.64 | 0.77 | 0.90 |
| A4 | 0.44 | 0.59 | 0.75 | 0.48 | 0.64 | 0.79 | 0.67 | 0.82 | 0.97 | 0.66 | 0.80 | 0.94 | 0.67 | 0.79 | 0.92 | 0.38 | 0.51 | 0.64 | 0.59 | 0.69 | 0.81 | 0.67 | 0.79 | 0.96 | 0.54 | 0.62 | 0.72 | 0.54 | 0.66 | 0.78 | 0.47 | 0.58 | 0.70 | 0.50 | 0.63 | 0.75 | 0.58 | 0.70 | 0.83 | 0.64 | 0.77 | 0.90 | 0.59 | 0.72 | 0.85 |
| A5 | 0.69 | 0.84 | 1.00 | 0.61 | 0.76 | 0.91 | 0.67 | 0.82 | 0.97 | 0.71 | 0.86 | 1.00 | 0.56 | 0.69 | 0.82 | 0.56 | 0.69 | 0.82 | 0.65 | 0.76 | 0.92 | 0.69 | 0.81 | 1.00 | 0.60 | 0.70 | 0.84 | 0.37 | 0.49 | 0.61 | 0.56 | 0.67 | 0.79 | 0.55 | 0.68 | 0.80 | 0.55 | 0.68 | 0.80 | 0.56 | 0.69 | 0.82 | 0.62 | 0.74 | 0.87 |
| A6 | 0.50 | 0.66 | 0.81 | 0.52 | 0.67 | 0.82 | 0.64 | 0.79 | 0.94 | 0.69 | 0.83 | 0.97 | 0.56 | 0.69 | 0.82 | 0.59 | 0.72 | 0.85 | 0.63 | 0.73 | 0.88 | 0.67 | 0.79 | 0.96 | 0.60 | 0.70 | 0.84 | 0.54 | 0.66 | 0.78 | 0.51 | 0.63 | 0.74 | 0.48 | 0.60 | 0.73 | 0.40 | 0.53 | 0.65 | 0.44 | 0.56 | 0.69 | 0.41 | 0.54 | 0.67 |
| A7 | 0.38 | 0.53 | 0.69 | 0.64 | 0.79 | 0.94 | 0.70 | 0.85 | 1.00 | 0.71 | 0.86 | 1.00 | 0.59 | 0.72 | 0.85 | 0.69 | 0.85 | 1.00 | 0.56 | 0.65 | 0.76 | 0.56 | 0.65 | 0.76 | 0.57 | 0.66 | 0.78 | 0.51 | 0.63 | 0.76 | 0.49 | 0.60 | 0.72 | 0.43 | 0.55 | 0.68 | 0.40 | 0.53 | 0.65 | 0.44 | 0.56 | 0.69 | 0.36 | 0.49 | 0.62 |
| A8 | 0.69 | 0.84 | 1.00 | 0.70 | 0.85 | 1.00 | 0.70 | 0.85 | 1.00 | 0.66 | 0.80 | 0.94 | 0.74 | 0.87 | 1.00 | 0.56 | 0.69 | 0.82 | 0.69 | 0.81 | 1.00 | 0.69 | 0.81 | 1.00 | 0.51 | 0.58 | 0.68 | 0.54 | 0.66 | 0.78 | 0.51 | 0.63 | 0.74 | 0.55 | 0.68 | 0.80 | 0.55 | 0.68 | 0.80 | 0.56 | 0.69 | 0.82 | 0.56 | 0.69 | 0.82 |
| A9 | 0.47 | 0.63 | 0.78 | 0.42 | 0.58 | 0.73 | 0.42 | 0.58 | 0.73 | 0.66 | 0.80 | 0.94 | 0.74 | 0.87 | 1.00 | 0.49 | 0.62 | 0.74 | 0.67 | 0.79 | 0.96 | 0.65 | 0.76 | 0.92 | 0.51 | 0.58 | 0.68 | 0.76 | 0.88 | 1.00 | 0.77 | 0.88 | 1.00 | 0.75 | 0.88 | 1.00 | 0.70 | 0.83 | 0.95 | 0.67 | 0.79 | 0.92 | 0.59 | 0.72 | 0.85 |
| A10 | 0.66 | 0.81 | 0.97 | 0.67 | 0.82 | 0.97 | 0.64 | 0.79 | 0.94 | 0.63 | 0.77 | 0.91 | 0.64 | 0.77 | 0.90 | 0.56 | 0.69 | 0.82 | 0.54 | 0.61 | 0.71 | 0.59 | 0.69 | 0.81 | 0.54 | 0.62 | 0.72 | 0.63 | 0.76 | 0.88 | 0.60 | 0.72 | 0.84 | 0.68 | 0.80 | 0.93 | 0.75 | 0.88 | 1.00 | 0.72 | 0.85 | 0.97 | 0.74 | 0.87 | 1.00 |

Table A3.
Distance matrix.
Table A3.
Distance matrix.
| X1 | X2 | X3 | X4 | X5 | X6 | X7 | X8 | X9 | X10 | X11 | X12 | X13 | X14 | X15 | |||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| A1 | 0.00 | 0.00 | 0.00 | 0.09 | 0.09 | 0.09 | 0.27 | 0.27 | 0.27 | 0.06 | 0.06 | 0.06 | 0.15 | 0.15 | 0.15 | 0.33 | 0.36 | 0.38 | 0.06 | 0.08 | 0.12 | 0.09 | 0.13 | 0.19 | 0.00 | 0.00 | 0.00 | 0.41 | 0.41 | 0.41 | 0.21 | 0.21 | 0.21 | 0.18 | 0.18 | 0.18 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| A2 | 0.25 | 0.25 | 0.25 | 0.18 | 0.18 | 0.18 | 0.00 | 0.00 | 0.00 | 0.11 | 0.11 | 0.11 | 0.13 | 0.13 | 0.13 | 0.33 | 0.36 | 0.38 | 0.04 | 0.06 | 0.08 | 0.06 | 0.08 | 0.12 | 0.02 | 0.03 | 0.05 | 0.22 | 0.22 | 0.22 | 0.30 | 0.30 | 0.30 | 0.23 | 0.23 | 0.23 | 0.20 | 0.20 | 0.20 | 0.10 | 0.10 | 0.10 | 0.18 | 0.18 | 0.18 |
| A3 | 0.25 | 0.25 | 0.25 | 0.21 | 0.21 | 0.21 | 0.03 | 0.03 | 0.03 | 0.00 | 0.00 | 0.00 | 0.10 | 0.10 | 0.10 | 0.10 | 0.13 | 0.15 | 0.06 | 0.08 | 0.12 | 0.00 | 0.00 | 0.00 | 0.17 | 0.22 | 0.32 | 0.22 | 0.22 | 0.22 | 0.26 | 0.26 | 0.26 | 0.25 | 0.25 | 0.25 | 0.18 | 0.18 | 0.18 | 0.15 | 0.15 | 0.15 | 0.10 | 0.10 | 0.10 |
| A4 | 0.25 | 0.25 | 0.25 | 0.21 | 0.21 | 0.21 | 0.03 | 0.03 | 0.03 | 0.06 | 0.06 | 0.06 | 0.08 | 0.08 | 0.08 | 0.31 | 0.33 | 0.36 | 0.09 | 0.13 | 0.19 | 0.02 | 0.03 | 0.04 | 0.14 | 0.19 | 0.28 | 0.22 | 0.22 | 0.22 | 0.30 | 0.30 | 0.30 | 0.25 | 0.25 | 0.25 | 0.18 | 0.18 | 0.18 | 0.10 | 0.10 | 0.10 | 0.15 | 0.15 | 0.15 |
| A5 | 0.00 | 0.00 | 0.00 | 0.09 | 0.09 | 0.09 | 0.03 | 0.03 | 0.03 | 0.00 | 0.00 | 0.00 | 0.18 | 0.18 | 0.18 | 0.13 | 0.15 | 0.18 | 0.04 | 0.06 | 0.08 | 0.00 | 0.00 | 0.00 | 0.08 | 0.11 | 0.16 | 0.39 | 0.39 | 0.39 | 0.21 | 0.21 | 0.21 | 0.20 | 0.20 | 0.20 | 0.20 | 0.20 | 0.20 | 0.18 | 0.18 | 0.18 | 0.13 | 0.13 | 0.13 |
| A6 | 0.19 | 0.19 | 0.19 | 0.18 | 0.18 | 0.18 | 0.06 | 0.06 | 0.06 | 0.03 | 0.03 | 0.03 | 0.18 | 0.18 | 0.18 | 0.10 | 0.13 | 0.15 | 0.06 | 0.08 | 0.12 | 0.02 | 0.03 | 0.04 | 0.08 | 0.11 | 0.16 | 0.22 | 0.22 | 0.22 | 0.26 | 0.26 | 0.26 | 0.28 | 0.28 | 0.28 | 0.35 | 0.35 | 0.35 | 0.31 | 0.31 | 0.31 | 0.33 | 0.33 | 0.33 |
| A7 | 0.31 | 0.31 | 0.31 | 0.06 | 0.06 | 0.06 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.15 | 0.15 | 0.15 | 0.00 | 0.00 | 0.00 | 0.12 | 0.17 | 0.24 | 0.12 | 0.17 | 0.24 | 0.11 | 0.15 | 0.22 | 0.24 | 0.24 | 0.24 | 0.28 | 0.28 | 0.28 | 0.33 | 0.33 | 0.33 | 0.35 | 0.35 | 0.35 | 0.31 | 0.31 | 0.31 | 0.38 | 0.38 | 0.38 |
| A8 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.06 | 0.06 | 0.06 | 0.00 | 0.00 | 0.00 | 0.13 | 0.15 | 0.18 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.17 | 0.22 | 0.32 | 0.22 | 0.22 | 0.22 | 0.26 | 0.26 | 0.26 | 0.20 | 0.20 | 0.20 | 0.20 | 0.20 | 0.20 | 0.18 | 0.18 | 0.18 | 0.18 | 0.18 | 0.18 |
| A9 | 0.22 | 0.22 | 0.22 | 0.27 | 0.27 | 0.27 | 0.27 | 0.27 | 0.27 | 0.06 | 0.06 | 0.06 | 0.00 | 0.00 | 0.00 | 0.21 | 0.23 | 0.26 | 0.02 | 0.03 | 0.04 | 0.04 | 0.06 | 0.08 | 0.17 | 0.22 | 0.32 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.05 | 0.05 | 0.05 | 0.08 | 0.08 | 0.08 | 0.15 | 0.15 | 0.15 |
| A10 | 0.03 | 0.03 | 0.03 | 0.03 | 0.03 | 0.03 | 0.06 | 0.06 | 0.06 | 0.09 | 0.09 | 0.09 | 0.10 | 0.10 | 0.10 | 0.13 | 0.15 | 0.18 | 0.15 | 0.20 | 0.29 | 0.09 | 0.13 | 0.19 | 0.14 | 0.19 | 0.28 | 0.12 | 0.12 | 0.12 | 0.16 | 0.16 | 0.16 | 0.08 | 0.08 | 0.08 | 0.00 | 0.00 | 0.00 | 0.03 | 0.03 | 0.03 | 0.00 | 0.00 | 0.00 |
References
- Evolution of Vietnam’s Textiles & Garments Industry Amid COVID-19. Fi-bre2fashion. Available online: https://www.fibre2fashion.com/industry-article/8705/evolution-of-vietnam-s-textiles-garments-industry-amid-covid-19 (accessed on 22 June 2020).
- Handfield, R. Supply Chain Resource Cooperative. NC State University. Available online: https://scm.ncsu.edu/scm-articles/article/author/handfield (accessed on 22 January 2020).
- Durmić, E. The Evaluation of the Criteria for Sustainable Supplier Selection by Using the FUCOM Method. Oper. Res. Eng. Sci. Theory Appl. 2019, 2, 91–107. [Google Scholar] [CrossRef]
- Zavadskas, E.K.; Turskis, Z.; Stević, Ž.; Mardani, A. Modelling Procedure for the Selection of Steel Pipes Supplier by Applying Fuzzy AHP Method. Oper. Res. Eng. Sci. Theory Appl. 2020, 3, 39–53. [Google Scholar] [CrossRef]
- Badi, I.; Pamucar, D. Supplier selection for steelmaking company by using combined Grey-MARCOS methods. Decis. Mak. Appl. Manag. Eng. 2020, 3, 37–48. [Google Scholar] [CrossRef]
- Dweiri, F.T.; Kumar, S.; Khan, S.A.; Jain, V. Designing an integrated AHP based decision support system for supplier selection in automotive industry. Expert Syst. Appl. 2016, 62, 273–283. [Google Scholar] [CrossRef]
- Radovanović, M.; Ranđelović, A.; Jokić, Ž. Application of hybrid model fuzzy AHP-VIKOR in selection of the most efficient procedure for rectification of the optical sight of the long-range rifle. Decis. Mak. Appl. Manag. Eng. 2020, 3, 131–148. [Google Scholar] [CrossRef]
- Narasimhan, R. An Analytical Approach to Supplier Selection. J. Purch. Mater. Manag. 1983, 19, 27–32. [Google Scholar] [CrossRef]
- Tahriri, F.; Osman, M.R.; Ali, A.; Yusuff, R.; Esfandiary, A. AHP approach for supplier evaluation and selection in a steel manufacturing company. J. Ind. Eng. Manag. (JIEM) 2008, 1, 54–76. [Google Scholar]
- Wang, Y.-M.; Chin, K.-S.; Leung, J.P.-F. A note on the application of the data envelopment analytic hierarchy process for supplier selection. Int. J. Prod. Res. 2009, 47, 3121–3138. [Google Scholar] [CrossRef]
- Farzad, T.; Mohammad Rasid, O.; Aidy, A.; Rosnah Mohd, Y. A review of supplier selection methods in manufacturing industries. Suranaree J. Sci. Technol. 2008, 15, 201–208. [Google Scholar]
- Nydick, R.L.; Hill, R.P. Using the Analytic Hierarchy Process to Structure the Supplier Selection Procedure. Int. J. Purch. Mater. Manag. 1992, 28, 31–36. [Google Scholar] [CrossRef]
- Yang, C.; Chen, B. Supplier selection using combined analytical hierarchy process and grey relational analysis. J. Manuf. Technol. Manag. 2006, 17, 926–941. [Google Scholar] [CrossRef]
- Yücenur, G.N.; Vayvay, O.; Demirel, N. Çetin Supplier selection problem in global supply chains by AHP and ANP approaches under fuzzy environment. Int. J. Adv. Manuf. Technol. 2011, 56, 823–833. [Google Scholar] [CrossRef]
- Kasirian, M.N.; Yusuff, R.M. Application of AHP and ANP in supplier selection process—A case in an automotive company. Int. J. Manag. Sci. Eng. Manag. 2010, 5, 125–135. [Google Scholar] [CrossRef]
- Eshtehardian, E.; Ghodousi, P.; Bejanpour, A. Using ANP and AHP for the supplier selection in the construction and civil engineering companies; Case study of Iranian company. KSCE J. Civ. Eng. 2013, 17, 262–270. [Google Scholar] [CrossRef]
- Choudhury, S.; Howladar, P.; Majumder, M.; Saha, A.K. Application of Novel MCDM for Location Selection of Surface Water Treatment Plant. IEEE Trans. Eng. Manag. 2019, 1–13. [Google Scholar] [CrossRef]
- Wang, C.-N.; Nguyen, V.T.; Thai, H.T.N.; Duong, D.H. Multi-Criteria Decision Making (MCDM) Approaches for Solar Power Plant Location Selection in Viet Nam. Energies 2018, 11, 1504. [Google Scholar] [CrossRef]
- Tadić, S.R.; Krstić, M.; Roso, V.; Brnjac, N. Dry Port Terminal Location Selection by Applying the Hybrid Grey MCDM Model. Sustainability 2020, 12, 6983. [Google Scholar] [CrossRef]
- Emovon, I.; Oghenenyerovwho, O.S. Application of MCDM method in material selection for optimal design: A review. Results Mater. 2020, 7, 100115. [Google Scholar] [CrossRef]
- Singh, M.; Pant, M.; Godiyal, R.D.; Sharma, A.K. MCDM approach for selection of raw material in pulp and papermaking industry. Mater. Manuf. Process. 2020, 35, 241–249. [Google Scholar] [CrossRef]
- Mills, E.F.E.A.; Baafi, M.A.; Amowine, N.; Zeng, K. A Hybrid Grey Mcdm Approach for Asset Allocation: Evidence from China’s Shanghai Stock Exchange. J. Bus. Econ. Manag. 2020, 21, 446–472. [Google Scholar] [CrossRef]
- Biswas, S. Measuring performance of healthcare supply chains in India: A comparative analysis of multi-criteria deci-sion making methods. Decis. Mak. Appl. Manag. Eng. 2020, 3, 162–189. [Google Scholar] [CrossRef]
- Pi, W.-N.; Low, C. Supplier evaluation and selection via Taguchi loss functions and an AHP. Int. J. Adv. Manuf. Technol. 2005, 27, 625–630. [Google Scholar] [CrossRef]
- Timmerman, E. An Approach to Vendor Performance Evaluation. J. Purch. Mater. Manag. 1986, 22, 2–8. [Google Scholar] [CrossRef]
- Petrović, G.; Mihajlović, J.; Ćojbašić, Ž.; Madić, M.; Marinković, D. Comparison of three fuzzy mcdm methods for solving the supplier selection problem. Facta Univ. Ser. Mech. Eng. 2019, 17, 455–469. [Google Scholar] [CrossRef]
- Talluri, S.; Narasimhan, R. Vendor evaluation with performance variability: A max–min approach. Eur. J. Oper. Res. 2003, 146, 543–552. [Google Scholar] [CrossRef]
- Ng, W.L. An efficient and simple model for multiple criteria supplier selection problem. Eur. J. Oper. Res. 2008, 186, 1059–1067. [Google Scholar] [CrossRef]
- Guneri, A.F.; Yucel, A.; Ayyıldız, G. An integrated fuzzy-lp approach for a supplier selection problem in supply chain man-agement. Expert Syst. Appl. 2009, 36, 9223–9228. [Google Scholar] [CrossRef]
- Chaundry, S.S.; Fost, F.G.; Zydiak, J.L. Vendor selection with price breaks. Eur. J. Oper. Res. 1993, 70, 52–66. [Google Scholar]
- Rosenthal, E.C.; Zydiak, J.L.; Chaudhry, S.S. Vendor Selection with Bundling. Decis. Sci. 1995, 26, 35–48. [Google Scholar] [CrossRef]
- Ghodsypour, S.; O’Brien, C. The total cost of logistics in supplier selection, under conditions of multiple sourcing, multiple criteria and capacity constraint. Int. J. Prod. Econ. 2001, 73, 15–27. [Google Scholar] [CrossRef]
- Weber, C.A.; Ellram, L.M. Supplier Selection Using Multi-objective Programming: A Decision Support System Approach. Int. J. Phys. Distrib. Logist. Manag. 1993, 23, 3–14. [Google Scholar] [CrossRef]
- Gao, Z.; Tang, L. A multi-objective model for purchasing of bulk raw materials of a large-scale integrated steel plant. Int. J. Prod. Econ. 2003, 83, 325–334. [Google Scholar] [CrossRef]
- Kannan, D.; Khodaverdi, R.; Olfat, L.; Jafarian, A.; Diabat, A. Integrated fuzzy multi criteria decision making method and multi-objective programming approach for supplier selection and order allocation in a green supply chain. J. Clean. Prod. 2013, 47, 355–367. [Google Scholar] [CrossRef]
- Karpak, B.; Kasuganti, R.R.; Kumcu, E. Multi-Objective Decision-Making In Supplier Selection: An Application of Visual Interactive Goal Programming. J. Appl. Bus. Res. (JABR) 2011, 15, 57. [Google Scholar] [CrossRef][Green Version]
- Chang, C.-T.; Chen, H.-M.; Zhuang, Z.-Y. Integrated multi-choice goal programming and multi-segment goal programming for supplier selection considering imperfect-quality and price-quantity discounts in a multiple sourcing environment. Int. J. Syst. Sci. 2012, 45, 1101–1111. [Google Scholar] [CrossRef]
- Kuo, R.J.; Lin, Y.J. Supplier selection using analytic network process and data envelopment analysis. Int. J. Prod. Econ. 2012, 50, 2852–2863. [Google Scholar] [CrossRef]
- Chattopadhyay, R.; Chakraborty, S.; Chakraborty, S. An integrated D-MARCOS method for supplier selection in an iron and steel industry. Decis. Mak. Appl. Manag. Eng. 2020, 3, 49–69. [Google Scholar] [CrossRef]
- Ramakrishnan, K.R.; Chakraborty, S. A Cloud Topsis Model for Green Supplier Selection. Facta Univ. Ser. Mech. Eng. 2020, 18, 375. [Google Scholar] [CrossRef]
- Ho, W.; Xu, X.; Dey, P.K. Multi-criteria decision making approaches for supplier evaluation and selection: A literature review. Eur. J. Oper. Res. 2010, 202, 16–24. [Google Scholar] [CrossRef]
- Lin, K.-P.; Hung, K.-C.; Lin, Y.-T.; Hsieh, Y.-H. Green Suppliers Performance Evaluation in Belt and Road Using Fuzzy Weighted Average with Social Media Information. Sustainability 2017, 10, 5. [Google Scholar] [CrossRef]
- Jia, P.; Govindan, K.; Choi, T.-M.; Rajendran, S. Supplier Selection Problems in Fashion Business Operations with Sustainability Considerations. Sustainability 2015, 7, 1603–1619. [Google Scholar] [CrossRef]
- Fong, J.R.M.; Alcaraz, J.L.G.; Díaz-Reza, J.R.; Sáenz-Díez, J.C.; Blanco-Fernández, J. The Role of Green and Traditional Supplier Attributes on Business Performance. Sustainability 2017, 9, 1520. [Google Scholar] [CrossRef]
- Saaty, T.L. The Analytic Hierarchy Process—Planning, Priority Setting, Resource Allocation; McGraw-Hill: New York, NY, USA, 1980. [Google Scholar]
- Büyüközkan, G.; Feyzioğlu, O.; Nebol, E. Selection of the strategic alliance partner in logistics value chain. Int. J. Prod. Econ. 2008, 113, 148–158. [Google Scholar] [CrossRef]
- Zimmermann, H.-J. Fuzzy Set Theory—And Its Applications, 2nd ed.; Springer: Dordrecht, The Netherlands, 1991. [Google Scholar]
- Buckley, J. Fuzzy hierarchical analysis. Fuzzy Sets Syst. 1985, 17, 233–247. [Google Scholar] [CrossRef]
- Wei, G.-W. GRA method for multiple attribute decision making with incomplete weight information in intuitionistic fuzzy setting. Knowl. Based Syst. 2010, 23, 243–247. [Google Scholar] [CrossRef]
- Wei, G.-W. Gray relational analysis method for intuitionistic fuzzy multiple attribute decision making. Expert Syst. Appl. 2011, 38, 11671–11677. [Google Scholar] [CrossRef]
- Ross, T.J. Fuzzy Logic with Engineering Applications; Wiley: Hoboken, NJ, USA, 2010. [Google Scholar]
- Pan, N.-F. Fuzzy AHP approach for selecting the suitable bridge construction method. Autom. Constr. 2008, 17, 958–965. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).