Abstract
After the recent establishment of the Sustainable Development Goals and the Agenda 2030, the sustainable design of products in general and infrastructures in particular emerge as a challenging field for the development and application of multicriteria decision-making tools. Sustainability-related decision problems usually involve, by definition, a wide variety in number and nature of conflicting criteria, thus pushing the limits of conventional multicriteria decision-making tools practices. The greater the number of criteria and the more complex the relations existing between them in a decisional problem, the less accurate and certain are the judgments required by usual methods, such as the analytic hierarchy process (AHP). The present paper proposes a neutrosophic AHP completion methodology to reduce the number of judgments required to be emitted by the decision maker. This increases the consistency of their responses, while accounting for uncertainties associated to the fuzziness of human thinking. The method is applied to a sustainable-design problem, resulting in weight estimations that allow for a reduction of up to 22% of the conventionally required comparisons, with an average accuracy below 10% between estimates and the weights resulting from a conventionally completed AHP matrix, and a root mean standard error below 15%.
1. Introduction
Optimal decision-making has been an active field of scientific research since the 1970s. Ever since then, efforts have been made to develop a variety of mathematical multicriteria decision-making tools (MCDM) tools that cover a wide range of decisional problems. One of the most recent decision-making challenges is the sustainable design of products. The Sustainable Development Goals adopted by the United Nations in 2015 advocate for a profound shift in the conventional design practices. Based on the functionality and economic performance of the products, current practices usually fall short in addressing social and environmental impacts along the product’s life cycle. In particular and given the vast recognized effects that the construction sector has both on the environment and on the society [1], efforts have been made during the last years to optimize the response of construction-related products, such as bridges, buildings, and other infrastructures, on the different dimensions of sustainability. Studies have been conducted that aim to optimize the economic costs of both the construction [2,3] and the maintenance [4,5] of different types of infrastructures. Regarding the environmental impacts of structures, there has been increasing interest in reducing particular environmental effects, such as their carbon footprint [6,7] or their embodied energy [8], as well as in improving their overall environmental performance along with their life cycle on the basis of score-based standardized methods [9,10]. Only recently have studies been published on the analysis of social life-cycle impacts of infrastructures [11,12].
Although being an essential requirement, the separate assessment of the individual sustainability dimensions is still not sufficient for the sustainable design of a product, as it must only be addressed by assuming a holistic perspective, taking into consideration each and every of its dimensions simultaneously [13]. Given the different nature of the economic, environmental, and social criteria involved in finding the most sustainable solution to a design problem, the sustainable design of products emerges as a major field for the application of MCDM tools. Among the most popular MCDM methods is the so-called analytic hierarchy process (AHP), defined by Saaty [14]. The AHP method is conceived to aid the decision maker in structuring complex problems where multiple and conflicting criteria are involved. The method is based on determining, for each pair of criteria, how much more relevant one criterion is with respect to the other in order to make the final decision. AHP has been widely applied in assessing design problems in a variety of fields, such as energy management [15], transport management [16], or maintenance of infrastructures [17], among many others.
The need for a holistic approach to address sustainable-design problems relies on the complex and often intricate relations existing between the different criteria involved in the final decision [18]. However, Zadeh [19] posed that our ability to emit precise and meaningful statements decreases to the same extent that the complexity of the problem to be addressed increases. Consequently, given that AHP bases the assessment results on the subjective judgments emitted by the decision maker, the use of this method for assessing sustainable-design problems presents two major limitations that need to be resolved.
On the one hand, the use of AHP as defined by Saaty has been the object of severe criticism, as it presumes the judgments emitted by the decision maker to be certain. That assumption is not consistent with the rather diffuse nature of human thinking [20], in which vagueness increases with the complexity of the problem to be addressed. In such contexts, the fuzzy sets theory [21] has emerged as a powerful tool to mathematically model the vagueness associated to human reasoning. In contrast to classical sets theory, where the membership of an element in a set is always expressed in binary terms, the fuzzy logic allows one to handle with partial membership grades. A continuous membership function is a defined value in the real unit interval. Thus defined, the fuzzy sets theory establishes a practical baseline for modeling the non-probabilistic uncertainties of human thinking and has been therefore widely applied in decision-making problems in recent years [22,23,24].
In an attempt to further enhance the proven, but limited advantages of the fuzzy sets theory for modeling vague cognitive processes, other sets theories have been introduced over recent times. Among them, the neutrosophic sets theory introduced by Smarandache [25] constitutes the most advanced generalization of the fuzzy sets theory existing to date. Neutrosophic logic is based on the definition of three independent membership functions that represent the truth, the indeterminacy, and the falsehood of a statement. In doing so, the neutrosophic sets theory allows one to model not only imprecise statements, but also to deal successfully with paradoxes or statements that are inconsistent or based on incomplete information. From a practical point of view, only in very recent years the neutrosophic sets theory has reached a sufficient level of development to be applied in the resolution of real scientific and engineering problems. In recent times, the neutrosophic logic has been successfully applied to solve decision-making problems related to a variety of fields, such as investment strategies [26], supplier selection [27], or the design of bridges [13], among others.
In addition, besides the aforementioned limitation, the accuracy of the AHP method for weight estimation is also hindered by the size of the comparison matrix to be filled by the decision maker. In fact, this is not a limitation of the method itself but of the human capacity to process a huge amount of information. This was recognized by Saaty himself [28], who established seven as the maximum number of criteria that a person is able to evaluate with a certain consistency using his method. This is indeed a serious limitation when it comes to addressing the sustainable performance of a product, as sustainable assessments tend to rely on more than seven criteria. In recent times, research has been conducted on deriving AHP criteria weights from incomplete comparison matrices. Incomplete matrices allow one to reduce the number of comparisons needed by the classical AHP, namely n(n − 1)/2 (n being the number of criteria), to a more affordable number of judgments. This has also the advantage that the decision maker is not obliged to complete all entries of the matrix if they lack the knowledge to fill some of them.
Many of the matrix completion methods are based on the idea first suggested by Harker [29] of repairing the incomplete comparison matrix by maximizing its resulting consistency. Completion methods based on the consistency optimization have been developed from a classical perspective [30,31] as well as from the fuzzy logic [32]. Zhou [33] criticized the results derived from the use of such maximizing methods to be ideal and nonrealistic. To overcome that problem, Zhou suggested a DEMATEL-based completion method to restore AHP comparison matrices to their original state (whether it is consistent or not) and not to their ideal one. This method allows for the completion of AHP matrices maintaining the original consistency derived from the decision maker by analyzing the indirect relations existing between two criteria to derive the unknown entries.
The present paper aims to bridge the abovementioned existing gaps of the classical AHP method when coping with decision problems that involve a great amount of complexly related criteria, such as sustainable-design problems. Herein, a neutrosophic extension of the DEMATEL-based AHP matrix completion method is proposed to reduce the number of required comparisons to be made by the decision maker, while including in the decision problem the implicit nonprobabilistic information derived from the judgments emitted by him/her.
The rest of the paper is divided into the following sections: Section 2 presents relevant materials and methods: Section 2.1 introduces the classical AHP method, Section 2.2 describes the criteria weight derivation out of a neutrosophic AHP comparison matrix, and Section 2.3 presents a method for the completion of incomplete comparison matrices in a neutrosophic environment. Section 3 describes a sustainable-design decision problem as a case study for the application of the proposed neutrosophic completion technique. In Section 4, the obtained results are presented. Finally, in Section 5, conclusions on the performance of the proposed technique are drawn.
2. Materials and Methods
2.1. Preliminaries on Classical AHP Method
The classical AHP method, as defined by Saaty [14], allows one to derive the weights between alternatives or criteria involved in a decision-making process. The method requires an expert to complete a comparison matrix, where each element aij represents how much more relevant alternative i is with respect to alternative j for making the final decision according to expert’s knowledge of the problem. The matrix is filled with numerical values from the so-called Saaty’s fundamental scale, which allows for the conversion of semantic values into real numbers. The fundamental scale is a discrete set of integers that ranges from 1 to 9, with 1 meaning that both alternatives are equally relevant, and 9 that the first alternative is extremely more important than the second one.
Built this way, the classical AHP comparison matrix A = {aij} results in a square and reciprocal matrix, i.e., aij = 1/aji ∀i,j ∈ {1,...,n}, where n is the number of alternatives or criteria to be compared. It should be noted as well that aii = 1 ∀i ∈ {1,...,n}. The weights of each alternative are then obtained as the elements of the eigenvector associated to the greatest eigenvalue λmax of the comparison matrix A.
AHP method provides meaningful results if the comparison matrix is filled consistently. Saaty [14] proposed a mathematical way to evaluate the consistency of the matrix through the consistency index CI, defined as:
CI = (λmax − n)/(n − 1)
2.2. Analytic Hierarchy Process in a Neutrosophic Environment
Here, the application of the neutrosophic logic on the derivation of AHP-based criteria weights is exposed. First, some preliminaries on the neutrosophic logic and the basic neutrosophic arithmetic operations are presented. Then, the construction of a neutrosophic AHP comparison matrix that accounts for the nonprobabilistic uncertainties associated to the expert’s emitted judgments is described.
2.2.1. Neutrosophic Logic Fundamentals
Neutrosophic sets theory is a generalization of the fuzzy sets theory meant to model more cognitive information than the fuzzy logic, because it can handle indeterminacies and neutralities [34]. A neutrosophic set A in a finite universe set X is defined as:
where tA(x), iA(x), and fA(x) correspond to the truth, indeterminacy, and falsity functions of the element x ∈ X. Truth, indeterminacy, and falsity membership functions are defined in the unit interval [0, 1] and are independent, i.e., they satisfy:
A single-valued triangular neutrosophic number a = ⟨(a1, a2, a3); ta, ia, fa⟩ on the real number set is described with the following membership functions [35]:
The basic arithmetic operations between two single-valued triangular neutrosophic numbers a = ⟨(a1, a2, a3); ta, ia, fa⟩ and b = ⟨(b1, b2, b3); tb, ib, fb⟩ are defined as [36,37]:
It should be noted that the division operation is only valid if ta ≤ tb, ia ≥ ib, fa ≥ fb, tb ≠ 0, and ib, fb ≠ 1.
2.2.2. On the Construction of the Neutrosophic AHP Comparison Matrix
To incorporate the nonprobabilistic uncertainties associated to the judgments emitted by the decision maker, a neutrosophic AHP comparison matrix is constructed following the methodology proposed by Navarro et al. [13], where each element of the matrix aij is a single-valued neutrosophic number aij = ⟨(lij,mij,uij); tij, iij, fij⟩ ∀i,j ∈ {1,...,n}. The diagonal elements of the comparison matrix are defined as aii = ⟨(1,1,1); 0,0,0⟩ ∀i ∈ {1,...,n}. It is important to note that the reciprocal elements of the matrix are defined as aji = 1/aij = ⟨(1/uij,1/mij,1/lij); tij, iij, fij⟩ ∀i,j ∈ {1,...,n} [38].
The method requires from the decision maker to fill a conventional AHP matrix, together with the self-confidence degree, evaluated on the interval [0, 1], expressed by the expert on their comparisons. Considering these inputs, the central values mij of each matrix element aij correspond directly to the judgments emitted by the decision maker expressed according to the fundamental scale introduced by Saaty. The lower and upper bounds {lij, uij} of each triangular number are expressed in terms of the Saaty’s scale as well. These bounds can be obtained as:
where mij ± ∆(cij) represents the value of the extended Saaty’s fundamental scale after subtracting/adding a certain number of steps ∆(cij) to the central value mij. The extended fundamental scale is a discrete set that adds to Saaty’s fundamental scale its reciprocal values in an inverse order, thus ranging from 1/9 to 9. ∆(cij) is defined as a stepwise function that depends on the certainty cij emitted by the decision maker when expressing judgment aij (Table 1).

Table 1.
Steps on Saaty’s extended scale [8].
Obtaining the neutrosophic parameters {tij, iij, fij} expressing the reliability of each judgment aij emitted by the decision maker is now presented. The truth parameter tij can be derived from the expert’s assessment credibility [39]. Here, the expert’s credibility is related to the relevant experience that the decision maker expresses on the fields involved in the decision-making problem [40]:
where the expertise of the decision maker is addressed here in terms of p coefficients defined in the interval [0, 1]. Four coefficients are considered here to be relevant for determining the expert’s knowledge related to the sustainable design of infrastructures, measuring the expert’s experience in structural design, as well as in environmental, social, and economic assessments.
The indeterminacy iij can be obtained from the complementary of the certainty values cij expressed by the decision maker for each element of the comparison matrix:
At last, the parameter representing the falsehood fij of the expert’s statements is derived from the consistency of his/her resulting comparison matrix and is common for every statement:
where RI is a random index defined by Saaty [14] that reflects the coherency of a comparison nxn matrix filled with random values (Table 2), and CRlim is the limiting consistency ratio for a comparison matrix to be considered acceptably consistent. For more than 5 criteria, CRlim = 10%.

Table 2.
Steps on Saaty’s extended scale [8].
2.2.3. Derivation of Weights from a Neutrosophic Comparison Matrix
To derive the eigenvalue-based weights from an AHP matrix so as proposed by the classical method is nonpractical in fuzzy environments [41]. Buckley [42] presented an alternative procedure to derive weights from fuzzy comparison matrices that has been widely used since its publication. However, given that the extended Saaty’s fundamental scale is not equispaced, fuzzy weights derived from the application of Buckley’s method turn out to become unreasonably high and asymmetric definition ranges [43]. As a response to the abovementioned limitation, Enea and Piazza [44] proposed a procedure to derive acceptably constrained fuzzy ranges for the weights resulting from the application of Buckley’s method. This constriction method, originally defined for fuzzy numbers, was first successfully applied by Navarro [13] to determine weight boundaries in a neutrosophic environment. The method consists of the following two mathematical programming models to derive the lower and upper bounds (wl,i, wu,i) of a neutrosophic weight w as:
Both models are subject to following conditions:
2.2.4. Deneutrosophication Process
As a result from the above, weights wi for each of the decision criteria i are derived in the form of triangular neutrosophic numbers, namely wi = ⟨(wl,i, wm,i, wu,i); ti, ii, fi⟩. A so-called deneutrosophication technique is required to transform those weights into scalar numbers. Sodenkamp et al. [39] proposed a procedure for single-valued neutrosophic numbers based on two subsequent steps, which was extended for its application on generalized neutrosophic numbers by Navarro et al. [13]. Firstly, the neutrosophic weights are converted into triangular fuzzy numbers. The transfer function converting the neutrosophic membership functions ⟨μi(x),νi(x),λi(x)⟩ into a single fuzzy membership function ηi(x) is obtained as the distance between each point contained in the triad and the point corresponding to the neutrosophic point of optimum reliability ⟨1,0,0⟩:
The second step for obtaining the scalar weights consists in defuzzifying the fuzzy weights. Chu and Tao [45] proposed a defuzzification procedure based on obtaining an area index, which results from the rectangular area between the origin of the considered coordinate system (0, 0) and the centroid point (CoGx, CoGy) of the fuzzy weight. The final scalar weights Wi are obtained as:
where n is the number of criteria involved in the decision-making process.
2.3. Completion Method for Neutrosophic AHP Comparison Matrices
In this section, a methodology is presented to derive neutrosophic AHP comparison matrices out of an incomplete, conventional comparison matrix. The resulting synthetic matrix shall repair the incomplete matrix to its original consistency condition. First, the fundamentals of the classical DEMATEL technique are exposed. Then, a DEMATEL-based completion method on a neutrosophic environment is presented.
2.3.1. The Classical DEMATEL Technique
The MCDM DEMATEL method is conceived to convert complex causal relations between elements of any type into a structured and intelligible visual model, where factors are classified into effect and cause categories [46]. The classical method consists of four steps:
Step 1. Generation of a direct influence matrix DIM. Similar to the AHP method, experts are first asked to fill a comparison matrix. Here, the influence that factor i has on factor j is estimated using a four-levels scale of integers ranging from 0 to 3, each score representing “no influence”, “low influence”, “medium influence”, and “high influence”, respectively. For each expert k, a non-negative influence matrix DIMk = {zij}, where zij is the influence score assigned in accordance with the abovementioned scale. Diagonal elements are set to zero. The final direct influence matrix DIM is obtained as the average of the matrices DIMk obtained from the experts.
Step 2. Matrix normalization. The direct influence matrix DIM is now normalized to NIM by dividing each matrix element zij by s, defined as:
Step 3. Generation of the total relation matrix TRM. By definition, a total influence relation matrix TRM = {gij} can be obtained by aggregating direct and indirect effects as:
where I is represents the identity matrix.
Step 4. Derivation of the influential factors Ri and Ci. The influential factors Ri and Ci can be obtained as the sum of each row and column of the TRM, respectively. For a particular factor i, depending on whether Ri − Ci is positive or negative, it can be obtained if factor i falls in the cause or in the effect group, respectively.
2.3.2. Completion Method for Neutrosophic AHP Matrices
Given that DEMATEL method is conceived to reveal the non-evident relations existing between a set of factors and considering that both DEMATEL and AHP are based on the analysis of comparison matrices, Zhou [33] recently suggested a DEMATEL-inspired technique for restoring incomplete AHP comparison matrices to their initial state and consistency. Zhou’s method was limited to handling scalar comparison matrices.
A DEMATEL-based method is introduced here for repairing incomplete AHP comparison matrices A* = {aij} defined in a neutrosophic environment, i.e., where elements aij are defined by triangular neutrosophic numbers aij = ⟨(lij,mij,uij); tij, iij, fij⟩ ∀i,j ∈ {1,...,n}. The basic inputs for the problem are an incomplete, conventional comparison matrix AHP M* = {mij}, together with an incomplete certainty matrix C* = {cij}. It shall be noted that cij is known only if mij is known. The construction of the complete neutrosophic matrix consists of several steps, as follows:
First, the missing central values mij of the incomplete matrix M* are obtained following the technique proposed by Zhou et al. [33]:
Step 1.1. Generation of DIM. Given an incomplete scalar AHP matrix M* = {mij}, compute DIM = {zij}, where zij = mij if mij is known and zij = 0 if mij is unknown.
Step 1.2. Normalization of DIM. Compute the normalized influence matrix NIM by dividing each matrix element zij by s, as in classical DEMATEL (see Equation (23)).
Step 1.3. Compute total relation matrix TRM = {gij} as in classical DEMATEL (see Equation (24)).
Step 1.4. Estimate a complete and reciprocal pairwise comparison matrix M’ = {m’ij}, considering the relations revealed between factors by the total relation matrix TRM = {gij}:
Taking into consideration that the resulting synthetic comparison matrix M’ containing the central elements shall be reciprocal and considering the factors relation presented in Equation (25), each missing entry m*ij shall be derived.
Once the central elements are obtained, the upper and lower bounds {lij, uij} of each element aij shall be derived. For the known values of the input AHP matrix, the lower and upper bounds {lij, uij} shall be obtained according to Equation (12). The estimation of the missing bounds {l*ij, u*ij} consists of several steps:
Step 2.1. Two auxiliary square matrices L* = {lij} and U* = {uij} are constructed, where {lij, uij} = {0, 0} if mij is unknown.
Step 2.2. Normalization of L* and U*. Compute the normalized influence matrices by dividing each matrix element {lij, uij} as follows:
Step 2.3. Compute total relation matrices TRML = {gLij} and TRMU = {gUij} as in classical DEMATEL (see Equation (24)).
Step 2.4. The missing values {l*ij, u*ij} shall then be derived as:
The neutrosophic parameters {t*ij, i*ij, f*ij} of the missing entries shall reflect the reliability of the estimates. The expert’s credibility when handling complete neutrosophic AHP matrices is considered equal for every matrix entry according to Equation (13). Here, the expert’s credibility t*ij associated to the repaired missing elements. a*ij is proposed to be penalized by the number of missing judgments in the original AHP matrix M* = {mij}. The greater the number of missing elements, the less information is available to predict {l*ij, m*ij, u*ij}, and consequently the less reliable these estimates will be. The following formula is proposed for determining the missing truth membership function parameters t*ij:
where n* is the number of total missing judgments and n is the number of criteria involved in the decision-making process. From Equation (29) it follows that the expert’s credibility when assessing aij is zero if no elements are known (i.e., n* = n·(n − 1)/2), and equals to their average credibility if no element is unknown (i.e., n* = 0).
The indeterminacy i*ij of a missing entry is expected to be related to the certainty that the decision maker expresses when making comparisons that involve criteria i and j:
The indeterminacy iij for the remaining entries shall be obtained following Equation (14). At last, the falsity membership function parameter fij depends on the inconsistencies revealed by the expert’s judgments when filling the comparison matrix. The consistency of the responses shall only be evaluated from a complete matrix. Thus, it is proposed to determine the average expert’s incoherency fij from the synthetically completed matrix M’ including the central values mij. The inconsistency f*ij associated to the estimated missing values shall then be calculated as:
where n* is the number of total missing judgments and n is the number of criteria involved in the decision-making process. Although relying on a similar penalization idea as the definition of t*ij, Equation (31) has been slightly modified so that when no elements are known (i.e., n* = n·(n − 1)/2), the falsity parameter f*ij becomes 1, while if every entry is known, f*ij = fij ∀i,j ∈ {1,...,n}.
3. Problem Definition
The neutrosophic matrix completion method presented here is applied to a sustainability-based decision-making design problem. The problem consists of deriving the weights of the criteria considered relevant to find the most sustainable-design solution for a prestressed concrete bridge deck located in a coastal region. In such chloride-laden environments, the maintenance demand of concrete structures along their service lives can result in environmental, social, and economic impacts comparable in magnitude to those derived from the construction of the infrastructure itself. To address the sustainability life-cycle performance of alternative bridge-deck designs in aggressive environments, a set of nine decision criteria is proposed (Table 3). Two of them are related to the economic dimension of sustainability, and imply considering, on the one hand, the costs derived from the construction of the infrastructure, and on the other hand, the costs that result from maintenance and decommissioning of the structure.

Table 3.
Sustainability criteria relevant for bridge design in coastal regions [13].
The life-cycle impacts of an infrastructure shall be assessed in terms of the three environmental criteria on which the so-called life cycle assessment endpoint methodologies, such as ReCiPe [47], are based at the present. The first of these criteria accounts for the damage that the emissions derived from the different production and construction processes have on the human health. Such impact is usually measured in DALY (disability adjusted life years), representing the lifetime that a person is disabled due to disease derived from pollutants. The second environmental criterion considers the damage to the ecosystem. Such impact is usually measured as the local species loss over time at a particular location because of emissions and land occupation resulting from human activities. The third environmental aspect to be considered is the negative contribution of production and construction processes to natural resources scarcity. This can be measured in terms of the additional costs required for future mineral and fossil resource extraction.
The social dimension of sustainability can be addressed by means of four different criteria, which are defined after a hotspot analysis following the UNEP/SETAC guidelines [48] for social life cycle assessments. The first social criterion to be accounted for is the generation of employment and the conditions of such employment. This is measured in terms of effective working hours required by every construction and maintenance activity developed throughout the complete life cycle of the structure. When generating one hour of work, it is necessary to take into consideration the conditions of the employment generated, bearing in mind the safety of the work generated, if there we are contributing or not to gender discrimination, if such employment is fairly paid, or if the employment is generated in a region with high or low unemployment rates. The second social criterion considers the contribution to the economic development of regions, benefitting alternatives that imply an economic input to poorer areas. When choosing a design alternative in terms of sustainability, its associated maintenance needs shall be accounted for, as a bridge-deck solution that requires constant maintenance will affect both the accessibility of the locations connected by the infrastructure, as well as the driving safety of the users. At last, maintenance activities conducted on the infrastructure also imply negative impacts on the aesthetics of the site where the structure is located, as well as a series of externalities affecting the comfort of the local community, such as the generation of dust, noise, and vibrations.
The assessment of the relevance that each of the nine abovementioned criteria shall take when making a decision on the most sustainable-design alternative for a particular bridge design problem shall be done by means of the AHP method. Such methodology requires an expert to fill a 9 × 9 comparison matrix, which implies emitting 9·(9 − 1)/2 = 36 pairwise comparisons, some of them particularly difficult to conduct consistently attending to the different and complex nature of the criteria described above. The matrix completion methodology proposed here aims to provide a tool to reduce the number of judgments required by the decision maker without jeopardizing the overall consistency of their responses. Additionally, the incomplete comparison matrix is translated into a neutrosophic environment to take into account the nonprobabilistic uncertainties of the nonmissing matrix entries.
However, the goodness of the results obtained after applying the matrix completion method proposed here depends on the number of missing entries from the original AHP matrix. Here, an initially complete and consistent AHP matrix serves as the basis to determine how the number of missing judgments affects the obtained criteria weights. The complete baseline AHP matrix M is provided in Table 4, together with the certainty expressed by the expert for each comparison (Table 5).

Table 4.
Baseline complete AHP comparison matrix M.

Table 5.
Baseline complete certainty matrix C.
4. Results
Here, results are investigated on how the proposed neutrosophic completion method for incomplete comparison matrices performs depending on the number of missing entries.
4.1. Scalar Weights Derived from the Baseline Complete Comparison Matrix
To serve as the basis for comparison, the results obtained following the neutrosophic AHP technique presented in Section 2.2 are briefly presented. Table 6 summarizes the profile of the expert, together with the resulting neutrosophic characterization parameters derived according to Equations (13) to (15).

Table 6.
Neutrosophic profile of the baseline decision maker.
Figure 1 presents the triangular neutrosophic truth: indeterminacy and falsehood membership functions associated to the criteria weights. Additionally, Figure 1 shows the scalar weights that result after applying the deneutrosophication technique presented in Equations (21) and (22).
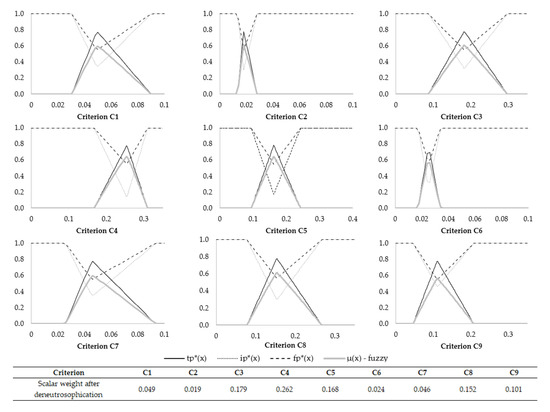
Figure 1.
Neutrosophic membership functions associated to the criteria weights derived from the baseline complete AHP comparison matrix.
4.2. Completion Results
The performance of the proposed neutrosophic completion technique is addressed considering four different scenarios for the completeness degree of the baseline matrix. In each scenario, a different number of entries is randomly selected and assumed missing. The number of missing entries is 3 for scenario 1, 5 for the second scenario, 8 for the third and 12 for the last one. This implies, respectively, a reduction of 8, 14, 22, and 33% of the number of comparisons required to be completed by the expert when following the AHP method conventionally. One thousand simulations are conducted for each scenario to generate unique incomplete matrices. For each simulation, the methodology presented in Section 2.3 is followed to generate complete neutrosophic matrices from which scalar criteria weights are derived.
Table 7 shows the obtained results for each of the nine criteria addressed. It can be observed that the maximum deviation of the mean estimated weights versus the baseline weights is 10.5% and is obtained for criterion C7 (development of local economies). This deviation corresponds to the scenario where 12 entries of the baseline matrix are considered missing.

Table 7.
Mean scalar criteria weights obtained for each scenario.
Figure 2 shows the scalar weights of each criterion (C1 to C9) resulting from the baseline complete matrix, together with the 5th and 95th percentile of the estimations resulting from scenarios 1 and 4. For the sake of simplicity, results of scenarios 2 and 3 have not been plotted, as they are enveloped by results of scenario 4. It can be observed that, despite the good fitting of the mean, the dispersion of the results increases significantly with the number of missing entries.
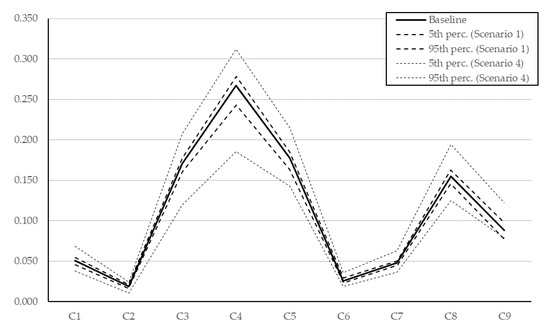
Figure 2.
Dispersion of the results for scenarios 1 (3 random entries of the baseline matrix missing) and 4 (12 random entries of the baseline matrix missing).
To measure the observed dispersion, the relative standard deviation is calculated for each scenario and criterion. The relative standard deviation is defined as the ratio between the standard deviation and the mean of a set of estimations. Table 8 shows the relative standard deviation (RSD) for each criterion and scenario. It can be observed that the dispersion increases as the number of nonmissing entries decreases.

Table 8.
Relative standard deviation of the criteria weights obtained for each scenario.
In view of the results, to evaluate the overall goodness of the proposed completion model, the root mean square error (RMSE) is applied. RMSE is used here to evaluate the differences between the predicted estimates and the baseline weights. The root mean square error of the weight estimate of a particular criterion i is defined as:
where N = 1000 is the sample size, wi is the scalar baseline weight of criterion i, and w*i,n is each of the 1000 weight estimates for criterion i for the incompleteness scenario under evaluation. Here, RMSE obtained for each criterion is normalized by the value of the corresponding baseline criterion. Figure 3 shows the normalized RMSE (N-RMSE) derived for each criterion and for each of the four analyzed scenarios. It can be observed that the mean N-RMSE, falling close to 11% when 22% of the required initial judgments are missing, increases with the number of missing entries. Such an increase is in accordance with the increasing dispersion of the estimates detected for scenarios 3 and 4.
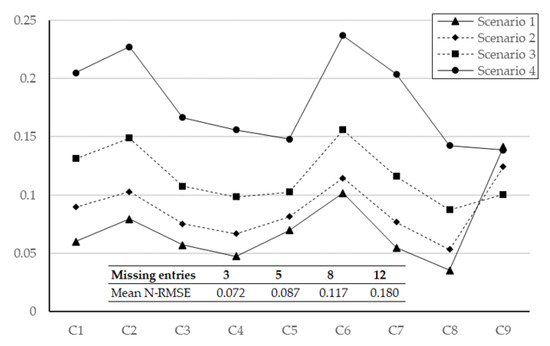
Figure 3.
Normalized RMSE resulting for the weight estimation of each criterion for different incompleteness degrees: scenario 1 (3 random entries of the baseline matrix missing), scenario 2 (5 random entries missing), scenario 3 (8 random entries missing), and scenario 4 (12 random entries missing).
4.3. Comparison of the Results Considering a Different Expert
Here, the proposed matrix completion method is applied to a different set of inputs corresponding to a new decision maker (expert 2 henceforth) in order to confirm the goodness of the results presented above for the baseline expert. For the sake of simplicity, the inputs for this second analysis are provided in Appendix A. Table A1 and Table A2 show, respectively, the expert’s complete comparison matrix and their confidence degree expressed for each of the opinions. Table A3 summarizes the neutrosophic characterization parameters corresponding to the second expert. The scalar criteria weights obtained for this second expert are given in Table A4, where weights of the baseline decision maker are also given for comparative purposes.
Again, 1000 randomly generated incomplete comparison matrices are constructed out of the second baseline matrix, assuming the same four incompleteness scenarios than those defined above. Table 9 shows the mean scalar criteria weights estimated when 3, 5, 8, and 12 of the entries of the complete comparison matrix are missing. The mean estimations are, on average, quite similar to those obtained for the first expert. It can be observed that the maximum deviation for the second expert is 10.1%, close to the 10.5% obtained for the first decision maker, although associated to different a criterion.

Table 9.
Second expert’s mean scalar criteria weights obtained for each scenario.
Table 10 presents the relative standard deviation of the obtained weights resulting from the second expert’s synthetical matrices. Similar dispersion results are observed when comparing with the first expert analyzed; although, in general terms, results from this second analysis are slightly more dispersed. However, the maximum absolute difference obtained in terms of the relative standard deviation is 4.5% and corresponds to the dispersion of the weight estimation of criterion C1 when 12 input entries are missing.

Table 10.
Second expert’s relative standard deviation of the criteria weights obtained for each scenario.
The normalized RMSE is obtained for this second analysis. The mean N-RMSE values for each of the four incompleteness scenarios are presented in Table 11. For comparative purposes, the N-RMSE are included in Table 11 as well. Again, when 22% of the judgments are missing (8 entries), the obtained N-RMSE still falls beneath 15%, irrespective of the configuration of the randomly generated incomplete matrix.

Table 11.
Second expert’s normalized RMSE resulting in the weight estimation of each criterion for different incompleteness degrees.
5. Conclusions
A neutrosophic completion technique is proposed in this paper for the derivation of AHP weights out of incomplete, higher-order comparison matrices. Such technique is useful when dealing with decision-making design problems, where a significant number of criteria are involved. The completion technique in this work has been applied to address a construction-related sustainability-based design problem, namely the evaluation of the sustainability life-cycle performance of different concrete bridge-deck alternatives located in a coastal region.
Results show that the maximum observed difference between the criteria weights obtained from a complete 9 × 9 AHP matrix and the estimated weights obtained from synthetically completed neutrosophic matrices is 10% on average for the worst case analyzed, namely when 33% of the required pairwise comparisons are missing. On the other hand, the dispersion measured in terms of the relative standard deviation is between 10 and 15%, when 22% of the entries are missing. From the analysis of the estimates derived from the 1000 randomly generated repaired comparison matrices, it is shown that for 14% of the entries missing, a N-RMSE of 11% is obtained, while when 22% of the entries are missing, the N-RMSE is still below 15%. Such results have been validated with the inputs of a second decision maker, where similar values have been obtained. Results require, however, further validation by analyzing a greater set of alternative decision makers. It shall also be noted that the restored comparison matrices might still result in poor consistency. A future line of research relates to the investigation and establishment of adequate neutrosophic consistency thresholds to allow for the acceptance/rejection of artificially completed comparison matrices.
In conclusion, the present paper proposes a powerful tool for reducing the number of judgments required to face MCDM problems based on AHP criteria weights derivation. Given that the proposed method has been validated with 1000 randomly generated synthetical matrices, the conclusions are valid irrespective of the entries missing. This is particularly advantageous when a great number of criteria are involved in the decision-making problem, as the decision maker is allowed to neglect those comparisons where he feels less confident about. In addition, working in a neutrosophic environment allows the designer to capture the nonprobabilistic uncertainties associated to the vagueness of human thinking, thus accounting for the valuable information derived from the consideration of the judgments’ reliability associated to the decision maker’s credibility, inconsistencies, and indeterminacies.
Author Contributions
This paper represents a result of teamwork. The authors jointly designed the research. I.J.N. drafted the manuscript. V.Y. and J.V.M. edited and improved the manuscript until all authors were satisfied with the final version. All authors have read and agreed to the published version of the manuscript.
Funding
The authors acknowledge the financial support of the Spanish Ministry of Economy and Business, along with FEDER funding (DIMALIFE Project: BIA2017-85098-R).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
Input data regarding the second decision maker are provided here. Table A1 shows the complete AHP comparison matrix of the second expert that serves as the basis for the exposed validation analysis.

Table A1.
Baseline complete AHP comparison matrix M for expert 2.
Table A1.
Baseline complete AHP comparison matrix M for expert 2.
| C1 | C2 | C3 | C4 | C5 | C6 | C7 | C8 | C9 | |
|---|---|---|---|---|---|---|---|---|---|
| C1 | 1 | 1/3 | 1/6 | 1/6 | 1/6 | 1/3 | 1/4 | 1/4 | 1/4 |
| C2 | 3 | 1 | 1/2 | 1/5 | 1/4 | 1/2 | 3 | 1/2 | 1/2 |
| C3 | 6 | 2 | 1 | 1 | 1/2 | 3 | 7 | 6 | 6 |
| C4 | 6 | 5 | 1 | 1 | 1/2 | 3 | 7 | 6 | 6 |
| C5 | 6 | 4 | 2 | 2 | 1 | 2 | 6 | 5 | 5 |
| C6 | 3 | 2 | 1/3 | 1/3 | 1/2 | 1 | 2 | 1/2 | 1/2 |
| C7 | 4 | 1/3 | 1/7 | 1/7 | 1/6 | 1/2 | 1 | 1/2 | 1/2 |
| C8 | 4 | 2 | 1/6 | 1/6 | 1/5 | 2 | 2 | 1 | 1 |
| C9 | 4 | 2 | 1/6 | 1/6 | 1/5 | 2 | 2 | 1 | 1 |
Table A2 shows the complete certainty matrix of the second expert that serves as the basis for the exposed validation analysis.

Table A2.
Baseline complete certainty matrix C for expert 2.
Table A2.
Baseline complete certainty matrix C for expert 2.
| C1 | C2 | C3 | C4 | C5 | C6 | C7 | C8 | C9 | |
|---|---|---|---|---|---|---|---|---|---|
| C1 | 1 | 0.8 | 0.5 | 0.7 | 0.9 | 0.8 | 0.8 | 0.6 | 0.2 |
| C2 | 0.8 | 1 | 0.7 | 0.8 | 0.6 | 0.6 | 0.4 | 0.7 | 0.7 |
| C3 | 1/2 | 2/3 | 1 | 0.8 | 0.8 | 0.7 | 0.8 | 0.7 | 0.6 |
| C4 | 0.7 | 0.8 | 0.8 | 1 | 0.8 | 0.3 | 0.4 | 0.5 | 0.6 |
| C5 | 0.9 | 0.6 | 0.8 | 0.8 | 1 | 0.2 | 0.7 | 0.6 | 0.4 |
| C6 | 0.8 | 0.6 | 0.7 | 0.3 | 0.2 | 1 | 0.8 | 0.8 | 0.4 |
| C7 | 0.8 | 0.4 | 0.8 | 0.4 | 0.7 | 0.8 | 1 | 0.5 | 0.5 |
| C8 | 0.6 | 0.7 | 0.7 | 0.5 | 0.6 | 0.8 | 0.5 | 1 | 0.4 |
| C9 | 0.2 | 0.7 | 0.6 | 0.6 | 0.4 | 0.4 | 0.5 | 0.4 | 1 |
Table A3 shows the neutrosophic characterization parameters of the second decision maker.

Table A3.
Neutrosophic profile of expert 2.
Table A3.
Neutrosophic profile of expert 2.
| Expert’s Profile Defining Parameters | Value |
|---|---|
| Knowledge degree in design of infrastructures | 0.60 |
| Expertise in economic assessments | 0.60 |
| Expertise in environmental assessments | 1.00 |
| Expertise in social life-cycle assessments | 0.80 |
| Expert’s credibility. Truth membership parameter t | 0.80 |
| Expressed mean self confidence | 0.66 |
| Expert’s certainty. Indeterminacy membership parameter i | 0.34 |
| Consistency ratio of the comparison matrix | 0.07 |
| Expert’s inconsistency. Falsehood membership parameter f | 0.72 |
Table A4 shows the resulting scalar weights derived from the second analysis after applying the deneutrosophication technique described in this paper.

Table A4.
Scalar criteria weights obtained for expert 2.
Table A4.
Scalar criteria weights obtained for expert 2.
| Scenario | C1 | C2 | C3 | C4 | C5 | C6 | C7 | C8 | C9 |
|---|---|---|---|---|---|---|---|---|---|
| Expert 1 | 0.049 | 0.019 | 0.179 | 0.262 | 0.168 | 0.024 | 0.046 | 0.152 | 0.101 |
| Expert 2 | 0.027 | 0.060 | 0.204 | 0.214 | 0.237 | 0.076 | 0.048 | 0.074 | 0.061 |
References
- Worrell, E.; Price, L.; Martin, N.; Hendriks, C.; Ozawa, L. Carbon dioxide emissions from the global cement industry. Annu. Rev. Energ. Environ. 2001, 26, 303–329. [Google Scholar] [CrossRef]
- García, J.; Yepes, V.; Martí, J.V. A hybrid k-means cuckoo search algorithm applied to the counterfort retaining walls problem. Mathematics 2020, 8, 555. [Google Scholar] [CrossRef]
- Penadés-Plà, V.; García-Segura, T.; Yepes, V. Robust design optimization for low-cost concrete box-girder bridge. Mathematics 2020, 8, 398. [Google Scholar] [CrossRef]
- Kim, S.; Frangopol, D.M. Multi-objective probabilistic optimum monitoring planning considering fatigue damage detection, maintenance, reliability, service life and cost. Struct. Multidisc. Optim. 2018, 57, 39–54. [Google Scholar] [CrossRef]
- García-Segura, T.; Yepes, V.; Frangopol, D.M. Multi-objective design of post-tensioned concrete road bridges using artificial neural networks. Struct. Multidiscip. Optim. 2017, 56, 139–150. [Google Scholar] [CrossRef]
- Van den Heede, P.; De Belie, N. A service life based global warming potential for high-volume fly ash concrete exposed to carbonation. Constr. Build. Mater. 2014, 55, 183–193. [Google Scholar] [CrossRef]
- García, J.; Martí, J.V.; Yepes, V. The Buttressed walls problem: An application of a hybrid clustering particle swarm optimization algorithm. Mathematics 2020, 8, 862. [Google Scholar] [CrossRef]
- García-Segura, T.; Penadés-Plà, V.; Yepes, V. Sustainable bridge design by metamodel-assisted multi-objective optimization and decision-making under uncertainty. J. Clean. Prod. 2018, 202, 904–915. [Google Scholar] [CrossRef]
- Gursel, A.P.; Ostertag, C. Comparative life-cycle impact assessment of concrete manufacturing in Singapore. Int. J. Life Cycle Assess. 2017, 22, 237–255. [Google Scholar] [CrossRef]
- Penadés-Plà, V.; Martí, J.V.; García-Segura, T.; Yepes, V. Life-cycle assessment: A comparison between two optimal post-tensioned concrete box-girder road bridges. Sustainability 2017, 9, 1864. [Google Scholar] [CrossRef]
- Navarro, I.J.; Yepes, V.; Martí, J.V. Social life cycle assessment of concrete bridge decks exposed to aggressive environments. Environ. Impact Assess. 2018, 72, 50–63. [Google Scholar] [CrossRef]
- Sierra, L.A.; Pellicer, E.; Yepes, V. Method for estimating the social sustainability of infrastructure projects. Environ. Impact Assess. 2017, 65, 41–53. [Google Scholar] [CrossRef]
- Navarro, I.J.; Yepes, V.; Martí, J.V. Sustainability assessment of concrete bridge deck designs in coastal environments using neutrosophic criteria weights. Struct. Infrastruct. Eng. 2020, 16, 949–967. [Google Scholar] [CrossRef]
- Saaty, T.L. The Analytic Hierarchy Process; McGraw-Hill: New York, NY, USA, 1980. [Google Scholar]
- Tavana, M.; Shaabani, A.; Javier Santos-Arteaga, F.; Raeesi Vanani, I. A review of uncertain decision-making methods in energy management using text mining and data analytics. Energies 2020, 13, 3947. [Google Scholar] [CrossRef]
- Yannis, G.; Kopsacheili, A.; Dragomanovits, A.; Petraki, V. State-of-the-art review on multi-criteria decision-making in the transport sector. J. Traffic Transp. Eng. 2020, 7, 413–431. [Google Scholar] [CrossRef]
- Navarro, I.J.; Penadés-Plà, V.; Martínez-Muñoz, D.; Rempling, R.; Yepes, V. Life cycle sustainability assessment for multi-criteria decision making in bridge design: A review. J. Civ. Eng. Manag. 2020, 26, 690–704. [Google Scholar] [CrossRef]
- Radwan, N.; Senousy, M.; Riad, A. Neutrosophic AHP multi-criteria decision making method applied on the selection of learning management system. Int. J. Adv. Comp. Technol. 2016, 8, 95–105. [Google Scholar]
- Hedelin, B. Complexity is no excuse. Sustain. Sci. 2019, 14, 733–749. [Google Scholar] [CrossRef]
- Zadeh, L. Outline of a new approach to the analysis of complex systems and decision processes. IEEE Trans. Sys. Man. Cyb. 1973, 3, 28–44. [Google Scholar] [CrossRef]
- Zadeh, L. Fuzzy sets. Inform. Control 1965, 8, 338–353. [Google Scholar] [CrossRef]
- Milošević, D.M.; Milošević, M.R.; Simjanović, D.J. Implementation of adjusted fuzzy AHP method in the assessment for reuse of industrial buildings. Mathematics 2020, 8, 1697. [Google Scholar] [CrossRef]
- Lin, C.-N. A fuzzy analytic hierarchy process-based analysis of the dynamic sustainable management index in leisure agriculture. Sustainability 2020, 12, 5395. [Google Scholar] [CrossRef]
- Salehi, S.; Ghazizadeh, M.J.; Tabesh, M.; Valadi, S.; Nia, S.P. A risk component-based model to determine pipes renewal strategies in water distribution networks. Struct. Infrastruct. Eng. 2019. [Google Scholar] [CrossRef]
- Smarandache, F. A Unifying Field in Logics, Neutrosophy: Neutrosophic Probability, Set and Logic; American Research Press: Rehoboth, DE, USA, 1999. [Google Scholar]
- Liu, P.; Liu, X. The neutrosophic number generalized weighted power averaging operator and its application in multiple attribute group decision making. Int. J. Mach. Learn. Cyb. 2018, 9, 347–358. [Google Scholar] [CrossRef]
- Peng, J.J.; Wang, J.; Yang, W. A multi-valued neutrosophic qualitative flexible approach based on likelihood for multi-criteria decision-making problems. Int. J. Syst. Sci. 2017, 48, 425–435. [Google Scholar] [CrossRef]
- Saaty, T.; Ozdemir, M. Why the magic number seven plus or minus two. Math. Comput. Model. 2003, 38, 233–244. [Google Scholar] [CrossRef]
- Harker, P.T. Incomplete pairwise comparisons in the analytic hierarchy process. Math. Mod. 1987, 9, 837–848. [Google Scholar] [CrossRef]
- Chen, K.; Kou, G.; Tarn, J.M.; Song, Y. Bridging the gap between missing and inconsistent values in eliciting preference from pairwise comparison matrices. Ann. Oper. Res. 2015, 235, 155–175. [Google Scholar] [CrossRef]
- Bozóki, S.; Fülöp, J.; Rónyai, L. On optimal completion of incomplete pairwise comparison matrices. Math. Comput. Model. 2010, 52, 318–333. [Google Scholar] [CrossRef]
- Dong, M.; Li, S.; Zhang, H. Approaches to group decision making with incomplete information based on power geometric operators and triangular fuzzy AHP. Expert Syst. Appl. 2015, 42, 7846–7857. [Google Scholar] [CrossRef]
- Zhou, X.; Hu, Y.; Deng, Y.; Deng, Y.; Chan, F.T.; Ishizaka, A. A DEMATEL-based completion method for incomplete pairwise comparison matrix in AHP. Ann. Oper. Res. 2018, 271, 1045–1066. [Google Scholar] [CrossRef]
- Sumathi, I.R.; Antony Crispin Sweety, C. New approach on differential equation via trapezoidal neutrosophic number. Complex Intell. Syst. 2019, 5, 417–424. [Google Scholar] [CrossRef]
- Deli, I.; Subas, Y. A ranking method of single valued neutrosophic numbers and its applications to multi-attribute decision making problems. Int. J. Mach. Learn. Cyb. 2017, 8, 1309–1322. [Google Scholar] [CrossRef]
- Ye, J. Subtraction and Division Operations of simplified neutrosophic sets. Information 2017, 8, 51. [Google Scholar] [CrossRef]
- Liang, R.; Wang, J.; Zhang, H. A multi-criteria decision-making method based on single-valued trapezoidal neutrosophic preference relations with complete weight information. Neural Comput. App. 2018, 30, 3383–3398. [Google Scholar] [CrossRef]
- Sodenkamp, M.A.; Tavana, M.; Di Caprio, D. An aggregation method for solving group multi-criteria decision-making problems with single-valued neutrosophic sets. Appl. Soft Comput. 2018, 71, 715–727. [Google Scholar] [CrossRef]
- Sierra, L.A.; Pellicer, E.; Yepes, V. Social sustainability in the life cycle of Chilean public infrastructure. J. Constr. Eng. Manag. 2016, 142, 05015020. [Google Scholar] [CrossRef]
- Abdel-Basset, M.; Manogaran, G.; Mohamed, M.; Chilamkurti, N. Three-way decisions based on neutrosophic sets and AHP-QFD framework for supplier selection problem. Future Gener. Comput. Syst. 2018, 89, 19–30. [Google Scholar] [CrossRef]
- Dubois, D. The role of fuzzy sets in decision sciences: Old techniques and new directions. Fuzzy Set. Syst. 2011, 184, 3–28. [Google Scholar] [CrossRef]
- Buckley, J.J. Fuzzy hierarchical analysis. Fuzzy Set. Syst. 1985, 17, 233–247. [Google Scholar] [CrossRef]
- Wang, Y.M.; Elhag, T.M. On the normalization of interval and fuzzy weights. Fuzzy Set. Syst. 2006, 157, 2456–2471. [Google Scholar] [CrossRef]
- Enea, M.; Piazza, T. Project selection by constrained fuzzy AHP. Fuzzy Optim. Decis. Mak. 2004, 3, 39–62. [Google Scholar] [CrossRef]
- Chu, T.; Tao, C. Ranking fuzzy numbers with an area between the centroid point and original point. Comput. Math. Appl. 2002, 43, 111–117. [Google Scholar] [CrossRef]
- Gabus, A.; Fontela, E. World Problems, an Invitation to Further Tought within the Framework of Dematel; Battelle Geneva Research Centre: Geneva, Switzerland, 1972. [Google Scholar]
- Goedkoop, M.; Heijungs, R.; Huijbregts, M.; De Schryver, A.; Struijs, J.; Van Zelm, R. ReCiPe 2008: A Life Cycle Impact Assessment Method Which Comprises Harmonised Category Indicators at the Midpoint and the Endpoint Level; Ministerie van Volkshuisvesting: The Hague, The Netherlands, 2009. [Google Scholar]
- UNEP/SETAC. Guidelines for Social Life Cycle Assessment of Products; UNEP/SETAC Life-Cycle Initiative: Paris, France, 2009. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).