On a Semilinear Parabolic Problem with Four-Point Boundary Conditions

Abstract

This paper studies a semilinear parabolic equation in 1D along with nonlocal boundary conditions. The value at each boundary point is associated with the value at an interior point of the domain, which is known as a four-point boundary condition. First, the solvability of a steady-state problem is addressed and a constructive algorithm for finding a solution is proposed. Combining this schema with the semi-discretization in time, a constructive algorithm for approximation of a solution to a transient problem is developed. The well-posedness of the problem is shown using the semigroup theory in C-spaces. Numerical experiments support the theoretical algorithms.

1. Introduction

Modeling of physical systems in transport theory is usually based on mass balance. Mathematical description frequently leads to an appropriate partial differential equation (PDE). If this process takes place in a bounded domain, then the governing PDE must be accompanied by suitable boundary conditions (BCs) describing the behavior of the unknown quantity outside the area of consideration. The BCs are of fundamental importance since they determine the explicit form of a solution (David Hilbert outlined 23 famous mathematical problems in 1900. One of them is “The general problem of boundary values” in relation to PDEs in bounded domains. BCs connect solutions with the exterior domain with some expectations/restrictions.). The classical heat conduction theory is based on the Fourier law and it leads to the parabolic heat conduction equation

$$\rho c_p{\partial }_{t}u-\nabla ·\left(k\nabla u\right)=F,$$

where $c_p$ is the specific heat capacity, $\rho$ stands for the mass density of the material, k is the thermal conductivity and u denotes the temperature. The initial state is described by the initial datum $u(x,t)=u_0\left(x\right)$. The heat equation is usually accompanied by one of the following three classical BCs

Dirichlet 

when temperature is prescribed on the surrounding surface;

Neumann 

when the normal component of the flux is given on the boundary;

Robin/Newton 

when a linear combination of the temperature and the normal component of the flux is known at the boundary.

Besides these standard types of BCs also the following two evolution BCs are known, cf. [1]

Carslaw 

$\rho c_{p}b{\partial }_{t}u+k\nabla u·\mathbf{\nu }=g$;

Jaeger 

$\rho c_{p}b{\partial }_{t}u+k\nabla u·\mathbf{\nu }+hu=g$.

All these BCs mentioned above are local, i.e., the relation between the temperature and the flux is taken at the same time and place. Researchers have already studied (under appropriate assumptions on the data functions) the well-posedness of problems involving those local boundary conditions.

On the other hand, there exist models with so-called nonlocal BCs. A. A. Samarskii and A.V. Bitsadze [2] are originators of problems with such BCs. Investigation of problems with various types of nonlocal boundary conditions is a hot topic presently, i.a. because multi-point boundary-value problems (BVPs) for ODEs have many applications in modeling and analyzing problems arising from electric power networks, electric railway systems, telecommunication lines and also in chemistry and analyzing kinetic reaction problems. They have been intensively studied e.g., in [3,4,5,6,7,8,9]. However, there are only a few papers devoted to time-dependent problems along with multi-point BCs, e.g., [10,11,12]. The article [11] deals with 3-point BCs subject to nonlinear parabolic Cauchy problem in $(0,\infty )\times (0,1)$

$$\begin{array}{cc}\hfill {\displaystyle {\partial }_{t}u(t,x)-{\partial }_x\left(g\left({\partial }_{x}u(t,x)\right)\right)}& {\displaystyle =f(t,x)}\hfill \\ \hfill u(t,0)& {\displaystyle =0}\hfill \\ \hfill u(t,\eta )& {\displaystyle =\beta u(t,1)}\hfill \\ \hfill u(0,x)& {\displaystyle =u_0\left(x\right),}\hfill \end{array}$$

where $\eta \in (0,1)$ and $\beta >1$ are given. The convergence of the solution towards the equilibrium solution was addressed in [12].

Alikhanov [13] studied a linear parabolic problem along with a 3-point BC. He showed the uniqueness and the continuous dependence of a solution on the initial data. A numerical finite-difference scheme was suggested and its convergence—assuming the existence of a very smooth exact solution $u\in C^{4,3}\left(\overline{\mathsf{\Omega }\times [0,T]}\right)$—was shown. The existence of a solution was not addressed. Using the method of energy inequalities, a priori estimates for the corresponding differential and finite-difference problems were obtained in a weighted $L_2$ norms. This proof technique has been generalized to multi-point BCs for linear parabolic problems in [14]. However, also here the assumption of existence of a very regular solution is needed to prove convergence of suggested approximation schemes. The existence of a solution was again not addressed. A compact difference scheme for the multi-point boundary-value problem of the heat equation has also been presented in [15].

The problem in this paper describes a transient semilinear heat equation in $(a,b)$ with two controllers located at the interior points $c,d$, where

$$a<c<d<b.$$

The physical application is controlled cooling of a rod. The role of both controllers is to adjust the boundary data to the measured temperature, i.e.,

$$u\left(a\right)=u\left(c\right),u\left(b\right)=u\left(d\right).$$

(1)

We assume perfect contact conditions at controller points c and d, i.e.,

$${\left[\left[u\left(x\right)\right]\right]}_{x=c}=0={\left[\left[u\left(x\right)\right]\right]}_{x=d},{\left[\left[u^{\prime }\left(x\right)\right]\right]}_{x=c}=0={\left[\left[u^{\prime }\left(x\right)\right]\right]}_{x=d}.$$

(2)

Here the ${\left[\left[w\left(x\right)\right]\right]}_{x=y}$ denotes the usual jump operator of the quantity $w\left(x\right)$ at the position $x=y$.

The main difficulty by stability analysis is the fact that one cannot prove that the governing (steady-state) differential operator is elliptic – due to the nonlocal BCs. Unfortunately, most solution methods rely on the ellipticity of the operator. That is why we first developed a new solution method for the steady-state differential problem. This is based on the principle of linear superposition. Secondly, we showed that the operator remains sectorial in an appropriate function space.

After that, we designed a numerical scheme for approximation of the solution to a semilinear parabolic equation accompanied with the four-point BCs (1), which is based on semi-discretization in time method. The convergence of approximations towards the exact solution is shown under much weaker regularity assumptions than it was done in [13,14]. Therefore, we conclude that the semilinear parabolic equation accompanied with the four-point BCs (1) is well-posed. Finally, we carried out some numerical experiments to support our results.

2. Linear Steady-State Case

In the study of the existence of solutions to ODEs major advancements have been made thanks to the so-called “Bernstein-Nagumo” conditions [16,17]. In this section, we derive a simple construction method for the solution of linear second order ODE-problems with nonlocal BCs. We will study the resolvent operator associated with this problem. This will be later applied to parabolic settings.

Let us consider the following nonlocal problem in $(a,b)$ for $r\in \mathbb{C}$

$$\begin{array}{cc}\hfill {\displaystyle ru\left(x\right)-u^{″}\left(x\right)}& {\displaystyle =f;}\hfill \\ \hfill u\left(a\right)=u\left(c\right)& {\displaystyle =\alpha ;}\hfill \\ \hfill u\left(d\right)=u\left(b\right)& {\displaystyle =\beta ,}\hfill \end{array}$$

(3)

with $\alpha$ and $\beta$ unknown. We look for a classic solution of (3). Under a classic solution we understand $C^2\left([a,b]\right)$ function, for which the interface condition (2) is naturally valid. The concept of a weak solution in not appropriate in this situation, because a weak solution may have jumps of the first derivative at the interface points $x=c,d$. We show a very simple constructive way for solving this problem, which is based on the principle of linear superposition.

Let us consider the following seven auxiliary problems

$$\begin{array}{ccc}\hfill {\displaystyle r{z}_1\left(x\right)-z_1^{″}\left(x\right)}& {\displaystyle =f}\hfill & {\displaystyle in(a,c);}\hfill \\ \hfill z_1\left(a\right)=z_1\left(c\right)& {\displaystyle =0,}\hfill \end{array}$$

(4)

$$\begin{array}{ccc}\hfill {\displaystyle r{w}_1\left(x\right)-w_1^{″}\left(x\right)}& {\displaystyle =0}\hfill & {\displaystyle in(a,c);}\hfill \\ \hfill w_1\left(a\right)=w_1\left(c\right)& {\displaystyle =1,}\hfill \end{array}$$

(5)

$$\begin{array}{ccc}\hfill {\displaystyle r{z}_2\left(x\right)-z_2^{″}\left(x\right)}& {\displaystyle =f}\hfill & {\displaystyle in(c,d);}\hfill \\ \hfill z_2\left(c\right)=z_2\left(d\right)& {\displaystyle =0,}\hfill \end{array}$$

(6)

$$\begin{array}{ccc}\hfill {\displaystyle r{w}_2\left(x\right)-w_2^{″}\left(x\right)}& {\displaystyle =0}\hfill & {\displaystyle in(c,d);}\hfill \\ \hfill w_2\left(c\right)& {\displaystyle =0;}\hfill \\ \hfill w_2\left(d\right)& {\displaystyle =1,}\hfill \end{array}$$

(7)

$$\begin{array}{ccc}\hfill {\displaystyle r{v}_2\left(x\right)-v_2^{″}\left(x\right)}& {\displaystyle =0}\hfill & {\displaystyle in(c,d);}\hfill \\ \hfill v_2\left(c\right)& {\displaystyle =1;}\hfill \\ \hfill v_2\left(d\right)& {\displaystyle =0,}\hfill \end{array}$$

(8)

$$\begin{array}{ccc}\hfill {\displaystyle r{z}_3\left(x\right)-z_3^{″}\left(x\right)}& {\displaystyle =f}\hfill & {\displaystyle in(d,b);}\hfill \\ \hfill z_3\left(d\right)=z_3\left(b\right)& {\displaystyle =0,}\hfill \end{array}$$

(9)

$$\begin{array}{ccc}\hfill {\displaystyle r{w}_3\left(x\right)-w_3^{″}\left(x\right)}& {\displaystyle =0}\hfill & {\displaystyle in(d,b);}\hfill \\ \hfill w_3\left(d\right)=w_3\left(b\right)& {\displaystyle =1.}\hfill \end{array}$$

(10)

Further we set ${u|}_{(a,c)}=u_1$, ${u|}_{(c,d)}=u_2$, ${u|}_{(d,b)}=u_3$, where

$$\begin{array}{cc}\hfill u_1& {\displaystyle =z_1+\alpha w_1;}\hfill \\ \hfill u_2& {\displaystyle =z_2+\alpha v_2+\beta w_2;}\hfill \\ \hfill u_3& {\displaystyle =z_3+\beta w_3.}\hfill \end{array}$$

(11)

Then we have

$${\left[\left[u\left(x\right)\right]\right]}_{x=c}=0={\left[\left[u\left(x\right)\right]\right]}_{x=d}.$$

There is a perfect contact at controller points, so we have to force

$${\left[\left[u^{\prime }\left(x\right)\right]\right]}_{x=c}=0={\left[\left[u^{\prime }\left(x\right)\right]\right]}_{x=d},$$

which implies

$$M\left(\begin{array}{c}\alpha \\ \beta \end{array}\right):=\left(\begin{array}{cc}{w}_1^{\prime }\left(c\right)-v_2^{\prime }\left(c\right)& {\displaystyle -w_2^{\prime }\left(c\right)}\\ -v_2^{\prime }\left(d\right)& {\displaystyle w_3^{\prime }\left(d\right)-w_2^{\prime }\left(d\right)}\end{array}\right)\left(\begin{array}{c}\alpha \\ \beta \end{array}\right)=\left(\begin{array}{c}{z}_2^{\prime }\left(c\right)-z_1^{\prime }\left(c\right)\\ z_2^{\prime }\left(d\right)-z_3^{\prime }\left(d\right)\end{array}\right).$$

(12)

The values of $\alpha ,\beta$ in (3) are the solution of (12).

In this way we can see that the solvability of the nonlocal problem (3) is linked to the solvability of the classical Dirichlet BVPs (4)–(8) and the solvability of the algebraic system (12). We have to check if the matrix M is invertible. To do this, we derive the formulas for solutions to particular problems, first. The general solution to $rp\left(x\right)-p^{″}\left(x\right)=0$ has the following form

$$p\left(x\right)=C_1{\mathrm{e}}^{\sqrt{r}x}+C_2{\mathrm{e}}^{-\sqrt{r}x}$$

with the constants $C_1,C_2$ depending on the boundary conditions under consideration. One can find the exact forms of the particular solutions, namely

$$\begin{array}{cc}\hfill {\displaystyle w_1\left(x\right)}& {\displaystyle =-\frac{\left({\mathrm{e}}^{-\sqrt{r}a}-{\mathrm{e}}^{-\sqrt{r}c}\right){\mathrm{e}}^{\sqrt{r}x}}{-{\mathrm{e}}^{-\sqrt{r}a}{\mathrm{e}}^{\sqrt{r}c}+{\mathrm{e}}^{-\sqrt{r}c}{\mathrm{e}}^{\sqrt{r}a}}+\frac{\left({\mathrm{e}}^{\sqrt{r}a}-{\mathrm{e}}^{\sqrt{r}c}\right){\mathrm{e}}^{-\sqrt{r}x}}{-{\mathrm{e}}^{-\sqrt{r}a}{\mathrm{e}}^{\sqrt{r}c}+{\mathrm{e}}^{-\sqrt{r}c}{\mathrm{e}}^{\sqrt{r}a}}}\hfill \\ & {\displaystyle =\frac{-{\mathrm{e}}^{\sqrt{r}(x-a)}+{\mathrm{e}}^{\sqrt{r}(x-c)}+{\mathrm{e}}^{\sqrt{r}(a-x)}-{\mathrm{e}}^{\sqrt{r}(c-x)}}{{\mathrm{e}}^{\sqrt{r}(a-c)}-{\mathrm{e}}^{\sqrt{r}(c-a)}}}\hfill \\ & {\displaystyle =\frac{sinh\left(\sqrt{r}(a-x)\right)+sinh\left(\sqrt{r}(x-c)\right)}{sinh\left(\sqrt{r}(a-c)\right)}}\hfill \\ & {\displaystyle =\frac{2sinh\left(\frac{\sqrt{r}}{2}(a-c)\right)cosh\left(\frac{\sqrt{r}}{2}(a+c-2x)\right)}{2sinh\left(\frac{\sqrt{r}}{2}(a-c)\right)cosh\left(\frac{\sqrt{r}}{2}(a-c)\right)}}\hfill \\ & {\displaystyle =\frac{cosh\left(\frac{\sqrt{r}}{2}(a+c-2x)\right)}{cosh\left(\frac{\sqrt{r}}{2}(a-c)\right)},}\hfill \end{array}$$

(13)

$$\begin{array}{cc}\hfill {\displaystyle v_2\left(x\right)}& {\displaystyle =\frac{{\mathrm{e}}^{-\sqrt{r}d}{\mathrm{e}}^{\sqrt{r}x}}{{\mathrm{e}}^{-\sqrt{r}d}{\mathrm{e}}^{\sqrt{r}c}-{\mathrm{e}}^{-\sqrt{r}c}{\mathrm{e}}^{\sqrt{r}d}}-\frac{{\mathrm{e}}^{\sqrt{r}d}{\mathrm{e}}^{-\sqrt{r}x}}{{\mathrm{e}}^{-\sqrt{r}d}{\mathrm{e}}^{\sqrt{r}c}-{\mathrm{e}}^{-\sqrt{r}c}{\mathrm{e}}^{\sqrt{r}d}}}\hfill \\ & {\displaystyle =\frac{{\mathrm{e}}^{\sqrt{r}(x-d)}-{\mathrm{e}}^{\sqrt{r}(d-x)}}{{\mathrm{e}}^{\sqrt{r}(c-d)}-{\mathrm{e}}^{\sqrt{r}(d-c)}}}\hfill \\ & {\displaystyle =\frac{sinh\left(\sqrt{r}(x-d)\right)}{sinh\left(\sqrt{r}(c-d)\right)},}\hfill \end{array}$$

(14)

$$\begin{array}{cc}\hfill {\displaystyle w_2\left(x\right)}& {\displaystyle =-\frac{{\mathrm{e}}^{-\sqrt{r}c}{\mathrm{e}}^{\sqrt{r}x}}{{\mathrm{e}}^{-\sqrt{r}d}{\mathrm{e}}^{\sqrt{r}c}-{\mathrm{e}}^{-\sqrt{r}c}{\mathrm{e}}^{\sqrt{r}d}}+\frac{{\mathrm{e}}^{\sqrt{r}c}{\mathrm{e}}^{-\sqrt{r}x}}{{\mathrm{e}}^{-\sqrt{r}d}{\mathrm{e}}^{\sqrt{r}c}-{\mathrm{e}}^{-\sqrt{r}c}{\mathrm{e}}^{\sqrt{r}d}}}\hfill \\ & {\displaystyle =\frac{{\mathrm{e}}^{\sqrt{r}(c-x)}-{\mathrm{e}}^{\sqrt{r}(x-c)}}{{\mathrm{e}}^{\sqrt{r}(c-d)}-{\mathrm{e}}^{\sqrt{r}(d-c)}}}\hfill \\ & {\displaystyle =\frac{sinh\left(\sqrt{r}(c-x)\right)}{sinh\left(\sqrt{r}(c-d)\right)},}\hfill \end{array}$$

(15)

$$\begin{array}{cc}\hfill {\displaystyle w_3\left(x\right)}& {\displaystyle =-\frac{\left(-{\mathrm{e}}^{-\sqrt{r}b}+{\mathrm{e}}^{-\sqrt{r}d}\right){\mathrm{e}}^{\sqrt{r}x}}{{\mathrm{e}}^{-\sqrt{r}b}{\mathrm{e}}^{\sqrt{r}d}-{\mathrm{e}}^{-\sqrt{r}d}{\mathrm{e}}^{\sqrt{r}b}}+\frac{\left(-{\mathrm{e}}^{\sqrt{r}b}+{\mathrm{e}}^{\sqrt{r}d}\right){\mathrm{e}}^{-\sqrt{r}x}}{{\mathrm{e}}^{-\sqrt{r}b}{\mathrm{e}}^{\sqrt{r}d}-{\mathrm{e}}^{-\sqrt{r}d}{\mathrm{e}}^{\sqrt{r}b}}}\hfill \\ & {\displaystyle =\frac{-{\mathrm{e}}^{\sqrt{r}(x-d)}+{\mathrm{e}}^{\sqrt{r}(x-b)}+{\mathrm{e}}^{\sqrt{r}(d-x)}-{\mathrm{e}}^{\sqrt{r}(b-x)}}{{\mathrm{e}}^{\sqrt{r}(d-b)}-{\mathrm{e}}^{\sqrt{r}(b-d)}}}\hfill \\ & {\displaystyle =\frac{sinh\left(\sqrt{r}(d-x)\right)+sinh\left(\sqrt{r}(x-b)\right)}{sinh\left(\sqrt{r}(d-b)\right)}}\hfill \\ & {\displaystyle =\frac{2sinh\left(\frac{\sqrt{r}}{2}(d-b)\right)cosh\left(\frac{\sqrt{r}}{2}(d+b-2x)\right)}{2sinh\left(\frac{\sqrt{r}}{2}(d-b)\right)cosh\left(\frac{\sqrt{r}}{2}(d-b)\right)}}\hfill \\ & {\displaystyle =\frac{cosh\left(\frac{\sqrt{r}}{2}(d+b-2x)\right)}{cosh\left(\frac{\sqrt{r}}{2}(d-b)\right)}.}\hfill \end{array}$$

(16)

Involving these relations into (12) we get

$$\mathit{M}=\left[\begin{array}{cc}-2\frac{\sqrt{r}\left({\mathrm{e}}^{-\sqrt{r}\left(a-d\right)}+{\mathrm{e}}^{\sqrt{r}\left(-d+c\right)}-{\mathrm{e}}^{-\sqrt{r}\left(-d+c\right)}-{\mathrm{e}}^{\sqrt{r}\left(a-d\right)}\right)}{\left({\mathrm{e}}^{-\sqrt{r}\left(a-c\right)}-{\mathrm{e}}^{\sqrt{r}\left(a-c\right)}\right)\left({\mathrm{e}}^{\sqrt{r}\left(-d+c\right)}-{\mathrm{e}}^{-\sqrt{r}\left(-d+c\right)}\right)}& 2\frac{\sqrt{r}}{{\mathrm{e}}^{\sqrt{r}\left(-d+c\right)}-{\mathrm{e}}^{-\sqrt{r}\left(-d+c\right)}}\\ -2\frac{\sqrt{r}}{{\mathrm{e}}^{\sqrt{r}\left(-d+c\right)}-{\mathrm{e}}^{-\sqrt{r}\left(-d+c\right)}}& 2\frac{\sqrt{r}\left(-{\mathrm{e}}^{-\sqrt{r}\left(b-c\right)}+{\mathrm{e}}^{\sqrt{r}\left(-d+c\right)}-{\mathrm{e}}^{-\sqrt{r}\left(-d+c\right)}+{\mathrm{e}}^{\sqrt{r}\left(b-c\right)}\right)}{\left(-{\mathrm{e}}^{-\sqrt{r}\left(b-d\right)}+{\mathrm{e}}^{\sqrt{r}\left(b-d\right)}\right)\left({\mathrm{e}}^{\sqrt{r}\left(-d+c\right)}-{\mathrm{e}}^{-\sqrt{r}\left(-d+c\right)}\right)}\end{array}\right].$$

The matrix M is regular if its determinant is different from 0. To check this, we rewrite $det\mathit{M}$ into a more suitable form for our purposes. To obtain this, we use basic functional relations between trigonometric and hyperbolic functions, namely

$$\begin{array}{ccc}\hfill {\displaystyle sinhz}& =\hfill & \frac{e^z-e^{-z}}{2},\forall z\in \mathbb{C},\hfill \\ \hfill coshz& =\hfill & \frac{e^z+e^{-z}}{2},\forall z\in \mathbb{C}.\hfill \end{array}$$

(17)

We may write

$$\begin{array}{cc}\hfill det\mathit{M}& {\displaystyle =-4r\left({\mathrm{e}}^{-\sqrt{r}\left(a-d\right)}+{\mathrm{e}}^{\sqrt{r}\left(-d+c\right)}-{\mathrm{e}}^{-\sqrt{r}\left(-d+c\right)}-{\mathrm{e}}^{\sqrt{r}\left(a-d\right)}\right)}\hfill \\ & {\displaystyle \times \frac{\left(-{\mathrm{e}}^{-\sqrt{r}\left(b-c\right)}+{\mathrm{e}}^{\sqrt{r}\left(-d+c\right)}-{\mathrm{e}}^{-\sqrt{r}\left(-d+c\right)}+{\mathrm{e}}^{\sqrt{r}\left(b-c\right)}\right)}{\left({\mathrm{e}}^{-\sqrt{r}\left(a-c\right)}-{\mathrm{e}}^{\sqrt{r}\left(a-c\right)}\right){\left({\mathrm{e}}^{\sqrt{r}\left(-d+c\right)}-{\mathrm{e}}^{-\sqrt{r}\left(-d+c\right)}\right)}^2\left(-{\mathrm{e}}^{-\sqrt{r}\left(b-d\right)}+{\mathrm{e}}^{\sqrt{r}\left(b-d\right)}\right)}}\hfill \\ & {\displaystyle +4\frac{r}{{\left({\mathrm{e}}^{\sqrt{r}\left(-d+c\right)}-{\mathrm{e}}^{-\sqrt{r}\left(-d+c\right)}\right)}^2}}\hfill \\ & {\displaystyle =\frac{4r\left({\mathrm{e}}^{\frac{1}{2}\sqrt{r}\left(a-b+c-d\right)}-{\mathrm{e}}^{-\frac{1}{2}\sqrt{r}\left(a-b+c-d\right)}\right)}{\left({\mathrm{e}}^{\sqrt{r}\left(-c+d\right)}-{\mathrm{e}}^{-\sqrt{r}\left(-c+d\right)}\right)\left({\mathrm{e}}^{\frac{1}{2}\sqrt{r}\left(a-c\right)}+{\mathrm{e}}^{-\frac{1}{2}\sqrt{r}\left(a-c\right)}\right)\left({\mathrm{e}}^{\sqrt{r}\left(b-d\right)}+\frac{1}{2}{\mathrm{e}}^{-\sqrt{r}\left(b-d\right)}\right)}}\hfill \\ & {\displaystyle =r\frac{sinh\left(\frac{1}{2}\sqrt{r}\left(a-b+c-d\right)\right)}{sinh\left(\sqrt{r}\left(-c+d\right)\right)cosh\left(\frac{1}{2}\sqrt{r}\left(a-c\right)\right)cosh\left(\frac{1}{2}\sqrt{r}\left(b-d\right)\right)}.}\hfill \end{array}$$

Using the relations (17) and

$$\left|\right|a|-|b\left|\right|\le |a-b|$$

for $z,a,b\in \mathbb{C}$, we can easily derive the following estimates

$$e^{|\Re z|}\frac{1-e^{-2|\Re z|}}{2}\le \left|sinhz\right|\le e^{|\Re z|},e^{|\Re z|}\frac{1-e^{-2|\Re z|}}{2}\le \left|coshz\right|\le e^{|\Re z|}.$$

(18)

Therefore

$$\begin{array}{cc}\hfill \left|det\mathit{M}\right|& {\displaystyle =\left|r\frac{sinh\left(\frac{1}{2}\sqrt{r}\left(a-b+c-d\right)\right)}{sinh\left(\sqrt{r}\left(-c+d\right)\right)cosh\left(\frac{1}{2}\sqrt{r}\left(a-c\right)\right)cosh\left(\frac{1}{2}\sqrt{r}\left(b-d\right)\right)}\right|}\hfill \\ & {\displaystyle \ge \left|r\right|\frac{1-e^{-|\Re \sqrt{r}|(-a+b-c+d)}}{2}.}\hfill \end{array}$$

Let $0\ne K\in \mathbb{R}$. A simple calculation yields

$$sinh\left(K\sqrt{r}\right)=0⟺e^{K\sqrt{r}}=e^{-K\sqrt{r}}⟺e^{2K\Re \sqrt{r}}{e}^{2Ki\Im \sqrt{r}}=1⟺\Re \sqrt{r}=0\wedge \Im \sqrt{r}=\frac{k\pi }{K}fork\in \mathbb{Z}.$$

It holds

$$\Re r+i\Im r=r={\left(\sqrt{r}\right)}^2={\Re }^2\sqrt{r}-{\Im }^2\sqrt{r}+2i\Re \sqrt{r}\Im \sqrt{r}.$$

(19)

If $\Re \sqrt{r}=0$ then

$$\Re r+i\Im r=-{\Im }^2\sqrt{r},$$

which implies

$$\Im r=0\wedge \Re r=-\frac{k^2{\pi }^2}{K^2}.$$

Thus, we have proved that

$$sinh\left(K\sqrt{r}\right)=0⟺\left(\Im r=0\wedge \Re r=-\frac{k^2{\pi }^2}{K^2}fork\in \mathbb{N}\cup \left\{0\right\}\right).$$

(20)

Analogously we deduce that

$$\begin{array}{cc}\hfill {\displaystyle cosh\left(K\sqrt{r}\right)=0}& {\displaystyle ⟺e^{K\sqrt{r}}=-e^{-K\sqrt{r}}}\hfill \\ & {\displaystyle ⟺e^{2K\Re \sqrt{r}}{e}^{2Ki\Im \sqrt{r}}=-1}\hfill \\ & {\displaystyle ⟺\Re \sqrt{r}=0\wedge \Im \sqrt{r}=\frac{(2k+1)\pi }{2K},}\hfill \end{array}$$

for $k\in \mathbb{Z}$. Using (19) we see that

$$\Im r=0\wedge \Re r=-{\left(\frac{(2k+1)\pi }{2K}\right)}^2.$$

Thus, we have proved that

$$cosh\left(K\sqrt{r}\right)=0⟺\left(\Im r=0\wedge \Re r=-{\left(\frac{(2k+1)\pi }{2K}\right)}^{2}fork\in \mathbb{N}\cup \left\{0\right\}\right).$$

(21)

We can clearly see that $det\mathit{M}=0$ if and only if $r=0$ or $sinh\left(\frac{1}{2}\sqrt{r}\left(a-b+c-d\right)\right)=0$, thus

$$det\mathit{M}=0⟺\left(\Im r=0\wedge \Re r=-\frac{4k^2{\pi }^2}{{(a-b+c-d)}^2}fork\in \mathbb{N}\cup \left\{0\right\}\right).$$

(22)

This concludes the proof that the nonlocal problem (3) can be solved using the classical Dirichlet BVPs (4)–(8) in the way described above if $det\mathit{M}\ne 0$.

3. Estimates for $\alpha ,\beta$

According to (12) we may write

$$\left(\begin{array}{c}\alpha \\ \beta \end{array}\right)=\frac{1}{detM}\left(\begin{array}{cc}{w}_3^{\prime }\left(d\right)-w_2^{\prime }\left(d\right)& {\displaystyle w_2^{\prime }\left(c\right)}\\ v_2^{\prime }\left(d\right)& {\displaystyle w_1^{\prime }\left(c\right)-v_2^{\prime }\left(c\right)}\end{array}\right)\left(\begin{array}{c}{z}_2^{\prime }\left(c\right)-z_1^{\prime }\left(c\right)\\ z_2^{\prime }\left(d\right)-z_3^{\prime }\left(d\right)\end{array}\right).$$

(23)

where

$$det\mathit{M}=r\frac{sinh\left(\frac{\sqrt{r}}{2}\left(a-b+c-d\right)\right)}{sinh\left(\sqrt{r}\left(-c+d\right)\right)cosh\left(\frac{\sqrt{r}}{2}\left(a-c\right)\right)cosh\left(\frac{\sqrt{r}}{2}\left(b-d\right)\right)}.$$

We may rewrite the matrix in (23) in a more suitable form, namely

$$\begin{array}{c}{\displaystyle \frac{1}{det\mathit{M}}\left(\begin{array}{cc}{w}_3^{\prime }\left(d\right)-w_2^{\prime }\left(d\right)& {\displaystyle w_2^{\prime }\left(c\right)}\\ v_2^{\prime }\left(d\right)& {\displaystyle w_1^{\prime }\left(c\right)-v_2^{\prime }\left(c\right)}\end{array}\right)=\frac{1}{det\mathit{M}}}\hfill \\ {\displaystyle \times \left[\begin{array}{cc}2\frac{\sqrt{r}\left({\mathrm{e}}^{-\sqrt{r}\left(b-c\right)}-{\mathrm{e}}^{\sqrt{r}\left(-d+c\right)}+{\mathrm{e}}^{-\sqrt{r}\left(-d+c\right)}-{\mathrm{e}}^{\sqrt{r}\left(b-c\right)}\right)}{\left(-{\mathrm{e}}^{-\sqrt{r}\left(b-d\right)}+{\mathrm{e}}^{\sqrt{r}\left(b-d\right)}\right)\left(-{\mathrm{e}}^{\sqrt{r}\left(-d+c\right)}+{\mathrm{e}}^{-\sqrt{r}\left(-d+c\right)}\right)}& 2\frac{\sqrt{r}}{-{\mathrm{e}}^{\sqrt{r}\left(-d+c\right)}+{\mathrm{e}}^{-\sqrt{r}\left(-d+c\right)}}\\ -2\frac{\sqrt{r}}{-{\mathrm{e}}^{\sqrt{r}\left(-d+c\right)}+{\mathrm{e}}^{-\sqrt{r}\left(-d+c\right)}}& -2\frac{\sqrt{r}\left(-{\mathrm{e}}^{-\sqrt{r}\left(a-d\right)}-{\mathrm{e}}^{\sqrt{r}\left(-d+c\right)}+{\mathrm{e}}^{-\sqrt{r}\left(-d+c\right)}+{\mathrm{e}}^{\sqrt{r}\left(a-d\right)}\right)}{\left({\mathrm{e}}^{-\sqrt{r}\left(a-c\right)}-{\mathrm{e}}^{\sqrt{r}\left(a-c\right)}\right)\left(-{\mathrm{e}}^{\sqrt{r}\left(-d+c\right)}+{\mathrm{e}}^{-\sqrt{r}\left(-d+c\right)}\right)}\end{array}\right]}\hfill \\ {\displaystyle =\frac{\sqrt{r}}{det\mathit{M}}\left[\begin{array}{cc}\frac{sinh\left(\sqrt{r}(c-b)\right)+sinh\left(\sqrt{r}(d-c)\right)}{sinh\left(\sqrt{r}(b-d)\right)sinh\left(\sqrt{r}(d-c)\right)}& \frac{1}{sinh\left(\sqrt{r}(d-c)\right)}\\ -\frac{1}{sinh\left(\sqrt{r}(d-c)\right)}& -\frac{sinh\left(\sqrt{r}(a-d)\right)+sinh\left(\sqrt{r}(d-c)\right)}{sinh\left(\sqrt{r}(c-a)\right)sinh\left(\sqrt{r}(d-c)\right)}\end{array}\right]}\hfill \\ {\displaystyle =\frac{sinh\left(\sqrt{r}\left(-c+d\right)\right)cosh\left(\frac{\sqrt{r}}{2}\left(a-c\right)\right)cosh\left(\frac{\sqrt{r}}{2}\left(b-d\right)\right)}{\sqrt{r}sinh\left(\frac{\sqrt{r}}{2}\left(a-b+c-d\right)\right)}}\hfill \\ {\displaystyle \times \left[\begin{array}{cc}\frac{2sinh\left(\frac{\sqrt{r}}{2}(d-b)\right)cosh\left(\frac{\sqrt{r}}{2}(2c-b-d)\right)}{sinh\left(\sqrt{r}(b-d)\right)sinh\left(\sqrt{r}(d-c)\right)}& \frac{1}{sinh\left(\sqrt{r}(d-c)\right)}\\ -\frac{1}{sinh\left(\sqrt{r}(d-c)\right)}& -\frac{2sinh\left(\frac{\sqrt{r}}{2}(a-c)\right)cosh\left(\frac{\sqrt{r}}{2}(a+c-2d)\right)}{sinh\left(\sqrt{r}(c-a)\right)sinh\left(\sqrt{r}(d-c)\right)}\end{array}\right]}\hfill \\ {\displaystyle =\frac{cosh\left(\frac{\sqrt{r}}{2}\left(a-c\right)\right)cosh\left(\frac{\sqrt{r}}{2}\left(b-d\right)\right)}{\sqrt{r}sinh\left(\frac{\sqrt{r}}{2}\left(a-b+c-d\right)\right)}}\hfill \\ {\displaystyle \times \left[\begin{array}{cc}\frac{2sinh\left(\frac{\sqrt{r}}{2}(d-b)\right)cosh\left(\frac{\sqrt{r}}{2}(2c-b-d)\right)}{sinh\left(\sqrt{r}(b-d)\right)}& 1\\ -1& -\frac{2sinh\left(\frac{\sqrt{r}}{2}(a-c)\right)cosh\left(\frac{\sqrt{r}}{2}(a+c-2d)\right)}{sinh\left(\sqrt{r}(c-a)\right)}\end{array}\right]}\hfill \\ {\displaystyle =\frac{cosh\left(\frac{\sqrt{r}}{2}\left(a-c\right)\right)cosh\left(\frac{\sqrt{r}}{2}\left(b-d\right)\right)}{\sqrt{r}sinh\left(\frac{\sqrt{r}}{2}\left(a-b+c-d\right)\right)}}\hfill \\ {\displaystyle \times \left[\begin{array}{cc}\frac{2sinh\left(\frac{\sqrt{r}}{2}(d-b)\right)cosh\left(\frac{\sqrt{r}}{2}(2c-b-d)\right)}{2sinh\left(\frac{\sqrt{r}}{2}(b-d)\right)cosh\left(\frac{\sqrt{r}}{2}(b-d)\right)}& 1\\ -1& -\frac{2sinh\left(\frac{\sqrt{r}}{2}(a-c)\right)cosh\left(\frac{\sqrt{r}}{2}(a+c-2d)\right)}{2sinh\left(\frac{\sqrt{r}}{2}(c-a)\right)cosh\left(\frac{\sqrt{r}}{2}(c-a)\right)}\end{array}\right]}\hfill \\ {\displaystyle =\frac{cosh\left(\frac{\sqrt{r}}{2}\left(a-c\right)\right)cosh\left(\frac{\sqrt{r}}{2}\left(b-d\right)\right)}{\sqrt{r}sinh\left(\frac{\sqrt{r}}{2}\left(a-b+c-d\right)\right)}\left[\begin{array}{cc}-\frac{cosh\left(\frac{\sqrt{r}}{2}(2c-b-d)\right)}{cosh\left(\frac{\sqrt{r}}{2}(b-d)\right)}& 1\\ -1& \frac{cosh\left(\frac{\sqrt{r}}{2}(a+c-2d)\right)}{cosh\left(\frac{\sqrt{r}}{2}(c-a)\right)}\end{array}\right].}\hfill \end{array}$$

Applying (18), we can estimate the particular entries of the last matrix as follows

$$\begin{array}{cc}\hfill {\displaystyle \left|\frac{cosh\left(\frac{\sqrt{r}}{2}\left(a-c\right)\right)cosh\left(\frac{\sqrt{r}}{2}\left(2c-b-d\right)\right)}{\sqrt{r}sinh\left(\frac{\sqrt{r}}{2}\left(a-b+c-d\right)\right)}\right|}& {\displaystyle \le \frac{1}{\left|\sqrt{r}\right|}\frac{{\mathrm{e}}^{\frac{|\Re \sqrt{r}|}{2}(c-a)}{\mathrm{e}}^{\frac{|\Re \sqrt{r}|}{2}(b+d-2c)}}{{\mathrm{e}}^{\frac{|\Re \sqrt{r}|}{2}(b-a+d-c)}\frac{1-e^{-|\Re \sqrt{r}|(b-a+d-c)}}{2}}}\hfill \\ & {\displaystyle =\frac{1}{\left|\sqrt{r}\right|}\frac{2}{1-e^{-|\Re \sqrt{r}|(b-a+d-c)}},}\hfill \end{array}$$

$$\begin{array}{cc}\hfill {\displaystyle \left|\frac{cosh\left(\frac{\sqrt{r}}{2}\left(a-c\right)\right)cosh\left(\frac{\sqrt{r}}{2}\left(b-d\right)\right)}{\sqrt{r}sinh\left(\frac{\sqrt{r}}{2}\left(a-b+c-d\right)\right)}\right|}& {\displaystyle \le \frac{1}{\left|\sqrt{r}\right|}\frac{{\mathrm{e}}^{\frac{|\Re \sqrt{r}|}{2}(c-a)}{\mathrm{e}}^{\frac{|\Re \sqrt{r}|}{2}(b-d)}}{{\mathrm{e}}^{\frac{|\Re \sqrt{r}|}{2}(b-a+d-c)}\frac{1-e^{-|\Re \sqrt{r}|(b-a+d-c)}}{2}}}\hfill \\ & {\displaystyle =\frac{1}{\left|\sqrt{r}\right|e^{|\Re \sqrt{r}|(d-c)}}\frac{2}{1-e^{-|\Re \sqrt{r}|(b-a+d-c)}}}\hfill \end{array}$$

and

$$\begin{array}{cc}\hfill {\displaystyle \left|\frac{cosh\left(\frac{\sqrt{r}}{2}\left(a+c-2d\right)\right)cosh\left(\frac{\sqrt{r}}{2}\left(b-d\right)\right)}{\sqrt{r}sinh\left(\frac{\sqrt{r}}{2}\left(a-b+c-d\right)\right)}\right|}& {\displaystyle \le \frac{1}{\left|\sqrt{r}\right|}\frac{{\mathrm{e}}^{\frac{|\Re \sqrt{r}|}{2}(2d-a-c)}{\mathrm{e}}^{\frac{|\Re \sqrt{r}|}{2}(b-d)}}{{\mathrm{e}}^{\frac{|\Re \sqrt{r}|}{2}(b-a+d-c)}\frac{1-e^{-|\Re \sqrt{r}|(b-a+d-c)}}{2}}}\hfill \\ & {\displaystyle =\frac{1}{\left|\sqrt{r}\right|}\frac{2}{1-e^{-|\Re \sqrt{r}|(b-a+d-c)}}.}\hfill \end{array}$$

According to (23) and the considerations above we have

$$\begin{array}{cc}\hfill {\displaystyle max\left\{\right|\alpha |,|\beta \left|\right\}}& {\displaystyle \le \frac{1}{\left|\sqrt{r}\right|}\frac{2\left(1+\frac{1}{e^{|\Re \sqrt{r}|(d-c)}}\right)}{1-e^{-|\Re \sqrt{r}|(b-a+d-c)}}max\left\{\right|z_2^{\prime }\left(c\right)-z_1^{\prime }\left(c\right)|,|z_2^{\prime }\left(d\right)-z_3^{\prime }\left(d\right)\left|\right\}}\hfill \\ & {\displaystyle \le \frac{4}{\left|\sqrt{r}\right|}\frac{1}{1-e^{-|\Re \sqrt{r}|(b-a+d-c)}}max\left\{\right|z_2^{\prime }\left(c\right)-z_1^{\prime }\left(c\right)|,|z_2^{\prime }\left(d\right)-z_3^{\prime }\left(d\right)\left|\right\}.}\hfill \end{array}$$

(24)

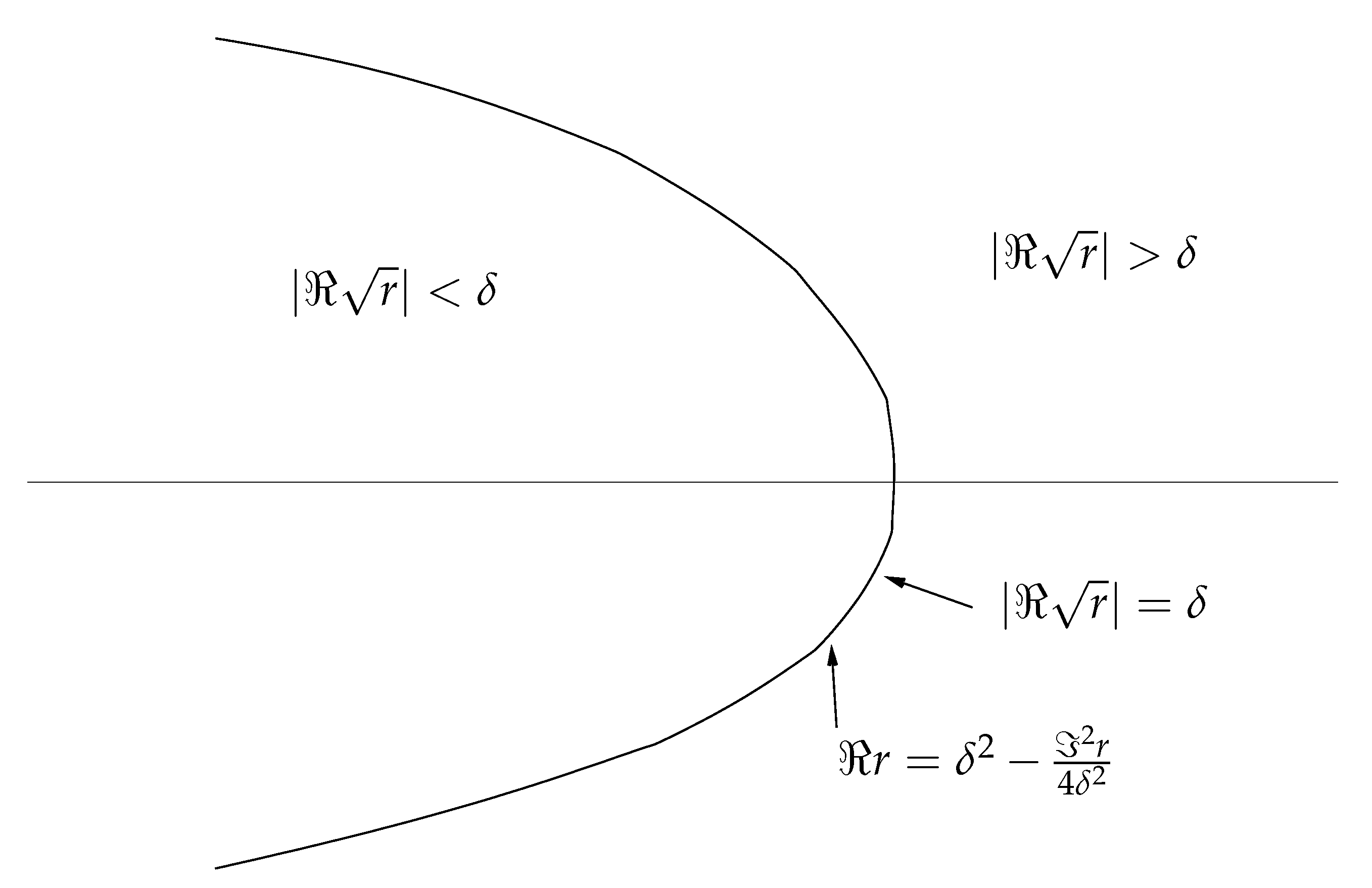
Now, we characterize all r for which $|\Re \sqrt{r}|\ge \delta >0$.

Using $\sqrt{r}=\Re \sqrt{r}+i\Im \sqrt{r}$ we have

$$r=\Re r+i\Im r={\Re }^2\sqrt{r}-{\Im }^2\sqrt{r}+2i\Re \sqrt{r}\Im \sqrt{r}.$$

This implies

$$\Re r={\Re }^2\sqrt{r}-{\Im }^2\sqrt{r}={\Re }^2\sqrt{r}-{\left(\frac{\Im r}{2\Re \sqrt{r}}\right)}^2={\Re }^2\sqrt{r}-\frac{{\Im }^{2}r}{4{\Re }^2\sqrt{r}}.$$

We see that if $|\Re \sqrt{r}|=\delta$ the complex numbers r lie on a horizontal parabola (see Figure 1)

$$\Re r={\delta }^2-\frac{{\Im }^{2}r}{4{\delta }^2}.$$

The top of the parabola is at the point $({\delta }^2,0)$. From this we conclude that if $r\in \mathbb{C}$ lies on the right-hand side of the horizontal parabola, then $|\Re \sqrt{r}|\ge \delta >0$. Clearly, there exists a sector $S_{-\overline{\delta },\overline{\varphi }}$ in the complex plane with $\overline{\delta }<0$

$$S_{-\overline{\delta },\overline{\varphi }}=\{r\in \mathbb{C};|arg(r+\overline{\delta })|\le \pi -\overline{\varphi },r\ne -\overline{\delta }\},\overline{\varphi }\in (0,\pi /2),$$

in which

$$\begin{array}{cc}\hfill {\displaystyle max\left\{\right|\alpha |,|\beta \left|\right\}}& {\displaystyle \le \frac{C\left(\overline{\delta }\right)}{\left|\sqrt{r}\right|}max\left\{\right|z_2^{\prime }\left(c\right)-z_1^{\prime }\left(c\right)|,|z_2^{\prime }\left(d\right)-z_3^{\prime }\left(d\right)\left|\right\}.}\hfill \end{array}$$

(25)

Our next concern is to derive estimates of $|z_i^{\prime }|$ at the points $c,d$ for $i=1,2,3$. This will be done in the next section, cf. (28).

4. Resolvent Estimate

Consider the problem (3). Let us denote $Au=-u^{″}$. We see A as an operator from $D\left(A\right)$ into $\mathbb{X}$, where

$$\begin{array}{cc}\hfill {\displaystyle D\left(A\right)}& {\displaystyle =\{u\in C^2\left([a,b]\right);u\left(a\right)=u\left(c\right),u\left(d\right)=u\left(b\right)\},}\hfill \\ \hfill \mathbb{X}& {\displaystyle =\{u\in C([a,b]);u(a)=u(c),u(d)=u(b\left)\right\}.}\hfill \end{array}$$

The norm in $\mathbb{X}$ is induced by $C\left(\right[a,b\left]\right)$ and denoted by $∥·∥$. We see that $\overline{D\left(A\right)}=\mathbb{X}$.

The goal of this section is to derive some uniform estimates (with respect to r) of the resolvent operator ${(rI+A)}^{-1}$ in an appropriate function space. We show that this can be achieved in the sector $S_{-\overline{\delta },\overline{\varphi }}$.

First, we address the closedness of A. Let $(u_n,A{u}_n)\to (u,y)$. Due to the fact that $A{u}_n$ is convergent, it is bounded. Applying the embedding theorem for continuous functions $C^2\subset C^1$ we have the boundedness and equi-continuity of $u_n^{\prime }$, i.e.,

$$|u_n^{\prime }\left(x\right)-u_n^{\prime }\left(y\right)|=\left|{\int }_x^y{u}_n^{″}\right|\le C|x-y|.$$

Using the Arzela–Ascolli theorem (Thm. 1.5.3 in [18]), we get the relative compactness of $u_n^{\prime }$, i.e., there exists a subsequence of $u_n^{\prime }$ that converges uniformly to some g. We know that $u_n$ converges pointwise to u. Thus, u is differentiable and $u^{\prime }=g$. Further we may write for any smooth function $\varphi$

$$\begin{array}{ccc}\hfill {\displaystyle {\int }_a^b{u}_n^{″}\varphi }& {\displaystyle =-{\int }_a^b{u}_n^{\prime }{\varphi }^{\prime }+}& {\displaystyle {\left.u_n^{\prime }\varphi \right|}_a^b}\\ \hfill \downarrow & \downarrow & \downarrow \\ \hfill {\displaystyle -{\int }_a^{b}y\varphi }& {\displaystyle =-{\int }_a^b{u}^{\prime }{\varphi }^{\prime }+}& {\displaystyle {\left.u^{\prime }\varphi \right|}_a^b}& {\displaystyle ={\int }_a^b{u}^{″}\varphi ,}\end{array}$$

which implies $Au=y$, i.e., the operator A is closed. The aim of this section is to prove that A, together with the nonlocal BCs (3), is a sectorial operator in a suitable function space, cf. [19,20,21].

According to (11) we have

$$\begin{array}{cc}\hfill {\displaystyle {∥u∥}_{C\left(\right[a,b\left]\right)}}& {\displaystyle \le {∥u_1∥}_{C\left(\right[a,c\left]\right)}+{∥u_2∥}_{C\left(\right[c,d\left]\right)}+{∥u_3∥}_{C\left(\right[d,b\left]\right)}}\hfill \\ & {\displaystyle \le {∥z_1∥}_{C\left(\right[a,c\left]\right)}+{∥z_2∥}_{C\left(\right[c,d\left]\right)}+{∥z_3∥}_{C\left(\right[d,b\left]\right)}}\hfill \\ & {\displaystyle +\left|\alpha \right|({∥w_1∥}_{C\left(\right[a,c\left]\right)}+{∥v_2∥}_{C\left(\right[c,d\left]\right)})+\left|\beta \right|({∥w_2∥}_{C\left(\right[c,d\left]\right)}+{∥w_3∥}_{C\left(\right[d,b\left]\right)}).}\hfill \end{array}$$

(26)

One can prove that a strongly elliptic partial differential operator of second order with continuous coefficients in a smooth bounded domain $\mathsf{\Omega }$ together with the homogeneous Dirichlet boundary condition generates an analytic semigroup in $L_p\left(\mathsf{\Omega }\right)$ for $1<p<\infty$. This is based on the resolvent estimate with respect to the $L_p\left(\mathsf{\Omega }\right)$-norm, see [21] (Chapter 7.3). In the analysis of our subject, we need to have a $C\left(\overline{\mathsf{\Omega }}\right)$-bound rather than an $L_p\left(\mathsf{\Omega }\right)$-bound. The resolvent estimate in the $C\left(\overline{\mathsf{\Omega }}\right)$-norm can be found in [22] and the $L_{\infty }\left(\mathsf{\Omega }\right)$-bound in [21] (Chapter 7.3).

The particular problem (4) is a classical homogeneous Dirichlet setting. The spectrum of the operator A is real and strict positive. In this standard case we have the following estimate, cf. [22]

$${∥{(rI+A)}^{-1}∥}_{\mathcal{L}\left(C\right([a,c]),C([a,c]\left)\right)}\le \frac{C}{|r+\delta |}for any r\in S_{-\overline{\delta },\overline{\varphi }}$$

and

$${∥z_1∥}_{C\left(\right[a,c\left]\right)}\le {∥{(rI+A)}^{-1}∥}_{\mathcal{L}\left(C\right([a,c]),C([a,c]\left)\right)}{∥f∥}_{C\left(\right[a,c\left]\right)}\le \frac{C}{|r+\delta |}{∥f∥}_{C\left(\right[a,c\left]\right)}.$$

(27)

Let us note that a similar estimate is also valid for $z_2$ and $z_3$ using the same argument. The situation for $v_2,w_1,w_2$ and $w_3$ is analogous. First, we have to get rid of the non-homogeneous BC by shifting the solution by an appropriate linear function g to get (e.g., $v_2=h-g$)

$$rh+Ah=rg$$

along with the homogeneous Dirichlet BCs. Then, using the same argumentation as for $z_1$, we get

$${∥h∥}_{C\left(\right[c,d\left]\right)})\le {∥{(rI+A)}^{-1}∥}_{\mathcal{L}\left(C\right([c,d]),C([c,d]\left)\right))}{∥rg∥}_{C\left(\right[c,d\left]\right)})\le \frac{C\left|r\right|}{|r+\delta |},$$

such that

$${∥v_2∥}_{C\left(\right[c,d\left]\right)})\le {∥g∥}_{C\left(\right[c,d\left]\right)})+{∥h∥}_{C\left(\right[c,d\left]\right)})\le C\left(1+\frac{\left|r\right|}{|r+\delta |}\right).$$

Analogously we arrive at the same kind of estimates for $w_1$, $w_2$ and $w_3$.

Let $0<\xi <1$. Then $A^{\xi }{(r+A)}^{-1}$ is a linear bounded operator and

$$\begin{array}{cc}\hfill {\displaystyle A^{\xi }{(r+A)}^{-1}}& {\displaystyle ={\left[A{(r+A)}^{-\frac{1}{\xi }}\right]}^{\xi }}\hfill \\ & {\displaystyle ={\left[(r+A-r){(r+A)}^{-\frac{1}{\xi }}\right]}^{\xi }}\hfill \\ & {\displaystyle ={\left[{(r+A)}^{1-\frac{1}{\xi }}-r{(r+A)}^{-\frac{1}{\xi }}\right]}^{\xi }}\hfill \\ & {\displaystyle ={\left[{\left\{{(r+A)}^{-1}\right\}}^{\frac{1}{\xi }-1}-r{\left\{{(r+A)}^{-1}\right\}}^{\frac{1}{\xi }}\right]}^{\xi }.}\hfill \end{array}$$

First, we note that for a bounded operator B and for $0\le \zeta \le 1$ we have

$$∥B^{\zeta }∥=\underset{∥x∥\le 1}{sup}∥B^{\zeta }x∥\le \underset{∥x∥\le 1}{sup}{∥Bx∥}^{\zeta }{∥x∥}^{1-\zeta }\le \underset{∥x∥\le 1}{sup}{∥Bx∥}^{\zeta }\le \underset{∥x∥\le 1}{sup}{∥B∥}^{\zeta }{∥x∥}^{\zeta }\le {∥B∥}^{\zeta }.$$

Using the inequality

$${(a+b)}^{\zeta }\le max\{1,2^{\zeta -1}\}\left(a^{\zeta }+b^{\zeta }\right),a,b\ge 0,\zeta \ge 0$$

we obtain (skipping the function space)

$$\begin{array}{cc}\hfill {\displaystyle ∥A^{\xi }{(r+A)}^{-1}∥}& {\displaystyle =∥{\left[{\left\{{(r+A)}^{-1}\right\}}^{\frac{1}{\xi }-1}-r{\left\{{(r+A)}^{-1}\right\}}^{\frac{1}{\xi }}\right]}^{\xi }∥}\hfill \\ & {\displaystyle \le {∥{\left\{{(r+A)}^{-1}\right\}}^{\frac{1}{\xi }-1}-r{\left\{{(r+A)}^{-1}\right\}}^{\frac{1}{\xi }}∥}^{\xi }}\hfill \\ & {\displaystyle \le {\left[∥{\left\{{(r+A)}^{-1}\right\}}^{\frac{1}{\xi }-1}∥+∥r{\left\{{(r+A)}^{-1}\right\}}^{\frac{1}{\xi }}∥\right]}^{\xi }}\hfill \\ & {\displaystyle \le C\left[{∥{(r+A)}^{-1}∥}^{1-\xi }+∥{(r+A)}^{-1}∥r^{\xi }\right]}\hfill \\ & {\displaystyle \le {C\left|r+\delta \right|}^{\xi -1}\left(1+{\left(\frac{\left|r\right|}{\left|r+\delta \right|}\right)}^{\xi }\right).}\hfill \end{array}$$

For the particular choice $\xi =\frac{1}{2}$ we have

$$∥A^{\frac{1}{2}}{(r+A)}^{-1}∥\le C{\left|r+\delta \right|}^{-\frac{1}{2}}\left(1+{\left(\frac{\left|r\right|}{\left|r+\delta \right|}\right)}^{\frac{1}{2}}\right).$$

In light of this we may write

$$|z_1^{\prime }\left(c\right)|\le {∥z_1^{\prime }∥}_{C\left(\right[a,c\left]\right)}\le C{\left|r+\delta \right|}^{-\frac{1}{2}}\left(1+{\left(\frac{\left|r\right|}{\left|r+\delta \right|}\right)}^{\frac{1}{2}}\right).$$

(28)

The same estimates are valid for $|z_2^{\prime }\left(c\right)|,|z_2^{\prime }\left(d\right)|$ and $|z_3^{\prime }\left(d\right)$.

Wrapping up the considerations above, we successively deduce that

$$\begin{array}{cc}\hfill {\displaystyle {∥u∥}_{C\left(\right[a,b\left]\right)}}& {\displaystyle \stackrel{\left(26\right)}{\le }{∥z_1∥}_{C\left(\right[a,c\left]\right)}+{∥z_2∥}_{C\left(\right[c,d\left]\right)}+{∥z_3∥}_{C\left(\right[d,b\left]\right)}}\hfill \\ & {\displaystyle +\left|\alpha \right|({∥w_1∥}_{C\left(\right[a,c\left]\right)}+{∥v_2∥}_{C\left(\right[c,d\left]\right)})+\left|\beta \right|({∥w_2∥}_{C\left(\right[c,d\left]\right)}+{∥w_3∥}_{C\left(\right[d,b\left]\right)})}\hfill \\ & {\displaystyle \le \frac{C}{|r+\delta |}\left({∥f∥}_{C\left(\right[a,c\left]\right)}+{∥f∥}_{C\left(\right[c,d\left]\right)}+{∥f∥}_{C\left(\right[d,b\left]\right)}\right)}\hfill \\ & {\displaystyle +C\left(1+\frac{\left|r\right|}{|r+\delta |}\right)\left(\left|\alpha \right|+\left|\beta \right|\right)}\hfill \\ & {\displaystyle \stackrel{\left(25\right)}{\le }\frac{C}{|r+\delta |}{∥f∥}_{C\left(\right[a,b\left]\right)}+\frac{C}{|\sqrt{r}|}max\left\{\right|z_2^{\prime }\left(c\right)-z_1^{\prime }\left(c\right)|,|z_2^{\prime }\left(d\right)-z_3^{\prime }\left(d\right)\left|\right\}}\hfill \\ & {\displaystyle \stackrel{\left(28\right)}{\le }\frac{C}{|r+\delta |}{∥f∥}_{C\left(\right[a,b\left]\right)}+\frac{C}{|\sqrt{r}|}{\left|r+\delta \right|}^{-\frac{1}{2}}\left(1+{\left(\frac{\left|r\right|}{\left|r+\delta \right|}\right)}^{\frac{1}{2}}\right)}\hfill \\ & {\displaystyle \le \frac{C}{|r+\delta |}{∥f∥}_{C\left(\right[a,b\left]\right)}+\frac{C}{|r+\delta |}\left(1+{\left(\frac{\left|r\right|}{\left|r+\delta \right|}\right)}^{\frac{1}{2}}\right){\left(\frac{\left|r+\delta \right|}{\left|r\right|}\right)}^{\frac{1}{2}}.}\hfill \end{array}$$

(29)

Finally, we conclude that

$${∥{(rI+A)}^{-1}∥}_{\mathcal{L}\left(C\right([a,b]),C([a,b]\left)\right))}\le \frac{C}{|r+\delta |},\forall r\in S_{-\overline{\delta },\overline{\varphi }}.$$

Thus, A is a sectorial operator in $\mathbb{X}$. For the definition of a sectorial operator we refer the reader to [19,20,21]. In our special situation it means that the spectrum is real, lies in a half plane and the resolvent operator obeys the inequality above.

5. Parabolic Problem

The aim of this section is to solve the following semilinear parabolic problem ($Au=-u_{xx}$)

$$\begin{array}{cc}\hfill {\displaystyle u_t(t,x)+Au(t,x)}& {\displaystyle =f(t,x,u(t,x),u_x(t,x))}\hfill \\ \hfill \alpha \left(t\right)& {\displaystyle =u(t,a)=u(t,c)}\hfill \\ \hfill \beta \left(t\right)& {\displaystyle =u(t,d)=u(t,b)}\hfill \\ \hfill u(0,x)& {\displaystyle =u_0\left(x\right)}\hfill \end{array}$$

(30)

for $t\in [0,T]$ and $x\in (a,b)$, along with the unknown functions $\alpha \left(t\right)$ and $\beta \left(t\right)$. We assume that f is a global Lipschitz continuous function in all variables.

The operator A is sectorial in $\mathbb{X}$. Therefore, we may involve the semigroup theory (cf. [19,20,21]) to conclude that:

Theorem 1.

Let f be a global Lipschitz continuous function in all variables and $u_0\in \mathbb{X}$. Then there exists a unique solution u to (30).

Semi-Discretization in Time

Rothe’s method (cf. [23]) represents a constructive method suitable for solving evolution problems with standard BCs. Using a simple discretization in time, a time-dependent problem is approximated by a sequence of elliptic BVPs which have to be solved successively with increasing time step. This standard procedure is in our case complicated by the nonlocal BCs. We will show how to apply this method to our nonlocal setting.

First, we divide the time interval $[0,T]$ into $n\in \mathbb{N}$ equidistant sub-intervals $[t_{i-1},t_i]$ for $t_i=i\tau$, where $\tau =\frac{T}{n}$. We introduce the following notation

$$z_i=z\left(t_i\right),\delta z_i=\frac{z_i-z_{i-1}}{\tau }$$

for any function z.

We are left with a recurrent system of nonlocal steady-state problems at each successive time point $t_i$, $i=1,\cdots ,n$

$$\begin{array}{c}\hfill \begin{array}{c}{\displaystyle \delta u_i+A{u}_i=f(t_{i-1},u_{i-1},u_{i-1}^{\prime }),}\hfill \\ {\alpha }_i=u_i\left(a\right)=u_i\left(c\right),\hfill \\ {\beta }_i=u_i\left(d\right)=u_i\left(b\right).\hfill \end{array}\end{array}$$

(31)

Please note that $u_0=u_0\left(x\right)$, which is a known function.

The problem (31) can be rewritten as follows

$$\begin{array}{c}{\displaystyle \frac{u_i}{\tau }+A{u}_i=f(t_{i-1},u_{i-1},u_{i-1}^{\prime })+\frac{u_{i-1}}{\tau },}\hfill \\ {\alpha }_i=u_i\left(a\right)=u_i\left(c\right),\hfill \\ {\beta }_i=u_i\left(d\right)=u_i\left(b\right).\hfill \end{array}$$

This is precisely the same form of the problem as we have studied in Section 2. Applying our constructive method using auxiliary problems (4)–(8), we get the approximations $u_i$ ($i=1,\cdots ,n$) obeying (31). The convergence of the approximations towards the exact solution and the error estimates can be obtained readily using the semigroup theory in Banach spaces. Let us note that this has already been studied in [24] under the assumption that A is a sectorial operator in $\mathbb{X}$ and

$$\Re \sigma \left(A\right)>{\delta }_0>0.$$

To meet this condition, we can redefine our problem by shifting the spectrum, i.e., instead of

$$u_t(t,x)+Au(t,x)=f(t,x,u(t,x),u_x(t,x))$$

we take

$$u_t(t,x)+pu(t,x)+Au(t,x)=f(t,x,u(t,x),u_x(t,x))+pu(t,x).$$

This means, considering $\tilde{A}u=pu+Au$ instead of $Au$. In light of this, we may write:

Theorem 2.

Let f be a global Lipschitz continuous function in all variables and $u_0\in C^2\left([a,b]\right)\cap \mathbb{X}$. Then there exists a unique solution u to (30). Moreover, the approximations $u_i$ defined by (31) obey

$$\underset{1\le i\le n}{max}{∥u\left(t_i\right)-u_i∥}_{C\left(\right[a,b\left]\right)}\le C\tau .$$

6. Numerical Experiments

The aim of this section is to demonstrate the efficiency of the proposed theoretical schemes described in the previous sections. We start with a steady-state case.

6.1. Steady-State Example

Consider the problem (3) with $r=1$, $a=\frac{\pi }{8},c=\frac{3\pi }{8},d=\frac{5\pi }{8},b=\frac{7\pi }{3}$. Let $u=sin\left(2x\right)$ be the exact solution and $f\left(x\right)=2+5sin\left(2x\right)$ be the corresponding right-hand-side.

We apply the Finite Element Method (FEM) with N discretization intervals using first order Lagrange polynomials (P1-FEM) to find an approximation of the solutions to auxiliary problems (4), (6) and (9). We approximate the first order derivatives appearing in (12) by the first order differences at the interior points c and d. Finally, we approximate the total error on the solution by

$$\begin{array}{ccc}\hfill E& :=& \underset{1⩽j⩽N}{max}\left|u\left(x_j\right)-u_j\right|,\hfill \end{array}$$

with $u_j\approx u\left(x_j\right)$, $j=0,\cdots ,N$.

The results are depicted in Figure 2, which validates the scheme described in Section 2.

6.2. Transient Problem

Now, we test the proposed method from Section 5. Let us consider the following semilinear parabolic problem

$$\begin{array}{cc}\hfill {\displaystyle u_t(t,x)+u(t,x)-u_{xx}(t,x)}& {\displaystyle =sin\left(u\right(t,x\left)\right)+f(t,x)}\hfill \\ \hfill \alpha \left(t\right)& {\displaystyle =u(t,a)=u(t,c)}\hfill \\ \hfill \beta \left(t\right)& {\displaystyle =u(t,d)=u(t,b)}\hfill \\ \hfill u(0,x)& {\displaystyle =u_0\left(x\right)}\hfill \end{array}$$

with unknown $\alpha \left(t\right)$ and $\beta \left(t\right)$.

We set $a=\frac{\pi }{8},c=\frac{3\pi }{8},d=\frac{5\pi }{8}$ and $b=\frac{7\pi }{3}$. The $f(t,x)$ is defined in such a way that

$$u(t,x)=2-e^{-t}cos\left(\pi t\right)sin\left(2x\right)$$

is the exact solution representing a damped transient wave.

The auxiliary problems (4), (6) and (9) are solved using the Finite Element Method (FEM) with N discretization intervals using first order Lagrange polynomials (P1-FEM). We approximate the first order derivatives appearing in (12) by the first order differences at the interior points c and d. Finally, we approximate the total error on the solution by

$$\begin{array}{ccc}\hfill E& :=& \underset{1⩽i⩽N_t}{max}\underset{1⩽j⩽N}{max}\left|u\left(t_i,x_j\right)-u_j^{\left(i\right)}\right|,\hfill \end{array}$$

with $u_j^{\left(i\right)}\approx u(t_i,x_j)$, $j=1,\cdots ,N$, $i=1,\cdots ,N_t$.

We investigate the dependence of the error on the discretization in time. For this reason, we take the number of space discretization intervals sufficiently large—in our case $N=2000$. Figure 3 shows the error between the numerical solution and the exact solution in a log-log scale for decreasing time step $\tau$.

7. Conclusions

Using the principle of linear superposition and Rothe’s method, the solution of a semilinear parabolic equation accompanied with the nonlocal BCs (1) can be approximated. The convergence of the approximations towards the exact solution and the error estimates follow from the fact that the (steady-state) differential operator of the proposed problem is sectorial in an appropriate function space and from existing applications of the semigroup theory in Banach spaces.