Generalized Hurst Hypothesis: Description of Time-Series in Communication Systems

1. Introduction

Complex systems represent themselves as diffusive systems, where the direct/deterministic physical laws are absent for their accurate description and, therefore, for further predictions. In other words, the direct fitting function derived from the first principles (or from an appropriate simple model) and corresponding to the deterministic law is absent. In these cases, the correlation analysis connecting different physical values plays a significant role. The trendless sequences (TLS), frequently defined as long-time series (LTS) or “noise”, describe fluctuations originated from different sources and represent the most difficult response for analysis and extraction of reliable and stable information. However, over the past 20–30 years, many researchers have been trying to extract reliable information from TLS. Notably, there has been significant progress in the analysis of the TLS achieved in electrochemistry [1,2,3,4,5] and other branches of sciences thanks to the works of Prof. Timashev, who proposed and developed the flicker-noise spectroscopy [6,7], and Prof. Yulmetyev, who applied the Mori–Zwanzig formalism [8,9,10] to describe many phenomena in different complex systems having diffusive nature. We should also mention a monograph written by Prof. Chen with his pupils [11], in which they provided an analysis of different types of model noises having presumably a fractal/scaling origin. Moreover, one can recall the $\beta$-distribution approach [12], when the analysis of real temporal-noises in biological systems is reduced to almost 10-20 robust parameters associated with the parameters of beta-distributions and their fitting functions. We should also note that this bell-like curve approach is based on the generalization of the detrended fluctuation analysis (DFA) developed by Peng et al. [13]. A new universal set of parameters for TLS description, which allows detecting anomalies in data, was introduced by Nigmatullin and Vorobev [14]. However, the proposed parameters do not have direct connection with fractal properties of the analyzed signal. The key idea of our study is that the analysis based on Hurst law captures fractal structure of data [15].

In this paper, we concentrate presumably on the generalization of the Hurst empirical law, which plays an important role in analysis of the different time-series. As it is known from Feder [15], this relationship characterizes the growth of the cumulative averaged values and can be expressed approximately as

$$\frac{R\left(x\right)}{S\left(x\right)}\stackrel{x\gg 1}{\cong }C·x^H,$$

(1)

where $R\left(x\right)=max\left(x\right)-min\left(x\right)$ is the range of a given TLS, $S\left(x\right)$ is its standard deviation, C is a positive constant and H is the power-law exponent, $H\in [0;1]$. This empirical law discovered by Hurst [16] has an asymptotic character and is valid for relatively large segments of some temporal series x. This asymptotic law is quite popular in the analysis of time-series in communication systems. Since in ordinary conditions network traffic usually has fractal structure, many researchers have used asymptotic Hurst law (1) to detect traffic anomalies. For example, Deka and Bhattacharyya [17] constructed TLS(s) based on time interval attributes of packets. They further calculated cross-correlation of the TLS(s) and estimated the values of the Hurst exponent for evaluation. They showed that in such kind of experiments it is possible to detect the differences between normal traffic and Distributed Denial of Service (DDoS) attacks just by analyzing the calculated values of the Hurst exponent.

A more deliberate work was done by Dymora and Mazurek [18], who studied fractal properties of network traffic as well. The researchers analyzed long-term properties, processing data in the range of several months. Asymptotic Hurst law (1) was applied to detect anomalies and Legendre spectrum was further studied to identify them more precisely. The researchers came to the conclusion that deviations of Hurst exponent from the standard values can be considered as signs of unauthorized actions.

Despite the difficulties in establishing any kind of explicit relation between the Hurst exponent and parameters of communication systems, Toral et al. [19] demonstrated that there is an empirical relationship between the Hurst exponent of traffic flows and the packet loss rate.

Hurst exponent is used to analyze communication systems at physical level as well. One of the applications is connected with flicker noise, which is quite common in electronic devices [20]. The effect of flicker noise is significant at low frequencies and it can seriously deteriorate the signal-to-noise ratio (SNR) of the received signal. The link between Hurst exponent and flicker noise is based on the fact that flicker noise can be described in the form of the fractal Brownian motion, which is known to be connected with the Hurst exponent [15].

Parshin and Parshin [21] used Hurst exponent for modelling and evaluation of flicker noise. In their next study, the same authors proposed flicker noise compensation algorithm [22] and concluded that for non-Gaussian flicker noise the compensation algorithm improves SNR by 20 dB.

Moreover, the Hurst exponent is frequently used not only in communication systems, but also in the analysis of financial time series [23], electroencephalography (EEG) [24] and many other fields. The main disadvantage of the empirical law (1) is that it has an asymptotic behavior, which implies that a relatively large number of data is needed for description of fractal properties of the analyzed signal. Since Hurst exponent is successfully used to analyze signals in various fields of science and technology, the introduction of a more universal tool based on the well-known asymptotic law (1) is expected to open new opportunities in the fields, where the empirical Hurst law was successfully applied.

The basic aim of this paper is to generalize expression (1) and apply this relationship for segments of temporal series x having an arbitrary length. A thorough analysis of previous results obtained by Sheng et al. [11] and Feder [15] allows suggesting three hypotheses that cover completely the chosen segment x:

$$GH\left(1\right)\equiv y_1(x,A,B,H)=\frac{R\left(x\right)}{S\left(x\right)}\cong A+B·x^H$$

(2)

$$GH\left(2\right)\equiv y_2(x,B_{0,1,2},H_{1,2})=\frac{R\left(x\right)}{S\left(x\right)}\cong B_0+B_1{x}^{H_1}+B_2{x}^{H_2}$$

(3)

$$GH\left(3\right)\equiv y_3(x,A_{0,1,2,3},H_{1,2,3})=\frac{R\left(x\right)}{S\left(x\right)}\cong A_0+A_1·x^{H_1}+A_2·x^{H_2}+A_3·x^{H_3}$$

(4)

For every hypothesis, we present an example of a TLS, namely, noises from radio and audio devices. We further analyze the deviation of the parameters figuring in (2)–(4) and present the statistics for the most important ones. To fit completely the given segment by these fitting functions, we use the eigen-coordinates (EC) method that was described in detail in the paper by Nigmatullin [25] and in the book by Nigmatullin et al. [26]. In the Appendix, we provide the desired transformations that allow transforming these non-linear fitting functions to the basic linear relationship:

$$Y\left(x_j\right)=\sum _{s=0}^{S-1}{C}_s{X}_s\left(x_j\right).$$

(5)

The relationship (5) allows applying the linear least square method (LLSM) and relate the constants $C_s$ figuring in (5) with initial fitting constants (three for GH(1), five for GH(2) and seven for GH(3)) figuring in (2)–(4) using some non-linear relationships.

The key contributions of this paper can be summarized as follows:

• We propose the generalization of asymptotic Hurst law (Section 2.1).
• The proposed method is not asymptotic, thus it does not impose any limitations on the size of the analyzed TLS.
• We test it on noise data described in Section 2.2.
• We analyze the importance of parameters of the generalized Hurst law (Section 3).
• We discuss the possible applications of the generalized Hurst law (Section 4).

2. Materials and Methods

2.1. Description of the Algorithm

Let us consider a TLS $x_i,i=0,\dots ,N-1$ of N elements. To calculate the $R\left(x\right)/S\left(x\right)$ ratio reflecting a specific and “universal” response of some complex system and described by the given TLS, we first divide the given TLS $x_i$ into $K=\lfloor \frac{N}{a}\rfloor$ segments of length $a<N$. Next, we calculate the $R\left(x\right)/S\left(x\right)$ ratio within the segments of length a, $2a$, …$Ka$. Thus we get K values obtained by calculation of $R\left(ka\right)/S\left(ka\right)$, $k=1,2,\dots K$. Then, we fit the ratios $R\left(ka\right)/S\left(ka\right)$ for each k using the hypotheses in (2)–(4) with respect to segments a, $2a$, …$Ka$. If the first hypothesis provides the fit with a relative error less than 2%, then it is accepted. The value of the relative error is defined by the conventional expression

$$Err(y,f)=\left(\frac{stdev(y-f)}{mean\left(\right|y\left|\right)}\right)·100\%,$$

(6)

where

$$stdev\left(Y\right)=\sqrt{\left(\frac{1}{N}\sum _{j=1}^N{Y}_j^2\right)},mean\left(Y\right)=\frac{1}{N}\sum _{j=1}^N{Y}_j$$

(7)

Here, $y_j,j=1,2,\dots ,N$ is the measured function and $f_j$ is the corresponding fitting function. For more complex hypotheses, we use the same criterion associated with the value of the relative error.

To accelerate these calculations, we apply reduction to three incident points (RTIP), the procedure used in [25,26]. The essence of this effective procedure lies in the following. We choose a segment of the length L that contains $y_1,y_2,\dots ,y_L={\left\{y\right\}}_L$ data points and then select only three points ($max\left({\left\{y\right\}}_L\right),mean\left({\left\{y\right\}}_L\right),min\left({\left\{y\right\}}_L\right)$) that are invariant with respect to $L!$ permutations corresponding to the chosen segment. Therefore, one can obtain the compressed TLS containing three subsequences of the length [$N/L$] that demonstrate the distributions of the maximum, mean and minimum values of the initial TLS, correspondingly. The evaluation of the correlations made with the help of the statistics of the fractional moments [27,28] shows that $L=10$ times compression is sufficient, because it leaves the correlation coefficient in the interval [0.9–0.975].

The initial length of a segment a is chosen individually for each hypothesis. Generally, it is quite close to the value of the compression parameter $L=10$. In our paper, we use $a=10$ and $a=20$ for different data. Finishing this section, one can describe the algorithm that is used for calculation of the fitting parameters figuring in (2)–(4). There are three parameters ($A,B,H$) for the first hypothesis (2), five ($B_{0,1,2},H_{1,2}$) for the second hypothesis (3) and seven ($A_{0,1,2,3},H_{1,2,3}$) for the third hypothesis (4). These parameters can be considered as the reduced parameters reflecting the behavior of a complex system, if responses of the chosen system are presented in the form of the TLS(s). Therefore, the algorithm is simple as it incorporates only the following three steps and cannot create uncontrollable errors related to its application:

• Select L and apply the RTIP-procedure, if necessary.
• Calculate the ratios $R\left(ka\right)/S\left(ka\right)$ up to $K=\lfloor \frac{N}{a}\rfloor$.
• Fit the obtained ratios to the hypothesis figuring in (2)–(4) with the help of the EC-method.

The basic linear relationship (5) for these non-linear hypotheses is given in the Appendix A. The value of the relative/dimensionless error is defined by expression (6).

2.2. Description of the Data

To test the aforementioned hypotheses in (2)–(4), we collected noise signals from radio and audio devices. In radio communication devices, the noise signal is the signal from the receiver when no other devices transmit signals in the receiver’s bandwidth. In audio devices, the noise signal is the signal of a microphone when there is no sound sources in the room. Radio receivers can be compared using noise figure, which is defined as the ratio of the receiver’s output noise power to the power of thermal noise in the input pins, expressed in $dB$. The lower the noise figure of a device is, the better performance it can offer. Noise from radio communication devices was captured in an ordinary laboratory environment, while noise from the audio device was recorded in a soundproof chamber.

We capture the digitalized orthogonal in-phase and quadrature components of the signal received by a radio device. Therefore, the captured signal can be represented as a vector of complex numbers $x_i\in \mathbb{C},i=1,\dots ,N$. We calculate the argument of every complex number $x_i$, thus obtaining new pure real signal $y_i=arg\left(x_i\right)$. This TLS is further used for $R/S$ calculation and fitting.

First, we analyzed the noise signal from Adalm Pluto Software defined radio (SDR). Pluto SDR is a programmable radio communication device, capable of receiving or transmitting signals. It features a 12-bit analog-to-digital converter (ADC) and a cascade of analog filters. The entire receiver path has Noise Figure below 3.5 dB. After careful analysis, we concluded that the phase of the noise is more suitable for the hypotheses in (2)–(4) than the power or absolute value of the signal. To test the first hypothesis, we used the phase of the noise from Pluto SDR. An example of the fit can be seen in Figure 1.

Second, we analyzed the noise signal from National Instruments USRP 2930 (Universal Software Radio Peripheral). NI USRP 2930 has a 14-bit ADC and its noise figure ranges from 5 to 7 dB. It has better ADC, but its noise figure is higher compared to Pluto SDR’s. After testing different hypotheses on the noise data from NI USRP 2930, we concluded that the phase of the noise suits the second hypothesis better. Figure 2 and Figure 3 present examples of a second-hypothesis fit.

Third, we recorded the noise of Audio-Technica AT2020USB+ condenser microphone. It has 16-bit ADC and allows performing stereo recording; therefore, there are two signals: left channel and right channel. After testing the third hypothesis on this data, we found that the differential noise signal is the most suitable one. That is, we subtract the right channel noise from the left-channel one and analyze the difference. Figure 4 demonstrates fitting using the third hypothesis.

Generally speaking, it is quite difficult to indicate what properties the TLS should have to be better described by the first, second or third hypothesis. Moreover, as the number of exponents in the hypothesis increases, so does the quality of fitting. We assigned the data to hypotheses based on the criteria that every hypothesis must provide fitting with the relative error no more than 1–2%.

To summarize the data description, we used three datasets of different origin:

• Phase of the Adalm Pluto SDR receiver noise, Hypothesis 1 (2)
• Phase of the NI-USRP 2930 receiver noise, Hypothesis 2 (3)
• Differential noise of AT2020USB+ microphone, Hypothesis 3 (4)

All the analyzed data are openly available in Github repository [29] for further analysis and for reproduction of the results obtained in the current research.

3. Results

The limited size of this paper does not allow us to present all the fitting parameters. However, given the criterion associated with the minimal value of the fitting error being less than 2%, one can demonstrate the obtained results.

Table 1. First hypothesis statistics.

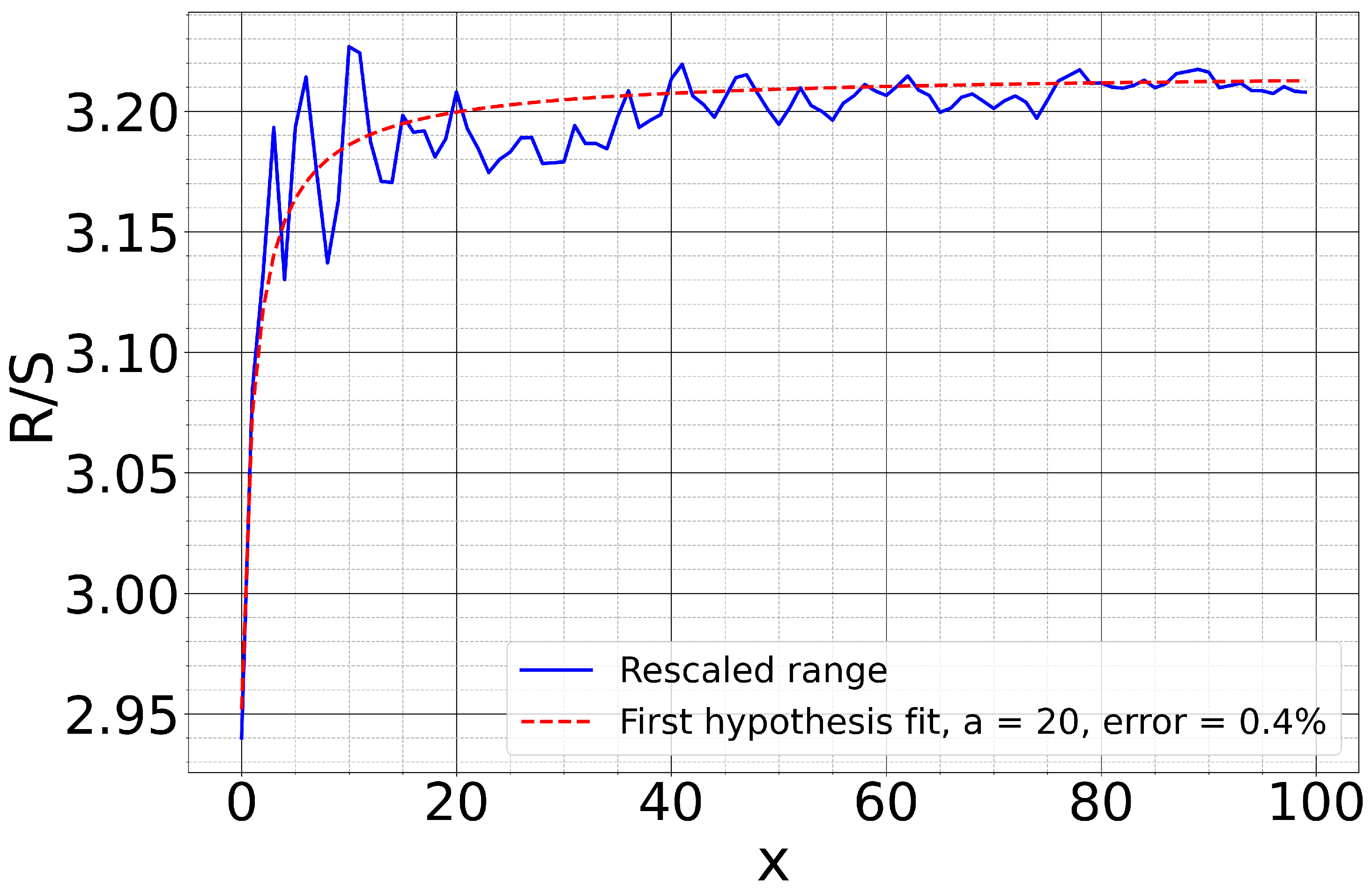
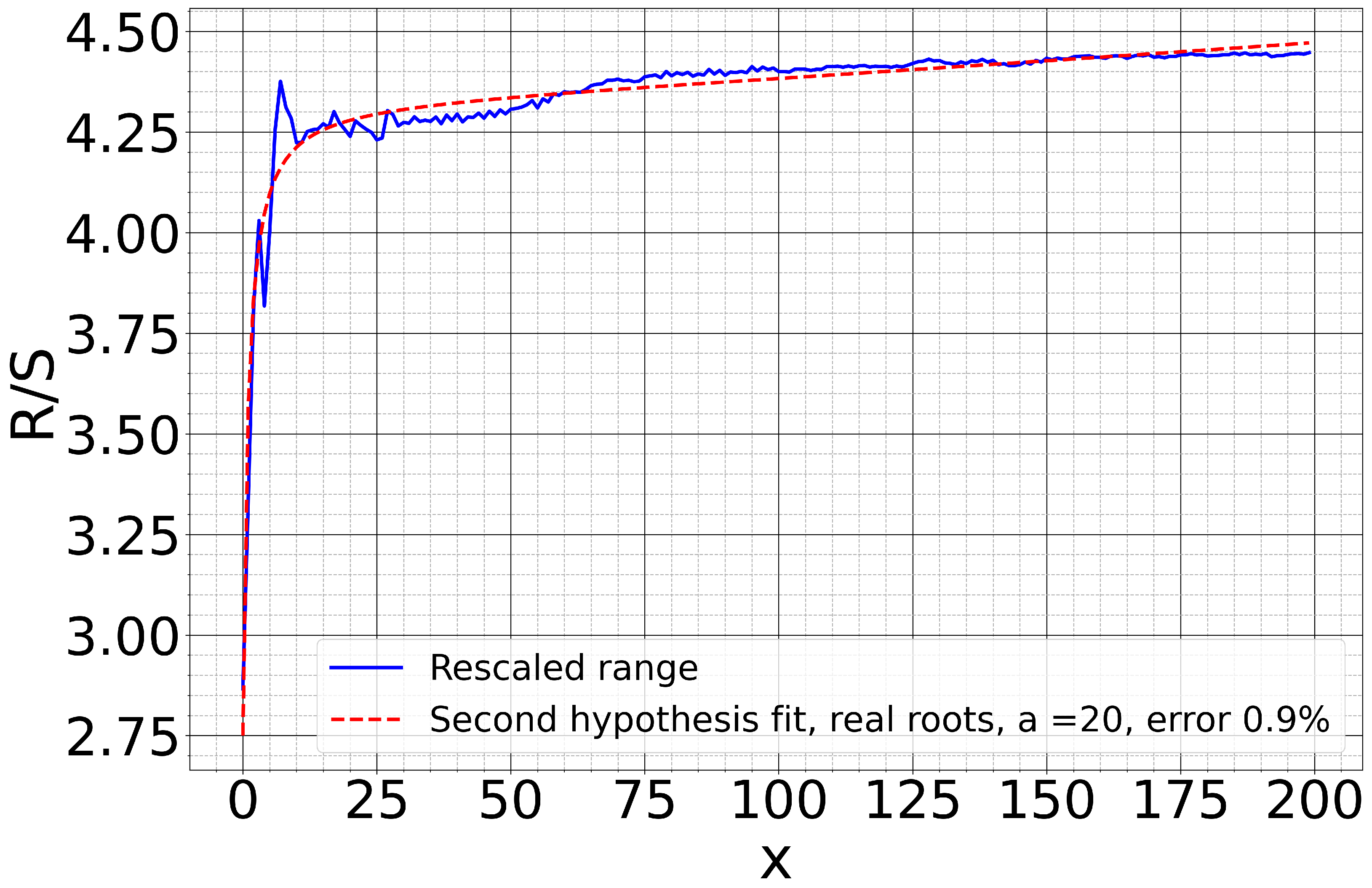
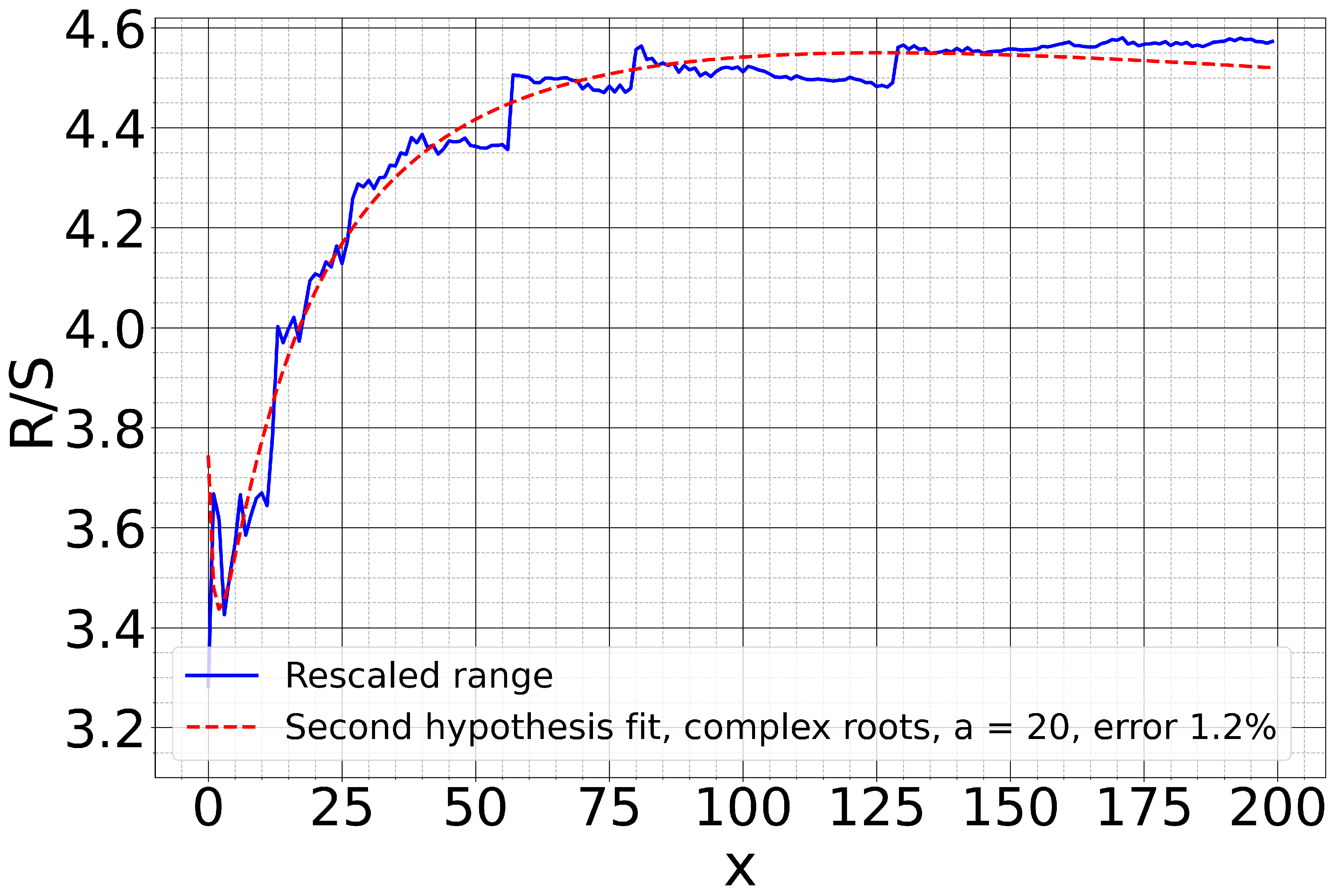
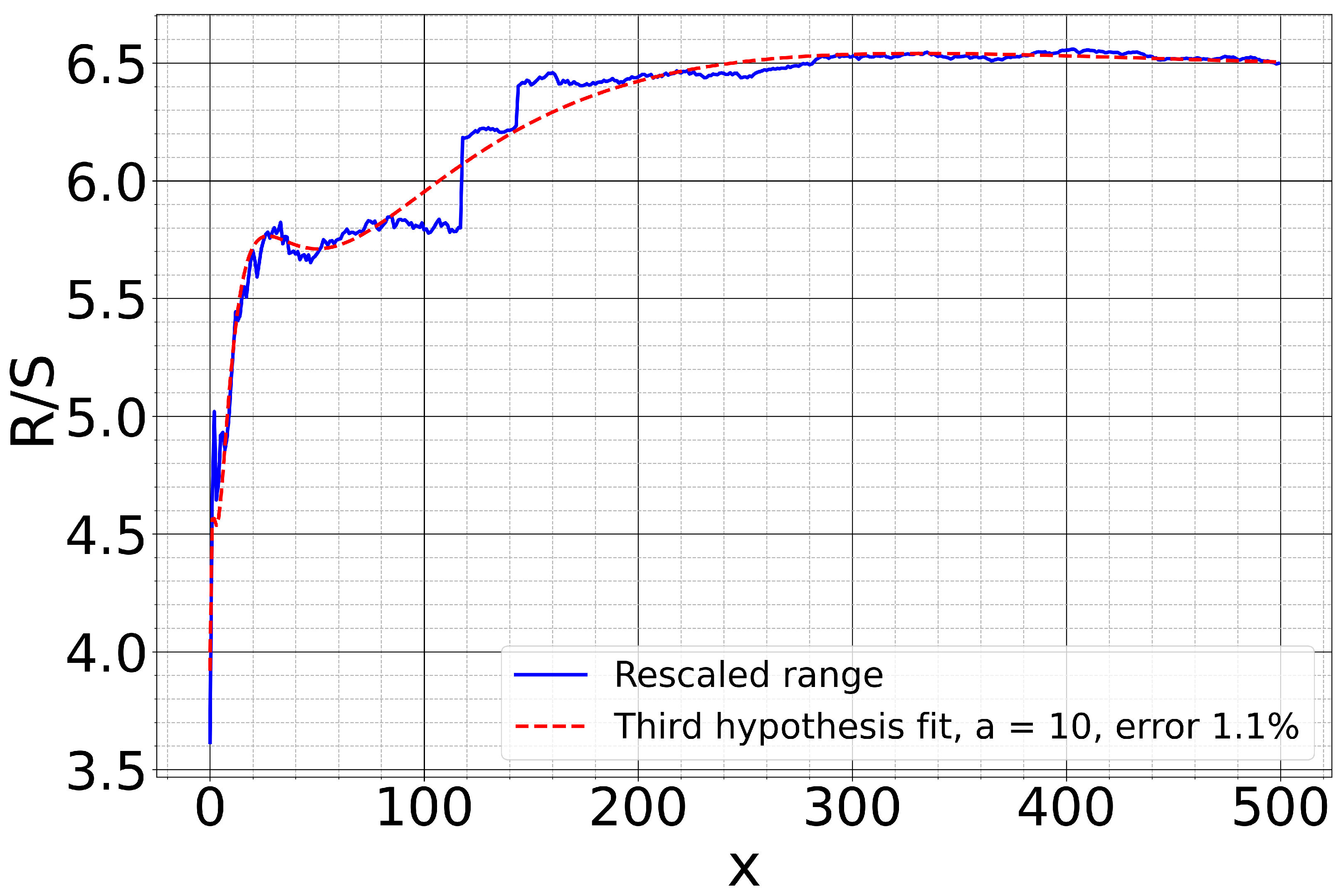
	Fit Error	H	A
mean	1.0%	−1.0	3.19
std	0.4%	0.1	0.02

,

Table 2. Third hypothesis statistics.

	Fit Error	${\mathit{B}}_2$	${\mathit{B}}_3$	Re(${\mathit{H}}_1$)	Im(${\mathit{H}}_1$)	${\mathit{H}}_3$
mean	2.0%	0.048	−0.05	−0.16	−0.04	−2.4
std	0.5%	0.5	0.59	0.25	0.4	0.5

and

Table 3. Second hypothesis statistics.

	Fit Error	${\mathit{B}}_0$	Re(${\mathit{H}}_{1,\mathit{compl}}$)	Im(${\mathit{H}}_{1,\mathit{compl}}$)	${\mathit{H}}_{1,\mathit{real}}$	${\mathit{H}}_{2,\mathit{real}}$
mean	1.0%	4.17	−0.05	0.55	0.59	−0.52
std	0.3%	0.4	0.07	0.15	0.43	0.38

present the key parameters corresponding to the hypotheses in (2)–(4) tested on the data described above. Some parameters have quite a large dispersion and cannot adequately represent properties of given TLSs. Such parameters are omitted in the tables; therefore, Table 1, Table 2 and Table 3 contain fewer fitting parameters than there are in Equations (2)–(4).

One peculiar feature of the second hypothesis is that Hurst-parameters $H_{1,2}$ may be not pure real, but complex conjugated numbers, and Figure 2 and Figure 3 illustrate such a case. For that reason, we provide statistics for both complex $H_{1,2,compl}$ and real $H_{1,2,real}$ parameters in Table 3. Although theoretically the same is correct for the third hypothesis, it turned out that two parameters $H_{1,2}$ are always complex-conjugated during the analysis of described data. Therefore, the statistics for real and imaginary part of $H_1$ is provided in Table 2.

The parameters B, (Hypothesis 1); $B_{1,2}$ (Hypothesis 2) and $B_1,A_{0,1,2,3}$ (Hypothesis 3) have random behavior and are not important. We emphasize that the hypothesis in (2) shows better results if the original TLS is limited (e.g., the phase of the signal). A limited signal has no sharp outliers, thus the $R\left(x\right)/S\left(x\right)$ curve is smooth without any sharp increases.

We stress that the first hypothesis, being the simplest one, fails to adequately fit the data for the second and third hypotheses. At the same time, the third hypothesis can describe data from every example presented. Since there is no explicit criterion for selection of the proper hypothesis, we choose the hypothesis by the value of the relative fitting error. However, the search for the criterion that can differentiate different types of noise merits further research.

4. Discussion

In this paper, we show how to transform TLS to the desired $R/S$ ratio. Furthermore, we propose the generalization of the well-known asymptotic Hurst law. The R/S ratio reflects the scaling properties of the complex system and can be applied as a reduced procedure to analyze various TLSs of different nature. To demonstrate the applicability of the method, we use it to analyze noise captured from radio devices and a microphone. In all cases, the relative fitting error does not exceed 2%. The fitting parameters in (2)–(4) can be used as quantitative parameters for further classification of the compared TLSs.

These new fitting parameters can also be used to estimate and compensate flicker noise in communication systems. Since similar algorithms based on the asymptotic Hurst law significantly improve the signal-to-noise ratio of the systems, we expect that the proposed method will ameliorate the results in this area. Furthermore, the proposed method is expected to become a more sophisticated tool in network traffic analysis, compared with the asymptotic Hurst law, which is currently widely used in this field. Such an approach may be useful in the radiometric identification task as well, when the transmitter devices are to be classified based on the difference of the received and the reference signal. The proposed generalized Hurst law may be used for classification of transmitters, as was done by Nigmatullin et al. [30]. The generalized Hurst law may yield more reliable results since it captures fractal properties of a TLS, which was difficult to do with the parameters proposed in [30]. The new set of parameters may also show good results in a task of weak signal detection.

From the theoretical point of view, the most interesting feature that follows from the analysis of data considered is related to the appearance of complex-conjugated power-law exponents. Up to now, we cannot provide a clear explanation from the physical point of view, but we think that these values can essentially change the analysis of the long-ranged temporal series and lead to a deeper understanding of the conventional Brownian motion [15]. These new relationships associated with the influence of the complex power-law exponents on the different types of random/complex motions merits further research. The examples shown in this paper definitely demonstrate their appearance in real data analysis and their possible corrections should be taken into account.