Abstract
One of the most challenging endeavors of contemporary research is to describe and analyze the dynamic behavior of time series arising from real-world systems. To address the need for analyzing long-range correlations and multifractal properties of multivariate time series, we generalize the multifractal detrended moving average algorithm (MFDMA) to the multivariate case and propose a multivariate MFDMA algorithm (MV-MFDMA). The validity and performance of the proposed algorithm are tested by conducting numerical simulations on synthetic multivariate monofractal and multifractal time series. The MV-MFDMA algorithm is then utilized to analyze raw, seasonally adjusted, and remainder components of five air pollutant time series. Results from all three cases reveal multifractal properties with persistent long-range correlations.
1. Introduction
Research of complex systems has become increasingly important in both natural and social sciences. Time series derived from complex real-world systems exhibit nonlinear behavior that cannot be characterized by linear statistical models. Namely, time series from financial, environmental, and many other fields often manifest long-term memory and frequent large fluctuations that cannot be adequately explained with normal-like distributions. Conventional econometric models such as ARMA, GARCH, and EGARCH fail to capture and accommodate these properties and the nature of such series. The scaling law mostly used to describe these types of time series is a power law with a scaling exponent that (at least) asymptotically describes the behavior of a quantity F as a function of a scale parameter s: [1]. The systems characterized by a scaling law typically represent fractals or multifractals, depending on whether they are described by one scaling exponent or by a multitude of scaling exponents [1,2].
Various methods have been developed to characterize the properties of fractals and multifractals. Detrended fluctuation analysis (DFA) is applied to time series data in various fields, but Peng et al. originally proposed it for identifying long-range dependence in DNA nucleotide sequences [3]. The DFA algorithm was extended to multifractal detrended fluctuation analysis (MFDFA) for describing the multifractal properties of time series [4]. Methods based on the moving average have also been developed. The first such method was introduced for estimating the Hurst exponent of self-affinity signals [5]. It was further extended to the detrending moving average (DMA) and the multifractal detrending moving average (MFDMA) by considering the second-order difference between the original time series and its moving average function [6]. The behavior of the multivariate time series has been widely studied [1,7,8,9,10,11,12]. The DFA and MFDFA have been recently extended to the multivariate cases (MVDFA and MV-MFDFA) to give insight into the multichannel data and auto-correlation behavior [1,12].
In this paper, inspired by Xiong and Shang [1] and Zhang et al. [12], we extend the method of MFDMA to a multivariate case (MV-MFDMA) to analyze the long-range correlations and multifractal properties of multivariate air pollutant time series data. A better understanding of the temporal and spatial variability of environmental time series is essential for modeling various phenomena. Algorithms that can handle multivariate time series have become exceedingly important, especially in dealing with environmental issues. Different environmental time series have been previously analyzed in the contexts of multifractality. For instance, Reference [13] used multifractal analysis on an air pollution index time series, while References [14,15] used six air pollutants for numerical experiments in their multifractal analysis. Fine particulate matter pollutants have been of interest for several research endeavors [16,17,18], while [19], for example, used a multifractal analysis on a time series from the European carbon futures markets. Multifractal analysis is often used for temperature analysis like [20] did for air temperature, or [21] for global methane concentrations and remotely-sensed temperature anomalies.
We chose data on air pollution as it directly impairs the environment, endangers entire ecosystems, causes biodiversity loses, and jeopardizes human health. Air pollution occurs when harmful or excessive amounts of gases, particles, and biological molecules are introduced into the atmosphere, whether they are of natural or anthropogenic origin. However, the consensus is that anthropogenic pollution is the main cause of most problems the environment faces today. Pollution is primarily caused by industrial activities, energy use, transport, and agricultural activities. Furthermore, some household activities, such as heating, can cause significant air pollution, although this is mostly relevant for developing and underdeveloped countries. Coordinated action and great willpower are needed to make positive changes because some pollutants, such as fine particulate matter and ground-level ozone continuously create significant health problems, while various emissions continue to damage the environment. Although air quality improvements are somewhat noticeable in recent years because of coordinated international actions and global, regional, and national policies, it is evident that a multidisciplinary approach is needed to advance this fundamentally important research area and create solutions to improve air quality.
Therefore, our paper has three objectives. We extend the MFDMA method to a multivariate case, suggest the MV-MFDMA algorithm, and then, conduct numerical experiments on multivariate processes to investigate the performance of the newly proposed MV-MFDMA. Finally, we apply the MV-MFDMA algorithm to explore the long-range correlations and multifractal properties of five air pollutant time series.
The remainder of the paper is organized as follows. We introduce the proposed MV-MFDMA algorithm in Section 2, while the validity of the MV-MFDMA algorithm is presented in Section 3. In Section 4, we outline the available data set and pre-processing analysis and provide the results obtained using air pollutant time series. Finally, the conclusions are drawn in Section 5.
2. Multivariate Multifractal Detrending Moving Average Analysis
In this section, we propose a multivariate multifractal detrended moving average algorithm (MV-MFDMA). Let , denote the p time series, where N is the number of observations in each time series. The newly constructed MV-MFDMA algorithm consists of the following steps.
- Step 1:
- Calculate cumulative sums of each time series :
- Step 2:
- Calculate the moving average function of each time series in a moving window of size n:where is the largest integer not larger than and is the smallest integer not smaller than . The parameter specifies the position of the moving window. In general, the moving average function includes data points in the past and data points in the future. Here, we consider three different values of parameter If , then the moving average function is calculated over all the past data points of the series, and hence, it refers to the backward moving average. For , the moving average function includes half past and half future data points in each window and refers to the central moving average. In the case of , the moving average function is calculated over all the future data points and refers to the forward moving average. For more details, see [6,22].
- Step 3:
- Calculate the series residue by subtracting the moving average function from :where t satisfies the criterion .
- Step 4:
- Divide the residue series into non-overlapping segments of equal length n. The segments are denoted by such that for with .
- Step 5:
- Calculate the fluctuation variance as a function of n for an arbitrary segment v:where and stands for the Euclidean norm.
- Step 6:
- Average over all local variances to obtain the order fluctuation function:where and If ,
- Step 7:
- Vary the values of segment size n to determine the power law relation between the function and the size scale n. If a time series exhibits multifractal properties, then for large values of n will follow a power law type of scaling relation, such as:where denotes the generalized Hurst exponent.
The generalized Hurst exponent can be attained by the slope of the log-log plot of versus n through the method of ordinary least squares. The scaling exponent when traces the scaling behavior of the segments with larger fluctuations. Similarly, it shows the scaling behavior of segments with small fluctuations for . Usually, the large fluctuations are identified by a smaller scaling exponent for multifractal series. For monofractal time series, is independent of q. If only short-range correlations or no correlations exist in the sequence, then the scaling exponent equals . In this case, the time series display a random walk behavior. However, if there is long-range power law correlation, then . Furthermore, if , the long-range auto-correlations are persistent, which indicates that an increase is likely to be followed by another increase. If , we have long-range auto-correlations with anti-persistent behavior [3,4]. In this case, an increase is likely to be followed by a decrease.
Such a defined generalized Hurst exponent is directly related to the multifractal scaling exponent : . The monofractal time series are characterized by a linear form for the multifractal scaling exponent. The multifractality of the time series can be characterized by the singularity spectrum of the Holder exponent . It is known that and . The singularity spectrum indicates the dimension of the subset of the series that is characterized by . The spectrum gives information about the relative dominance of various fractal exponents present in the series, while characterizes the strength of the singularity. The wider the spectrum, the richer the multifractality behavior.
Note that if , then the MV-MFDMA reduces to the standard MFDMA. On the other hand, if , the MV-MFDMA investigates the multifractal features and long-range correlation properties of the multivariate process of dimension i as a whole.
3. Numerical Experiments on Synthetic Data Sets
The validity of the proposed MV-MFDMA algorithm is investigated in this section by performing numerical simulations on synthetic multivariate time series data. Synthetic data are modeled by the autoregressive fractionally integrated moving-average process (ARFIMA) following the procedure in [12]. Let us recall that the long-range correlations in stochastic variables can be modeled as:
where follows a standard normal distribution, is a memory parameter related to the Hurst exponent , and , [12]. Then, the two-component ARFIMA process can be defined as:
where and follow a standard normal distribution , are the scaling parameters, and is a free parameter that controls the coupling strength between variables x and y [12]. If , then the variables x and y are fully decoupled and represent two separate ARFIMA processes. On the other hand, if W decreases from one to , then the correlations between variables x and y increase.
In the experiments, we considered multivariate monofractal time series, both independent and correlated. The length of each time series was . The results were averaged over 20 realizations of each type of test series.
3.1. Independent Multivariate Monofractal Series
We generated a trivariate uncorrelated monofractal time series with parameters corresponding to the scaling exponent using the ARFIMA model (9) and (10). These series were considered as uncorrelated since the initial data channels were realizations of mutually independent uncorrelated monofractal series [12].
Figure 1 displays the scaling exponents as a function of q and multifractal spectra obtained by applying the MV-MFDMA to trivariate uncorrelated monofractal series, for . As expected, regardless of , for trivariate uncorrelated monofractal series, the estimated scaling exponent equals . This result implies the monofractal properties of multivariate series and holds regardless of the parameter . The multifractal spectra confirms the validity of the algorithm.
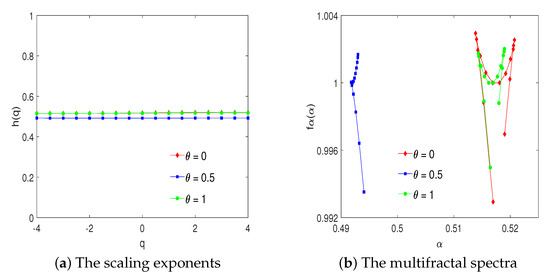
Figure 1.
Uncorrelated monofractal series.
Next, we simulated trivariate anti-correlated and correlated monofractal time series with the following scaling exponents: and ; see Figure 2. The results show that is independent of q and practicality equal to and , respectively. These results hold regardless of the chosen parameter .
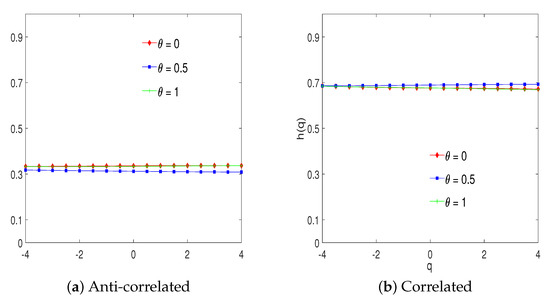
Figure 2.
Independent monofractal series: the scaling exponents.
3.2. Correlated Bivariate Monofractal Series
The MV-MFDMA method was also applied and tested on the correlated bivariate time series simulated by the two-component ARFIMA model following the procedure in [12]. The following values of a free parameter controlling the coupling strength between time series were considered: , while the parameters of the model corresponded to scaling coefficients . Figure 3 shows the average MV-MFDMA results of correlated bivariate time series with different correlation levels for . If we fix the coupling parameter W, the scaling exponents do not depend on the value of q and are nearly equal to the value of . This result is in harmony with the scaling exponent of individual univariate series. Moreover, even if we change the coupling parameter W, the scaling exponents remain the same for different values of q.
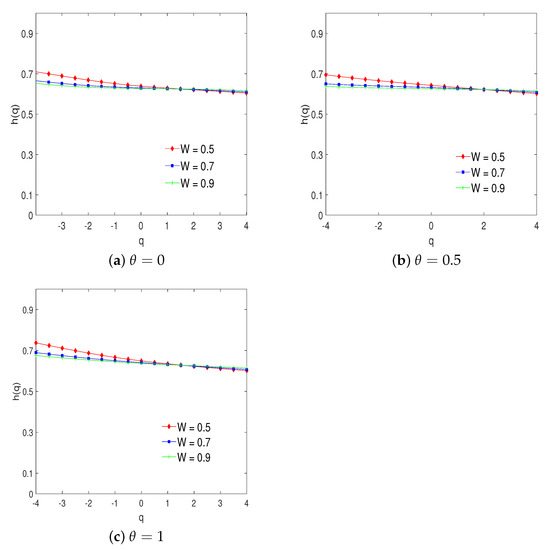
Figure 3.
Correlated monofractal series: the scaling exponents.
3.3. Multivariate Multifractal Series
Finally, we applied the MV-MFDMA to multifractal time series simulated by the following binomial multifractal model:
where and is the number of the digits equal to one in the binary representation of index k [12]. More precisely, we simulated trivariate time series according to (11) and chose , and , respectively. The proposed algorithm was applied to the generated series, and the obtained results are shown in Figure 4 in terms of scaling exponent and multifractal spectra for . We also present the same results for individual time series.
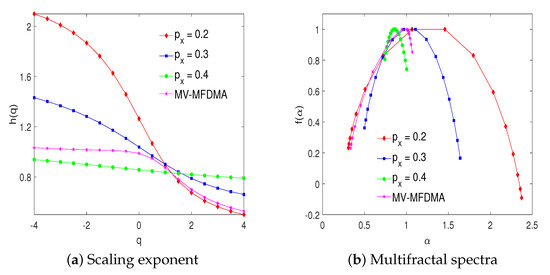
Figure 4.
Multifractal series.
The individual univariate time series manifest the expected multifractal characteristics, while it can be observed that the scaling exponents of the considered trivariate multifractal series obtained by the new MV-MFDMA vary among the scaling exponents of individual univariate series. For negative values of q, the scaling exponents of the trivariate multifractal series are most harmonized to the scaling exponents of a univariate series for . On the other hand, for positive values of q, it is most adjusted to the scaling exponents of a univariate series for . This phenomenon was also revealed in [12]. The large fluctuations of univariate series with have a major impact on the large fluctuation of multivariate series. Similarly, the major impact on the small fluctuations of multivariate series originates from the small fluctuations of univariate series with .
Based on the presented results, we can observe that the MV-MFDMA algorithm preserves the properties of the univariate MFDMA. Namely, it is known that algorithms based on the multifractal detrending moving average are sensitive to the sample size, the selection of the scaling range, the choice of q-orders, and the position of the moving window [23]. These algorithms require a larger sample size, i.e., a larger number of observations are needed to obtain a more accurate estimation of the multifractal spectrum. Then, the accuracy is also influenced by the selection of the appropriate scaling range. Equal spacing between scales is suggested, where the scaling range varies from 10 to [23]. The choice of the q-orders should include both positive and negative values. It is evident from the presented results that the algorithm depends on the position of the moving window. According to [24], the lowest accuracy is obtained when , while and provide higher accuracy.
A comparison of the proposed MV-MFDMA algorithm with other algorithms for detecting multifractal properties is given in Table 1.

Table 1.
Comparison of the algorithms for detecting multifractality.
4. Air Pollutant Time Series via MV-MFDMA
In this section, we present the data and analyze the multifractal properties of multivariate air pollutant time series. We performed the MV-MFDMA algorithm on raw series, seasonally adjusted series, and remainder components and then compared the results.
4.1. Data
Data for this paper were acquired from [25]. For the purposes of testing the MV-MFDMA, we used datasets of five air pollutants presented in Table 2. To obtain uniform series in terms of length, values were used only on days when all five variables were measured.

Table 2.
Variables.
Table 3 provides the descriptive statistics of the air pollutant time series. Positive values of skewness indicate that the distributions of all air pollutants are positively skewed. Kurtosis is greater than three for all air pollutants, which indicates that the homogeneity of the distribution in all cases is leptokurtic in relation to the normal distribution. The Jarque–Bera test rejects the null hypothesis of normality in air pollutants’ series distribution, which is further corroborated by the fact that kurtosis is larger than three, and there is no zero skewness in any of the five cases. The statistics of the augmented Dickey–Fuller (ADF) unit root test based on both the Akaike (AIC) and Schwarz information criterion (SIC) reject the null hypothesis of a unit root at the 1% significance level. Additionally, the Philips–Perron (PP) test also rejects the null hypothesis of a unit root at the same significance level. Both the ADF and PP tests were done for both the trend and intercept and just the intercept cases. The t-statistics for all six cases of unit root tests are also presented in Table 3 and indicate that the air pollutants series are stationary.

Table 3.
Descriptive statistics: raw data series.
The state of California was chosen because it is usually singled out as a leader in air pollution among other U.S. states. Even though all air pollutants are high in California, the O3 levels particularly stand out. Since seasonal trends can sometimes influence the multifractal behavior of time series, it is preferable to perform seasonal decomposition; see for example [15,26,27]. It is interesting to note that a common approach for analyzing trendless fluctuations is absent. Nigmatullin and Vorobev [28] stated that in most cases, authors use traditional methods, such as the Fourier method, the wavelet method, Yulmenteyev’s method, and Timashev’s method or some additional processing algorithms that are also based on conventional methods containing some model assumptions and treatment methods associated with continuous mathematics. Nigmatullin, Lino, and Maione [29] pointed out that these sets of methods solve some specific tasks, but cannot be viewed as universal. To address this gap, a universal “platform” for treating various types of different trendless sequences has been proposed (see [28,29] for more details). For the purposes of this paper, we adjusted the considered time series by performing seasonal and trend decomposition using LOESS (STL) decomposition [30]. Through this algorithm, each time series is additively decomposed into deterministic trends, seasonal components, and stochastic remainder components. Removing seasonal components from the raw time series does not significantly influence the descriptive statistics results. All the descriptive statistics and unit root tests conclusions from the raw data are valid for the seasonally adjusted data as well (see Appendix A). Figure 5 shows that the seasonal components of all time series are characterized by the annual oscillation. Figure 5 also demonstrates, among others, the evolution trend of five air pollutant concentration series. The PM2.5 and SO2 series are more prone to extreme spikes, whereas NO2, CO, and O3 concentrations have somewhat different trends in winter and summer, indicating a seasonal inclination. On the other hand, the trend components are characterized by a very small range of variability and do not show a large temporal evolution. The range of variability is the largest for series NO2 and PM2.5. The remainder components of all time series do not display discernible patterns, and there are small fluctuations around zero.
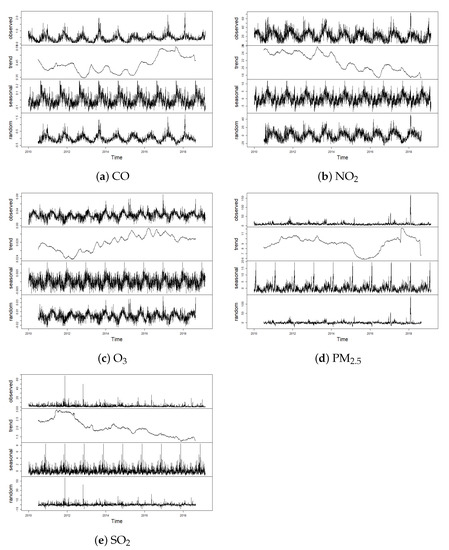
Figure 5.
STL decomposition of air pollutant time series.
4.2. Results
The MV-MFDMA presented in Section 2 was applied to the above-mentioned raw and seasonally adjusted air pollutant time series obtained upon removal of the seasonal components, as well as on the remainder components of the series. Applying multifractal analysis on the remainder components ensures the identification of the dynamic characteristics of air pollutants’ inner fluctuations and enhances the robustness of the results. We set the range of time scale n to be , where N is the length of each time series.
Figure 6 illustrates the behavior of the MV-MFDMA fluctuation function versus time in the logarithmic scale for all three case: raw, seasonally adjusted, and remainder. The plots are presented for and fixed . All curves are approximately linear under large scales, indicating the power law behavior and the presence of multifractality. The MV-MFDMA fluctuation functions have quite similar behavior in all three cases, while we can note that fluctuations are the smallest for the remainder components. Fluctuations are observed regardless of the q values for small values. That is, the results show crossover time scales, i.e., different scaling laws and scaling exponents for time scales (where for raw and for the other two cases). When , we find that the MV-MFDMA fluctuation functions nicely respect the scaling relation, i.e., scale well with the scale size. Additionally, although not displayed, the MV-MFDMA is tested for . The results confirm the power law behavior and demonstrate the absence of large fluctuations.
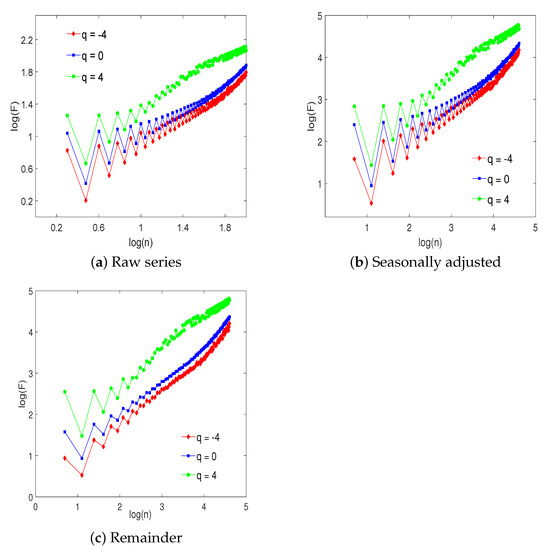
Figure 6.
Power law dependence of the fluctuation functions with respect to the scale (log-log plots).
Figure 7 shows the values of the generalized Hurst exponents versus q, where the variation of q belongs to the interval for raw, seasonally adjusted, and remainder series. In all cases for , we observe the dependence of MV-MFDMA on q. The MV-MFDMA monotonically decreases when the value of q increases. This result implies the multifractality of the examined time series. It is interesting to note that raw and seasonally adjusted series display almost the same behavior of the generalized Hurst exponents for all values of parameter . On the contrary, the values of the generalized Hurst exponents for the remainder series are above for , which indicates a strong long-term persistence. However, in the cases of the forward and backward moving average, the values of are lower.
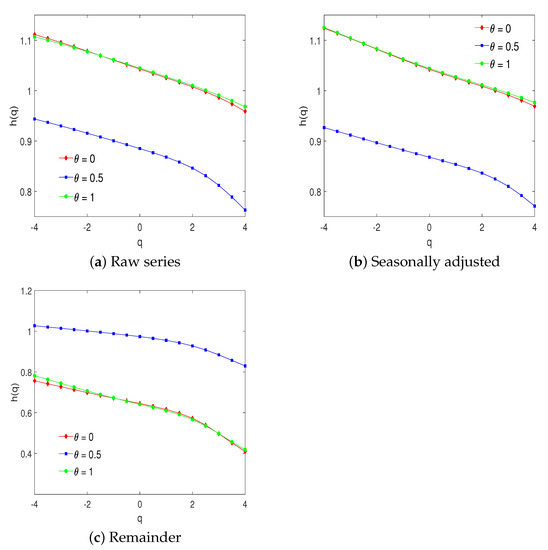
Figure 7.
Generalized Hurst exponents.
Figure 8 displays the multifractal spectra of via the Legendre transform. The shapes of the inverted U parabola of the spectra confirm the fact of the multifractality in the time series. The smallest range of the multifractality is observed when . The results hold for all raw, seasonally adjusted, and remainder series.
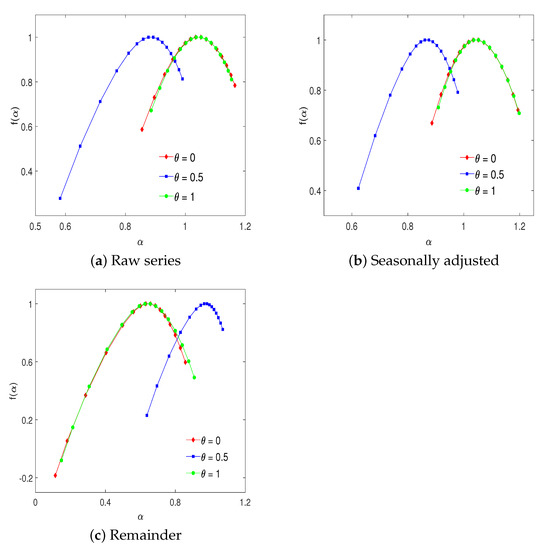
Figure 8.
The multifractal spectra.
With the aim of quantifying the degree of the multifractality of the multivariate system, we use the following measures (12) and (13) [12]:
The larger the measures of and , the richer and stronger the degree of multifractality of the time series is. Table 4, Table 5 and Table 6 present the scaling exponent and the multifractality degrees and for the individual and multivariate air pollutants for all levels and for raw, seasonally adjusted, and remainder series, respectively.

Table 4.
The scaling exponent , multifractality degrees , and : raw series.

Table 5.
The scaling exponent , multifractality degrees , and : seasonally adjusted series.

Table 6.
The scaling exponent , multifractality degrees , and : remainder component.
Raw and seasonally adjusted series have similar characteristics of multifractal parameters. For and , the values of are approximately around one, while in the case of , the values are a bit lower, namely and for raw and seasonally adjusted series, respectively. This holds for both individual and multivariate time series. The results imply that both individual and multivariate series show persistent long-range correlation. Analogous to , noise can be deducted in the case of the scaling exponent of multivariate time series less than one. In the case of the remainder components, the fluctuations are also characterized by a long-term persistence. However, the values of suggest that the remainder components are characterized by a weak persistence suggesting stable trends in the next period. In summary, multivariate series of five air pollutants show consistent, positive autocorrelation behavior. In all three cases, an interesting fact is that all values of and are significantly larger than zero. On the other hand, the values for multivariate air pollutants range around those values for individual time series and are lower than the maximum values of the individuals in each case. Both the and values in the remainder components are higher than the values of both raw and seasonally adjusted series. This finding reveals that the considered air pollutants can be characterized by multifractality behavior. Furthermore, since the relationship always exists among the individuals, it possibly makes the multifractal level weaker. As a result, the and values for multivariate time series are smaller than the maximum and average of the and values of individuals.
5. Conclusions
The multivariate approach and analysis may have a key role in cases when a high degree of uncertainty and coupling underlying dynamical mechanics is present. Hence, in this paper, we introduced the multivariate multifractal detrended moving average analysis (MV-MFDMA) as a multivariate generalization of the MFDMA method. The proposed method provides a way to analyze and investigate fractal dynamics information in multivariate time series data sets generated by complex systems. The validity of the proposed method was investigated by conducting numerical simulations on synthetic monofractal and multifractal time series. The correlation properties of multivariate monofractal time series are in line with the univariate case, and the fractal behavior of correlated bivariate time series is independent of its correlation level. In the case of the multivariate multifractal series, the multivariate system exhibits multifractal properties. The corresponding multifractal degree decreases with the decreasing of the multifractal degree of individual series. According to our simulation results, the MV-MFDMA represents a reliable technique for measuring the long-term correlations of non-stationary multivariate time series.
The MV-MFDMA was also utilized to investigate the multifractal properties of air pollutant time series where the individual air pollutants were considered as different variables from the same system. We analyzed raw and seasonally adjusted time series of air pollutants obtained upon removing the annual oscillations. We found that air pollutants exhibited multifractal auto-correlation behavior, even after removing the seasonal pattern. In both cases, the air pollutant time series data exhibited multifractal properties, with persistent long-range correlations. In order to capture the dynamic characteristics of the inner fluctuations of the air pollutants, we also applied the algorithm to the stochastic remainder components of the time series. The results confirmed that multivariate time series of air pollutants possessed multifractal properties and exhibited long-term persistence such that an increase (decrease) in the previous period will be followed by an increase (decrease) in the next period.
The findings of this paper provide an elevated understanding of the evolutionary activity and temporal links of five air pollutants in the state of California. In general, it is necessary to achieve a better comprehension of the associations between different air pollution time series to manage the environmental air quality based on evidence. Researchers from any scientific field that operate with multivariate frequent time series are encouraged to apply the proposed algorithm since it provides an improvement in detecting long-range correlations and multifractal properties of multichannel data. However, the proposed algorithm has certain limitations. It applies only to frequent and large-dimensional multivariate time series with an equal length N. Moreover, when applying the proposed algorithm, it is suggested to use an equal spacing between scales, where the scaling range varies from 10 to , while the q-orders should include both positive and negative values. Finally, in some cases, seasonality can influence the selected time series, so if that is the case, the series should be firstly depersonalized before applying the algorithm. Future research papers can use the proposed MV-MFDMA algorithm, not only the environmental quality ones, but on the widest range of different real-world complex system time series, for example on financial, economic, meteorological, and health care time series. Therefore, directions for future research should go towards studying new time series when a better comprehension of their interconnections is necessary.
Author Contributions
Conceptualization, M.K. and P.M.; methodology M.K.; software, M.D.; validation, M.D.; writing, all; visualization, M.D.; supervision, J.M. All authors read and agreed to the published version of the manuscript.
Funding
This research has been funded by the Ministry of Education, Science and Technological Development of the Republic of Serbia.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Collected data are available from the authors.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; nor in the decision to publish the results.
Appendix A
Table A1 presents descriptive statistics of seasonally adjusted series.

Table A1.
Descriptive statistics: seasonally adjusted series.
Table A1.
Descriptive statistics: seasonally adjusted series.
| CO | NO2 | O3 | PM2.5 | SO2 | ||
|---|---|---|---|---|---|---|
| Mean | 0.4381 | 21.4366 | 0.0279 | 8.8198 | 1.9964 | |
| Std. Dev. | 0.2422 | 10.7698 | 0.0088 | 7.4037 | 2.6018 | |
| Skewness | 1.2054 | 0.3761 | 0.1193 | 6.5486 | 6.0940 | |
| Kurtosis | 6.0841 | 3.0578 | 3.7585 | 96.2279 | 102.8836 | |
| Jarque–Bera | 2131.856 * | 79.1695 * | 87.9690 * | 1,233,060 * | 1,408,679 * | |
| Observations | 3339 | 3339 | 3339 | 3339 | 3339 | |
| ADF (AIC) | intercept | −4.3080 * | −4.6241 * | −6.5685 * | −12.3825 * | −7.2438 * |
| trend and intercept | −4.4298 * | −4.7864 * | −6.5767 * | −12.3867 * | −8.5387 * | |
| ADF (SIC) | intercept | −5.8546 * | −5.7474 * | −7.9224 * | −16.3571 * | −10.2605 * |
| trend and intercept | −5.9854 * | −5.9493 * | −7.9653 * | 16.3589 * | −11.4403 * | |
| PP | intercept | −26.7990 * | −33.2027 * | −39.6205 * | −19.1607 * | −51.9978 * |
| trend and intercept | −26.9846 * | −34.1516 * | −39.8951 * | −19.1657 * | −49.5006 * |
Note: ADF—augmented Dickey–Fuller unit root test; PP—Philips–Perron unit root test; AIC—Akaike information criterion; SIC—Schwarz information criterion; *—stat. sig. < 0.01.
References
- Xiong, H.; Shang, P. Detrended fluctuation analysis of multivariate time series. Commun. Nonlinear Sci. 2017, 42, 12–21. [Google Scholar] [CrossRef]
- Ihlen, E.A.F. Introduction to multifractal detrended fluctuation analysis in Matlab. Front. Physiol. 2012, 3, 141. [Google Scholar] [CrossRef]
- Peng, C.K.; Buldyrev, S.V.; Havlin, S.; Simons, M.; Stanley, H.E.; Goldberger, A.L. Mosaic organization of DNA nucleotides. Phys. Rev. E 1994, 49, 1685–1689. [Google Scholar] [CrossRef] [PubMed]
- Kantelhardt, J.W.; Zschiegner, S.A.; Koscielny-Bunde, E.; Havlin, S.; Bunde, A.; Stanley, H.E. Multifractal detrended fluctuation analysis of nonstationary time series. Physica A 2002, 316, 87–114. [Google Scholar] [CrossRef]
- Vandewalle, N.; Ausloos, M. Crossing of two mobile averages: A method for measuring the roughness exponent. Phys. Rev. E 1998, 58, 6832–6834. [Google Scholar] [CrossRef]
- Gu, G.-F.; Zhou, W.-X. Detrending moving average algorithm for multifractals. Phys. Rev. E 2010, 82, 011136. [Google Scholar] [CrossRef] [PubMed]
- Flores-Marquez, E.L.; Ramírez-Rojas, A.; Telesca, L. Multifractal detrended fluctuation analysis of earthquake magnitude series of Mexican South Pacific Region. Appl. Math. Comput. 2015, 265, 1106–1114. [Google Scholar] [CrossRef]
- Wang, Y.; Wu, C. Futures Markets: New Evidence from Multifractal Detrending Moving Average Analysis. Comput. Econ. 2013, 42, 393–414. [Google Scholar] [CrossRef]
- Mali, P. Multifractal detrended moving average analysis of global temperature records. J. Stat. Mech. Theory Exp. 2016, 2016, 013201. [Google Scholar] [CrossRef][Green Version]
- Ahmed, M.U.; Mandic, D.P. Multivariate multi-scale entropy: A tool for complexity analysis of multichannel data. Phys. Rev. E 2011, 84, 061918. [Google Scholar] [CrossRef]
- Cao, L.; Mees, A.; Judd, K. Dynamics from multivariate time series. Physica D 1998, 121, 75–88. [Google Scholar] [CrossRef]
- Zhang, X.; Zeng, M.; Meng, Q. Multivariate multifractal detrended fluctuation analysis of 3D wind field signals. Physica A 2018, 490, 513–523. [Google Scholar] [CrossRef]
- Manimaran, P.; Narayana, A.C. Multifractal detrended cross-correlation analysis on air pollutants of University of Hyderabad Campus, India. Physica A 2018, 502, 228–235. [Google Scholar] [CrossRef]
- Fan, Q.; Liu, S.; Wang, K. Multiscale multifractal detrended fluctuation analysis of multivariate time series. Physica A 2019, 532, 121864. [Google Scholar] [CrossRef]
- Wang, F.; Fan, Q. Coupling correlation detrended analysis for multiple nonstationary series. Commun. Nonlinear Sci. 2021, 94, 105579. [Google Scholar] [CrossRef]
- Zhang, C.; Ni, Z.; Ni, L.; Li, J.; Zhou, L. Asymmetric multifractal detrending moving average analysis in time series of PM2.5 concentration. Physica A 2016, 457, 322–330. [Google Scholar] [CrossRef]
- Zhang, C.; Wang, X.; Chen, S.; Zou, L.; Zhang, X.; Tang, C. A study on daily PM2.5 concentrations in Hong Kong using the EMD-based MFDFA method. Physica A 2019, 530, 121182. [Google Scholar] [CrossRef]
- Zhang, C.; Wang, X.; Chen, S.; Zou, L.; Tang, C. Coupling detrended fluctuation analysis of the relationship between PM2.5 concentration and weather elements. Physica A 2019, 531, 121757. [Google Scholar] [CrossRef]
- Zou, S.; Zhang, T. Multifractal detrended cross-correlation analysis of the relation between price and volume in European carbon futures markets. Physica A 2020, 537, 122310. [Google Scholar] [CrossRef]
- Da Silva, H.S.; Silva, J.R.S.; Stosic, T. Multifractal analysis of air temperature in Brazil. Physica A 2020, 549, 124333. [Google Scholar] [CrossRef]
- Tzanis, C.G.; Koutsogiannis, I.; Philippopoulos, K.; Kalamaras, N. Multifractal detrended cross-correlation analysis of global methane and temperature. Remote Sens. 2020, 12, 557. [Google Scholar] [CrossRef]
- Wang, Y.; Wu, C.; Pan, Z. Multifractal detrending moving average analysis on the US Dollar exchange rates. Physica A 2011, 390, 3512–3523. [Google Scholar] [CrossRef]
- Xi, C.P.; Zhang, S.-N.; Xiong, G.; Zhao, H.-C. A comparative study of multifractal detrended fluctuation analysis and multifractal detrended moving average algorithm to estimate the multifractal spectrum. Acta Phys. Sin. 2015, 64, 136403. [Google Scholar]
- Lai, S.; Wan, L.; Zeng, Z. Comparative Study of Sliding Window Multifractal Detrended Fluctuation Analysis and Multifractal Moving Average Algorithm. J. Phys. Conf. Ser. 2019, 1345, 042086. [Google Scholar] [CrossRef]
- United States Environmental Protection Agency: Outdoor Air Quality Data. Available online: https://www.epa.gov/outdoor-air-quality-data/download-daily-data (accessed on 15 August 2020).
- Kalamaras, N.; Tzanis, C.G.; Deligiorgi, D.; Philippopoulos, K.; Koutsogiannis, I. Distribution of air temperature multifractal characteristics over Greece. Atmosphere 2019, 10, 45. [Google Scholar] [CrossRef]
- Krzyszczak, J.; Baranowski, P.; Zubik, M.; Hoffmann, H. Temporal scale influence on multifractal properties of agro-meteorological time series. Agric. For. Meteorol. 2017, 239, 223–235. [Google Scholar] [CrossRef]
- Nigmatullin, R.; Vorobev, A. The “Universal” Set of Quantitative Parameters for Reading of the Trendless Sequences. Fluct. Noise Lett. 2019, 18, 1950023. [Google Scholar] [CrossRef]
- Nigmatullin, R.; Lino, P.; Maione, G. Reduction of Trendless Sequences of Data by Universal Parameters. In New Digital Signal Processing Methods; Springer: Cham, Switzerland, 2020; pp. 409–429. [Google Scholar]
- Cleveland, R.B.; Cleveland, W.S.; McRae, J.E.; Terpenning, I. STL: A seasonal-trend decomposition procedure based on loess. J. Off. Stat. 1990, 6, 3–73. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).