Abstract
The torque density and efficiency of synchronous reluctance machines (SynRMs) are greatly affected by the geometry of the rotor. Hence, an optimal design of the SynRM rotor geometry is highly recommended to achieve optimal performance (i.e., torque density, efficiency, and power factor). This paper studies the impact of considering the current angle as a variable during the optimization process on the resulting optimal geometry of the SynRM rotor. Various cases are analyzed and compared for different ranges of current angles during the optimization process. The analysis is carried out using finite element magnetic simulation. The obtained optimal geometry is prototyped for validation purposes. It is observed that when considering the effect of the current angle during the optimization process, the output power of the optimal geometry is about 3.32% higher than that of a fixed current angle case. In addition, during the optimization process, the case which considers the current angle as a variable has reached the optimal rotor geometry faster than that of a fixed current angle case. Moreover, it is observed that for a fixed current angle case, the torque ripple is affected by the selected value of the current angle. The torque ripple is greatly decreased by about 34.20% with a current angle of 45° compared to a current angle of 56.50°, which was introduced in previous literature.
1. Introduction
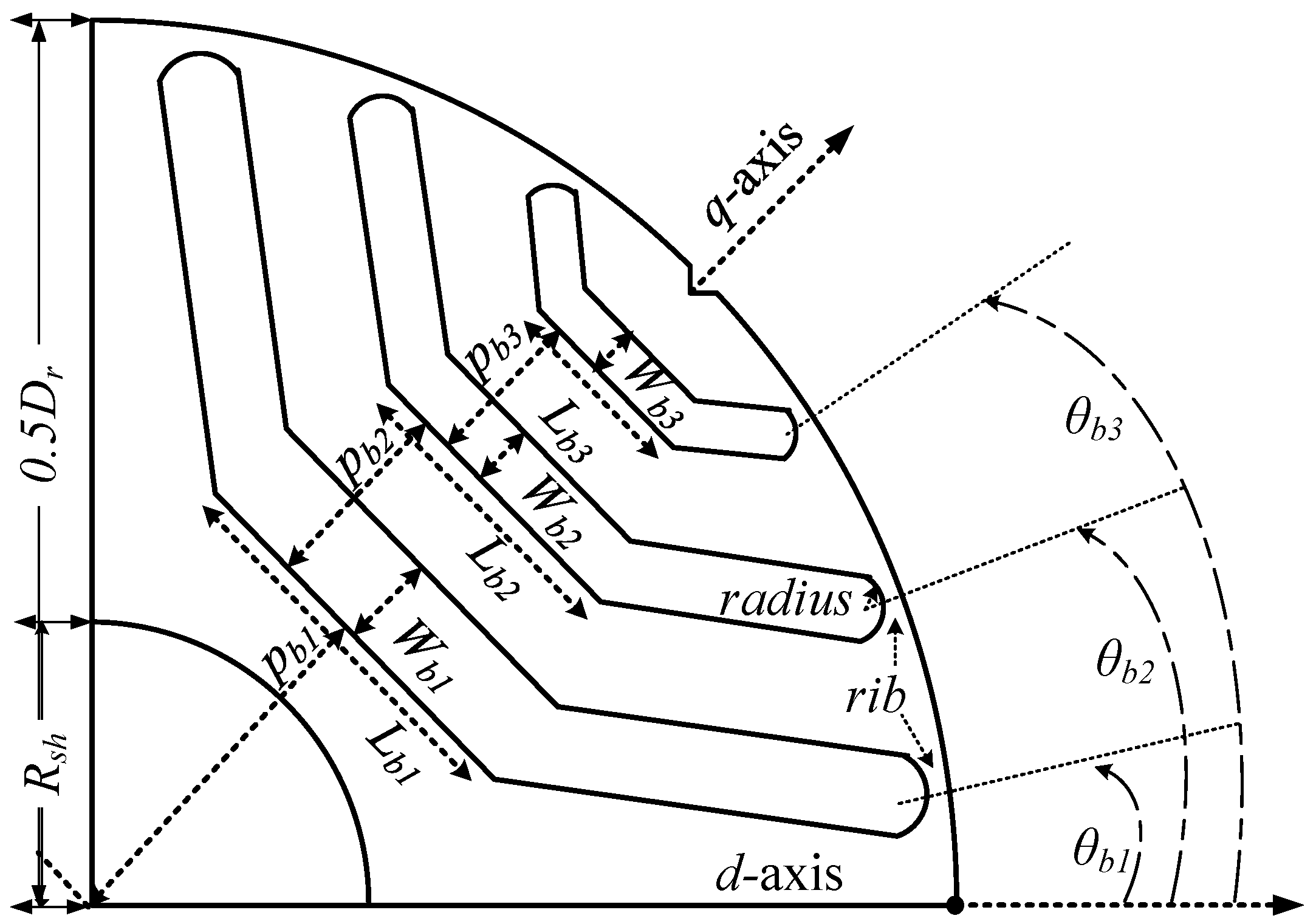
Recently, interest in synchronous reluctance machines (SynRMs) has increased remarkably thanks to their advantages compared to other types of electrical machines [1,2,3,4,5]. They offer a good torque density, a high efficiency, and a wide range of operating speeds [6]. In addition to their simple and robust structure, they have no windings, cages, and permanent magnets in their rotor, resulting in very low rotor losses and hence good thermal management [2]. These advantages make SynRMs a good competitor compared to the other electric machines in several electric drive systems in different industrial applications such as hospitals and aerospace [7]. It is evident through the literature that the performance of SynRMs (torque ripple, average torque, efficiency, and power factor) greatly depends on the saliency ratio (the ratio between the direct and quadrature axis inductances) [8]. This ratio is a function of several parameters of the machine design such as the winding, magnetic material, and rotor flux-barriers [9,10,11]. Starting from the standard stator design of the induction machine, the rotor flux barrier parameters are key elements in the performance of the SynRM. There are several parameters in the rotor as sketched in Figure 1. Therefore, it is evident that an optimization process is necessary to optimally select the parameters of the SynRM rotor.
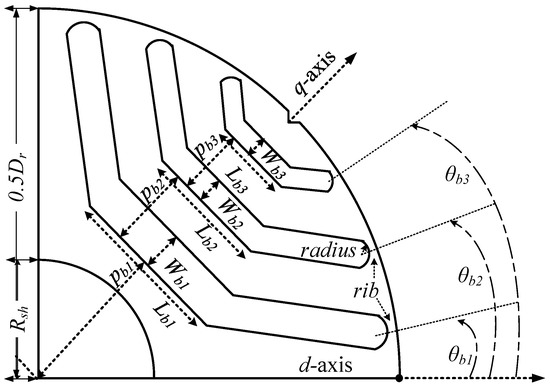
Figure 1.
Rotor geometry of one pole of synchronous reluctance machines (SynRM).
Through literature, several research papers about the optimization of SynRMs can be found [12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29]. Various optimization schemes have been reported and applied to SynRM design. For example, in [12], the rotor of the SynRM was optimized using a multi-objective differential evolution algorithm for high-speed applications focusing on selecting the barrier angles and the magnetic insulation ratio. The other geometrical parameters of the rotor were derived from these two parameters (the barrier angles and the magnetic insulation ratio). In [13], the optimal number of flux barriers and rotor poles of the SynRM were optimally selected by applying a weighted-factor using a multi-objective optimization technique. A circular rotor shape was used in [14] to maximize the torque and to minimize the torque ripple of the SynRM using a multi-objective genetic algorithm. In this design, a circular rotor was adopted in order to minimize the number of parameters and to get a time-efficient optimization process. Three different geometries for rotor flux barriers (one rotor has a circular flux barrier and the other two rotors use a rectangular flux barrier) were studied and compared in [15]. The design process uses the same optimization algorithm proposed in [14]. It was shown that the rectangular flux barrier has fewer structural challenges and lower inertia at high speed. In addition, it is preferred especially for machines with inserted permanent magnet (PM inside the flux-barriers. In [16], an alternative technique for the development of asymmetric flux barriers with rotor skewing is proposed in combination with design optimization to enhance average torque and reduce torque ripple. Although the torque ripple in this method is below 3%, the number of optimization variables in this method is relatively high between 29 and 37. This results in a slower and complicated optimization process. In [17], the rotor of the SynRM was optimized using three different popular optimization algorithms (simulated annealing, differential evolution, and genetic algorithm) to minimize the torque ripple and maximize the torque per Joule loss ratio. The differential evolution algorithm has shown the best result in terms of repeatability of the results and convergence time. It was demonstrated in [18,19,20,21] that the rotors with skewing techniques have reduced torque ripple significantly. In [22], the rotor of the SynRM was optimized to maximize the saliency ratio and minimize the thickness of the iron ribs. The rotor was made ribless in [23] to obtain an improved power factor, torque, and efficiency.
In [24], a generalized formula was proposed to select the widths and angles of the flux-barriers considering additional factors such as stator and rotor slot opening and number of slots. However, the torque ripple is still high. Furthermore, a preliminary design for the flux-barrier widths was introduced in [25] without considering the influence of the different number of stator slots. The effect of the number of stator slots was considered in [26] and the torque ripple was reduced from 23.38% to 12.3%. All the previous studies about the rotor design of the SynRM did not consider the current angle as a design variable during the design and optimization procedures. The current angle was fixed based on a rule of thumb or primary simulation i.e., in the range of 45° to 60° as in [26]. In [27], a simultaneous structural and magnetic topology optimization technique was developed for the rotor of the SynRM using solid isotropic with material penalization. The total structural compliance, torque ripple, and the average torque were simultaneously considered in this method. In [28], a new technique was proposed to design the rotor of the SynRM. A symmetrical rotor geometry with fluid shaped barriers was used in this optimization method. The optimal design in this method was chosen using the communication between MATLAB and Flux 2D. In [29], a line start SynRM was optimized using an optimization topology that uses the normalized Gaussian network. The computational time was reduced in this method as it separates out unpromising geometries. The effect of the current angle on the final optimal geometry of the SynRM has not been investigated before as far as we know.
This paper studies the effect of considering the current angle during the optimization process on the final optimal geometry of the rotor of the SynRM. Different cases are analyzed and compared for different ranges of current angles during the optimization process. This way, in some cases, the saturation level in the machine is enforced during the optimization process by varying the current angle range. Finite element magnetic simulation is carried out and compared for the optimal geometries. Finally, experimental results are conducted to validate the simulation results.
2. Design Optimization of SynRMs
2.1. Hybrid PSOGWO Technique
In this paper, the hybrid particle swarm optimizer and grey wolf optimizer (PSOGWO) algorithm was used to determine the best parameters in order to obtain the optimal rotor design of the SynRM. The following paragraphs briefly describe the core idea and the updating process of the PSO, GWO, and hybrid PSOGWO.
PSO was originally proposed by Kennedy and Eberhart to simulate the social behavior of a flock of birds [30,31]. In order to determine the best solution, every particle, representing a candidate solution, updates continuously its position and velocity. The following relation can be used to estimate the new step size of each particle.
where w is the inertia factor; C1 and C2 denote the cognitive and the social coefficients; r1 and r2 denote random; t is the iteration number; i is the particle number; Pbest is the local best; Gbest is the global best.
The first section of (1) provides the exploration capability of the PSO. Whereas, the second section moves the particle towards the best position ever achieved by itself. The last section of (1) moves the particle according to the best position achieved by all the particles in the population. The core idea of GWO is extracted from the behavior of grey wolves. GWO simulates the hunting process and the leadership hierarchy of grey wolves [32]. Grey wolves exist at the highest level of the food chain and are regarded as predators.
The hunting mechanism contains two chief sections: tracking and catching the prey, then encircling and attacking the prey until movement stops. During the hunting process, prey is encircled by the grey wolves. To simulate the encircling behavior, the next relations can be considered [32]:
where t is the current iteration; Xp and X denote the position of the prey and the location of grey wolves, respectively.
A and C denote the coefficients vectors that are estimated using the following relations:
r1 and r2 are random values; a is constant that reduces linearly from 2 to 0 over the optimization process.
The process update of grey wolves is carried out based on the following relation;
For every iteration, the best three wolves are represented by Xα, Xβ, and Xδ;
Finally, the updated position of the prey is provided by the average of three values of positions assessed as the best solutions:
The fundamental idea of the hybrid PSOGWO is to integrate the capability of social thinking of the PSO with the local search ability of the GWO. A PSO suffers from shortcomings like catching the local minimum. Therefore, to avoid this disadvantage, the GWO was used to reduce the chance of trapping on the local minimum. Moreover, the GWO has the advantage of preserving a balance between exploitation and exploration during the optimizing procedure. More details about the mathematical modeling and physical meaning of the hybrid PSOGWO can be found in [33].
2.2. Optimization Process
In the optimization process, a stator of a standard induction machine of 5.5 kW with the parameters listed in Table 1 was employed. The stator geometry was kept fixed during the optimization process. Based on the number of stator slots and poles, the number of rotor flux-barriers could be identified which was selected to be three per pole [34,35]. Twelve rotor parameters, θb1, θb2, θb3, Wb1, Wb2, Wb3, Lb1, Lb2, Lb3, pb1, pb2, and pb3, sketched in Figure 1 were considered during the optimization process. To avoid the conflicts in the obtained geometry, some constraints were made as shown in Figure 1 and Table 2. As mentioned before, the main core of this paper is to study the influence of considering the current angle during the optimization process on the final optimal geometry of the SynRM. Therefore, in this research, different ranges of the current angle were considered (five cases) as in Table 3. The ranges of the current angles were selected based on the fact that the current angle of the maximum torque of the SynRMs equaled 45° (i.e., d-axis current = q-axis current) when neglecting the saturation effect. Nevertheless, when considering the saturation effect, the current angle deviated from 45°. Therefore, in this paper, we tried to enforce different ranges of the current angle to around 45° to determine the impact on the final optimal geometry; this will be shown in the next paragraphs. Although the range of case 5 locates within the case 4 range, there were different optimal geometries obtained based on the two cases. This was why we were trying to narrow the search region of the current angle as in case 5 and to increase this range as in case 4 and even to keep the current angle fixed as in case 3.

Table 1.
Parameters of the SynRM.

Table 2.
Rotor variables upper and lower limits.

Table 3.
Range of current angle for different cases.
The hybrid PSOGWO algorithm presented before was implemented to obtain the optimal rotor geometrical parameters and the current angle of each case in order to maximize the output torque and minimize the torque ripple of the machine. The cost function of the optimization is given as follows:
where, Tr and Tav are the torque ripple in percent and the average torque of the SynRM.
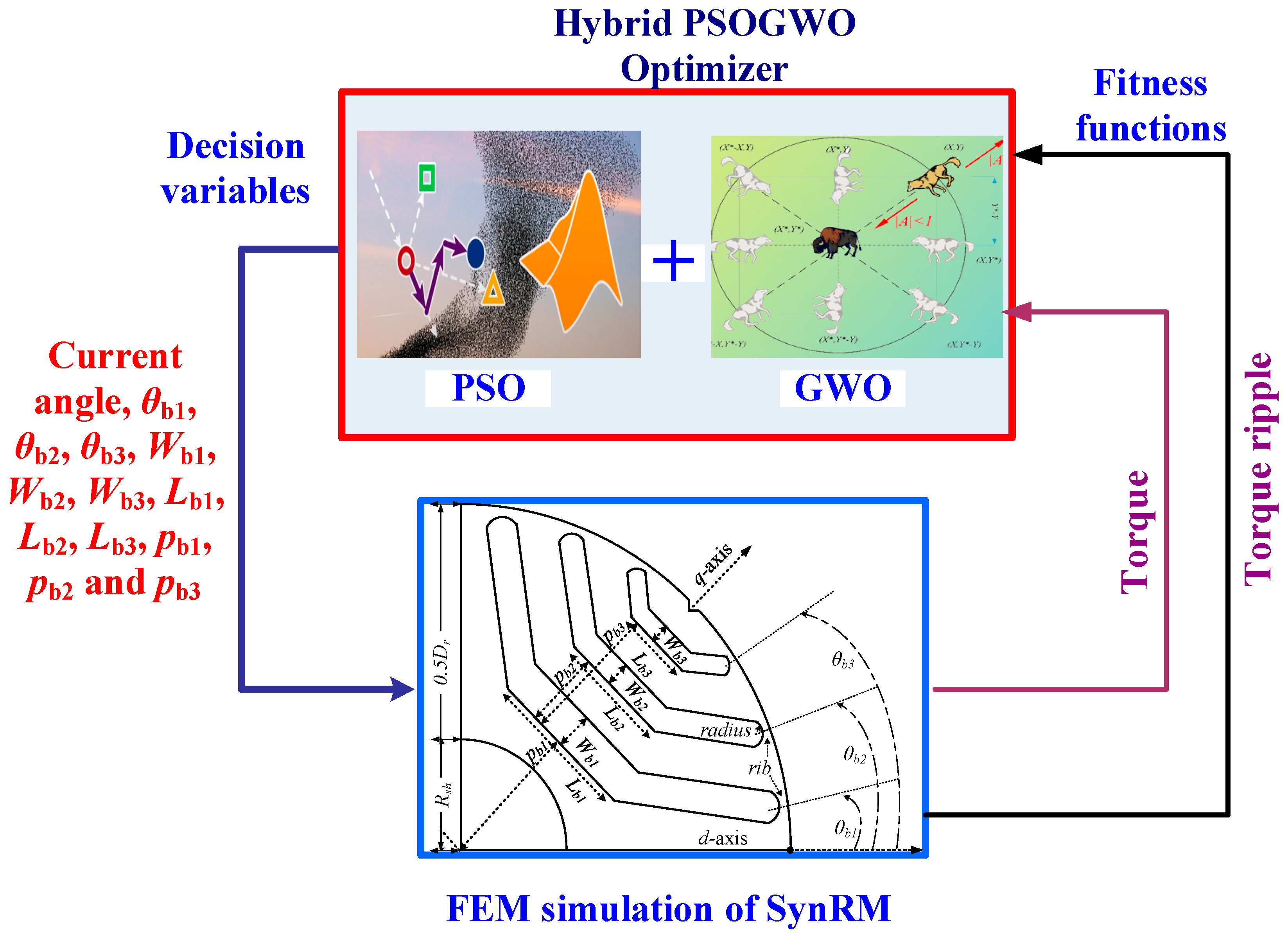
The flow chart of the optimization loop is described in Figure 2. The finite element model (FEM) of the machine, in which the equations that represent the machine were solved numerically, was coupled with the PSOGWO technique to obtain the optimal geometry [1]. The losses were determined as in [8]. Later on, FEM is used to evaluate the performance of the obtained optimal machine.
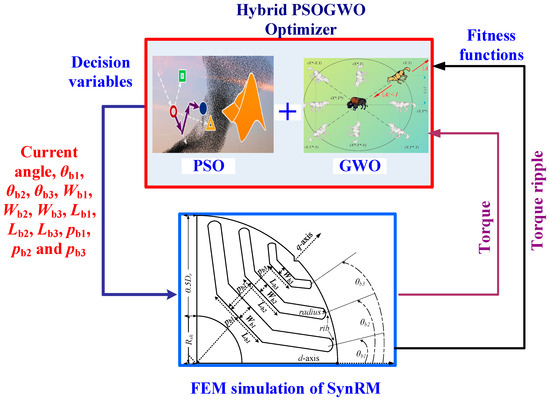
Figure 2.
Flow chart of the optimization process.
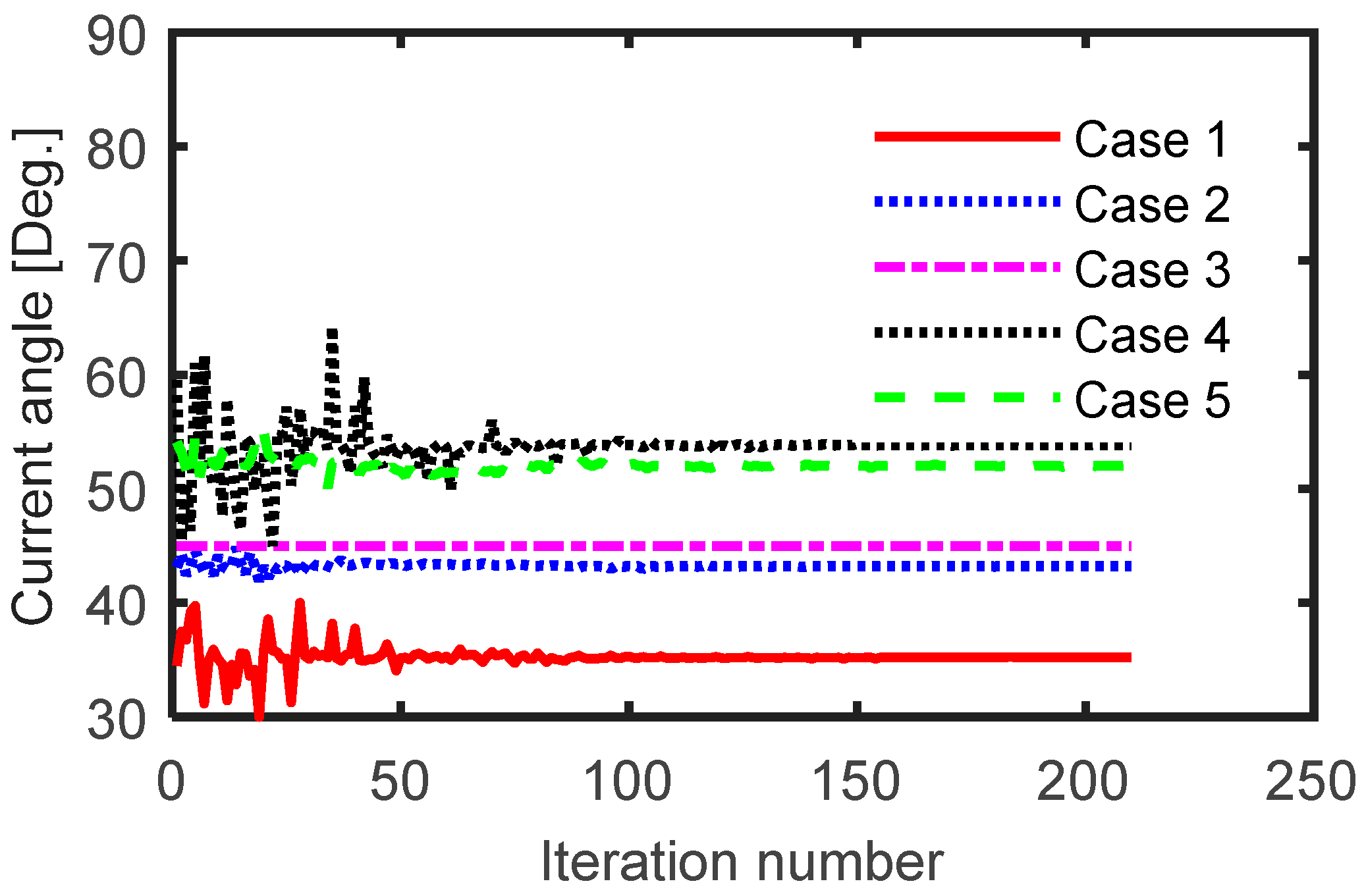
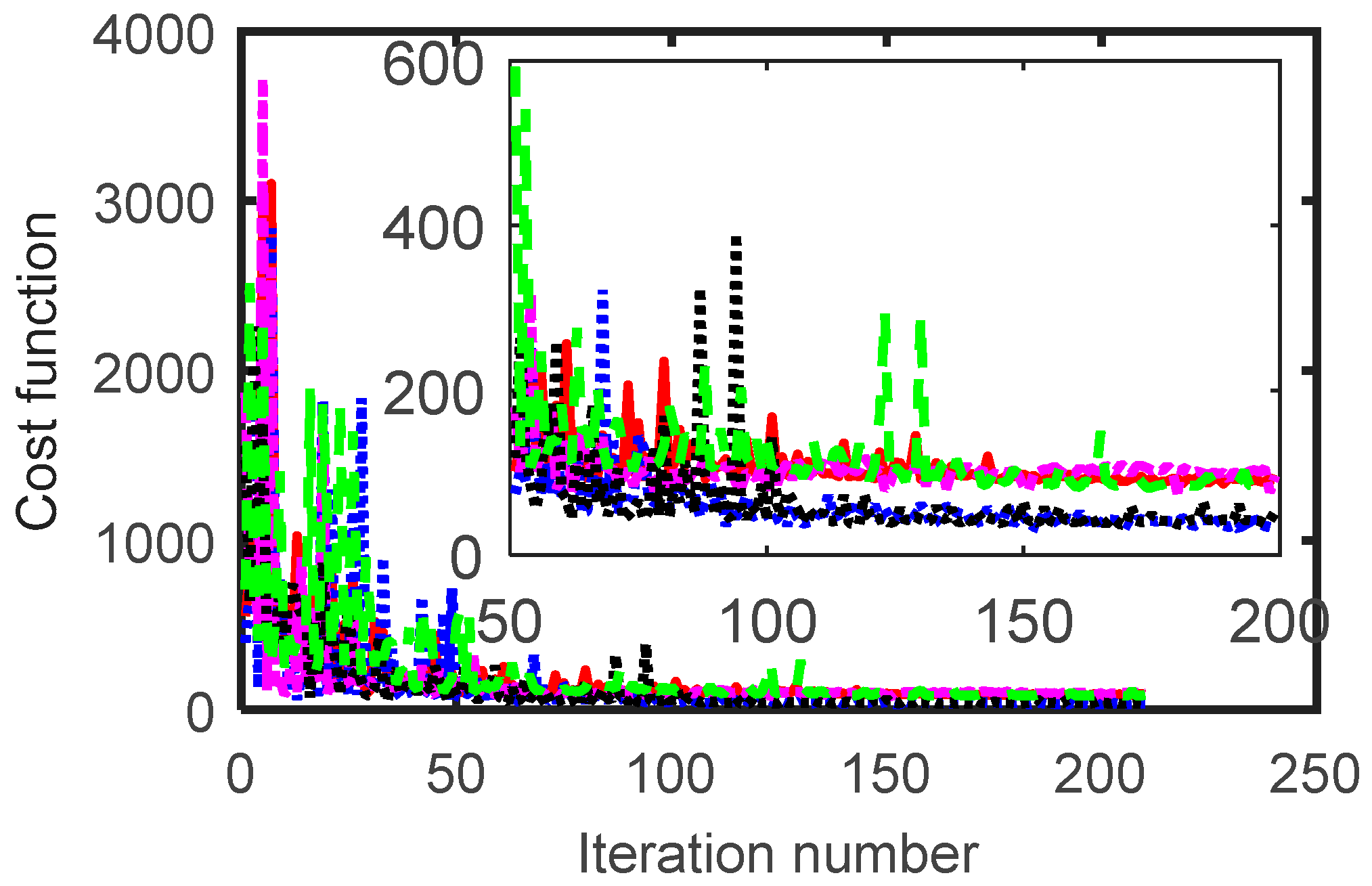
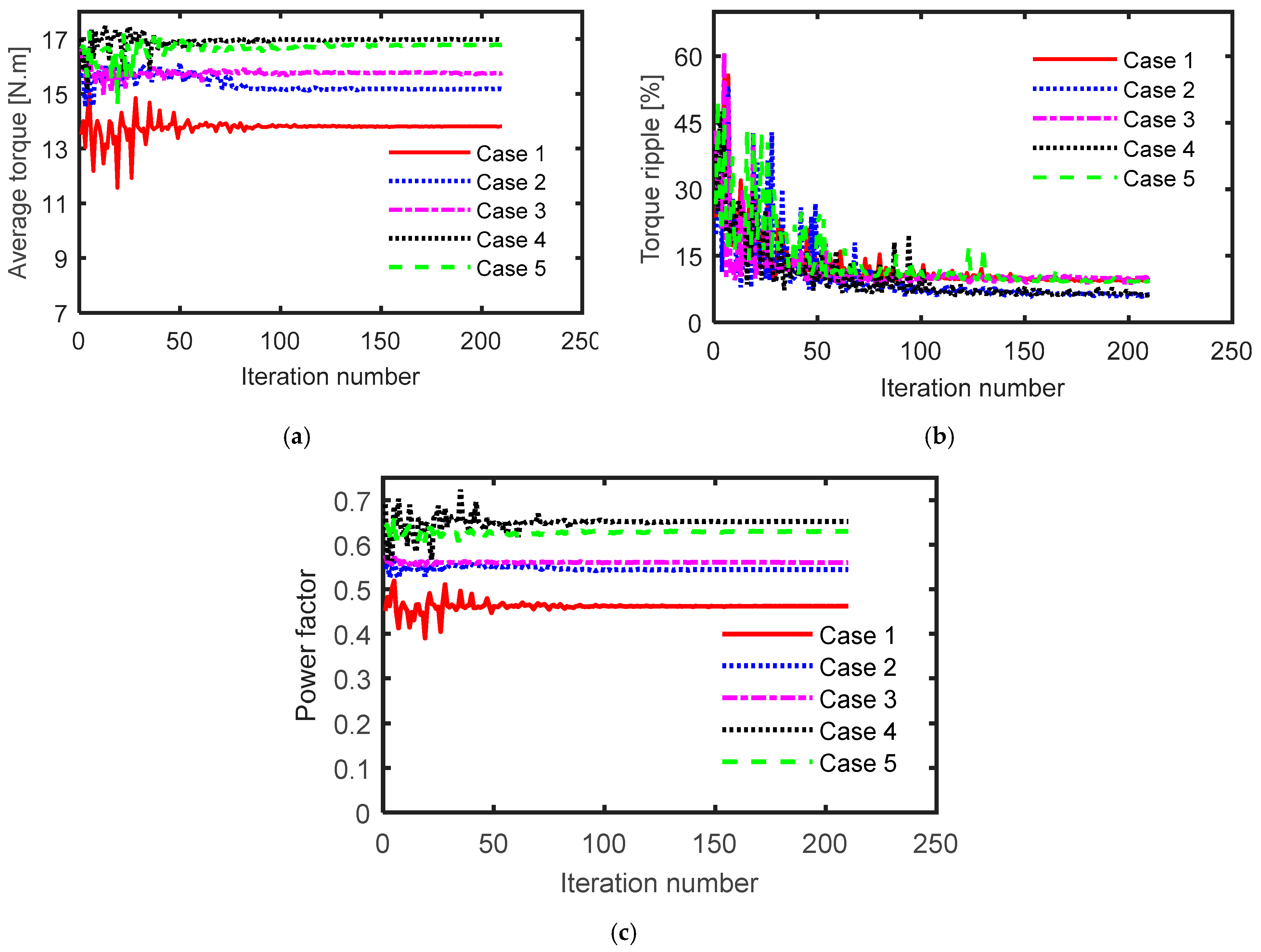
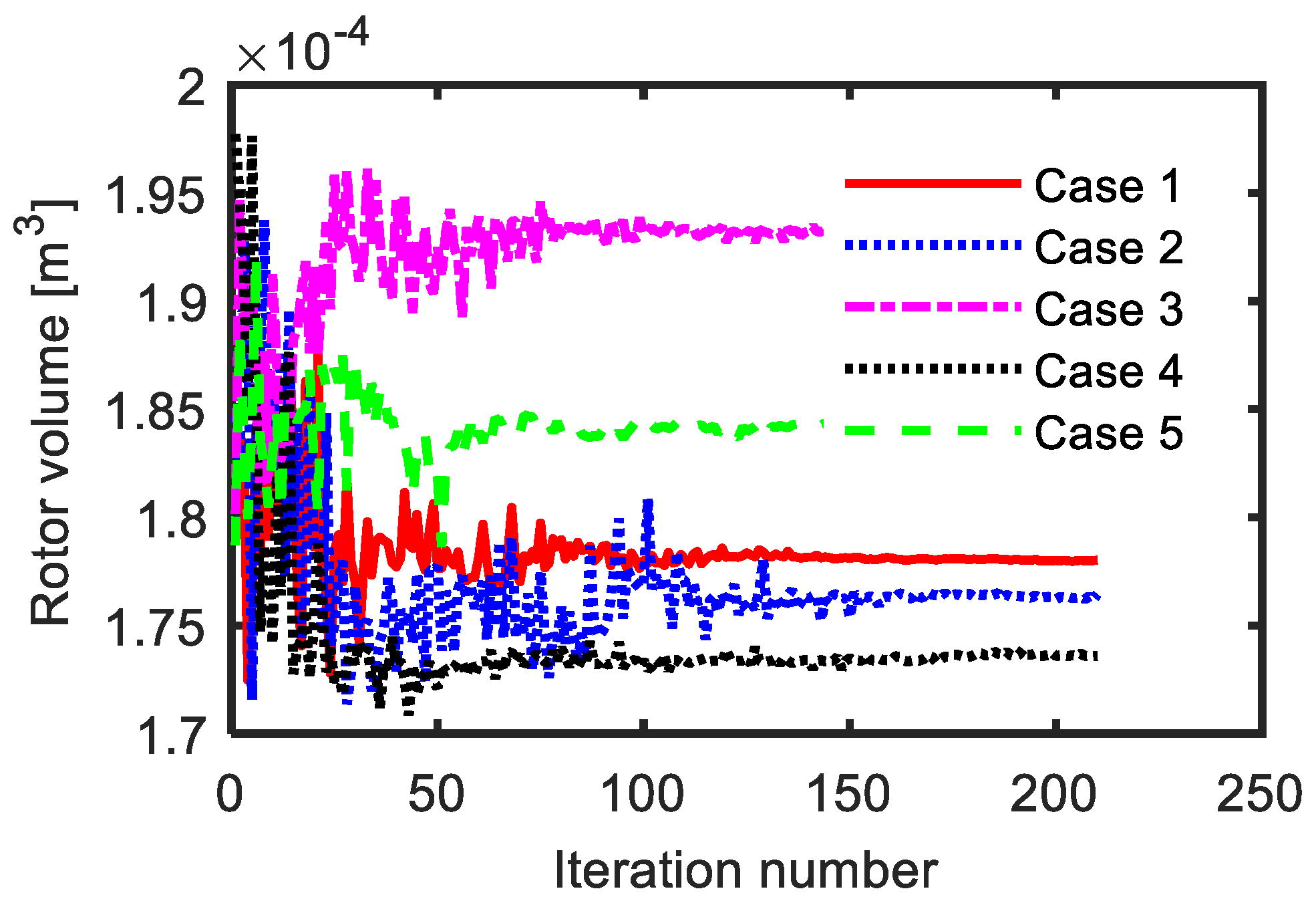
As mentioned before, five different ranges of the current angle were considered (see Table 3). For each case, the range of the current angle was set and the optimization process was completed. The number of designs for each case was 210. Figure 3 shows the variation of current angle versus iteration number during the optimization process for different cases. The cost function versus the iteration number is reported in Figure 4. Figure 5 shows some performance indicators of the SynRM for different cases. Notice that the results in this section were obtained at different current angles. Therefore, it was not possible to compare the performance indicators of the five cases. However, this will be done in the next section. Moreover, it was proved from Figure 5 that the average torque and the power factor were greatly affected by the value of the current angle in a specific case (between different designs), while the impact on the torque ripple was lower. Figure 6 and Table 4 reveal that the iron volume of the obtained rotor geometry depended on the considered current angle during the optimization process. Figure 6 shows that the third case, which considered a fixed value for the current angle (45°), gave the largest rotor iron volume, while the fourth case, which considered sufficient range of current angle variation in which the current angle of maximum torque and minimum torque ripple of the SynRM existed, gave the lowest iron volume of the rotor. The rotor iron volume of the third case was about 11% higher than that of the fourth case. This meant that the inertia of the SynRM based on the fourth case was lower resulting in a fast-dynamic machine.
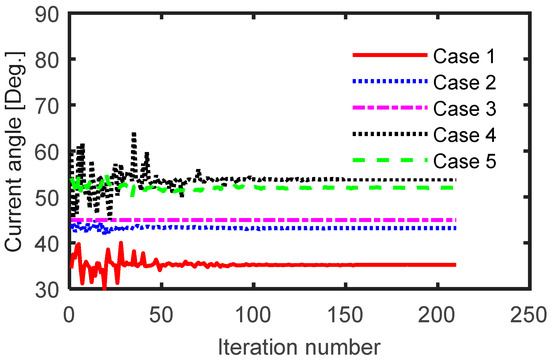
Figure 3.
Variation of current angle versus iteration number for different cases.
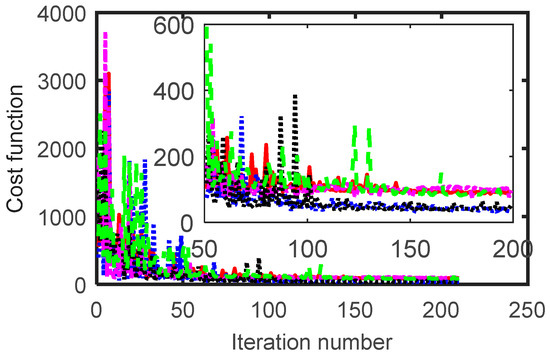
Figure 4.
Cost function at different iteration number of the optimization technique.
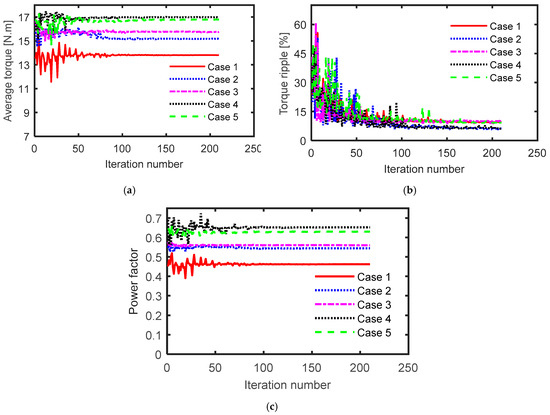
Figure 5.
(a) Average torque, (b) torque ripple, and (c) power factor versus iteration number for different cases.
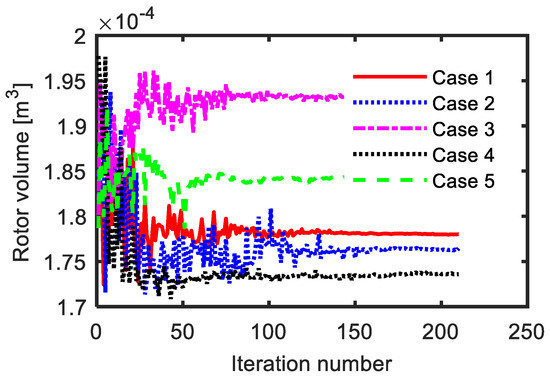
Figure 6.
Rotor iron volume versus iteration number for different cases.

Table 4.
Final optimal geometry for the SynRM for different case studies.
Figure 3, Figure 4, Figure 5 and Figure 6 show that the steady-state response of the optimization process was not delayed considering the current angle, while in some cases, the response became even faster. The optimization process of cases 1 and 4 reached its steady-state after about 80 and 60 iterations respectively compared to about 70 iterations for the third case. In contrast, the fifth case had a slower performance as shown in the zoomed view of Figure 4.
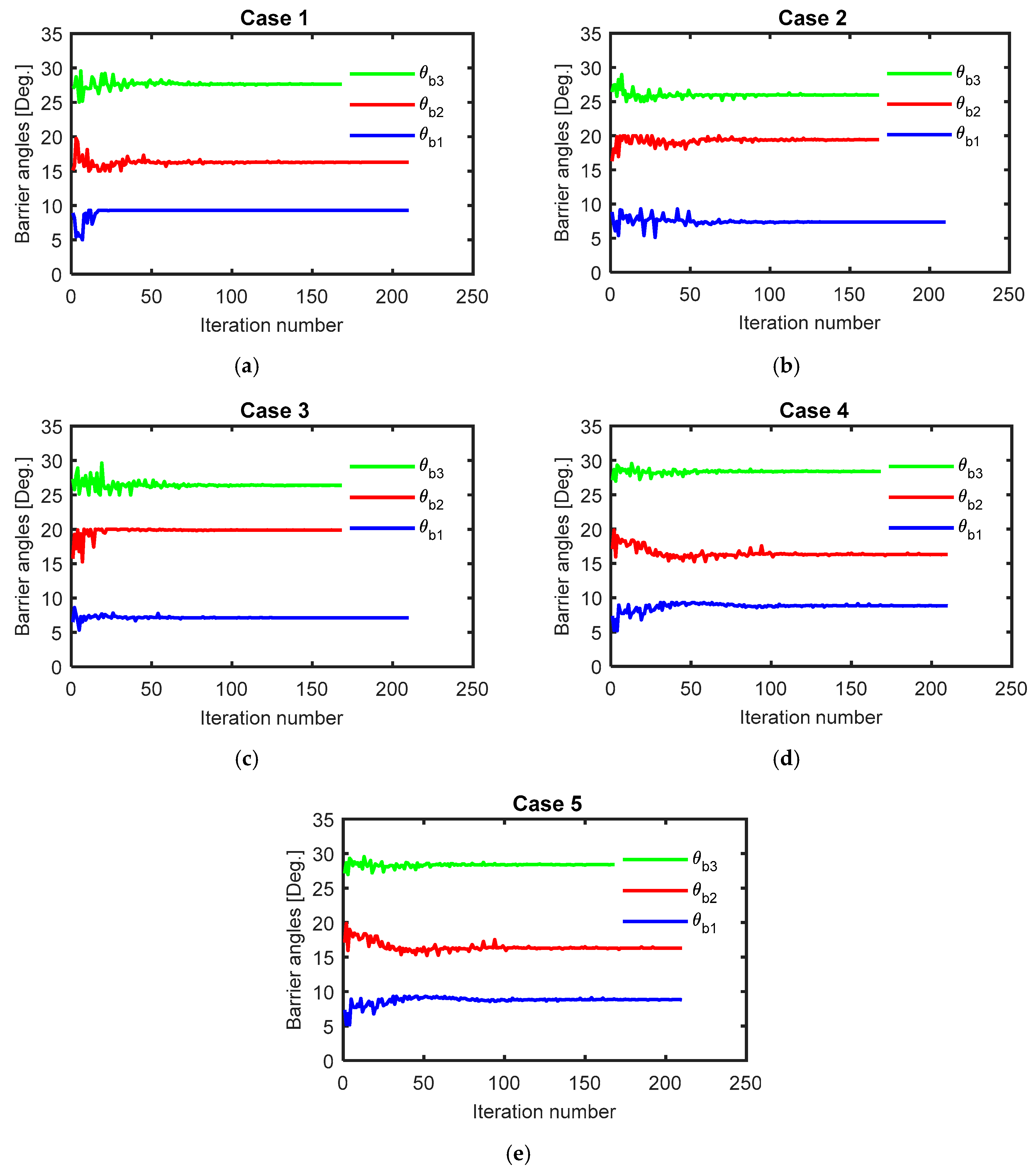
Figure 7, Figure 8, Figure 9 and Figure 10 and Table 4 show the final optimal geometry of the rotor flux-barrier angles, lengths, widths, and positions for different cases. In Figure 7, it is found that the flux-barrier angles were greatly varied when considering different ranges of current angle during the optimization process. For example, in the first case (with current angle range from 30°: 40°), the flux-barriers angles changed by about 2° to 6° compared to the optimal geometry proposed in [26] and by about 2° to 3.5° compared to the third case. However, when the current angle was kept fixed to 45° in the third case during the optimization process, the obtained optimal geometry for this case was different compared to the optimal geometry presented in [26] which used a current angle equal to 56.50°. This proved that the optimized geometry was sensitive to the chosen value of the current angle for fixed current angle cases.
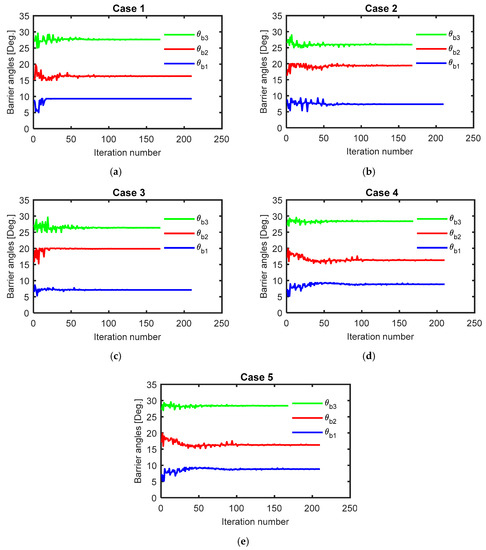
Figure 7.
Optimal geometry of flux barrier angles for different cases, (a) case 1, (b) case 2, (c) case 3, (d) case 4 and (e) case 5.
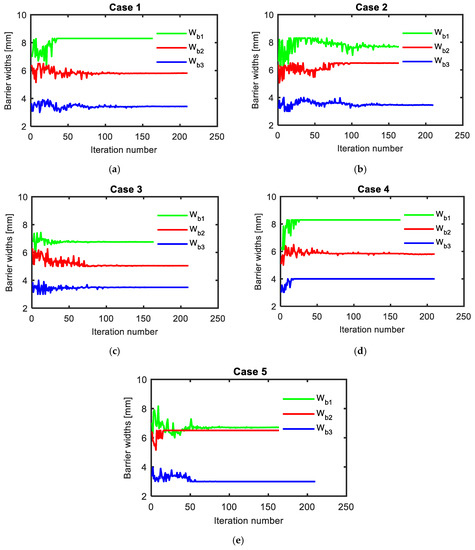
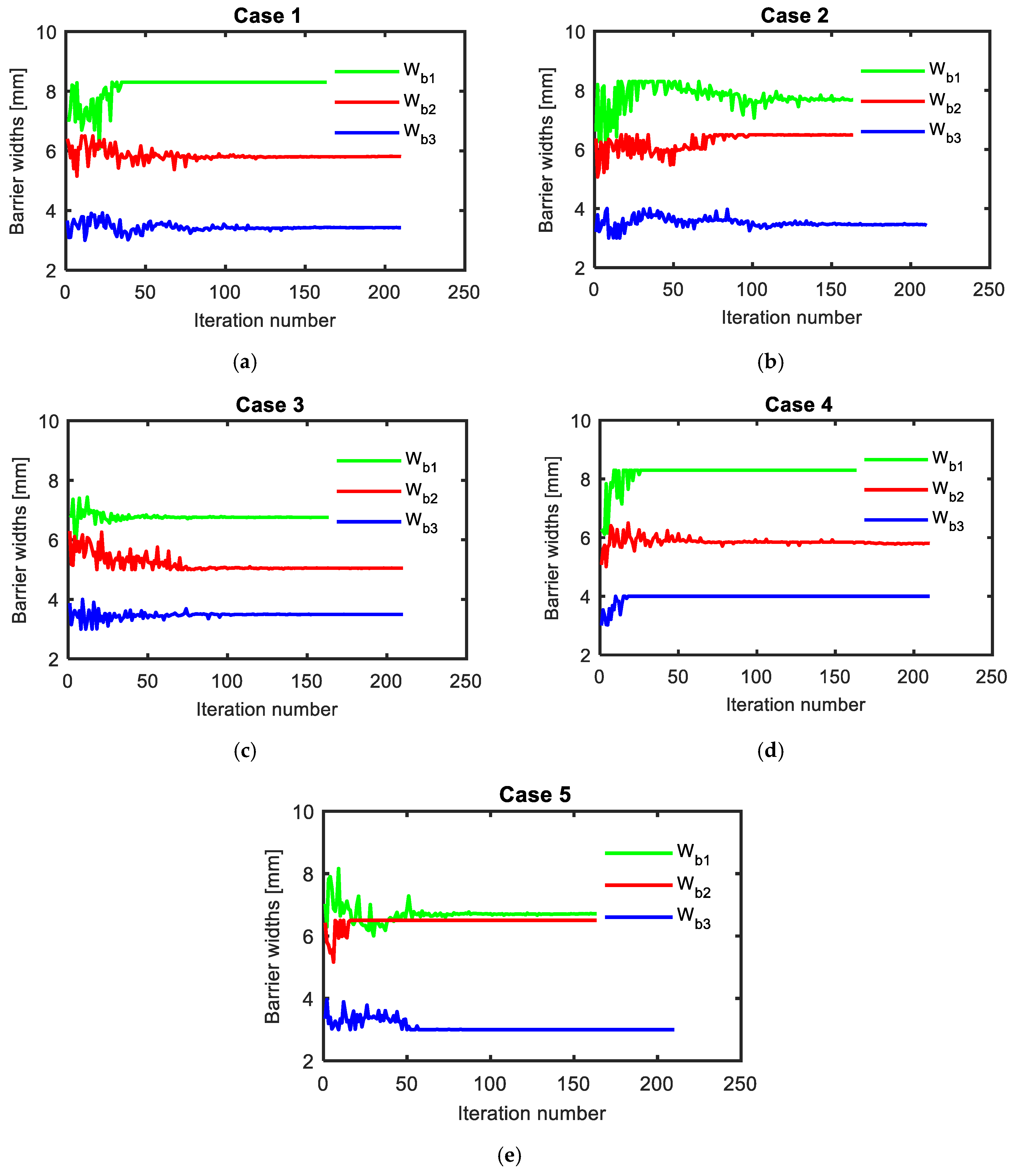
Figure 8.
Optimal geometry of flux barrier widths for different cases, (a) case 1, (b) case 2, (c) case 3, (d) case 4 and (e) case 5.
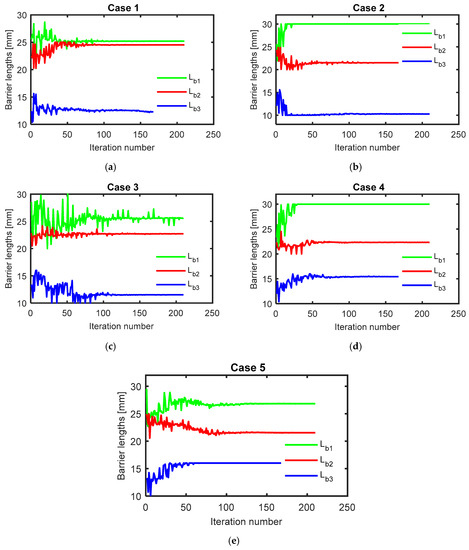
Figure 9.
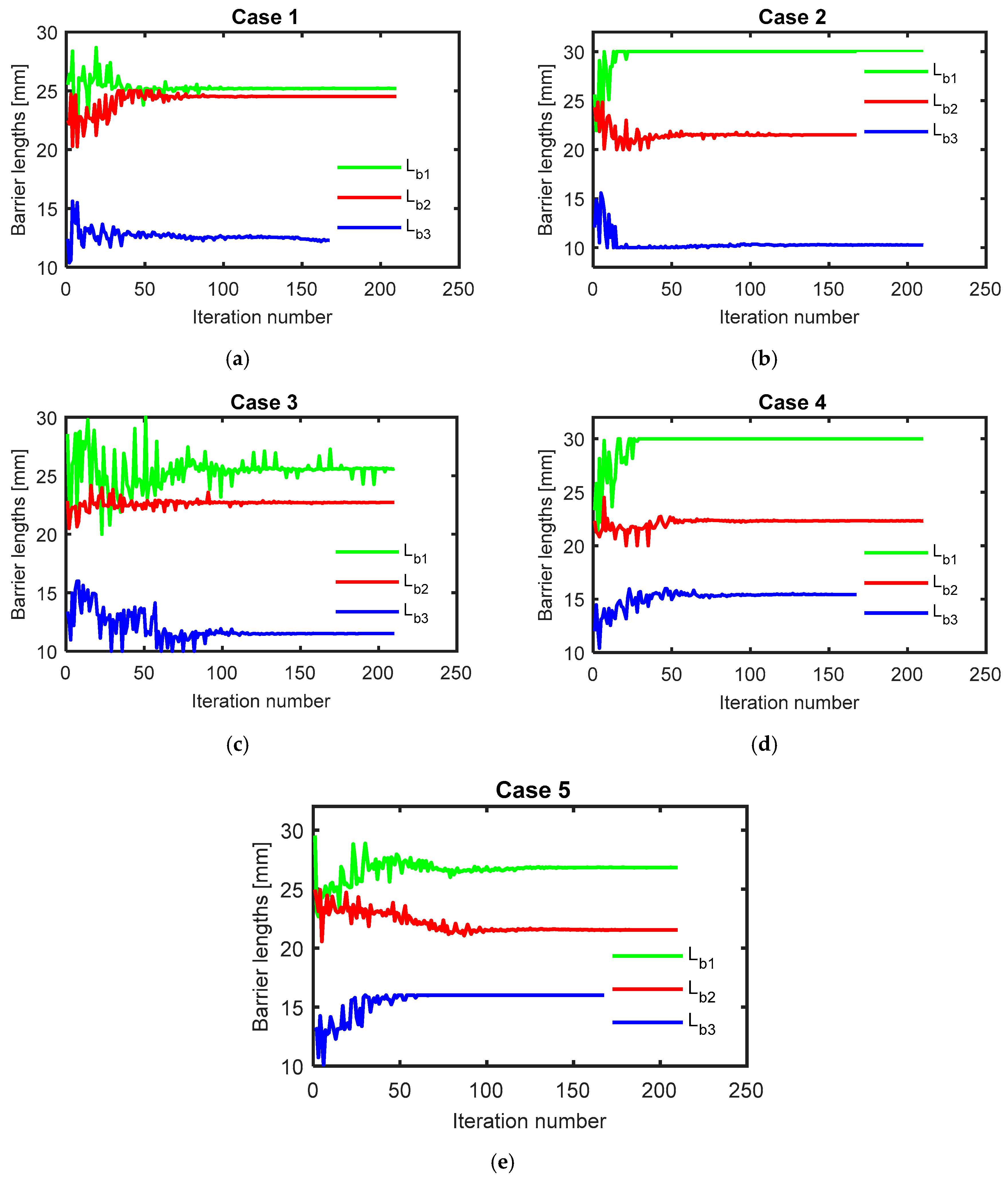
Optimal geometry of flux barrier lengths for different cases, (a) case 1, (b) case 2, (c) case 3, (d) case 4 and (e) case 5.
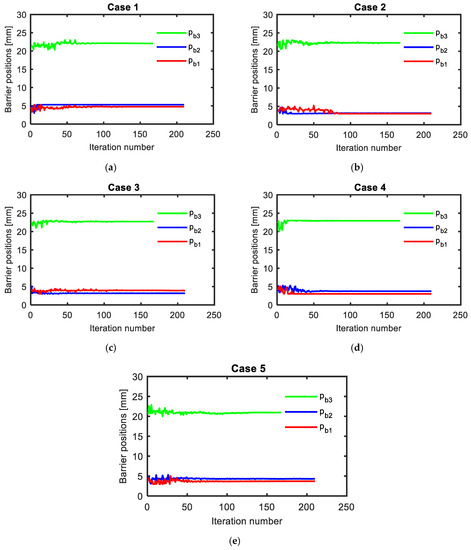
Figure 10.
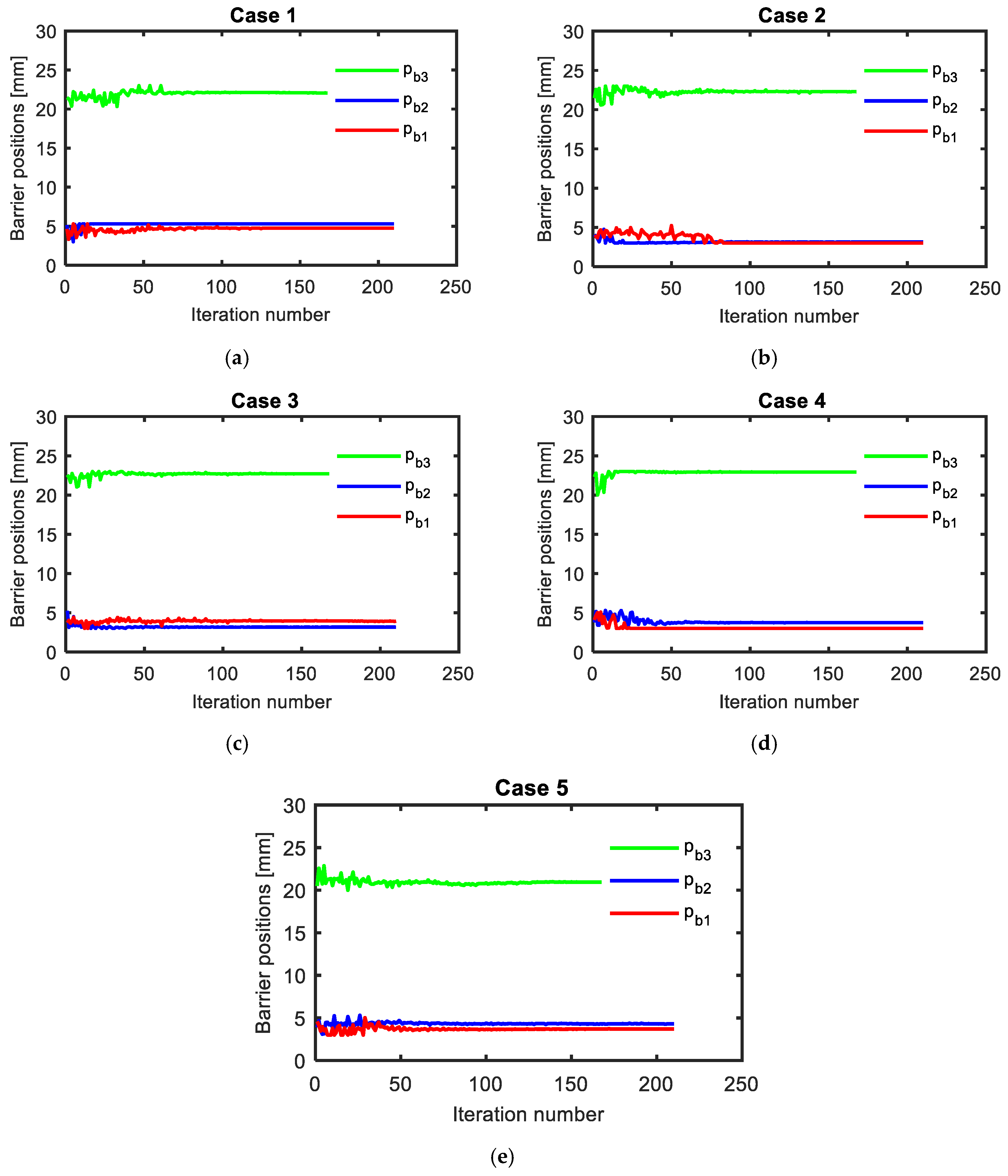
Optimal geometry of flux barrier positions for different cases, (a) case 1, (b) case 2, (c) case 3, (d) case 4 and (e) case 5.
In addition, the optimal dimensions of the flux-barriers widths were also varied with current angles as shown in Figure 8. The flux-barriers optimal widths, Wb1, Wb2, and Wb3 were changed by about 1.54, 0.75, and 0.7 mm respectively for the first case compared to their values in the third case. In addition, the flux-barriers optimal lengths, Lb1, Lb2, and Lb3 were changed by about 0.40, 1.82, and 0.88 mm respectively for the first case compared to their values in the third case as shown in Figure 9. Moreover, Figure 10 shows that the flux-barriers optimal positions, pb1, pb2, and pb3 were changed by about 0.65, 1.40, and 1.58 mm respectively for the first case compared to their values in the third case.
3. Performance Analysis of SynRM
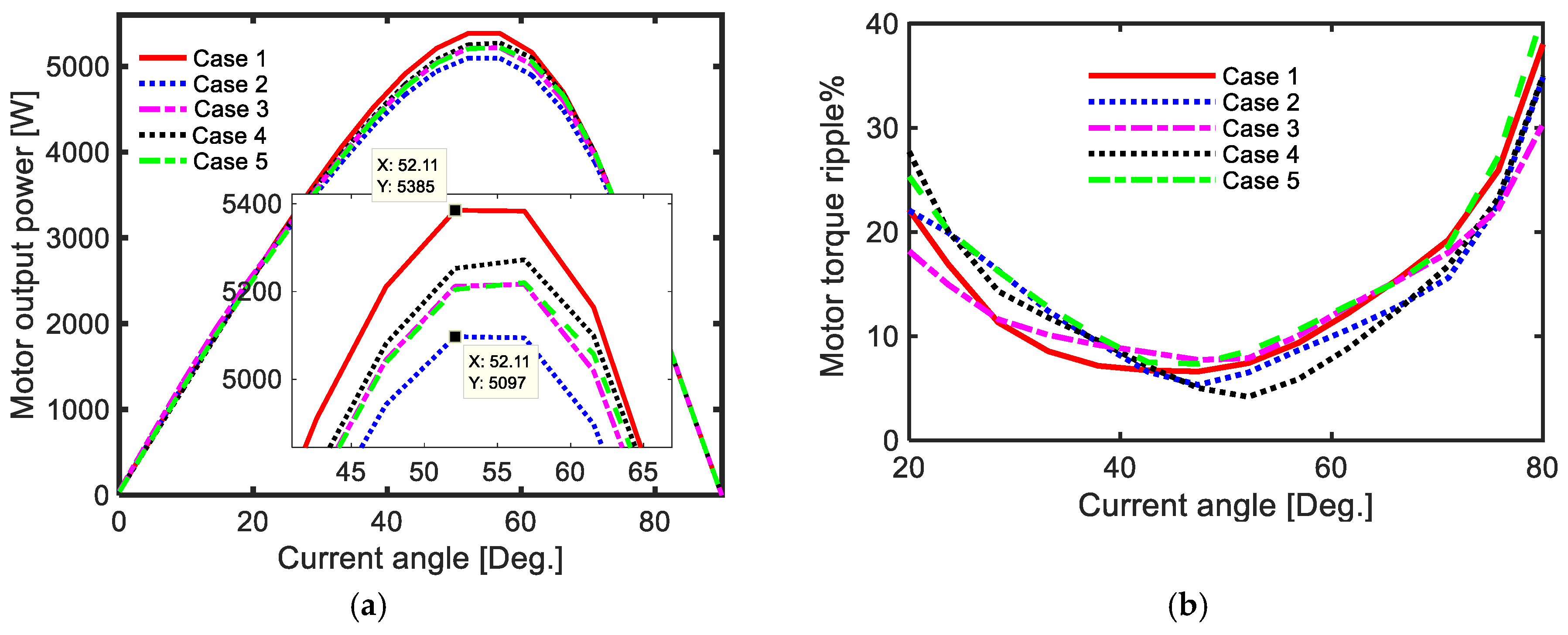
The performance of the optimal geometry of the rotor of the three-phase SynRM for different case studies was studied and compared using finite element magnetic simulations. The optimal geometry for each case is shown in Table 5. Figure 11a shows the output power of the three-phase SynRM for different cases at rated conditions (speed = 3000 rpm and RMS current = 12.23 A) and at different current angles. It was been found from Table 5 and Figure 11a that the first case gave the highest output power and the second case gave the lowest output power at the rated condition and at the optimal current angle. The optimal current angle was the angle that maximized the output power. The optimal current angle was 52.11° for both the first, the second, and the third case as shown in Figure 11a and Table 5, while it was 56.8° for the other cases. The output power in the first case was 5.65% higher than the second case. Moreover, the first case had about 3.32% higher output power compared to the third case. Note that the current angle in the third case was fixed during the optimization process while the effect of the current angle was considered in the first case as discussed in the previous section.

Table 5.
Performance of the optimal geometry for different case studies of the three-phase SynRM using finite element model (FEM) simulation.
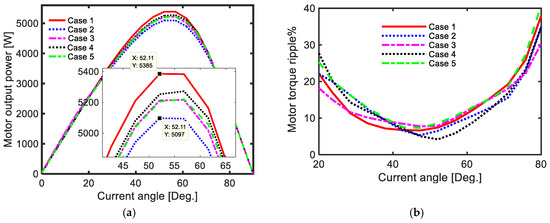
Figure 11.
(a) Motor output power and (b) torque ripple at different current angles and at rated conditions for the optimal geometry of different cases.
Figure 11b shows the torque ripple of the three-phase SynRM for different cases at the rated conditions and at different current angles. The torque ripple decreased with the increase in current angle till it reached its minimum value then it increased again. It was found that the torque ripple had the lowest value in the fourth case, about 5.85%, while the fifth case gave the maximum value of the torque ripple: about 10.58%. The torque ripple for the first case was 7.4%. However, the torque ripple in the third case which used a fixed current angle during the optimization process was about 7.9%. The chosen value of the current angle for the fixed current angle cases significantly affected the obtained torque ripple at the optimal current angle. This was highly obvious in [26], which used a current angle equal to 56.5° and the obtained torque ripple with the optimal angle in [26] was about 12%.
To summarize, the much higher output power and lower torque ripple of our work compared to [26] justified research of the current angle in the geometrical optimization process, as was the goal of this paper.
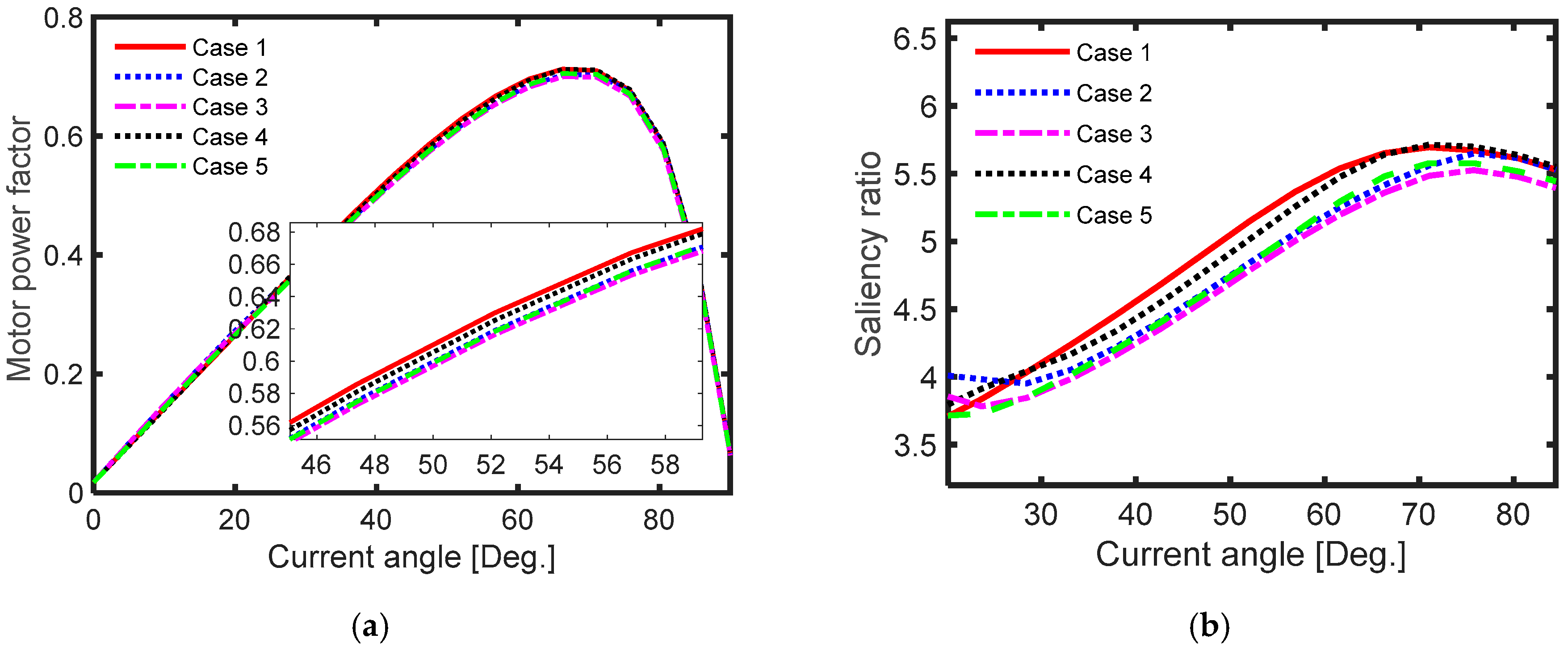
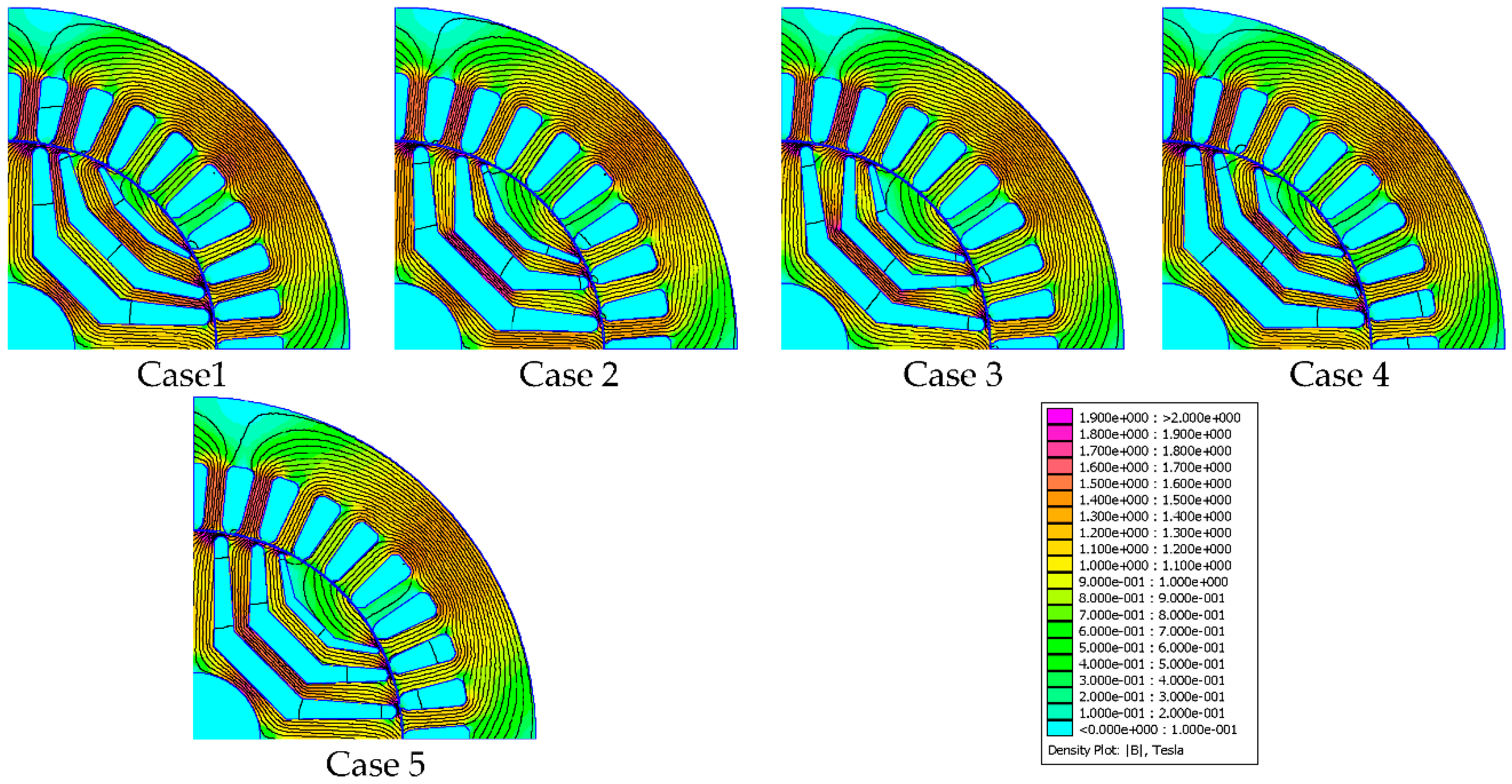
Figure 12 shows the power factor and the saliency ratio for the optimal geometry for different cases studied at rated conditions and at different current angles. It is noted that the fourth case had the highest value of the power factor. It was 0.6628. This was due to its higher optimal current angle compared to the first case. The power factor of the first case was 0.6297. Figure 12b shows that the first case gave the highest saliency ratio and the second case gave the lowest saliency ratio. In addition, the saliency ratio of the first case was about 11.7% higher than its value in the third case. The distribution of flux density at the same instant of the optimal geometry is shown in Figure 13 for the various study cases. It was been found that the rotor geometry calculated from the first case had less saturated area compared to other studied cases.
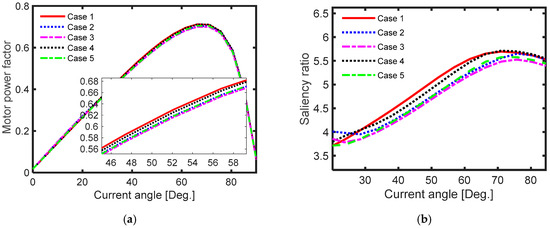
Figure 12.
(a) Motor power factor and (b) saliency ratio at different current angles and at rated conditions for the optimal geometry of different cases.
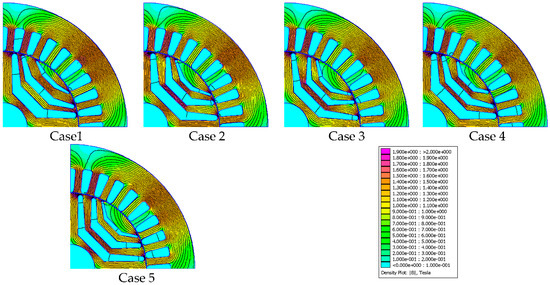
Figure 13.
Flux density distribution of the optimal geometry for different cases.
From the previous analysis and discussion, it was evident that considering the current angle during the optimization process of SynRMs was beneficial. Besides, it also observed that the range of the current angle played a role in the maximum output torque and torque ripple value.
4. Experimental Results
Figure 14a shows a complete experimental test bench to validate the simulation results presented before. It consisted of a 5.5 kW three-phase SynRM with a 36-slot stator and four-pole rotor as in case 4. The stator and the rotor are shown in Figure 14b. The three-phase SynRM was coupled with a 10 kW three-phase induction motor. The SynRM implemented in this paper required a control system, as it had no rotor cage. Hence, the desired speed of the three-phase SynRM was achieved using an induction motor, as the three-phase SynRM worked in the mode of torque control. A three-phase inverter based on space vector modulation with a 6.6 kHz switching frequency and 600 V DC bus voltage was used to control the three-phase SynRM. A digital signal processing (DSP1103) was used to obtain the required switching pulses. Incremental encoder and torque sensor were used to measure the rotor speed and the average torque respectively. The input electrical power for the three-phase SynRM was computed using a power analyzer.

Figure 14.
(a) The complete experimental setup and (b) three-phase SynRM stator and rotor.
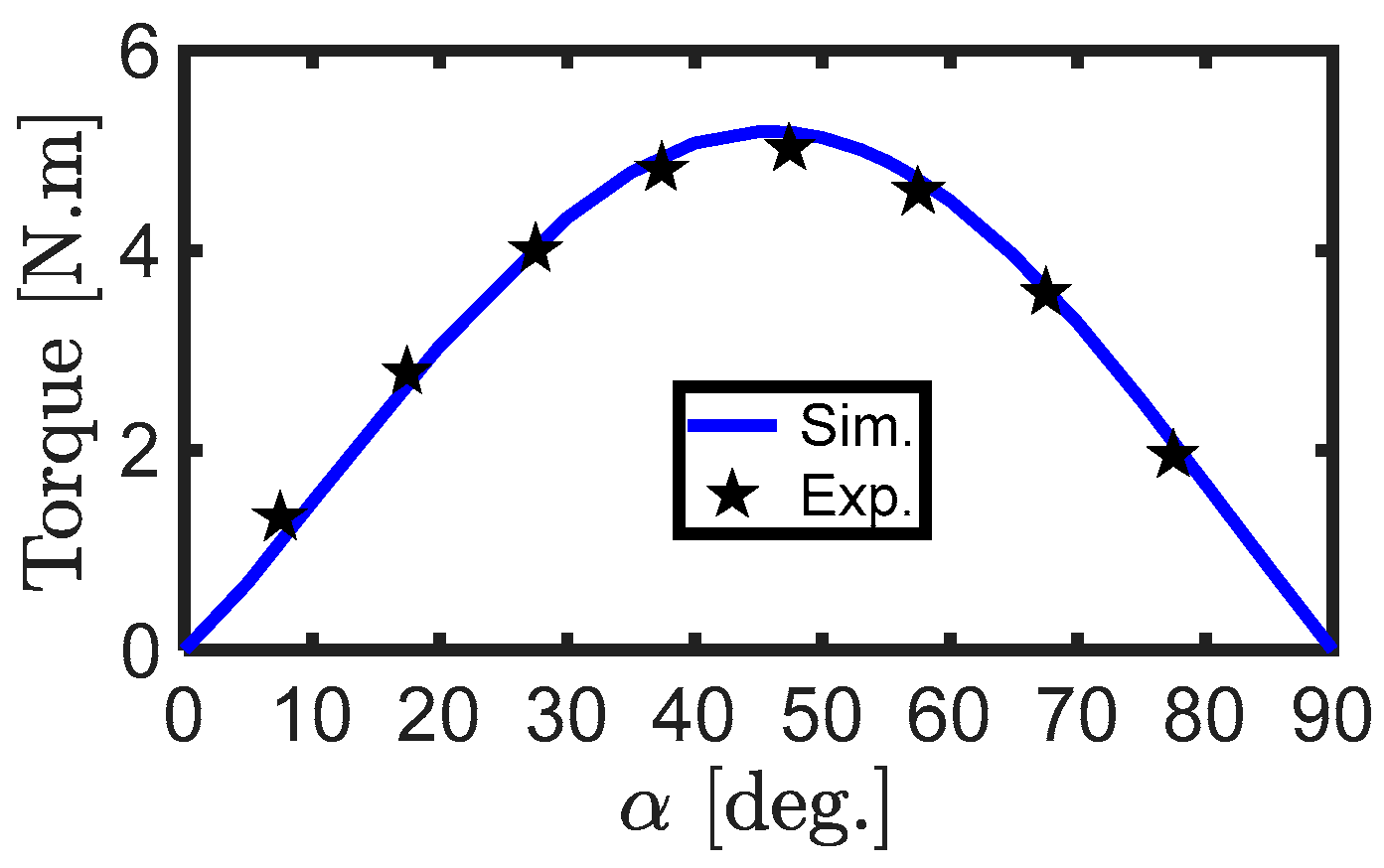
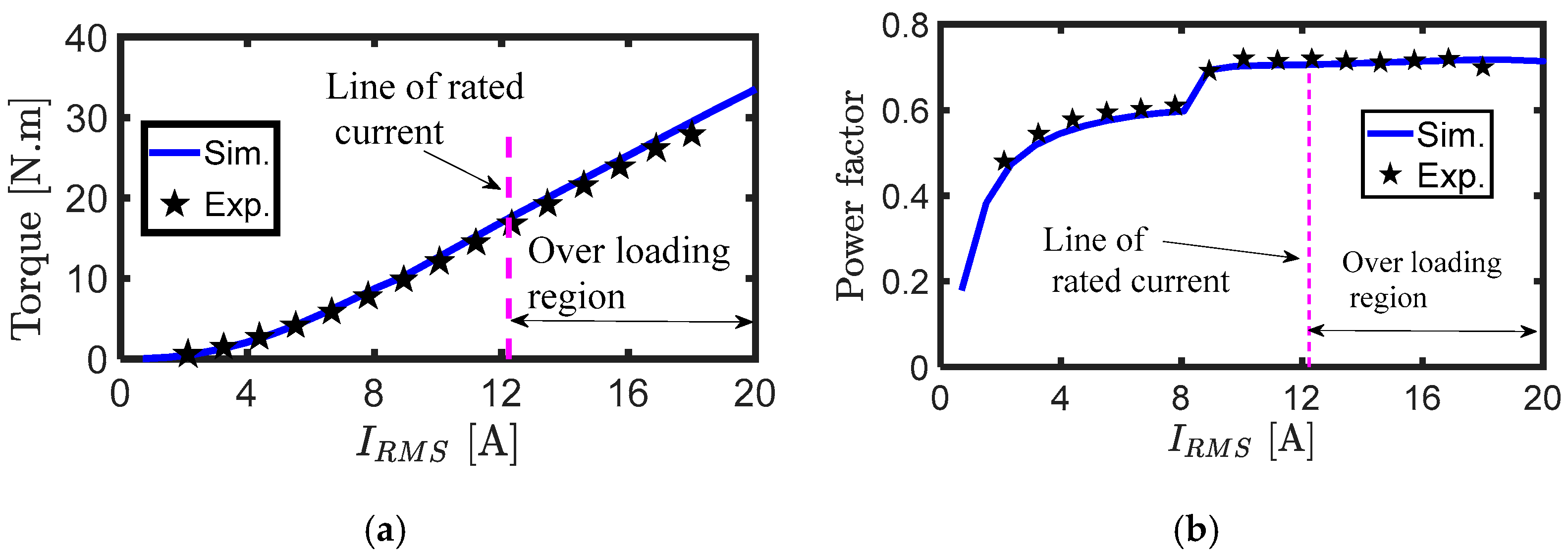
To validate the implemented simulation model, various measurements were obtained on the prototype. Figure 15 shows the simulated and measured value of the SynRM output torque at half the rated speed and current (speed = 1500 rpm and RMS current= 6.1 A) at different current angles. There was good agreement between the simulated and average values. The average torque and power factor measured and simulated values at different line currents including overloading to double the rated current, at an optimal current angle, and at one-third the rated speed as shown in Figure 16a and Figure 16b respectively. The torque was linearly varied with the current as shown in Figure 16a. Figure 16b shows that there was a step-change in the power factor. This was due to the change of optimal current angle with line current.
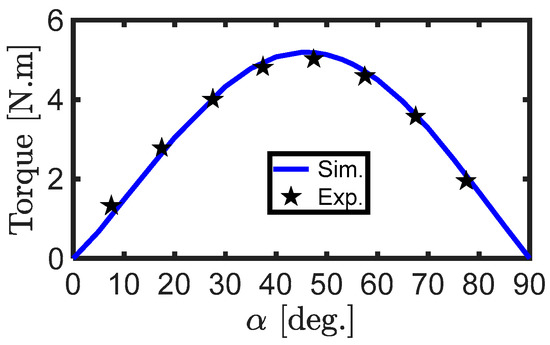
Figure 15.
Simulated and measured output torque at different current angles at half the rated current and half the rated speed.
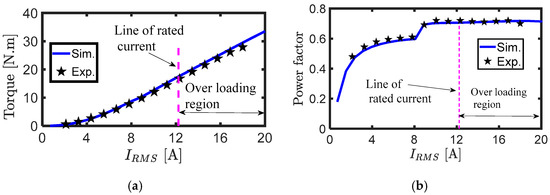
Figure 16.
(a) Average output torque and (b) power factor at different line currents, at an optimal current angle, and at .
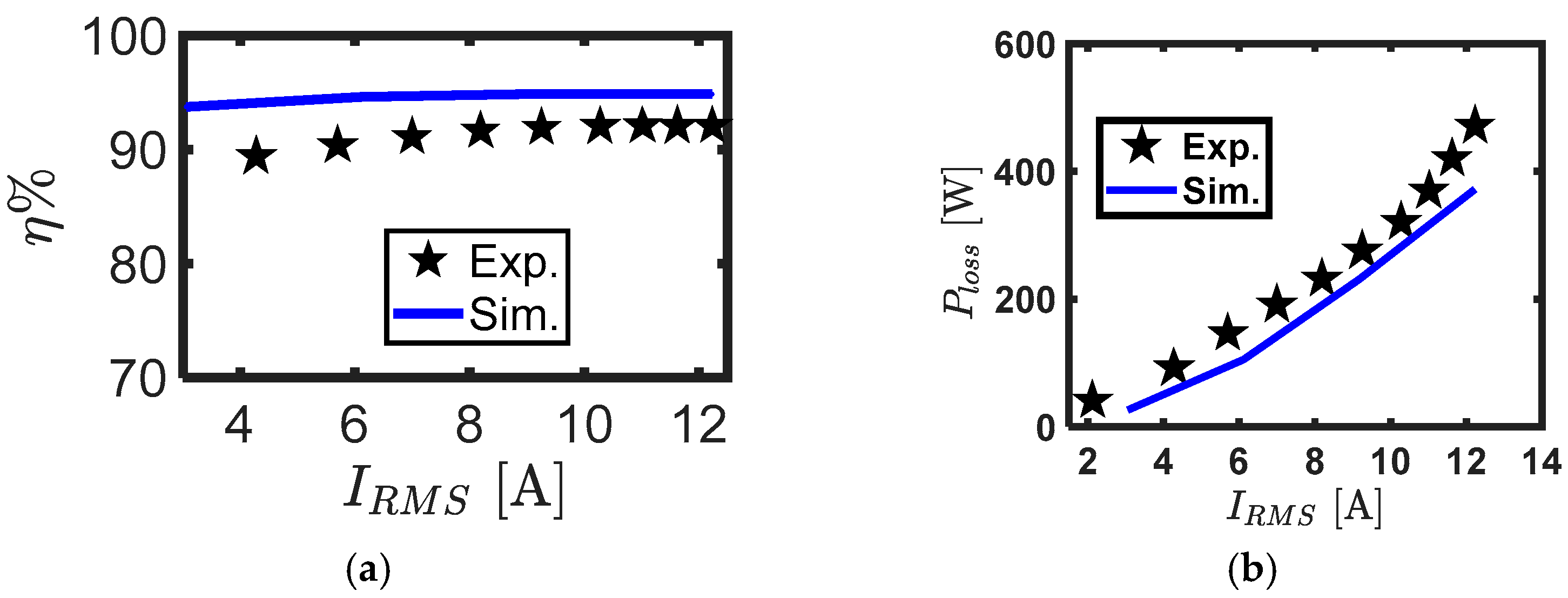
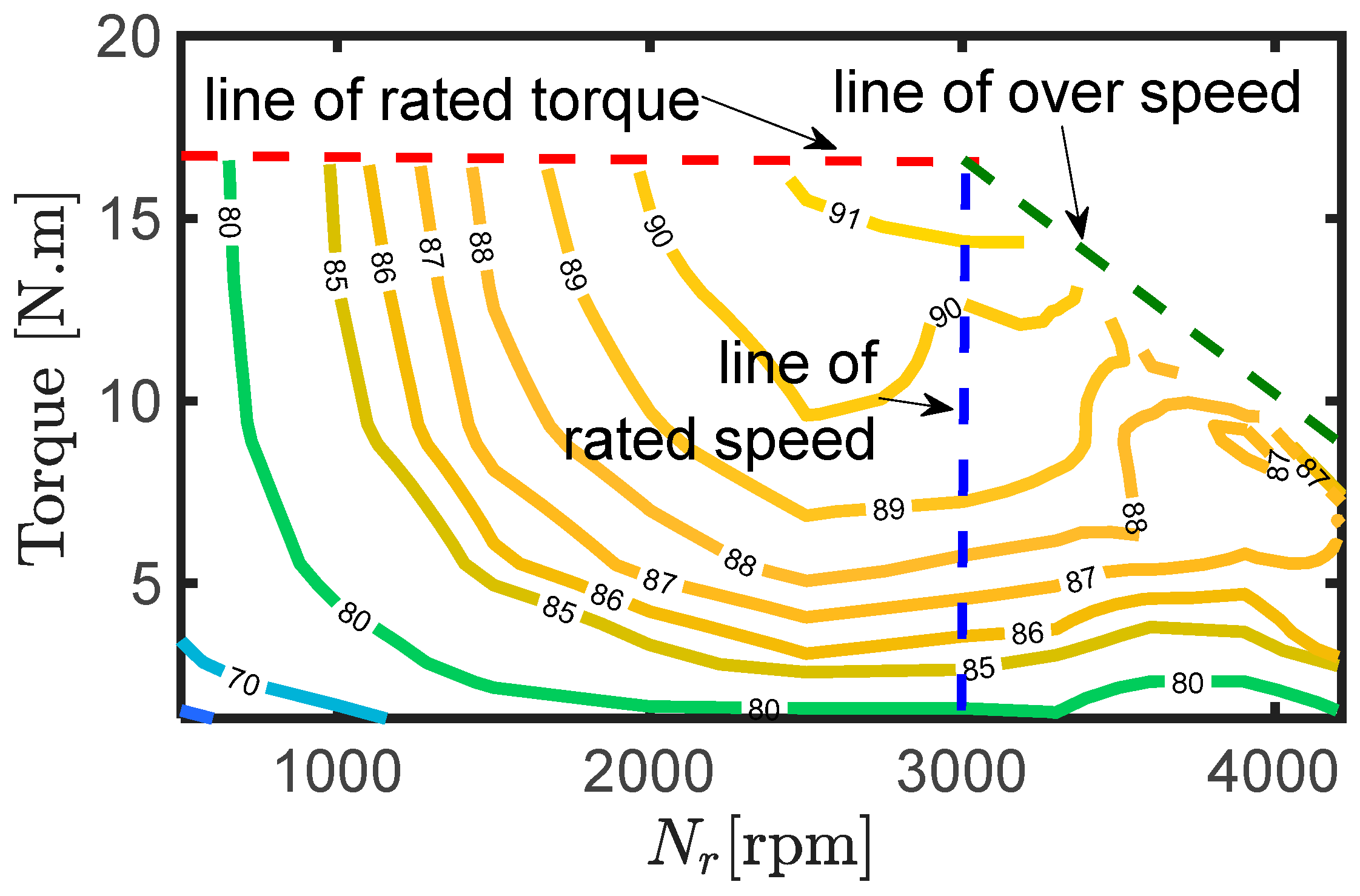
Figure 17 shows the measured and simulated values for the efficiency and total losses of the SynRM at different line currents, at rated speed, and at an optimal current angle. There was a slight difference between the simulated and measured values of efficiency and losses. This was due to neglecting the effect of mechanical and switching losses and the inaccurate iron loss simulation model parameters. Figure 18 shows the efficiency map of the complete drive system at different rotor speeds and at optimal current angles including the flux weakening region.
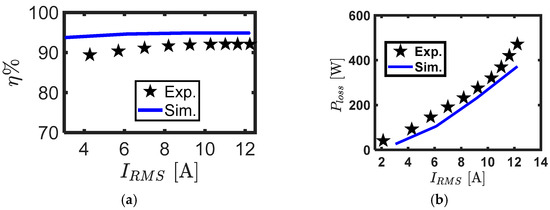
Figure 17.
(a) Efficiency, (b) SynRM total losses at different line currents, optimal current angle, and at rated speed.
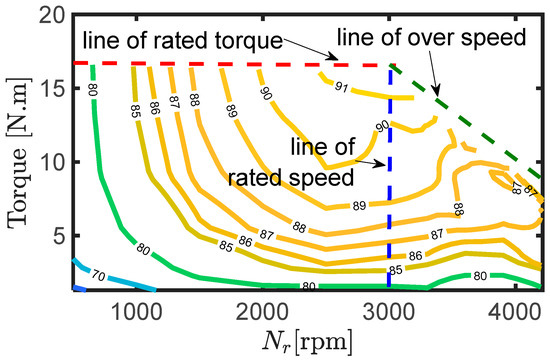
Figure 18.
Efficiency map of the complete drive system at optimal current angles.
5. Conclusions
This paper has investigated the influence of considering the current angle on the final optimal geometry when designing the rotor of a synchronous reluctance motor. Five cases for different ranges of current angles have been studied and compared using finite element simulation. It is proved that considering the current angle on the SynRM rotor design is effective to obtain improved performance of the SynRM. It is observed that the output power is increased by about 3.32% when the current angle is considered as a variable during the rotor design optimization process compared to the fixed current angle case. In addition, the selection of the appropriate current angle value for fixed current angle cases has a significant influence on the torque ripple of the optimized rotor geometry. Further, it is also noticed that the range of the current angle plays a role in the maximum output torque and torque ripple value. Moreover, it is found that for a fixed current angle case (angle = 45°), the torque ripple of the optimal geometry is greatly decreased by 34.20% compared to a case of current angle equal to 56.50°, which is the reference case in literature [26]. In the end, a test bench for a 5.5 kW three-phase SynRM has been carried out to validate the simulated results.
Author Contributions
Conceptualization, K.B.T., M.N.I., H.R. and P.S., validation, K.B.T., M.N.I., H.R., writing—original draft preparation, K.B.T., M.N.I., H.R., writing—review and editing, M.N.I., H.R., and P.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Bacco, G.; Bianchi, N.; Mahmoud, H. A Nonlinear Analytical Model for the Rapid Prediction of the Torque of Synchronous Reluctance Machines. IEEE Trans. Energy Convers. 2018, 33, 1539–1546. [Google Scholar] [CrossRef]
- Tawfiq, K.B.; Ibrahim, M.N.; El-Kholy, E.E.; Sergeant, P. Refurbishing three-phase synchronous reluctance machines to multiphase machines. Electr. Eng. 2020. [Google Scholar] [CrossRef]
- Ibrahim, M.N.; Sergeant, P.; Rashad, E.E.M. Combined Star-Delta Windings to Improve Synchronous Reluctance Motor Performance. IEEE Trans. Energy Convers. 2016, 31, 1479–1487. [Google Scholar] [CrossRef]
- Bianchi, N.; Bolognani, S.; Bon, D.; Pré, M.D. Torque Harmonic Compensation in a Synchronous Reluctance Motor. IEEE Trans. Energy Convers. 2008, 23, 466–473. [Google Scholar] [CrossRef]
- Tawfiq, K.B.; Ibrahim, M.N.; El-Kholy, E.E.; Sergeant, P. Performance Improvement of Existing Three Phase Synchronous Reluctance Machine: Stator Upgrading to 5-Phase With Combined Star-Pentagon Winding. IEEE Access 2020, 8, 143569–143583. [Google Scholar] [CrossRef]
- Ibrahim, M.N.F.; Sergeant, P.; Rashad, E.M. Relevance of Including Saturation and Position Dependence in the Inductances for Accurate Dynamic Modeling and Control of SynRMs. IEEE Trans. Ind. Appl. 2017, 53, 151–160. [Google Scholar] [CrossRef]
- Vagati, A. Synchronous Reluctance Drives: A New Alternative (Tutorial Course Notes); IEEE Press: Piscataway, NJ, USA, 1994; Chapter 6; pp. 1–27. [Google Scholar]
- Ibrahim, M.N.; Sergeant, P.; Rashad, E.M. Synchronous Reluctance Motor Performance Based on Different Electrical Steel Grades. IEEE Trans. Magn. 2015, 51, 1–4. [Google Scholar] [CrossRef]
- Zhao, W.; Zhao, F.; Lipo, T.A.; Kwon, B.-I. Optimal Design of a Novel V-Type Interior Permanent Magnet Motor with Assisted Barriers for the Improvement of Torque Characteristics. IEEE Trans. Magn. 2014, 50, 1–4. [Google Scholar] [CrossRef]
- Davoli, M.; Bianchini, C.; Torreggiani, A.; Immovilli, F. A design method to reduce pulsating torque in PM assisted synchronous reluctance machines with asymmetry of rotor barriers. In Proceedings of the IECON 2016—42nd Annual Conference of the IEEE Industrial Electronics Society, Florence, Italy, 24–26 October 2016; pp. 1566–1571. [Google Scholar]
- Baek, J.; Bonthu, S.; Choi, S. Design of five-phase permanent magnet assisted synchronous reluctance machine for low output torque ripple applications. IET Electr. Power Appl. 2016, 10, 339–346. [Google Scholar] [CrossRef]
- Babetto, C.; Bacco, G.; Bianchi, N. Synchronous Reluctance Machine Optimization for High-Speed Applications. IEEE Trans. Energy Convers. 2018, 33, 1266–1273. [Google Scholar] [CrossRef]
- Howard, E.; Kamper, M.J. Weighted Factor Multiobjective Design Optimization of a Reluctance Synchronous Machine. IEEE Trans. Ind. Appl. 2016, 52, 2269–2279. [Google Scholar] [CrossRef]
- Cupertino, F.; Pellegrino, G.; Armando, E.; Gerada, C. A SyR and IPM machine design methodology assisted by optimization algorithms. In Proceedings of the 2012 IEEE Energy Conversion Congress and Exposition (ECCE), Raleigh, NC, USA, 15–20 September 2012; pp. 3686–3691. [Google Scholar] [CrossRef]
- Pellegrino, G.; Cupertino, F.; Gerada, C. Automatic Design of Synchronous Reluctance Motors Focusing on Barrier Shape Optimization. IEEE Trans. Ind. Appl. 2015, 51, 1465–1474. [Google Scholar] [CrossRef]
- Howard, E.; Kamper, M.J.; Gerber, S. Asymmetric Flux Barrier and Skew Design Optimization of Reluctance Synchronous Machines. IEEE Trans. Ind. Appl. 2015, 51, 3751–3760. [Google Scholar] [CrossRef]
- Cupertino, F.; Pellegrino, G.; Gerada, C. Design of Synchronous Reluctance Motors With Multiobjective Optimization Algorithms. IEEE Trans. Ind. Appl. 2014, 50, 3617–3627. [Google Scholar] [CrossRef]
- Vagati, A.; Pastorelli, M.A.; Francheschini, G.; Petrache, S.C. Design of low-torque-ripple synchronous reluctance motors. IEEE Trans. Ind. Appl. 1998, 34, 758–765. [Google Scholar] [CrossRef]
- Muteba, M.; Twala, B.; Nicolae, D.V. Torque ripple minimization in synchronous reluctance motor using a sinusoidal rotor lamination shape. In Proceedings of the 2016 XXII International Conference on Electrical Machines (ICEM), Lausanne, Switzerland, 4–7 September 2016; pp. 606–611. [Google Scholar]
- Arafat, A.; Choi, S. Active current harmonic suppression for torque ripple minimization at open phase faults in a five-phase PMa-SynRM. IEEE Trans. Ind. Electron. 2019, 66, 922–931. [Google Scholar] [CrossRef]
- Bianchi, N.; Degano, M.; Fornasiero, E. Sensitivity analysis of torque ripple reduction of synchronous reluctance and interior PM motors. IEEE Trans. Ind. Appl. 2015, 51, 187–195. [Google Scholar] [CrossRef]
- Donaghy-Spargo, C.M. Electromagnetic–mechanical design of synchronous reluctance rotors with fine features. IEEE Trans. Magn. 2017, 53, 1–8. [Google Scholar] [CrossRef]
- Bao, Y.; Degano, M.; Wang, S.; Chuan, L.; Zhang, H.; Xu, Z.; Gerada, C. A Novel Concept of Ribless Synchronous Reluctance Motor for Enhanced Torque Capability. IEEE Trans. Ind. Electron. 2020, 67, 2553–2563. [Google Scholar] [CrossRef]
- Taghavi, S.; Pillay, P. A novel grain-oriented lamination rotor core assembly for a synchronous reluctance traction motor with a reduced torque ripple algorithm. IEEE Trans. Ind. Appl. 2016, 52, 3729–3738. [Google Scholar] [CrossRef]
- Moghaddam, R.R. Synchronous Reluctance Machine (SynRM) in Variable Speed Drives (VSD) Applications. Ph.D. Thesis, KTH Royal Institute of Technology, Stockholm, Sweden, 2011. [Google Scholar]
- Ibrahim, M.N.; Sergeant, P.; Rashad, E. Simple Design Approach for Low Torque Ripple and High Output Torque Synchronous Reluctance Motors. Energies 2016, 9, 942. [Google Scholar] [CrossRef]
- Guo, F.; Brown, I.P. Simultaneous Magnetic and Structural Topology Optimization of Synchronous Reluctance Machine Rotors. IEEE Trans. Magn. 2020, 56, 1–12. [Google Scholar] [CrossRef]
- Uberti, F.; Frosini, L.; Szabo, L. An Optimization Procedure for a Synchronous Reluctance Machine with Fluid Shaped Flux Barriers. In Proceedings of the 2020 International Conference on Electrical Machines (ICEM), Gothenburg, Sweden, 23–26 August 2020; pp. 389–395. [Google Scholar] [CrossRef]
- Lolova, I.; Barta, J.; Bramerdorfer, G.; Silber, S. Topology optimization of line-start synchronous reluctance machine. In Proceedings of the 2020 19th International Conference on Mechatronics—Mechatronika (ME), Prague, Czech Republic, 2–4 December 2020; pp. 1–7. [Google Scholar] [CrossRef]
- Eberhart, R.; Kennedy, J. A new optimizer using particle swarm theory. In Proceedings of the Sixth International Symposium on Micro Machine and Human Science, MHS’95, Nagoya, Japan, 4–6 October 1995; pp. 39–43. [Google Scholar]
- Abdalla, O.; Rezk, H.; Ahmed, E.M. Wind driven optimization algorithm based global MPPT for PV system under non-uniform solar irradiance. Sol. Energy 2019, 180, 429–444. [Google Scholar] [CrossRef]
- Mohamed, A.; Diab, A.A.Z.; Rezk, H. Partial shading mitigation of PV systems via different meta-heuristic techniques. Renew. Energy 2019, 130, 1159–1175. [Google Scholar] [CrossRef]
- Şenel, F.A.; Gökçe, F.; Yüksel, A.S.; Yiğit, T. A novel hybrid PSO–GWO algorithm for optimization problems. Eng. Comput. 2019, 35, 1359–1373. [Google Scholar] [CrossRef]
- Wang, K.; Zhu, Z.Q. Torque ripple reduction of synchronous reluctance machines optimal slot/pole and flux-barrier layer number combinations. Int. J. Comput. Math. Electr. Electron. Eng. 2015, 34, 3–17. [Google Scholar] [CrossRef]
- Palmieri, M.; Perta, M.; Cupertino, F.; Pellegrino, G. Effect of the numbers of slots and barriers on the optimal design of synchronous reluctance machines. In Proceedings of the 2014 International Conference on Optimization of Electrical and Electronic Equipment (OPTlM), Brasov, Romania, 22–24 May 2014. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).