Mutual Influence of Geometric Parameters and Mechanical Properties on Thermal Stresses in Composite Laminated Plates with Rectangular Holes
Abstract
1. Introduction
2. Literature Review
3. Analytical Solution
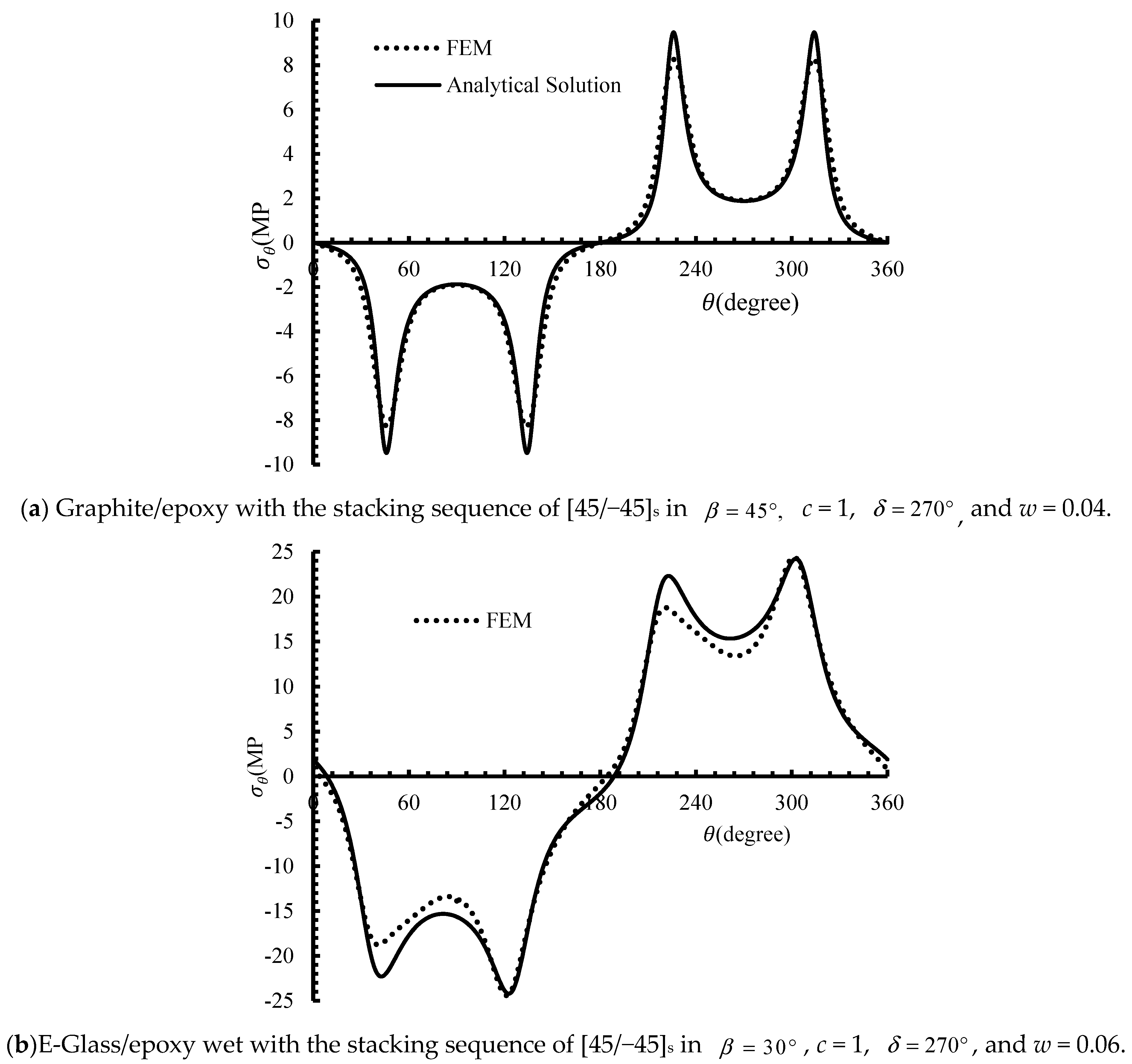
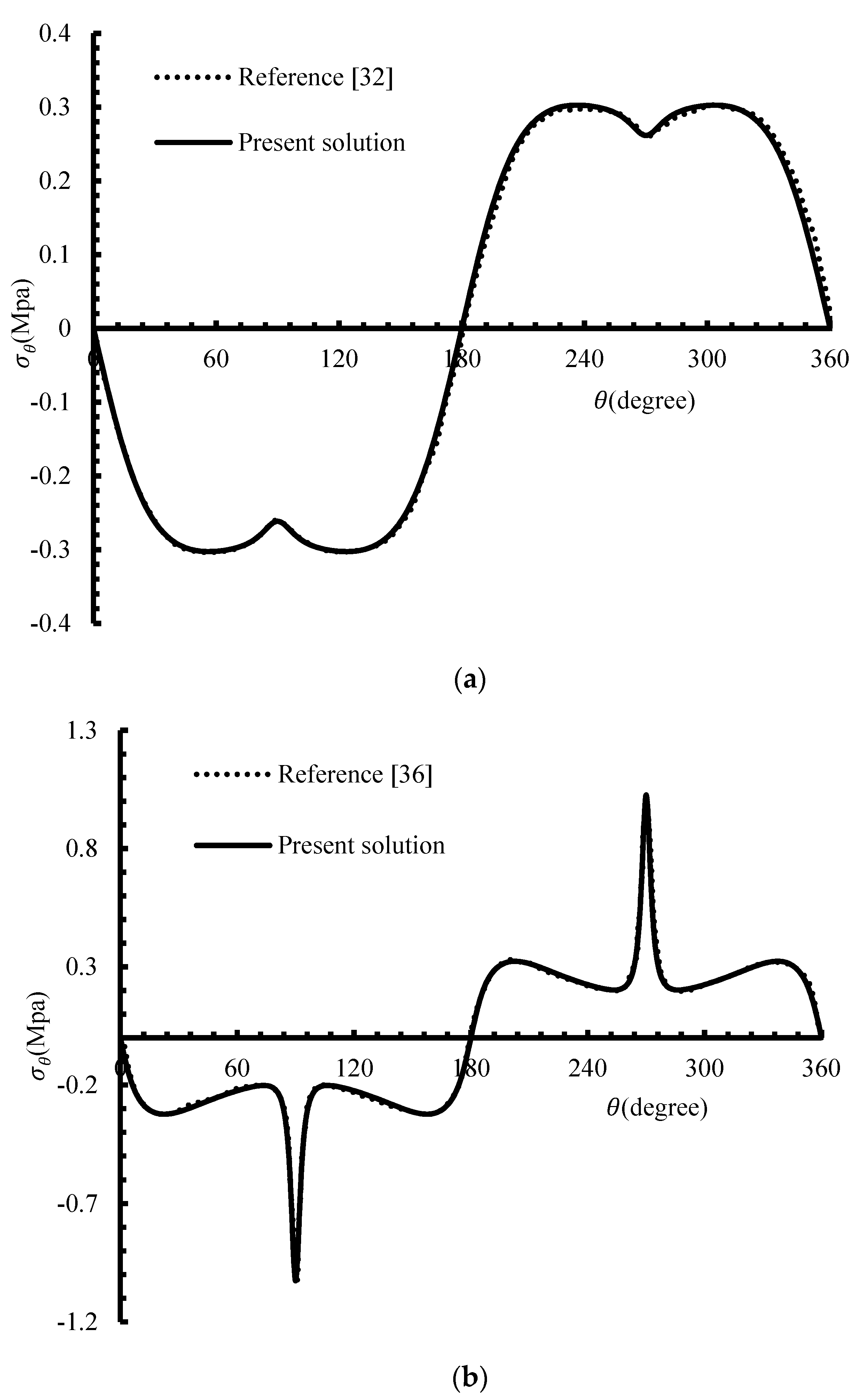
4. Validation of the Analytical Solution
5. Results and Discussion
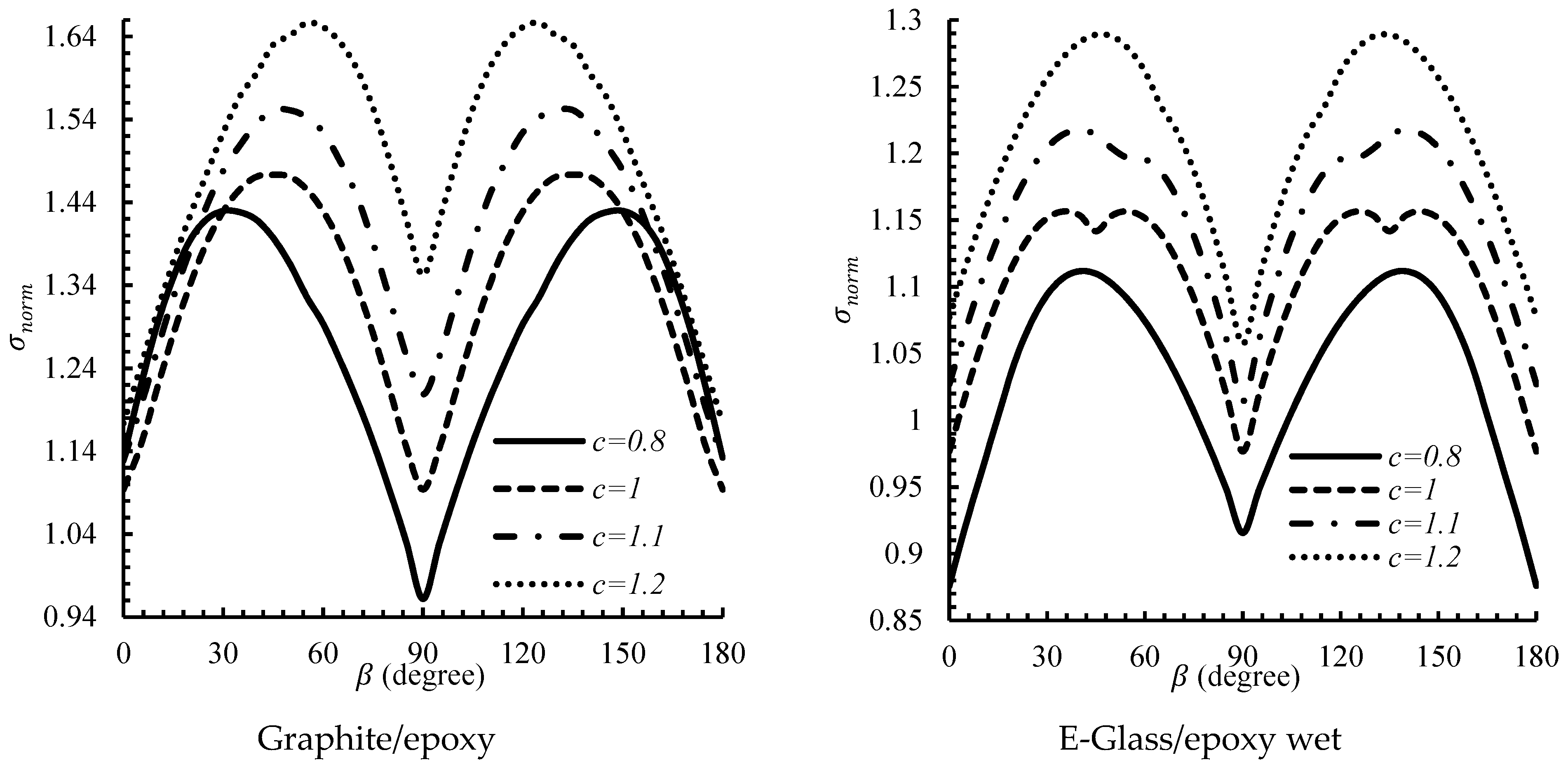
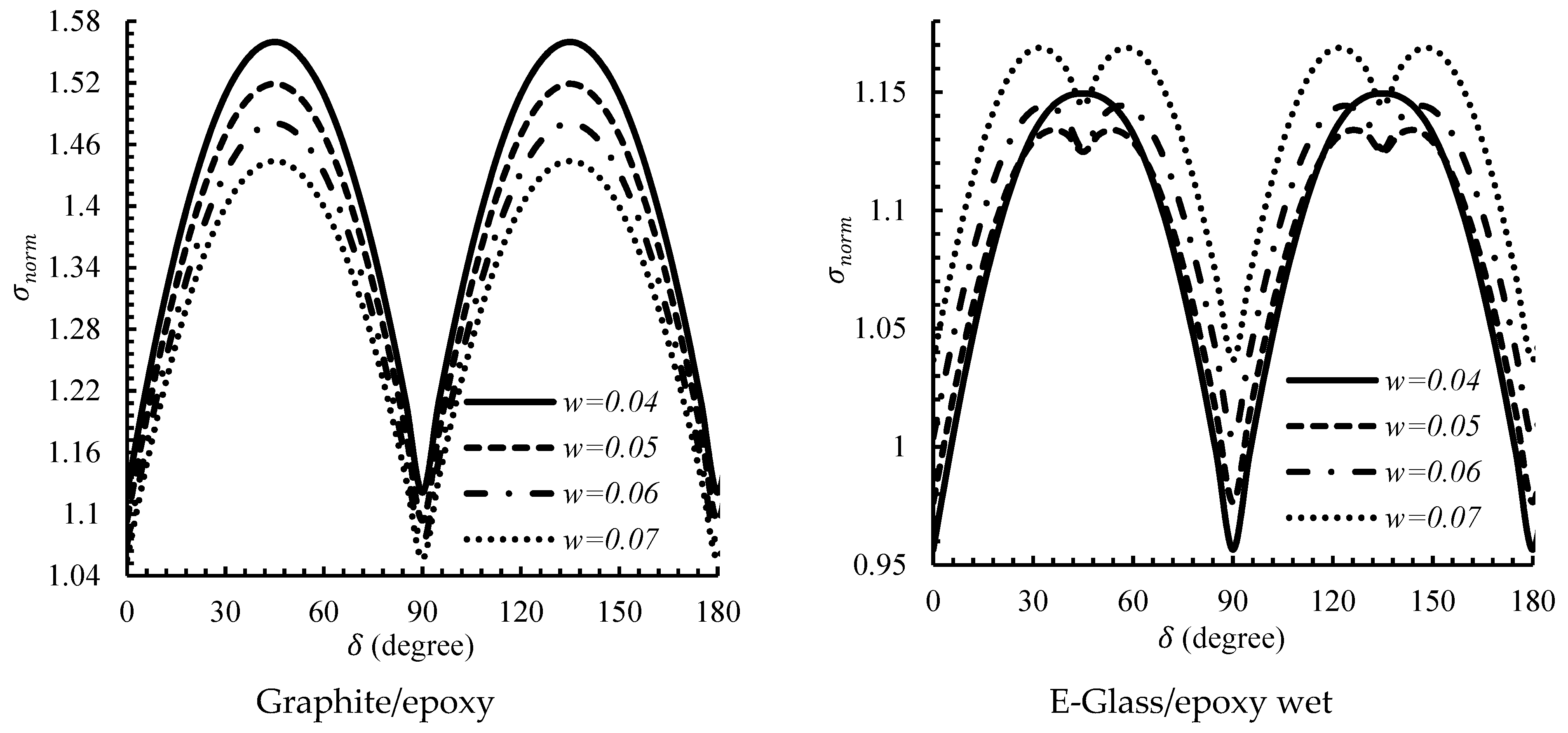
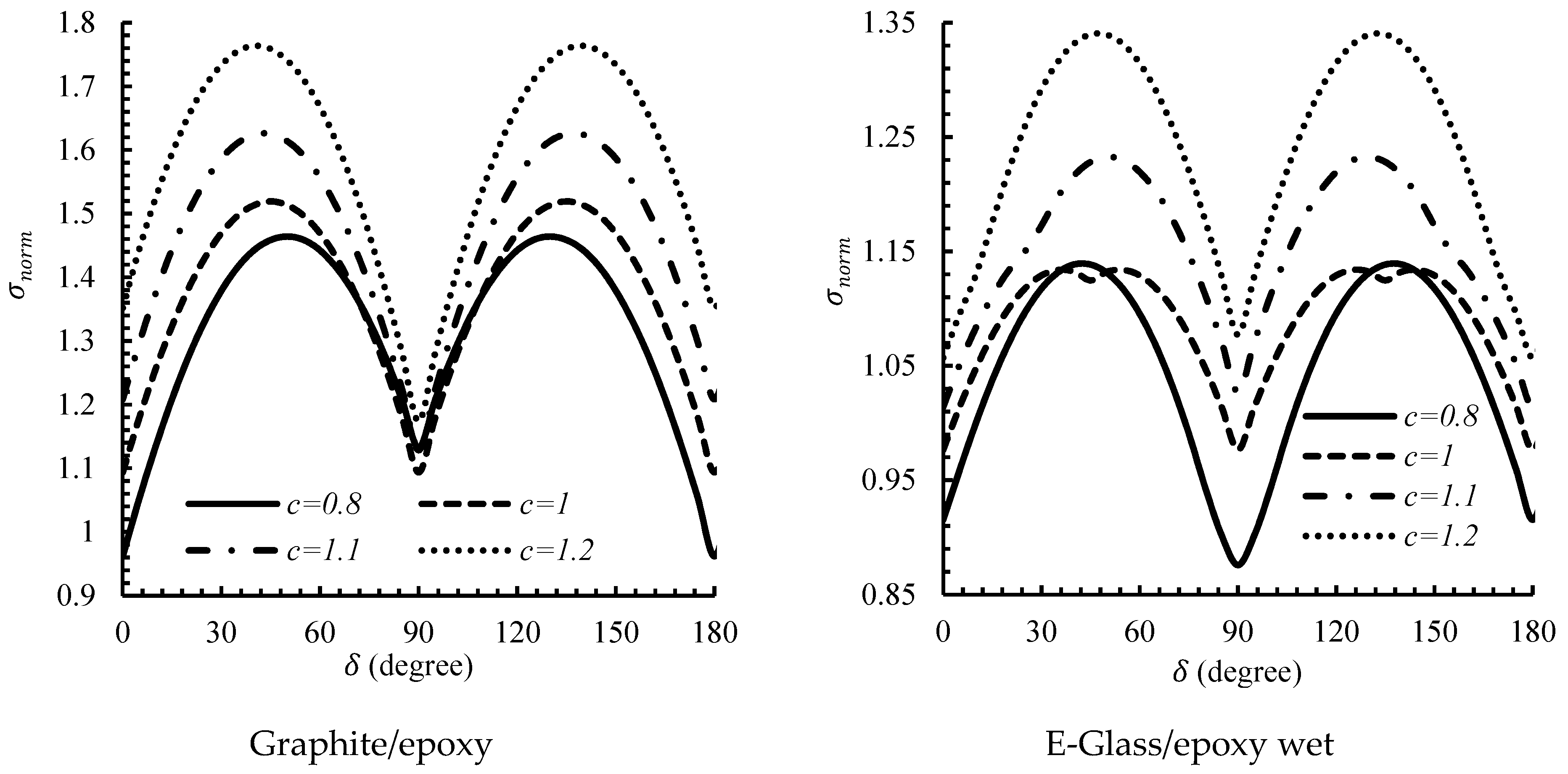
5.1. Effect of Hole Rotation Angles
5.2. Effect of Heat Flux Angle
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Bitsadze, L. Explicit solution of one boundary value problem of thermoelasticity for a circle with diffusion, microtemperatures, and microconcentrations. Acta Mech. 2020, 231, 3551–3563. [Google Scholar] [CrossRef]
- Sarkar, N. Thermoelastic responses of a finite rod due to nonlocal heat conduction. Acta Mech. 2020, 231, 947–955. [Google Scholar] [CrossRef]
- Alshaya, A.; Lin, S.J. Hybrid stress analysis of a near-surface circular hole in finite structures. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2019, 234, 1366–1381. [Google Scholar] [CrossRef]
- Song, H.P.; Song, K.; Schiavone, P.; Gao, C.F. Design of a neutral elastic inhomogeneity via thermal expansion. Acta Mech. 2020, 231, 2867–2876. [Google Scholar] [CrossRef]
- Jafari, M.; Chaleshtari, M.H.B.; Abdolalian, H.; Craciun, E.-M.; Feo, L. Determination of forces and moments per unit length in symmetric exponential FG plates with a quasi-triangular hole. Symmetry 2020, 12, 834. [Google Scholar] [CrossRef]
- Wang, X.; Schiavone, P. Uniformity of stresses inside a non-elliptical inhomogeneity near an irregularly shaped hole in plane elasticity. Mech. Mater. 2020, 145, 103389. [Google Scholar] [CrossRef]
- Blesa Gracia, J.; Rammerstorfer, F.G. Increase in buckling loads of plates by introduction of cutouts. Acta Mech. 2019, 230, 2873–2889. [Google Scholar] [CrossRef]
- Wang, S.R.; Wang, Y.H.; Gong, J.; Wang, Z.L.; Huang, Q.X.; Kong, F.L. Failure mechanism and constitutive relation for an anchorage segment of an anchor cable under pull-out loading. Acta Mech. 2020, 231, 3305–3317. [Google Scholar] [CrossRef]
- Jafari, M.; Hoseyni, S.A.M.; Altenbach, H.; Craciun, E.-M. Optimum design of infinite perforated orthotropic and isotropic plates. Mathematics 2020, 8, 569. [Google Scholar] [CrossRef]
- Groza, G.; Jianu, M.; Pop, N. Infinitely differentiable functions represented into Newton interpolating series. Carpathian J. Math. 2014, 30, 309–316. [Google Scholar]
- Jafari, M.; Bayati Chaleshtari, M.H. Using dragonfly algorithm for optimization of orthotropic infinite plates with a quasi-triangular cut-out. Eur. J. Mech. A/Solids 2017, 66, 1–14. [Google Scholar] [CrossRef]
- Lekhnitskii, S.G. Anisotropic Plates, 2nd ed.; Gordon and Breach Science: New York, NY, USA, 1968. [Google Scholar]
- Florence, A.L.; Goodier, J.N. Thermal stress at spherical cavities and circular holes in uniform heat flow. J. Appl. Mech. 1959, 26, 293–294. [Google Scholar]
- Florence, A.L.; Goodier, J.N. Thermal stresses due to disturbance of uniform heat flow by an insulated ovaloid hole. J. Appl. Mech. 1960, 27, 635–639. [Google Scholar] [CrossRef]
- Hasebe, N.; Wang, X. Complex variable method for thermal stress problem. J. Therm. Stresses 2005, 28, 595–648. [Google Scholar] [CrossRef]
- Tarn, J.Q.; Wang, Y.M. Thermal stresses in anisotropic bodies with a hole or a rigid inclusion. J. Therm. Stresses 1993, 16, 455–471. [Google Scholar] [CrossRef]
- Chao, C.K.; Chang, K.W. Contact stresses in an infinite plate containing a rigid circular inclusion under thermal loads. Acta Mech. 2001, 152, 95–108. [Google Scholar] [CrossRef]
- Wang, X.; Dong, M.C.; Lu, G. Thermal elastic-plastic stress analysis of an anisotropic structure. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2003, 217, 723–733. [Google Scholar] [CrossRef]
- Ukadgaonker, V.G.; Rao, D.K.N. A general solution for stresses around holes in symmetric laminates under inplane loading. Compos. Struct. 2000, 49, 339–354. [Google Scholar] [CrossRef]
- Sharma, D.S. Stresses around polygonal hole in an infinite laminated composite plate. Eur. J. Mech. A/Solids 2015, 54, 44–52. [Google Scholar] [CrossRef]
- Goyat, V.; Verma, S.; Garg, R.K. Reduction of stress concentration for a rounded rectangular hole by using a functionally graded material layer. Acta Mech. 2017, 228, 3695–3707. [Google Scholar] [CrossRef]
- Dai, M.; Yang, H.-B.; Schiavone, P. Stress concentration around an elliptical hole with surface tension based on the original Gurtin–Murdoch model. Mech. Mater. 2019, 135, 144–148. [Google Scholar] [CrossRef]
- Damghani, M.; Harrison, C.; Kennedy, D. The effects of composite laminate stiffness and loading on stress resultant concentration factor around a hole. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2018, 232, 1033–1049. [Google Scholar] [CrossRef]
- Choi, H.J. Thermal stresses due to a uniform heat flow disturbed by a pair of offset parallel cracks in an infinite plane with orthotropy. Eur. J. Mech. A/Solids 2017, 63, 1–13. [Google Scholar] [CrossRef]
- Xiao, J.; Xu, Y.; Zhang, F. An analytic solution for the problem of two symmetrical edge cracks emanating from a circular hole with surface effect under antiplane shear. Acta Mech. 2018, 229, 4915–4925. [Google Scholar] [CrossRef]
- Guo, L.-C.; Noda, N. An analytical method for thermal stresses of a functionally graded material cylindrical shell under a thermal shock. Acta Mech. 2010, 214, 71–78. [Google Scholar] [CrossRef]
- Khan, K.A.; Barello, R.; Muliana, A.H.; Lévesque, M. Coupled heat conduction and thermal stress analyses in particulate composites. Mech. Mater. 2011, 43, 608–625. [Google Scholar] [CrossRef]
- Zhang, Z.; Demir, K.; Gu, G.X. Computational analysis of thermally induced stress concentration in structures with geometric constraints. Mech. Mater. 2019, 133, 102–110. [Google Scholar] [CrossRef]
- Li, L.; Jia, P.; Pan, W. Temperature effect on the tensile behaviors of carbon/polyimide composite laminate. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2016, 231, 4592–4602. [Google Scholar] [CrossRef]
- Mahmoudi, H.; Atefi, G. Analytical solution for thermal stresses in a hollow cylinder under periodic thermal loading. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2011, 226, 1705–1724. [Google Scholar] [CrossRef]
- Jafari, M.; Nazari, M.B.; Taherinasab, A. Thermal stress analysis in metallic plates with a non-circular hole subjected to uniform heat flux. Eur. J. Mech. A/Solids 2016, 59, 356–363. [Google Scholar] [CrossRef]
- Jafari, M.; Bagher Nazari, M.; Taheri Nasab, A. Study of the effective parameters on stress distribution around triangular hole in metallic plates subjected to uniform heat flux. J. Therm. Stresses 2016, 39, 333–344. [Google Scholar] [CrossRef]
- Rasouli, M.; Jafari, M. Thermal stress analysis of infinite anisotropic plate with elliptical hole under uniform heat flux. J. Therm. Stresses 2016, 39, 1341–1355. [Google Scholar] [CrossRef]
- Chao, C.K.; Chen, F.M.; Lin, T.H. Thermal stresses induced by a remote uniform heat flow interacting with two circular inclusions. J. Therm. Stresses 2017, 40, 564–582. [Google Scholar] [CrossRef]
- Chao, C.-K.; Gao, B. Mixed boundary-value problems of two-dimensional anisotropic thermoelasticity with elliptic boundaries. Int. J. Solids Struct. 2001, 38, 5975–5994. [Google Scholar] [CrossRef]
- Chiang, C.-R. Thermal stress at a circular hole in cubic crystals under uniform heat flow. Acta Mech. 2018, 229, 3963–3969. [Google Scholar] [CrossRef]
- Jafari, M.; Jafari, M. Thermal stress analysis of orthotropic plate containing a rectangular hole using complex variable method. Eur. J. Mech. A/Solids 2019, 73, 212–223. [Google Scholar] [CrossRef]
- Jafari, M.; Jafari, M. Effect of hole geometry on the thermal stress analysis of perforated composite plate under uniform heat flux. J. Compos. Mater. 2018, 53, 1079–1095. [Google Scholar] [CrossRef]
- Hahn, D.W.; Özişik, M.N. Heat Conduction Fundamentals. In Heat Conduction, 3rd ed.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2012; pp. 1–39. [Google Scholar]

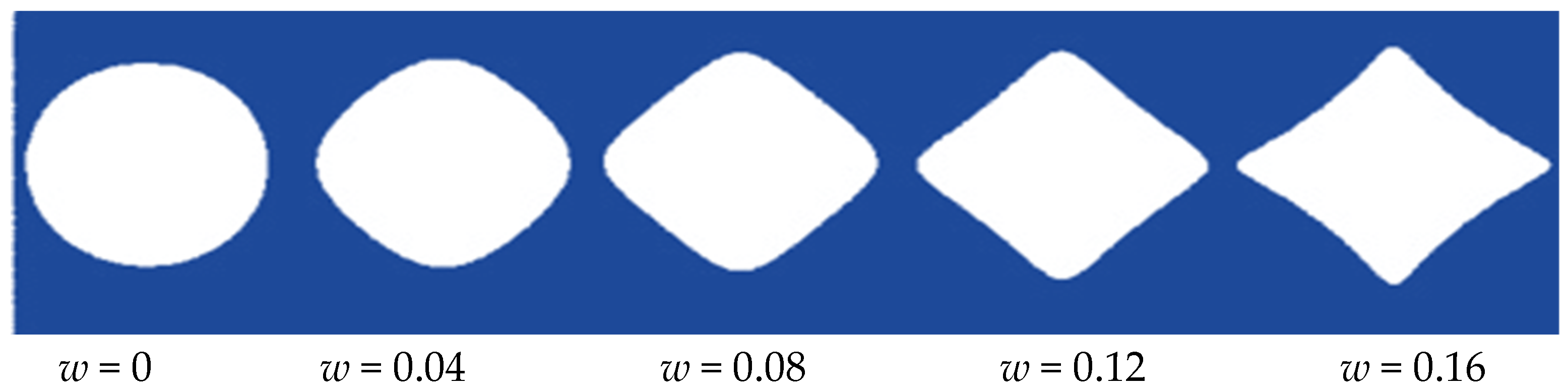
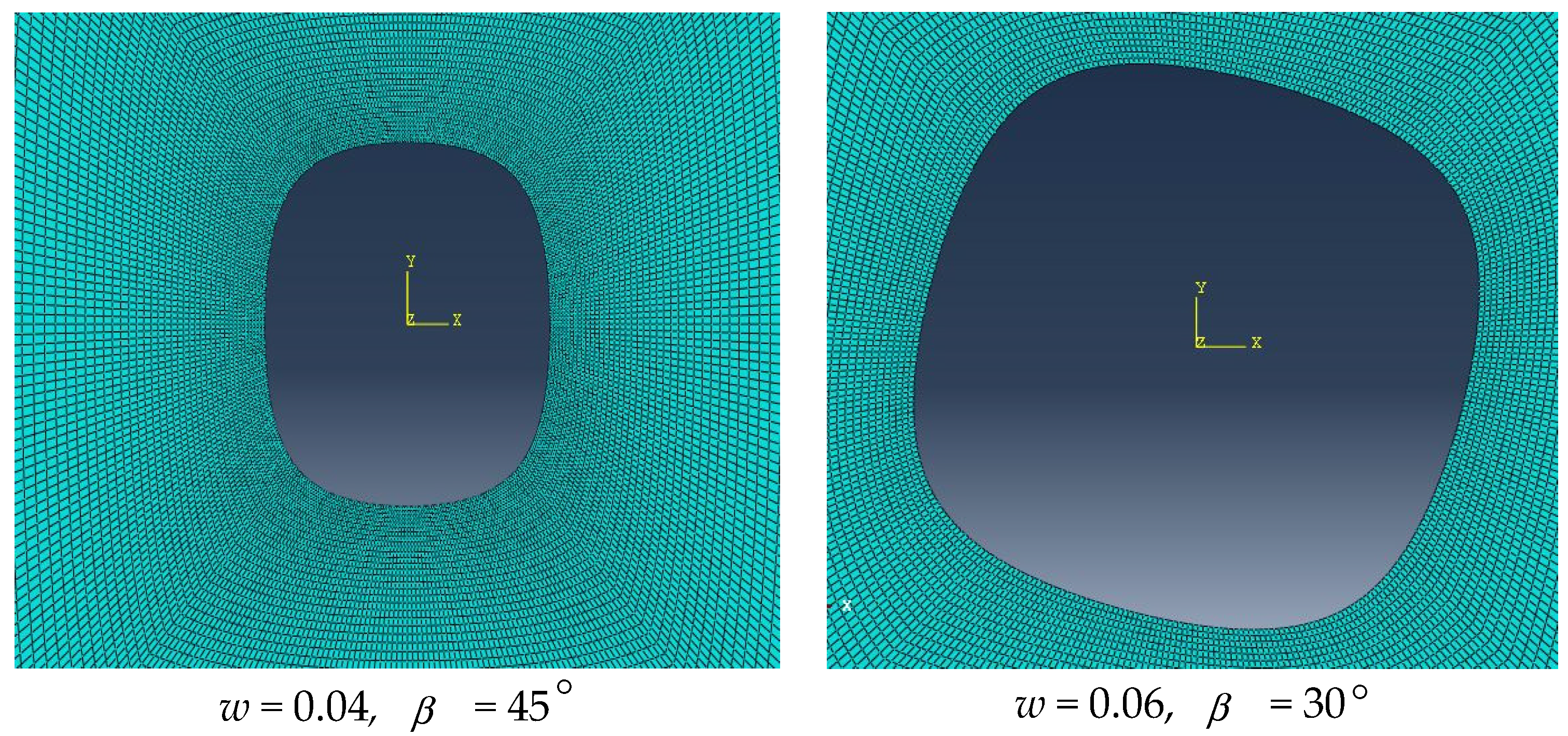



| Material | E11 (GPa) | E22 (GPa) | G12 (GPa) | υ12 | α11 (K−1) | α22 (K−1) | K11 (Wm−1 K−1) | K22 (Wm−1 K−1) |
|---|---|---|---|---|---|---|---|---|
| Graphite/epoxy | 144.8 | 9.7 | 4.1 | 0.3 | −3 × 10−6 | 2.8 × 10−5 | 4.62 | 0.72 |
| E-Glass/epoxy wet | 35 | 9 | 4.7 | 0.28 | 5.5 × 10−6 | 2.5 × 10−5 | 2.2 | 1.1 |
| , , | ||||||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chaleshtari, M.H.B.; Jafari, M.; Khoramishad, H.; Craciun, E.-M. Mutual Influence of Geometric Parameters and Mechanical Properties on Thermal Stresses in Composite Laminated Plates with Rectangular Holes. Mathematics 2021, 9, 311. https://doi.org/10.3390/math9040311
Chaleshtari MHB, Jafari M, Khoramishad H, Craciun E-M. Mutual Influence of Geometric Parameters and Mechanical Properties on Thermal Stresses in Composite Laminated Plates with Rectangular Holes. Mathematics. 2021; 9(4):311. https://doi.org/10.3390/math9040311
Chicago/Turabian StyleChaleshtari, Mohammad Hossein Bayati, Mohammad Jafari, Hadi Khoramishad, and Eduard-Marius Craciun. 2021. "Mutual Influence of Geometric Parameters and Mechanical Properties on Thermal Stresses in Composite Laminated Plates with Rectangular Holes" Mathematics 9, no. 4: 311. https://doi.org/10.3390/math9040311
APA StyleChaleshtari, M. H. B., Jafari, M., Khoramishad, H., & Craciun, E.-M. (2021). Mutual Influence of Geometric Parameters and Mechanical Properties on Thermal Stresses in Composite Laminated Plates with Rectangular Holes. Mathematics, 9(4), 311. https://doi.org/10.3390/math9040311







