Existence and Global Attractivity of Pseudo Almost Periodic Solutions for Clifford-Valued Fuzzy Neural Networks with Proportional Delays

Abstract

In this paper, Clifford-valued fuzzy neural networks with proportional delays, whose leakage term coefficients are also Clifford numbers, are considered. Based on the Banach fixed point theorem and differential inequality technique, we use a direct method to obtain the existence, uniqueness, and global attractivity of pseudo almost periodic solutions for the considered networks. Finally, we provide a numerical example to illustrate the feasibility of our results. Our results are new.

1. Introduction

The Clifford-valued neural network is a generalization of a real-valued neural network, complex-valued neural network, and quaternion-valued neural network, and has been shown superior to a real-valued neural network [1,2]. Because the multiplication of Clifford algebra does not meet the commutative law, there are few results on the dynamics of Clifford-valued neural networks [3,4,5,6,7,8,9,10,11]. Many existing results are obtained by decomposing a Clifford-valued system into a real-value system [3,4,5,6]. Therefore, it is a meaningful and challenging work to study the dynamics of Clifford-valued systems via a direct method; that is, without decomposing Clifford-valued systems into real-valued systems [7,8,9,10,11].

Since time delay is inevitable in modeling real systems, in recent years, as an important mathematical model, systems with proportional time delays play important roles in many application fields, such as physics, biological systems, neural network systems, and control science [12,13]. Therefore, many scholars have studied the dynamics of neural networks with proportional delays. For example, in [14], the existence and global attractiveness of pseudo almost periodic solutions for a class of fuzzy cellular neural networks with multiple proportional delays are obtained by using the fixed point theorem of contractive mapping and differential inequality technique, in [15], the existence, uniqueness, and exponential stability of anti-periodic solutions for recurrent neural networks with multiple delays are established by using the Lyapunov method and inequality technique. In [16], the finite time synchronization problem of a class of fuzzy cellular neural networks with time-varying coefficients and proportional delays is investigated. In [17], a class of competitive neural networks with multiple proportional delays is studied, and a new sufficient condition for the global exponential stability of such a network is obtained.

On the other hand, in the mathematical modeling of practical problems, uncertainty or fuzziness is a factor to be considered. On the basis of traditional cellular neural networks, fuzzy cellular neural networks [18] were first proposed in 1996. They are neural networks that incorporate fuzzy logic into the structure of traditional cellular neural networks. They have important applications in image processing and pattern recognition; therefore, fuzzy neural networks have been widely studied [14,15,16,17,18,19,20,21].

In addition, almost periodic oscillation and pseudo almost periodic oscillation are important dynamics of neural networks. Many authors have studied the existence and stability of almost periodic solutions [5,13] and pseudo almost periodic solutions [22,23,24,25,26] of neural networks, including stochastic neural networks [27] and fuzzy neural networks [28,29].

Moreover, recently, the existence and global exponential stability of $(\mu ,\nu )$-pseudo almost periodic solutions to a class of Clifford-valued higher order Hopfield neural networks, with bounded multiple discrete delays whose leakage term coefficients are also Clifford numbers, is studied in [30]. Proportional delays are a class of unbounded delays. Neural networks with proportional delays are a class of neural networks with important theoretical and application values. However, up until now, the results of almost periodic oscillation of neural networks with proportional delays and whose leakage term coefficients are also Clifford numbers, have not been reported.

Inspired by the above analysis, the purpose of this paper is to study the existence and attraction of pseudo almost periodic solutions for a class of Clifford-valued fuzzy neural networks with proportional delays and whose leakage term coefficients are also Clifford numbers. To the best of our knowledge, this is the first paper to study the existence and attractivity of pseudo almost periodic solutions of Clifford-valued neural networks with proportional delay and whose leakage coefficients are also Clifford numbers.

The rest of the paper is arranged as follows. In Section 2, we review some concepts, introduce some lemmas, and give the model’s description. In Section 3, by using the direct method, we establish the existence of pseudo almost periodic solutions for the network under consideration. In Section 4, we study the global attractivity of pseudo almost periodic solutions. In Section 5, we give a numerical example to illustrate the feasibility of our results. Finally, we draw a brief conclusion in Section 6.

2. Model Description and Preliminaries

The real Clifford algebra over ${\mathbb{R}}^m$ is defined as

$$\begin{array}{c}\hfill \mathcal{A}=\left\{\sum _{A\in \mathsf{\Omega }}{x}^A{e}_A,x^A\in \mathbb{R}\right\},\end{array}$$

where $\mathsf{\Omega }=\{\varnothing ,1,2,\cdots A,\cdots ,12\cdots m\}$, $e_A=e_{{\hslash }_1}{e}_{{\hslash }_2}\cdots e_{{\hslash }_k}=e_{{\hslash }_1{\hslash }_2\cdots {\hslash }_k}$ for $A={\hslash }_1{\hslash }_2\cdots {\hslash }_k$, $1<{\hslash }_1<{\hslash }_2<\cdots <{\hslash }_k<m$. In addition, $e_{\varnothing }=e_0=1$ and $e_{\hslash },\hslash =1,2,\cdots ,m$ are said to be Clifford generators and satisfy $e_p^2=1,p=1,2,\cdots ,s$, $e_p^2=-1,p=s+1,s+2,\cdots ,m$, $e_p{e}_q+e_q{e}_p=0,p\ne q$, where $p,q=1,2,\cdots ,m$.

For $x={\sum }_A{x}^A{e}_A\in \mathcal{A}$, we define ${\parallel x\parallel }_{\mathcal{A}}=\underset{A}{max}\left\{\right|x_A\left|\right\}$ and for $x={(x_1,x_2,\cdots ,x_n)}^T\in {\mathcal{A}}^n$, we define ${\parallel x\parallel }_{{\mathcal{A}}^n}=\underset{1\le p\le n}{max}\{\parallel x_p{\parallel }_{\mathcal{A}}\}$, then $(\mathcal{A},{\parallel ·\parallel }_{\mathcal{A}})$ and $({\mathcal{A}}^n,{\parallel ·\parallel }_{{\mathcal{A}}^n})$ are Banach spaces. For $x={\sum }_A{x}^A{e}_A$, we define $x^c={\displaystyle \sum _{A\ne \varnothing }}{x}^A{e}_A$ and $x^{\varnothing }=x-x^c$.

According to [19], for $x=\sum x^A{e}_A,y=\sum y^A{e}_A\in \mathcal{A}$, we define

$$\begin{array}{c}\hfill x\bigvee y=\sum (x^A\bigvee y^A)e_A\mathrm{and}x\bigwedge y=\sum (x^A\bigwedge y^A)e_A,\end{array}$$

where $x^A\bigvee y^A=max\{x^A,y^A\},x^A\bigwedge y^A=min\{x^A,y^A\}.$

The model we want to study in this paper is as follows:

$$\begin{array}{cc}\hfill {\dot{x}}_i\left(t\right)=& -c_i\left(t\right)x_i\left(t\right)+\sum _{j=1}^n{a}_{ij}\left(t\right)f_j\left(x_j\left(t\right)\right)+\sum _{j=1}^n{b}_{ij}\left(t\right)g_j\left(x_j\left(q_{ij}t\right)\right)+\underset{j=1}{\overset{n}{\bigvee }}{\alpha }_{ij}\left(t\right)h_j\left(x_j\left(q_{ij}t\right)\right)\hfill \\ \hfill & +\underset{j=1}{\overset{n}{\bigwedge }}{\beta }_{ij}\left(t\right)h_j\left(x_j\left(q_{ij}t\right)\right)+\underset{j=1}{\overset{n}{\bigvee }}{S}_{ij}\left(t\right)v_j\left(t\right)+\underset{j=1}{\overset{n}{\bigwedge }}{T}_{ij}\left(t\right)v_j\left(t\right)+I_i\left(t\right),i=1,2,\dots ,n,\hfill \end{array}$$

(1)

where n is the number of neurons in layers, $x_i\left(t\right)\in \mathcal{A}$ represents the state of the ith unit at time t, $\mathcal{A}$ is a Clifford algebra; $c_i\left(t\right)\in \mathcal{A}$ is the rate with which the ith unit will reset its potential to the resting state in isolation when disconnected from the network and external inputs; $a_{ij}\left(t\right),b_{ij}\left(t\right)\in \mathcal{A}$ correspond to the first-order and second-order connection weights of the fuzzy neural network; ${\alpha }_{ij}\left(t\right)\in \mathcal{A}$ is the fuzzy feedback MAX template; ${\beta }_{ij}\left(t\right)\in \mathcal{A}$ is the fuzzy feedback MIN template; $S_{ij}\left(t\right)$ and $T_{ij}\left(t\right)\in \mathcal{A}$ are the fuzzy feed-forward MAX template and the fuzzy feed-forward MIN template; $v_j\left(t\right)\in \mathcal{A}$ is the input of the jth neuron; $I_i\left(t\right)\in \mathcal{A}$ stands for the external inputs; $f_j\left(t\right),g_j\left(t\right),h_j\left(t\right)\in \mathcal{A}$ are the activation functions; $0<q_{ij}<1$ is the proportional coefficient of proportional delay.

For convenience, we will adopt the following notations:

$${\overline{c}}_i^{\varnothing }=\underset{t\in \mathbb{R}}{inf}\left\{{\parallel c_i^{\varnothing }\left(t\right)\parallel }_{\mathcal{A}}\right\},{\overline{c}}_i^c=\underset{t\in \mathbb{R}}{sup}\left\{{\parallel c_i^c\left(t\right)\parallel }_{\mathcal{A}}\right\},a_{ij}^{+}=\underset{t\in \mathbb{R}}{sup}\left\{{\parallel a_{ij}\left(t\right)\parallel }_{\mathcal{A}}\right\},$$

$$b_{ij}^{+}=\underset{t\in \mathbb{R}}{sup}\left\{{\parallel b_{ij}\left(t\right)\parallel }_{\mathcal{A}}\right\},{\alpha }_{ij}^{+}=\underset{t\in \mathbb{R}}{sup}\left\{{\parallel {\alpha }_{ij}\left(t\right)\parallel }_{\mathcal{A}}\right\},{\beta }_{ij}^{+}=\underset{t\in \mathbb{R}}{sup}\left\{{\parallel {\beta }_{ij}\left(t\right)\parallel }_{\mathcal{A}}\right\},$$

The initial values of system (1) are given by

$$x_i\left(s\right)={\phi }_i\left(s\right),s\in [q{t}_0,t_0],$$

where ${\phi }_i\in C([q{t}_0,t_0],\mathbb{R}),q=\underset{1\le j\le n}{min}\left\{q_{ij}\right\}$.

Let $BC(\mathbb{R},{\mathcal{A}}^n)$ be the collection of all bounded and continuous functions from $\mathbb{R}$ to ${\mathcal{A}}^n$. The space $(BC(\mathbb{R},{\mathcal{A}}^n),{\parallel ·\parallel }_0)$ is a Banach space when it is endowed with the norm:

$$\begin{array}{c}\hfill {\parallel f\parallel }_0=\underset{t\in \mathbb{R}}{sup}{\parallel f\left(t\right)\parallel }_{{\mathcal{A}}^n},\end{array}$$

where $f\in BC(\mathbb{R},{\mathcal{A}}^n)$.

Definition 1

([20]). A function $f\in BC(\mathbb{R},{\mathcal{A}}^n)$ is called to an almost periodic function, if for every $\epsilon >0$, there exists $l=l\left(\epsilon \right)>0$ such that for each interval with length $l\left(\epsilon \right)$, one can find a number $\tau \in [a,a+l(\epsilon \left)\right]$ satisfying

$$\begin{array}{c}\hfill {\parallel f(t+\tau )-f\left(t\right)\parallel }_{{\mathcal{A}}^n}<\epsilon ,\forall t\in \mathbb{R}.\end{array}$$

All of these functions will be denoted by $AP(\mathbb{R},{\mathcal{A}}^n)$.

Definition 2

([20]). A function $f\in BC(\mathbb{R},{\mathcal{A}}^n)$ is said to be pseudo almost periodic, if it can be written as $f=f_1+f_2$, where $f_1\in AP(\mathbb{R},{\mathcal{A}}^n)$, $f_2\in PA{P}_0(\mathbb{R},{\mathcal{A}}^n)$ and

$$\begin{array}{c}\hfill PA{P}_0(\mathbb{R},{\mathcal{A}}^n)=\left\{f\in BC(\mathbb{R},{\mathcal{A}}^n)|\underset{T\to +\infty }{lim}\frac{1}{2T}{\int }_{-T}^T{\parallel f\left(t\right)\parallel }_{{\mathcal{A}}^n}dt=0\right\}.\end{array}$$

Lemma 1

([20]). If $f,g\in PAP(\mathbb{R},{\mathcal{A}}^n)$, then $f+g,fg\in PAP(\mathbb{R},{\mathcal{A}}^n)$.

Lemma 2

([20]). Let $f\in C(\mathcal{A},{\mathcal{A}}^n)$ satisfy the Lipschitz condition and $g\in PAP(\mathbb{R},{\mathcal{A}}^n)$, then $f\left(g(·)\right)\in PAP(\mathbb{R},{\mathcal{A}}^n)$.

Lemma 3

( [21]). If $0<q<1$, $t\in \mathbb{R}$, $x\in PAP(\mathbb{R},{\mathcal{A}}^n)$, then $x\left(qt\right)\in PAP(\mathbb{R},{\mathcal{A}}^n)$.

Using the same proof method as Lemma 2 in [14], we can prove

Lemma 4.

Assume that $x,y\in PAP(\mathbb{R},\mathcal{A})$, then we have $x\bigvee y,x\bigwedge y\in PAP(\mathbb{R},\mathcal{A})$.

Lemma 5

([20]). The space $(PAP(\mathbb{R},{\mathcal{A}}^n),\parallel ·{\parallel }_0)$ is a Banach space.

Similar to the proof of Corollary 1 in [18], one can easily show that

Lemma 6.

If ${\alpha }_{ij},{\beta }_{ij}\in C(\mathbb{R},\mathcal{A}),f\in C(\mathbb{R},\mathcal{A}),x,y\in \mathcal{A}$. Then we have

$$\begin{array}{cc}\hfill {\parallel \underset{j=1}{\overset{n}{\bigwedge }}{\alpha }_{ij}\left(t\right)f_j\left(x\right)-\underset{j=1}{\overset{n}{\bigwedge }}{\alpha }_{ij}\left(t\right)f_j\left(y\right)\parallel }_{\mathcal{A}}\le & \sum _{j=1}^n\parallel {\alpha }_{ij}{\left(t\right)\parallel }_{\mathcal{A}}{\parallel f_j\left(x\right)-f_j\left(y\right)\parallel }_{\mathcal{A}},\hfill \\ \hfill \parallel \underset{j=1}{\overset{n}{\bigvee }}{\beta }_{ij}\left(t\right)f_j\left(x\right)-\underset{j=1}{\overset{n}{\bigvee }}{\beta }_{ij}\left(t\right)f_j\left(y\right){\parallel }_{\mathcal{A}}\le & \sum _{j=1}^n\parallel {\beta }_{ij}{\left(t\right)\parallel }_{\mathcal{A}}{\parallel f_j\left(x\right)-f_j\left(y\right)\parallel }_{\mathcal{A}}.\hfill \end{array}$$

Lemma 7

([20]). Let $G\left(t\right)={\int }_{-\infty }^t{e}^{-{\int }_s^{t}a\left(u\right)du}F\left(s\right)ds$, where $a\in AP(\mathbb{R},{\mathbb{R}}^{+})$ with $\underset{t\in \mathbb{R}}{inf}a\left(t\right)>0$ and $F\in PAP(\mathbb{R},{\mathcal{A}}^n)$, then $G\in PAP(\mathbb{R},{\mathcal{A}}^n)$.

The assumptions used in this paper are as follows:

(H₁) 

For $i,j=1,2,\dots n,c_i^{\varnothing }\in AP(\mathbb{R},{\mathbb{R}}^{+})$ with ${\overline{c}}_i^{\varnothing }>0$,$c_i^c,a_{ij},b_{ij},{\alpha }_{ij},{\beta }_{ij}\in PAP(\mathbb{R},\mathcal{A})$,

$S_{ij},T_{ij},I_i\in PAP(\mathbb{R},\mathcal{A})$.

(H₂) 

For $j=1,2,\cdots n$, functions $f_j,g_j,h_j\in C(\mathcal{A},\mathcal{A})$ satisfy there exist constants

$K_j,L_j,M_j,N_j$, such that for any $s,t\in \mathcal{A}$,

$$\begin{array}{c}\hfill \parallel f_j\left(s\right)-f_j{\left(t\right)\parallel }_{\mathcal{A}}\le K_j{\parallel s-t\parallel }_{\mathcal{A}},{\parallel g_j\left(s\right)-g_j\left(t\right)\parallel }_{\mathcal{A}}\le L_j{\parallel s-t\parallel }_{\mathcal{A}},\end{array}$$

$$\begin{array}{c}\hfill {\parallel h_j\left(s\right)-h_j\left(t\right)\parallel }_{\mathcal{A}}\le M_j{\parallel s-t\parallel }_{\mathcal{A}},{\parallel I_j\left(s\right)-I_j\left(t\right)\parallel }_{\mathcal{A}}\le N_j{\parallel s-t\parallel }_{\mathcal{A}},\end{array}$$

and $f_j\left(0\right)=g_j\left(0\right)=h_j\left(0\right)=0.$

(H₃) 

The constant

$$\begin{array}{c}\hfill \delta :=\underset{1\le i\le n}{max}\left\{\frac{1}{{\overline{c}}_i^{\varnothing }}\left({\overline{c}}_i^c+\sum _{j=1}^n{a}_{ij}^{+}{K}_j+\sum _{j=1}^n{b}_{ij}^{+}{L}_j+\sum _{j=1}^n{\alpha }_{ij}^{+}{M}_j+\sum _{j=1}^n{\beta }_{ij}^{+}{M}_j\right)\right\}<1.\end{array}$$

3. Pseudo Almost Periodic Solutions

In this section, by the contracting mapping principle, we will study the existence of pseudo almost periodic solutions of (1).

For $i,j=1,2,\dots ,n$, we define

$$\begin{array}{cc}\hfill F_i(t,x)=& -c_i^c\left(t\right)x_i\left(t\right)+\sum _{j=1}^n{a}_{ij}\left(t\right)f_j\left(x_j\left(t\right)\right)+\sum _{j=1}^n{b}_{ij}\left(t\right)g_j\left(x_j\left(q_{ij}t\right)\right)+\underset{j=1}{\overset{n}{\bigvee }}{\alpha }_{ij}\left(t\right)h_j\left(x_j\left(q_{ij}t\right)\right)\hfill \\ \hfill & +\underset{j=1}{\overset{n}{\bigwedge }}{\beta }_{ij}\left(t\right)h_j\left(x_j\left(q_{ij}t\right)\right)+I_i\left(t\right),i=1,2,\dots ,n.\hfill \end{array}$$

Obviously, if $x={(x_1,x_2,\cdots x_n)}^T$ is a solution of the integral equation:

$$\begin{array}{c}\hfill x_i\left(t\right)={\int }_{-\infty }^t{e}^{-{\int }_s^t{c}_i^{\varnothing }\left(u\right)du}\left[F_i(s,x)+\underset{j=1}{\overset{n}{\bigvee }}{S}_{ij}\left(s\right)v_j\left(s\right)+\underset{j=1}{\overset{n}{\bigwedge }}{T}_{ij}\left(s\right)v_j\left(s\right)+I_i\left(s\right)\right]ds,i=1,2,\dots ,n,\end{array}$$

then x is a solution of system (1).

Let $B=(PAP(\mathbb{R},{\mathcal{A}}^n),\parallel ·{\parallel }_0)$ and

$$\begin{array}{cc}\hfill \tilde{\phi }\left(t\right)=& ({\int }_{-\infty }^t{e}^{-{\int }_s^t{c}_1^{\varnothing }\left(u\right)du}\left(\underset{j=1}{\overset{n}{\bigvee }}{S}_{1j}\left(s\right)v_j\left(s\right)+\underset{j=1}{\overset{n}{\bigwedge }}{T}_{1j}\left(s\right)v_j\left(s\right)+I_1\left(s\right)\right)ds,\cdots ,\hfill \\ \hfill & {\int }_{-\infty }^t{e}^{-{\int }_s^t{c}_n^{\varnothing }\left(u\right)du}\left(\underset{j=1}{\overset{n}{\bigvee }}{S}_{nj}\left(s\right)v_j\left(s\right)+\underset{j=1}{\overset{n}{\bigwedge }}{T}_{nj}\left(s\right)v_j\left(s\right)+I_n\left(s\right)\right)ds{)}^T.\hfill \end{array}$$

Define

$$\begin{array}{c}\hfill B_{\delta }=\left\{\phi \in B|{\parallel \phi -\tilde{\phi }\parallel }_0\le \frac{\delta N}{1-\delta }\right\},\end{array}$$

where $\delta$ is mentioned in (H₃) and N is a positive constant satisfying $N\ge \parallel \tilde{\phi }{\parallel }_0$, then we have

$$\begin{array}{c}\hfill {\parallel \phi \parallel }_0\le {\parallel \phi -\tilde{\phi }\parallel }_0+\parallel \tilde{\phi }{\parallel }_0\le \frac{\delta N}{1-\delta }+N=\frac{N}{1-\delta }.\end{array}$$

Theorem 1.

If assumptions (H₁)–(H₃) hold, then system (1) has a unique pseudo almost periodic solution in $B_{\delta }=\{\phi \in B|{\parallel \phi -\tilde{\phi }\parallel }_0\le \frac{\delta N}{1-\delta }\}$.

Proof. 

Consider the mapping $T:B\to BC(\mathbb{R},{\mathcal{A}}^n)$ defined by setting $T\phi =(T_1\phi ,T_2\phi ,\cdots$, $T_n{\phi )}^T$, where

$$\begin{array}{c}\hfill \left(T_i\phi \right)\left(t\right)={\int }_{-\infty }^t{e}^{-{\int }_s^t{c}_i^{\varnothing }\left(u\right)du}\left[F_i(s,x)+\underset{j=1}{\overset{n}{\bigvee }}{S}_{ij}\left(s\right)v_j\left(s\right)+\underset{j=1}{\overset{n}{\bigwedge }}{T}_{ij}\left(s\right)v_j\left(s\right)+I_i\left(s\right)\right]ds.\end{array}$$

By Lemmas 1–4, we obtain $F_i\in PAP(\mathbb{R},\mathcal{A})$. Further, by Lemma 7, we have $T\phi \in PAP(\mathbb{R},\mathcal{A})$.

We will divide the rest of the proof into two steps.

Step 1, we will verify $T:B_{\delta }\to B_{\delta }$ is a self-mapping. For any $\phi \in B_{\delta }$, we have

$$\begin{array}{cc}\hfill {\parallel T\phi -\tilde{\phi }\parallel }_0\le & \underset{t\in \mathbb{R}}{sup}\left\{\underset{1\le i\le n}{max}\right\{{\int }_{-\infty }^t{e}^{-{\int }_s^t{c}_i^{\varnothing }\left(u\right)du}({\parallel c_i^c\left(s\right){\phi }_i\left(s\right)\parallel }_{\mathcal{A}}+\sum _{j=1}^n{\parallel a_{ij}\left(s\right)f_j\left({\phi }_j\left(s\right)\right)\parallel }_{\mathcal{A}}\hfill \\ \hfill & +\sum _{j=1}^n{\parallel b_{ij}\left(s\right)g_j\left({\phi }_j\left(q_{ij}s\right)\right)\parallel }_{\mathcal{A}}+\sum _{j=1}^n{\parallel {\alpha }_{ij}\left(s\right)h_j\left({\phi }_j\left(q_{ij}s\right)\right)\parallel }_{\mathcal{A}}\hfill \\ \hfill & +\sum _{j=1}^n{\parallel {\beta }_{ij}\left(s\right)h_j\left({\phi }_j\left(q_{ij}s\right)\right)\parallel }_{\mathcal{A}}\left)ds\right\}\}\hfill \\ \hfill \le & \underset{t\in \mathbb{R}}{sup}\left\{\underset{1\le i\le n}{max}\right\{{\int }_{-\infty }^t{e}^{-{\int }_s^t{c}_i^{\varnothing }\left(u\right)du}({\overline{c}}_i^c{\parallel \phi \parallel }_0+\sum _{j=1}^n{a}_{ij}^{+}{K}_j{\parallel \phi \parallel }_0+\sum _{j=1}^n{b}_{ij}^{+}{L}_j{\parallel \phi \parallel }_0\hfill \\ \hfill & +\sum _{j=1}^n{\alpha }_{ij}^{+}{M}_j{\parallel \phi \parallel }_0+\sum _{j=1}^n{\beta }_{ij}^{+}{M}_j{\parallel \phi \parallel }_0\left)ds\right\}\}\hfill \\ \hfill \le & \underset{1\le i\le n}{max}\left\{\frac{1}{{\overline{c}}_i^{\varnothing }}\left({\overline{c}}_i^c+\sum _{j=1}^n\left[a_{ij}^{+}{K}_j+b_{ij}^{+}{L}_j+{\alpha }_{ij}^{+}{M}_j+{\beta }_{ij}^{+}{M}_j\right]\right)\right\}{\parallel \phi \parallel }_0\hfill \\ \hfill \le & \frac{\delta N}{1-\delta }.\hfill \end{array}$$

Hence, $\phi \left(B_{\delta }\right)\subset B_{\delta }$.

Step 2, we will show T is a contractive mapping. For any $\phi ,\psi \in B_{\delta }$, we find

$$\begin{array}{cc}\hfill {\parallel T\phi -T\psi \parallel }_0\le & \underset{t\in \mathbb{R}}{sup}\left\{\underset{1\le i\le n}{max}\right\{{\int }_{-\infty }^t{e}^{-{\int }_s^t{c}_i^{\varnothing }\left(u\right)du}({\parallel c_i^c\left(s\right)({\phi }_i\left(s\right)-{\psi }_i\left(s\right))\parallel }_{\mathcal{A}}\hfill \\ \hfill & +\sum _{j=1}^n{\parallel a_{ij}\left(s\right)(f_j\left({\phi }_j\left(s\right)\right)-f_j\left({\psi }_j\left(s\right)\right))\parallel }_{\mathcal{A}}\hfill \\ \hfill & +\sum _{j=1}^n{\parallel b_{ij}\left(s\right)(g_j\left({\phi }_j\left(q_{ij}s\right)\right)-g_j\left({\psi }_j\left(q_{ij}s\right)\right))\parallel }_{\mathcal{A}}\hfill \\ \hfill & +\sum _{j=1}^n{\parallel {\alpha }_{ij}\left(s\right)(h_j\left({\phi }_j\left(q_{ij}s\right)\right)-h_j\left({\psi }_j\left(q_{ij}s\right)\right))\parallel }_{\mathcal{A}}\hfill \\ \hfill & +\sum _{j=1}^n{\parallel {\beta }_{ij}\left(s\right)(h_j\left({\phi }_j\left(q_{ij}s\right)\right)-h_j\left({\psi }_j\left(q_{ij}s\right)\right))\parallel }_{\mathcal{A}}\left)ds\right\}\}\hfill \\ \hfill \le & \underset{t\in \mathbb{R}}{sup}\left\{\underset{1\le i\le n}{max}\right\{{\int }_{-\infty }^t{e}^{-{\int }_s^t{c}_i^{\varnothing }\left(u\right)du}({\overline{c}}_i^c{\parallel \phi -\psi \parallel }_0\hfill \\ \hfill & +\sum _{j=1}^n{a}_{ij}^{+}{K}_j{\parallel \phi -\psi \parallel }_0+\sum _{j=1}^n{b}_{ij}^{+}{L}_j{\parallel \phi -\psi \parallel }_0\hfill \\ \hfill & +\sum _{j=1}^n{\alpha }_{ij}^{+}{M}_j{\parallel \phi -\psi \parallel }_0+\sum _{j=1}^n{\beta }_{ij}^{+}{M}_j{\parallel \phi -\psi \parallel }_0\left)ds\right\}\}\hfill \\ \hfill \le & \underset{1\le i\le n}{max}\left\{\frac{1}{{\overline{c}}_i^{\varnothing }}\right({\overline{c}}_i^c+\sum _{j=1}^n{a}_{ij}^{+}{K}_j+\sum _{j=1}^n{b}_{ij}^{+}{L}_j\hfill \\ \hfill & +\sum _{j=1}^n{\alpha }_{ij}^{+}{M}_j+\sum _{j=1}^n{\beta }_{ij}^{+}{M}_j\left)\right\}{\parallel \phi -\psi \parallel }_0\hfill \\ \hfill \le & \delta {\parallel \phi -\psi \parallel }_0.\hfill \end{array}$$

Noticing that $\delta <1$, T is a contracting mapping. Therefore, system (1) possesses a unique one pseudo almost periodic solution in $B_{\delta }$. This completes the proof. □

4. Global Attractivity

Our result on the global attractivity of pseudo almost periodic solutions of system (1) is as follows:

Theorem 2.

If conditions (H₁)–(H₃) hold, then system (1) has a unique pseudo almost periodic solution x satisfying that there exist constants $\lambda >0$ and $M>1$, such that

$$\begin{array}{c}\hfill {\parallel x\left(t\right)-y\left(t\right)\parallel }_{{\mathcal{A}}^n}\le M({\parallel \phi -\psi \parallel }_{\xi }+\epsilon )e^{-\lambda ln\frac{1+t}{1+t_0}},t>t_0,\end{array}$$

where y is an arbitrary solution of system (1) with initial value φ, ψ is the initial value of x and ${\parallel \phi -\psi \parallel }_{\xi }=\underset{s\in [q{t}_0,t_0]}{sup}{\parallel \phi \left(s\right)-\psi \left(s\right)\parallel }_{{\mathcal{A}}^n}$.

Proof. 

If $x\left(t\right)$ is the pseudo almost periodic solution of system (1) with initial value $\phi$ and y is an arbitrary solution of system (1) with the initial value $\psi$. Let $z\left(t\right)=x\left(t\right)-y\left(t\right).$ Then, for $i=1,2,\dots ,n$, one gets

$$\begin{array}{cc}\hfill z_i^{\prime }\left(t\right)=& -c_i\left(t\right)z_i\left(t\right)+\sum _{j=1}^n{a}_{ij}\left(t\right)(f_j\left(x_j\left(t\right)\right)-f_j\left(y_j\left(t\right)\right))+\sum _{j=1}^n{b}_{ij}\left(t\right)(g_j\left(x_j\left(q_{ij}t\right)\right)-g_j\left(x_j\left(q_{ij}t\right)\right))\hfill \\ \hfill & +\underset{j=1}{\stackrel{n}{\bigvee }}{\alpha }_{ij}\left(t\right)(h_j\left(x_j\left(q_{ij}t\right)\right)-h_j\left(y_j\left(q_{ij}t\right)\right))+\underset{j=1}{\stackrel{n}{\bigwedge }}{\beta }_{ij}\left(t\right)(h_j\left(x_j\left(q_{ij}t\right)\right)-h_j\left(y_j\left(q_{ij}t\right)\right)).\hfill \end{array}$$

(2)

From (H₃), for $i=1,2,\dots ,n$, we have

$$\begin{array}{cc}\hfill \underset{t\ge 0}{sup}& \{-{\overline{c}}_i^{\varnothing }+(\parallel c_i^c{\left(t\right)\parallel }_{\mathcal{A}}+\sum _{j=1}^n\parallel a_{ij}{\left(t\right)\parallel }_{\mathcal{A}}{K}_j+\sum _{j=1}^n{\parallel b_{ij}\left(t\right)\parallel }_{\mathcal{A}}{L}_j\hfill \\ \hfill & +\sum _{j=1}^n\parallel {\alpha }_{ij}{\left(t\right)\parallel }_{\mathcal{A}}{M}_j+\sum _{j=1}^n{\parallel {\beta }_{ij}\left(t\right)\parallel }_{\mathcal{A}}{M}_j\left)\right\}<0.\hfill \end{array}$$

(3)

Let $K_i$ be defined by

$$\begin{array}{cc}\hfill K_i\left(\theta \right)=& \underset{t\in \mathbb{R}}{sup}\{\theta -{\overline{c}}_i^{\varnothing }+(\parallel c_i^c{\left(t\right)\parallel }_{\mathcal{A}}+\sum _{j=1}^n\parallel a_{ij}{\left(t\right)\parallel }_{\mathcal{A}}{K}_j+\sum _{j=1}^n{\parallel b_{ij}\left(t\right)\parallel }_{\mathcal{A}}{L}_j{e}^{\theta ln\frac{1}{q_{ij}}}\hfill \\ \hfill & +\sum _{j=1}^n\parallel {\alpha }_{ij}{\left(t\right)\parallel }_{\mathcal{A}}{M}_j{e}^{\theta ln\frac{1}{q_{ij}}}+\sum _{j=1}^n{\parallel {\beta }_{ij}\left(t\right)\parallel }_{\mathcal{A}}{M}_j{e}^{\theta ln\frac{1}{q_{ij}}}\left)\right\},i=1,2,\dots ,n,\hfill \end{array}$$

where $\theta \in [0,\underset{1\le i\le n}{min}{\overline{c}}_i^{\varnothing }]$. Then, from (3), we have

$$\begin{array}{cc}\hfill K_i\left(0\right)=& \underset{t\in \mathbb{R}}{sup}\{-{\overline{c}}_i^{\varnothing }+(\parallel c_i^c{\left(t\right)\parallel }_{\mathcal{A}}+\sum _{j=1}^n\parallel a_{ij}{\left(t\right)\parallel }_{\mathcal{A}}{K}_j+\sum _{j=1}^n{\parallel b_{ij}\left(t\right)\parallel }_{\mathcal{A}}{L}_j\hfill \\ \hfill & +\sum _{j=1}^n\parallel {\alpha }_{ij}{\left(t\right)\parallel }_{\mathcal{A}}{M}_j+\sum _{j=1}^n{\parallel {\beta }_{ij}\left(t\right)\parallel }_{\mathcal{A}}{M}_j\left)\right\}<0,i=1,2,\dots ,n.\hfill \end{array}$$

Since $K_i\left(0\right)=0$, $K_i\left(\theta \right)\to \infty$ as $\theta \to \infty$ and the continuity of $K_i\left(\theta \right)$, we can take a constant $\lambda \in (0,\underset{1\le i\le n}{min}\left\{{\overline{c}}_i^{\varnothing }\right\})$, such that $K_i\left(\lambda \right)<0$ and

$$\begin{array}{cc}\hfill \underset{t\in \mathbb{R}}{sup}& \{\frac{\lambda }{1+t}-{\overline{c}}_i^{\varnothing }+(\parallel c_i^c{\left(t\right)\parallel }_{\mathcal{A}}+\sum _{j=1}^n\parallel a_{ij}{\left(t\right)\parallel }_{\mathcal{A}}{K}_j+\sum _{j=1}^n{\parallel b_{ij}\left(t\right)\parallel }_{\mathcal{A}}{L}_j{e}^{\lambda ln\frac{1}{q_{ij}}}\hfill \\ \hfill & +\sum _{j=1}^n\parallel {\alpha }_{ij}{\left(t\right)\parallel }_{\mathcal{A}}{M}_j{e}^{\lambda ln\frac{1}{q_{ij}}}+\sum _{j=1}^n{\parallel {\beta }_{ij}\left(t\right)\parallel }_{\mathcal{A}}{M}_j{e}^{\lambda ln\frac{1}{q_{ij}}}\left)\right\}\hfill \\ \hfill <& \underset{t\in \mathbb{R}}{sup}\{\lambda -{\overline{c}}_i^{\varnothing }+(\parallel c_i^c{\left(t\right)\parallel }_{\mathcal{A}}+\sum _{j=1}^n\parallel a_{ij}{\left(t\right)\parallel }_{\mathcal{A}}{K}_j+\sum _{j=1}^n{\parallel b_{ij}\left(t\right)\parallel }_{\mathcal{A}}{L}_j{e}^{\lambda ln\frac{1}{q_{ij}}}\hfill \\ \hfill & +\sum _{j=1}^n\parallel {\alpha }_{ij}{\left(t\right)\parallel }_{\mathcal{A}}{M}_j{e}^{\lambda ln\frac{1}{q_{ij}}}+\sum _{j=1}^n{\parallel {\beta }_{ij}\left(t\right)\parallel }_{\mathcal{A}}{M}_j{e}^{\lambda ln\frac{1}{q_{ij}}}\left)\right\}<0,i=1,2,\dots ,n.\hfill \end{array}$$

Noting that

$$\begin{array}{c}\hfill ln\frac{1+t}{1+q_{ij}t}\le ln\frac{1}{q_{ij}},t\ge 0,i,j=1,2,\dots ,n,\end{array}$$

for any $\epsilon >0,M>1$, we have that

$$\begin{array}{c}\hfill {\parallel z\left(t\right)\parallel }_{{\mathcal{A}}^n}\le M({\parallel \phi -\psi \parallel }_{\xi }+\epsilon )e^{-\lambda ln\frac{1+t}{1+t_0}},t\in [q{t}_0,t_0].\end{array}$$

We claim that

$$\begin{array}{c}\hfill {\parallel z\left(t\right)\parallel }_{{\mathcal{A}}^n}\le M({\parallel \phi -\psi \parallel }_{\xi }+\epsilon )e^{-\lambda ln\frac{1+t}{1+t_0}},t>t_0.\end{array}$$

(4)

To prove (4) holds, we will prove for every $d>1$, the following inequality holds.

$$\begin{array}{c}\hfill {\parallel z\left(t\right)\parallel }_{{\mathcal{A}}^n}\le dM({\parallel \phi -\psi \parallel }_{\xi }+\epsilon )e^{-\lambda ln\frac{1+t}{1+t_0}},t\in [t_0,+\infty ).\end{array}$$

(5)

If (5) does not hold, then there must be some $\theta >1$, such that

$$\begin{array}{c}\hfill \{\begin{array}{c}{\parallel z\left(\theta \right)\parallel }_{{\mathcal{A}}^n}=dM({\parallel \phi -\psi \parallel }_{\xi }+\epsilon )e^{-\lambda ln\frac{1+\theta }{1+t_0}}\hfill \\ {\parallel z\left(t\right)\parallel }_{{\mathcal{A}}^n}<dM({\parallel \phi -\psi \parallel }_{\xi }+\epsilon )e^{-\lambda ln\frac{1+t}{1+t_0}},t\in [q{t}_0,\theta ),\hfill \end{array}\end{array}$$

(6)

which combined with (2), for $i=1,2,\dots ,n$, we have

$$\begin{array}{cc}\hfill {\parallel z_i\left(\theta \right)\parallel }_{\mathcal{A}}=& \parallel z_i\left(t_0\right)e^{-{\int }_{t_0}^{\theta }{c}_i^{\varnothing }\left(u\right)du}+{\int }_{t_0}^{\theta }{e}^{-{\int }_s^{\theta }{c}_i^{\varnothing }\left(u\right)du}(c_i^c\left(s\right)z_i\left(s\right)\hfill \\ \hfill & +\sum _{j=1}^n{a}_{ij}\left(s\right)(f_j\left(x_j\left(s\right)\right)-f_j\left(y_j\left(s\right)\right))+\sum _{j=1}^n{b}_{ij}\left(s\right)(g_j\left(x_j\left(q_{ij}s\right)\right)-g_j\left(y_j\left(q_{ij}s\right)\right))\hfill \\ \hfill & +\sum _{j=1}^n{\beta }_{ij}\left(s\right)(h_j\left(x_j\left(q_{ij}s\right)\right)-h_j\left(y_j\left(q_{ij}s\right)\right))\hfill \\ \hfill & +\sum _{j=1}^n{\alpha }_{ij}\left(s\right)(h_j\left(x_j\left(q_{ij}s\right)\right)-h_j\left(y_j\left(q_{ij}s\right)\right))ds{\parallel }_{\mathcal{A}})\hfill \\ \hfill \le & {\parallel z_i\left(t_0\right)\parallel }_{\mathcal{A}}{e}^{-{\int }_{t_0}^{\theta }{\overline{c}}_i^{\varnothing }du}+{\int }_{t_0}^{\theta }{e}^{-{\int }_s^{\theta }{\overline{c}}_i^{\varnothing }du}({\parallel c_i^c\left(t\right)\parallel }_{\mathcal{A}}{\parallel z_i\left(s\right)\parallel }_{\mathcal{A}}\hfill \\ \hfill & +\sum _{j=1}^n\parallel a_{ij}{\left(s\right)\parallel }_{\mathcal{A}}{K}_j{\parallel z_j\left(s\right)\parallel }_{\mathcal{A}}+\sum _{j=1}^n{\parallel b_{ij}\left(s\right)\parallel }_{\mathcal{A}}{L}_j{\parallel z_j\left(q_{ij}s\right)\parallel }_{\mathcal{A}}\hfill \\ \hfill & +\sum _{j=1}^n\parallel {\alpha }_{ij}{\left(s\right)\parallel }_{\mathcal{A}}{M}_j{\parallel z_j\left(q_{ij}s\right)\parallel }_{\mathcal{A}}+\sum _{j=1}^n{\parallel {\beta }_{ij}\left(s\right)\parallel }_{\mathcal{A}}{M}_j{\parallel z_j\left(q_{ij}s\right)\parallel }_{\mathcal{A}})ds\hfill \\ \hfill \le & M({\parallel \phi -\psi \parallel }_{\xi }+\epsilon )e^{-{\int }_{t_0}^{\theta }{\overline{c}}_i^{\varnothing }du}+dM({\parallel \phi -\psi \parallel }_{\xi }+\epsilon ){\int }_{t_0}^{\theta }{e}^{-{\int }_s^{\theta }{\overline{c}}_i^{\varnothing }du}({\parallel c_i^c\left(s\right)\parallel }_{\mathcal{A}}{e}^{-\lambda ln\frac{1+s}{1+t_0}}\hfill \\ \hfill & +\sum _{j=1}^n\parallel a_{ij}{\left(s\right)\parallel }_{\mathcal{A}}{K}_j{e}^{-\lambda ln\frac{1+s}{1+t_0}}+\sum _{j=1}^n{\parallel b_{ij}\left(s\right)\parallel }_{\mathcal{A}}{L}_j{e}^{-\lambda ln\frac{1+q_{ij}s}{1+t_0}}\hfill \\ \hfill & +\sum _{j=1}^n\parallel {\alpha }_{ij}{\left(s\right)\parallel }_{\mathcal{A}}{M}_j{e}^{-\lambda ln\frac{1+q_{ij}s}{1+t_0}}+\sum _{j=1}^n{\parallel {\beta }_{ij}\left(s\right)\parallel }_{\mathcal{A}}{M}_j{e}^{-\lambda ln\frac{1+q_{ij}s}{1+t_0}})ds\hfill \\ \hfill =& dM({\parallel \phi -\psi \parallel }_{\xi }+\epsilon )e^{-\lambda ln\frac{1+\theta }{1+t_0}}(\frac{1}{d}{e}^{-{\int }_{t_0}^{\theta }({\overline{c}}_i^{\varnothing }-\frac{\lambda }{1+u})du}\hfill \\ \hfill & +{\int }_{t_0}^{\theta }{e}^{-{\int }_s^{\theta }({\overline{c}}_i^{\varnothing }-\frac{\lambda }{1+u})du}(\parallel c_i^c{\left(s\right)\parallel }_{\mathcal{A}}+\sum _{j=1}^n\parallel a_{ij}{\left(s\right)\parallel }_{\mathcal{A}}{K}_j+\sum _{j=1}^n{\parallel b_{ij}\left(s\right)\parallel }_{\mathcal{A}}{L}_j{e}^{\lambda ln\frac{1+s}{1+q_{ij}s}}\hfill \\ \hfill & +\sum _{j=1}^n\parallel {\alpha }_{ij}{\left(s\right)\parallel }_{\mathcal{A}}{M}_j{e}^{\lambda ln\frac{1+s}{1+q_{ij}s}}+\sum _{j=1}^n{\parallel {\beta }_{ij}\left(s\right)\parallel }_{\mathcal{A}}{M}_j{e}^{\lambda ln\frac{1+s}{1+q_{ij}s}}\left)ds\right)\hfill \end{array}$$

$$\begin{array}{cc}\hfill \le & dM({\parallel \phi -\psi \parallel }_{\xi }+\epsilon )e^{-\lambda ln\frac{1+\theta }{1+t_0}}(\frac{1}{d}{e}^{-{\int }_{t_0}^{\theta }({\overline{c}}_i^{\varnothing }-\frac{\lambda }{1+u})du}\hfill \\ \hfill & +{\int }_{t_0}^{\theta }{e}^{-{\int }_s^{\theta }({\overline{c}}_i^{\varnothing }-\frac{\lambda }{1+u})du}(\parallel c_i^c{\left(s\right)\parallel }_{\mathcal{A}}+\sum _{j=1}^n\parallel a_{ij}{\left(s\right)\parallel }_{\mathcal{A}}{K}_j+\sum _{j=1}^n{\parallel b_{ij}\left(s\right)\parallel }_{\mathcal{A}}{L}_j{e}^{\lambda ln\frac{1}{q_{ij}}}\hfill \\ \hfill & +\sum _{j=1}^n\parallel {\alpha }_{ij}{\left(s\right)\parallel }_{\mathcal{A}}{M}_j{e}^{\lambda ln\frac{1}{q_{ij}}}+\sum _{j=1}^n{\parallel {\beta }_{ij}\left(s\right)\parallel }_{\mathcal{A}}{M}_j{e}^{\lambda ln\frac{1}{q_{ij}}}\left)ds\right)\hfill \\ \hfill \le & dM({\parallel \phi -\psi \parallel }_{\xi }+\epsilon )e^{-\lambda ln\frac{1+\theta }{1+t_0}}(\frac{1}{d}{e}^{-{\int }_{t_0}^{\theta }({\overline{c}}_i^{\varnothing }-\frac{\lambda }{1+u})du}\hfill \\ \hfill & +{\int }_{t_0}^{\theta }{e}^{-{\int }_s^{\theta }({\overline{c}}_i^{\varnothing }-\frac{\lambda }{1+u})du}\left({\overline{c}}_i^{\varnothing }-\frac{\lambda }{1+s}\right)ds)\hfill \\ \hfill \le & dM({\parallel \phi -\psi \parallel }_{\xi }+\epsilon )e^{-\lambda ln\frac{1+\theta }{1+t_0}}\left(1-\left(1-\frac{1}{d}\right)e^{-{\int }_{t_0}^{\theta }({\overline{c}}_i^{\varnothing }-\frac{\lambda }{1+u})du}\right)\hfill \\ \hfill <& dM({\parallel \phi -\psi \parallel }_{\xi }+\epsilon )e^{-\lambda ln\frac{1+\theta }{1+t_0}},\hfill \end{array}$$

this yields that,

$${\parallel z\left(\theta \right)\parallel }_{{\mathcal{A}}^n}<dM({\parallel \phi -\psi \parallel }_{\xi }+\epsilon )e^{-\lambda ln\frac{1+\theta }{1+t_0}},$$

which contradicts (6). Hence, (5) holds. Letting $d\to 1$, we derive that (4) holds. The proof is complete. □

5. An Example

Our numerical example is as follows.

Example 1.

In system (1), let $n=m=2,s=0$ and for $i,j=1,2$, take

$$x_i\left(t\right)=x_i^0\left(t\right)e_0+x_i^1\left(t\right)e_1+x_i^2\left(t\right)e_2+x_i^{12}\left(t\right)e_{12},$$

$$f_j\left(x_j\right)=\frac{1}{25}{e}_0{sin}^2{x}_j^1+\frac{1}{30}{e}_{1}tanh(x_j^{12}+x_j^0)+\frac{1}{35}{e}_{2}sin{x}_j^2+\frac{1}{40}{e}_{12}{tanh}^2{x}_j^0,$$

$$g_j\left(x_j\right)=\frac{1}{50}{e}_0{sin}^2{x}_j^1+\frac{1}{52}{e}_{1}tanh(x_j^{12}+x_j^0)+\frac{1}{80}{e}_2{tanh}^2{x}_j^2+\frac{1}{55}{e}_{12}sin{x}_j^0,$$

$$h_j\left(x_j\right)=\frac{1}{100}{e}_0{sin}^2{x}_j^0+\frac{1}{50}{e}_{1}sin(x_j^1+x_j^0)+\frac{1}{70}{e}_{2}sin{x}_j^2+\frac{1}{60}{e}_{12}{sin}^2{x}_j^{12},$$

$$c_1\left(t\right)=(3.1-0.1sin\sqrt{5}t)e_0+(2.1+0.2sint)e_1+(2-0.5cos\sqrt{3}t)e_2+(2+0.1sint)e_{12},$$

$$c_2\left(t\right)=(3.1-0.1sin\sqrt{5}t)e_0+(2-0.5sint)e_1+(2-0.1sin\sqrt{3}t)e_2+(2-0.4sint)e_{12},$$

$$\left(\begin{array}{c}{I}_1\left(t\right)\hfill \\ I_2\left(t\right)\hfill \end{array}\right)=\left(\begin{array}{c}2e_{0}sint+e_{1}cos\sqrt{3}t+0.3e_{2}sin\sqrt{5}t+2e_{12}sint\hfill \\ (2sint+\frac{2}{1+t^2})e_0+0.5e_{1}cos\sqrt{3}t+0.2e_{2}sin\sqrt{2}t+2e_{12}cost\hfill \end{array}\right),$$

$$\left(\begin{array}{cc}{a}_{11}\left(t\right)\hfill & a_{12}\left(t\right)\hfill \\ a_{21}\left(t\right)\hfill & a_{22}\left(t\right)\hfill \end{array}\right)=\left(\begin{array}{cc}0.02e_{0}sin\sqrt{2}t+0.03e_{1}sint\hfill & 0.05e_{2}sin\sqrt{2}t+0.05e_{12}cos\sqrt{3}t\hfill \\ 0.02e_{1}sin\sqrt{2}t+0.08e_{2}sint\hfill & 0.07e_{0}cost+0.09e_{12}sin\sqrt{3}t\hfill \end{array}\right),$$

$$\left(\begin{array}{cc}{b}_{11}\left(t\right)\hfill & b_{12}\left(t\right)\hfill \\ b_{21}\left(t\right)\hfill & b_{22}\left(t\right)\hfill \end{array}\right)=\left(\begin{array}{cc}0.01e_{0}sint+0.06e_{1}cos\sqrt{5}t\hfill & 0.08e_{2}sin\sqrt{7}t+0.09e_{12}cos\sqrt{3}t\hfill \\ 0.05e_{1}sint+0.11e_{2}cos\sqrt{2}t\hfill & 0.01e_{0}cos\sqrt{6}t+0.03e_{12}sin\sqrt{5}t\hfill \end{array}\right),$$

$$\left(\begin{array}{cc}{\alpha }_{11}\left(t\right)\hfill & {\alpha }_{12}\left(t\right)\hfill \\ {\alpha }_{21}\left(t\right)\hfill & {\alpha }_{22}\left(t\right)\hfill \end{array}\right)=\left(\begin{array}{cc}0.01e_{0}sin\sqrt{3}t+0.02e_{1}sint\hfill & 0.02e_{2}cos\sqrt{2}t+0.05e_{12}sin\sqrt{3}t\hfill \\ 0.02e_{1}sint+0.03e_{2}sin\sqrt{2}t\hfill & 0.03e_{0}sin\sqrt{3}t+0.01e_{12}cos\sqrt{2}t\hfill \end{array}\right),$$

$$\left(\begin{array}{cc}{\beta }_{11}\left(t\right)\hfill & {\beta }_{12}\left(t\right)\hfill \\ {\beta }_{21}\left(t\right)\hfill & {\beta }_{22}\left(t\right)\hfill \end{array}\right)=\left(\begin{array}{cc}0.03e_{0}sint+0.02e_{1}sin\sqrt{3}t\hfill & 0.02e_{2}sin\sqrt{2}t+0.03e_{12}sin\sqrt{3}t\hfill \\ 0.08e_{1}sin\sqrt{2}t+0.02e_{2}cos\sqrt{3}t\hfill & 0.01e_{0}sin\sqrt{3}t+0.04e_{12}sin\sqrt{7}t\hfill \end{array}\right),$$

$$\left(\begin{array}{cc}{S}_{11}\left(t\right)\hfill & S_{12}\left(t\right)\hfill \\ S_{21}\left(t\right)\hfill & S_{22}\left(t\right)\hfill \end{array}\right)=\left(\begin{array}{cc}0.05e_{0}sin\sqrt{7}t+0.01e_{1}sin\sqrt{3}t\hfill & 0.07e_{2}sin\sqrt{7}t+0.02e_{12}sin\sqrt{3}t\hfill \\ 0.03e_{1}sin\sqrt{3}t+0.02e_{2}sin\sqrt{2}t\hfill & 0.03e_{0}cos\sqrt{2}t+0.05e_{12}sin\sqrt{3}t\hfill \end{array}\right),$$

$$\left(\begin{array}{cc}{T}_{11}\left(t\right)\hfill & T_{12}\left(t\right)\hfill \\ T_{21}\left(t\right)\hfill & T_{22}\left(t\right)\hfill \end{array}\right)=\left(\begin{array}{cc}0.01e_{0}sin\sqrt{2}t+0.06e_{1}sint\hfill & 0.05e_{2}sin\sqrt{3}t+0.05e_{12}cos\sqrt{2}t\hfill \\ 0.02e_{1}sint+0.03e_{2}sin\sqrt{2}t\hfill & 0.07e_{0}cost+0.09e_{12}sin\sqrt{3}t\hfill \end{array}\right),$$

$$v_1\left(t\right)=v_2\left(t\right)=\frac{1}{11}{e}_{0}sin\sqrt{3}t+\frac{1}{12}{e}_{1}cos\sqrt{2}t+\frac{1}{10}{e}_{2}sin\sqrt{5}t+\frac{1}{15}{e}_{12}sint,$$

$$q_{11}=0.5,q_{12}=0.4,q_{21}=0.4,q_{22}=0.3.$$

By a simple calculation, we have

$$K_j=\frac{1}{25},L_j=\frac{1}{50},M_j=\frac{1}{50},{\overline{c}}_1^{\varnothing }={\overline{c}}_2^{\varnothing }=3,{\overline{c}}_1^c=2.2,{\overline{c}}_2^c=2.5,q=0.3,$$

$$a_{11}^{+}=0.03,a_{12}^{+}=0.05,a_{21}^{+}=0.08,a_{22}^{+}=0.09,b_{11}^{+}=0.06,b_{12}^{+}=0.09,b_{21}^{+}=0.05,b_{22}^{+}=0.03,$$

$${\alpha }_{11}^{+}=0.02,{\alpha }_{12}^{+}=0.05,{\alpha }_{21}^{+}=0.03,{\alpha }_{22}^{+}=0.03,{\beta }_{11}^{+}=0.03,{\beta }_{12}^{+}=0.03,{\beta }_{21}^{+}=0.08,{\beta }_{22}^{+}=0.04.$$

Besides, we can get

$$\frac{1}{{\overline{c}}_1^{\varnothing }}\left({\overline{c}}_1^c+\sum _{j=1}^2{a}_{1j}^{+}{K}_j+\sum _{j=1}^2{b}_{1j}^{+}{L}_j+\sum _{j=1}^2{\alpha }_{1j}^{+}{M}_j+\sum _{j=1}^2{\beta }_{1j}^{+}{M}_j\right)\approx 0.7364<1,$$

$$\frac{1}{{\overline{c}}_2^{\varnothing }}\left({\overline{c}}_2^c+\sum _{j=1}^2{a}_{2j}^{+}{K}_j+\sum _{j=1}^2{b}_{2j}^{+}{L}_j+\sum _{j=1}^2{\alpha }_{2j}^{+}{M}_j+\sum _{j=1}^2{\beta }_{2j}^{+}{M}_j\right)\approx 0.8373<1$$

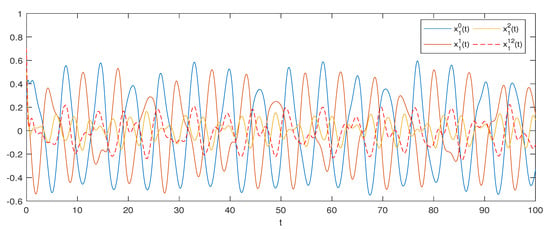
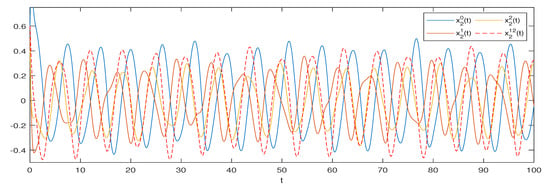
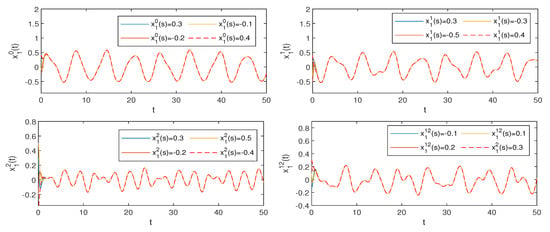
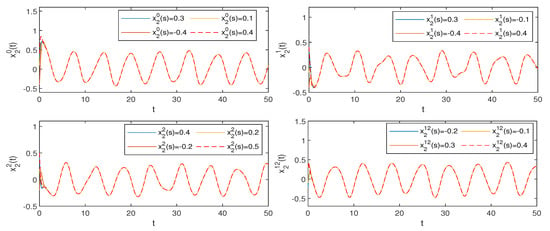
and $\delta \approx 0.8373<1$. Hence, conditions (H₁)–(H₃) of are verified. Consequently, by Theorem 2, system (1) possesses a unique one pseudo almost periodic solution that is globally attractive (see Figure 1, Figure 2, Figure 3 and Figure 4).

Figure 1. The states $x_1^0,x_1^1,x_1^2,x_1^{12}$ of (1) with different initial values.

Figure 2. The states $x_2^0,x_2^1,x_2^2,x_2^{12}$ of (1) with different initial values.

Figure 3. The stability of states $x_1^0,x_1^1,x_1^2,x_1^{12}$ of (1) with different initial values.

Figure 4. The stability of states $x_2^0,x_2^1,x_2^2,x_2^{12}$ of (1) with different initial values.

Remark 1.

No known results can be used to draw the conclusion of Example 1.

6. Conclusions

In this paper, we studied the existence and global attractivity of pseudo almost periodic solutions for a class of Clifford-valued fuzzy neural networks with proportional delays whose leakage coefficients were also Clifford numbers by the direct method. Our results are new. Our method can be used to study the existence and attractivity of pseudo almost periodic solutions for other types of Clifford-valued neural networks with proportional delays, and to study the existence and attractivity of almost automorphic solutions of Clifford-valued neural networks with proportional delays.