A New Synchronization Method for Time-Delay Fractional Complex Chaotic System and Its Application
Abstract
:1. Introduction
- (1)
- The adomian decomposition algorithm is used to research the time-delay fractional complex system. According to the complexity algorithm and bifurcation diagram, the chaotic characteristics are analyzed from two aspects: Parameters and fractional-order.
- (2)
- The definition of MFPDFS for the time-delay fractional complex system is proposed, and feedback control is added to design the controller to realize the MFPDFS.
- (3)
- According to the designed MFPDFS controller, a WSCs secure communication scheme is designed. The signal at the receiver consists of the sum of the information signal and the time-delay fractional complex chaotic signal.
2. Dynamics Characteristics of the Time-Delay Fractional Complex System
2.1. The Dissipation
2.2. Time Chaotic Attractor
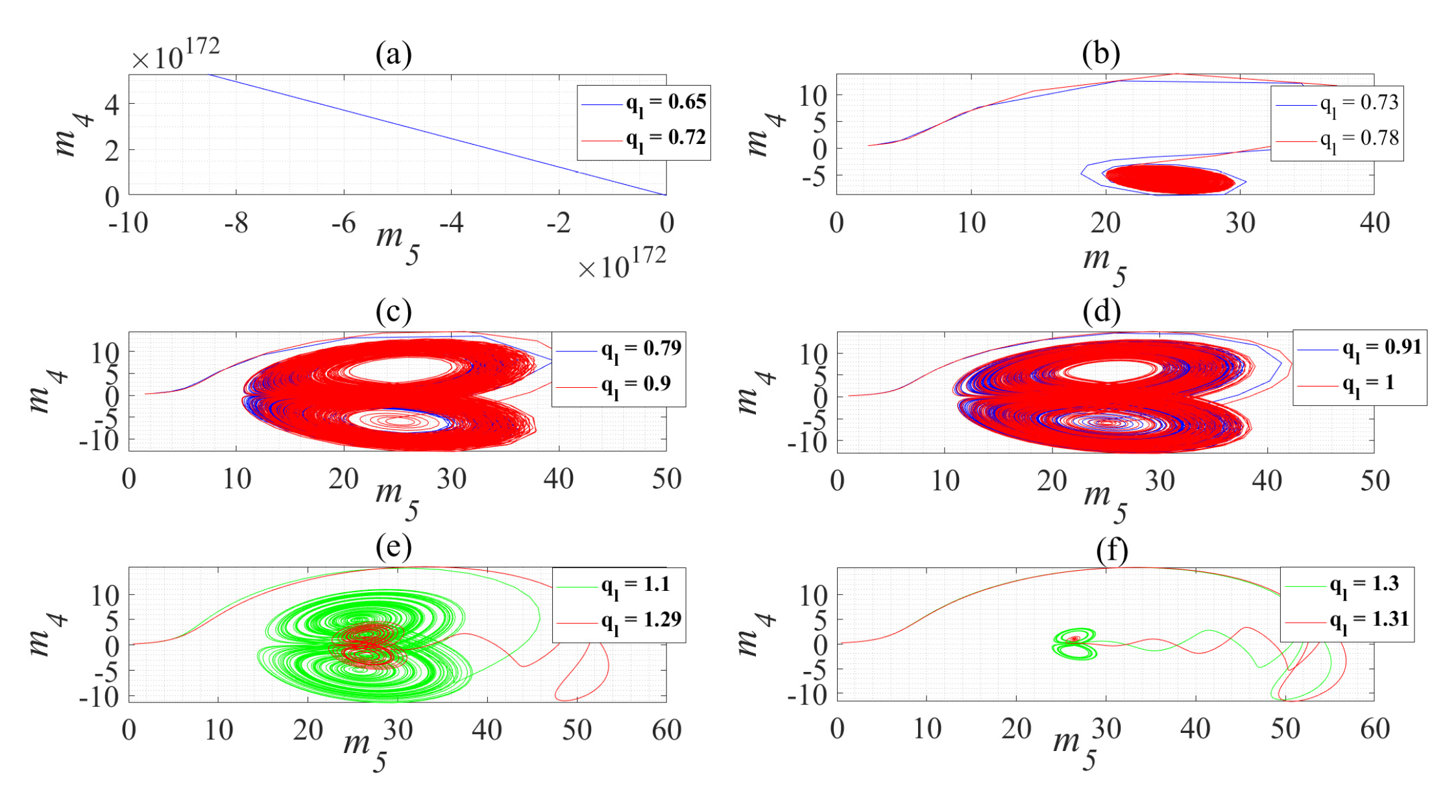
2.3. Coexistence Attractor
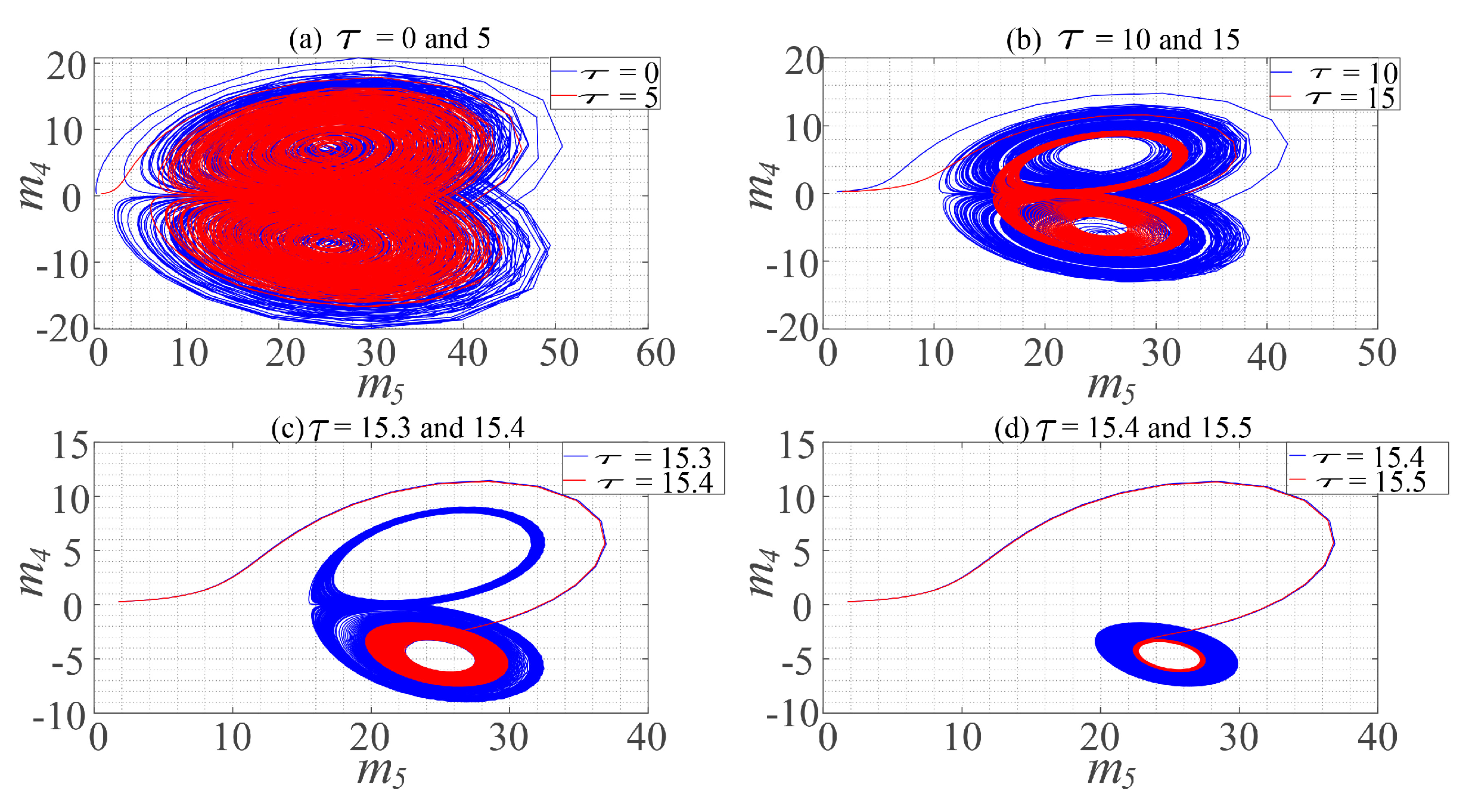
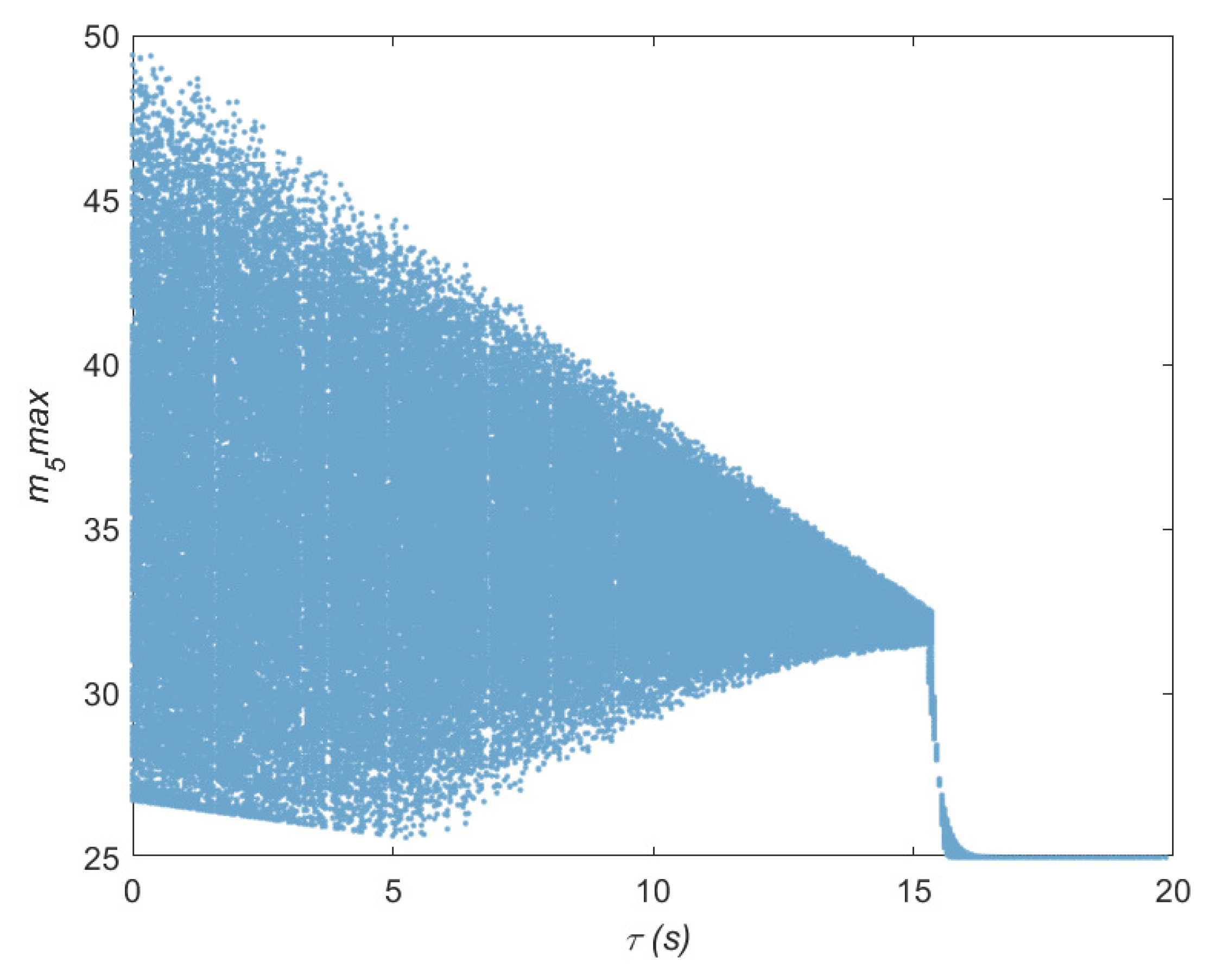
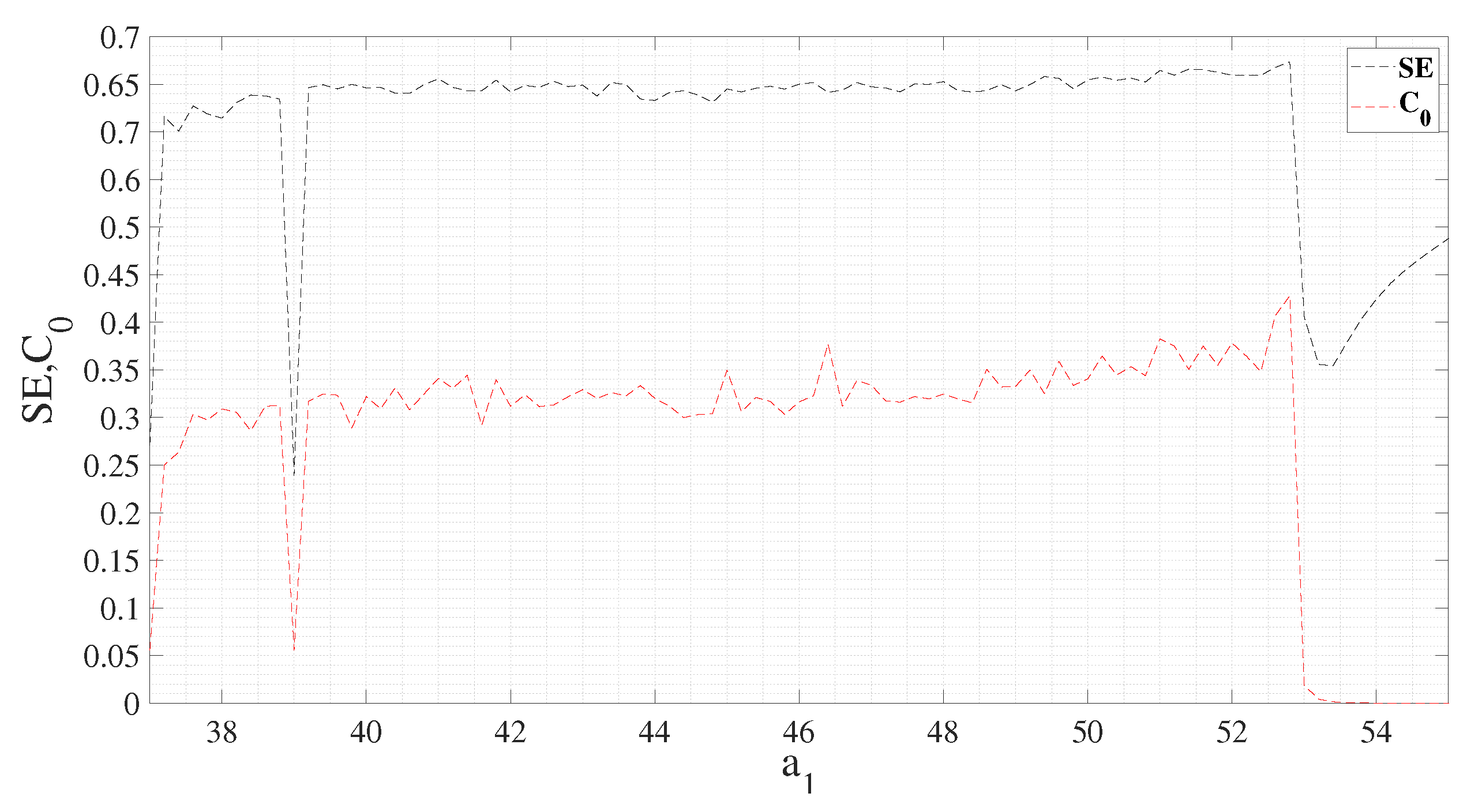
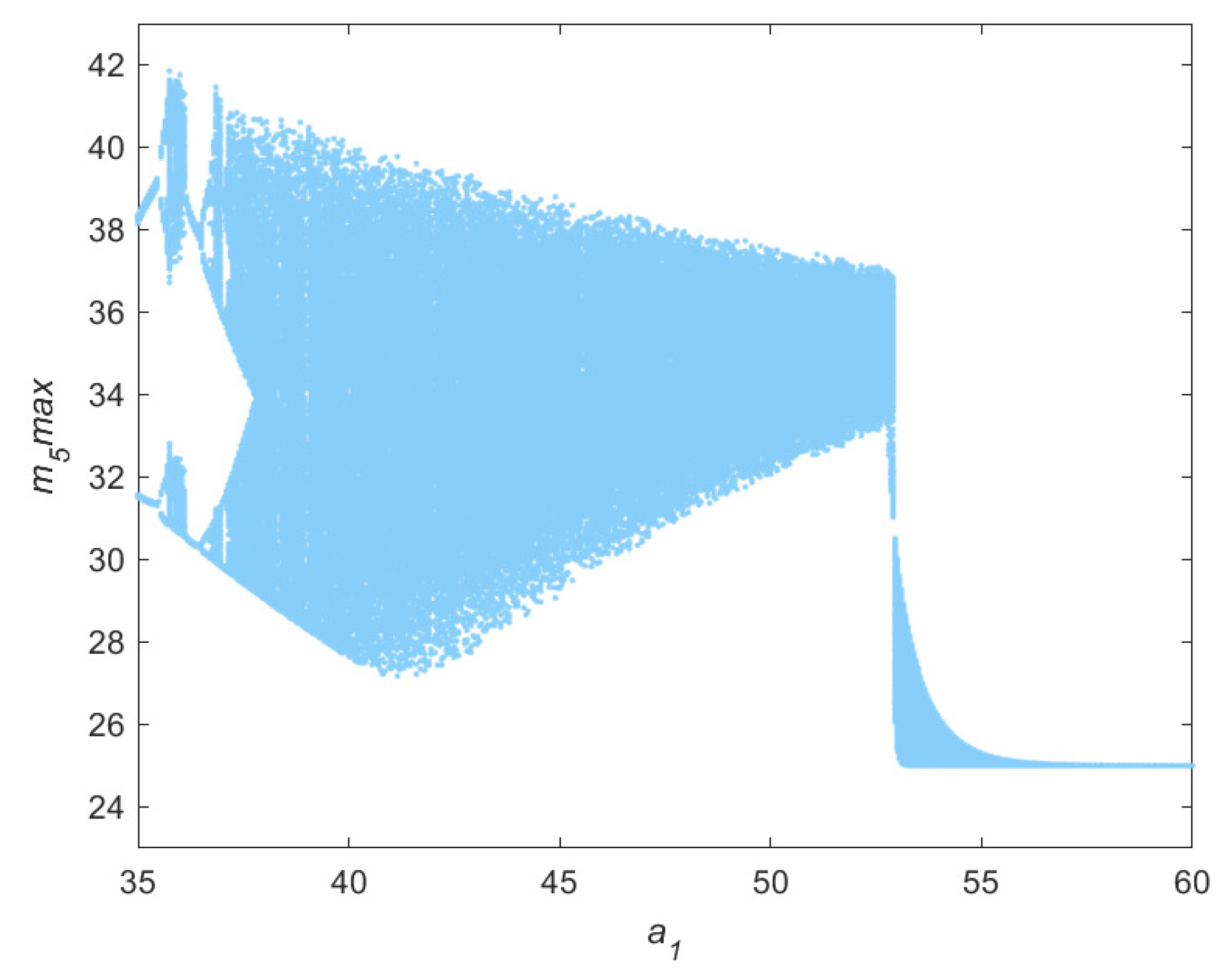
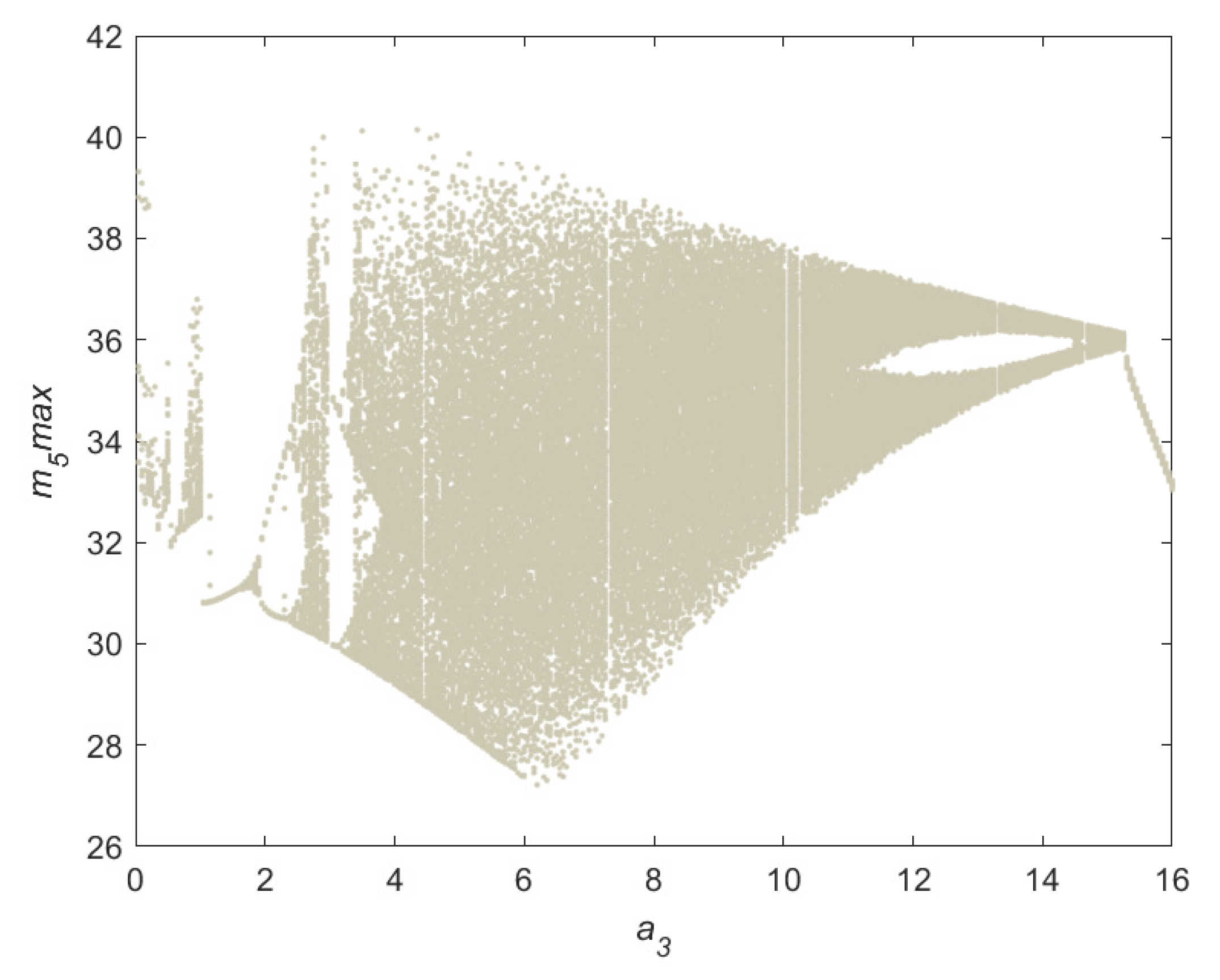
2.4. Parameter Space and Analysis of Its Chaotic Characteristics
2.5. Fractional-Order Changes and Complexity Analysis
3. Modified Fractional Projective Difference Function Synchronization
3.1. Definition of MFPDFS
3.2. Design of the MFPDFS Controller
4. Speech Secure Communication Scheme
5. Numerical Simulation Experiment
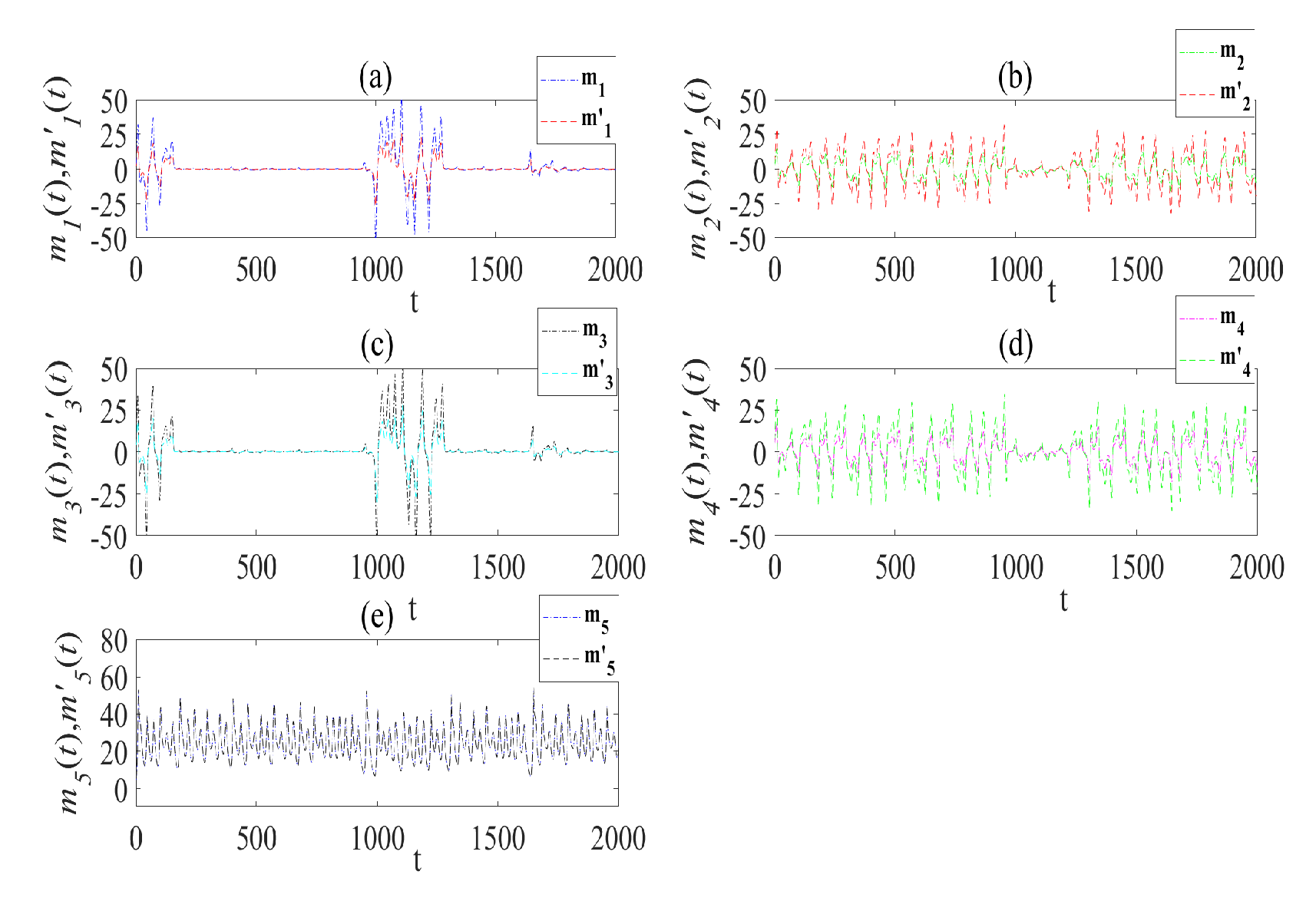
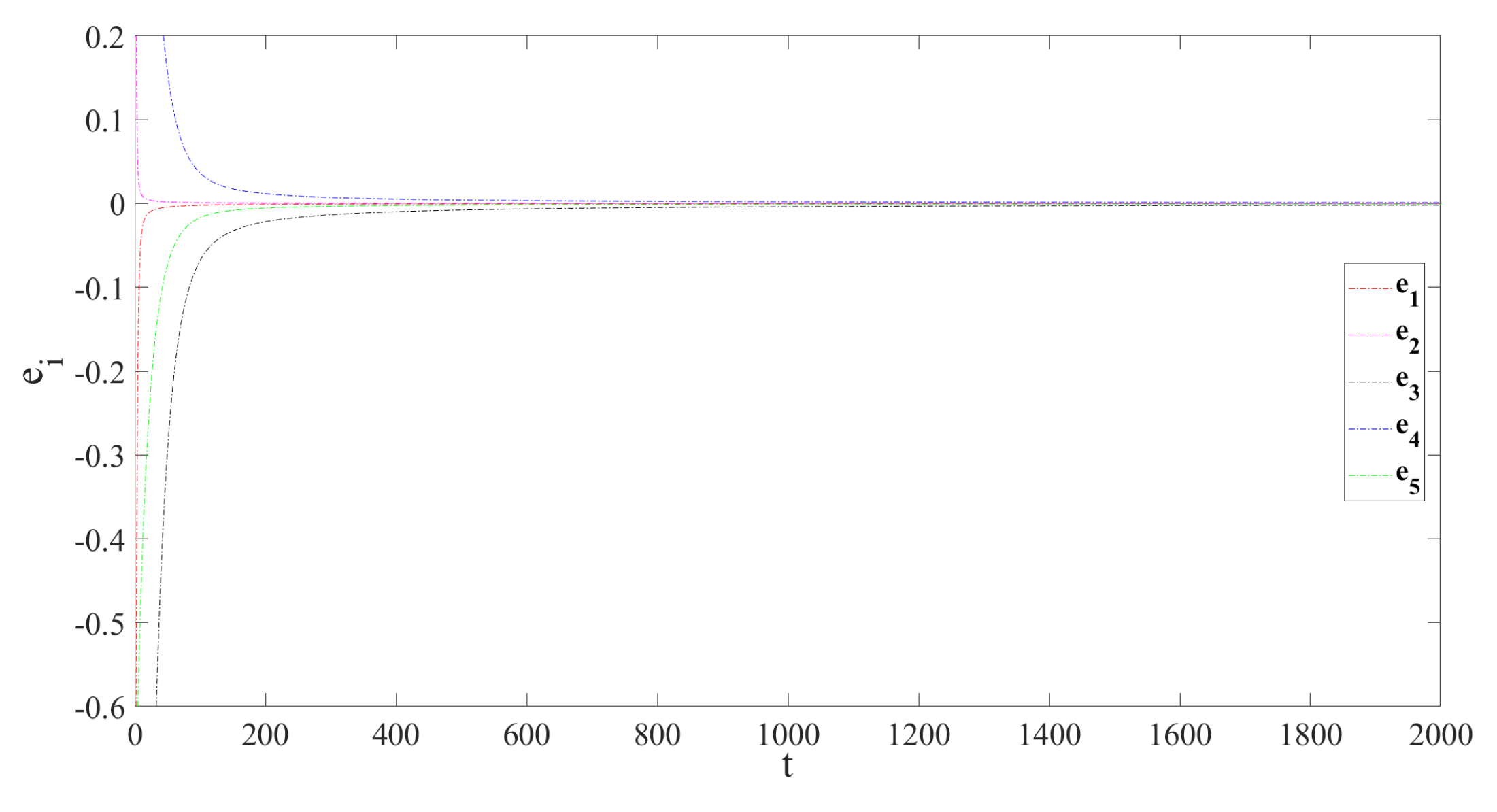
5.1. MFPDFS Controller Simulation Experiment
5.2. SNR Test Experiment
5.3. Speech Communication Simulation
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Gao, X.; Yu, J.B. Chaos in the fractional order periodically forced complex Duffing’s oscillators. Chaos Solitons Fractals 2005, 26, 1097–1104. [Google Scholar] [CrossRef]
- Reza, B.; Ali, B.M. Synchronization of different fractional order chaotic systems with time-varying parameter and orders. ISA Trans. 2018, 80, 399–410. [Google Scholar]
- Chai, L.; Liu, J.; Chen, G.; Zhao, X. Dynamics and synchronization of a complex-valued star network. Sci. China Technol. Sci. 2021, 64, 2729–2743. [Google Scholar] [CrossRef]
- Liu, J.; Chen, G.; Zhao, X. Generalized synchronization and parameters identification of different-dimensional chaotic systems in the complex field. Fractals 2021, 29, 2150081. [Google Scholar] [CrossRef]
- Zhao, X.; Liu, J.; Zhang, F.; Jiang, C. Complex generalized synchronization in complex-variable chaotic system. Eur. Phys.-J.-Spec. Top. 2021, 230, 2035–2041. [Google Scholar] [CrossRef]
- Zheng, Y. Fuzzy prediction-based feedback control of fractional order chaotic systems. Optik 2015, 126, 5645–5649. [Google Scholar] [CrossRef]
- Li, R.; Wu, H. Secure communication on fractional-order chaotic systems via adaptive sliding mode control with teaching–learning–feedback-based optimization. Nonlinear Dyn. 2019, 95, 1221–1243. [Google Scholar] [CrossRef]
- Jiang, J.; Cao, D.; Chen, H. Sliding mode control for a class of variable-order fractional chaotic systems. J. Frankl. Inst. 2020, 357, 10127–10158. [Google Scholar] [CrossRef]
- Wu, X.; Bao, H.; Cao, J. Finite-time inter-layer projective synchronization of Caputo fractional-order two-layer networks by sliding mode control. J. Frankl. Inst. 2020, 358, 1002–1020. [Google Scholar] [CrossRef]
- Chan, J.; Lee, T.H.; Tan, C.P. Secure Communication Through a Chaotic System and a Sliding-Mode Observer. IEEE Trans. Syst. Man Cybern. Syst. 2020, 99, 1–13. [Google Scholar] [CrossRef]
- Khettab, K.; Ladaci, S.; Bensafia, Y. Fuzzy adaptive control of fractional order chaotic systems with unknown control gain sign using a fractional order Nussbaum gain. IEEE/ CAA J. Autom. Sin. 2019, 6, 816–823. [Google Scholar] [CrossRef]
- Pisarchik, A.; Jaimes-Reátegui, R.; Rodríguez-Flores, C.; García-López, J.; Huerta-Cuellar, G.; Martín-Pasquín, F. Secure chaotic communication based on extreme multistability. J. Frankl. Inst. 2021, 358, 2561–2575. [Google Scholar] [CrossRef]
- Bendoukha, S.; Abdelmalek, S. The fractional chua chaotic system: Dynamics, synchronization, and application to secure communications. Int. J. Nonlinear Sci. Numer. Simul. 2019, 20, 77–88. [Google Scholar] [CrossRef]
- Liu, J.; Wang, Z.; Shu, M.; Zhang, F.; Leng, S.; Sun, X. Secure Communication of Fractional Complex Chaotic Systems Based on Fractional Difference Function Synchronization. Complexity 2019, 2019, 7242791. [Google Scholar] [CrossRef] [Green Version]
- Zhang, L.; Sun, K.; Liu, W.; He, S. A novel color image encryption scheme using fractional-order hyperchaotic system and DNA sequence operations. Chin. Phys. B 2017, 26, 98–106. [Google Scholar] [CrossRef]
- Lai, Q.; Norouzi, B.; Liu, F. Dynamic analysis, circuit realization, control design and image encryption application of an extended Lü system with coexisting attractors. Chaos Solitons Fractals 2018, 114, 230–245. [Google Scholar] [CrossRef]
- Wang, R.; Zhang, Y.; Chen, Y.; Chen, X.; Xi, L. Fuzzy neural network-based chaos synchronization for a class of fractional-order chaotic systems: An adaptive sliding mode control approach. Nonlinear Dyn. 2020, 100, 1275–1287. [Google Scholar] [CrossRef]
- Bhatnagar, G.; Wu, Q. Biometric Inspired Multimedia Encryption Based on Dual Parameter Fractional Fourier Transform. IEEE Trans. Syst. Man Cybern. Syst. 2014, 44, 1234–1247. [Google Scholar] [CrossRef]
- Cai, X.; Xu, W.; Wang, L.; Chen, G. Towards High-Data-Rate Noncoherent Chaotic Communication: A Multiple-Mode Differential Chaos Shift Keying System. IEEE Trans. Wirel. Commun. 2021, 20, 4888–4901. [Google Scholar] [CrossRef]
- Luo, C.; Wang, X. Chaos in the fractional-order complex Lorenz system and its synchronization. Nonlinear Dyn. 2013, 71, 241–257. [Google Scholar] [CrossRef]
- Luo, C.; Wang, X. Chaos generated from the fractional-order complex Chen system and its application to digital secure communication. Int. J. Mod. Phys. C 2013, 24, 1350025–1350047. [Google Scholar] [CrossRef]
- Liu, X.; Hong, L.; Yang, L. Fractional-order complex T system: Bifurcations, chaos control, and synchronization. Nonlinear Dyn. 2013, 75, 589–602. [Google Scholar] [CrossRef]
- Jiang, C.; Liu, S.; Luo, C. A New Fractional-Order Chaotic Complex System and Its Anti-synchronization. Abstr. Appl. Anal. 2014, 2014, 326354. [Google Scholar] [CrossRef]
- Caputo, M. Linear models of dissipation whose Q is almost frequency independent-II. Geophys. J. R. Astron. Soc. 1967, 13, 529–539. [Google Scholar] [CrossRef]
- Adomian, G. A new approach to nonlinear partial differential equations. J. Math. Anal. Appl. 1984, 102, 420–434. [Google Scholar] [CrossRef] [Green Version]
- Lei, T.; He, J.; Fu, H.; Dai, W. Dynamics analysis of fractional-order Lü chaotic system with time-delay based on adomian decomposition. Sci. Technol. Eng. 2020, 20, 12711–12716. [Google Scholar]
- Zhao, X.; Liu, J.; Liu, H.; Zhang, F. Solution of the fractional-order chaotic system based on Adomian decomposition algorithm and its complexity analysis. IEEE Access 2020, 8, 28774–28781. [Google Scholar] [CrossRef]
- He, S.; Sun, K.; Wang, H. The Adomian Decomposition Method of Fractional Chaotic System and Its Complexity Analysis. Acta Phys. Sin. 2014, 63, 030502-72. Available online: https://kns.cnki.net/kcms/detail/detail.aspx?dbcode=CJFD&dbname=CJFD2014\&filename=WLXB201403008&uniplatform=NZKPT&v=V24QuWTxDUAhbliYoNbKsbw7oINjDjLglTLqZwfnxRC8cuBJFzuDArofKIvV_Ghj (accessed on 11 November 2021).
- Matignon, D. Stability results for fractional differential equations with applications to control processing. Comput. Eng. Syst. Appl. 1996, 2, 963–968. [Google Scholar]



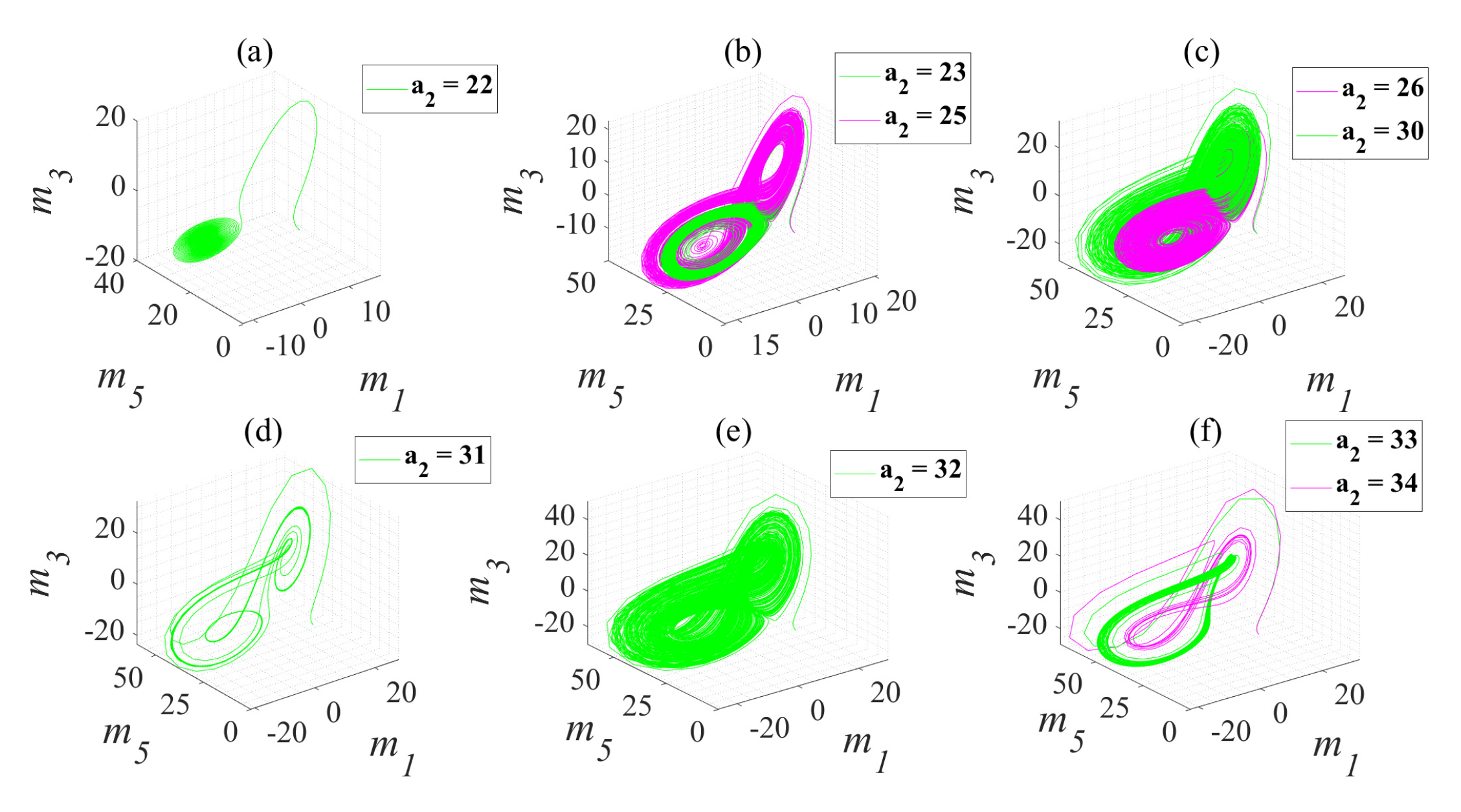
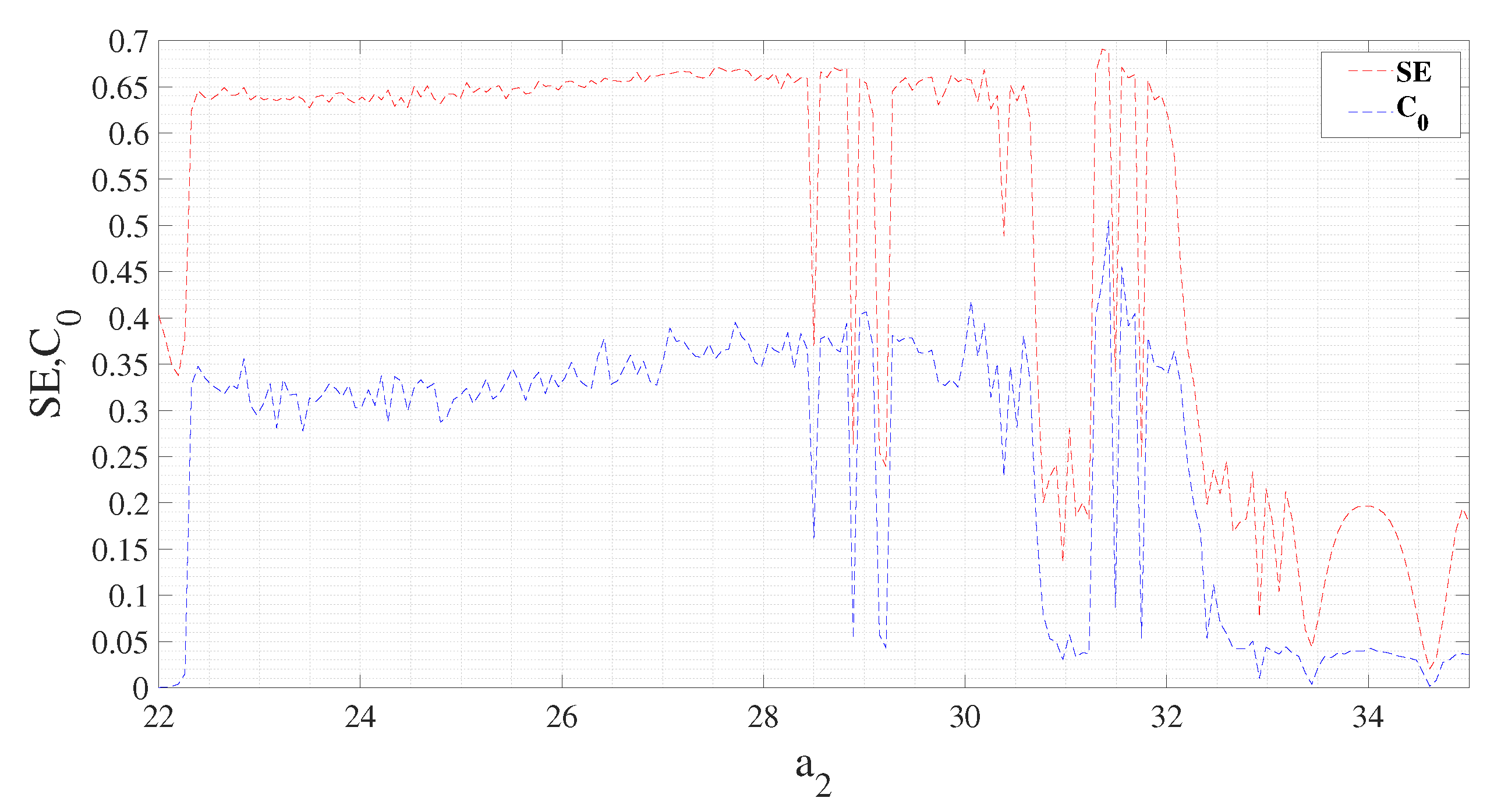
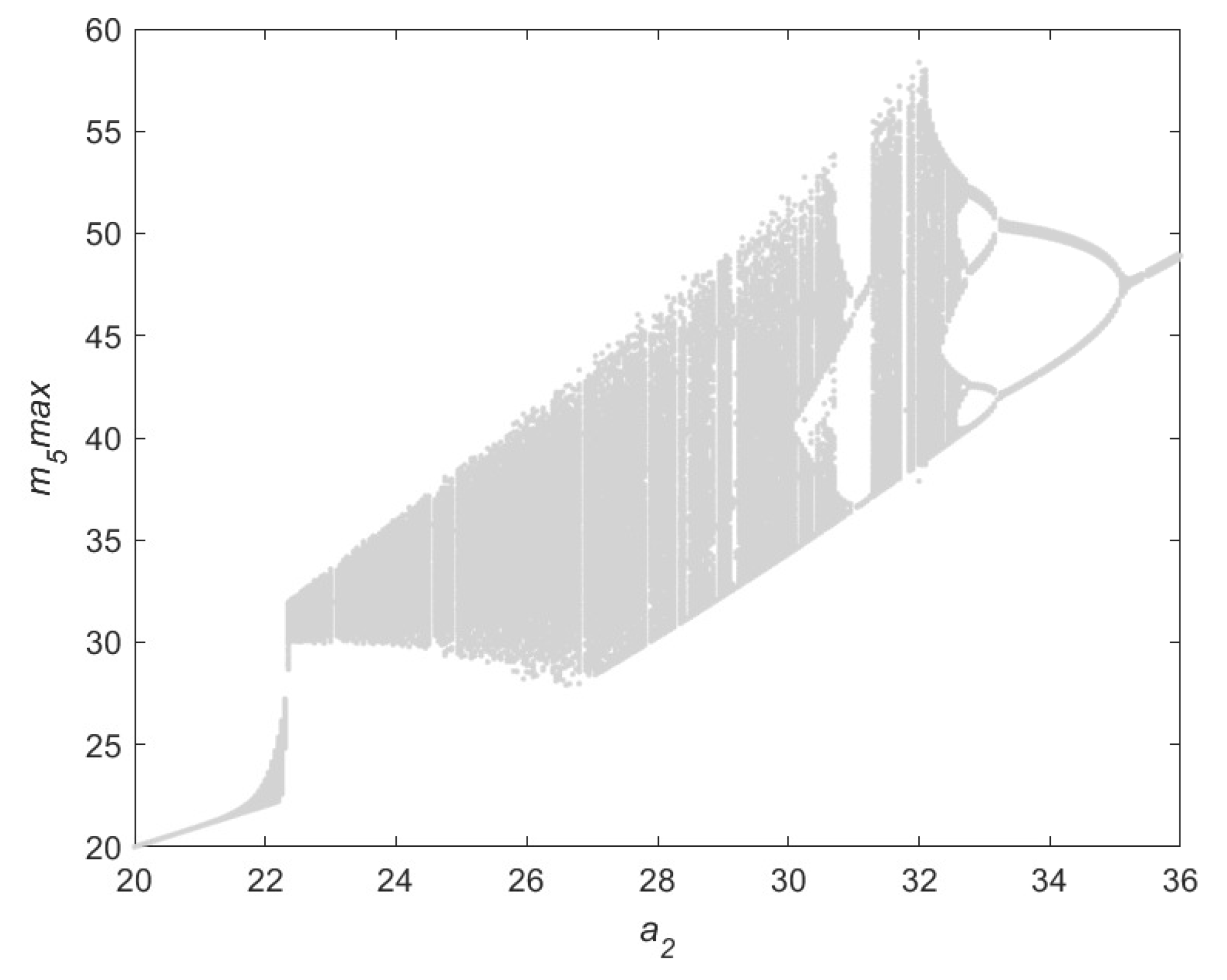
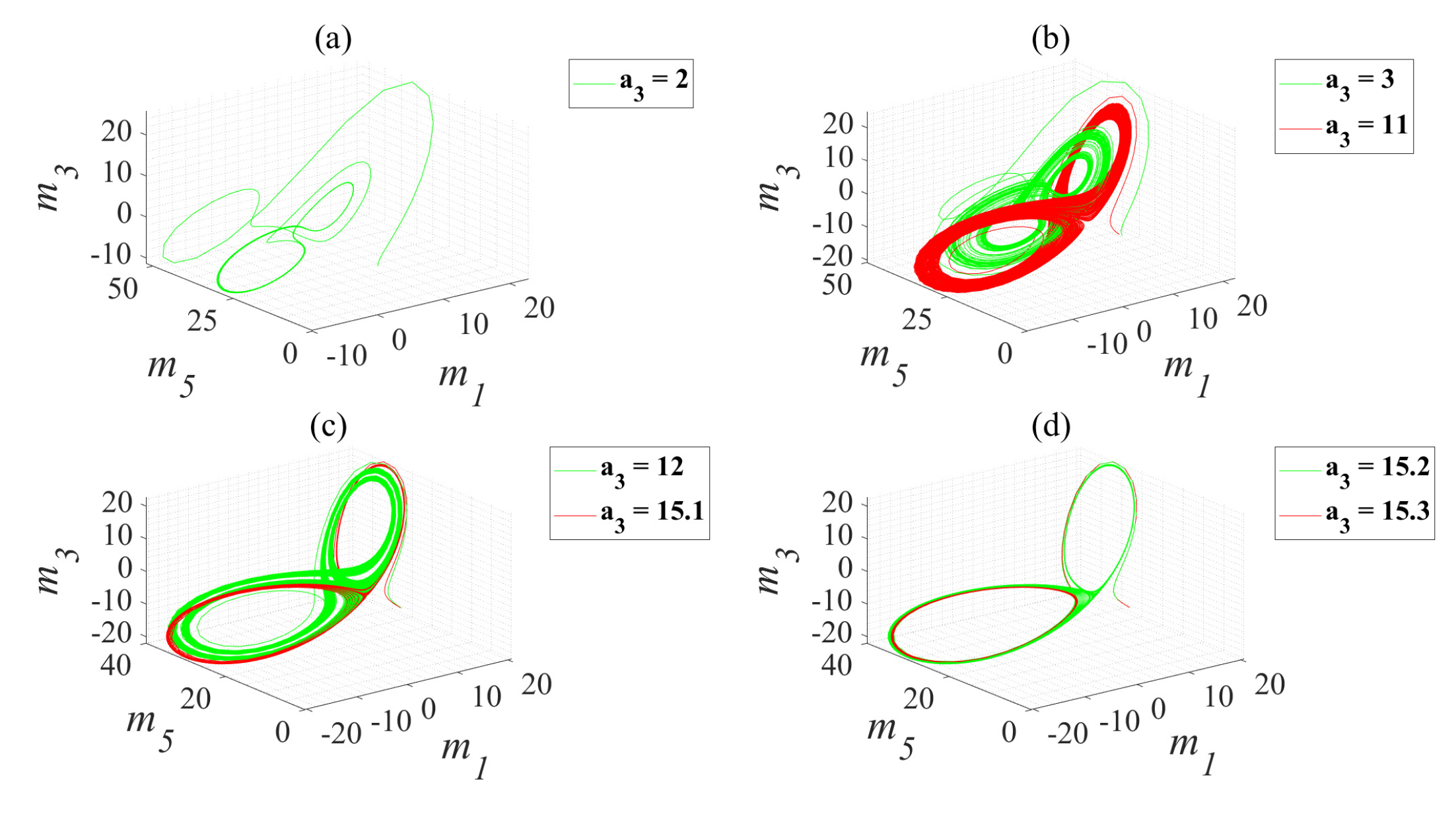
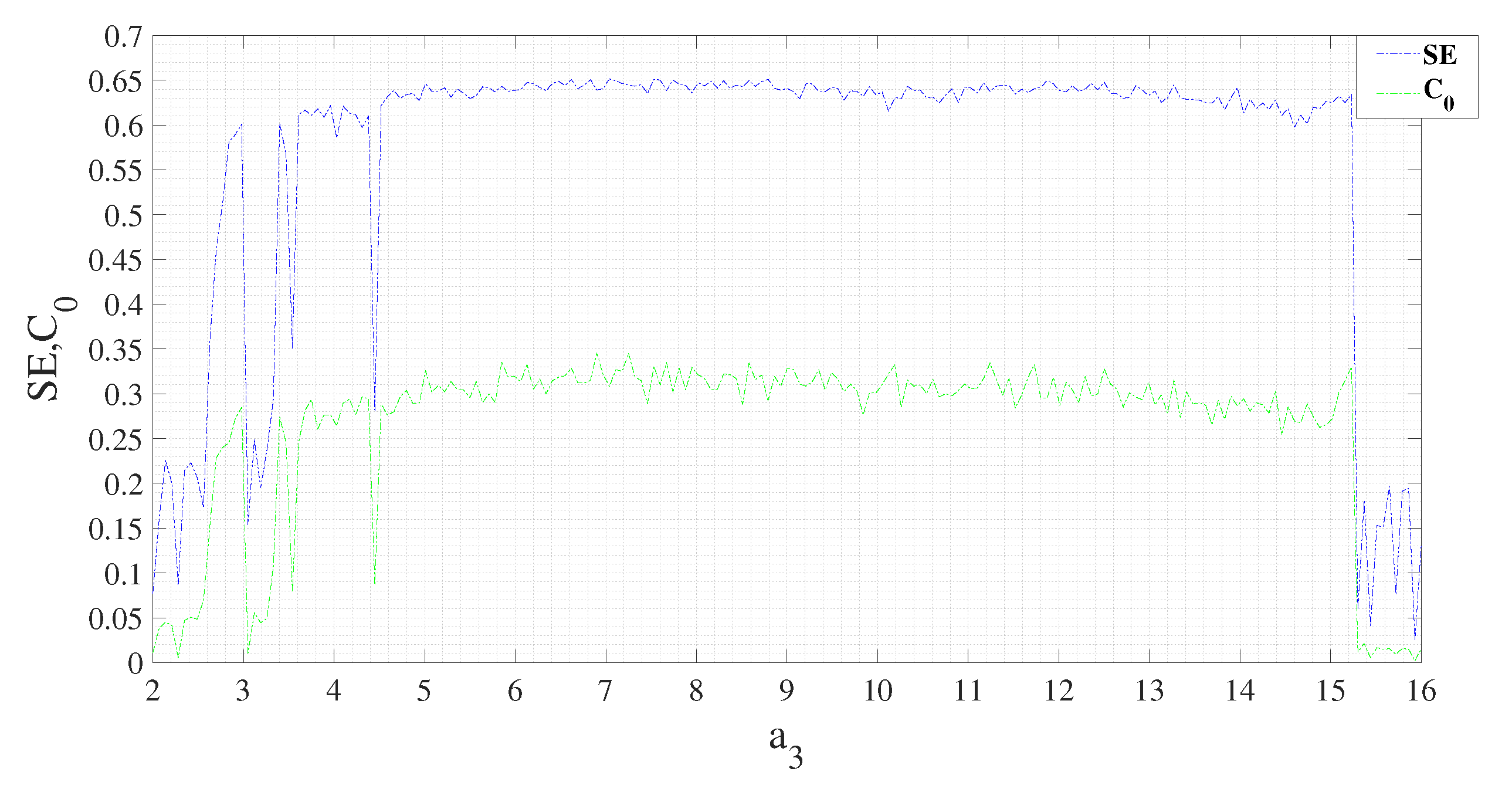
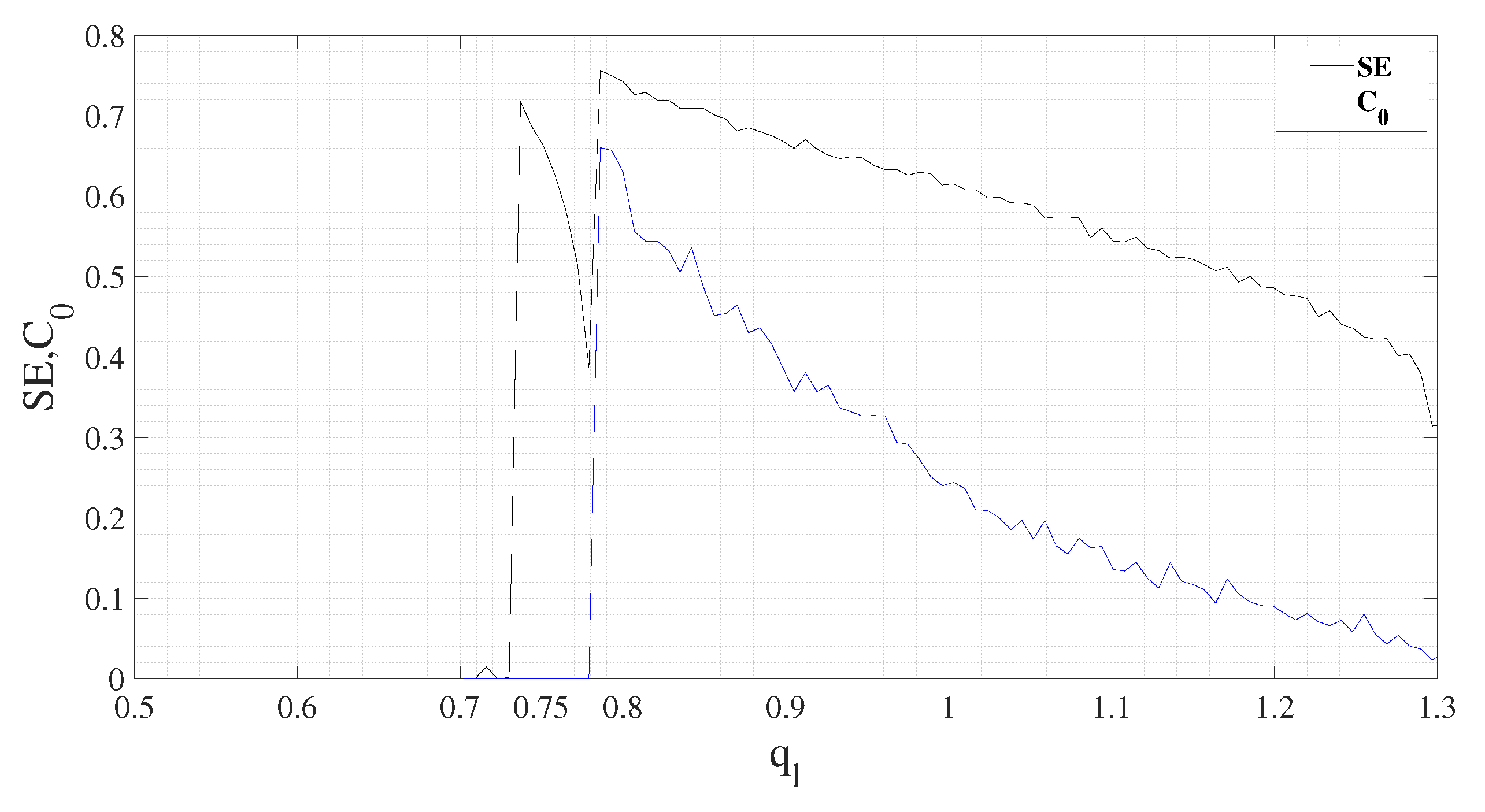
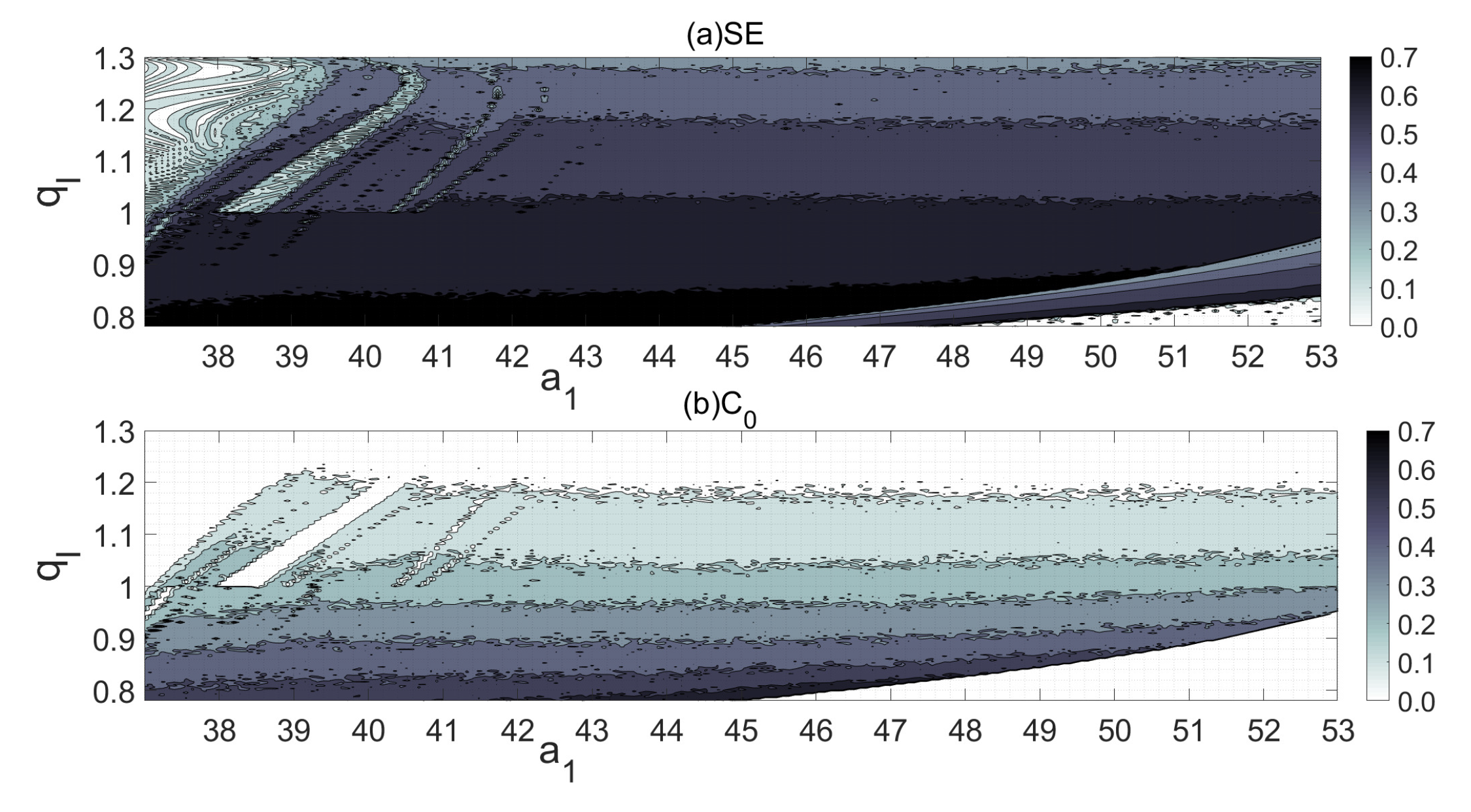

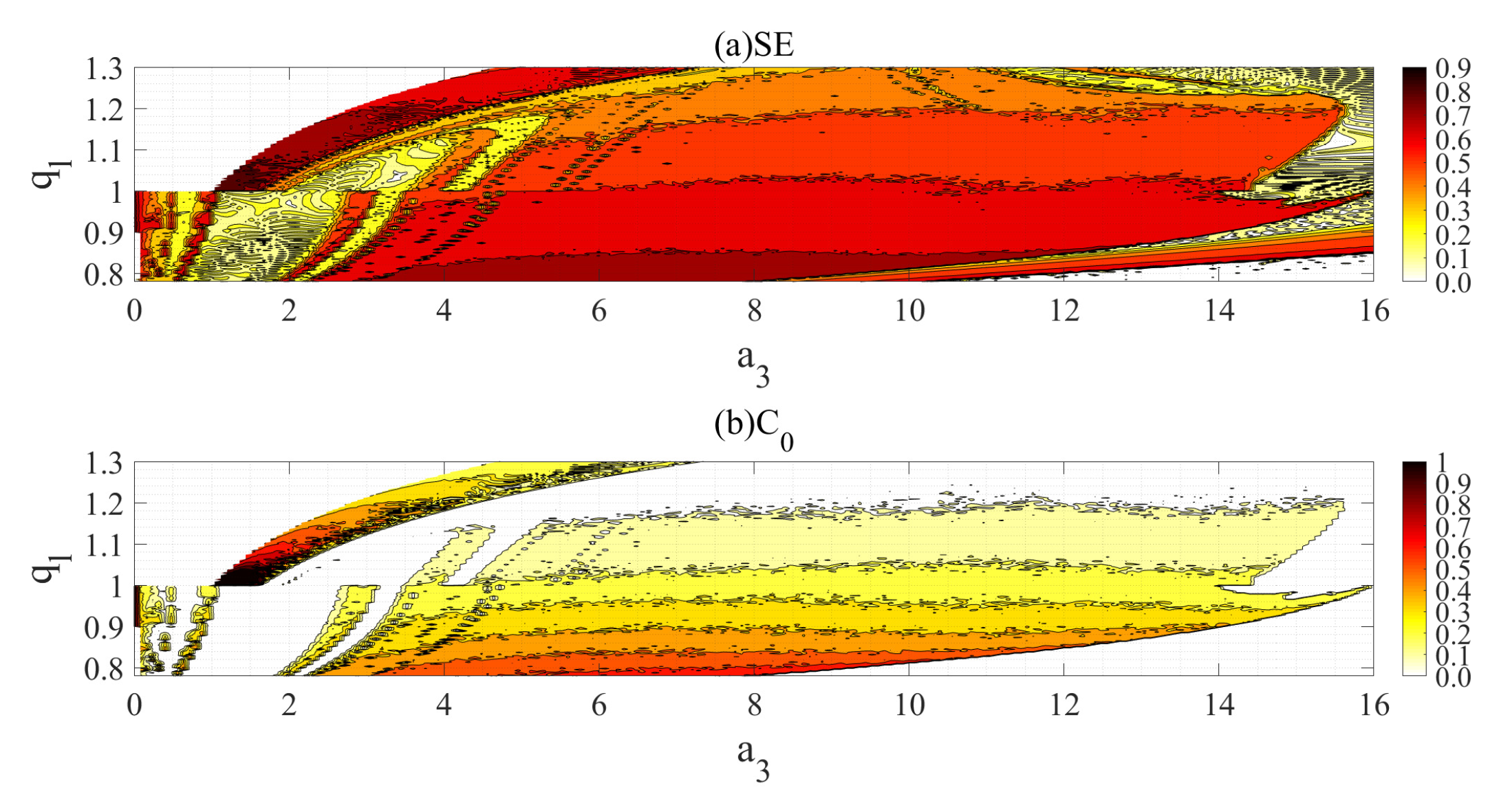



| SE | Dynamic State | ||
|---|---|---|---|
| 0 | 0 | Non-chaotic | |
| 0.71–0.38 | 0 | Non-chaotic | |
| 0.75–0.38 | 0.66–0.24 | Chaotic | |
| 0.67–0.61 | 0.38–0.24 | Chaotic | |
| 0.61–0.31 | 0.24–0.02 | Chaotic | |
| 0 | 0 | Non-chaotic |
| SNR | |||
|---|---|---|---|
| 0.5 | 292.9168 | 0.0325 | 39.5465 |
| 0.8 | 292.9168 | 0.0208 | 41.4847 |
| 0.9 | 292.9168 | 0.0637 | 36.6239 |
| 1 | 292.9168 | 0.1301 | 33.5259 |
| 1.5 | 292.9168 | 0.8129 | 25.5671 |
| SNR | |||
|---|---|---|---|
| 0.5 | 292.9168 | 0.0393 | 38.7253 |
| 0.8 | 292.9168 | 0.0356 | 39.1553 |
| 0.9 | 292.9168 | 0.0989 | 34.7150 |
| 1 | 292.9168 | 0.1945 | 31.7777 |
| 1.5 | 292.9168 | 1.1568 | 24.0348 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, J.; Ma, C.; Wang, X.; Zhang, F.; van Wyk, M.A.; Kou, L. A New Synchronization Method for Time-Delay Fractional Complex Chaotic System and Its Application. Mathematics 2021, 9, 3305. https://doi.org/10.3390/math9243305
Guo J, Ma C, Wang X, Zhang F, van Wyk MA, Kou L. A New Synchronization Method for Time-Delay Fractional Complex Chaotic System and Its Application. Mathematics. 2021; 9(24):3305. https://doi.org/10.3390/math9243305
Chicago/Turabian StyleGuo, Junmei, Chunrui Ma, Xinheng Wang, Fangfang Zhang, Michaël Antonie van Wyk, and Lei Kou. 2021. "A New Synchronization Method for Time-Delay Fractional Complex Chaotic System and Its Application" Mathematics 9, no. 24: 3305. https://doi.org/10.3390/math9243305
APA StyleGuo, J., Ma, C., Wang, X., Zhang, F., van Wyk, M. A., & Kou, L. (2021). A New Synchronization Method for Time-Delay Fractional Complex Chaotic System and Its Application. Mathematics, 9(24), 3305. https://doi.org/10.3390/math9243305







