Hierarchical Quasi-Fractional Gradient Descent Method for Parameter Estimation of Nonlinear ARX Systems Using Key Term Separation Principle
Abstract
:1. Introduction
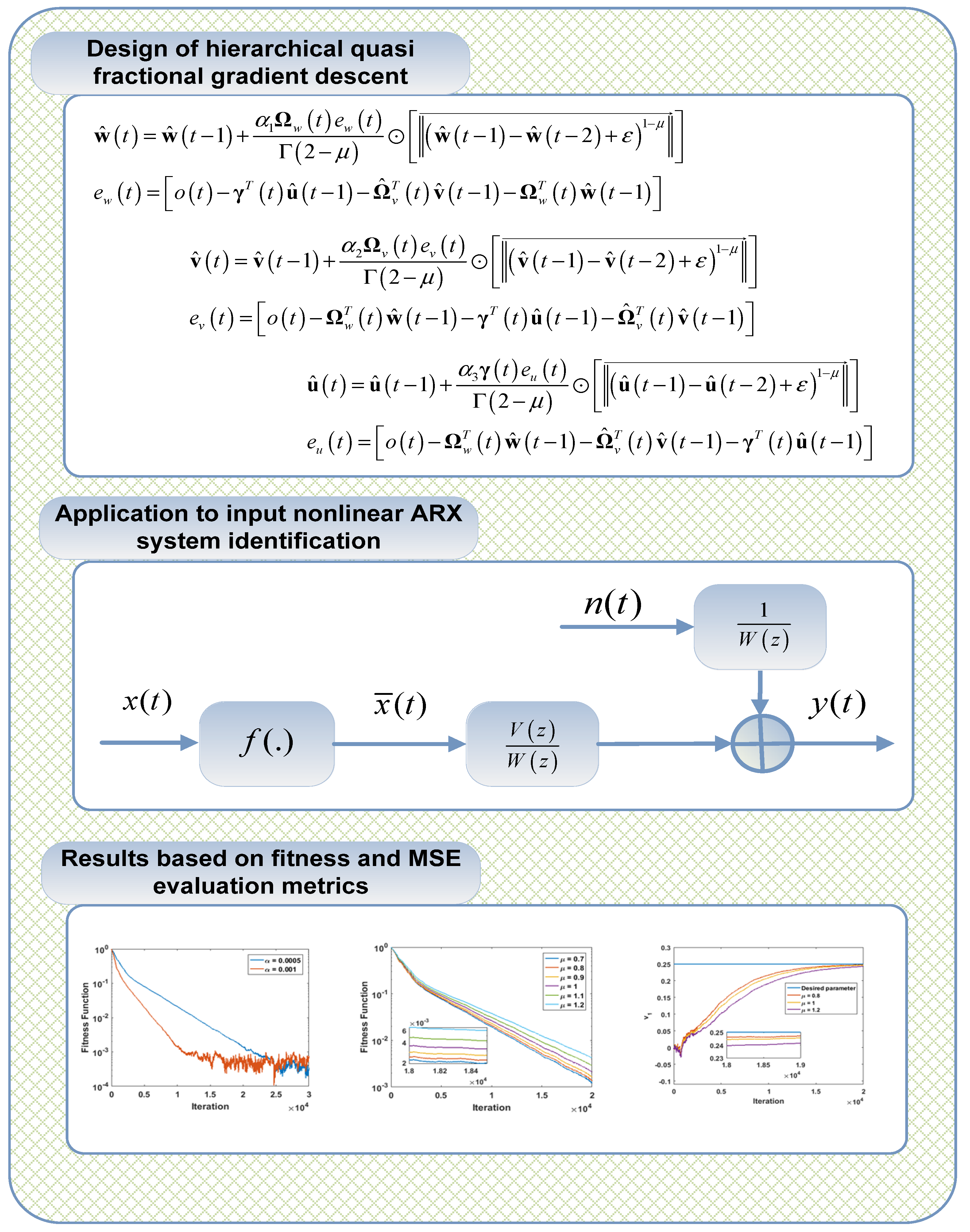
- A novel hierarchical quasi-fractional gradient descent, HQFGD, algorithm is presented by integrating the hierarchical identification theory and key term separation technique with the quasi-fractional gradient method.
- The hierarchical identification procedure decomposes the system into subsystems, thus reducing the overall dimensions of the system, and the key term separation technique allows one to avoid the overparameterization issue.
- The accuracy and robustness of the proposed HQFGD is established through effective parameter estimation of input nonlinear autoregressive exogenous noise, INARX, systems under different disturbance conditions, fractional orders and learning rate variations.
- The comparison with the standard counterpart validates the efficacy of the proposed HQFGD scheme in terms of convergence sped and estimation accuracy.
2. Nonlinear ARX System Model
3. Hierarchical Gradient Descent Method
4. Hierarchical Quasi Fractional Gradient Descent Method
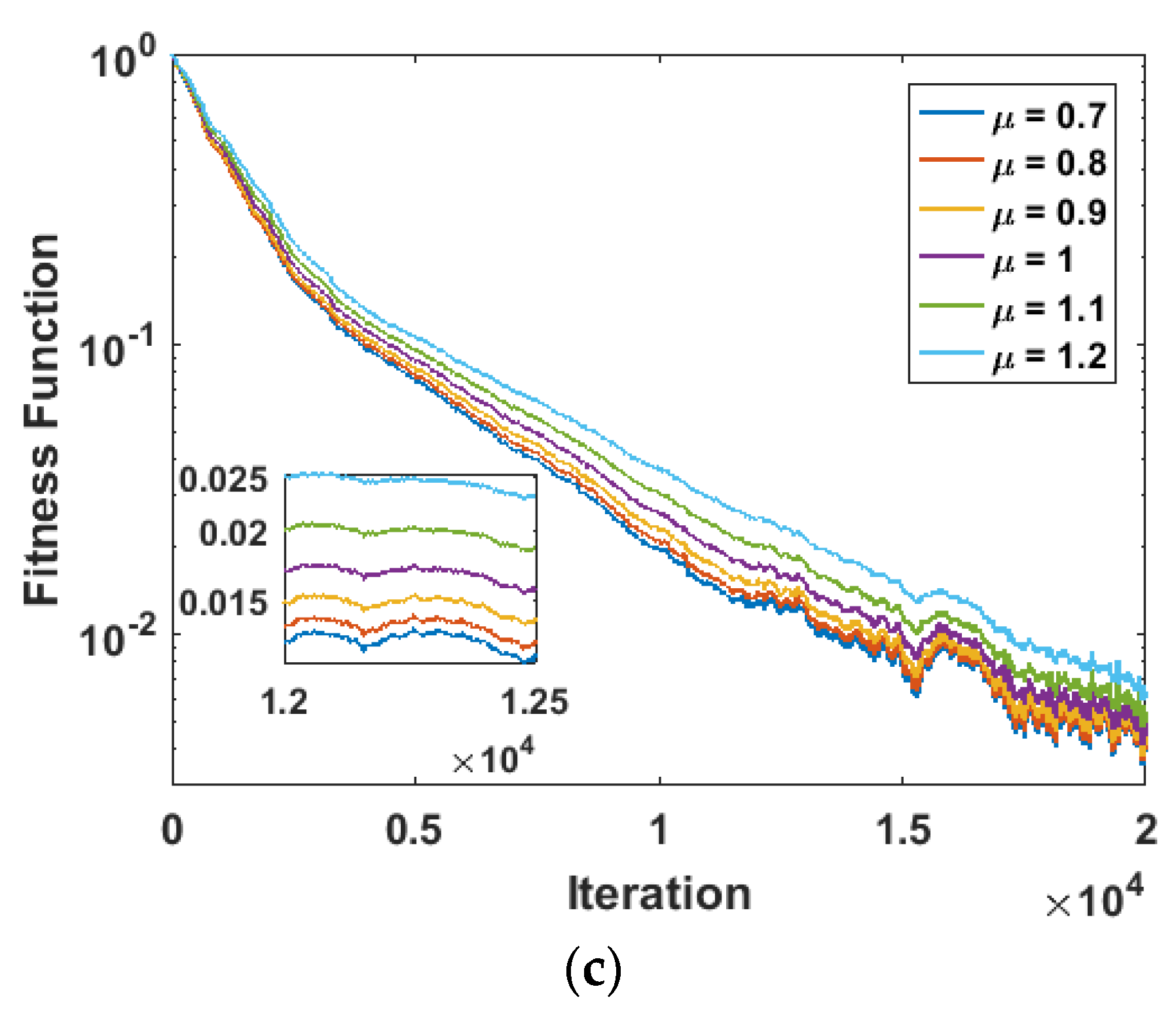
5. Results and Discussion
6. Conclusions
- A novel design of hierarchical quasi-fractional gradient descent, HQFGD, is presented for effective parameter estimation of input nonlinear autoregressive systems with exogeneous disturbance, i.e., INARX systems.
- The HQFGD is developed by incorporating the hierarchical identification principle and key term separation idea into the structure of QFGD. The hierarchical identification procedure decomposes the INARX system into different subsystems and reduces the computational complexity of the conventional counterpart.
- The HQFGD effectively estimates the parameters of the INARX system by considering only the actual system parameters and avoiding estimation of the redundant parameters due to overparameterization problems caused by the product of the cross terms.
- The HQFGD is accurate, robust, and convergent in comparison with the standard counterpart for parameter estimation of INARX systems.
- The HQFGD is relatively better with regard to convergence speed than the conventional HGD for = 0.8 and 0.9, while the HQFGD is relatively better than the HGD as regards final accuracy for = 1.1 and 1.2.
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Sabatier, J.; Agrawal, O.P.; Machado, J.T. Advances in Fractional Calculus, 1st ed.; Springer: Dordrecht, The Netherlands, 2007; Volume 4. [Google Scholar]
- Machado, J.T.; Kiryakova, V.; Mainardi, F. Recent history of fractional calculus. Commun. Nonlinear Sci. Numer. Simul. 2011, 16, 1140–1153. [Google Scholar] [CrossRef] [Green Version]
- Tejado, I.; Pérez, E.; Valério, D. Fractional calculus in economic growth modelling of the group of seven. Fract. Calc. Appl. Anal. 2019, 22, 139–157. [Google Scholar] [CrossRef]
- Rashid, S.; Hammouch, Z.; Aydi, H.; Ahmad, A.G.; Alsharif, A.M. Novel computations of the time-fractional Fisher’s model via generalized fractional integral operators by means of the Elzaki transform. Fractal Fract. 2021, 5, 94. [Google Scholar] [CrossRef]
- Sun, H.; Zhang, Y.; Baleanu, D.; Chen, W.; Chen, Y. A new collection of real world applications of fractional calculus in science and engineering. Commun. Nonlinear Sci. Numer. Simul. 2018, 64, 213–231. [Google Scholar] [CrossRef]
- Masood, Z. Fractional Dynamics of Stuxnet Virus Propagation in Industrial Control Systems. Mathematics 2021, 9, 2160. [Google Scholar] [CrossRef]
- Valério, D.; Ortigueira, M.D.; Tenreiro, J.M.; Lopes, A.M. Continuous-time fractional linear systems: Steady-state responses. In Volume 6 Applications in Control; De Gruyter: Berlin, Germany, 2019; pp. 149–174. [Google Scholar]
- Christ, L.F.; Valério, D.; Coelho, R.M.; Vinga, S. Models of bone metastases and therapy using fractional derivatives. J. Appl. Nonlinear Dyn. 2018, 7, 81–94. [Google Scholar] [CrossRef]
- Pires, E.S.; Machado, J.T.; de Moura Oliveira, P.B.; Cunha, J.B.; Mendes, L. Particle swarm optimization with fractional-order velocity. Nonlinear Dyn. 2010, 61, 295–301. [Google Scholar] [CrossRef] [Green Version]
- Mousavi, Y.; Alfi, A. Fractional calculus-based firefly algorithm applied to parameter estimation of chaotic systems. Chaos Solitons Fractals 2018, 114, 202–215. [Google Scholar] [CrossRef]
- Ray, P.K.; Paital, S.R.; Mohanty, A.; Foo, Y.E.; Krishnan, A.; Gooi, H.B.; Amaratunga, G.A. A hybrid firefly-swarm optimized fractional order interval type-2 fuzzy PID-PSS for transient stability improvement. IEEE Trans. Ind. Appl. 2019, 55, 6486–6498. [Google Scholar] [CrossRef]
- Muhammad, Y.; Khan, R.; Raja, M.A.Z.; Ullah, F.; Chaudhary, N.I.; He, Y. Design of fractional swarm intelligent computing with entropy evolution for optimal power flow problems. IEEE Access 2020, 8, 111401–111419. [Google Scholar] [CrossRef]
- Yousri, D.; Mirjalili, S. Fractional-order cuckoo search algorithm for parameter identification of the fractional-order chaotic, chaotic with noise and hyper-chaotic financial systems. Eng. Appl. Artif. Intell. 2020, 92, 103662. [Google Scholar] [CrossRef]
- Kiani-B, A.; Fallahi, K.; Pariz, N.; Leung, H. A chaotic secure communication scheme using fractional chaotic systems based on an extended fractional Kalman filter. Commun. Nonlinear Sci. Numer. Simul. 2009, 14, 863–879. [Google Scholar] [CrossRef]
- Wang, X.; Zhang, F.; Kung, H.T.; Johnson, V.C.; Latif, A. Extracting soil salinization information with a fractional-order filtering algorithm and grid-search support vector machine (GS-SVM) model. Int. J. Remote Sens. 2020, 41, 953–973. [Google Scholar] [CrossRef]
- Zahoor, R.M.A.; Qureshi, I.M. A modified least mean square algorithm using fractional derivative and its application to system identification. Eur. J. Sci. Res. 2009, 35, 14–21. [Google Scholar]
- Khan, A.A.; Shah, S.M.; Raja, M.A.Z.; Chaudhary, N.I.; He, Y.; Machado, J.A.T. Fractional LMS and NLMS Algorithms for Line Echo Cancellation. Arab. J. Sci. Eng. 2021, 46, 9385–9398. [Google Scholar] [CrossRef]
- Raja, M.A.Z.; Akhtar, R.; Chaudhary, N.I.; Zhiyu, Z.; Khan, Q.; Rehman, A.U.; Zaman, F. A new computing paradigm for the optimization of parameters in adaptive beamforming using fractional processing. Eur. Phys. J. Plus 2019, 134, 275. [Google Scholar] [CrossRef]
- Shah, S.M.; Samar, R.; Raja, M.A.Z.; Dynamics, N. Fractional-order algorithms for tracking Rayleigh fading channels. Nonlinear Dyn. 2018, 92, 1243–1259. [Google Scholar] [CrossRef]
- Yin, W.; Wei, Y.; Liu, T.; Wang, Y. A novel orthogonalized fractional order filtered-x normalized least mean squares algorithm for feedforward vibration rejection. Mech. Syst. Signal Process. 2019, 119, 138–154. [Google Scholar] [CrossRef]
- Chaudhary, N.I.; Ahmed, M.; Khan, Z.A.; Zubair, S.; Raja, M.A.Z.; Dedovic, N. Design of normalized fractional adaptive algorithms for parameter estimation of control autoregressive autoregressive systems. Appl. Math. Model. 2018, 55, 698–715. [Google Scholar] [CrossRef]
- Khan, Z.A.; Chaudhary, N.I.; Zubair, S. Fractional stochastic gradient descent for recommender systems. Electron. Mark. 2019, 29, 275–285. [Google Scholar] [CrossRef]
- Khan, Z.A.; Zubair, S.; Chaudhary, N.I.; Raja, M.A.Z.; Khan, F.A.; Dedovic, N. Design of normalized fractional SGD computing paradigm for recommender systems. Neural Comput. Appl. 2020, 32, 10245–10262. [Google Scholar] [CrossRef]
- Chaudhary, N.I.; Aslam, M.S.; Baleanu, D.; Raja, M.A.Z. Design of sign fractional optimization paradigms for parameter estimation of nonlinear Hammerstein systems. Neural Comput. Appl. 2020, 32, 8381–8399. [Google Scholar] [CrossRef]
- Chaudhary, N.I.; Zubair, S.; Raja, M.A.Z. A new computing approach for power signal modeling using fractional adaptive algorithms. ISA Trans. 2017, 68, 189–202. [Google Scholar] [CrossRef]
- Shoaib, B.; Qureshi, I.M. Adaptive step-size modified fractional least mean square algorithm for chaotic time series prediction. Chin. Phys. B 2014, 23, 050503. [Google Scholar] [CrossRef]
- Cheng, S.; Wei, Y.; Sheng, D.; Chen, Y.; Wang, Y. Identification for Hammerstein nonlinear ARMAX systems based on multi-innovation fractional order stochastic gradient. Signal Process. 2018, 142, 1–10. [Google Scholar] [CrossRef]
- Chaudhary, N.I.; Raja MA, Z.; He, Y.; Khan, Z.A.; Machado, J.T. Design of multi innovation fractional LMS algorithm for parameter estimation of input nonlinear control autoregressive systems. Appl. Math. Model. 2021, 93, 412–425. [Google Scholar] [CrossRef]
- Aslam, M.S.; Chaudhary, N.I.; Raja, M.A.Z. A sliding-window approximation-based fractional adaptive strategy for Hammerstein nonlinear ARMAX systems. Nonlinear Dyn. 2017, 87, 519–533. [Google Scholar] [CrossRef]
- Zubair, S.; Chaudhary, N.I.; Khan, Z.A.; Wang, W. Momentum fractional LMS for power signal parameter estimation. Signal Process. 2018, 142, 441–449. [Google Scholar] [CrossRef]
- Chaudhary, N.I.; Zubair, S.; Aslam, M.S.; Raja, M.A.Z.; Machado, J.T. Design of momentum fractional LMS for Hammerstein nonlinear system identification with application to electrically stimulated muscle model. Eur. Phys. J. Plus 2019, 134, 407. [Google Scholar] [CrossRef]
- Cheng, S.; Wei, Y.; Chen, Y.; Li, Y.; Wang, Y. An innovative fractional order LMS based on variable initial value and gradient order. Signal Process. 2017, 133, 260–269. [Google Scholar] [CrossRef]
- Chaudhary, N.I.; Latif, R.; Raja, M.A.Z.; Machado, J.T. An innovative fractional order LMS algorithm for power signal parameter estimation. Appl. Math. Model. 2020, 83, 703–718. [Google Scholar] [CrossRef]
- Chen, Y.; Gao, Q.; Wei, Y.; Wang, Y. Study on fractional order gradient methods. Appl. Math. Comput. 2017, 314, 310–321. [Google Scholar] [CrossRef]
- Wei, Y.; Kang, Y.; Yin, W.; Wang, Y. Generalization of the gradient method with fractional order gradient direction. J. Frankl. Inst. 2020, 357, 2514–2532. [Google Scholar] [CrossRef]
- Liu, J.; Zhai, R.; Liu, Y.; Li, W.; Wang, B.; Huang, L. A quasi fractional order gradient descent method with adaptive stepsize and its application in system identification. Appl. Math. Comput. 2021, 393, 125797. [Google Scholar] [CrossRef]
- Chen, H.; Xiao, Y.; Ding, F. Hierarchical gradient parameter estimation algorithm for Hammerstein nonlinear systems using the key term separation principle. Appl. Math. Comput. 2014, 247, 1202–1210. [Google Scholar] [CrossRef]
- Ding, F.; Chen, H.; Xu, L.; Dai, J.; Li, Q.; Hayat, T. A hierarchical least squares identification algorithm for Hammerstein nonlinear systems using the key term separation. J. Frankl. Inst. 2018, 355, 3737–3752. [Google Scholar] [CrossRef]
- Ding, F.; Ma, H.; Pan, J.; Yang, E. Hierarchical gradient-and least squares-based iterative algorithms for input nonlinear output-error systems using the key term separation. J. Frankl. Inst. 2021, 358, 5113–5135. [Google Scholar] [CrossRef]
- Giri, F.; Bai, E.W. Block-Oriented Nonlinear System Identification, 1st ed.; Springer: London, UK, 2010; Volume 1. [Google Scholar]
- Billings, S.A. Nonlinear System Identification: NARMAX Methods in the Time, Frequency, and Spatio-Temporal Domains; John Wiley & Sons: Hoboken, NJ, USA, 2013; Volume 1. [Google Scholar]
- Schoukens, J.; Ljung, L. Nonlinear system identification: A user-oriented road map. IEEE Control Syst. Mag. 2019, 39, 28–99. [Google Scholar]
- Le, F.; Markovsky, I.; Freeman, C.T.; Rogers, E. Recursive identification of Hammerstein systems with application to electrically stimulated muscle. Control Eng. Pract. 2012, 20, 386–396. [Google Scholar] [CrossRef] [Green Version]
- Mehmood, A.; Zameer, A.; Chaudhary, N.I.; Raja, M.A.Z. Backtracking search heuristics for identification of electrical muscle stimulation models using Hammerstein structure. Appl. Soft Comput. 2019, 84, 105705. [Google Scholar] [CrossRef]
- Mehmood, A.; Zameer, A.; Chaudhary, N.I.; Ling, S.H.; Raja, M.A.Z. Design of meta-heuristic computing paradigms for Hammerstein identification systems in electrically stimulated muscle models. Neural Comput. Appl. 2020, 32, 12469–12497. [Google Scholar] [CrossRef]
- Mehmood, A.; Chaudhary, N.I.; Zameer, A.; Raja, M.A.Z. Novel computing paradigms for parameter estimation in power signal models. Neural Comput. Appl. 2020, 32, 6253–6282. [Google Scholar] [CrossRef]
- Mehmood, A.; Shi, P.; Raja, M.A.Z.; Zameer, A.; Chaudhary, N.I. Design of backtracking search heuristics for parameter estimation of power signals. Neural Comput. Appl. 2020, 33, 1479–1496. [Google Scholar] [CrossRef]
- Prasad, V.; Mehta, U. Modeling and parametric identification of Hammerstein systems with time delay and asymmetric dead-zones using fractional differential equations. Mech. Syst. Signal Process. 2022, 167, 108568. [Google Scholar] [CrossRef]
- Prasad, V.; Kothari, K.; Mehta, U. Parametric identification of nonlinear fractional Hammerstein models. Fractal Fract. 2020, 4, 2. [Google Scholar] [CrossRef] [Green Version]
- Atangana, A.; Shafiq, A. Differential and integral operators with constant fractional order and variable fractional dimension. Chaos Solitons Fractals 2019, 127, 226–243. [Google Scholar] [CrossRef]
- Ghanbari, B.; Atangana, A. A new application of fractional Atangana–Baleanu derivatives: Designing ABC-fractional masks in image processing. Phys. A Stat. Mech. Its Appl. 2020, 542, 123516. [Google Scholar] [CrossRef]
- Atangana, A. Modelling the spread of COVID-19 with new fractal-fractional operators: Can the lockdown save mankind before vaccination? Chaos Solitons Fractals 2020, 136, 109860. [Google Scholar] [CrossRef]
- Shi, L.; Wang, X.; Hou, H. Research on Optimization of Array Honeypot Defense Strategies Based on Evolutionary Game Theory. Mathematics 2021, 9, 805. [Google Scholar] [CrossRef]
- Posypkin, M.; Khamisov, O. Automatic Convexity Deduction for Efficient Function’s Range Bounding. Mathematics 2021, 9, 134. [Google Scholar] [CrossRef]
- Lera, D.; Posypkin, M.; Sergeyev, Y.D. Space-filling curves for numerical approximation and visualization of solutions to systems of nonlinear inequalities with applications in robotics. Appl. Math. Comput. 2021, 390, 125660. [Google Scholar] [CrossRef]





| Noise | MSE | |||||||
|---|---|---|---|---|---|---|---|---|
| 0.02 | 0.7 | 1.3499 | 0.7503 | 0.2504 | 1.0004 | 0.4998 | 0.9004 | 9.71 × 10−8 |
| 0.8 | 1.3498 | 0.7503 | 0.2504 | 1.0004 | 0.4998 | 0.9004 | 9.01 × 10−8 | |
| 0.9 | 1.3498 | 0.7503 | 0.2503 | 1.0004 | 0.4999 | 0.9004 | 8.01 × 10−8 | |
| 1.0 | 1.3498 | 0.7502 | 0.2502 | 1.0004 | 0.4999 | 0.9004 | 6.92 × 10−8 | |
| 1.1 | 1.3497 | 0.7502 | 0.2500 | 1.0004 | 0.4999 | 0.9003 | 6.75 × 10−8 | |
| 1.2 | 1.3496 | 0.7500 | 0.2496 | 1.0006 | 0.4999 | 0.9003 | 1.24 × 10−7 | |
| 0.09 | 0.7 | 1.3496 | 0.7511 | 0.2516 | 1.0012 | 0.4994 | 0.9014 | 1.28 × 10−6 |
| 0.8 | 1.3496 | 0.7511 | 0.2516 | 1.0012 | 0.4994 | 0.9013 | 1.21 × 10−6 | |
| 0.9 | 1.3496 | 0.7510 | 0.2515 | 1.0011 | 0.4995 | 0.9013 | 1.10 × 10−6 | |
| 1.0 | 1.3496 | 0.7510 | 0.2513 | 1.0011 | 0.4995 | 0.9012 | 9.53 × 10−7 | |
| 1.1 | 1.3495 | 0.7508 | 0.2510 | 1.0011 | 0.4995 | 0.9012 | 7.77 × 10−7 | |
| 1.2 | 1.3495 | 0.7507 | 0.2505 | 1.0011 | 0.4996 | 0.9011 | 6.10 × 10−7 | |
| 0.2 | 0.7 | 1.3486 | 0.7531 | 0.2546 | 1.0036 | 0.4983 | 0.9038 | 1.05 × 10−5 |
| 0.8 | 1.3487 | 0.7530 | 0.2544 | 1.0035 | 0.4984 | 0.9037 | 9.87 × 10−6 | |
| 0.9 | 1.3487 | 0.7528 | 0.2542 | 1.0033 | 0.4984 | 0.9036 | 9.07 × 10−6 | |
| 1.0 | 1.3488 | 0.7527 | 0.2539 | 1.0031 | 0.4985 | 0.9035 | 8.05 × 10−6 | |
| 1.1 | 1.3488 | 0.7525 | 0.2535 | 1.0029 | 0.4986 | 0.9033 | 6.81 × 10−6 | |
| 1.2 | 1.3489 | 0.7523 | 0.2528 | 1.0028 | 0.4988 | 0.9030 | 5.00 × 10−6 | |
| 1.3500 | 0.7500 | 0.2500 | 1.0000 | 0.5000 | 0.9000 | 0 |
| Noise | MSE | |||||||
|---|---|---|---|---|---|---|---|---|
| 0.02 | 0.7 | 1.3498 | 0.7507 | 0.2509 | 1.0010 | 0.4997 | 0.9006 | 4.46 × 10−7 |
| 0.8 | 1.3498 | 0.7507 | 0.2509 | 1.0010 | 0.4997 | 0.9006 | 4.27 × 10−7 | |
| 0.9 | 1.3498 | 0.7506 | 0.2509 | 1.0009 | 0.4997 | 0.9005 | 4.00 × 10−7 | |
| 1.0 | 1.3498 | 0.7506 | 0.2508 | 1.0009 | 0.4998 | 0.9005 | 3.64 × 10−7 | |
| 1.1 | 1.3498 | 0.7506 | 0.2508 | 1.0008 | 0.4998 | 0.9005 | 3.20 × 10−7 | |
| 1.2 | 1.3498 | 0.7505 | 0.2507 | 1.0007 | 0.4998 | 0.9005 | 2.70 × 10−7 | |
| 0.09 | 0.7 | 1.3494 | 0.7524 | 0.2530 | 1.0036 | 0.4991 | 0.9020 | 5.41 × 10−6 |
| 0.8 | 1.3494 | 0.7523 | 0.2530 | 1.0035 | 0.4991 | 0.9019 | 5.19 × 10−6 | |
| 0.9 | 1.3494 | 0.7522 | 0.2529 | 1.0033 | 0.4991 | 0.9019 | 4.85 × 10−6 | |
| 1.0 | 1.3494 | 0.7521 | 0.2528 | 1.0031 | 0.4991 | 0.9019 | 4.41 × 10−6 | |
| 1.1 | 1.3494 | 0.7519 | 0.2527 | 1.0028 | 0.4991 | 0.9018 | 3.88 × 10−6 | |
| 1.2 | 1.3494 | 0.7518 | 0.2526 | 1.0024 | 0.4992 | 0.9017 | 3.27 × 10−6 | |
| 0.2 | 0.7 | 1.3482 | 0.7567 | 0.2580 | 1.0106 | 0.4973 | 0.9055 | 4.36 × 10−5 |
| 0.8 | 1.3481 | 0.7562 | 0.2580 | 1.0103 | 0.4974 | 0.9054 | 4.14 × 10−5 | |
| 0.9 | 1.3480 | 0.7559 | 0.2578 | 1.0098 | 0.4974 | 0.9054 | 3.86 × 10−5 | |
| 1.0 | 1.3480 | 0.7556 | 0.2576 | 1.0091 | 0.4974 | 0.9052 | 3.51 × 10−5 | |
| 1.1 | 1.3480 | 0.7552 | 0.2573 | 1.0083 | 0.4975 | 0.9051 | 3.08 × 10−5 | |
| 1.2 | 1.3481 | 0.7547 | 0.2569 | 1.0073 | 0.4976 | 0.9049 | 2.59 × 10−5 | |
| 1.3500 | 0.7500 | 0.2500 | 1.0000 | 0.5000 | 0.9000 | 0 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chaudhary, N.I.; Raja, M.A.Z.; Khan, Z.A.; Cheema, K.M.; Milyani, A.H. Hierarchical Quasi-Fractional Gradient Descent Method for Parameter Estimation of Nonlinear ARX Systems Using Key Term Separation Principle. Mathematics 2021, 9, 3302. https://doi.org/10.3390/math9243302
Chaudhary NI, Raja MAZ, Khan ZA, Cheema KM, Milyani AH. Hierarchical Quasi-Fractional Gradient Descent Method for Parameter Estimation of Nonlinear ARX Systems Using Key Term Separation Principle. Mathematics. 2021; 9(24):3302. https://doi.org/10.3390/math9243302
Chicago/Turabian StyleChaudhary, Naveed Ishtiaq, Muhammad Asif Zahoor Raja, Zeshan Aslam Khan, Khalid Mehmood Cheema, and Ahmad H. Milyani. 2021. "Hierarchical Quasi-Fractional Gradient Descent Method for Parameter Estimation of Nonlinear ARX Systems Using Key Term Separation Principle" Mathematics 9, no. 24: 3302. https://doi.org/10.3390/math9243302
APA StyleChaudhary, N. I., Raja, M. A. Z., Khan, Z. A., Cheema, K. M., & Milyani, A. H. (2021). Hierarchical Quasi-Fractional Gradient Descent Method for Parameter Estimation of Nonlinear ARX Systems Using Key Term Separation Principle. Mathematics, 9(24), 3302. https://doi.org/10.3390/math9243302






