The Integral Mittag-Leffler, Whittaker and Wright Functions

Abstract

Integral Mittag-Leffler, Whittaker and Wright functions with integrands similar to those which already exist in mathematical literature are introduced for the first time. For particular values of parameters, they can be presented in closed-form. In most reported cases, these new integral functions are expressed as generalized hypergeometric functions but also in terms of elementary and special functions. The behavior of some of the new integral functions is presented in graphical form. By using the MATHEMATICA program to obtain infinite sums that define the Mittag-Leffler, Whittaker, and Wright functions and also their corresponding integral functions, these functions and many new Laplace transforms of them are also reported in the Appendices for integral and fractional values of parameters.

1. Introduction

The appearance of special functions of mathematical physics was associated with solutions of particular ordinary differential equations, while the integral special functions arrived much later in mathematical literature after properties of these functions were investigated. Integral special functions were introduced as new special functions, which can be applied in many circumstances, especially in operational calculus, where they are frequently serving as direct and inverse integral transforms. The form of an integrand is identical for all integral functions, but limits of integration are different in order to assure the convergence of defined integrals. There are two types of integral special functions: those with elementary functions in their integrands and those with special functions. To the first group belong the exponential integral $-\mathrm{Ei}\left(-x\right)$, the sine and cosine integrals, $\mathrm{si}\left(x\right)$, $\mathrm{Si}\left(x\right)$, $\mathrm{ci}\left(x\right)$ and $\mathrm{Ci}\left(x\right)$, and the corresponding integrals of hyperbolic trigonometric functions, $\mathrm{Shi}\left(x\right)$ and $\mathrm{Chi}\left(x\right)$. These functions are defined in the following way [1,2,3,4,5]

$$\begin{array}{c}{\displaystyle {\mathrm{E}}_1\left(x\right)=-\mathrm{Ei}\left(-x\right)={\int }_x^{\infty }\frac{e^{-t}}{t}dt,x>0,}\hfill \\ {\displaystyle \mathrm{Si}\left(x\right)={\int }_0^x\frac{sint}{t}dt,}\hfill \\ {\displaystyle \mathrm{si}\left(x\right)=-{\int }_x^{\infty }\frac{sint}{t}dt=\mathrm{Si}\left(x\right)-\frac{\pi }{2},}\hfill \\ {\displaystyle \mathrm{Ci}\left(x\right)=-{\int }_x^{\infty }\frac{cost}{t}dt=\gamma +lnx-{\int }_0^x\frac{1-cost}{t}dt=-\mathrm{ci}\left(x\right),}\hfill \\ {\displaystyle \mathrm{Shi}\left(x\right)={\int }_0^x\frac{sinht}{t}dt,}\hfill \\ {\displaystyle \mathrm{Chi}\left(x\right)=\gamma +lnx-{\int }_0^x\frac{1-cosht}{t}dt,}\hfill \end{array}$$

(1)

where $\gamma$ is the Euler–Mascheroni constant. As can be observed in (1), the integral special functions have integrands in the form, $f\left(t\right)/t$, and the intervals of integrations are $0<t<x$ or $x<t<\infty$. Few direct and inverse integral transforms are presented below to illustrate their applications, for example, in the Laplace transformation [6,7,8],

$$F\left(s\right)≔\mathcal{L}\left[f\left(t\right)\right]≔{\int }_0^{\infty }{e}^{-st}f\left(t\right)dt,$$

(2)

we have

$$\begin{array}{c}{\displaystyle \mathcal{L}\left[\frac{1}{\sqrt{t}}\mathrm{Ei}\left(-t\right)\right]=-2\sqrt{\frac{\pi }{s}}ln\left(\sqrt{s}+\sqrt{s+1}\right),\mathrm{Re}s>0,}\hfill \\ {\displaystyle \mathcal{L}\left[\mathrm{Si}\left(t\right)\right]=\frac{{cot}^{-1}s}{s},\mathrm{Re}s>0,}\hfill \\ {\displaystyle \mathcal{L}\left[\mathrm{si}\left(t\right)\right]=\frac{{tan}^{-1}s}{s},}\hfill \\ {\displaystyle \mathcal{L}\left[\mathrm{Ci}\left(t\right)\right]=-\frac{ln\left(1+s^2\right)}{2s},}\hfill \\ {\displaystyle {\mathcal{L}}^{-1}\left[\frac{ln\left(s+b\right)}{s+a}\right]=e^{-at}\left[ln\left(b-a\right)-\mathrm{Ei}\left(\left(a-b\right)t\right)\right],\mathrm{Re}\left(s-a\right)>0,}\hfill \\ {\displaystyle {\mathcal{L}}^{-1}\left[\frac{lns}{s^2+1}\right]=cost\mathrm{Si}\left(t\right)-sint\mathrm{Ci}\left(t\right),\mathrm{Re}s>0,}\hfill \\ {\displaystyle {\mathcal{L}}^{-1}\left[\frac{slns}{s^2+1}\right]=-sint\mathrm{Si}\left(t\right)-cost\mathrm{Ci}\left(t\right).}\hfill \end{array}$$

(3)

Integrands in the second group of integral special functions include special functions, the most well-known and applied of which are the integral Bessel functions (see, e.g., [3,7,9,10,11,12,13])

$$\begin{array}{c}{\displaystyle {\mathrm{Ji}}_{\nu }\left(x\right)=-{\int }_x^{\infty }\frac{J_{\nu }\left(t\right)}{t}dt,}\hfill \\ {\displaystyle {\mathrm{Yi}}_{\nu }\left(x\right)=-{\int }_x^{\infty }\frac{Y_{\nu }\left(t\right)}{t}dt,}\hfill \\ {\displaystyle {\mathrm{Ii}}_{\nu }\left(x\right)=-{\int }_0^x\frac{I_{\nu }\left(t\right)}{t}dt,}\hfill \\ {\displaystyle {\mathrm{Ki}}_{\nu }\left(x\right)=-{\int }_x^{\infty }\frac{K_{\nu }\left(t\right)}{t}dt.}\hfill \end{array}$$

(4)

Already in 1929, van der Pol [9] showed that it is possible to express the differentiation with respect to the order of the Bessel function of the first kind as a convolution integral, which includes the integral Bessel function of the zero-order:

$$\frac{\partial J_{\nu }\left(t\right)}{\partial \nu }=\frac{1}{2}{\int }_0^t{\mathrm{Ji}}_0\left(t-x\right)\left[J_{\nu -1}\left(x\right)-J_{\nu +1}\left(x\right)\right]dx.$$

(5)

The integral Bessel functions of the zero-order are inverse transforms of the following Laplace transforms [7]

$$\begin{array}{c}{\displaystyle {\mathcal{L}}^{-1}\left[\frac{{sinh}^{-1}s}{s}\right]={\mathrm{Ji}}_0\left(t\right),}\hfill \\ {\displaystyle {\mathcal{L}}^{-1}\left[\frac{{\left({sinh}^{-1}s\right)}^2}{s}\right]={\mathrm{Yi}}_0\left(t\right),}\hfill \\ {\displaystyle {\mathcal{L}}^{-1}\left[ln\left(s+\sqrt{s^2+1}\right)-\frac{\pi i}{2}\right]={\mathrm{Ii}}_0\left(t\right),}\hfill \\ {\displaystyle {\mathcal{L}}^{-1}\left[\frac{{\left({cosh}^{-1}s\right)}^2}{2s}+\frac{{\pi }^2}{8s}\right]={\mathrm{Ki}}_0\left(t\right).}\hfill \end{array}$$

(6)

In analogy to the integral Bessel functions and with the possibility of extension to other special functions, this work introduces three new integral functions. Furthermore, these integral functions guide us toward the establishment of integrals and series. Section 2 explores the integral Mittag-Leffler functions. Section 3 and Section 4 discuss the integral Whittaker and Wright functions, respectively. Section 5 contains concluding remarks.

In order to preserve the applied form of notation, the following two integral functions are introduced:

$$\mathrm{Fi}\left(x\right)={\int }_0^x\frac{f\left(t\right)-f\left(0\right)}{t}dt,$$

(7)

and

$$\mathrm{fi}\left(x\right)={\int }_x^{\infty }\frac{f\left(t\right)}{t}dt.$$

(8)

To ensure convergence of integrals in (7) or in (8), which depends on the behavior of $f\left(t\right)/t$ integrands at the origin and at infinity, the forms of integral functions $\mathrm{Fi}\left(x\right)$ or $\mathrm{fi}\left(x\right)$ are chosen. Since the explicit expressions for $f\left(t\right)$ functions are sometimes given in the form of $f\left(t^{\alpha }\right)$ where $\alpha =\pm \frac{1}{2},\pm 1,2,3,\dots$ the corresponding change of integration variables for these equations is desired.

In the case of Mittag-Leffler, Whittaker and Wright functions, for some values of parameters, by using the MATHEMATICA program, it was possible to obtain these integral functions in a closed-form. Derived integral functions are tabulated and also in some cases graphically presented (see [3]).

2. The Integral Mittag-Leffler Functions

The classical one-parameter and the two-parameter Mittag-Leffler functions are defined by [14]:

$$\begin{array}{c}{\displaystyle {\mathrm{E}}_{\alpha }\left(x\right)=\sum _{k=0}^{\infty }\frac{x^k}{\Gamma \left(\alpha k+1\right)},\mathrm{Re}\alpha >0,}\hfill \\ {\displaystyle {\mathrm{E}}_{\alpha ,\beta }\left(x\right)=\sum _{k=0}^{\infty }\frac{x^k}{\Gamma \left(\alpha k+\beta \right)},\mathrm{Re}\alpha >0,\mathrm{Re}\beta >0.}\hfill \end{array}$$

(9)

In this investigation, they are only considered for positive real values of the argument, i.e., $x>0$. In the particular case of positive rational $\alpha$ with $\alpha =p/q$ and p and q positive coprimes, Mittag-Leffler functions are given as a finite sum of generalized hypergeometric functions (see (A3) in Appendix A).

The Laplace transforms of the Mittag-Leffler functions are derived directly from (2) and (9), and we have:

$$\begin{array}{c}{\displaystyle \mathcal{L}\left[{\mathrm{E}}_{\alpha }\left(t\right)\right]={\int }_0^{\infty }{e}^{-st}\left[\sum _{k=0}^{\infty }\frac{t^k}{\Gamma \left(\alpha k+1\right)}\right]dt=\sum _{k=0}^{\infty }\frac{k!}{\Gamma \left(\alpha k+1\right)}{\left(\frac{1}{s}\right)}^{k+1},}\hfill \\ {\displaystyle \mathcal{L}\left[{\mathrm{E}}_{\alpha ,\beta }\left(t\right)\right]={\int }_0^{\infty }{e}^{-st}\left[\sum _{k=0}^{\infty }\frac{t^k}{\Gamma \left(\alpha k+\beta \right)}\right]dt=\sum _{k=0}^{\infty }\frac{k!}{\Gamma \left(\alpha k+\beta \right)}{\left(\frac{1}{s}\right)}^{k+1},}\hfill \\ \mathrm{Re}s>1.\hfill \end{array}$$

(10)

For particular values of parameters $\alpha$ and $\beta$, the explicit form of the Mittag-Leffler functions can be obtained by applying the MATHEMATICA program to sums of infinite series in (9), and these results are presented in Appendix A. Using Equation (10), many new Laplace transforms of the Mittag-Leffler functions were evaluated, and they are also reported in Appendix A. Similarly as in the case when $\alpha$ is positive rational, the Laplace transforms of the Mittag-Leffler functions can be expressed by the finite sum of products of generalized hypergeometric functions (see (A4) in Appendix A).

The integral Mittag-Leffler functions are introduced by considering their exponential behavior as a function of real, positive variable x (see Appendix A).

$$\begin{array}{c}{\displaystyle {\mathrm{Ei}}_{\alpha }\left(x\right)={\int }_0^x\frac{{\mathrm{E}}_{\alpha }\left(t\right)-1}{t}dt,}\hfill \\ {\displaystyle {\mathrm{Ei}}_{\alpha ,\beta }\left(x\right)={\int }_0^x\frac{{\mathrm{E}}_{\alpha ,\beta }\left(t\right)-1/\Gamma \left(\beta \right)}{t}dt.}\hfill \end{array}$$

(11)

Formally, by introducing (9) into (11) we have

$$\begin{array}{c}{\displaystyle {\mathrm{Ei}}_{\alpha }\left(x\right)=\sum _{k=1}^{\infty }\frac{x^k}{k\Gamma \left(\alpha k+1\right)},}\hfill \\ {\displaystyle {\mathrm{Ei}}_{\alpha ,\beta }\left(x\right)=\sum _{k=1}^{\infty }\frac{x^k}{k\Gamma \left(\alpha k+\beta \right)}.}\hfill \end{array}$$

(12)

For several values of parameters $\alpha$ and $\beta$, it is possible to derive the integral Mittag-Leffler functions in a closed-form by applying the MATHEMATICA program to the sums of infinite series in (12). These functions are presented in Table 1 and Table 2. As it is observable, most of these integral functions are expressed as generalized hypergeometric series. Typical behavior of one-parameter and two-parameter integral Mittag-Leffler functions is illustrated in Figure 1 and Figure 2.

Table 1. The integral Mittag-Leffler functions derived for some values of parameters $\alpha$ and $\beta$ by using (12).

$\mathit{\alpha }$	$\mathit{\beta }$	${\mathbf{Ei}}_{\mathit{\alpha },\mathit{\beta }}\left(\mathit{x}\right)$
$\frac{1}{3}$	$\frac{1}{5}$	$\frac{x}{\Gamma \left(\frac{8}{15}\right)}{}_2{F}_2\left(\left.\begin{array}{c}1,\frac{1}{3}\\ \frac{8}{15},\frac{4}{3}\end{array}\right|x^3\right)+\frac{x^2}{2\Gamma \left(\frac{13}{15}\right)}{}_2{F}_2\left(\left.\begin{array}{c}1,\frac{2}{3}\\ \frac{13}{15},\frac{5}{3}\end{array}\right|x^3\right)+\frac{5x^3}{3\Gamma \left(\frac{1}{5}\right)}{}_2{F}_2\left(\left.\begin{array}{c}1,1\\ \frac{6}{5},2\end{array}\right|x^3\right)$
$\frac{1}{3}$	$\frac{1}{4}$	$\frac{x}{\Gamma \left(\frac{7}{12}\right)}{}_2{F}_2\left(\left.\begin{array}{c}1,\frac{1}{3}\\ \frac{7}{12},\frac{4}{3}\end{array}\right|x^3\right)+\frac{x^2}{2\Gamma \left(\frac{11}{12}\right)}{}_2{F}_2\left(\left.\begin{array}{c}1,\frac{2}{3}\\ \frac{11}{12},\frac{5}{3}\end{array}\right|x^3\right)+\frac{4x^3}{3\Gamma \left(\frac{1}{4}\right)}{}_2{F}_2\left(\left.\begin{array}{c}1,1\\ \frac{5}{4},2\end{array}\right|x^3\right)$
$\frac{1}{3}$	$\frac{1}{2}$	$\frac{2x^3}{3\sqrt{\pi }}{}_2{F}_2\left(\left.\begin{array}{c}1,1\\ \frac{3}{2},2\end{array}\right|x^3\right)+\frac{x}{\Gamma \left(\frac{5}{6}\right)}{}_2{F}_2\left(\left.\begin{array}{c}1,\frac{1}{3}\\ \frac{5}{6},\frac{4}{3}\end{array}\right|x^3\right)+\frac{3x^2}{\Gamma \left(\frac{1}{6}\right)}{}_2{F}_2\left(\left.\begin{array}{c}1,\frac{2}{3}\\ \frac{7}{6},\frac{5}{3}\end{array}\right|x^3\right)$
$\frac{1}{3}$	$\frac{3}{2}$	$\frac{x}{\Gamma \left(\frac{11}{6}\right)}{}_2{F}_2\left(\left.\begin{array}{c}1,\frac{1}{3}\\ \frac{4}{3},\frac{11}{6}\end{array}\right|x^3\right)+\frac{18x^2}{7\Gamma \left(\frac{1}{6}\right)}{}_2{F}_2\left(\left.\begin{array}{c}1,\frac{2}{3}\\ \frac{5}{3},\frac{13}{6}\end{array}\right|x^3\right)+\frac{4x^3}{9\sqrt{\pi }}{}_2{F}_2\left(\left.\begin{array}{c}1,1\\ 2,\frac{5}{2}\end{array}\right|x^3\right)$
$\frac{1}{2}$	$\frac{1}{2}$	$\frac{x^2}{\sqrt{\pi }}{}_2{F}_2\left(\left.\begin{array}{c}1,1\\ \frac{3}{2},2\end{array}\right|x^2\right)+e^{x^2}F\left(x\right),F\left(x\right)=e^{-x^2}{\int }_0^x{e}^{t^2}dt$
$\frac{1}{2}$	1	$-\frac{\gamma }{2}-lnx+\frac{\mathrm{Ei}\left(x^2\right)}{2}+\frac{2x}{\sqrt{\pi }}{}_2{F}_2\left(\left.\begin{array}{c}\frac{1}{2},1\\ \frac{3}{2},\frac{3}{2}\end{array}\right|x^2\right)$
$\frac{1}{2}$	2	$\frac{1}{2}\left(1-\gamma +\mathrm{Ei}\left(x^2\right)+\frac{1-e^{x^2}}{x^2}\right)-lnx+\frac{4x}{3\sqrt{\pi }}{}_2{F}_2\left(\left.\begin{array}{c}\frac{1}{2},1\\ \frac{3}{2},\frac{3}{2}\end{array}\right|x^2\right)$
$\frac{1}{2}$	3	$\frac{2+4x^2+\left(3-2\gamma \right)x^4-2e^{x^2}\left(1+x^2\right)+2x^4\left(\mathrm{Ei}\left(x^2\right)-2lnx\right)}{8x^4}+\frac{8x}{15\sqrt{\pi }}{}_2{F}_2\left(\left.\begin{array}{c}\frac{1}{2},1\\ \frac{3}{2},\frac{7}{2}\end{array}\right|x^2\right)$
$\frac{1}{2}$	4	$\frac{12+18x^2\left(1+x^2\right)+\left(11-6\gamma \right)x^6-6e^{x^2}\left(2+x^2+x^4\right)+3x^6\left(2\mathrm{Ei}\left(x^2\right)-4lnx\right)}{72x^6}+\frac{16x}{105\sqrt{\pi }}{}_2{F}_2\left(\left.\begin{array}{c}\frac{1}{2},1\\ \frac{3}{2},\frac{9}{2}\end{array}\right|x^2\right)$
$\frac{1}{2}$	$\beta$	$\frac{x^2}{2\Gamma \left(\beta +1\right)}{}_2{F}_2\left(\left.\begin{array}{c}1,1\\ 2,\beta +1\end{array}\right|x^2\right)+\frac{x}{\Gamma \left(\beta +\frac{1}{2}\right)}{}_2{F}_2\left(\left.\begin{array}{c}\frac{1}{2},1\\ \frac{3}{2},\beta +\frac{1}{2}\end{array}\right|x^2\right)$
1	$\frac{1}{4}$	$\frac{x}{\Gamma \left(\frac{5}{4}\right)}{}_2{F}_2\left(\left.\begin{array}{c}1,1\\ \frac{5}{4},2\end{array}\right|x\right)$
1	$\frac{1}{3}$	$\frac{x}{\Gamma \left(\frac{4}{3}\right)}{}_2{F}_2\left(\left.\begin{array}{c}1,1\\ \frac{4}{3},2\end{array}\right|x\right)$
1	$\frac{1}{2}$	$\frac{2x}{\sqrt{\pi }}{}_2{F}_2\left(\left.\begin{array}{c}1,1\\ \frac{3}{2},2\end{array}\right|x\right)$
1	1	$-\gamma -lnx+\mathrm{Chi}\left(x\right)+\mathrm{Shi}\left(x\right)$
1	$\frac{3}{2}$	$\frac{4x}{3\sqrt{\pi }}{}_2{F}_2\left(\left.\begin{array}{c}1,1\\ \frac{5}{2},2\end{array}\right|x\right)$
1	$\beta$	$\frac{x}{\Gamma \left(\beta +1\right)}{}_2{F}_2\left(\left.\begin{array}{c}1,1\\ 2,1+\beta \end{array}\right|x\right)$

Table 2. The integral Mittag-Leffler functions derived for some values of parameters $\alpha$ and $\beta$ by using (12).

$\mathit{\alpha }$	$\mathit{\beta }$	${\mathbf{Ei}}_{\mathit{\alpha },\mathit{\beta }}\left(\mathit{x}\right)$
$\frac{3}{2}$	$\frac{1}{2}$	$\frac{4x^2}{15\sqrt{\pi }}{}_2{F}_4\left(\left.\begin{array}{c}1,1\\ \frac{7}{6},\frac{3}{2},\frac{11}{6},2\end{array}\right|\frac{x^2}{27}\right)+\frac{x}{48}{}_1{F}_3\left(\left.\begin{array}{c}\frac{1}{2}\\ \frac{2}{3},\frac{4}{3},\frac{3}{2}\end{array}\right|\frac{x^2}{27}\right)$
$\frac{3}{2}$	1	$\frac{4x}{3\sqrt{\pi }}{}_2{F}_4\left(\left.\begin{array}{c}\frac{1}{2},1\\ \frac{5}{6},\frac{7}{6},\frac{3}{2},\frac{3}{2}\end{array}\right|\frac{x^2}{27}\right)+\frac{x^2}{12}{}_2{F}_4\left(\left.\begin{array}{c}1,1\\ \frac{4}{3},\frac{5}{3},2,2\end{array}\right|\frac{x^2}{27}\right)$
$\frac{3}{2}$	$\frac{3}{2}$	$\frac{x}{2}{}_1{F}_3\left(\left.\begin{array}{c}\frac{1}{2}\\ \frac{4}{3},\frac{3}{2},\frac{5}{3}\end{array}\right|\frac{x^2}{27}\right)+\frac{8x^2}{105\sqrt{\pi }}{}_2{F}_4\left(\left.\begin{array}{c}1,1\\ \frac{3}{2},\frac{11}{6},2,\frac{13}{6}\end{array}\right|\frac{x^2}{27}\right)$
$\frac{3}{2}$	2	$\frac{8x}{15\sqrt{\pi }}{}_2{F}_4\left(\left.\begin{array}{c}\frac{1}{2},1\\ \frac{7}{6},\frac{3}{2},\frac{3}{2},\frac{11}{6}\end{array}\right|\frac{x^2}{27}\right)+\frac{x^2}{48}{}_2{F}_4\left(\left.\begin{array}{c}1,1\\ \frac{5}{3},2,2,\frac{7}{3}\end{array}\right|\frac{x^2}{27}\right)$
2	$\frac{1}{4}$	$\frac{16x}{5\Gamma \left(\frac{1}{4}\right)}{}_2{F}_3\left(\left.\begin{array}{c}1,1\\ \frac{9}{8},\frac{11}{8},2\end{array}\right|\frac{x}{4}\right)$
2	$\frac{1}{3}$	$\frac{9x}{4\Gamma \left(\frac{1}{3}\right)}{}_2{F}_3\left(\left.\begin{array}{c}1,1\\ \frac{7}{6},\frac{5}{3},2\end{array}\right|\frac{x}{4}\right)$
2	$\frac{1}{2}$	$\frac{9x}{3\sqrt{\pi }}{}_2{F}_3\left(\left.\begin{array}{c}1,1\\ \frac{5}{4},\frac{7}{4},2\end{array}\right|\frac{x}{4}\right)$
2	1	$-2\gamma -lnx+2\mathrm{Chi}\left(\sqrt{x}\right)$
2	2	$2-2\gamma -lnx-\frac{2sinh\sqrt{x}}{\sqrt{x}}+2\mathrm{Chi}\left(\sqrt{x}\right)$
2	3	$\frac{x}{24}{}_2{F}_3\left(\left.\begin{array}{c}1,1\\ 2,\frac{5}{2},3\end{array}\right|\frac{x}{4}\right)$
2	4	$\frac{x}{120}{}_2{F}_3\left(\left.\begin{array}{c}1,1\\ 2,\frac{7}{2},3\end{array}\right|\frac{x}{4}\right)$
2	$\beta$	$\frac{x}{\Gamma \left(\beta +2\right)}{}_2{F}_3\left(\left.\begin{array}{c}1,1\\ 2,\frac{\beta }{2}+1,\frac{\beta +3}{2}\end{array}\right|\frac{x}{4}\right)$
3	1	$\frac{x}{6}{}_2{F}_4\left(\left.\begin{array}{c}1,1\\ \frac{4}{3},\frac{5}{3},2,2\end{array}\right|\frac{x}{27}\right)$
3	$\beta$	$\frac{x}{\Gamma \left(\beta +3\right)}{}_2{F}_4\left(\left.\begin{array}{c}1,1\\ 2,\frac{\beta }{3}+1,\frac{\beta +4}{3},\frac{\beta +5}{3}\end{array}\right|\frac{x}{27}\right)$
4	1	$\frac{x}{24}{}_2{F}_5\left(\left.\begin{array}{c}1,1\\ \frac{5}{4},\frac{3}{2},\frac{7}{4},2,2\end{array}\right|\frac{x}{256}\right)$
4	$\beta$	$\frac{x}{\Gamma \left(\beta +4\right)}{}_2{F}_5\left(\left.\begin{array}{c}1,1\\ 2,\frac{\beta }{4}+1,\frac{\beta +5}{4},\frac{3}{2}+\frac{\beta }{4},\frac{\beta +7}{4}\end{array}\right|\frac{x}{256}\right)$
5	1	$\frac{x}{120}{}_2{F}_6\left(\left.\begin{array}{c}1,1\\ \frac{6}{5},\frac{7}{5},\frac{8}{5},\frac{9}{5},2,2\end{array}\right|\frac{x}{3125}\right)$
5	$\beta$	$\frac{x}{\Gamma \left(\beta +5\right)}{}_2{F}_6\left(\left.\begin{array}{c}1,1\\ 2,\frac{\beta }{5}+1,\frac{\beta +6}{5},\frac{\beta +7}{5},\frac{\beta +8}{5},\frac{\beta +9}{5}\end{array}\right|\frac{x}{3125}\right)$

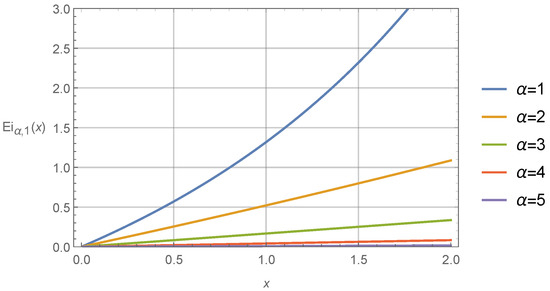
Figure 1. The integral one-parameter Mittag-Leffler function ${\mathrm{Ei}}_{\alpha ,1}\left(x\right)$ as a function of variable x and parameters $\alpha$.

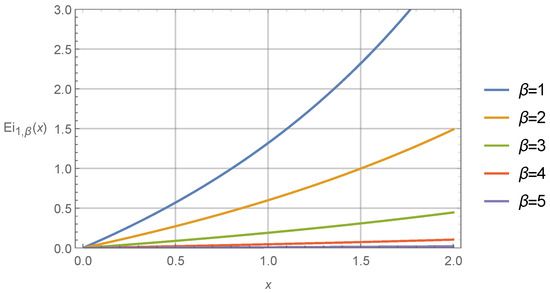
Figure 2. The integral two-parameter Mittag-Leffler function ${\mathrm{Ei}}_{1,\beta }\left(x\right)$ as a function of variable x and parameters $\beta$.

Evidently, also direct integration, by using (11), leads to the integral Mittag-Leffler functions. For example, for ${\mathrm{E}}_2\left(x\right)=cosh\sqrt{x}$, according to (1), we have

$${\mathrm{Ei}}_2\left(x\right)={\int }_0^x\frac{cosh\sqrt{t}-1}{t}dt=-2\gamma -lnx+2\mathrm{Chi}\sqrt{x},$$

(13)

and as expected, this result is identical to that derived from (12) (see Table 1 and Table 2).

Applying the formulas (A1) and (A2) given in Appendix A, the integral Mittag-Leffler function for positive rational values of parameter $\alpha$ with $\alpha =p/q$ and $p,q$ positive coprimes is

$$\begin{array}{ccc}& & {\mathrm{Ei}}_{p/q,\beta }\left(x\right)\hfill \\ & =& \sum _{k=1}^q\frac{x^k}{k\Gamma \left(k/q+\beta \right)}{}_2{F}_q\left(\left.\begin{array}{c}1,k/q\\ b_0,\dots ,b_{p-1},k/q+1\end{array}\right|\frac{x^q}{p^p}\right).\hfill \end{array}$$

(14)

where

$$b_j=\frac{k}{q}+\frac{\beta +j}{p}.$$

In addition, using the sums in (12), it is possible to derive the Laplace transforms of the integral Mittag-Leffler functions:

$$\begin{array}{c}{\displaystyle \mathcal{L}\left[{\mathrm{Ei}}_{\alpha }\left(t\right)\right]={\int }_0^{\infty }{e}^{-st}\left[\sum _{k=0}^{\infty }\frac{t^{k+1}}{\left(k+1\right)\Gamma \left(\alpha \left(k+1\right)+1\right)}\right]dt}\hfill \\ {\displaystyle =\sum _{k=0}^{\infty }\frac{\left(k+1\right)!}{\left(k+1\right)\Gamma \left(\alpha \left(k+1\right)+1\right)}{\left(\frac{1}{s}\right)}^{k+2},\mathrm{Re}s>1.}\hfill \\ {\displaystyle \mathcal{L}\left[{\mathrm{Ei}}_{\alpha ,\beta }\left(t\right)\right]={\int }_0^{\infty }{e}^{-st}\left[\sum _{k=0}^{\infty }\frac{t^{k+1}}{\left(k+1\right)\Gamma \left(\alpha \left(k+\beta \right)+1\right)}\right]dt}\hfill \\ {\displaystyle =\sum _{k=0}^{\infty }\frac{\left(k+1\right)!}{\left(k+1\right)\Gamma \left(\alpha \left(k+1\right)+\beta \right)}{\left(\frac{1}{s}\right)}^{k+2},\mathrm{Re}s>1.}\hfill \end{array}$$

(15)

The evaluated Laplace transforms of the integral Mittag-Leffler functions are presented in Table 3 and Table 4.

Table 3. The Laplace transforms of the integral Mittag-Leffler functions ${\mathrm{Ei}}_{\alpha ,\beta }$ derived for some values of parameters $\alpha$ and $\beta$ by using (15).

$\mathit{\alpha }$	$\mathit{\beta }$	$\mathcal{L}\left[{\mathbf{Ei}}_{\mathit{\alpha },\mathit{\beta }}\left(\mathit{t}\right)\right]$
1	$\frac{1}{5}$	$\frac{5}{\Gamma \left(\frac{1}{5}\right)s^2}{}_2{F}_1\left(\left.\begin{array}{c}1,1\\ \frac{6}{5}\end{array}\right|\frac{1}{s}\right)$
1	$\frac{1}{4}$	$\frac{4}{\Gamma \left(\frac{1}{4}\right)s^2}{}_2{F}_1\left(\left.\begin{array}{c}1,1\\ \frac{5}{4}\end{array}\right|\frac{1}{s}\right)$
1	$\frac{1}{3}$	$\frac{3}{\Gamma \left(\frac{1}{6}\right)s^2}{}_2{F}_1\left(\left.\begin{array}{c}1,1\\ \frac{4}{3}\end{array}\right|\frac{1}{s}\right)$
1	$\frac{1}{2}$	$\frac{2{csc}^{-1}\left(\sqrt{s}\right)}{\sqrt{\pi }s\sqrt{s-1}}$
1	1	$-\frac{1}{s}ln\left(1-\frac{1}{s}\right)$
1	$\frac{3}{2}$	$\frac{4}{\sqrt{\pi }s}\left[1-\sqrt{s-1}{csc}^{-1}\left(\sqrt{s}\right)\right]$
1	$\beta$	$\frac{1}{s^2\Gamma \left(\beta +1\right)}{}_2{F}_1\left(\left.\begin{array}{c}1,1\\ \beta +1\end{array}\right|\frac{1}{s}\right)$
$\frac{3}{2}$	$\frac{1}{2}$	$\frac{8}{15\sqrt{\pi }{s}^3}{}_2{F}_2\left(\left.\begin{array}{c}1,1\\ \frac{7}{6},\frac{11}{6}\end{array}\right|\frac{4}{27s^2}\right)+\frac{1}{s^2}{}_2{F}_2\left(\left.\begin{array}{c}\frac{1}{2},1\\ \frac{2}{3},\frac{4}{3}\end{array}\right|\frac{4}{27s^2}\right)$
$\frac{3}{2}$	1	$\frac{4}{3\sqrt{\pi }{s}^2}{}_3{F}_3\left(\left.\begin{array}{c}\frac{1}{2},1,1\\ \frac{5}{6},\frac{7}{6},\frac{3}{2}\end{array}\right|\frac{4}{27s^2}\right)+\frac{1}{6s^3}{}_3{F}_3\left(\left.\begin{array}{c}1,1,\frac{3}{2}\\ \frac{4}{3},\frac{5}{6},2\end{array}\right|\frac{4}{27s^2}\right)$
$\frac{3}{2}$	$\frac{3}{2}$	$\frac{1}{2s^2}{}_2{F}_2\left(\left.\begin{array}{c}\frac{1}{2},1\\ \frac{4}{3},\frac{5}{3}\end{array}\right|\frac{4}{27s^2}\right)+\frac{16}{105\sqrt{\pi }{s}^3}{}_2{F}_2\left(\left.\begin{array}{c}1,1\\ \frac{11}{6},\frac{13}{6}\end{array}\right|\frac{4}{27s^2}\right)$
$\frac{3}{2}$	2	$\frac{8}{15\sqrt{\pi }{s}^2}{}_3{F}_3\left(\left.\begin{array}{c}\frac{1}{2},1,1\\ \frac{7}{6},\frac{3}{2},\frac{11}{6}\end{array}\right|\frac{4}{27s^2}\right)+\frac{1}{24s^3}{}_3{F}_3\left(\left.\begin{array}{c}1,1,\frac{3}{2}\\ \frac{5}{3},2,\frac{7}{3}\end{array}\right|\frac{4}{27s^2}\right)$
2	$\frac{1}{5}$	$\frac{25}{6\Gamma \left(\frac{1}{5}\right)s^2}{}_2{F}_2\left(\left.\begin{array}{c}1,1\\ \frac{11}{10},\frac{8}{5}\end{array}\right|\frac{1}{4s}\right)$
2	$\frac{1}{4}$	$\frac{16}{5\Gamma \left(\frac{1}{4}\right)s^2}{}_2{F}_2\left(\left.\begin{array}{c}1,1\\ \frac{9}{8},\frac{13}{8}\end{array}\right|\frac{1}{4s}\right)$
2	$\frac{1}{3}$	$\frac{9}{4\Gamma \left(\frac{1}{3}\right)s^2}{}_2{F}_2\left(\left.\begin{array}{c}1,1\\ \frac{7}{6},\frac{5}{3}\end{array}\right|\frac{1}{4s}\right)$
2	$\frac{1}{2}$	$\frac{4}{3\sqrt{\pi }{s}^2}{}_2{F}_2\left(\left.\begin{array}{c}1,1\\ \frac{5}{4},\frac{7}{4}\end{array}\right|\frac{1}{4s}\right)$
2	1	$\frac{1}{2s^2}{}_2{F}_2\left(\left.\begin{array}{c}1,1\\ \frac{3}{2},2\end{array}\right|\frac{1}{4s}\right)$
2	2	$\frac{1}{6s^2}{}_2{F}_2\left(\left.\begin{array}{c}1,1\\ \frac{5}{2},2\end{array}\right|\frac{1}{4s}\right)$
2	3	$\frac{1}{24s^2}{}_2{F}_2\left(\left.\begin{array}{c}1,1\\ \frac{5}{2},3\end{array}\right|\frac{1}{4s}\right)$
2	4	$\frac{1}{120s^2}{}_2{F}_2\left(\left.\begin{array}{c}1,1\\ \frac{7}{2},3\end{array}\right|\frac{1}{4s}\right)$
2	$\beta$	$\frac{1}{\Gamma \left(\beta +2\right)s^2}{}_2{F}_2\left(\left.\begin{array}{c}1,1\\ 1+\frac{\beta }{2},\frac{\beta +3}{2}\end{array}\right|\frac{1}{4s}\right)$

Table 4. The Laplace transforms of the integral Mittag-Leffler functions ${\mathrm{Ei}}_{\alpha ,\beta }$ derived for some values of parameters $\alpha$ and $\beta$ by using (15).

$\mathit{\alpha }$	$\mathit{\beta }$	$\mathcal{L}\left[{\mathbf{Ei}}_{\mathit{\alpha },\mathit{\beta }}\left(\mathit{t}\right)\right]$
3	$\frac{1}{5}$	$\frac{125}{66\Gamma \left(\frac{1}{5}\right)s^2}{}_2{F}_3\left(\left.\begin{array}{c}1,1\\ \frac{16}{15},\frac{7}{5},\frac{26}{15}\end{array}\right|\frac{1}{27s}\right)$
3	$\frac{1}{4}$	$\frac{64}{25\Gamma \left(\frac{1}{4}\right)s^2}{}_2{F}_3\left(\left.\begin{array}{c}1,1\\ \frac{13}{12},\frac{17}{12},\frac{7}{4}\end{array}\right|\frac{1}{27s}\right)$
3	$\frac{1}{3}$	$\frac{27}{28\Gamma \left(\frac{1}{3}\right)s^2}{}_2{F}_3\left(\left.\begin{array}{c}1,1\\ \frac{10}{9},\frac{13}{9},\frac{10}{9}\end{array}\right|\frac{1}{27s}\right)$
3	$\frac{1}{2}$	$\frac{27}{15\sqrt{\pi }{s}^2}{}_2{F}_3\left(\left.\begin{array}{c}1,1\\ \frac{7}{6},\frac{3}{2},\frac{11}{6}\end{array}\right|\frac{1}{27s}\right)$
3	1	$\frac{1}{6s^2}{}_2{F}_3\left(\left.\begin{array}{c}1,1\\ \frac{4}{3},\frac{5}{3},2\end{array}\right|\frac{1}{27s}\right)$
3	3	$\frac{1}{120s^2}{}_2{F}_3\left(\left.\begin{array}{c}1,1\\ 2,\frac{7}{3},\frac{8}{3}\end{array}\right|\frac{1}{27s}\right)$
3	$\beta$	$\frac{1}{\Gamma \left(\beta +3\right)s^2}{}_2{F}_3\left(\left.\begin{array}{c}1,1\\ 1+\frac{\beta }{3},\frac{\beta +4}{3},\frac{\beta +5}{3}\end{array}\right|\frac{1}{27s}\right)$
4	1	$\frac{1}{24s^2}{}_2{F}_4\left(\left.\begin{array}{c}1,1\\ \frac{5}{4},\frac{3}{2},\frac{7}{4},2\end{array}\right|\frac{1}{256s}\right)$
4	4	$\frac{1}{5040s^2}{}_2{F}_4\left(\left.\begin{array}{c}1,1\\ 2,\frac{9}{4},\frac{5}{2},\frac{11}{4}\end{array}\right|\frac{1}{256s}\right)$
4	$\beta$	$\frac{1}{\Gamma \left(\beta +4\right)s^2}{}_2{F}_4\left(\left.\begin{array}{c}1,1\\ 1+\frac{\beta }{4},\frac{\beta +5}{3},\frac{3}{2}+\frac{\beta }{4},\frac{\beta +7}{4}\end{array}\right|\frac{1}{256s}\right)$
5	1	$\frac{1}{120s^2}{}_2{F}_5\left(\left.\begin{array}{c}1,1\\ \frac{6}{5},\frac{7}{5},\frac{8}{5},\frac{9}{5}\end{array}\right|\frac{1}{3125s}\right)$
5	$\beta$	$\frac{1}{\Gamma \left(\beta +5\right)s^2}{}_2{F}_5\left(\left.\begin{array}{c}1,1\\ 1+\frac{\beta }{5},\frac{\beta +6}{5},\frac{\beta +7}{5},\frac{\beta +8}{5},\frac{\beta +9}{5}\end{array}\right|\frac{1}{3125s}\right)$

The Laplace transforms of the integral Mittag-Leffler functions with positive rational parameter $\alpha$ with $\alpha =p/q$ and $p,q$ positive coprimes can be evaluated from:

$$\begin{array}{ccc}& & \mathcal{L}\left[{\mathrm{Ei}}_{p/q,\beta }\left(t\right)\right]\hfill \\ & =& \frac{1}{s^2}\sum _{k=0}^{q-1}\frac{k!s^{-k}}{\Gamma \left(\frac{p}{q}\left(k+1\right)+\beta \right)}{}_{q+1}{F}_p\left(\left.\begin{array}{c}1,a_0,\dots ,a_{q-1}\\ b_0,\dots ,b_{p-1}\end{array}\right|\frac{{\left(q/s\right)}^q}{p^p}\right).\hfill \end{array}$$

(16)

where

$$\begin{array}{ccc}\hfill a_j& =& \frac{k+1+j}{q},\hfill \\ \hfill b_j& =& \frac{k}{q}+\frac{\beta +j}{p}.\hfill \end{array}$$

Furthermore, the following relation is satisfied:

$$\mathcal{L}\left[{\mathrm{Ei}}_{p/q,\beta }\left(t\right)\right]=\frac{1}{p^{p/q}s}\mathcal{L}\left[{\mathrm{E}}_{p/q,\beta }\left(t\right)\right].$$

(17)

3. The Integral Whittaker Functions

In 1903, Whittaker [15] showed that it is possible to express some special functions such as Bessel functions, parabolic cylinder functions, error functions, incomplete gamma functions, and logarithm and cosine integrals in terms of a new function suggested by him, i.e., the Whittaker function. Two Whittaker functions are applied today, and they are defined by using the Kummer confluent hypergeometric function [3,4]:

$$\begin{array}{c}{\displaystyle {\mathrm{M}}_{\kappa ,\mu }\left(x\right)=x^{\mu -1/2}{e}^{-x/2}{}_1{F}_1\left(\left.\begin{array}{c}\mu -\kappa +\frac{1}{2}\\ 1+2\mu \end{array}\right|x\right),}\hfill \\ {\displaystyle {\mathrm{W}}_{\kappa ,\mu }\left(x\right)=\frac{\Gamma \left(-2\mu \right)}{\Gamma \left(\frac{1}{2}-k-\mu \right)}{\mathrm{M}}_{\kappa ,\mu }\left(x\right)+\frac{\Gamma \left(2\mu \right)}{\Gamma \left(\frac{1}{2}-k+\mu \right)}{\mathrm{M}}_{\kappa ,-\mu }\left(x\right).}\hfill \end{array}$$

(18)

This permits us to introduce four integral Whittaker functions:

$$\begin{array}{c}{\displaystyle {\mathrm{Mi}}_{\kappa ,\mu }\left(x\right)={\int }_0^x\frac{{\mathrm{M}}_{\kappa ,\mu }\left(t\right)}{t}dt,}\hfill \\ {\displaystyle {\mathrm{mi}}_{\kappa ,\mu }\left(x\right)={\int }_x^{\infty }\frac{{\mathrm{M}}_{\kappa ,\mu }\left(t\right)}{t}dt.}\hfill \end{array}$$

(19)

and

$$\begin{array}{c}{\displaystyle {\mathrm{Wi}}_{\kappa ,\mu }\left(x\right)={\int }_0^x\frac{{\mathrm{W}}_{\kappa ,\mu }\left(t\right)}{t}dt,}\hfill \\ {\displaystyle {\mathrm{wi}}_{\kappa ,\mu }\left(x\right)={\int }_x^{\infty }\frac{{\mathrm{W}}_{\kappa ,\mu }\left(t\right)}{t}dt.}\hfill \end{array}$$

(20)

The integral Whittaker functions with particular values of parameters $\kappa$ and $\mu$ can be expressed in terms of elementary and special functions. These cases, derived using the MATHEMATICA program, are presented in Table 5, Table 6, Table 7, Table 8 and Table 9. Several integral Whittaker functions ${\mathrm{Mi}}_{\kappa ,\mu }\left(x\right)$, ${\mathrm{mi}}_{\kappa ,\mu }\left(x\right)$, ${\mathrm{Wi}}_{\kappa ,\mu }\left(x\right)$ and ${\mathrm{wi}}_{\kappa ,\mu }\left(x\right)$ as a function of variable x at fixed values of parameters $\kappa$ and $\mu$ are plotted in Figure 3, Figure 4, Figure 5 and Figure 6. Similarly, a long list of the Whittaker functions ${\mathrm{M}}_{\kappa ,\mu }\left(x\right)$ and ${\mathrm{W}}_{\kappa ,\mu }\left(x\right)$ with integer and fractional parameters was prepared (see Appendix B). In some cases, it was possible to obtain for them their Laplace transforms, and they are also reported in Appendix B.

Table 5. The integral Whittaker functions ${\mathrm{Mi}}_{\kappa ,\mu }$ derived for some values of parameters $\kappa$ and $\mu$ by using (18) and (19).

$\mathit{\kappa }$	$\mathit{\mu }$	${\mathbf{Mi}}_{\mathit{\kappa },\mathit{\mu }}\left(\mathit{x}\right)$
$-\frac{5}{2}$	0	$e^{x/2}\left[\sqrt{x}\left(x+1\right)+2F\left(\sqrt{\frac{x}{2}}\right)\right],F\left(x\right)=e^{-x^2}{\int }_0^x{e}^{t^2}dt$
$-\frac{3}{2}$	0	$2\sqrt{x}{e}^{x/2}$
$-\frac{3}{2}$	$\frac{1}{2}$	$\frac{1}{6}\left[\left(8x+3\pi x{\mathbf{L}}_0\left(\frac{x}{2}\right)\right)I_1\left(\frac{x}{2}\right)+\left(-\pi x{\mathbf{L}}_1\left(\frac{x}{2}\right)+6x+4\right)I_0\left(\frac{x}{2}\right)-4\right]$
$-\frac{3}{2}$	1	$2e^{x/2}\left[\sqrt{x}-\sqrt{2}F\left(\sqrt{\frac{x}{2}}\right)\right]$
$-\frac{3}{2}$	$\frac{3}{2}$	$\frac{2}{5}\left[\left(-8+8x+3\pi x{\mathbf{L}}_0\left(\frac{x}{2}\right)\right)I_1\left(\frac{x}{2}\right)+\left(-3\pi x{\mathbf{L}}_1\left(\frac{x}{2}\right)+2x-12\right)I_0\left(\frac{x}{2}\right)+12\right]$
$-\frac{3}{2}$	2	$8\left[\sqrt{2\pi }\mathrm{erf}\left(\sqrt{\frac{x}{2}}\right)+\frac{e^{-x/2}}{x^{-3/2}}\left(2\left(x-1\right)+e^x\left(x\left(x-4\right)+2\right)\right)\right]$
$-\frac{3}{2}$	$\frac{5}{2}$	$\frac{16}{7}\left[20+\left(5\pi x{\mathbf{L}}_1\left(\frac{x}{2}\right)+18x-44\right)I_0\left(\frac{x}{2}\right)+\frac{1}{x}\left(-5\pi x^2{\mathbf{L}}_0\left(\frac{x}{2}\right)+8x\left(x-9\right)+96\right)I_1\left(\frac{x}{2}\right)\right]$
$-\frac{3}{2}$	3	$30\left[x^{-5/2}{e}^{-x/2}\left(48+2e^x\left(x^3-12x^2+24x-24\right)\right)+3\sqrt{2\pi }\mathrm{erfi}\left(\sqrt{\frac{x}{2}}\right)\right]$
$-\frac{1}{2}$	0	$\sqrt{2\pi }\mathrm{erfi}\left(\sqrt{\frac{x}{2}}\right)$
$-\frac{1}{2}$	$\frac{1}{2}$	$\frac{1}{2}\left[-\pi x{\mathbf{L}}_0\left(\frac{x}{2}\right)I_1\left(\frac{x}{2}\right)+\left(\pi x{\mathbf{L}}_1\left(\frac{x}{2}\right)+2x+4\right)I_0\left(\frac{x}{2}\right)-4\right]$
$-\frac{1}{2}$	1	$8x^{-1/2}sinh\left(\frac{x}{2}\right)-2\sqrt{2\pi }\mathrm{erf}\left(\sqrt{\frac{x}{2}}\right)$
$-\frac{1}{2}$	$\frac{3}{2}$	$2\left(\pi x{\mathbf{L}}_0\left(\frac{x}{2}\right)+8\right)I_1\left(\frac{x}{2}\right)-2\left(\pi x{\mathbf{L}}_1\left(\frac{x}{2}\right)+2x-4\right)I_0\left(\frac{x}{2}\right)-8$
$-\frac{1}{2}$	2	$48x^{-3/2}{e}^{-x/2}\left[\left(x-1\right)e^x+1\right]-12\sqrt{2\pi }\mathrm{erfi}\left(\sqrt{\frac{x}{2}}\right)$
0	$\frac{1}{8}$	$\frac{8}{5}{x}^{5/8}{}_1{F}_2\left(\left.\begin{array}{c}\frac{5}{16}\\ \frac{9}{8},\frac{21}{16}\end{array}\right|\frac{x^2}{16}\right)$
0	$\frac{1}{7}$	$\frac{14}{9}{x}^{9/14}{}_1{F}_2\left(\left.\begin{array}{c}\frac{9}{28}\\ \frac{8}{7},\frac{37}{28}\end{array}\right|\frac{x^2}{16}\right)$
0	$\frac{1}{6}$	$\frac{3}{2}{x}^{2/3}{}_1{F}_2\left(\left.\begin{array}{c}\frac{1}{3}\\ \frac{7}{6},\frac{4}{3}\end{array}\right|\frac{x^2}{16}\right)$
0	$\frac{1}{5}$	$\frac{10}{7}{x}^{7/10}{}_1{F}_2\left(\left.\begin{array}{c}\frac{7}{20}\\ \frac{6}{5},\frac{27}{20}\end{array}\right|\frac{x^2}{16}\right)$
0	$\frac{1}{4}$	$\frac{4}{3}{x}^{3/4}{}_1{F}_2\left(\left.\begin{array}{c}\frac{3}{8}\\ \frac{5}{4},\frac{11}{8}\end{array}\right|\frac{x^2}{16}\right)$
0	$\frac{1}{3}$	$\frac{6}{5}{x}^{5/6}{}_1{F}_2\left(\left.\begin{array}{c}\frac{5}{12}\\ \frac{4}{3},\frac{17}{12}\end{array}\right|\frac{x^2}{16}\right)$
0	$\frac{1}{2}$	$2\mathrm{Shi}\left(\frac{x}{2}\right)$
0	1	$\frac{2}{3}{x}^{3/2}{}_1{F}_2\left(\left.\begin{array}{c}\frac{3}{4}\\ \frac{7}{4},2\end{array}\right|\frac{x^2}{16}\right)$
0	$\frac{3}{2}$	$\frac{24}{x}sinh\left(\frac{x}{2}\right)-12$
0	2	$\frac{2}{5}{x}^{5/2}{}_1{F}_2\left(\left.\begin{array}{c}\frac{5}{4}\\ \frac{9}{4},3\end{array}\right|\frac{x^2}{16}\right)$
0	$\frac{5}{2}$	$60\left[x^{-2}\left(6xcosh\left(\frac{x}{2}\right)-2sinh\left(\frac{x}{2}\right)\right)-\mathrm{Shi}\left(\frac{x}{2}\right)\right]$

Table 6. The integral Whittaker functions ${\mathrm{Mi}}_{\kappa ,\mu }$ derived for some values of parameters $\kappa$ and $\mu$ by using (18) and (19).

$\mathit{\kappa }$	$\mathit{\mu }$	${\mathbf{Mi}}_{\mathit{\kappa },\mathit{\mu }}\left(\mathit{x}\right)$
$\frac{1}{2}$	0	$\sqrt{2\pi }\mathrm{erf}\left(\sqrt{\frac{x}{2}}\right)$
$\frac{1}{2}$	$\frac{1}{2}$	$\frac{1}{2}\left[-\pi x{\mathbf{L}}_0\left(\frac{x}{2}\right)I_1\left(\frac{x}{2}\right)+\left(\pi x{\mathbf{L}}_1\left(\frac{x}{2}\right)+2x-4\right)I_0\left(\frac{x}{2}\right)+4\right]$
$\frac{1}{2}$	1	$2\sqrt{2\pi }\mathrm{erfi}\left(\sqrt{\frac{x}{2}}\right)-8x^{-1/2}sinh\left(\frac{x}{2}\right)$
$\frac{1}{2}$	$\frac{3}{2}$	$-2\left(\pi x{\mathbf{L}}_0\left(\frac{x}{2}\right)+8\right)I_1\left(\frac{x}{2}\right)+2\left(\pi x{\mathbf{L}}_1\left(\frac{x}{2}\right)+2x+4\right)I_0\left(\frac{x}{2}\right)+8$
$\frac{1}{2}$	$\frac{5}{2}$	$\begin{array}{c}16\left[\left(\pi x{\mathbf{L}}_0\left(\frac{x}{2}\right)+8\right)I_1\left(\frac{x}{2}\right)-\left(\pi x{\mathbf{L}}_1\left(\frac{x}{2}\right)+2x+4\right)I_0\left(\frac{x}{2}\right)+4\right]\hfill \\ +8x^2{}_2{F}_3\left(\left.\begin{array}{c}1,1\\ 2,2,2\end{array}\right|\frac{x^2}{16}\right)-4x^2{}_2{F}_3\left(\left.\begin{array}{c}1,1\\ 2,2,3\end{array}\right|\frac{x^2}{16}\right)\hfill \end{array}$
1	0	$\frac{\sqrt{x}}{30}\left[60{}_1{F}_2\left(\left.\begin{array}{c}\frac{1}{4}\\ 1,\frac{5}{4}\end{array}\right|\frac{x^2}{16}\right)+3x^2{}_1{F}_2\left(\left.\begin{array}{c}\frac{5}{4}\\ 2,\frac{9}{4}\end{array}\right|\frac{x^2}{16}\right)-20x{}_1{F}_2\left(\left.\begin{array}{c}\frac{3}{4}\\ 1,\frac{7}{4}\end{array}\right|\frac{x^2}{16}\right)\right]$
1	$\frac{1}{2}$	$2\left(1-e^{-x/2}\right)$
1	1	$-\frac{2x^{3/2}}{45}\left[-20{}_1{F}_2\left(\left.\begin{array}{c}\frac{3}{4}\\ 1,\frac{7}{4}\end{array}\right|\frac{x^2}{16}\right)+5x^2{}_1{F}_2\left(\left.\begin{array}{c}\frac{3}{4}\\ \frac{7}{4},\frac{3}{4}\end{array}\right|\frac{x^2}{16}\right)+3x{}_1{F}_2\left(\left.\begin{array}{c}\frac{5}{4}\\ 2,\frac{9}{4}\end{array}\right|\frac{x^2}{16}\right)\right]$
$\frac{3}{2}$	0	$2\sqrt{x}{e}^{-x/2}$
$\frac{3}{2}$	$\frac{1}{2}$	$\frac{1}{6}\left[x\left(\pi {\mathbf{L}}_0\left(\frac{x}{2}\right)-8\right)I_1\left(\frac{x}{2}\right)+\left(\pi x{\mathbf{L}}_1\left(\frac{x}{2}\right)-6x+4\right)I_0\left(\frac{x}{2}\right)+4\right]$
$\frac{3}{2}$	1	$\sqrt{2\pi }\mathrm{erf}\left(\sqrt{\frac{x}{2}}\right)-2\sqrt{x}{e}^{-x/2}$
$\frac{3}{2}$	$\frac{3}{2}$	$\frac{1}{5}\left[2\left(-3\pi {\mathbf{L}}_0\left(\frac{x}{2}\right)+8x+8\right)I_1\left(\frac{x}{2}\right)+\left(6\pi x{\mathbf{L}}_1\left(\frac{x}{2}\right)-4x+24\right)I_0\left(\frac{x}{2}\right)+24\right]$
2	$\frac{1}{2}$	$x{e}^{-x/2}$
2	$\frac{3}{2}$	$4-2\left(2+x\right)e^{-x/2}$
2	$\frac{5}{2}$	$-5x^{-2}\left(6\left(2+x\right)e^x-2x{\left(3+x\right)}^2-12\right)+30\mathrm{Shi}\left(\frac{x}{2}\right)$

Table 7. The integral Whittaker functions ${\mathrm{mi}}_{\kappa ,\mu }$ derived for some values of parameters $\kappa$ and $\mu$ by using (18) and (19).

$\mathit{\kappa }$	$\mathit{\mu }$	${\mathbf{mi}}_{\mathit{\kappa },\mathit{\mu }}\left(\mathit{x}\right)$
$\frac{1}{2}$	0	$\sqrt{2\pi }\mathrm{erfc}\left(\sqrt{\frac{x}{2}}\right)$
1	$\frac{1}{2}$	$2e^{-x/2}$
$\frac{3}{2}$	1	$2\sqrt{x}{e}^{-x/2}+\sqrt{2\pi }\mathrm{erfc}\left(\sqrt{\frac{x}{2}}\right)$
2	$\frac{1}{2}$	$-e^{-x/2}$
2	$\frac{3}{2}$	$2\left(2+x\right)e^{-x/2}$
$\frac{5}{2}$	1	$-\frac{2}{3}{x}^{3/2}{e}^{-x/2}$
$\frac{5}{2}$	2	$2\sqrt{x}\left(3+x\right)e^{-x/2}+3\sqrt{2\pi }\mathrm{erfc}\left(\sqrt{\frac{x}{2}}\right)$
3	$\frac{1}{2}$	$\frac{1}{3}\left[2+\left(x-2\right)x\right]e^{-x/2}$
3	$\frac{3}{2}$	$-\frac{1}{2}{x}^2{e}^{-x/2}$
4	$\frac{1}{2}$	$-\frac{x}{12}\left[12+\left(x-6\right)x\right]e^{-x/2}$
4	$\frac{3}{2}$	$\frac{1}{10}\left[8+{\left(x-2\right)}^{2}x\right]e^{-x/2}$

Table 8. The integral Whittaker functions ${\mathrm{Wi}}_{\kappa ,\mu }$ derived for some values of parameters $\kappa$ and $\mu$ by using (18) and (20).

$\mathit{\kappa }$	$\mathit{\mu }$	${\mathbf{Wi}}_{\mathit{\kappa },\mathit{\mu }}\left(\mathit{x}\right)$
$-\frac{3}{2}$	0	$-2\sqrt{x}{e}^{-x/2}\mathrm{Ei}\left(-x\right)+\sqrt{2\pi }\mathrm{erfc}\left(\sqrt{\frac{x}{2}}\right)$
$\frac{1}{4}$	$\frac{1}{4}$	$2^{1/4}\gamma \left(\frac{1}{4},\frac{x}{2}\right)$
$\frac{1}{2}$	0	$\sqrt{2\pi }\mathrm{erf}\left(\sqrt{\frac{x}{2}}\right)$
1	$-\frac{1}{2}$	$2\left(1-e^{-x/2}\right)$
1	$\frac{1}{2}$	$2\left(1-e^{-x/2}\right)$
$\frac{3}{2}$	0	$-2\sqrt{x}{e}^{-x/2}$
$\frac{3}{2}$	1	$\sqrt{2\pi }\mathrm{erf}\left(\sqrt{\frac{x}{2}}\right)-2\sqrt{x}{e}^{-x/2}$
2	$-\frac{1}{2}$	$-2x{e}^{-x/2}$
2	$\frac{1}{2}$	$-2x{e}^{-x/2}$
2	$\frac{3}{2}$	$4-2\left(2+x\right)e^{-x/2}$
$\frac{5}{2}$	0	$\sqrt{2\pi }\mathrm{erf}\left(\sqrt{\frac{x}{2}}\right)-2\sqrt{x}\left(x-1\right)e^{-x/2}$
3	$\frac{3}{2}$	$-2x^2{e}^{-x/2}$
3	$\frac{5}{2}$	$16-2\left[8+\left(4+x\right)x\right]e^{-x/2}$
4	$-\frac{1}{2}$	$-2x\left[12+\left(x-6\right)x\right]e^{-x/2}$
4	$\frac{1}{2}$	$-2x\left[12+\left(x-6\right)x\right]e^{-x/2}$
4	$\frac{3}{2}$	$16-2\left[8+x{\left(x-2\right)}^2\right]e^{-x/2}$
4	$\frac{5}{2}$	$-2x^3{e}^{-x/2}$

Table 9. The integral Whittaker functions ${\mathrm{wi}}_{\kappa ,\mu }$ derived for some values of parameters $\kappa$ and $\mu$ by using (18) and (20).

$\mathit{\kappa }$	$\mathit{\mu }$	${\mathbf{wi}}_{\mathit{\kappa },\mathit{\mu }}\left(\mathit{x}\right)$
$-\frac{1}{2}$	1	$2x^{-1/2}{e}^{-x/2}-\sqrt{2\pi }\mathrm{erfc}\left(\sqrt{\frac{x}{2}}\right)$
$-\frac{1}{2}$	2	$2x^{-3/2}{e}^{-x/2}$
$-\frac{1}{2}$	3	$\frac{1}{3}\left[-2\left(x-6\right)\left(x+2\right)x^{-5/2}{e}^{-x/2}+\sqrt{2\pi }\mathrm{erfc}\left(\sqrt{\frac{x}{2}}\right)\right]$
0	$-\frac{5}{2}$	$\frac{1}{2}\mathrm{Ei}\left(-\frac{x}{2}\right)+3x^{-2}\left(x+2\right)e^{-x/2}$
0	$-\frac{3}{2}$	$2x^{-1}{e}^{-x/2}$
0	$-\frac{1}{2}$	$-\mathrm{Ei}\left(-\frac{x}{2}\right)$
$\frac{1}{2}$	0	$\sqrt{2\pi }\mathrm{erfc}\left(\sqrt{\frac{x}{2}}\right)$
1	$-\frac{1}{2}$	$2e^{-x/2}$
1	$\frac{1}{2}$	$2e^{-x/2}$
1	$\frac{5}{2}$	$2x^{-2}\left[6+x\left(6+x\right)\right]e^{-x/2}$
$\frac{3}{2}$	0	$2\sqrt{x}{e}^{-x/2}$
$\frac{3}{2}$	1	$\sqrt{2\pi }\mathrm{erfc}\left(\sqrt{\frac{x}{2}}\right)+2\sqrt{x}{e}^{-x/2}$
2	$\frac{1}{2}$	$2x{e}^{-x/2}$
2	$\frac{3}{2}$	$2\left(2+x\right)e^{-x/2}$
$\frac{5}{2}$	0	$\sqrt{2\pi }\mathrm{erfc}\left(\sqrt{\frac{x}{2}}\right)+2\sqrt{x}\left(x-1\right)e^{-x/2}$
$\frac{5}{2}$	1	$2x^{3/2}{e}^{-x/2}$
3	$-\frac{1}{2}$	$2\left[2+x\left(x-2\right)\right]e^{-x/2}$
3	$\frac{1}{2}$	$2\left[2+x\left(x-2\right)\right]e^{-x/2}$
3	$\frac{3}{2}$	$2x^2{e}^{-x/2}$
3	$\frac{5}{2}$	$2\left[8+x\left(4+x\right)\right]e^{-x/2}$
4	$-\frac{1}{2}$	$2x\left[12+\left(x-6\right)x\right]e^{-x/2}$
4	$\frac{1}{2}$	$2x\left[12+\left(x-6\right)x\right]e^{-x/2}$
4	$\frac{3}{2}$	$2\left[8+{\left(x-2\right)}^{2}x\right]e^{-x/2}$

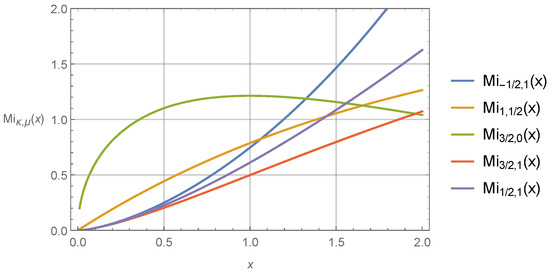
Figure 3. The integral Whittaker functions ${\mathrm{Mi}}_{\kappa ,\mu }\left(x\right)$ as a function of variable x at fixed values of parameters $\kappa$ and $\mu$.

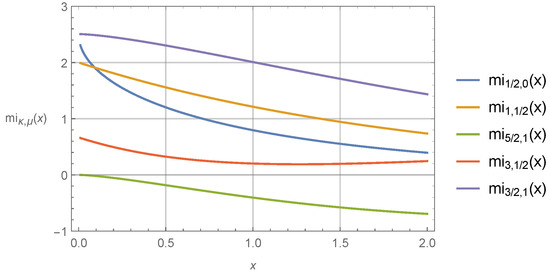
Figure 4. The integral Whittaker functions ${\mathrm{mi}}_{\kappa ,\mu }\left(x\right)$ as a function of variable x at fixed values of parameters $\kappa$ and $\mu$.

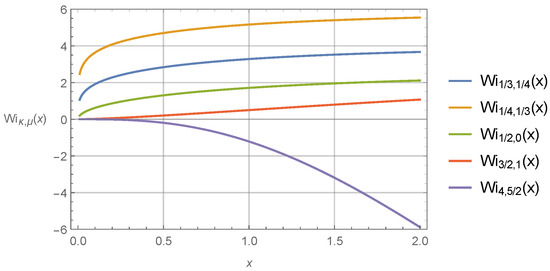
Figure 5. The integral Whittaker functions ${\mathrm{Wi}}_{\kappa ,\mu }\left(x\right)$ as a function of variable x at fixed values of parameters $\kappa$ and $\mu$.

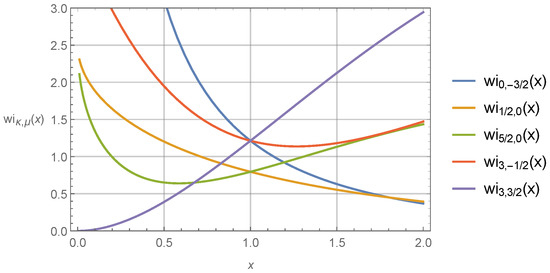
Figure 6. The integral Whittaker functions ${\mathrm{wi}}_{\kappa ,\mu }\left(x\right)$ as a function of variable x at fixed values of parameters $\kappa$ and $\mu$.

There is a number of recurrence relations between the Whittaker functions, for example [3,4]

$$\begin{array}{c}2\mu \left[{\mathrm{M}}_{\kappa -1/2,\mu -1/2}\left(t\right)-{\mathrm{M}}_{\kappa +1/2,\mu -1/2}\left(t\right)\right]=t^{1/2}{\mathrm{M}}_{\kappa ,\mu }\left(t\right),\\ \left(\kappa +\mu \right){\mathrm{W}}_{\kappa -1/2,\mu }\left(t\right)+{\mathrm{W}}_{\kappa +1/2,\mu }\left(t\right)=t^{1/2}{\mathrm{W}}_{\kappa ,\mu +1/2}\left(t\right),\end{array}$$

(21)

and this leads to integrals that are expressed in terms of the integral Whittaker functions

$$\begin{array}{c}{\displaystyle {\int }_0^x\frac{{\mathrm{M}}_{\kappa ,\mu }\left(t\right)}{t^{1/2}}dt=2\mu \left[{\mathrm{Mi}}_{\kappa -1/2,\mu -1/2}\left(t\right)-{\mathrm{Mi}}_{\kappa +1/2,\mu -1/2}\left(t\right)\right],}\\ {\displaystyle {\int }_0^x\frac{{\mathrm{W}}_{\kappa ,\mu +1/2}\left(t\right)}{t^{1/2}}dt=\left(\kappa +\mu \right){\mathrm{Wi}}_{\kappa -1/2,\mu }\left(t\right)+{\mathrm{Wi}}_{\kappa +1/2,\mu }\left(t\right).}\end{array}$$

(22)

Using the following representation of the Whittaker functions [5]

$${\mathrm{M}}_{\kappa ,\mu }\left(t\right)=t^{\mu +1/2}\sum _{n=0}^{\infty }{}_2{F}_1\left(\left.\begin{array}{c}-n,\mu -\kappa +\frac{1}{2}\\ 1+2\mu \end{array}\right|2\right)\frac{{\left(-t/2\right)}^n}{n!},$$

(23)

it is possible to obtain the integral Whittaker functions in terms of a rapidly convergent alternating series as follows:

$${\mathrm{Mi}}_{\kappa ,\mu }\left(x\right)=x^{\mu +1/2}\sum _{n=0}^{\infty }{}_2{F}_1\left(\left.\begin{array}{c}-n,\mu -\kappa +\frac{1}{2}\\ 1+2\mu \end{array}\right|2\right)\frac{{\left(-x/2\right)}^n}{n!\left(\frac{1}{2}+\mu +n\right)}.$$

(24)

There is a number of particular cases where the integral Whittaker functions can be written in a closed-form, for example, from [5]

$${\mathrm{M}}_{\kappa ,\kappa -1/2}\left(x\right)=x^{\kappa }{e}^{-x/2},$$

(25)

we have

$${\mathrm{Mi}}_{\kappa ,\kappa -1/2}\left(x\right)=2^{\kappa }\gamma \left(\kappa ,\frac{x}{2}\right),$$

(26)

but [5]

$${\mathrm{M}}_{\kappa ,\kappa -1/2}\left(x\right)={\mathrm{W}}_{\kappa ,\kappa -1/2}\left(x\right)={\mathrm{W}}_{\kappa ,-\kappa +1/2}\left(x\right)=e^{-x/2}{x}^{\kappa },$$

(27)

and therefore

$${\mathrm{Mi}}_{\kappa ,\kappa -1/2}\left(x\right)={\mathrm{Wi}}_{\kappa ,\kappa -1/2}\left(x\right)={\mathrm{Wi}}_{\kappa ,-\kappa +1/2}\left(x\right)=2^{\kappa }\gamma \left(\kappa ,\frac{x}{2}\right).$$

(28)

Furthermore, from [5]

$${\mathrm{M}}_{0,\mu }\left(x\right)=2^{2\mu +1/2}\Gamma \left(\mu +1\right)\sqrt{\frac{t}{2}}{I}_{\mu }\left(\frac{x}{2}\right),$$

(29)

follows that

$${\mathrm{Mi}}_{0,\mu }\left(x\right)=\frac{x^{\mu +1/2}}{\mu +1/2}{}_1{F}_2\left(\left.\begin{array}{c}\frac{2\mu +1}{4}\\ \mu +1,\frac{2\mu +5}{4}\end{array}\right|\frac{x^2}{16}\right).$$

(30)

Similary from

$${\mathrm{W}}_{0,\mu }\left(x\right)=\sqrt{\frac{x}{\pi }}{K}_{\mu }\left(\frac{x}{2}\right),$$

(31)

we have

$${\mathrm{Wi}}_{0,\mu }\left(x\right)=\frac{\sqrt{\pi }}{2sin\pi \mu }\left[\frac{4^{\mu }{\mathrm{Mi}}_{0,-\mu }\left(x\right)}{\Gamma \left(1-\mu \right)}-\frac{4^{-\mu }{\mathrm{Mi}}_{0,\mu }\left(x\right)}{\Gamma \left(1+\mu \right)}\right],$$

(32)

and in a general case

$${\mathrm{Wi}}_{\kappa ,\mu }\left(x\right)=\frac{\Gamma \left(-2\mu \right){\mathrm{Mi}}_{\kappa ,\mu }\left(x\right)}{\Gamma \left(\frac{1}{2}-\kappa -\mu \right)}+\frac{\Gamma \left(2\mu \right){\mathrm{Mi}}_{\kappa ,-\mu }\left(x\right)}{\Gamma \left(\frac{1}{2}-\kappa +\mu \right)}.$$

(33)

For $\kappa =\pm 1/2$, it is possible to obtain

$${\mathrm{Wi}}_{\pm \frac{1}{2},\mu }\left(x\right)={\mathrm{F}}_{\mu }^{\pm }\left(x\right)+{\mathrm{F}}_{-\mu }^{\pm }\left(x\right),$$

(34)

where we have set

$$\begin{array}{ccc}\hfill {\mathrm{F}}_{\mu }^{\pm }\left(x\right)& =& \frac{2x^{1/2+\mu }\Gamma \left(-2\mu \right)}{\left(1+2\mu \right)\Gamma \left(\frac{1}{2}\mp \frac{1}{2}-\mu \right)}\hfill \\ & & \left[{}_1{F}_2\left(\left.\begin{array}{c}\frac{1}{4}+\frac{\mu }{2}\\ \frac{1}{2}+\mu ,\frac{3}{4}+\frac{\mu }{2}\end{array}\right|\frac{x^2}{16}\right)\mp \frac{x/2}{3+2\mu }{}_1{F}_2\left(\left.\begin{array}{c}\frac{3}{4}+\frac{\mu }{2}\\ \frac{3}{2}+\mu ,\frac{7}{4}+\frac{\mu }{2}\end{array}\right|\frac{x^2}{16}\right)\right].\hfill \end{array}$$

(35)

Since [16]

$$\begin{array}{ccc}& & {}_2{F}_1\left(\left.\begin{array}{c}-n,\lambda \\ 2\lambda +1\end{array}\right|2\right)\hfill \\ & =& \frac{\Gamma \left(\lambda +\frac{1}{2}\right)}{\sqrt{\pi }}\left[\left(\frac{1+{\left(-1\right)}^n}{2}\right)\frac{\Gamma \left(\frac{n+1}{2}\right)}{\Gamma \left(\lambda +\frac{n+1}{2}\right)}+\left(\frac{1-{\left(-1\right)}^n}{2}\right)\frac{\Gamma \left(\frac{n}{2}+1\right)}{\Gamma \left(\lambda +\frac{n}{2}+1\right)}\right],\hfill \end{array}$$

(36)

and

$$\begin{array}{ccc}& & {}_2{F}_1\left(\left.\begin{array}{c}-n,\lambda \\ 2\lambda -1\end{array}\right|2\right)\hfill \\ & =& \frac{\Gamma \left(\lambda -\frac{1}{2}\right)}{\sqrt{\pi }}\left[\left(\frac{1+{\left(-1\right)}^n}{2}\right)\frac{\Gamma \left(\frac{n+1}{2}\right)}{\Gamma \left(\lambda +\frac{n-1}{2}\right)}-\left(\frac{1-{\left(-1\right)}^n}{2}\right)\frac{\Gamma \left(\frac{n}{2}+1\right)}{\Gamma \left(\lambda +\frac{n}{2}\right)}\right],\hfill \end{array}$$

(37)

by introducing $\lambda =\mu$ and $\lambda =\mu +1$, after some steps, it leads to

$$\begin{array}{ccc}& & {\mathrm{Mi}}_{\pm \frac{1}{2},\mu }\left(x\right)\hfill \\ & =& \frac{x^{\mu +1/2}}{\mu +1/2}\left[{}_1{F}_2\left(\left.\begin{array}{c}\frac{\mu }{2}+\frac{1}{4}\\ \mu +\frac{1}{2},\frac{\mu }{2}+\frac{3}{4}\end{array}\right|\frac{x^2}{16}\right)\mp \frac{x/2}{2\mu +3}{}_1{F}_2\left(\left.\begin{array}{c}\frac{\mu }{2}+\frac{3}{4}\\ \mu +\frac{3}{2},\frac{\mu }{2}+\frac{7}{4}\end{array}\right|\frac{x^2}{16}\right)\right].\hfill \end{array}$$

(38)

4. The Integral Wright Functions

In 1933 [17] and in 1940 [18], Wright introduced new special functions that were considered as a kind of generalization of the Bessel functions. However, today they play a significant independent role in mathematics and in solutions of physical problems by modeling space diffusion, stochastic processes, probability distributions and other diverse natural phenomena [19,20]. The Wright functions are defined by the following series

$${\mathrm{W}}_{\alpha ,\beta }\left(x\right)=\sum _{k=0}^{\infty }\frac{x^k}{k!\Gamma \left(\alpha k+\beta \right)}.$$

(39)

If the parameter $\alpha$ is a positive real number, they are called the Wright functions of the first kind, and when $-1<\alpha <0$, the Wright functions of the second kind.

Furthermore, consider the following functions:

$$\begin{array}{c}{\mathrm{F}}_{\alpha }\left(x\right)={\mathrm{W}}_{-\alpha ,0}\left(-x\right),0<\alpha <1,\hfill \\ {\mathrm{M}}_{\alpha }\left(x\right)={\mathrm{W}}_{-\alpha ,1-\alpha }\left(-x\right),0<\alpha <1,\hfill \\ {\mathrm{F}}_{\alpha }\left(x\right)=\alpha x{M}_{\alpha }\left(x\right).\hfill \end{array}$$

(40)

These functions with negative arguments x and with particular values of parameters are frequently named as the Mainardi functions and are denoted as ${\mathrm{F}}_{\alpha }\left(x\right)$ and ${\mathrm{M}}_{\alpha }\left(x\right)$ [19,20].

Their explicit form is

$$\begin{array}{c}{\displaystyle {\mathrm{F}}_{\alpha }\left(x\right)=\sum _{k=1}^{\infty }\frac{{\left(-x\right)}^k}{k!\Gamma \left(-\alpha k\right)}}\hfill \\ {\displaystyle =-\frac{1}{\pi }\sum _{k=1}^{\infty }\frac{{\left(-x\right)}^k}{k!}\Gamma \left(\alpha k+1\right)sin\left(\pi \alpha k\right),}\hfill \\ {\displaystyle {\mathrm{M}}_{\alpha }\left(x\right)=\sum _{k=0}^{\infty }\frac{{\left(-x\right)}^k}{k!\Gamma \left(-\alpha \left(k+1\right)+1\right)}}\hfill \\ {\displaystyle =\frac{1}{\pi }\sum _{k=0}^{\infty }\frac{{\left(-x\right)}^k}{k!}\Gamma \left(\alpha \left(k+1\right)\right)sin\left(\pi \alpha \left(k+1\right)\right).}\hfill \end{array}$$

(41)

For positive rational $\alpha =p/q$, where $p,q$ are positive coprimes, we have obtained reduction formulas for ${\mathrm{F}}_{p/q}\left(x\right)$ and ${\mathrm{M}}_{p/q}\left(x\right)$ in Appendix C. Furthermore, by applying the MATHEMATICA program to sums of infinite series in (39), it is possible to obtain the Wright functions of the first and second kinds for particular values of parameters $\alpha$ and $\beta$ in an explicit form (Appendix C). The Laplace transforms of these functions are expressed in terms of the Mittag-Leffler functions, so they are omitted here [19,20,21].

The two-parameter ${\mathrm{E}}_{\alpha ,\beta }\left(t\right)$ Mittag-Leffler functions defined in (9) differ only by the absence of factorials from the Wright functions and, therefore, the form of series in (39) leads to the integral Wright function, which is similar to that introduced in (11) and (12).

$${\mathrm{Wi}}_{\alpha ,\beta }\left(x\right)={\int }_0^x\frac{{\mathrm{W}}_{\alpha ,\beta }\left(t\right)-1/\Gamma \left(\beta \right)}{t}dt.$$

(42)

Unfortunately, the notation is the same as the integral Whittaker functions. In an explicit form from (39), we have

$${\mathrm{Wi}}_{\alpha ,\beta }\left(x\right)=\sum _{k=1}^{\infty }\frac{x^k}{kk!\Gamma \left(\alpha k+\beta \right)}.$$

(43)

For p and q positive coprimes, applying (A1) and (A2), the corresponding expression to (14) is

$$\begin{array}{ccc}& & {\mathrm{Wi}}_{p/q,\beta }\left(x\right)\hfill \\ & =& \sum _{k=1}^{q-1}\frac{x^k}{kk!\Gamma \left(\frac{p}{q}k+\beta \right)}{}_2{F}_{p+q}\left(\left.\begin{array}{c}1,k/q\\ b_0,\dots ,b_{p-1},c_0,\dots ,c_{q-1}\end{array}\right|\frac{x^q}{p^p{q}^q}\right),\hfill \\ & & b_j=\frac{k}{q}+\frac{\beta +j}{p},c_j=\frac{k+1+j}{q}.\hfill \end{array}$$

(44)

In the case of the Mainardi functions, we have

$$\begin{array}{c}{\displaystyle {\mathrm{Fi}}_{p/q}\left(x\right)=-\frac{1}{\pi }\sum _{k=1}^q\frac{{\left(-x\right)}^k}{kk!}\Gamma \left(\frac{p}{q}k+1\right)sin\left(\pi \frac{p}{q}k\right)S_k\left(x\right),}\hfill \\ {\displaystyle {\mathrm{Mi}}_{p/q}\left(x\right)=\frac{1}{\pi }\sum _{k=1}^q\frac{{\left(-x\right)}^k}{kk!}sin\left(\pi \frac{p}{q}\left(k+1\right)\right)\Gamma \left(\frac{p}{q}\left(k+1\right)\right)S_k\left(x\right),}\hfill \end{array}$$

(45)

where

$$\begin{array}{ccc}& & S_k\left(x\right)={}_{p+2}{F}_{q+1}\left(\left.\begin{array}{c}1,\frac{k}{q},a_0,\dots ,a_{p-1}\\ \frac{k}{q}+1,b_0,\dots ,b_{q-1}\end{array}\right|\frac{{\left(-1\right)}^{p+q}{x}^q{p}^p}{q^q}\right),\hfill \\ & & a_j=\frac{k}{q}+\frac{j+1}{p},b_j=\frac{k+1+j}{q}.\hfill \end{array}$$

(46)

In Table 10 and Table 11, the integral Wright functions derived with the help of MATHEMATICA program for some values of parameters $\alpha$ and $\beta$ are derived. There are many other expressions for these functions, which are available using this program, but being long and complex, they were omitted. The integral Mainardi fuctions ${\mathrm{Fi}}_{\alpha }\left(x\right)$ and ${\mathrm{Mi}}_{\alpha }\left(x\right)$ for $0<\alpha <1$, are presented in Table 12 and Table 13. As can be expected, most of these integral functions are expressed in terms of generalized hypergeometric functions.

Table 10. The integral Wright functions ${\mathrm{Wi}}_{\alpha ,\beta }$ derived for some values of parameters $\alpha$ and $\beta$ by using (43).

$\mathit{\alpha }$	$\mathit{\beta }$	${\mathbf{Wi}}_{\mathit{\alpha },\mathit{\beta }}\left(\mathit{x}\right)$
$-1$	$\frac{1}{2}$	$\frac{1}{\sqrt{\pi }}\left[ln4-2ln\left(\sqrt{1+x}+1\right)\right]$
$-1$	$\frac{3}{2}$	$\frac{x}{\sqrt{\pi }}{}_3{F}_2\left(\left.\begin{array}{c}\frac{1}{2},1,1\\ 2,2\end{array}\right|-x\right)$
$-1$	$\beta$	$\frac{x}{\Gamma \left(\beta -1\right)}{}_3{F}_2\left(\left.\begin{array}{c}1,1,2-\beta \\ 2,2\end{array}\right|-x\right)$
0	$-\frac{4}{3}$	$\frac{-\gamma -lnx+\mathrm{Chi}\left(x\right)+\mathrm{Shi}\left(x\right)}{\Gamma \left(-4/3\right)}$
0	$\beta$	$\frac{-\gamma -lnx+\mathrm{Chi}\left(x\right)+\mathrm{Shi}\left(x\right)}{\Gamma \left(\beta \right)}$
$\frac{1}{2}$	0	$-\frac{1}{2}+\frac{1}{2}{}_0{F}_2\left(\left.\begin{array}{c}-\\ \frac{1}{2},1\end{array}\right|\frac{x^2}{4}\right)+\frac{x}{\sqrt{\pi }}{}_0{F}_2\left(\left.\begin{array}{c}-\\ \frac{1}{2},\frac{3}{2}\end{array}\right|\frac{x^2}{4}\right)$
$\frac{1}{2}$	$\frac{1}{2}$	$\frac{x^2}{2\sqrt{\pi }}{}_2{F}_4\left(\left.\begin{array}{c}1,1\\ \frac{3}{2},\frac{3}{2},2,2\end{array}\right|\frac{x^2}{4}\right)+x{}_1{F}_3\left(\left.\begin{array}{c}\frac{1}{2}\\ 1,\frac{3}{2},\frac{3}{2}\end{array}\right|\frac{x^2}{4}\right)$
$\frac{1}{2}$	1	$\frac{x}{4}\left[\frac{8}{\sqrt{\pi }}{}_1{F}_3\left(\left.\begin{array}{c}\frac{1}{2}\\ \frac{3}{2},\frac{3}{2},\frac{3}{2}\end{array}\right|\frac{x^2}{4}\right)+x{}_2{F}_4\left(\left.\begin{array}{c}1,1\\ \frac{3}{2},\frac{3}{2},2,2\end{array}\right|\frac{x^2}{4}\right)\right]$
$\frac{1}{2}$	2	$\frac{x^2}{8}{}_2{F}_4\left(\left.\begin{array}{c}1,1\\ \frac{3}{2},2,2,3\end{array}\right|\frac{x^2}{4}\right)+\frac{4x}{3\sqrt{\pi }}{}_1{F}_3\left(\left.\begin{array}{c}\frac{1}{2}\\ \frac{3}{2},\frac{3}{2},\frac{5}{2}\end{array}\right|\frac{x^2}{4}\right)$
$\frac{1}{2}$	$\beta$	$\frac{x^2}{4\Gamma \left(1+\beta \right)}{}_2{F}_4\left(\left.\begin{array}{c}1,1\\ \frac{3}{2},2,2,\beta +1\end{array}\right|\frac{x^2}{4}\right)+\frac{x}{\Gamma \left(\frac{1}{2}+\beta \right)}{}_1{F}_3\left(\left.\begin{array}{c}\frac{1}{2}\\ \frac{3}{2},\frac{3}{2},\beta +\frac{1}{2}\end{array}\right|\frac{x^2}{4}\right)$
1	$-\frac{3}{2}$	$-\frac{x}{2\sqrt{\pi }}{}_2{F}_3\left(\left.\begin{array}{c}1,1\\ -\frac{1}{2},2,2\end{array}\right|x\right)$
3	$\frac{3}{2}$	$\frac{x}{\sqrt{\pi }}{}_2{F}_3\left(\left.\begin{array}{c}1,1\\ \frac{1}{2},2,2\end{array}\right|x\right)$
1	0	$-1+I_0\left(2\sqrt{x}\right)$
1	$\frac{1}{4}$	$\frac{x}{\Gamma \left(5/4\right)}{}_2{F}_3\left(\left.\begin{array}{c}1,1\\ \frac{5}{2},2,2\end{array}\right|x\right)$
1	$\frac{1}{2}$	$-\frac{2\gamma +ln4+lnx-2\mathrm{Chi}\left(2\sqrt{x}\right)}{\sqrt{\pi }}$
1	1	$x{}_2{F}_3\left(\left.\begin{array}{c}1,1\\ 2,2,2\end{array}\right|x\right)$
1	$\frac{3}{2}$	$-\frac{1}{\sqrt{\pi x}}\left[2sinh\left(2\sqrt{x}\right)-2\sqrt{x}\left(2\gamma -2+ln4-2\mathrm{Chi}\left(2\sqrt{x}\right)\right)\right]$
1	$\beta$	$x{}_2{F}_3\left(\left.\begin{array}{c}1,1\\ 2,2,\beta +1\end{array}\right|x\right)$

Table 11. The integral Wright functions ${\mathrm{Wi}}_{\alpha ,\beta }$ derived for some values of parameters $\alpha$ and $\beta$ by using (43).

$\mathit{\alpha }$	$\mathit{\beta }$	${\mathbf{Wi}}_{\mathit{\alpha },\mathit{\beta }}\left(\mathit{x}\right)$
$\frac{3}{2}$	$\frac{1}{2}$	$\frac{2x^2}{15\sqrt{\pi }}{}_2{F}_6\left(\left.\begin{array}{c}1,1\\ \frac{7}{2},\frac{3}{2},\frac{3}{2},\frac{11}{6},2,2\end{array}\right|\frac{x^2}{108}\right)+x{}_1{F}_5\left(\left.\begin{array}{c}\frac{1}{2}\\ \frac{2}{3},1,\frac{4}{3},\frac{3}{2},\frac{3}{2}\end{array}\right|\frac{x^2}{108}\right)$
2	$\frac{1}{4}$	$\frac{16x}{5\Gamma \left(1/4\right)}{}_2{F}_4\left(\left.\begin{array}{c}1,1\\ \frac{9}{8},\frac{13}{8},2,2\end{array}\right|\frac{x}{4}\right)$
2	$\frac{1}{3}$	$\frac{9x}{4\Gamma \left(1/3\right)}{}_2{F}_4\left(\left.\begin{array}{c}1,1\\ \frac{7}{6},\frac{5}{3},2,2\end{array}\right|\frac{x}{4}\right)$
2	$\frac{1}{2}$	$\frac{4x}{3\sqrt{\pi }}{}_2{F}_4\left(\left.\begin{array}{c}1,1\\ \frac{5}{4},\frac{7}{4},2,2\end{array}\right|\frac{x}{4}\right)$
2	1	$\frac{x}{2}{}_2{F}_4\left(\left.\begin{array}{c}1,1\\ \frac{3}{2},2,2,2\end{array}\right|\frac{x}{4}\right)$
2	2	$\frac{x}{6}{}_2{F}_4\left(\left.\begin{array}{c}1,1\\ \frac{5}{2},2,2,2\end{array}\right|\frac{x}{4}\right)$
2	$\beta$	$\frac{x}{\Gamma \left(\beta +2\right)}{}_2{F}_4\left(\left.\begin{array}{c}1,1\\ 2,2,\frac{\beta }{2}+1,\frac{\beta +3}{2}\end{array}\right|\frac{x}{4}\right)$
3	1	$\frac{x}{6}{}_2{F}_4\left(\left.\begin{array}{c}1,1\\ \frac{4}{3},\frac{5}{3},2,2\end{array}\right|\frac{x}{27}\right)$
3	$\beta$	$\frac{x}{\Gamma \left(\beta +3\right)}{}_2{F}_5\left(\left.\begin{array}{c}1,1\\ 2,2,\frac{\beta }{3}+1,\frac{\beta +4}{3},\frac{\beta +5}{3}\end{array}\right|\frac{x}{27}\right)$
4	$\beta$	$\frac{x}{\Gamma \left(\beta +4\right)}{}_2{F}_6\left(\left.\begin{array}{c}1,1\\ 2,2,\frac{\beta }{4}+1,\frac{\beta +5}{4},\frac{\beta +6}{4},\frac{\beta +7}{4}\end{array}\right|\frac{x}{256}\right)$
5	$\beta$	$\frac{x}{\Gamma \left(\beta +5\right)}{}_2{F}_7\left(\left.\begin{array}{c}1,1\\ 2,2,\frac{\beta }{4}+1,\frac{\beta +6}{5},\frac{\beta +7}{5},\frac{\beta +8}{5},\frac{\beta +9}{5}\end{array}\right|\frac{x}{3125}\right)$

Table 12. The integral Mainardi function ${\mathrm{Fi}}_{\alpha }$ derived for some values of parameter $\alpha$ by using (45).

$\mathit{\alpha }$	${\mathbf{Fi}}_{\mathit{\alpha }}\left(\mathit{x}\right)$
$\frac{3}{4}$	$\begin{array}{c}-x\left[\frac{1}{\Gamma \left(-\frac{3}{4}\right)}{}_3{F}_3\left(\left.\begin{array}{c}\frac{1}{4},\frac{7}{12},\frac{11}{12}\\ \frac{1}{2},\frac{3}{4},\frac{5}{4}\end{array}\right|-\frac{27x^4}{256}\right)+\frac{x}{144}\right.\hfill \\ \left.\left(\frac{8x}{\Gamma \left(-\frac{9}{4}\right)}{}_3{F}_3\left(\left.\begin{array}{c}\frac{3}{4},\frac{13}{12},\frac{17}{12}\\ \frac{5}{4},\frac{3}{2},\frac{7}{4}\end{array}\right|-\frac{27x^4}{256}\right)-\frac{27}{\sqrt{\pi }}{}_3{F}_4\left(\left.\begin{array}{c}\frac{1}{2},\frac{5}{6},\frac{7}{6}\\ \frac{3}{4},\frac{5}{4},\frac{3}{2}\end{array}\right|-\frac{27x^4}{256}\right)\right)\right]\hfill \end{array}$
$\frac{2}{3}$	$\frac{x}{4}\left[\frac{x}{\Gamma \left(-\frac{4}{3}\right)}{}_2{F}_2\left(\left.\begin{array}{c}\frac{2}{3},\frac{7}{6}\\ \frac{4}{3},\frac{5}{3}\end{array}\right|-\frac{4x^3}{27}\right)-\frac{4}{\Gamma \left(-\frac{2}{3}\right)}{}_2{F}_2\left(\left.\begin{array}{c}\frac{1}{3},\frac{5}{6}\\ \frac{2}{3},\frac{4}{3}\end{array}\right|-\frac{4x^3}{27}\right)\right]$
$\frac{1}{2}$	$\frac{1}{2}\mathrm{erf}\left(\frac{x}{2}\right)$
$\frac{1}{3}$	$\frac{x}{4}\left[\frac{x}{\Gamma \left(-\frac{2}{3}\right)}{}_1{F}_2\left(\left.\begin{array}{c}\frac{2}{3}\\ \frac{4}{3},\frac{5}{3}\end{array}\right|\frac{x^3}{27}\right)-\frac{4}{\Gamma \left(-\frac{1}{3}\right)}{}_1{F}_2\left(\left.\begin{array}{c}\frac{1}{3}\\ \frac{2}{3},\frac{4}{3}\end{array}\right|\frac{x^3}{27}\right)\right]$
$\frac{1}{4}$	$\begin{array}{c}-x\left[\frac{1}{\Gamma \left(-\frac{1}{4}\right)}{}_1{F}_3\left(\left.\begin{array}{c}\frac{1}{4}\\ \frac{1}{2},\frac{3}{4},\frac{5}{4}\end{array}\right|-\frac{x^4}{256}\right)+\frac{x}{72}\right.\hfill \\ \left.\left(\frac{9}{\sqrt{\pi }}{}_1{F}_3\left(\left.\begin{array}{c}\frac{1}{2}\\ \frac{3}{4},\frac{5}{4},\frac{3}{2}\end{array}\right|-\frac{x^4}{256}\right)+\frac{4x}{\Gamma \left(-\frac{3}{4}\right)}{}_3{F}_4\left(\left.\begin{array}{c}\frac{3}{4}\\ \frac{5}{4},\frac{3}{2},\frac{7}{4}\end{array}\right|-\frac{x^4}{256}\right)\right)\right]\hfill \end{array}$

Table 13. The integral Mainardi function ${\mathrm{Mi}}_{\alpha }$ derived for some values of parameter $\alpha$ by using (45).

$\mathit{\alpha }$	${\mathbf{Mi}}_{\mathit{\alpha }}\left(\mathit{x}\right)$
$\frac{3}{4}$	$\begin{array}{c}\frac{x}{96}\left[\frac{48}{\sqrt{\pi }}{}_3{F}_3\left(\left.\begin{array}{c}\frac{1}{4},\frac{5}{6},\frac{7}{6}\\ \frac{3}{4},\frac{5}{4},\frac{5}{4}\end{array}\right|-\frac{27x^4}{256}\right)\right.\hfill \\ \left.+\frac{24x}{\Gamma \left(-\frac{5}{4}\right)}{}_3{F}_3\left(\left.\begin{array}{c}\frac{1}{2},\frac{13}{12},\frac{17}{12}\\ \frac{5}{4},\frac{3}{2},\frac{3}{2}\end{array}\right|-\frac{27x^4}{256}\right)+\frac{x^3}{\Gamma \left(-\frac{11}{4}\right)}{}_4{F}_4\left(\left.\begin{array}{c}1,1,\frac{19}{12},\frac{23}{12}\\ \frac{3}{2},\frac{7}{4},2,2\end{array}\right|-\frac{27x^4}{256}\right)\right]\hfill \end{array}$
$\frac{2}{3}$	$-\frac{x^3}{18\Gamma \left(-\frac{5}{3}\right)}{}_3{F}_3\left(\left.\begin{array}{c}1,1,\frac{11}{6}\\ \frac{5}{3},2,2\end{array}\right|-\frac{4x^3}{27}\right)-\frac{x}{\Gamma \left(-\frac{1}{3}\right)}{}_2{F}_2\left(\left.\begin{array}{c}\frac{1}{3},\frac{7}{6}\\ \frac{4}{3},\frac{4}{3}\end{array}\right|-\frac{4x^3}{27}\right)$
$\frac{1}{2}$	$\frac{1}{2\sqrt{\pi }}\left[\mathrm{Chi}\left(\frac{x^2}{4}\right)-\mathrm{Shi}\left(\frac{x^2}{4}\right)-ln\left(\frac{x^2}{4}\right)-\gamma \right]$
$\frac{1}{3}$	$-\frac{x^3}{18\Gamma \left(-\frac{1}{3}\right)}{}_2{F}_3\left(\left.\begin{array}{c}1,1\\ \frac{5}{3},2,2\end{array}\right|\frac{x^3}{27}\right)-\frac{x}{\Gamma \left(\frac{1}{3}\right)}{}_1{F}_2\left(\left.\begin{array}{c}\frac{1}{3}\\ \frac{4}{3},\frac{4}{3}\end{array}\right|\frac{x^3}{27}\right)$
$\frac{1}{4}$	$\begin{array}{c}-\frac{x}{\sqrt{\pi }}{}_1{F}_3\left(\left.\begin{array}{c}\frac{1}{4}\\ \frac{3}{4},\frac{5}{4},\frac{5}{4}\end{array}\right|-\frac{x^4}{256}\right)\hfill \\ \left.+\frac{x^2}{4\Gamma \left(\frac{1}{4}\right)}{}_1{F}_3\left(\left.\begin{array}{c}\frac{1}{2}\\ \frac{5}{4},\frac{3}{2},\frac{3}{2}\end{array}\right|-\frac{x^4}{256}\right)+\frac{x^4}{96\Gamma \left(-\frac{1}{4}\right)}{}_2{F}_4\left(\left.\begin{array}{c}1,1\\ \frac{3}{2},\frac{7}{4},2,2\end{array}\right|-\frac{x^4}{256}\right)\right]\hfill \end{array}$

5. Conclusions

For the first time, three new special functions are presented in this investigation: the integral Mittag-Leffler functions, the integral Whittaker functions, and the integral Wright functions. These functions are defined in the mathematical literature in the same manner as other elementary and special integral functions. It is feasible to generate these functions in an explicit form for certain parameters values using the MATHEMATICA application. These integral functions are often represented in terms of generalized hypergeometric functions. The behavior of some of them is shown graphically. In the Appendices, a large number of Mittag-Leffler, Whittaker, and Wright functions with integral and fractional parameters, as well as their Laplace transforms, are presented in tabular form.

It may be observed that, generally, it is highly possible to make general integral functions such as (19) and (20) by using generalized hypergeometric ${}_p{F}_p\left(t\right)$, because they converge in the whole complex t-plane, or, for every real number t.