Abstract
Emotion plays an important role in decision making. In an emergency, panic can spread among crowds through person-to-person communications and can cause harmful effects on society. The aim of this paper is to propose a new theoretical model in the context of epidemiology to describe the spread of panic under an emergency. First, according to divisions in personality in the context of psychology, groups are divided into a level-headed group and an impatient group. Second, individuals in the two groups have unique personalities. Thus, the level-headed group only infects within the group, while the impatient group considers emotional infection within the group and cross infection between the groups. Then, a nonlinear infection rate is used to describe the probability of infection after an infected person contacts a susceptible person, which is more in line with the real situation. After that, the level-headed group–impatient group nonlinear SIRS panic spreading model is developed. Stable analysis of the model is obtained using the Lyapunov function method to study the stability of the panic-free equilibrium and panic-permanence equilibrium. Finally, simulations are carried out to dynamically describe the spread process of group emotional contagion.
1. Introduction
In recent years, public safety emergencies, such as fires, earthquakes, and stampedes have occurred frequently, which have led to public panic and caused a certain psychological burden on people [1]. In an emergency, individual behaviors are affected by many factors, for example, personal emotion [2], conformity behavior [3], familiarity with the surrounding environment [4], social relations [5,6], etc.
Emotion has a significant influence on group movements [7]. In an emergency, people become panicked because of unpredictable external factors, which affect people’s decision making [8]. Emotion is contagious and spreads rapidly among people, which is a natural process and is unconscious and uncontrolled [9]. Recently, studies have shown that emotion is a very important factor that affects individual behavior in an emergency [10,11,12,13]. Emotions can mainly be divided into positive emotions and negative emotions [14]. It has been found that negative emotions are easily spread among a group, which is not conducive to the group’s movements. In order to study the spread rules of negative emotions, Bosse et al. [15] introduced team leaders to simulate the contagion process of internal emotions. The addition of police or leaders could generate positive emotions and inhibit negative emotions in the group [16]. The abovementioned theory analyzed how negative emotions spread in groups. Xu et al. [17] identified the contagion of individual positive emotions and negative emotions, and considered crowd density and the emotion influence radius on the overall emotions of a crowd. Group movements were influenced by individual emotions. In an emergency, individuals were also vulnerable to the emotions of others, and this made it easier for people to aggregate together [18]; however, not all emotions are negative. Liu et al. [19] pointed out that emotional contagion might facilitate the spread of information among a group. Emotional simulation research has had an important impact on public security. Traditional methods focus on the interaction between individuals or groups, while ignoring the impact of emotional factors on the groups.
Group emotional contagion is a process of mutual spread between individuals, which is similar to the process of virus transmission in the epidemiology model [20]. There are mainly two classes of traditional contagions: the susceptible-infected-susceptible (SIS) model and the susceptible-infected-recovered (SIR) model [21,22,23]. On this basis, combining a knowledge of psychology and sociology, these were applied to emotion modeling, which simulated the psychological state of individuals under an emergency, and widely used in the field of emotion contagion [24,25,26,27,28,29,30,31]. Hill et al., adopted the traditional SIS (susceptible-infected-susceptible) epidemiological model and data from the Framingham Heart Disease Research Center to illustrate that emotion can spread through social networks [24]. According to the susceptible-infected-susceptible (SIS) model, Zhao et al. studied that panic spreads in a subway emergency according to passenger density: characteristic of subway cars with confined spaces and passengers’ psychological factors [25]. Pei et al. analyzed emotional contagion in political rally scenes [26]. Based on cellular automata, Fu et al. [27] structured a new CA-SIRS model to simulate the dynamics of a crowd’s emotional contagion in an emergency. Ni et al. [28] added an emotional stability node to the SIR model and simulated the contagion process under a group emotional contagion model. Hossain et al. [29] investigated the spread of panic in a predator–prey model and performed dynamic analyses. With the passage of time, some people in the panic crowd will become anxious [27,30]. In order to describe the panic propagation mechanism and how to stop the spread of panic, Cornes et al. [31] focused on reliable parameters from a real video, and simulated the process of evacuation in a panic spread event.
In this paper, based on the above research, according to the SIR epidemiological model and combining it with divisions of personality in psychology, the groups were divided into a level-headed group and an impatient group. Emotional contagion existed not only in within the group, but also cross infection between the different groups was considered, and a panic spreading model was established. The remainder of this paper comprises the following: the level-headed group–impatient group nonlinear SIRS panic spreading model is constructed in Section 2. In Section 3, the local asymptotic stability and the global asymptotic stability of the proposed model are analyzed, respectively. Numerical simulations to explain the theoretical results are carried out in Section 4. Finally, brief conclusions are drawn in Section 5.
2. Level-Headed Group–Impatient Group Nonlinear SIRS Panic Spreading Model
This paper considers the classical SIR model, and the three epidemiological categories are represented by three variables: susceptible, infected, and recovered, denoted by S(t), I(t), and R(t), respectively In order to construct the level-headed group–impatient group nonlinear SIRS panic spreading model, we made the following assumptions.
- (I)
- Drawing on the divisions in personality by Jung [32], the groups were divided into a level-headed group and an impatient group. Level-headed individuals have meticulous thinking and will calm down in the face of difficulty. On the contrary, impatient individuals are reckless and adventurous, and are vulnerable to the emotional influence of others. The level-headed group and the impatient group are both classified into three categories: susceptible, infected, and recovered, denoted by S1, I1, and R1 and S2, I2, and R2 at time t, respectively.
- (II)
- Several traditional infection rates have been widely used in various fields, namely the bilinear infection rate, , and the standard infection rate, . A characteristic of these two infection rates is that the number of infected individuals increases linearly, which is obviously limited and overly idealistic for academic research. Whether it is the level-headed group or the impatient group, the panic emotion tends to show a nonlinear relationship with the group through the process of spreading, which is more in line with real situations. S and I in the infection rate are considered as a function of time t. The nonlinear infection rate is [33]
- (III)
- Emotion spreads not only within groups but also between different groups to susceptible people. Based on the characteristics of each group, we consider that the impatient group is affected by panic contagion, not only within the group but also occurring through cross infection from the level-headed group. Furthermore, in the level-headed group, panic is contagious from infected individuals to susceptible individuals.
- (IV)
- Susceptible individuals in the level-headed group and the impatient group can become recovered individuals; however, they do not have permanent immunity and may become susceptible individuals again with a certain probability.
New recruitments to both the level-headed group and the impatient group are susceptible, and the rate is denoted by and , respectively. The death rate of humans is the rate, d. Level-headed and impatient recovered individuals lose immunity and return to being susceptible at rates of and , respectively. Infected individuals from the level-headed group and impatient group can recover at rates of and , respectively. All parameters are non-negative.
Consequently, the level-headed group–impatient group nonlinear SIRS panic spreading model with non-permanent immunity is established, of which the equations are
The unique solution of Equation (2) is positively invariant, which satisfies the initial conditions in . According to Equation (2), we analyzed the condition for the existence of panic-free equilibrium and the infected individuals of the level-headed group and the impatient group were both zero. The panic-free equilibrium, , always exists. The panic-permanence equilibrium, , of Equation (2) should satisfy the following equations
According to the method given by Van Den Driessche and Watmough [34], we can obtain the basic reproduction number, , in the panic-free state, where , then, , , , and . Let , then Equation (2) can be written as
where
We can obtain
Hence, the basic reproduction number of Equation (2) is the spectral radius of matrix , and we obtain
From Equation (3), if and , we can solve the second and third equations. We can obtain
Substituting for (8) and (9) in the first equation of Equation (3), we can obtain
where
Similarly, solving the fifth and the sixth equations of Equation (3), we can find that
Substituting for (12) and (13) in the fourth equation of Equation (3), we obtain
The only positive root, , exists only if it has the following conditions , as .
It holds that under the condition . We can deduce the panic-permanence equilibrium, .
In summary, we have the following results.
- (i)
- If and , is unique in the panic-free equilibrium.
- (ii)
- If and , two equilibria exist, the panic-free equilibrium, , and the panic-permanence equilibrium, , respectively.
3. Stability Analysis of Level-Headed Group–Impatient Group SIRS Panic Spreading Model
In this section, we analyze the stability of the level-headed group–impatient group nonlinear SIRS panic spreading model in detail, and study the local and global stability of the panic-free equilibrium and panic-permanence equilibrium, respectively.
3.1. Locally Stable Analysis of the Model
Theorem 1.
If and, panic-free equilibriumis locally asymptotically stable.
Proof of Theorem 1.
The Jacobian matrix of Equation (2) at is
The corresponding characteristic equation is
The eigenvalues for J () are
Since the values of all parameters are positive, it is obvious that ,, and are all negative. When the basic reproduction number (7) satisfies and , the other two eigenvalues and are both negative through calculation.
Theorem 2.
If and, the panic-permanence equilibrium,, is locally asymptotically stable.
Proof of Theorem 2.
Refer to Appendix A.
3.2. Global Stability Analysis of Level-Headed Sub-Model
Considering that the first three equations of Equation (2) contain only the level-headed group, we analyzed the dynamic behavior of the level-headed group. The level-headed sub-model is as follows
Theorem 3.
If , the panic-free equilibrium,, is globally asymptotically stable.
Proof of Theorem 3.
The above sub-model, Equation (17), can be rewritten as
We adopt the new Lyapunov function method [35,36]
where
Since , we have . Through calculation, we can further obtain
where , therefore .
According to the above analysis, we determine that the panic-free equilibrium, , is globally asymptotically stable.
Theorem 4.
If, the panic-permanence equilibrium,, is globally asymptotically stable.
Proof of Theorem 4.
See Appendix A.
3.3. Global Stability of the Model
Theorem 5.
If , the panic-free equilibrium,, is globally asymptotically stable.
Proof of Theorem 5.
We use traditional methods to structure the Lyapunov function
According to Theorem 3, the panic-free equilibrium, , is globally asymptotically stable if . Therefore, we only consider that the variable is in the panic-free state, given by
The panic-free equilibrium, , is globally asymptotically stable if .
Theorem 6.
If , the panic-permanence equilibrium,, is globally asymptotically stable.
Proof of Theorem 6.
We can construct the Lyapunov function as follows
Thus, the panic-permanence equilibrium, , is globally asymptotically stable by the LaSalle invariance principle [37].
From the above analysis, we can arrive at the following conclusion:
- (i)
- If and , the panic-free equilibrium, , is globally asymptotically stable.
- (ii)
- If and , the panic-permanence equilibrium, , is globally asymptotically stable.
4. Numerical Simulations and Analysis
In this section, we carry out the corresponding numerical simulations for our proposed theoretical model. In combination with the discussion and analyses above, the model simulation and numerical simulation results of equilibrium stability are given.
4.1. Simulation of Equilibrium Stability
We set the key parameters as follows: , , , , , , , , , and , and give the initial values of , , , , , and .
Through calculation, we can obtain the basic reproduction numbers, , and . The death of infected people, in other words, as can be seen in Figure 1, the panic-free equilibrium is not only locally asymptotically stable but also globally asymptotically stable.
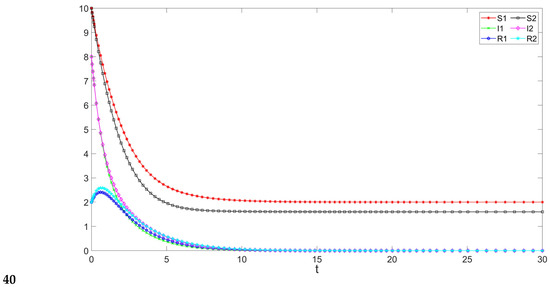
Figure 1.
The stability of the panic-free equilibrium, .
Some parameters of the model are set as follows: , , , , , , , , , and , and give the initial values: , , , , , and . The basic reproduction numbers, and , are obtained through calculation. According to numerical simulations in Figure 2, the solutions of the model tend to the panic-permanence equilibrium. We can get the equilibriums, , and they are locally asymptotically stable and globally asymptotically stable when infected people exist.
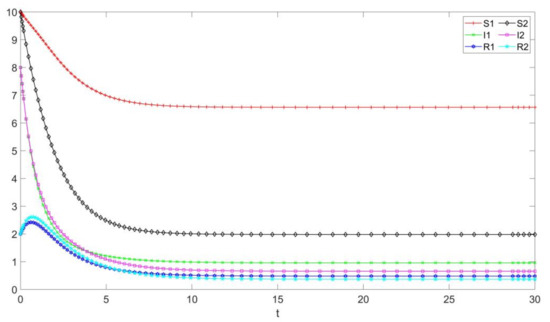
Figure 2.
The stability of the panic-permanence equilibrium, .
4.2. Analysis of Numerical Simulation
We keep some parameters fixed as follows: , , , , , , , , , and . Then, we choose initial values as: , , , , , and .
As can be seen from Figure 3, in the initial stage of panic contagion, the number of susceptible people in both the level-headed group and the impatient group decrease sharply, and the recovered people of the two groups show a rapid increase in a very short time. As time varies, each group adapts to changes in the environment. The number of recovered in the group gradually increases, while the infected group decreases over time. Finally, the level-headed group and the impatient group reach a stable state, and the panic emotion dies out and drops to zero, which accords with realistic events.
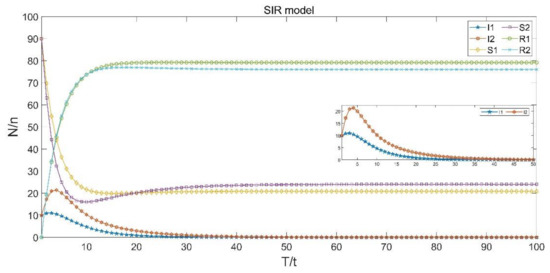
Figure 3.
Three types of groups change in both of the populations.
As shown in Figure 4, the change range of the impatient group is much more drastic than the level-headed group and the curve fluctuates greatly. The peak point of the impatient group is greater than that of the level-headed group. The two groups adapt to the changes in environment, and the number of each group decreases significantly and tends to gradually become stable. We can obtain the characteristics of the two groups. The impatient group is greatly affected by environmental changes, and the contagion process is fairly drastic, while the emotions of the level-headed group are stable and slowly recover. The infection rate of the impatient group is greater than that of the level-headed group. Therefore, an increase in the infection rate will speed up the spread of panic in the group, then the emotional contagion intensity of the whole group increases, and the group contagion is more obvious.
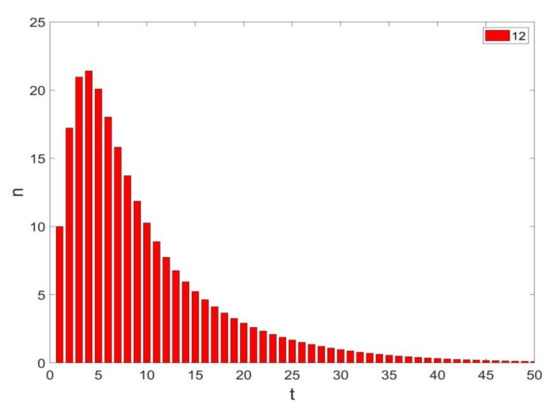
Figure 4.
Number of panic-infected people, I (t), versus time varying over the level-headed group and the impatient group.
We know that the impatient group changes more drastically than the level-headed group, and Figure 5 and Figure 6 illustrate this conclusion. In the early stage, for the recovered and susceptible people, the changing speed of the impatient group is faster than that of the level-headed group. With changes over time, the group reaches a steady state. Recovered people do not have permanent immunity, so they will become susceptible people once again. Therefore, the number of susceptible people in the impatient group is greater than that in the level-headed group, and the number of recovered people in the level-headed group is greater than that in the impatient group. We can see that a higher infection rate and recovery rate can promote a frequent spread of emotions between groups, and the contact between groups can promote recovery of the group.
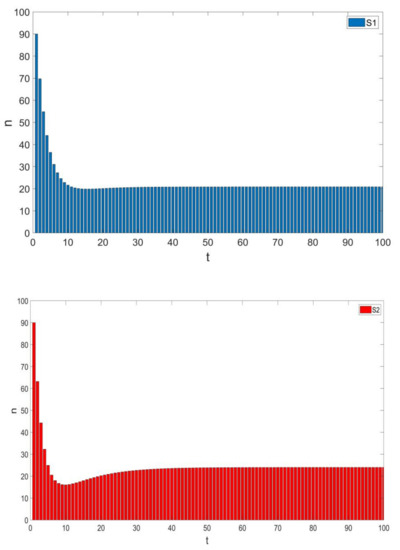
Figure 5.
Number of panic-susceptible people, S (t), versus time, varying over the level-headed group and the impatient group.
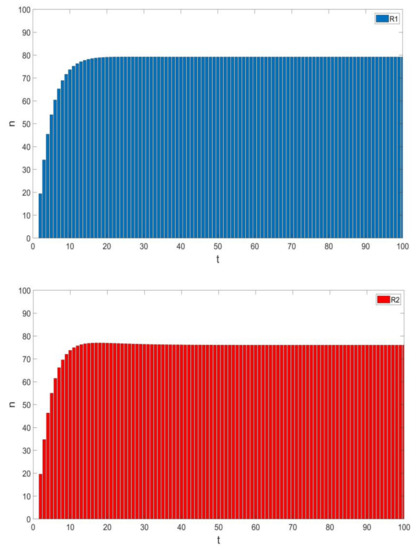
Figure 6.
Number of panic-recovered people, R (t), versus time, varying over the level-headed group and the impatient group.
From Figure 4, Figure 5 and Figure 6, we can obtain that the increase in the infection rate can promote the spread of panic. On the other hand, the recovery rate of impatience is higher than that of the level-headed recovery. At the same time, due to the non-permanent immunity of recovered people, they will become susceptible people again with a certain probability. Therefore, it can be seen that the increase in communication between groups can also inhibit the spread of panic.
5. Conclusions
In this paper, we studied the dynamic spread rules of the emotion panic in groups. According to the divisions of personality in psychology, the groups are broken down into a level-headed group and an impatient group. The level-headed group is only infected within the group, while the impatient group is infected not only by those within the group but also via cross infection outside from the level-headed group. We propose the nonlinear SIRS panic spreading model. We obtain the threshold value of panic contagion and discuss the local and global asymptomatic stability of the panic-free and panic-permanence equilibrium of the proposed model, which is also confirmed through numerical simulations.
The simulation results indicate that the contagion and recovery process of the impatient group is strong, whereas the level-headed group is relatively stable and the recovery is relatively slow in an emergency, which is in line with personal psychological characteristics. The infection rate and recovery rate have dual roles; they can allow the spread of emotions between groups more frequently and can enhance the level of panic, but the communication between groups can inhibit the spread of panic and can promote the recovery of group emotions. The simulation results verify our conjecture.
Our research may provide guidance for panic spread in an emergency. However, the complexity of personal emotional changes are different for different scenarios and situations. Future research will look into small groups [38,39], external influence [40], and social reinforcement [41] factors of emotional contagion. In this specific scenario, we should consider how crowd movement and efficient strategies could be properly implemented. Therefore, it is necessary to explore detailed modeling based on research from psychology and other external factors to obtain more realistic simulation results.
Author Contributions
Conceptualization, R.L.; methodology, R.L.; software, R.L.; validation, R.L.; investigation, H.L. and Q.S.; writing—original draft preparation, R.L.; resources, H.L. and Q.S.; supervision, H.L. and Q.S.; project administration, H.L. and Q.S. All authors have read and agreed to the published version of the manuscript.
Funding
Natural Science Foundation of China (71771112), and Project of Liaoning Provincial Federation Social Science Circles of China (L20BGL047).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
In the appendix, we give the proofs of Theorems 2 and 4.
Appendix A.1. Proof of Theorem 2
We use the Jacobian matrix of Equation (2) to illustrate.
The characteristic equation at can be written as the following equation
We can obtain two negative eigenvalues, ,
where
If and , so , then . Thus, all eigenvalues of the characteristic equation have negative roots. Therefore, the panic-permanence equilibrium, , is locally asymptotically stable.
Appendix A.2. Proof of Theorem 4
Equation (2) is rewritten as follows
The second equation of Equation (A7) can be written as follows
We choose the Lyapunov function
where
From the first Equation of (7), if , we get
Since Equation (A11) < 0 and Equation (A12) < 0, we can obtain .
Hence, the panic-permanence equilibrium, , is globally asymptotically stable.
References
- Ross, W.; Gorod, A.; Ulieru, M. A Socio-Physical Approach to Systemic Risk Reduction in Emergency Response and Prepar-edness. IEEE Trans. Syst. Man Cybern. Syst. 2015, 45, 1125–1137. [Google Scholar]
- Mao, Y.; Li, Z.; Li, Y.; He, W. Emotion-based diversity crowd behavior simulation in public emergency. Vis. Comput. 2019, 35, 1725–1739. [Google Scholar] [CrossRef]
- Low, D.J. Following the crowd. Nature 2000, 407, 465–466. [Google Scholar] [CrossRef]
- Meier, S.T.; Bützler, J.; Schlick, C.M. The influence of information presented on digital escape route signage on decision-making under mentally and emotionally strenuous conditions. In Proceedings of 19th Triennial Congress of the IEA, Melbourne, Australia, 9–14 August 2015; Volume 1, p. 1. [Google Scholar]
- Che, X.; Niu, Y.; Shui, B.; Fu, J.; Fei, G.; Goswami, P.; Zhang, Y. A novel simulation framework based on information asymmetry to evaluate evacuation plan. Vis. Comput. 2015, 31, 853–861. [Google Scholar] [CrossRef]
- Fu, L.; Song, W.; Lo, S.M. A fuzzy-theory-based method for studying the effect of information transmission on nonlinear crowd dispersion dynamics. Commun. Nonlinear Sci. Numer. Simul. 2017, 42, 682–698. [Google Scholar] [CrossRef]
- Bon, G.L. The Crowd, A Study of the Popular Mind. Am. J. Sociol. 1897, 2, 734–735. [Google Scholar]
- Durupınar, F.; Gudukbay, U.; Aman, A.; Badler, N.I.; Durupinar, F. Psychological Parameters for Crowd Simulation: From Audiences to Mobs. IEEE Trans. Vis. Comput. Graph. 2015, 22, 2145–2159. [Google Scholar] [CrossRef]
- Olson, K.R. A Literature Review of Social Mood. J. Behav. Finance 2006, 7, 193–203. [Google Scholar] [CrossRef]
- Quarantelli, E.L. The Sociology of Panic. Int. Encycl. Soc. Behav. Sci. 2001, 11020–11023. [Google Scholar]
- Bosse, T.; Duell, R.; Memon, Z.A.; Treur, J.; van der Wal, C.N. Multi-Agent Model for Emotion Contagion Spirals Integrated within a Supporting Ambient Agent Model; Springer: Berlin/Heidelberg, Germany, 2009; pp. 48–67. [Google Scholar]
- Ta, X.H.; Gaudou, B.; Longin, D.; Ho, T.V. Emotional contagion model for group evacuation simulation. Informatica 2017, 41, 169–182. [Google Scholar]
- Li, C.; Lv, P.; Manocha, D.; Wang, H.; Li, Y.; Zhou, B.; Xu, M. ACSEE: Antagonistic Crowd Simulation Model with Emotional Contagion and Evolutionary Game Theory. IEEE Trans. Affect. Comput. 2019, 99, 1. [Google Scholar] [CrossRef]
- Liu, Z.; Zhang, T.; Lan, Q. An Extended SISa Model for Sentiment Contagion. Discret. Dyn. Nat. Soc. 2014, 2014, 1–7. [Google Scholar] [CrossRef]
- Bosse, T.; Duell, R.; Memon, Z.; Treur, J.; van der Wal, N. Agent-Based Modeling of Emotion Contagion in Groups. Cogn. Comput. 2014, 7, 111–136. [Google Scholar] [CrossRef] [Green Version]
- Mao, Y.; Du, X.; Li, Y.; He, W. An emotion based simulation framework for complex evacuation scenarios. Graph. Model. 2019, 102, 1–9. [Google Scholar] [CrossRef]
- Xu, T.; Shi, D.; Chen, J.; Li, T.; Lin, P.; Ma, J. Dynamics of emotional contagion in dense pedestrian crowds. Phys. Lett. A 2020, 384, 126080. [Google Scholar] [CrossRef]
- Liu, Z.; Liu, T.; Ma, M.; Hsu, H.-H.; Ni, Z.; Chai, Y.J. A perception-based emotion contagion model in crowd emergent evacuation simulation. Comput. Animat. Virtual Worlds 2018, 29, e1817. [Google Scholar] [CrossRef]
- Liu, T.; Liu, Z.; Chai, Y.J.; Wang, J.; Lin, X.; Huang, P. Simulating evacuation crowd with emotion and personality. Artif. Life Robot. 2018, 24, 59–67. [Google Scholar] [CrossRef]
- Kermack, W.O.; Mckendrick, A.G.A. A Contribution to the Mathematical Theory of Epidemics. Proceedings of The Royal Society A Mathematical Physical and Engineering Sciences 1927, 115, 700–721. [Google Scholar]
- Anderson, R.M.; May, R.M. Infectious Diseases of Human: Dynamics and Control; Oxford University Press (OUP): Oxford, UK, 1992. [Google Scholar]
- Hethcote, H.W.; Driessche, P.V.D. An SIS epidemic model with variable population size and a delay. J. Math. Biol. 1995, 34, 177–194. [Google Scholar] [CrossRef]
- Beretta, E.; Takeuchi, Y. Global stability of an SIR epidemic model with time delays. J. Math. Biol. 1995, 33, 250–260. [Google Scholar] [CrossRef]
- Hill, A.L.; Rand, D.; Nowak, M.A.; Christakis, N.A. Emotions as infectious diseases in a large social network: The SISa model. Proc. R. Soc. B Boil. Sci. 2010, 277, 3827–3835. [Google Scholar] [CrossRef]
- Zhao, H.; Jiang, J.; Xu, R.; Ye, Y. SIRS Model of Passengers’ Panic Propagation under Self-Organization Circumstance in the Subway Emergency. Math. Probl. Eng. 2014, 2014, 1–12. [Google Scholar] [CrossRef] [Green Version]
- Lv, P.; Zhang, Z.; Li, C.; Guo, Y.; Zhou, B.; Xu, M. Crowd Behavior Evolution with Emotional Contagion in Political Rallies. IEEE Trans. Comput. Soc. Syst. 2019, 6, 377–386. [Google Scholar] [CrossRef]
- Fu, L.; Song, W.; Lv, W.; Lo, S. Simulation of emotional contagion using modifed sir model: A cellular automaton approach. Phys. A 2014, 405, 380–391. [Google Scholar]
- Ni, X.; Zhou, H.; Chen, W. Addition of an Emotionally Stable Node in the SOSa-SPSa Model for Group Emotional Contagion of Panic in Public Health Emergency: Implications for Epidemic Emergency Responses. Int. J. Environ. Res. Public Health 2020, 17, 5044. [Google Scholar] [CrossRef]
- Hossain, M.; Pal, N.; Samanta, S. Impact of fear on an eco-epidemiological model. Chaos Solitons Fractals 2020, 134, 109718. [Google Scholar] [CrossRef]
- Fu, L.; Song, W.; Lv, W.; Liu, X.; Lo, S. Multi-grid simulation of counter flow pedestrian dynamics with emotion propagation. Simul. Model. Pr. Theory 2016, 60, 1–14. [Google Scholar] [CrossRef]
- Cornes, F.; Frank, G.; Dorso, C. Fear propagation and the evacuation dynamics. Simul. Model. Pr. Theory 2019, 95, 112–133. [Google Scholar] [CrossRef]
- Jung, C.G. Collected works of C.G. Jung. In Psychology and Alchemy; Princeton University Press: Princeton, NJ, USA, 1980; Volume 12. [Google Scholar]
- Xiao, D.; Ruan, S. Global analysis of an epidemic model with nonmonotone incidence rate. Math. Biosci. 2007, 208, 419–429. [Google Scholar] [CrossRef]
- Driessche, P.V.D.; Watmough, J. Reproduction numbers and sub-threshold endemic equilibria for compartmental models of disease transmission. Math. Biosci. 2002, 180, 29–48. [Google Scholar] [CrossRef]
- Cruz, V.-D.-L. On the global stability of SIS, SIR and SIRS epidemic models with standard incidence. Chaos Solitons Fractals 2011, 44, 1106–1110. [Google Scholar]
- Tang, Q.; Teng, Z.; Abdurahman, X. A New Lyapunov Function for SIRS Epidemic Models. Bull. Malays. Math. Sci. Soc. 2017, 40, 237–258. [Google Scholar] [CrossRef]
- Lasalle, J.P. The Stability of Dynamical Systems; SIAM: Philadelphia, PA, USA, 1976; pp. 1096–1105. [Google Scholar]
- Li, Y.; Liu, H.; Zheng, X.; Han, Y.; Li, L. A Top–Bottom Clustering Algorithm Based on Crowd Trajectories for Small Group Classification. IEEE Access 2019, 7, 29679–29698. [Google Scholar] [CrossRef]
- Huang, K.; Zheng, X.; Yang, Y.; Wang, T. Behavioral evolution in evacuation crowd based on heterogeneous rationality of small groups. Appl. Math. Comput. 2015, 266, 501–506. [Google Scholar] [CrossRef]
- Zhou, R.; Ou, Y.; Tang, W.; Wang, Q.; Yu, B. An Emergency Evacuation Behavior Simulation Method Combines Personality Traits and Emotion Contagion. IEEE Access 2020, 8, 66693–66706. [Google Scholar] [CrossRef]
- Hébert-Dufresne, L.; Scarpino, S.V.; Young, J.-G. Macroscopic patterns of interacting contagions are indistinguishable from social reinforcement. Nat. Phys. 2020, 16, 426–431. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).