Abstract
This paper examines the hybrid nanoparticles and the magnetic field impacts on the mixed convection boundary layer flow and heat transfer caused by an inclined shrinking–stretching surface in a hybrid nanofluid. Silver (Ag) is added into a MgO–water nanofluid to form Ag-MgO–water hybrid nanofluid. By making use of proper similarity transformations, the governing equations are transformed to ordinary differential equations. The problem is numerically solved with the help of the MATLAB function bvp4c. The influences of the chosen parameters on the temperature, velocity, heat transfer rate and the skin friction coefficient are addressed and graphically illustrated. The results show that increasing the magnetic parameter substantially improves the heat transfer rate and increases the skin friction coefficient. The findings also suggest that increasing the nanoparticle volume fraction (Ag) improves the skin friction coefficient while decreasing the heat transfer rate. For both stretching and shrinking instances, non-unique (dual) solutions are discovered. Only the first solution is stable, according to the temporal stability analysis of the dual solutions.
1. Introduction
Heat transfer enhancement has gained much attention in current years, caused by its numerous uses in engineering and industries. In most applications, heat transfer fluids are utilized as cooling fluids, such as water, paraffin oil, diathermic oil, ethylene glycol, naphthenic mineral oil, vegetable oil, etc. However, these common fluids have poor thermal conductivity, which minimizes the amount of heat transferred. Thus, an innovative method of improving heat transfer in fluids is by adding nanosized particles in the base fluid to create a nanofluid mixture. It was presented by Choi and Eastman [1]. Nanofluids possess a significantly higher thermal conductivity than regular fluids. Therefore, nanofluids are widely used for a wide range of applications, such as nuclear reactor cooling, cooling of vehicles and machinery, electronic device cooling, biomedicine, etc. [2]. Consequently, many researchers have investigated the behaviors and properties of nanofluids for different aspects, numerically and experimentally. For example, Tiwari and Das [3] have proposed mathematical models of nanofluids that study the nanofluids’ behavior, considering the solid volume fractions of nanoparticles’ effects. The governing equations were numerically solved by the finite volume method (FEM). Several researchers have used the Tiwari–Das nanofluid model extensively; see [4,5,6,7,8,9,10,11,12,13,14,15].
The study of magnetohydrodynamics (MHD) flow is fundamental in the industry and has applications in a variety of fields, including petroleum products and metallurgical operations [16]. The rate of cooling in these processes has a huge impact on the finished product’s qualities, which can be regulated using a magnetic field and electrically conductive fluids. Various studies looked at the impact of applying a magnetic field on a nanofluid. The stretching surface and convective stagnation point flow of an incompressible nanofluid were used by Tian et al. [17] to study the magnetohydrodynamic flow numerically. The entropy of the boundary layer flow was investigated by Rashid et al. [18] using nanofluid generated by the shrinking porous surface. Moreover, Gopal et al. [19] revealed the effects of electric and magnetic force with viscosity dissipation on nanofluids of higher-order chemical processing over a continuously stretching porous wall. Furthermore, mixed convection flow (forced and free convection flow) has numerous engineering applications, for example, electrical engineering and chemical engineering, to name a few. As a result, numerous experts have looked into the mixed convection flow of nanofluids. The flow of a mixed convection nanofluid boundary layer toward a shrinking–stretching sheet at a stagnation point has been analyzed by Othman et al. [20]. The impact of physical variables on nanofluids’ flow, mass transfer, and heat transfer has been studied. Moreover, Ziaei-Rad et al. [21] reviewed the study of the mixed convection boundary layer nanofluid flow past a permeable inclined surface problem. In contrast, the numerical simulation of heat transfer and mixed convection nanofluid flow in a trapezoidal channel in a porous medium was carried out by El-shorbagy et al. [22]. Besides, in nanofluids, several researchers examined the MHD mixed convection flow past a stretching sheet. Over a stretching permeable sheet, Chamkha et al. [23] illustrated the MHD mixed convection nanofluid flow. The impact of viscous dissipation and a changing magnetic field on entropy production in MHD mixed convection nanofluid flow via a non-linear stretching surface were numerically explored by Matin et al. [24]. Besides, Ibrahim et al. [25] examined the impacts of viscous dissipation, thermal radiation, chemical reaction, suction, and heat generation of the MHD mixed convection boundary layer nanofluid flow with a stretching permeable sheet. Additionally, Vasanthakumari and Pondy [26] addressed the MHD mixed convection flow of a nanofluid across the inclined stretching sheet, having internal heat generation taken into account. Moreover, Gupta et al. [27] analyzed the joined impacts of the chemical reaction, magnetic field, and thermal radiation on the mixed convection incompressible nanofluid flow and heat transfer toward a stagnation point across an inclined stretching sheet.
In recent years, scientists and researchers are still looking for a better fluid to replace nanofluid and obtain a highly efficient heat transfer fluid. Their efforts led to the term: hybrid nanofluid. Hybrid nanofluids are an extension of nanofluids that contain two distinct types of nanoparticles mixed together in a base fluid. Hybrid nanofluids can enhance thermal characteristics better than regular nanofluids. The comparison between hybrid and traditional nanofluid in terms of the heat transfer characteristics was made by Devi and Devi [28]. They discovered that the hybrid nanofluid’s heat transfer rate is greater than the traditional nanofluid, even in the occurrence of a magnetic field. Furthermore, because of the benefits of hybrid nanofluids, researchers are eager to work toward hybrid nanofluids as heat transfer fluid. For instance, this includes the influence of Cu-–water hybrid nanofluid flow and heat transfer along a permeable moving sheet were described by Waini et al. [29]. According to the findings, in comparison to nanofluids containing single type of nanoparticles, hybrid nanofluids improve heat transfer properties. At present, many researchers are interested in the presence of dual solutions for the mixed convection flow. Zainal et al. [30] studied the MHD mixed convection flow across a vertical flat plate in a hybrid nanofluid with convective boundary conditions. They discovered dual solutions in both assisting and opposing flow regions. Waini et al. [31] analyzed the steady flow of mixed convection hybrid nanofluids over a vertical surface in a porous medium. Several dual solutions were found within a specific set of buoyancy parameters. Furthermore, the usage of hybrid nanoparticles causes the boundary layer to separate more slowly. Rostami et al. [32] evaluated the steady laminar MHD-mixed convection stagnation point flow over a vertical permeable flat plate in a hybrid nanofluid. Within a specific range of the buoyancy parameter, dual solutions have been reported, and the stability of these solutions has been determined. Jamaludin et al. [33] examined the MHD mixed convection stagnation point flow and heat transfer in Cu-A–water hybrid nanofluid above a permeable shrinking–stretching surface. Thus, a full report on the behavior of both lower and higher branch solutions was presented. The dual solutions were determined by Khashi’ie et al. [34] when they used hybrid nanofluids to study the mixed convection flow via a vertical plate embedded in a porous medium.
A numerical study of a hybrid nanofluid flow problem over a stretching–shrinking sheet has grabbed scientists’ and researchers’ intension in recent years. In a hybrid nanofluid, Waini et al. [35] carried out a numerical analysis of the unsteady flow and heat transfer toward a shrinking–stretching surface. They concluded that the velocity for Cu-A–water hybrid nanofluid increases with the increase in the suction parameter. They also discovered that the use of the hybrid nanofluid under the influence of the suction force could cause a further decrease in the temperature. Khashi’ie et al. [36] numerically investigated the impact of the convective condition and velocity slip on the three-dimensional hybrid nanofluids flow past a stretching–shrinking surface. They discovered that the increase in Biot and slip parameters can improve the heat transfer rates, but increasing the copper solid volume fraction has the opposite effect. In addition, using an Ag-MgO–water hybrid nanofluid, a numerical examination of the influence of boundary layer flow and heat transfer past an inclined permeable stretching–shrinking surface was carried out by Anuar et al. [37]. They found that when the angle of inclination and suction parameters increase, the local Nusselt number rises. The findings also show that raising the volume fraction of Ag nanoparticles in MgO–water nanofluid reduces the local Nusselt number. Furthermore, the hybrid nanofluid flow problem past a stretching–shrinking sheet was revealed numerically by Roşca and Pop [38], Anuar et al. [39], Wahid et al. [40] and Waini et al. [41], taking into account the various physical parameters.
Motivated by the above literature, the flat plate has been used in several research articles in two different positions; horizontal and vertical. Conversely, the inclined flat plate has received less interest. Nevertheless, there has never been a study of MHD mixed convection on an inclined stretching–shrinking sheet employing a hybrid nanofluid. As a result of the knowledge gap mentioned above, the current study attempts to enhance the work of Anuar et al. [37]. It can be performed by examining the MHD mixed convection flow of a hybrid nanofluid over an inclined permeable stretching–shrinking surface with suction force effects. The present model considers the solid volume fractions of nanoparticles while examining hybrid nanofluid behavior. The base fluid contains two distinct nanoparticles (Ag and MgO). Utilizing the similarity transformation approach, the governing equations with boundary conditions are transformed into a system of ordinary differential equations. The equations system is then solved using the MATLAB boundary value problem solver (bvp4c). In tabular and graphical representations, the impacts of many physical factors on heat transfer and flow characteristics are presented and explained. The stability analysis is carried out once the dual solutions for both stretching and shrinking instances are found. Furthermore, the difference has been presented with the previously published data to validate the obtained numerical results.
2. Formulation of the Problem
The mixed convection of magnetohydrodynamic flow of a hybrid nanofluid induced by an inclined permeable stretching–shrinking surface with an angle of inclination as displayed in Figure 1 is considered, where - and -axes are the dimensional Cartesian coordinates. Here, the -axis extends along the plate while the -axis normal to it. We assume that the velocity of the stretching–shrinking surface is , where is a positive constant. Additionally, the surface temperature of the sheet is considered as , where is a constant and the constant ambient temperature is signified as . In addition, denotes the mass flux velocity. A uniform magnetic field is applied normal to the plate. Meanwhile, the size of nanoparticles in the hybrid nanofluid is assumed to be uniform, and the agglomeration effect is neglected since the hybrid nanofluid is formed as a stable compound. Under the presumptions outlined above, the governing boundary layer equations of the hybrid nanofluid by employing the usual approximations of the boundary layer for the continuity, momentum and energy equations can be written as (see Devi and Devi [28], Afridi et al. [42] and Anuar et al. [37]):
subject to the boundary conditions [37]:
where and are the hybrid nanofluid velocity components along and directions. Here, signifies the temperature of the hybrid nanofluid, denotes the inclination angle, symbolizes the uniform magnetic field, implies the acceleration due to gravity and represents the parameter of the stretching–shrinking sheet with and are for the shrinking and stretching sheets, respectively, while for the static surface. Meanwhile, and are the dynamic viscosity, density, thermal conductivity, electrical conductivity, thermal expansion coefficient and heat capacity of the Ag-MgO–water hybrid nanofluid, respectively, which have the following definitions (see Devi and Devi [28]):
where the subscripts 1 and 2 represent MgO solid fraction and Ag solid fraction, while the subscripts and symbolize hybrid nanofluid and fluid, respectively. Furthermore, and indicate the volume fractions of MgO and Ag nanoparticles, respectively, where signifies the regular fluid. The required hybrid nanofluid is formed by adding Ag nanoparticles into MgO–water. The thermophysical properties of silver (Ag), magnesium oxide (MgO) and water are provided in Table 1, as reported by Abu-Libdeh et al. [43], Khan et al. [44] and Ghalambaz et al. [45]. As stated in [45], the thermal conductivity of the hybrid nanofluid is evaluated through curve fitting of the experimental data of Esfe et al. [46].
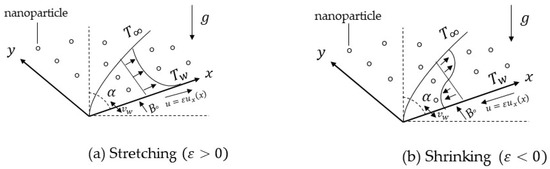
Figure 1.
The schematic problem flow.

Table 1.
The physical thermal characteristics of nanoparticles and water.
Following Anuar et al. [37], to obtain the similarity solutions for the Equations (1)–(4), the appropriate similarity transformations are employed as follows:
where signifies as dimensionless velocity, symbolizes the dimensionless temperature, and are the similarity variable and the kinematic viscosity, respectively. Meanwhile, is the stream function and the components of velocity are defined as and . Utilizing these definitions, the continuity Equation (1) is fully satisfied, and the velocities are expressed as:
such that:
Here, indicates the constant mass flux parameter where for injection and for suction.
Substituting the similarity variables (6) into governing Equations (2) and (3), one obtains the following similarity equations:
The boundary conditions (4) are converted to:
Note that is the mixed convection parameter or the buoyancy parameter, where is the Grashof number and represents the local Reynold number. Furthermore, demonstrates the opposing buoyancy force while signifies the assisting buoyancy force. Moreover, and are the magnetic parameter and the Prandtl number, respectively.
Next, the local Nusselt number and the skin friction coefficient are the parameters of physical interest, which can be defined as follows:
By substituting (6) into Equation (12), one obtains:
3. Stability Analysis
The numerical results reveal that there are non-uniqueness solutions from the boundary value problem (9)–(11) for a specific value of the physical parameters. As a result, a stability analysis, as shown in Merkin [47] as well as Weidman et al. [48], is used to identify the most trustworthy and stable solution and thus physically reliable. We have,
thus, the new dimensionless time variable is considered. By using variables in (6), the new similarity variables are introduced as:
Applying Equation (16) into Equations (14) and (15), the following system of equations are attained:
With the following initial and boundary conditions:
Following Weidman et al. [48], to examine the stability of the dual solutions , we write:
by which is an unknown eigenvalue parameter, while functions and are small relative to and , respectively. Thus, by substituting Equation (20) into (17) and (18) along with the conditions (19), and by taking , we can express the linear eigenvalue problem as follows:
Subject to the linearized conditions:
Following Harris et al. [49], resting the boundary condition on leads to the determination of the smallest eigenvalues . In the current work, the condition as is relaxed, which is replaced by the new boundary condition .
4. Numerical Method
The governing Equations (9) and (10) subject to the boundary restrictions (11) are solved numerically by the aid of the bvp4c function in MATLAB software. The bvp4c solver is explained in detail by Shampine et al. [50]. This solver uses the finite difference method that implements the three stages of the Lobatto IIIa formula. The syntax of the solver is defined by “sol=bvp4c (@OdeBVP, @OdeBC, solinit, options)”. To start the bvp4c routine, we need to convert Equations (9) and (10) into a system of first-order ordinary differential equations and rewrite them as follows:
The initial and boundary conditions (11) become:
The dual solutions are explored using two different initial guesses for the values of and . The appropriate initial guess and thickness of the boundary layer, must be chosen relying on the parameters applied, to obtain the required results. To validate the current numerical procedure, the values of are compared to cases that have been reported in Roşca and Pop [51] and Anuar et al. [37] for regular fluid () with various values of and when , and as elucidated in Table 2, which shows a favorable agreement. Additionally, Table 3 compares the values of for regular fluid () for various values of when and with those reported in Roşca and Pop [51] and Anuar et al. [37]. As a result, these tables indicate that the current results are valid and reliable. Thus, we can conclude that the developed algorithm for studying numerically the hybrid nanofluids flow can be used with great confidence.

Table 2.
Comparison of when ( ) with diverse values of and when and .

Table 3.
Comparison of when with diverse values of when and .
5. Results
The present work aims to investigate the influence of governing parameters such as suction parameter, , nanoparticle volume fraction parameter, , , mixed convection parameter, , stretching–shrinking parameter, , magnetic parameter, , and inclination angle parameter, , on the reduced skin friction f″ and the reduced Nusselt number which are presented in Figure 2 and Figure 3 as well as the dimensionless velocity and temperature which are displayed in Figure 4 and Figure 5. From these figures, it can be seen that two solutions exist for Equations (9)–(11) in the range of for both inclined permeable stretching and shrinking sheet, a unique solution found when and no solution is obtained when , where signifies the critical value of which the dual solutions are joined.
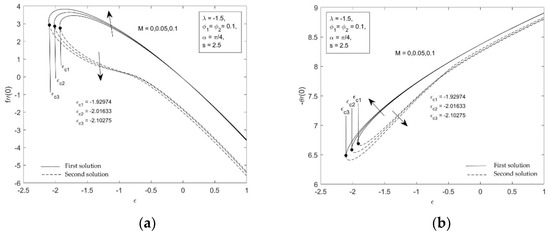
Figure 2.
Skin friction coefficient and local Nusselt number against for various values of .
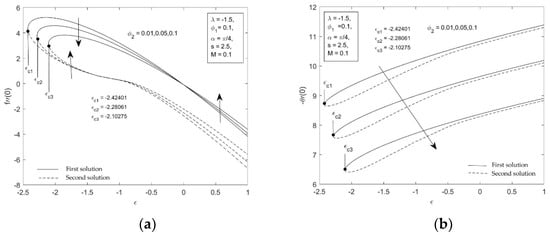
Figure 3.
Skin friction coefficient local Nusselt number against for various values of .
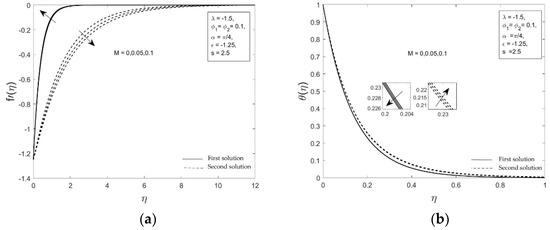
Figure 4.
Velocity profiles and temperature profiles for various values of .
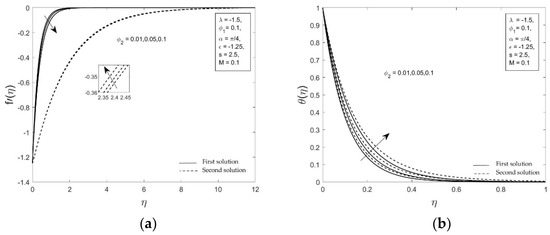
Figure 5.
Velocity profiles and temperature profiles for various values of .
For more details, Figure 2 displays the effect of on the reduced skin friction f″ and the reduced Nusselt number against when and . It can be seen that the rise of augments both and because of the reverse force known as the Lorentz force. As a result of the resistance to the motion of the fluid particles, this force appears to reduce fluid velocity. The synchronization of the magnetic and electric fields resulting from the creation of the Lorentz force appears to slow down the fluid movement. The boundary layer is becoming increasingly thin (see Figure 4a) as upsurges due to the postponed flow, thus increasing of and . From these figures, the behavior of the critical value of the stretching–shrinking parameter is going down with the incrementing of . The critical values of for are and , respectively.
The variations of the reduced skin friction coefficient and the reduced Nusselt number with some rates of together with three varying values of solid volume fraction , are illustrated in Figure 3 where and . Figure 3a highlights that the value of is increasing for the second solution; however, dual behaviors are found for the first solution of , where these values are decrementing at the shrinking region but increasing at the stretching region when the value of boosts, because of the increase in the volume fraction of nanoparticles raises the viscosity of the fluid. Hence, this helped to recover the coefficient of the skin friction along the surface. Moreover, Figure 3b conveys that the reduced Nusselt number (heat transfer rate) is reduced as the nanoparticle volume fraction augments for both inclined stretching and shrinking surfaces. Meanwhile, the values of appear to increase with the decrease of , but for , the opposite trend is observed. The critical values of are observed for solid volume fraction where and , respectively.
The profiles of and for certain physical parameters are presented in Figure 4 and Figure 5. From these figures, it is noticeable that there are dual solutions for the velocity profiles and the temperature profiles , which asymptotically satisfy the conditions (11), indicating that the current numerical findings are valid. The distribution of velocity profiles and the temperature profiles for numerous values of the magnetic parameter when and are presented in Figure 4. As seen in Figure 4a, the velocity appears to increase with the increase of for the first solution. Furthermore, a different direction is observed for the second solution. Meanwhile, Figure 4b exposes that the rise in causes a decrease in the temperature for the first solution, whereas an increment activity is preserved in the second solution. The Lorentz force is a resistive force that resists the fluid movement, resulting in decreasing manner of the velocity and the temperature for the first solutions, as shown in Figure 4. As a result, the velocity gradient as well as the temperature gradient at the surface increases, which in turn increases the skin friction coefficient and the Nusselt number. These findings are in agreement with the outcomes presented in Figure 2. Conversely, the second solutions show a different behavior, which is related to the stability of the solution that will be explained later.
Figure 5 shows the solid volume fraction effect toward the velocity profiles and the temperature profiles when and . As depicted in Figure 5a, the velocity increases in absolute sense for the first solution. This outcome demonstrates that the momentum boundary layer thickness increases in response to the increase of , thus reducing the magnitude of the velocity gradient at the surface. This finding is due to the opposing flow caused by the buoyancy force (represented by ). However, Figure 5b shows that the rise in significantly raises the temperature for both solutions. The magnification of the nanoparticle volume fraction enhances the thermal conductivity of hybrid nanofluid, thus raising the temperature, which in turn reduces the magnitude of the temperature gradient at the surface, . Thus, the Nusselt number, which represents the heat transfer rate at the surface decreases as increases. This finding is consistent with the results presented in Figure 3b.
The present mathematical model can be applied to predict the results of experiment works. Moreover, the present study also investigates the stability of the solutions in the long run. Figure 6 shows the variations of the eigenvalues γ against λ, while the other parameters are fixed. Referring to Equation (20), the unsteady (time dependent) solution converges to the steady (time independent) state solution as time evolves () if γ is positive. In contrast, the solution diverges if The sign of γ determines either decay or growth of the disturbance, which then determines the flow stability as time passes. It is evident from Figure 6 that γ is positive for the first solution, while it is negative for the second solution. Therefore, the first solution is stable and thus physically reliable as , while the second solution is not. Spangenberg et al. [52] have reported in their experimental work on turbulent boundary layer under strong adverse pressure gradient that dual solutions were obtained as a function of how the pressure gradient was realized. Another example of non-unique flow was reported by Aidun et al. [53], where they observed experimentally that the primary steady state flow in a through-flow lid-driven cavity was non-unique and only one of the multiple steady-state patterns can stabilize in the cavity. Although the second solutions are deprived of physical significance, they are still of interest from mathematical point of view. These solutions are also solutions to the differential equations, which satisfy the far field boundary conditions asymptotically. Similar equations may arise in other situations, where the lower branch solutions could have more realistic meaning [54].
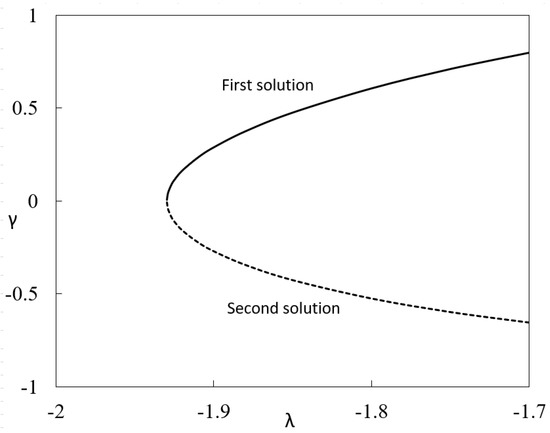
Figure 6.
Plot of eigenvalue γ against λ for .
6. Conclusions
The MHD mixed convection flow problem past an inclined permeable shrinking–stretching surface in a hybrid Ag-MgO–water nanofluid was investigated. Similarity transformations were utilized to help in obtaining the similarity equations. These equations were solved numerically using the MATLAB program’s boundary value problem solver, bvp4c. The significant findings are summarized as follows:
- Dual solutions are found for both stretching and shrinking scenarios , while the solutions came together at . Furthermore, there are no solutions for .
- The temporal stability analysis shows that only the first solution is stable over time.
- Deferred boundary layer separation occurs in the presence of nanoparticle volume fraction as well as the magnetic parameter.
- The temperature and velocity increase by raising the nanoparticle volume fraction and magnetic parameter .
- The skin friction coefficient as well as the heat transfer rate increases dramatically as magnetic parameter is raised.
- The augmentation of the nanoparticle volume fraction increases the skin friction coefficient but slows down the heat transmission across the inclined shrinking surface.
Author Contributions
Conceptualization, A.I.; funding acquisition, A.I.; methodology, S.A. and I.W.; Supervision, A.I. and S.E.A.; validation, I.W.; writing—original draft, S.A.; writing—review and editing, A.I., I.W. and S.E.A. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Universiti Kebangsaan Malaysia (project code: DIP-2020-001).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Acknowledgments
The financial supports received from the Universiti Kebangsaan Malaysia (Project Code: DIP-2020-001) and the Universiti Teknikal Malaysia Melaka are gratefully acknowledged.
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
| positive constants | |
| uniform magnetic field | |
| skin friction coefficient | |
| specific heat at constant pressure | |
| dimensionless velocity | |
| acceleration due to gravity | |
| Grashof number | |
| thermal conductivity of the fluid | |
| magnetic parameter | |
| local Nusselt number | |
| Prandtl number | |
| local Reynold number | |
| constant mass flux parameter | |
| time (s) | |
| fluid temperature | |
| surface temperature | |
| ambient temperature | |
| elements of velocity in and directions, respectively | |
| velocity of the stretching–shrinking surface | |
| mass flux velocity | |
| Cartesian coordinates | |
| thermal expansion coefficient | |
| eigenvalue | |
| parameter of stretching–shrinking sheet | |
| similarity variable | |
| dimensionless temperature | |
| mixed convection parameter | |
| dynamic viscosity of the fluid | |
| kinematic viscosity of the fluid | |
| Density of the fluid | |
| heat capacity of the fluid | |
| electrical conductivity of the fluid | |
| dimensionless time variable | |
| nanoparticle volume fractions for MgO (magnesium oxide) | |
| nanoparticle volume fractions for Ag (silver) | |
| stream function | |
| base fluid | |
| nanofluid | |
| hybrid nanofluid | |
| first nanoparticle (MgO) | |
| second nanoparticle (Ag) | |
References
- Choi, S.U.S.; Eastman, J.A. Enhancing Thermal Conductivity of Fluids with Nanoparticles. In Proceedings of the 1995 International Mechanical Engineering Congress and Exhibition, San Francisco, CA, USA, 12–17 November 1995; Volume 66, pp. 99–105. [Google Scholar]
- Wong, K.V.; De Leon, O. Applications of nanofluids: Current and future. Nanotechnol. Energy 2017, 105–132. [Google Scholar] [CrossRef] [Green Version]
- Tiwari, R.K.; Das, M.K. Heat transfer augmentation in a two-sided lid-driven differentially heated square cavity utilizing nanofluids. Int. J. Heat Mass Transf. 2007, 50, 2002–2018. [Google Scholar] [CrossRef]
- Sheremet, M.A.; Pop, I.; Nazar, R. Natural convection in a square cavity filled with a porous medium saturated with a nanofluid using the thermal nonequilibrium model with a Tiwari and Das nanofluid model. Int. J. Mech. Sci. 2015, 100, 312–321. [Google Scholar] [CrossRef]
- Mehmood, A.; Iqbal, M.S. Heat transfer analysis in natural convection flow of nanofluid past a wavy cone. J. Mol. Liq. 2016, 223, 1178–1184. [Google Scholar] [CrossRef]
- Dinarvand, S.; Hosseini, R.; Pop, I. Axisymmetric mixed convective stagnation-point flow of a nanofluid over a vertical permeable cylinder by Tiwari-Das nanofluid model. Powder Technol. 2017, 311, 147–156. [Google Scholar] [CrossRef]
- Dinarvand, S.; Pop, I. Free-convective flow of copper/water nanofluid about a rotating down-pointing cone using Tiwari-Das nanofluid scheme. Adv. Powder Technol. 2017, 28, 900–909. [Google Scholar] [CrossRef]
- Hayat, T.; Ijaz, M.; Qayyum, S.; Ayub, M.; Alsaedi, A. Mixed convective stagnation point flow of nanofluid with Darcy-Fochheimer relation and partial slip. Results Phys. 2018, 9, 771–778. [Google Scholar] [CrossRef]
- Aghamajidi, M.; Yazdi, M.; Dinarvand, S.; Pop, I. Tiwari-Das nanofluid model for magnetohydrodynamics (MHD) natural-convective flow of a nanofluid adjacent to a spinning down-pointing vertical cone. Propuls. Power Res. 2018, 7, 78–90. [Google Scholar] [CrossRef]
- Umavathi, J.C.; Hemavathi, K. Flow and heat transfer of composite porous medium saturated with nanofluid. Propuls. Power Res. 2019, 8, 173–181. [Google Scholar] [CrossRef]
- Dero, S.; Rohni, A.M.; Saaban, A. The dual solutions and stability analysis of nanofluid flow using tiwari-das modelover a permeable exponentially shrinking surface with partial slip conditions. J. Eng. Appl. Sci 2019, 14, 4569–4582. [Google Scholar] [CrossRef] [Green Version]
- Dogonchi, A.S.; Chamkha, A.J.; Hashemi-Tilehnoee, M.; Seyyedi, S.M.; Ganji, D.D. Effects of homogeneous-heterogeneous reactions and thermal radiation on magneto-hydrodynamic Cu-water nanofluid flow over an expanding flat plate with non-uniform heat source. J. Cent. South Univ. 2019, 26, 1161–1171. [Google Scholar] [CrossRef]
- Benzema, M.; Benkahla, Y.K.; Labsi, N.; Ouyahia, S.-E.; El Ganaoui, M. Second law analysis of MHD mixed convection heat transfer in a vented irregular cavity filled with Ag–MgO/water hybrid nanofluid. J. Therm. Anal. Calorim. 2019, 137, 1113–1132. [Google Scholar] [CrossRef]
- Sreedevi, P.; Reddy, P.S. Effect of magnetic field and thermal radiation on natural convection in a square cavity filled with TiO2 nanoparticles using Tiwari-Das nanofluid model. Alex. Eng. J. 2021, 61, 1529–1541. [Google Scholar] [CrossRef]
- Sreedevi, P.; Reddy, P.S.; Suryanarayana Rao, K.V. Effect of magnetic field and radiation on heat transfer analysis of nanofluid inside a square cavity filled with silver nanoparticles: Tiwari–Das model. Waves Random Complex Media 2021, 1–19. [Google Scholar] [CrossRef]
- Abel, M.S.; Tawade, J.V.; Shinde, J.N. The effects of MHD flow and heat transfer for the UCM fluid over a stretching surface in presence of thermal radiation. Adv. Math. Phys. 2012, 2012. [Google Scholar] [CrossRef]
- Tian, X.-Y.; Li, B.-W.; Hu, Z.-M. Convective stagnation point flow of a MHD non-Newtonian nanofluid towards a stretching plate. Int. J. Heat Mass Transf. 2018, 127, 768–780. [Google Scholar] [CrossRef]
- Rashid, I.; Sagheer, M.; Hussain, S. Entropy formation analysis of MHD boundary layer flow of nanofluid over a porous shrinking wall. Phys. A Stat. Mech. Its Appl. 2019, 536, 122608. [Google Scholar] [CrossRef]
- Gopal, D.; Saleem, S.; Jagadha, S.; Ahmad, F.; Almatroud, A.O.; Kishan, N. Numerical analysis of higher order chemical reaction on electrically MHD nanofluid under influence of viscous dissipation. Alex. Eng. J. 2021, 60, 1861–1871. [Google Scholar] [CrossRef]
- Othman, N.A.; Yacob, N.A.; Bachok, N.; Ishak, A.; Pop, I. Mixed convection boundary-layer stagnation point flow past a vertical stretching/shrinking surface in a nanofluid. Appl. Therm. Eng. 2017, 115, 1412–1417. [Google Scholar] [CrossRef]
- Ziaei-Rad, M.; Kasaeipoor, A.; Mehdi Rashidi, M.; Lorenzini, G. A similarity solution for mixed-convection boundary layer nanofluid flow on an inclined permeable surface. J. Therm. Sci. Eng. Appl. 2017, 9. [Google Scholar] [CrossRef]
- El-Shorbagy, M.A.; Eslami, F.; Ibrahim, M.; Barnoon, P.; Xia, W.-F.; Toghraie, D. Numerical investigation of mixed convection of nanofluid flow in a trapezoidal channel with different aspect ratios in the presence of porous medium. Case Stud. Therm. Eng. 2021, 25, 100977. [Google Scholar] [CrossRef]
- Chamkha, A.J.; Aly, A.M.; Al-Mudhaf, H.F. Laminar MHD mixed convection flow of a nanofluid along a stretching permeable surface in the presence of heat generation or absorption effects. Int. J. Microscale Nanoscale Therm. Fluid Transp. Phenom. 2011, 2, 51. [Google Scholar]
- Matin, M.H.; Nobari, M.R.H.; Jahangiri, P. Entropy analysis in mixed convection MHD flow of nanofluid over a non-linear stretching sheet. J. Therm. Sci. Technol. 2012, 7, 104–119. [Google Scholar] [CrossRef]
- Ibrahim, S.M.; Lorenzini, G.; Kumar, P.V.; Raju, C.S.K. Influence of chemical reaction and heat source on dissipative MHD mixed convection flow of a Casson nanofluid over a nonlinear permeable stretching sheet. Int. J. Heat Mass Transf. 2017, 111, 346–355. [Google Scholar] [CrossRef]
- Vasanthakumari, R.; Pondy, P. Mixed convection of silver and titanium dioxide nanofluids along inclined stretching sheet in presence of MHD with heat generation and suction effect. Math. Model. Eng. Probl. 2018, 5, 123–129. [Google Scholar] [CrossRef]
- Gupta, S.; Kumar, D.; Singh, J. MHD mixed convective stagnation point flow and heat transfer of an incompressible nanofluid over an inclined stretching sheet with chemical reaction and radiation. Int. J. Heat Mass Transf. 2018, 118, 378–387. [Google Scholar] [CrossRef]
- Devi, S.S.U.; Devi, S.P.A. Numerical investigation of three-dimensional hybrid Cu–Al2O3/water nanofluid flow over a stretching sheet with effecting Lorentz force subject to Newtonian heating. Can. J. Phys. 2016, 94, 490–496. [Google Scholar] [CrossRef]
- Waini, I.; Ishak, A.; Pop, I. Flow and heat transfer of a hybrid nanofluid past a permeable moving surface. Chin. J. Phys. 2020, 66, 606–619. [Google Scholar] [CrossRef]
- Zainal, N.A.; Nazar, R.; Naganthran, K.; Pop, I. MHD mixed convection stagnation point flow of a hybrid nanofluid past a vertical flat plate with convective boundary condition. Chin. J. Phys. 2020, 66, 630–644. [Google Scholar] [CrossRef]
- Waini, I.; Ishak, A.; Groşan, T.; Pop, I. Mixed convection of a hybrid nanofluid flow along a vertical surface embedded in a porous medium. Int. Commun. Heat Mass Transf. 2020, 114, 104565. [Google Scholar] [CrossRef]
- Rostami, M.N.; Dinarvand, S.; Pop, I. Dual solutions for mixed convective stagnation-point flow of an aqueous silica–alumina hybrid nanofluid. Chin. J. Phys. 2018, 56, 2465–2478. [Google Scholar] [CrossRef]
- Jamaludin, A.; Naganthran, K.; Nazar, R.; Pop, I. MHD mixed convection stagnation-point flow of Cu-Al2O3/water hybrid nanofluid over a permeable stretching/shrinking surface with heat source/sink. Eur. J. Mech. 2020, 84, 71–80. [Google Scholar] [CrossRef]
- Khashi’ie, N.S.; Arifin, N.M.; Pop, I. Non-Darcy mixed convection of hybrid nanofluid with thermal dispersion along a vertical plate embedded in a porous medium. Int. Commun. Heat Mass Transf. 2020, 118, 104866. [Google Scholar] [CrossRef]
- Waini, I.; Ishak, A.; Pop, I. Unsteady flow and heat transfer past a stretching/shrinking sheet in a hybrid nanofluid. Int. J. Heat Mass Transf. 2019, 136, 288–297. [Google Scholar] [CrossRef]
- Khashi’ie, N.S.; Arifin, N.M.; Pop, I.; Nazar, R.; Hafidzuddin, E.H.; Wahi, N. Three-dimensional hybrid nanofluid flow and heat transfer past a permeable stretching/shrinking sheet with velocity slip and convective condition. Chin. J. Phys. 2020, 66, 157–171. [Google Scholar] [CrossRef]
- Anuar, N.S.; Bachok, N.; Pop, I. Influence of buoyancy force on Ag-MgO/water hybrid nanofluid flow in an inclined permeable stretching/shrinking sheet. Int. Commun. Heat Mass Transf. 2021, 123, 105236. [Google Scholar] [CrossRef]
- Roşca, N.C.; Pop, I. Hybrid nanofluids flows determined by a permeable power-Law stretching/shrinking sheet modulated by orthogonal surface shear. Entropy 2021, 23, 813. [Google Scholar] [CrossRef] [PubMed]
- Anuar, N.S.; Bachok, N.; Pop, I. Cu-Al2O3/water hybrid nanofluid stagnation point flow past MHD stretching/shrinking sheet in presence of homogeneous-heterogeneous and convective boundary conditions. Mathematics 2020, 8, 1237. [Google Scholar] [CrossRef]
- Wahid, N.S.; Arifin, N.M.; Khashi’ie, N.S.; Pop, I. Hybrid nanofluid slip flow over an exponentially stretching/shrinking permeable sheet with heat generation. Mathematics 2021, 9, 30. [Google Scholar] [CrossRef]
- Waini, I.; Ishak, A.; Pop, I. Transpiration effects on hybrid nanofluid flow and heat transfer over a stretching/shrinking sheet with uniform shear flow. Alexandria Eng. J. 2020, 59, 91–99. [Google Scholar] [CrossRef]
- Afridi, M.I.; Qasim, M.; Khan, I.; Shafie, S.; Alshomrani, A.S. Entropy generation in magnetohydrodynamic mixed convection flow over an inclined stretching sheet. Entropy 2017, 19, 10. [Google Scholar] [CrossRef] [Green Version]
- Abu-Libdeh, N.; Redouane, F.; Aissa, A.; Mebarek-Oudina, F.; Almuhtady, A.; Jamshed, W.; Al-Kouz, W. Hydrothermal and entropy investigation of Ag/MgO/H2O hybrid nanofluid natural convection in a novel shape of porous cavity. Appl. Sci. 2021, 11, 1722. [Google Scholar] [CrossRef]
- Khan, U.; Zaib, A.; Abu Bakar, S.; Ishak, I. Stagnation-point flow of a hybrid nanoliquid over a non-isothermal stretching/shrinking sheet with characteristics of inertial and microstructure. Case Stud. Therm. Eng. 2021, 26, 101150. [Google Scholar] [CrossRef]
- Ghalambaz, M.; Doostani, A.; Izadpanahi, E.; Chamkha, A.J. Conjugate natural convection flow of Ag–MgO/water hybrid nanofluid in a square cavity. J. Therm. Anal. Calorim. 2020, 139, 2321–2336. [Google Scholar] [CrossRef]
- Esfe, M.H.; Arani, A.A.A.; Rezaie, M.; Yan, W.-M.; Karimipour, A. Experimental determination of thermal conductivity and dynamic viscosity of Ag–MgO/water hybrid nanofluid. Int. Commun. Heat Mass Transf. 2015, 66, 189–195. [Google Scholar] [CrossRef]
- Merkin, J.H. On dual solutions occurring in mixed convection in a porous medium. J. Eng. Math. 1986, 20, 171–179. [Google Scholar] [CrossRef]
- Weidman, P.D.; Kubitschek, D.G.; Davis, A.M.J. The effect of transpiration on self-similar boundary layer flow over moving surfaces. Int. J. Eng. Sci. 2006, 44, 730–737. [Google Scholar] [CrossRef]
- Harris, S.D.; Ingham, D.B.; Pop, I. Mixed convection boundary-layer flow near the stagnation point on a vertical surface in a porous medium: Brinkman model with slip. Transp. Porous Media 2009, 77, 267–285. [Google Scholar] [CrossRef]
- Shampine, L.F.; Gladwell, I.; Shampine, L.; Thompson, S. Solving ODEs with Matlab; Cambridge University Press: Cambridge, UK, 2003; ISBN 0521530946. [Google Scholar]
- Roşca, A.V.; Pop, I. Flow and heat transfer over a vertical permeable stretching/shrinking sheet with a second order slip. Int. J. Heat Mass Transf. 2013, 60, 355–364. [Google Scholar] [CrossRef]
- Spangenberg, W.G.; Rowland, W.R.; Mease, N.E. Fluid Mechanics of Internal Flows; Elsevier: Amsterdam, The Netherlands, 1967. [Google Scholar]
- Aidun, C.K.; Triantafillopoulos, N.G.; Benson, J.D. Global stability of a lid-driven cavity with throughflow. Phys. Fluids 1991, A3, 2081–2091. [Google Scholar] [CrossRef]
- Ishak, A.; Merkin, J.H.; Nazar, R.; Pop, I. Mixed convection boundary layer flow over a permeable vertical surface with prescribed wall heat flux. Z. Angew. Math. Phys. 2008, 59, 100–123. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).