Towards Parameter Identification of a Behavioral Model from a Virtual Reality Experiment
Abstract
:1. Introduction
- The presence of non-linearities in the mathematical model due to the imitation processes;
- The small number of data.
- Is it possible to estimate all of the model’s parameters from the physiological measurements provided by virtual reality?
- What is the minimal number of discrete time measurements needed to be sure of the parameter estimation procedure results?
2. The Different Behaviors and Their Modeling
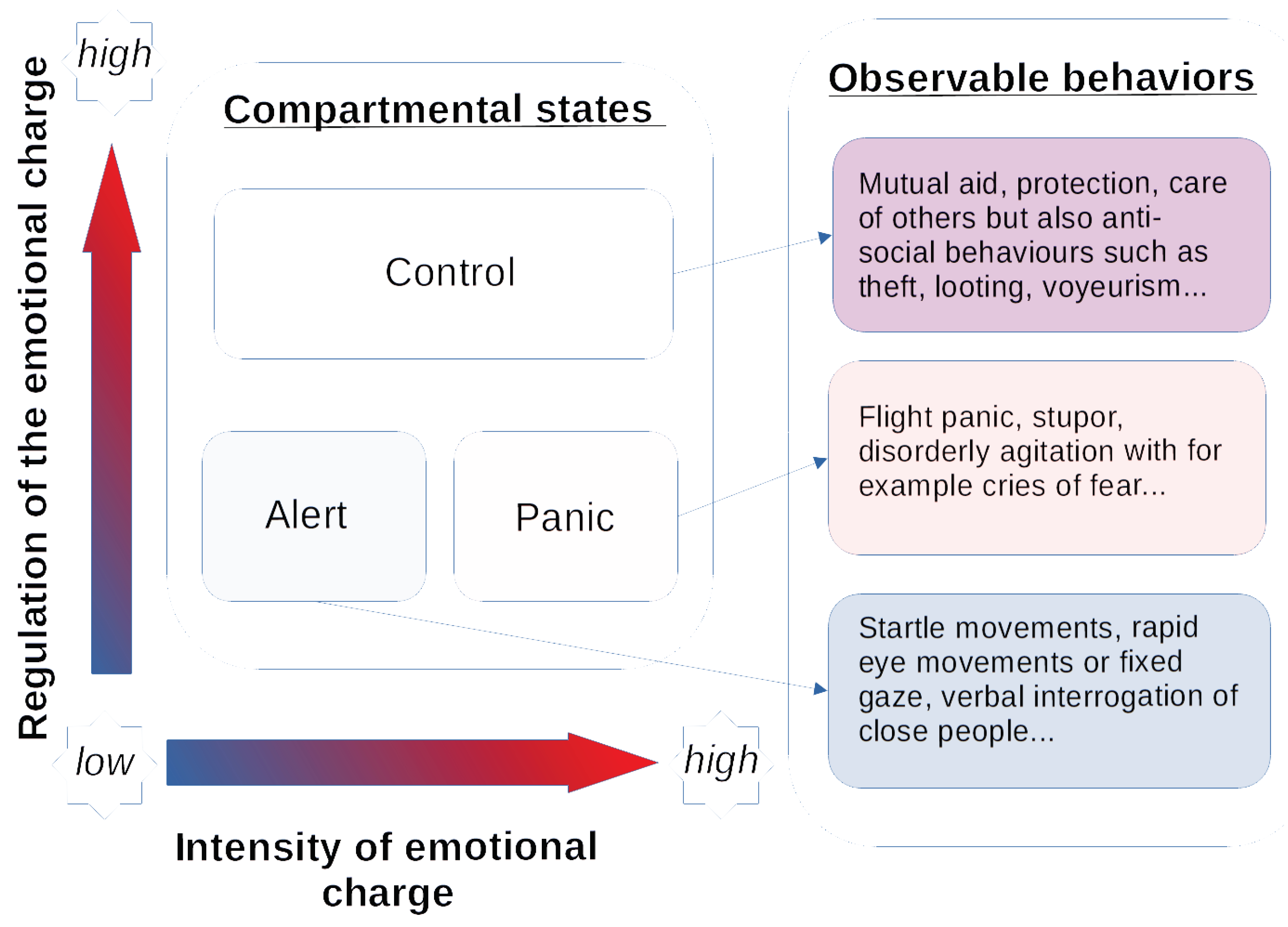
2.1. Emotional Load and Its Regulation
- The alert state corresponds to a low emotional charge and low regulation. It relates to a phase of assimilation of information relative to the event, a moment when people search in a very short time for information about the scenario they are experiencing. It marks a break from everyday behavior. Alert behaviors are often described by startle movements, rapid eye movements or a fixed gaze, and verbal interrogation of people close by;
- The controlled state corresponds to an emotional charge which is more or less strong. This emotional charge is regulated which is why this behavior is controlled. People can regulate their emotions, to act and adapt their behavior to the crisis context. The controlled behavior does not ensure the safety of the person or the individual’s survival. It concerns behaviors such as mutual aid, protection and care of others but also anti-social behaviors, such as theft, looting, and voyeurism;
- The panic state corresponds to a high emotional charge and a low regulation insufficient to provide a controlled behavior. Individuals in panic can adopt behaviors of panic flight, stupor, and disorderly agitation with cries of fear, for example.
2.2. Modeling the Dynamics of Human Behavior: Cross-References between the Social and Mathematical Sciences
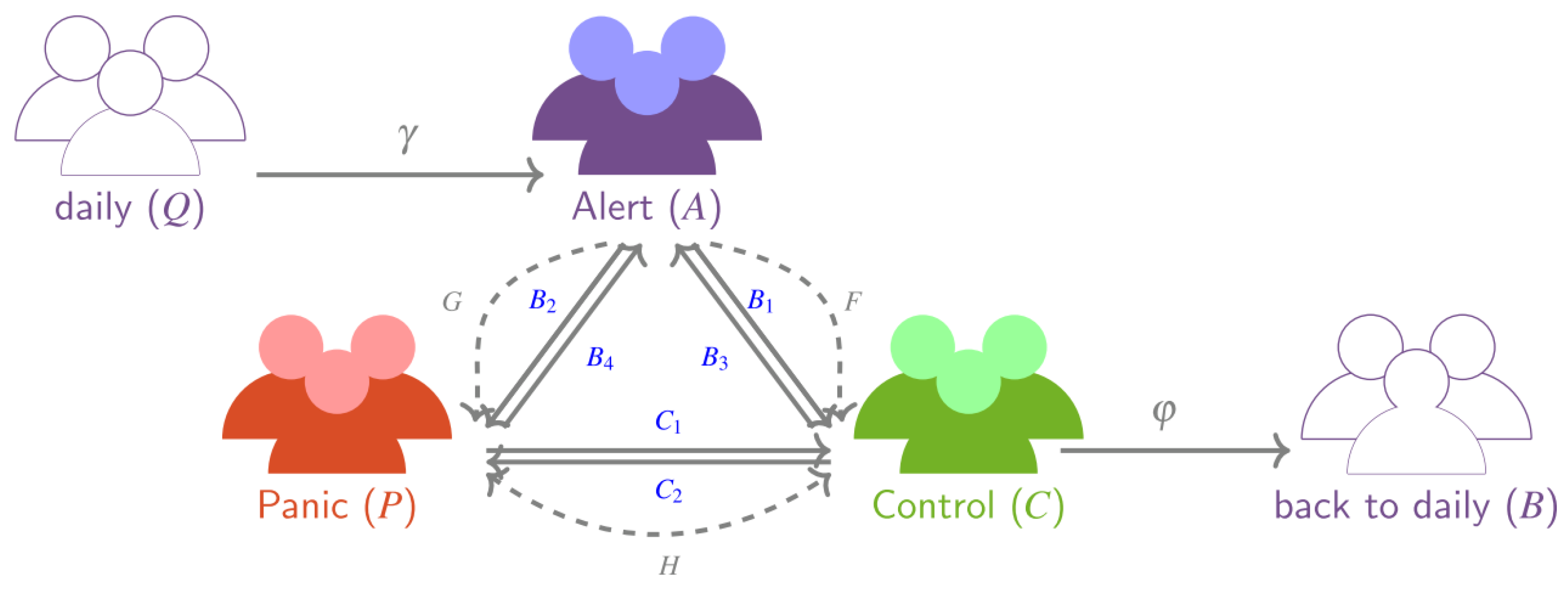
2.2.1. Structural Components of the APC Model
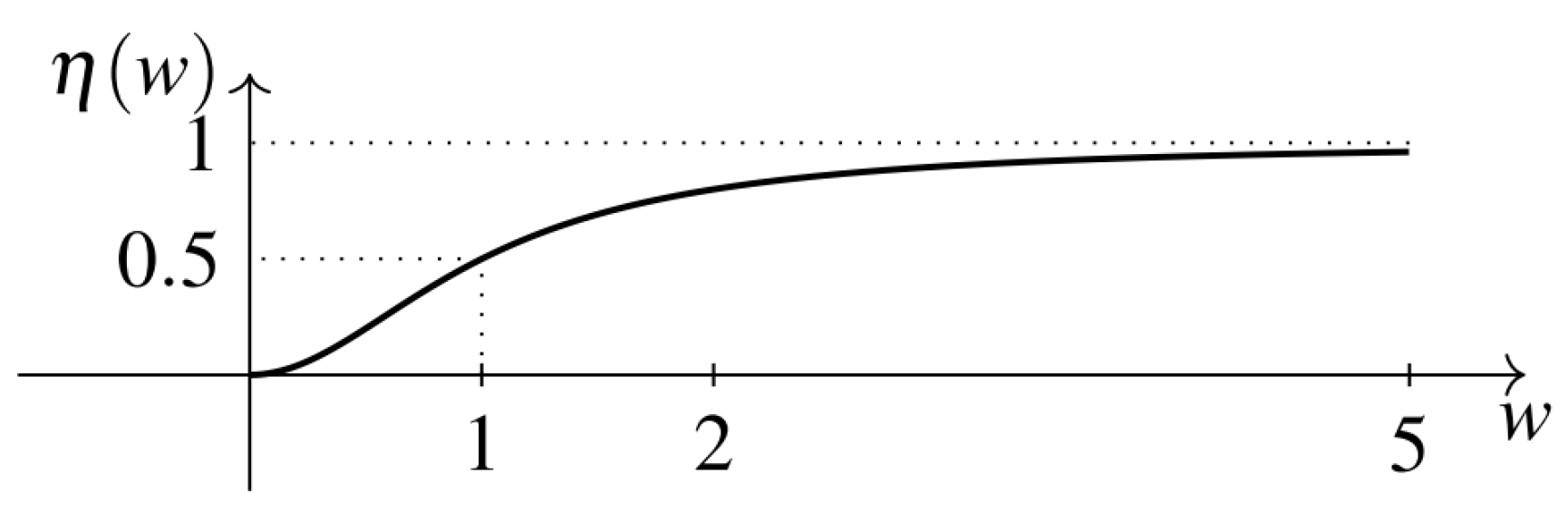
2.2.2. Imitation Processes
2.2.3. The Complete Model
3. The Virtual Reality (VR) Experiment
3.1. The VR Experimental Procedure and Sample
- First scenario (neutral scenario): in this experimental condition, the person is alone without any virtual person;
- Second scenario (organized scenario): in this experimental condition, the person is in the presence of virtual persons with a suitable behavior (escape from the tsunami by walking quickly in the right direction and without shouting);
- Third scenario (non-organized scenario): in this experimental condition, the person is in the presence of virtual persons with an unsuitable behavior (escape by running in all directions and shouting).
3.2. Measurements
4. The Link between the Mathematical Model and the Experimental Data
4.1. Observed Variables of the Mathematical Model
4.2. Modeling the Beginning and the End of the Catastrophe
5. Identifiability and Minimal Number of Observation Data
5.1. Identifiability
5.1.1. Definition
5.1.2. Method
- Functions of and are known;
- , , .
5.1.3. Identifiability of the APC Model with No Imitation
5.1.4. Identifiability of the Imitation Parameters
5.1.5. Identifiability of the Complete Model
5.2. Minimal Number of Observation Data
- 1.
- The functionis a differentiable function with respect to the first variable;
- 2.
- The function ϕ defined at Equation (11) is injective;
- 3.
- The Wronskian defined at Proposition 2 is not identically equal to zero.
- From the results of Section 3, we can conclude that a parameter estimation procedure can be implemented to estimate the intrinsic parameters using the data provided in Table 1. There is a unique parameter vector that allows the model outputs to fit the data of this table in the case of noisy-free measurements;
- One could be tempted to estimate all the parameters of the model from the second and third scenario. However, from Remark 4, order derivatives of output-polynomials are higher and there are not enough measurement points to have the local identifiability.
6. Parameter Estimation
6.1. Minimization Problem
6.2. Results
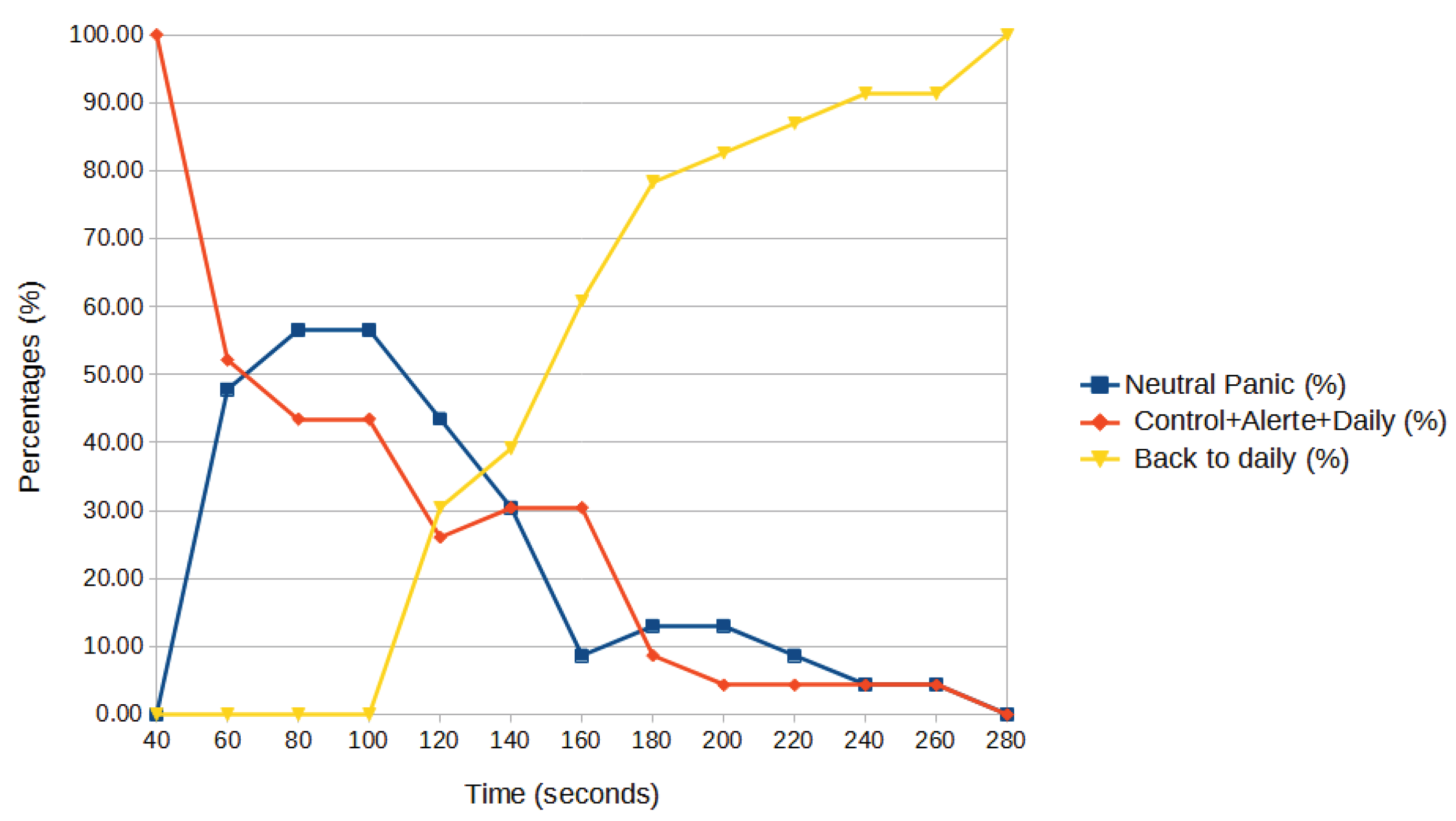
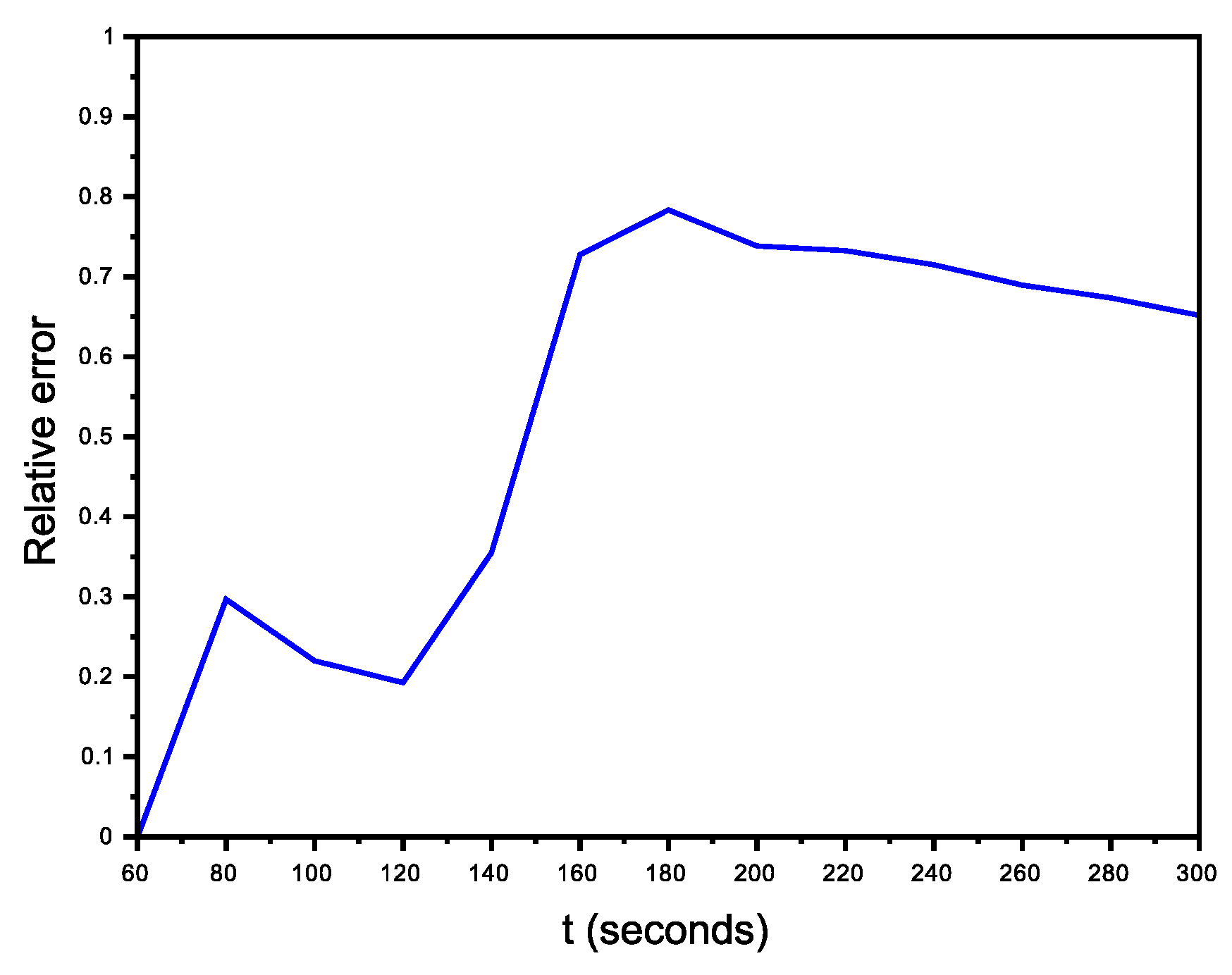
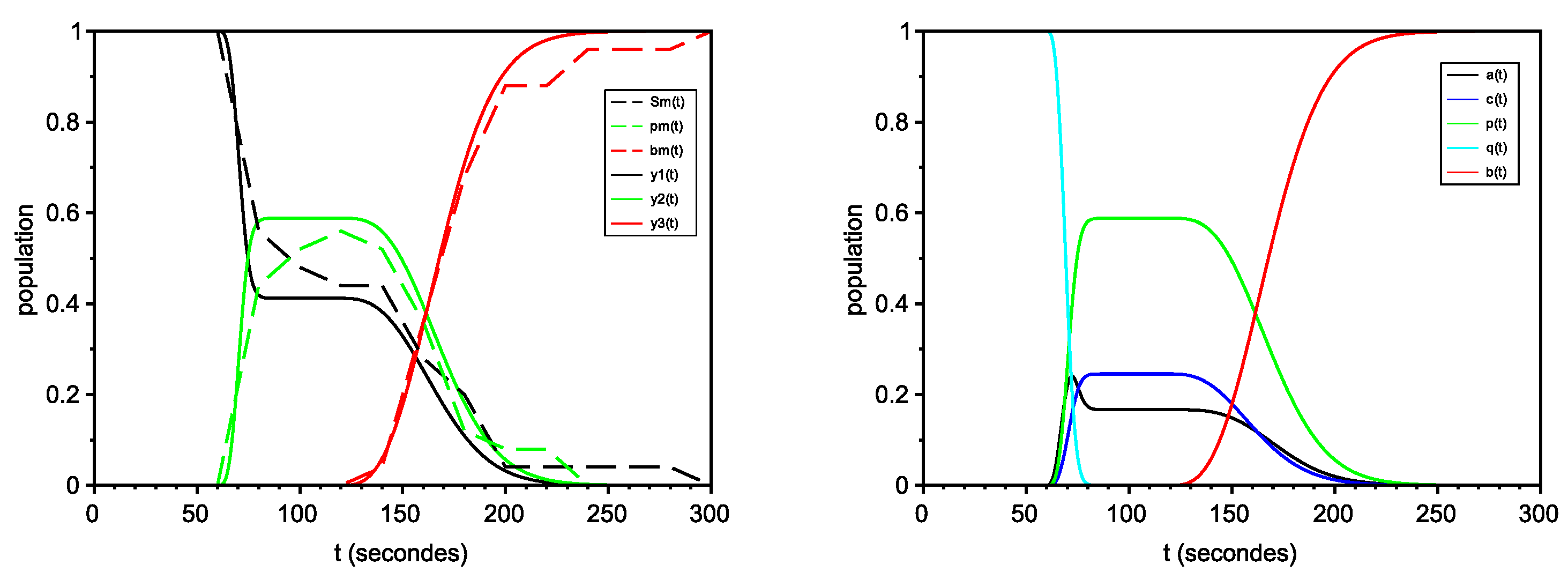
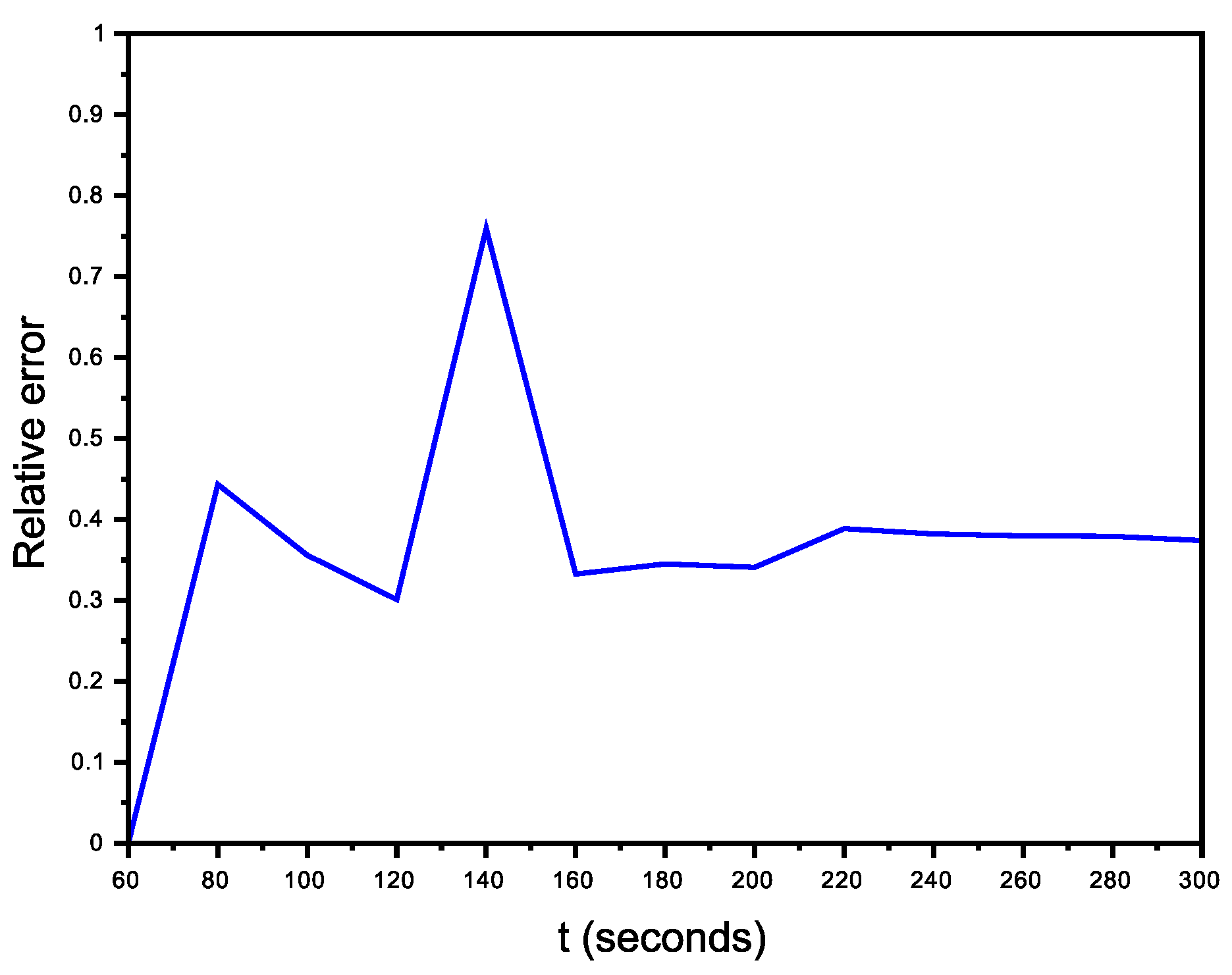
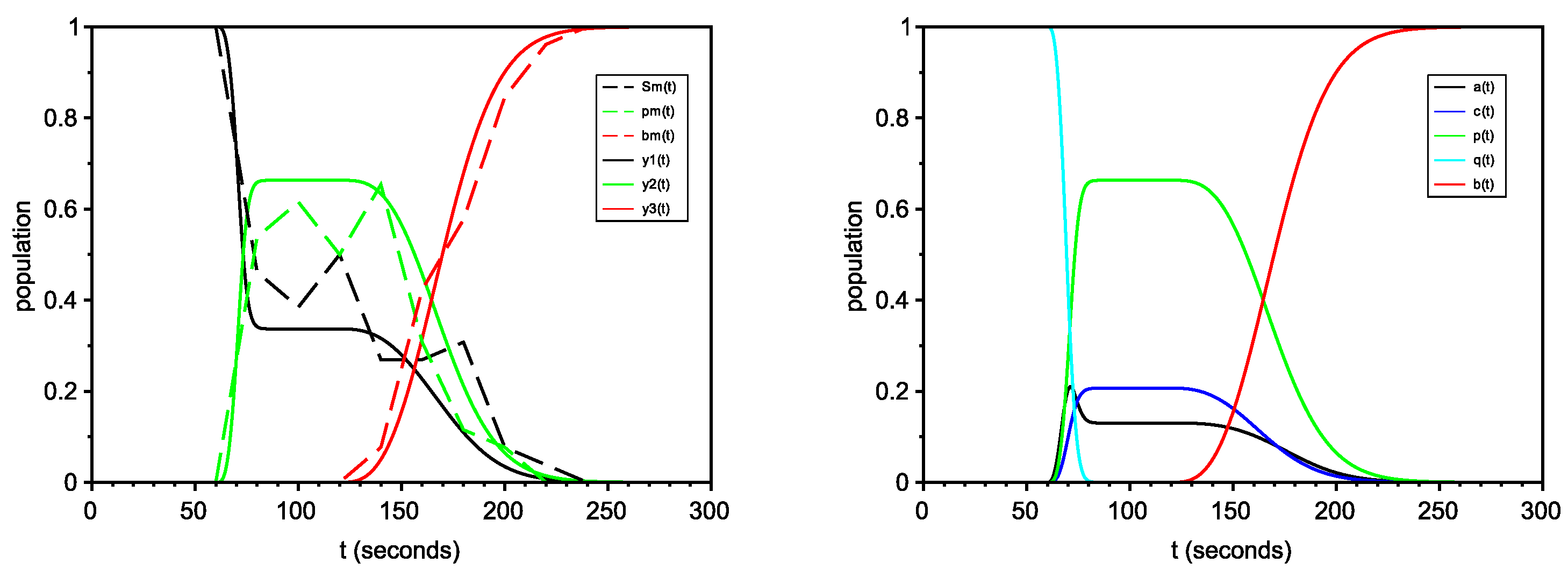
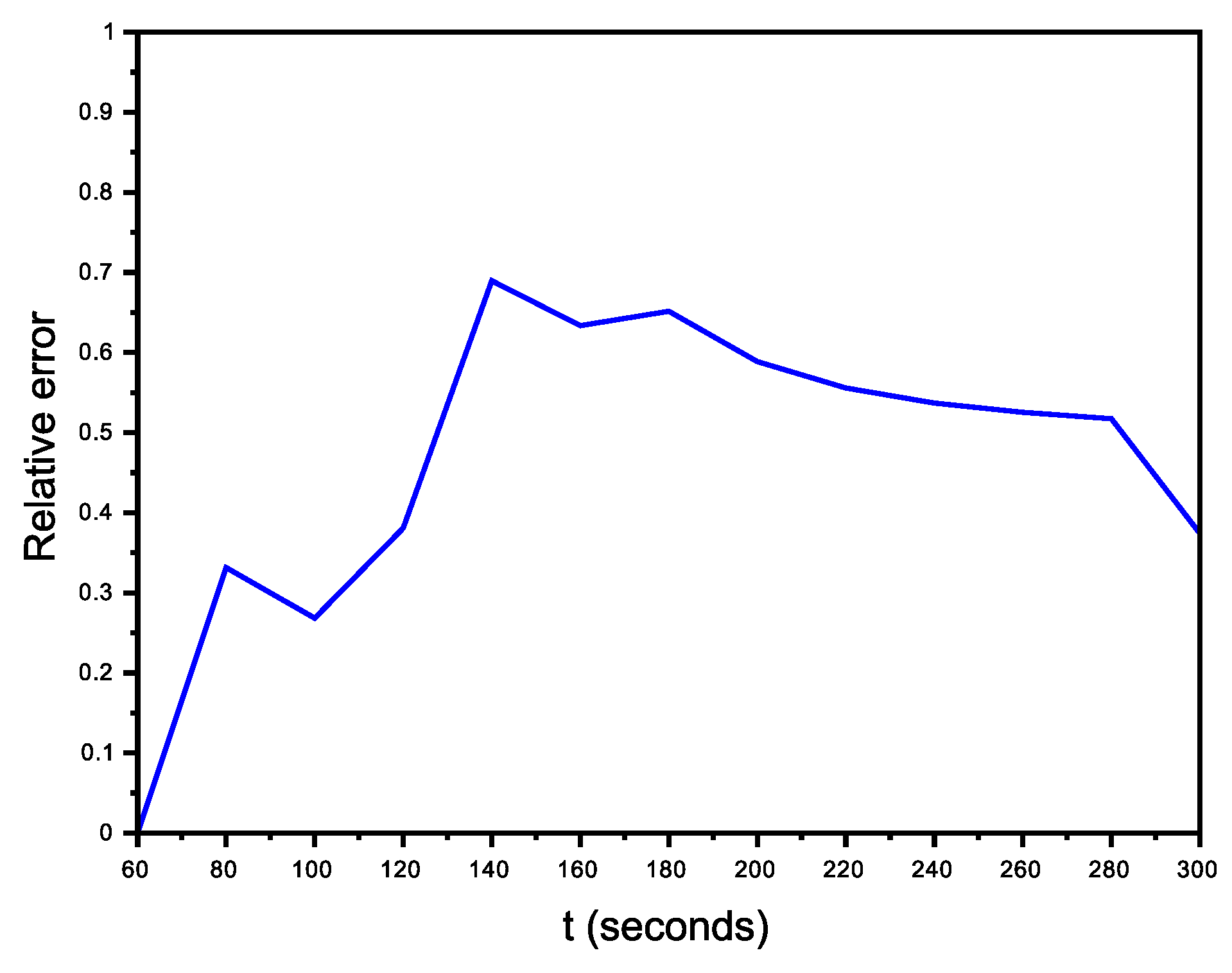
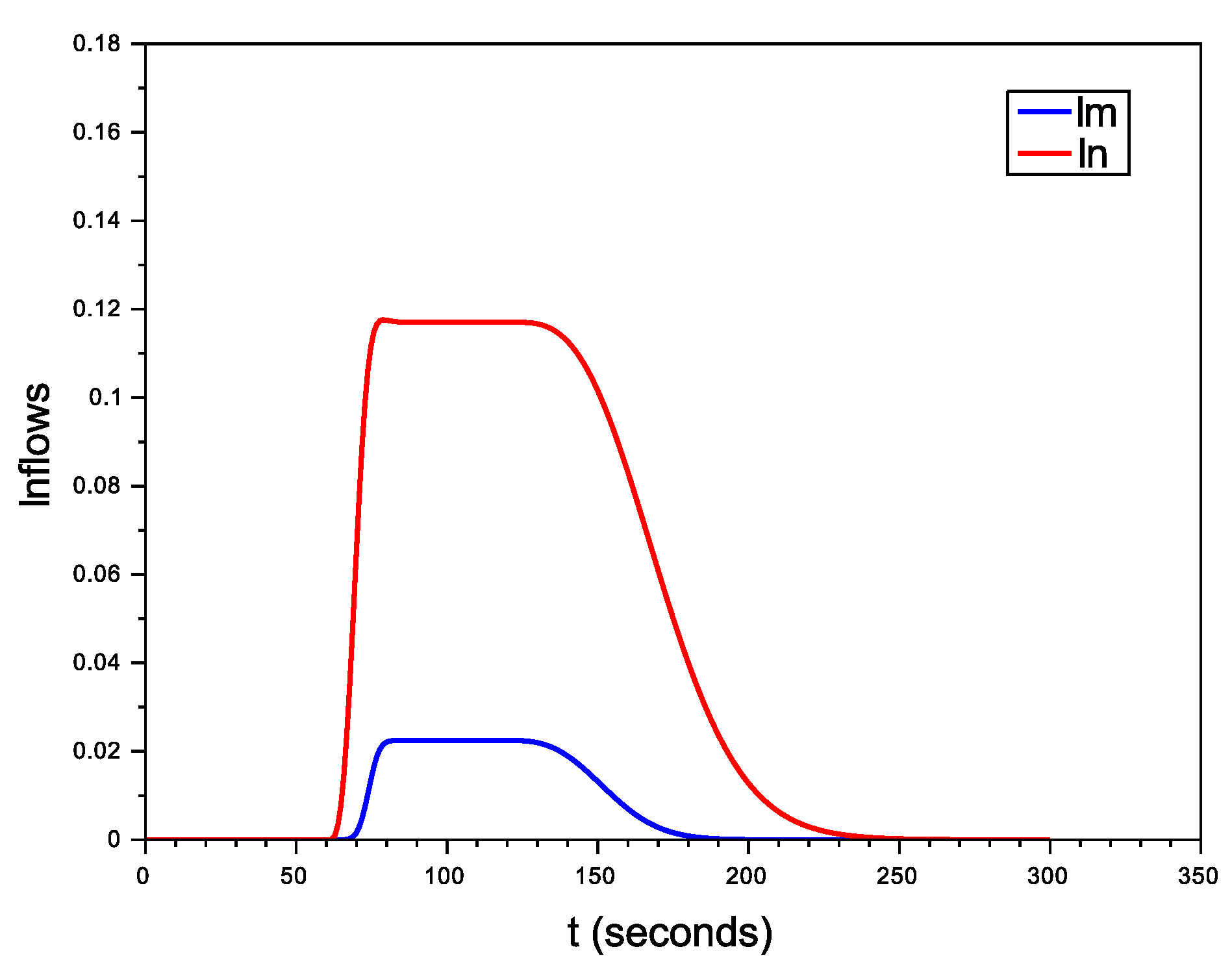
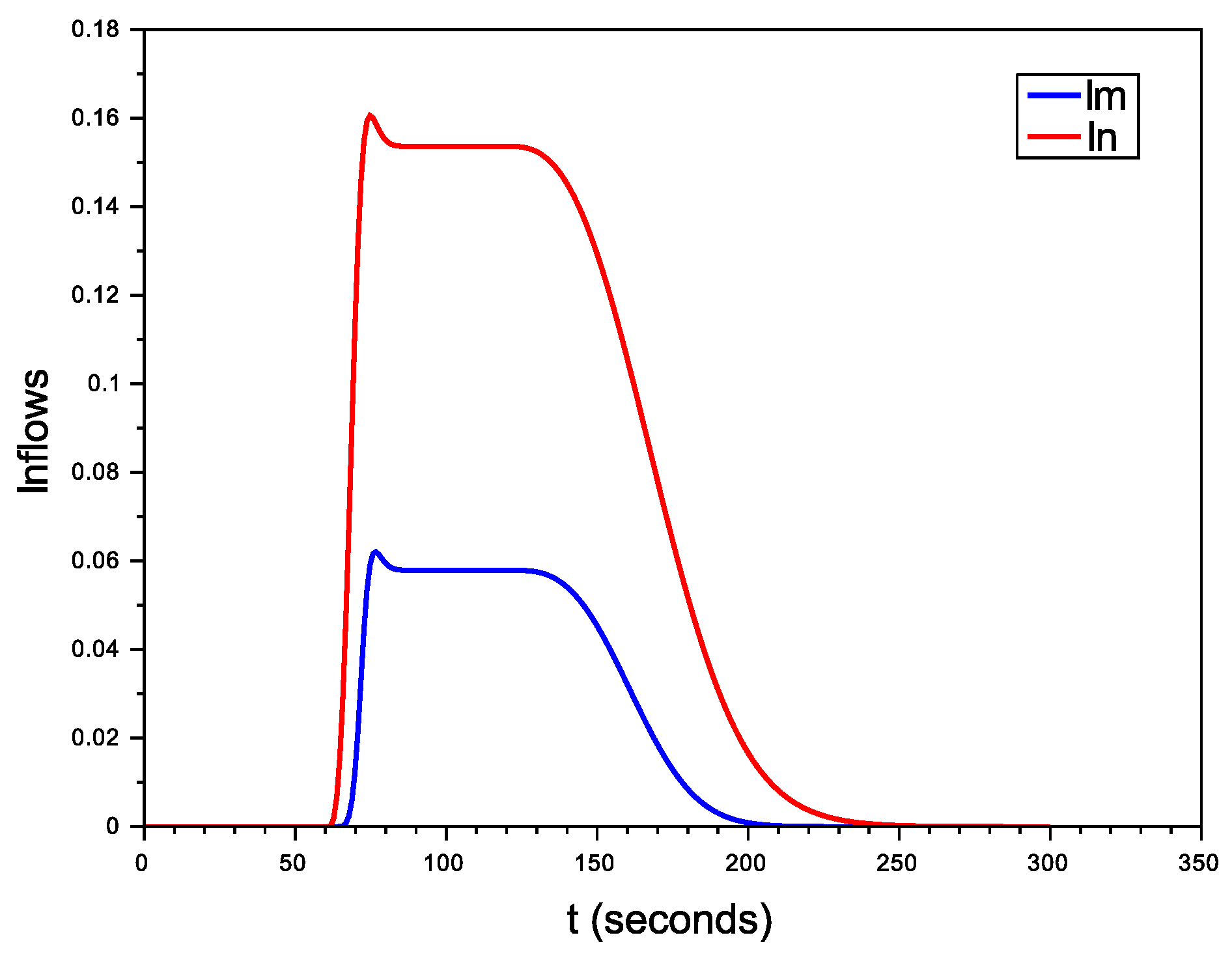
6.2.1. Scenario with No Avatars
6.2.2. Organized Scenario
6.2.3. Non-Organized Scenario
7. Conclusions and Research Perspectives
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Boschetti, L.; Provitolo, D.; Tric, E. A method to analyze territory rezilience to natural hazards, the example of the French Riviera against tsunami. In Proceedings of the EGU General Assembly Conference Abstracts, Vienna, Austria, 23–28 April 2017; Volume 19, p. 12935. [Google Scholar]
- Cantin, G.; Verdière, N.; Lanza, V.; Aziz-Alaoui, M.; Charrier, R.; Bertelle, C.; Provitolo, D.; Dubos-Paillard, E. Mathematical modeling of human behaviors during catastrophic events: Stability and bifurcations. Int. J. Bifurc. Chaos 2016, 26, 1630025. [Google Scholar] [CrossRef]
- Cornes, F.; Frank, G.; Dorso, C. Fear propagation and the evacuation dynamics. Simul. Model. Pract. Theory 2019, 95, 112–133. [Google Scholar] [CrossRef]
- Helbing, D.; Johansson, A. Pedestrian, Crowd and Evacuation Dynamics. Encycl. Complex. Syst. Sci. 2010, 16, 697–716. [Google Scholar] [CrossRef] [Green Version]
- Verdière, N.; Lanza, V.; Charrier, R.; Provitolo, D.; Dubos-Paillard, E.; Bertelle, C.; Aziz-Alaoui, M. Mathematical modeling of human behaviors during catastrophic events. In Proceedings of the International Conference on Complex Systems and Applications, Le Havre, France, 23–26 June 2014; pp. 67–74. [Google Scholar]
- Provitolo, D.; Dubos-Paillard, E.; Muller, J.P. Emergent human behaviour during a disaster: Thematic versus complex systems approaches. In Proceedings of the European Conference on Complex System, Vienna, Austria, 15 September 2011; pp. 1–11. [Google Scholar]
- Reghezza-Zitt, M.; Rufat, S. Resilience Imperative: Uncertainty, Risks and Disasters; Elsevier: Amsterdam, The Netherlands, 2015. [Google Scholar]
- Venel, J. Mathematical and Numerical Modelling of Crowd Motion. Ph.D. Thesis, Université Paris Sud—Paris XI, Orsay, France, 2008. [Google Scholar]
- Verdière, N.; Cantin, G.; Provitolo, D.; Lanza, V.; Dubos-Paillard, E.; Charrier, R.; Aziz-Alaoui, M.; Bertelle, C. Understanding and simulation of human behaviors in areas affected by disasters: From the observation to the conception of a mathematical model. Glob. J. Hum. Soc. Sci. 2015, 15, 7–15. [Google Scholar]
- Lanza, V.; Charrier, R.; Verdière, N.; Dubos-Paillard, E.; Navarro, O.; Provitolo, D.; Bertelle, C.; Cantin, G.; Aziz-Alaoui, M. Mathematical and geographical approach in the modeling of a network of human behavioral systems. In Proceedings of the XTerM2019, Le Havre, France, 26–28 June 2019. [Google Scholar]
- Wheatley, T.; Wegner, D.M. Psychology of Automaticity of Action. In International Encyclopedia of the Social and Behavioral Sciences; Elsevier: Amsterdam, The Netherlands, 2001. [Google Scholar]
- Zachariadis, V.; Amos, J.; Kohn, B. Simulating Pedestrian Route Choice Behaviour under Transient Traffic Conditions; Emerald Group Publishing Limited: Bingley, UK, 2009; pp. 113–135. [Google Scholar] [CrossRef]
- Zeng, Z.; Nakamura, H.; Chen, P. The 9th International Conference on Traffic and Transportation Studies (ICTTS 2014). A Modified Social Force Model for Pedestrian Behavior Simulation at Signalized Crosswalks. Procedia-Soc. Behav. Sci. 2014, 138, 521–530. [Google Scholar] [CrossRef] [Green Version]
- Mehdi, M.; Kapadia, M.; Thrash, T.; Sumner, R.; Gross, M.; Helbing, D.; Holscher, C. Crowd behaviour during high-stress evacuations in an immersive virtual environment. J. R. Soc. Interface 2016, 13, 20160414. [Google Scholar] [CrossRef]
- Mao, Y.; Fan, Z.; Zhao, J.; Zhang, Q.; He, W. An emotional contagion based simulation for emergency evacuation peer behavior decision. Simul. Model. Pract. Theory 2019, 96, 101936. [Google Scholar] [CrossRef]
- Selye, H. Stress in Health and Disease; Butterworths: Boston, MA, USA, 1976. [Google Scholar]
- Daly, A.C.; Gavaghan, D.; Cooper, J.; Tavener, S. Inference-based assessment of parameter identifiability in nonlinear biological models. J. R. Soc. Interface 2018, 15, 20180318. [Google Scholar] [CrossRef] [PubMed]
- Villaverde, A.F.; Tsiantis, N.; Banga, J.R. Full observability and estimation of unknown inputs, states and parameters of nonlinear biological models. J. R. Soc. Interface 2019, 16, 20190043. [Google Scholar] [CrossRef] [Green Version]
- Haupt, R.L.; Haupt, S.E. Practical Genetic Algorithms, 2nd ed.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2003. [Google Scholar]
- Russell, J.A. A circumplex model of affect. J. Personal. Soc. Psychol. 1980, 39, 1161–1178. [Google Scholar] [CrossRef]
- Gross, J.J. Emotion Regulation: Current Status and Future Prospects. Psychol. Inq. 2015, 26, 1–26. [Google Scholar] [CrossRef]
- Gratz, K.; Roemer, L. Multidimensional Assessment of Emotion Regulation and Dysregulation: Development, Factor Structure, and Initial Validation of the Difficulties in Emotion Regulation Scale. J. Psychopathol. Behav. Assess. 2004, 26, 41–54. [Google Scholar] [CrossRef]
- Kaufman, E.A.; Xia, M.; Fosco, G.; Yaptangco, M.; Skidmore, C.R.; Crowell, S.E. The difficulties in emotion regulation scale short form (DERS-SF): Validation and replication in adolescent and adult samples. J. Psychopathol. Behav. Assess. 2015, 38, 443–455. [Google Scholar] [CrossRef]
- Festinger, L. A Theory of Social Comparison Processes. Hum. Relations 1954, 7, 117–140. [Google Scholar] [CrossRef]
- Bargh, J.A.; Chen, M.; Burrows, L. Automaticity of social behavior: Direct effects of trait construct and stereotype activation on action. J. Personal. Soc. Psychol. 1996, 71, 230–244. [Google Scholar] [CrossRef]
- Gao, L.Q.; Hethcote, H.W. Disease transmission models with density-dependent demographics. J. Math. Biol. 1992, 30, 717–731. [Google Scholar] [CrossRef] [PubMed]
- Boschetti, L.; Mansour, I.; Provitolo, D.; Tric, E.; Grilli, S.; Nemati, F.; Larroque, C. The Mediterranean French coastal exposed to tsunami risk: From hazard to territorial vulnerability studies. In Proceedings of the AAG 2019, Washington, DC, USA, 3–7 April 2019. [Google Scholar]
- Verhulst, E.; Richard, P.; Provitolo, D.; Navarro, O. Virtual Tsunami: Navigation technique and user behavior analysis during emergency. In Proceedings of the 1st International Conference for Multi-Area Simulation—ICMASim, Angers, France, 8–10 October 2019. [Google Scholar]
- Laborde, S.; Mosley, E.; Thayer, J. Heart Rate Variability and Cardiac Vagal Tone in Psychophysiological Research—Recommendations for Experiment Planning, Data Analysis, and Data Reporting. Front. Psychol. 2017, 8, 213. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Boonnithi, S.; Phongsuphap, S. Comparison of heart rate variability measures for mental stress detection. In Proceedings of the 2011 Computing in Cardiology, Hangzhou, China, 18–21 September 2011; Volume 38. [Google Scholar]
- Navarro, O.; Krien, N.; Rommel, D.; Deledalle, A.; Lemée, C.; Coquet, M.; Mercier, D.; Fleury-Bahi, G. Coping strategies regarding coastal flooding risk in a context of climate change in a French Caribbean island. Environ. Behav. 2020, 53, 636–660. [Google Scholar] [CrossRef]
- Denis-Vidal, L.; Joly-Blanchard, G.; Noiret, C.; Petitot, M. An algorithm to test identifiability of non-linear systems. In Proceedings of the 5th IFAC NOLCOS, St. Petersburg, Russia, 4–6 July 2001; Volume 7, pp. 174–178. [Google Scholar]
- Verdière, N.; Orange, S. A systematic approach for doing an a priori identifiability study of dynamical nonlinear models. Math. Biosci. 2019, 308, 105–113. [Google Scholar] [CrossRef]
- Miao, H.; Xia, X.; Perelson, A.S.; Wu, H. On identifiability of nonlinear ODE models and applications in viral dynamics. SIAM Rev. 2011, 53, 3–39. [Google Scholar] [CrossRef] [PubMed]
- Xia, X.; Moog, C.H. Identifiability of nonlinear systems with application to HIV/AIDS models. IEEE Trans. Autom. Control 2003, 48, 330–336. [Google Scholar] [CrossRef]
- Kiranyaz, S.; Ince, T.; Gabbouj, M. Optimization Techniques: An Overview; Springer: Berlin/Heidelberg, Germany, 2014. [Google Scholar]
- Walter, E.; Pronzato, L. Identification of Parametric Models from Experimental Data; Springer: Berlin/Heidelberg, Germany, 1997. [Google Scholar]
- Kazarlis, S.A.; Papadakis, S.E.; Theocharis, J.B.; Petridis, V. Microgenetic algorithms as generalized hill-climbing operators for GA optimization. IEEE Trans. Evol. Comput. 2001, 5, 204–217. [Google Scholar] [CrossRef]
- Gen, M.; Cheng, R. Genetic Algorithms and Engineering Optimization; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 1999. [Google Scholar]





| Sex | |||
|---|---|---|---|
| Condition | Women | Men | Total |
| First scenario | 14 | 15 | 29 |
| Organized scenario | 15 | 15 | 30 |
| Non organized scenario | 14 | 15 | 29 |
| Total | 43 | 45 | 88 |
| Times (s) | 40 | 60 | 80 | 0. 100 | 120 | 140 | 160 | 180 | 200 | 220 | 240 | 260 | 280 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Neutral | P (%) | 0.00 | 47.83 | 56.52 | 56.52 | 43.48 | 30.43 | 8.70 | 13.04 | 13.04 | 8.70 | 4.35 | 4.35 | 0.00 |
| EAC (%) | 100.00 | 52.17 | 43.48 | 43.48 | 26.09 | 30.43 | 30.43 | 8.70 | 4.35 | 4.35 | 4.35 | 4.35 | 0.00 | |
| BD (%) | 0.00 | 0.00 | 0.00 | 0.00 | 30.43 | 39.13 | 60.87 | 78.26 | 82.61 | 86.96 | 91.30 | 91.30 | 100.00 | |
| Organized | P (%) | 0.00 | 44.00 | 52.00 | 56.00 | 52.00 | 36.00 | 12.00 | 8.00 | 8.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| EAC (%) | 100.00 | 56.00 | 48.00 | 44.00 | 44.00 | 28.00 | 20.00 | 4.00 | 4.00 | 4.00 | 4.00 | 4.00 | 0.00 | |
| BD (%) | 0.00 | 0.00 | 0.00 | 0.00 | 4.00 | 36.00 | 68.00 | 88.00 | 88.00 | 96.00 | 96.00 | 96.00 | 100.00 | |
| Non | P (%) | 0.00 | 53.85 | 61.54 | 50.00 | 65.38 | 30.77 | 11.54 | 7.69 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| Organized | EAC (%) | 100.00 | 46.15 | 38.46 | 50.00 | 26.92 | 26.92 | 30.77 | 7.69 | 3.85 | 0.00 | 0.00 | 0.00 | 0.00 |
| BD (%) | 0.00 | 0.00 | 0.00 | 0.00 | 7.69 | 42.31 | 57.69 | 84.62 | 96.15 | 100.00 | 100.00 | 100.00 | 100.00 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Verdière, N.; Navarro, O.; Naud, A.; Berred, A.; Provitolo, D. Towards Parameter Identification of a Behavioral Model from a Virtual Reality Experiment. Mathematics 2021, 9, 3175. https://doi.org/10.3390/math9243175
Verdière N, Navarro O, Naud A, Berred A, Provitolo D. Towards Parameter Identification of a Behavioral Model from a Virtual Reality Experiment. Mathematics. 2021; 9(24):3175. https://doi.org/10.3390/math9243175
Chicago/Turabian StyleVerdière, Nathalie, Oscar Navarro, Aude Naud, Alexandre Berred, and Damienne Provitolo. 2021. "Towards Parameter Identification of a Behavioral Model from a Virtual Reality Experiment" Mathematics 9, no. 24: 3175. https://doi.org/10.3390/math9243175
APA StyleVerdière, N., Navarro, O., Naud, A., Berred, A., & Provitolo, D. (2021). Towards Parameter Identification of a Behavioral Model from a Virtual Reality Experiment. Mathematics, 9(24), 3175. https://doi.org/10.3390/math9243175








