Prediction of Hydraulic Jumps on a Triangular Bed Roughness Using Numerical Modeling and Soft Computing Methods
Abstract
:1. Introduction
2. Materials and Methods
2.1. Dimensional Analysis
2.2. The FLOW-3D® Model
2.2.1. Turbulence Model
2.2.2. Boundary Conditions
2.2.3. Checking Stability and Convergence Criterion
2.2.4. Numerical Domain
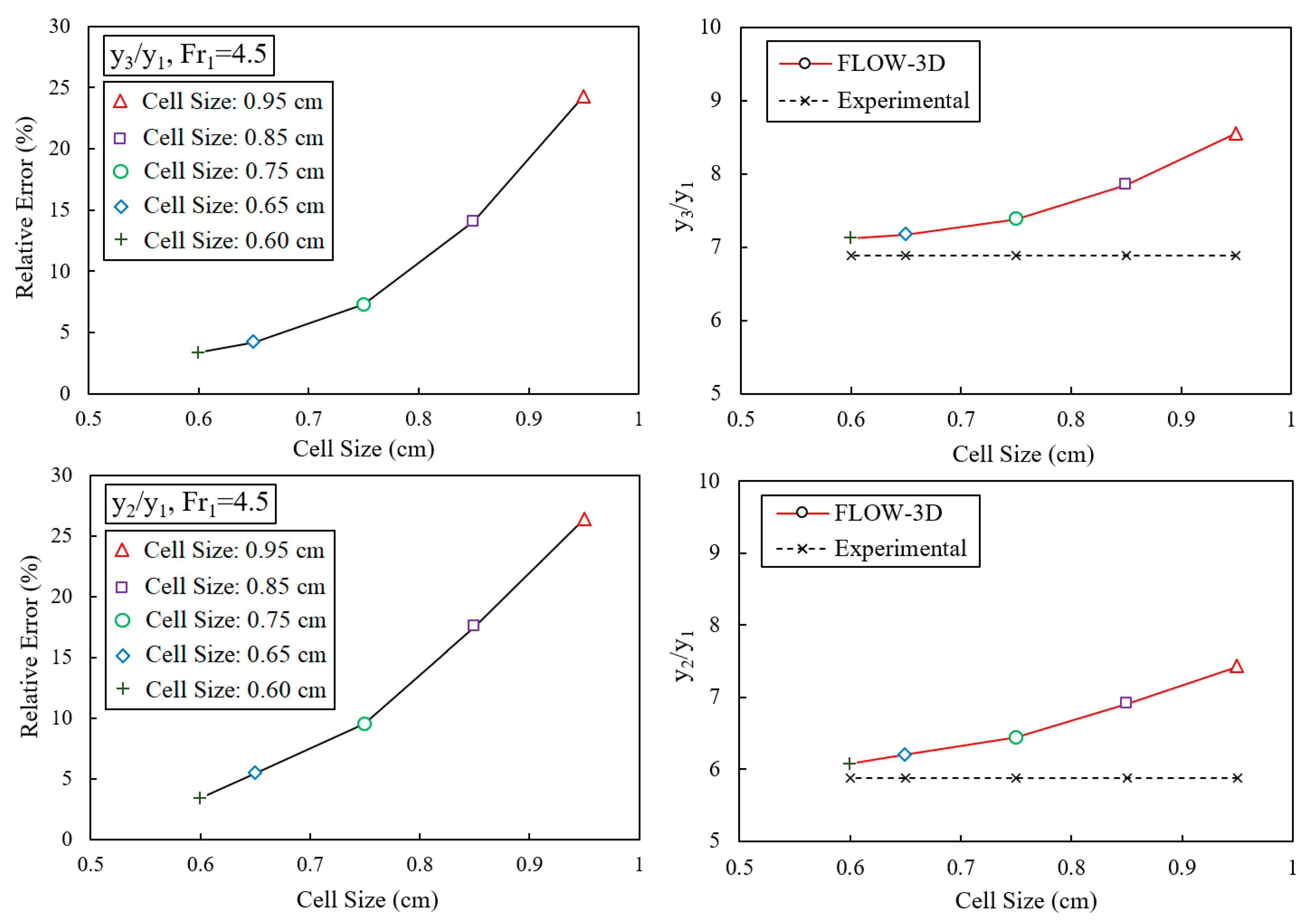
2.2.5. Mesh Size Sensitivity Analysis
2.3. Artificial Intelligence Methods
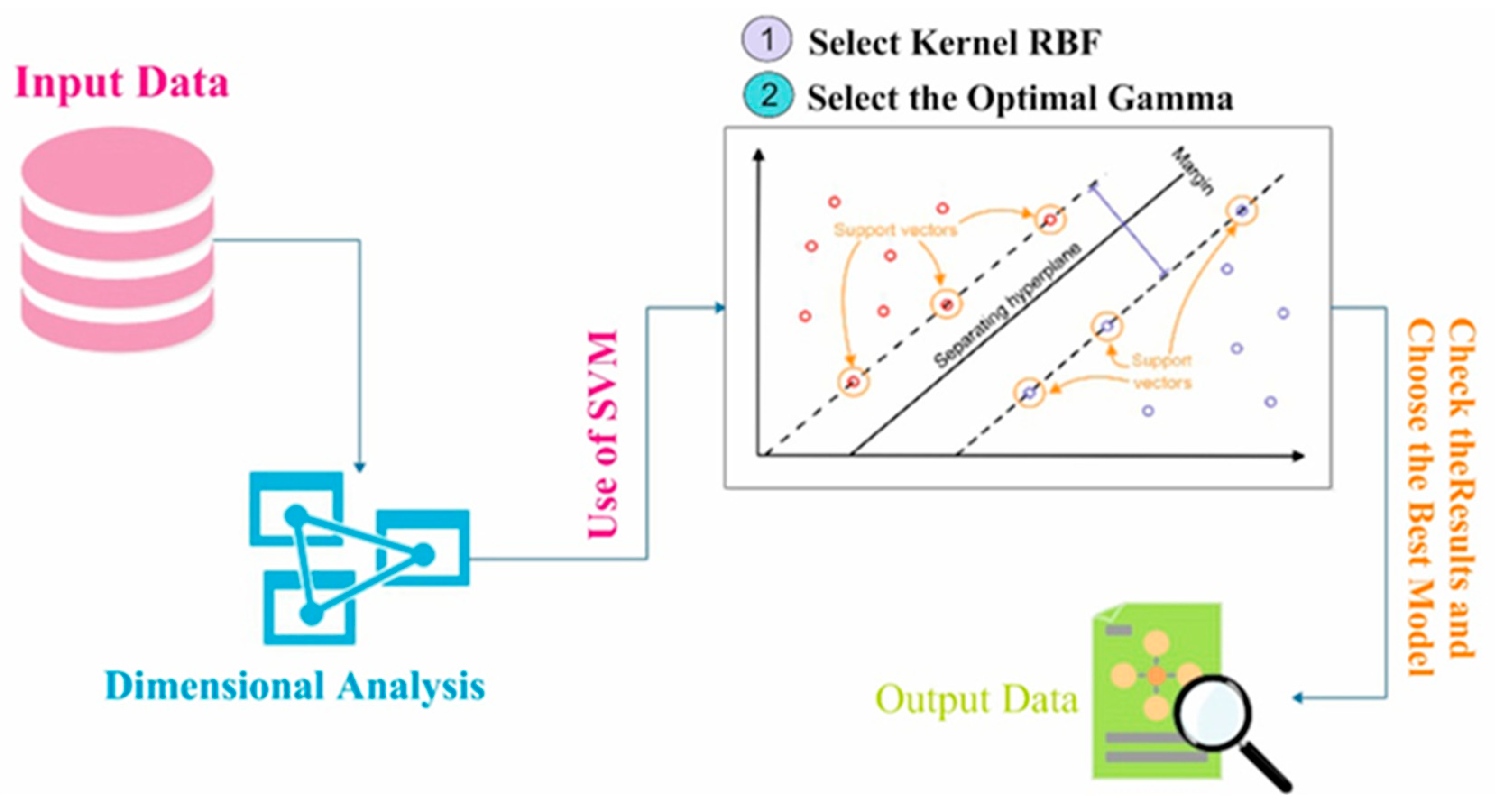
2.3.1. Support Vector Machine (SVM)
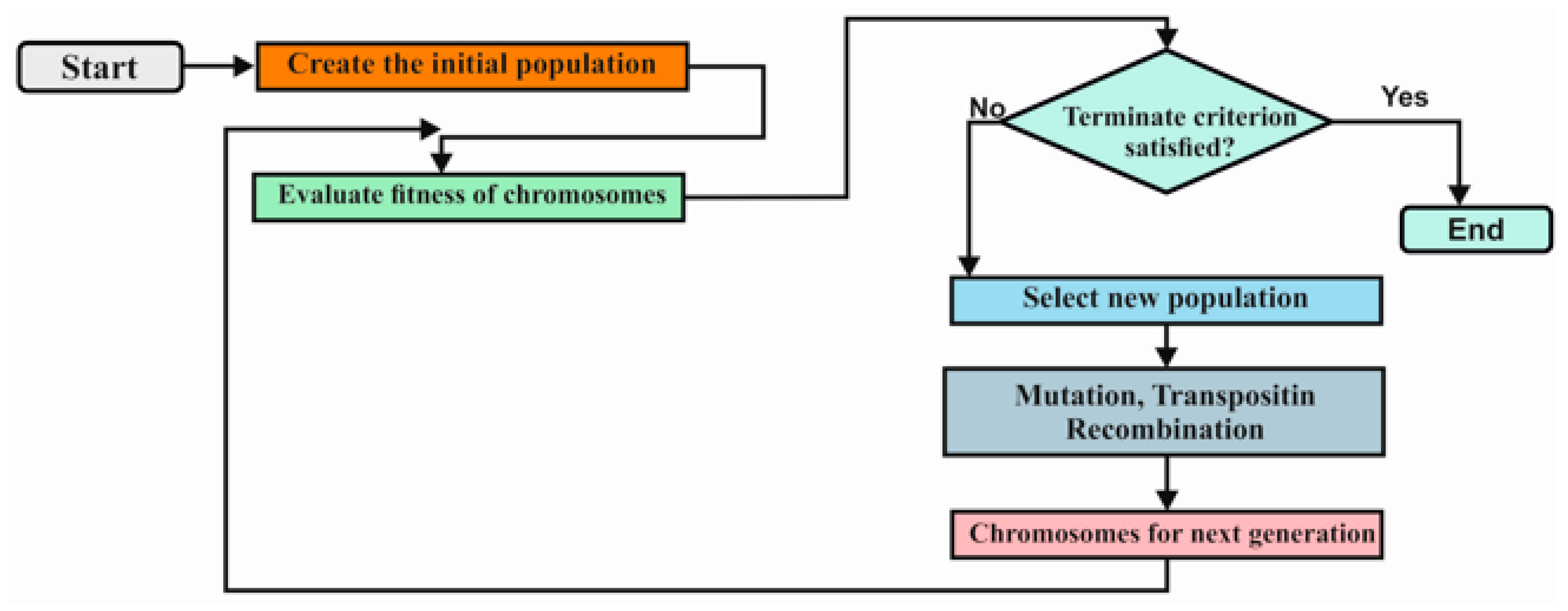
2.3.2. Gene Expression Programming (GEP)
2.3.3. Random Forest (RF)
2.4. Evaluation Criteria
3. Results
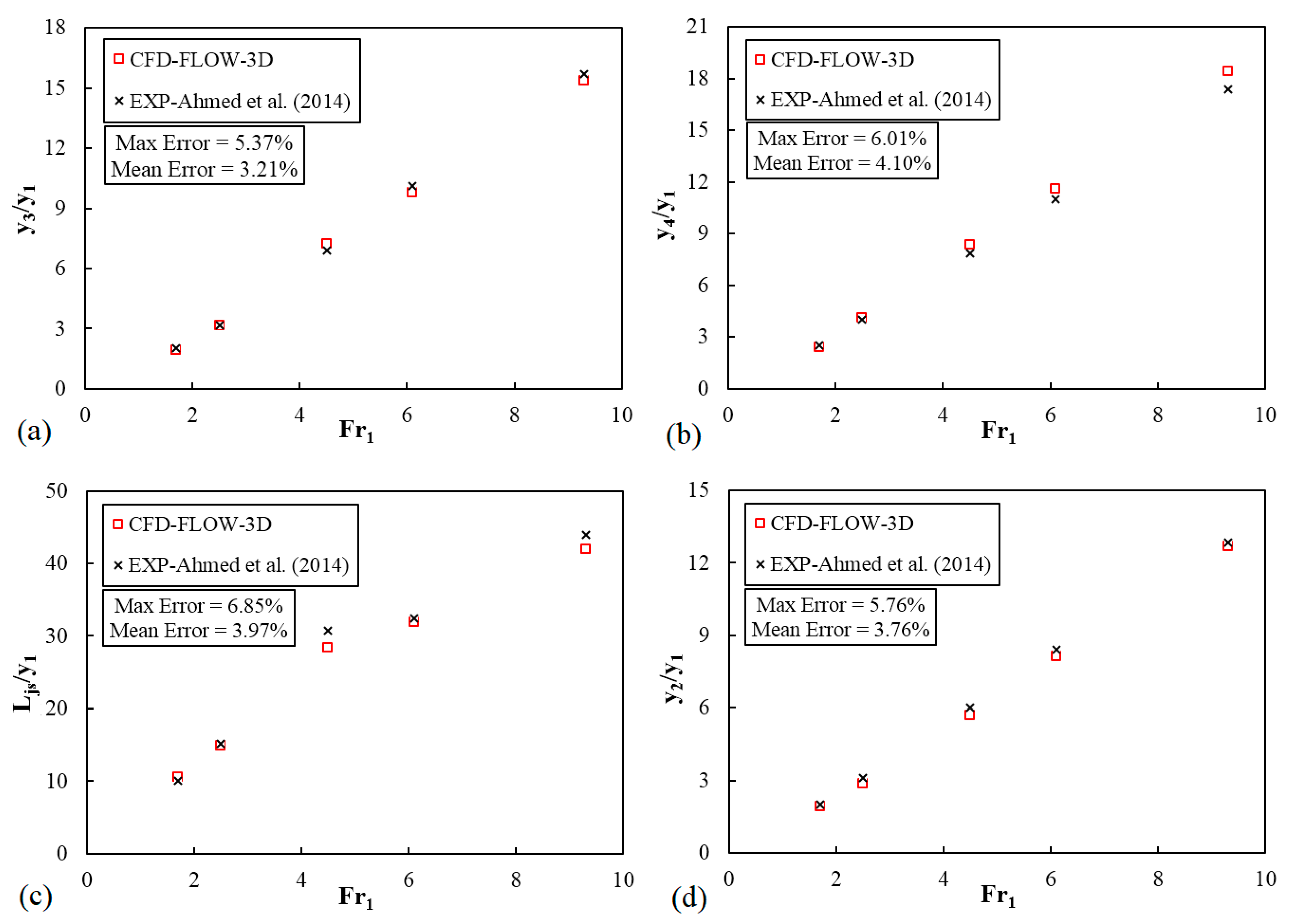
3.1. Validity of the FLOW-3D® Model Results
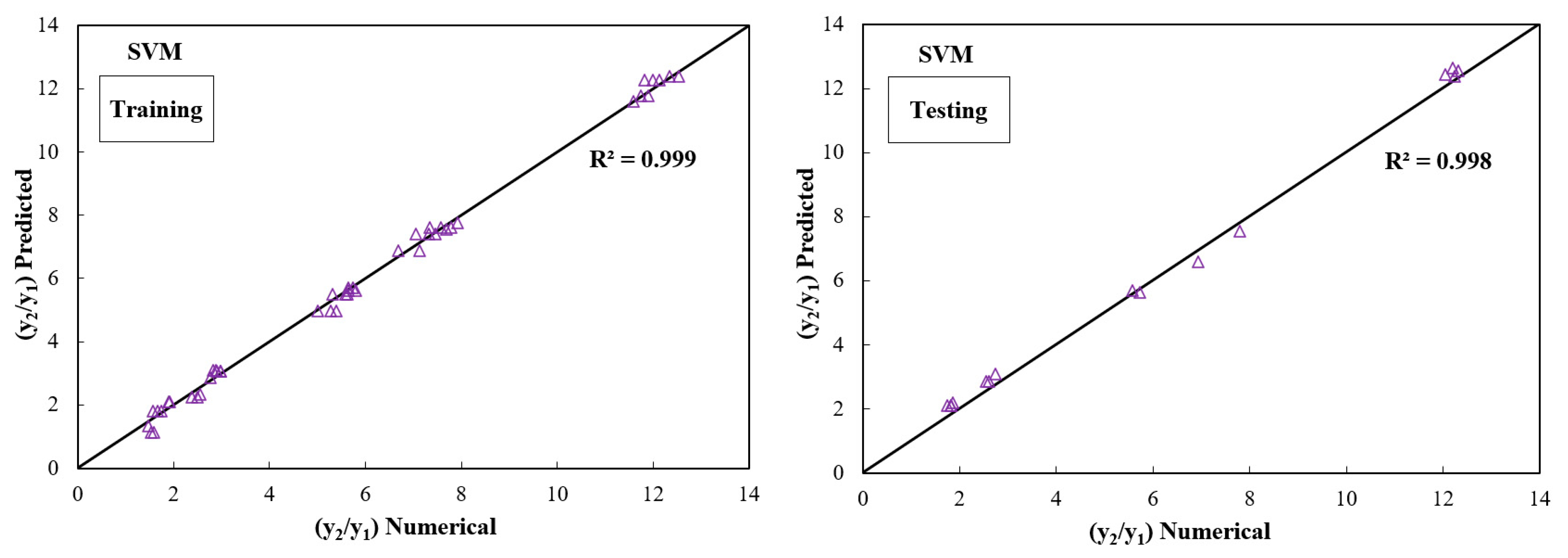
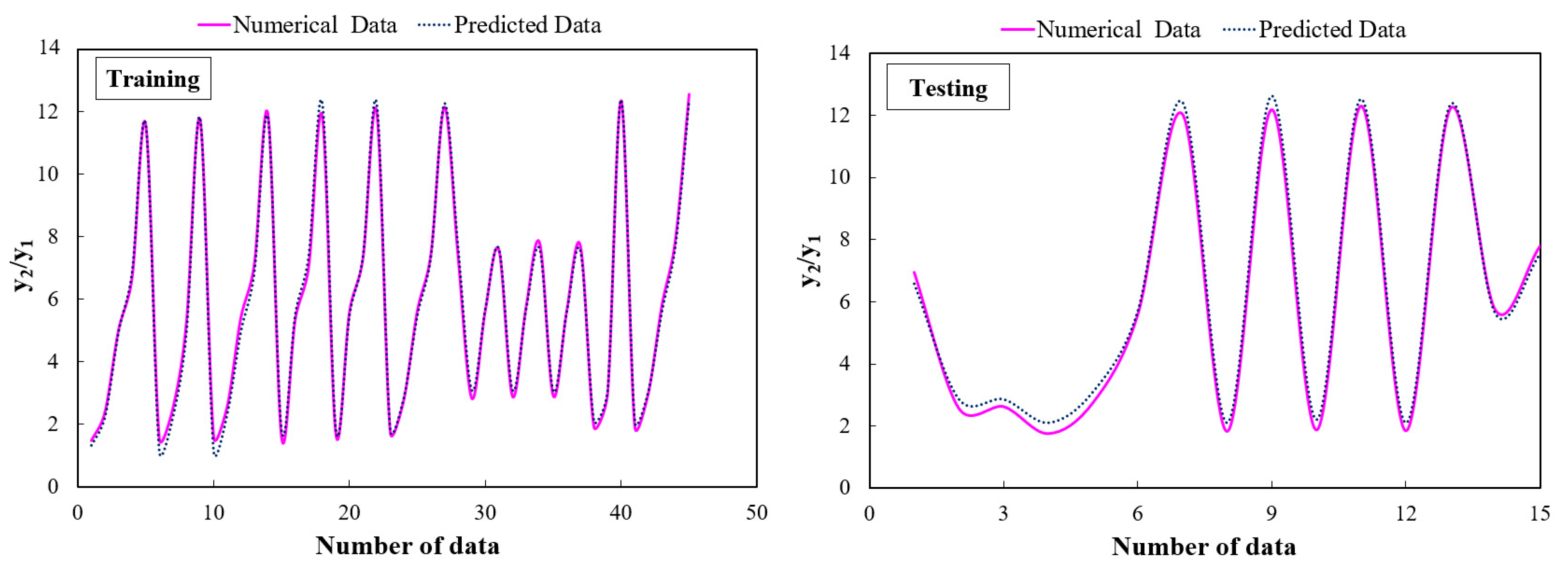
3.2. Sequent Depth Ratio in the Free Jump (y2/y1)
3.3. Submerged Depth Ratio in Submerged Jump (y3/y1)
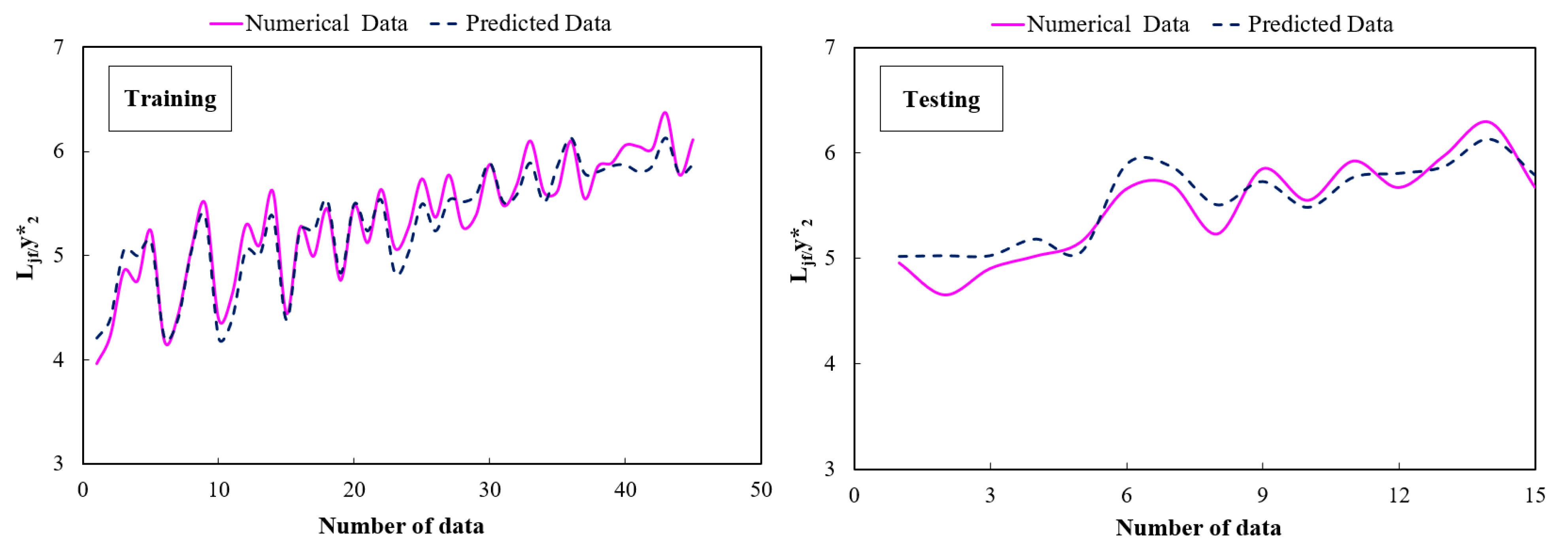
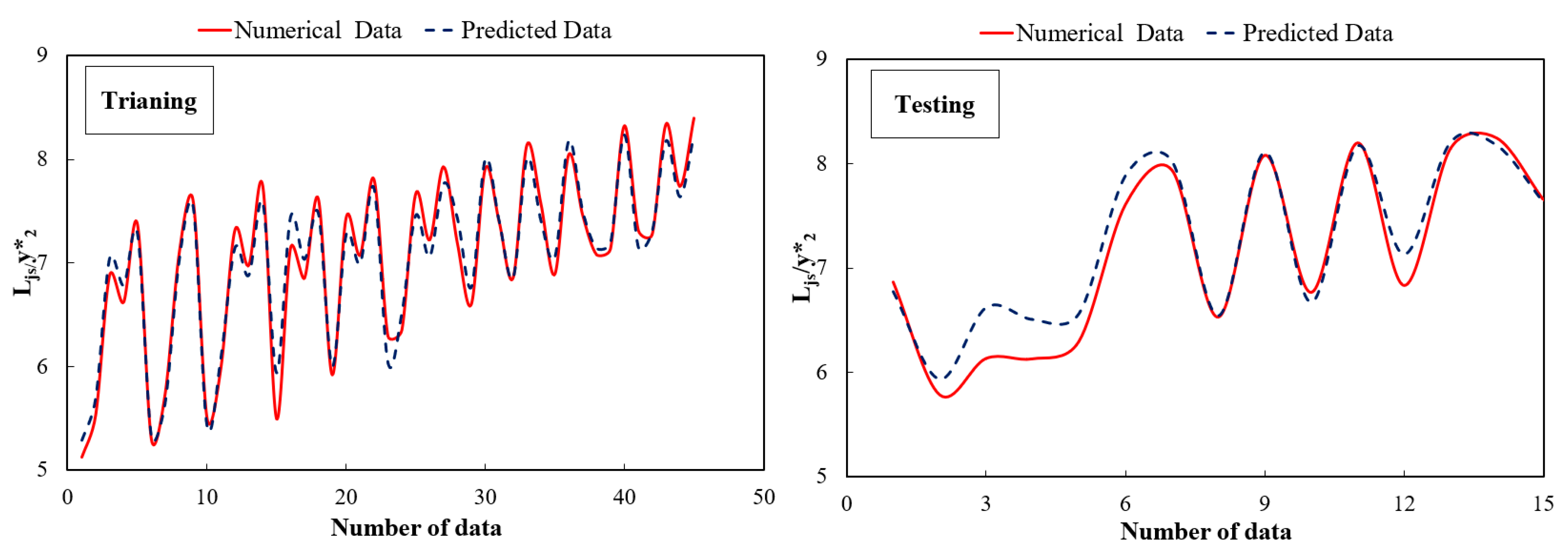
3.4. The Length Ratio of Jumps (/)
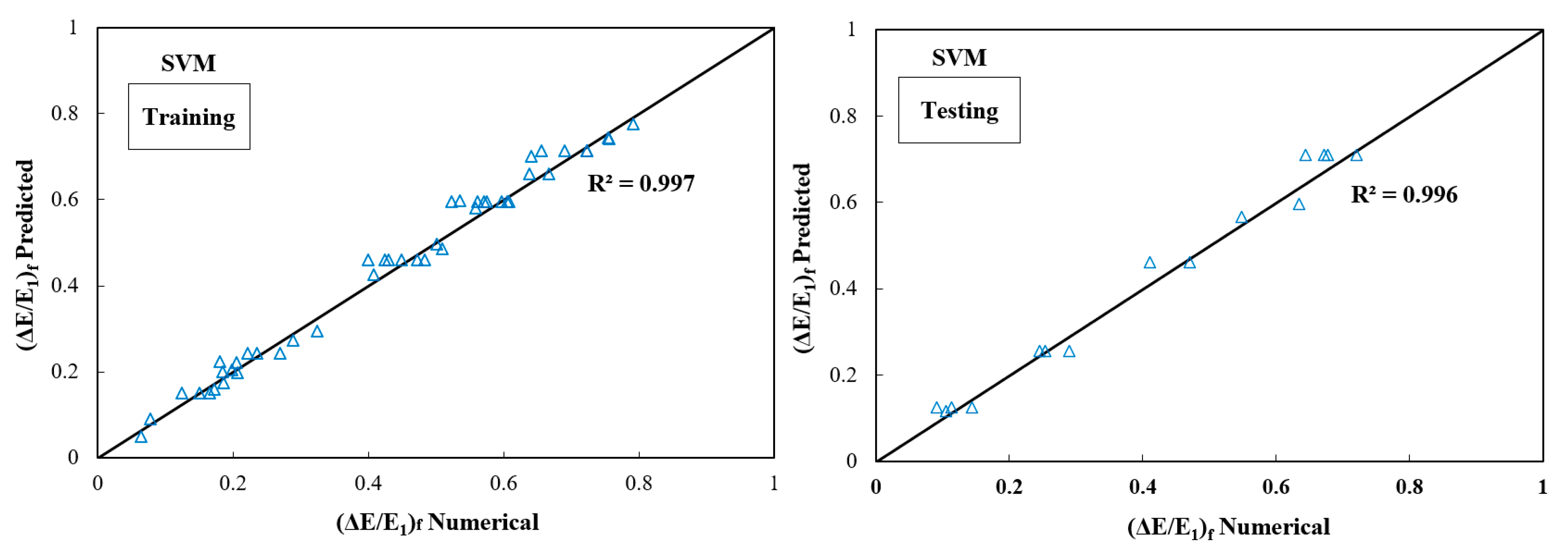
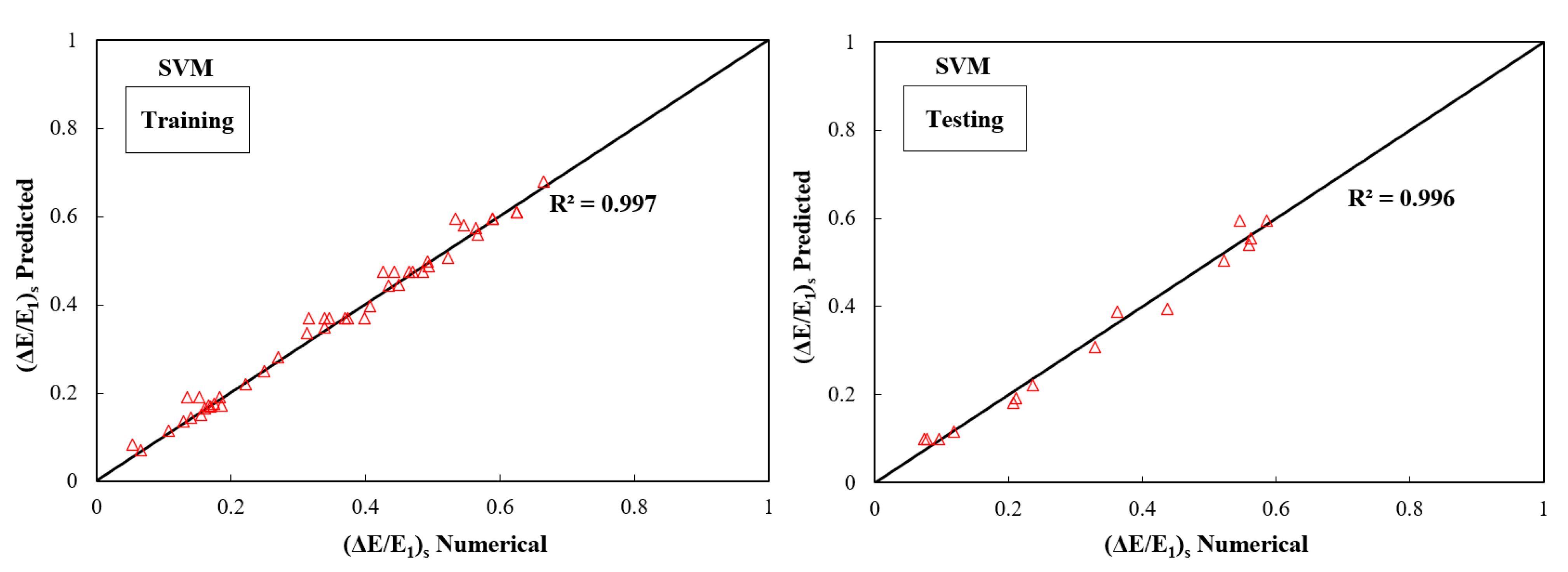
3.5. The Energy Dissipation (ΔE/E1)
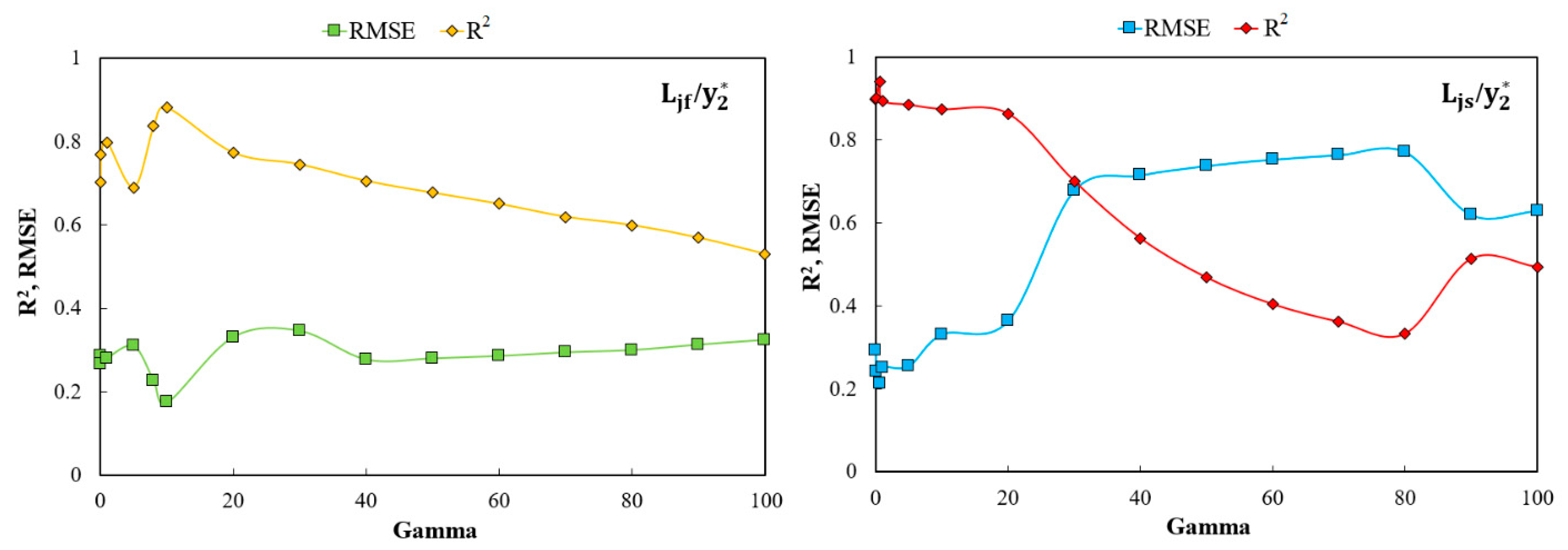
3.6. Sensitivity Analysis
4. Conclusions
- By comparing the results of the two experiments (physical and numerical), the FLOW-3D® software can accurately predict the characteristics of free and submerged hydraulic jumps. The overall mean value of relative error between numerical results and experimental data is 4.1%, which confirms the numerical model’s ability to predict the characteristics of the free and submerged jumps.
- The SVM model with the RMSE = 0.2075 and R2 = 0.9966 for the training phase and RMSE = 0.2990 and R2 = 0.9960 for the testing phase in predicting the y2/y1 is the best model and close to the FLOW-3D® result.
- For the y3/y1, the SVM model with values of RMSE = 0.3391 and R2 = 0.9964 for the testing phase is close to the FLOW-3D® model. The SVM model also performed better in predicting y4/y1 and had very little error. After the SVM model, the GEP model also provided acceptable results in estimating (y3/y1) and (y4/y1).
- The SVM model demonstrated better statistical criteria among other models (i.e., GEP and RF) and has high accuracy in predicting the relative length of free and submerged hydraulic jumps. Furthermore, the best result for predicting the in the optimal gamma is 10 (γ = 10) and the in the optimal gamma is 0.60 (γ = 0.60).
- For energy dissipation due to (ΔE/E1)f and (ΔE/E1)S, for the testing phase, SVM model with R2 = 0.9848 and RMSE = 0.031 as well as R2 = 0.9843 and RMSE = 0.0238 were recognized as the best models, respectively.
- The Fr1 has the greatest effect on predicting the (y3/y1) based on sensitivity analysis. By omitting this parameter, the prediction accuracy is significantly reduced. The SF and T/I are also involved in the (y3/y1), but the impact of each is less than the Fr1.
- Relationships with good correlation coefficients for the mentioned parameters in free and submerged hydraulic jumps were presented based on numerical results.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Notation
| Q | Discharge (L3T−1) |
| d | Gate opening (L) |
| E1, E2 | Specific energy at the beginning and after the free jump (L) |
| E3, E4 | Specific energy at the beginning and after the submerged jump (L) |
| ΔE | Energy dissipation (L) |
| y1 | Inlet depth of the hydraulic jump (L) |
| y2 | Sequent depth of the free jump (L) |
| y3 | Submerged depth (L) |
| y4 | Tailwater depth (L) |
| Ljf | Length of the free jump (L) |
| Ljs | Length of the submerged jump (L) |
| u1 | Inlet horizontal velocity (LT−1) |
| g | Gravitational acceleration (LT−2) |
| I | Distance of triangular roughness (L) |
| T | Roughness height (L) |
| Fr1 | Inlet Froude number (-) |
| Re1 | Inlet Reynolds number (-) |
| SF | Submergence factor (-) |
| t | Time (T) |
| p | Pressure (ML−1T−2) |
| F | Fraction function |
| ρ | Mass density of water (ML−3) |
| Kinematic viscosity of water (LT−1) | |
| μ | Dynamic viscosity of fluid (ML−1T−1) |
| k | Turbulence kinetic energy (L2T−3) |
| ε | Turbulence dissipation rate (L2T−3) |
| µeff | Effective viscosity (ML−1T−1) |
| Gk | The generation of turbulent kinetic energy caused by the average velocity gradient |
| Gb | The generation of turbulent kinetic energy caused by buoyancy |
| Sk, Sε | Source terms |
| SVM | Support Vector Machine |
| GEP | Gene Expression Programming |
| RF | Random Forest |
| R2 | Correlation coefficient |
| RMSE | Root Mean Square Error |
| NRMSE | Normalized Root Mean Square of Error |
| MAPE | Mean Absolute Percentage Error |
References
- Ebrahimi, S.; Salmasi, F.; Abbaspour, A. Numerical study of hydraulic jump on rough beds stilling basins. J. Civ. Eng. Urban. 2013, 3, 19–24. [Google Scholar]
- Chanson, H. Hydraulics of Open Channel Flow; Elsevier: Amsterdam, The Netherlands, 2004. [Google Scholar]
- McCorquodale, J.A.; Khalifa, A.M. Submerged radial hydraulic jump. J. Hydraul. Div. 1980, 106, 355–367. [Google Scholar] [CrossRef]
- Smith, C.D. The submerged hydraulic jump in an abrupt lateral expansion. J. Hydraul. Res. 1989, 27, 257–266. [Google Scholar] [CrossRef]
- Graber, S.D.; Ohtsu, I.; Yasuda, Y.; Ishikawa, M. Submerged Hydraulic Jumps below Abrupt Expansions. J. Hydraul. Eng. 2001, 127, 84–85. [Google Scholar] [CrossRef]
- Vallé, B.L.; Pasternack, G.B. Submerged and unsubmerged natural hydraulic jumps in a bedrock step-pool mountain channel. Geomorphology 2006, 82, 146–159. [Google Scholar] [CrossRef]
- Dey, S.; Sarkar, A. Characteristics of turbulent flow in submerged jumps on rough beds. J. Eng. Mech. 2008, 134, 49–59. [Google Scholar] [CrossRef]
- Tokyay, N.; Evcimen, T.; Şimşek, Ç. Forced hydraulic jump on non-protruding rough beds. Can. J. Civ. Eng. 2011, 38, 1136–1144. [Google Scholar] [CrossRef]
- Samadi-Boroujeni, H.; Ghazali, M.; Gorbani, B.; Nafchi, R.F. Effect of triangular corrugated beds on the hydraulic jump characteristics. Can. J. Civ. Eng. 2013, 40, 841–847. [Google Scholar] [CrossRef]
- Ead, S.; Rajaratnam, N. Hydraulic jumps on corrugated beds. J. Hydraul. Eng. 2002, 128, 656–663. [Google Scholar] [CrossRef]
- Carollo, F.G.; Ferro, V.; Pampalone, V. Hydraulic jumps on rough beds. J. Hydraul. Eng. 2007, 133, 989–999. [Google Scholar] [CrossRef]
- Pagliara, S.; Lotti, I.; Palermo, M. Hydraulic jump on rough bed of stream rehabilitation structures. J. Hydro-Environ. Res. 2008, 2, 29–38. [Google Scholar] [CrossRef]
- Abbaspour, A.; Hosseinzadeh Dalir, A.; Farsadizadeh, D.; Sadraddini, A.A. Effect of sinusoidal corrugated bed on hydraulic jump characteristics. J. Hydro-Environ. Res. 2009, 3, 109–117. [Google Scholar] [CrossRef]
- Chanson, H. Momentum considerations in hydraulic jumps and bores. J. Irrig. Drain. Eng. 2012, 138, 382–385. [Google Scholar] [CrossRef] [Green Version]
- Ahmed, H.M.A.; El Gendy, M.; Mirdan, A.M.H.; Ali, A.A.M.; Haleem, F.S.F.A. Effect of corrugated beds on characteristics of submerged hydraulic jump. Ain Shams Eng. J. 2014, 5, 1033–1042. [Google Scholar] [CrossRef] [Green Version]
- Palermo, M.; Pagliara, S. Semi-theoretical approach for energy dissipation estimation at hydraulic jumps in rough sloped channels. J. Hydraul. Res. 2018, 56, 786–795. [Google Scholar] [CrossRef]
- Pourabdollah, N.; Heidarpour, M.; Koupai, J.A. Characteristics of free and submerged hydraulic jumps in different stilling basins. Water Manag. 2020, 173, 121–131. [Google Scholar] [CrossRef]
- Habibzadeh, A.; Rajaratnam, N.; Loewen, M. Characteristics of the flow field downstream of free and submerged hydraulic jumps. Water Manag. 2019, 172, 180–194. [Google Scholar] [CrossRef]
- Gharangik, A.M.; Chaudhry, M.H. Numerical simulation of hydraulic jump. J. Hydraul. Eng. 1991, 117, 1195–1211. [Google Scholar] [CrossRef]
- Ma, F.; Hou, Y.; Prinos, P. Numerical calculation of submerged hydraulic jumps. J. Hydraul. Res. 2001, 39, 493–503. [Google Scholar] [CrossRef]
- Mousavi, S.N.; Júnior, R.S.; Teixeira, E.D.; Bocchiola, D.; Nabipour, N.; Mosavi, A.; Shamshirband, S. Predictive Modeling the Free Hydraulic Jumps Pressure through Advanced Statistical Methods. Mathematics 2020, 8, 323. [Google Scholar] [CrossRef] [Green Version]
- Abbaspour, A.; Farsadizadeh, D.; Dalir, A.H.; Sadraddini, A.A. Numerical study of hydraulic jumps on corrugated beds using turbulence models. Turk. J. Eng. Environ. Sci. 2009, 33, 61–72. [Google Scholar]
- Chern, M.-J.; Syamsuri, S. Effect of corrugated bed on hydraulic jump characteristic using SPH method. J. Hydraul. Eng. 2013, 139, 221–232. [Google Scholar] [CrossRef]
- Bayon, A.; Valero, D.; García-Bartual, R.; Vallés-Morán, F.J.; López-Jiménez, P.A. Performance assessment of OpenFOAM and FLOW-3D in the numerical modeling of a low Reynolds number hydraulic jump. Environ. Model. Softw. 2016, 80, 322–335. [Google Scholar] [CrossRef]
- Nikmehr, S.; Aminpour, Y. Numerical Simulation of Hydraulic Jump over Rough Beds. Period. Polytech. Civ. Eng. 2020, 64, 396–407. [Google Scholar] [CrossRef]
- Ghaderi, A.; Dasineh, M.; Aristodemo, F.; Ghahramanzadeh, A. Characteristics of free and submerged hydraulic jumps over different macroroughnesses. J. Hydroinform. 2020, 22, 1554–1572. [Google Scholar] [CrossRef]
- Ghaderi, A.; Dasineh, M.; Aristodemo, F.; Aricò, C. Numerical Simulations of the Flow Field of a Submerged Hydraulic Jump over Triangular Macroroughnesses. Water 2021, 13, 674. [Google Scholar] [CrossRef]
- Karbasi, M.; Azamathulla, H.M. GEP to predict characteristics of a hydraulic jump over a rough bed. KSCE J. Civ. Eng. 2016, 20, 3006–3011. [Google Scholar] [CrossRef]
- Roushangar, K.; Ghasempour, R. Explicit prediction of expanding channels hydraulic jump characteristics using gene expression programming approach. Hydrol. Res. 2017, 49, 815–830. [Google Scholar] [CrossRef]
- Roushangar, K.; Ghasempour, R. Evaluation of the impact of channel geometry and rough elements arrangement in hydraulic jump energy dissipation via SVM. J. Hydroinform. 2018, 21, 92–103. [Google Scholar] [CrossRef]
- Roushangar, K.; Homayounfar, F. Prediction Characteristics of Free and Submerged Hydraulic Jumps on Horizontal and Sloping Beds using SVM Method. KSCE J. Civ. Eng. 2019, 23, 4696–4709. [Google Scholar] [CrossRef]
- Naseri, M.; Othman, F. Determination of the length of hydraulic jumps using artificial neural networks. Adv. Eng. Softw. 2012, 48, 27–31. [Google Scholar] [CrossRef]
- Nasrabadi, M.; Mehri, Y.; Ghassemi, A.; Omid, M.H. Predicting submerged hydraulic jump characteristics using machine learning methods. Water Supply 2021. [Google Scholar] [CrossRef]
- Huš, M.; Grilc, M.; Pavlišič, A.; Likozar, B.; Hellman, A. Multiscale modelling from quantum level to reactor scale: An example of ethylene epoxidation on silver catalysts. Catal. Today 2019, 338, 128–140. [Google Scholar] [CrossRef]
- Hager, W.H.; Bremen, R. Classical hydraulic jump: Sequent depths. J. Hydraul. Res. 1989, 27, 565–585. [Google Scholar] [CrossRef]
- Fürst, J.; Halada, T.; Sedlář, M.; Krátký, T.; Procházka, P.; Komárek, M. Numerical Analysis of Flow Phenomena in Discharge Object with Siphon Using Lattice Boltzmann Method and CFD. Mathematics 2021, 9, 1734. [Google Scholar] [CrossRef]
- Hirt, C.W.; Nichols, B.D. Volume of fluid (VOF) method for the dynamics of free boundaries. J. Comput. Phys. 1981, 39, 201–225. [Google Scholar] [CrossRef]
- Nazari-Sharabian, M.; Nazari-Sharabian, A.; Karakouzian, M.; Karami, M. Sacrificial piles as scour countermeasures in river bridges a numerical study using flow-3D. Civ. Eng. J. 2020, 6, 1091–1103. [Google Scholar] [CrossRef]
- Abbasi, S.; Fatemi, S.; Ghaderi, A.; Di Francesco, S. The Effect of Geometric Parameters of the Antivortex on a Triangular Labyrinth Side Weir. Water 2021, 13, 14. [Google Scholar] [CrossRef]
- Chiu, C.-L.; Fan, C.-M.; Tsung, S.-C. Numerical Modeling for Periodic Oscillation of Free Overfall in a Vertical Drop Pool. J. Hydraul. Eng. 2017, 143, 04016077. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, W.; Hu, X.; Liu, F. Experimental and numerical research on trapezoidal sharp-crested side weirs. Flow Meas. Instrum. 2018, 64, 83–89. [Google Scholar] [CrossRef]
- Ghaderi, A.; Daneshfaraz, R.; Dasineh, M.; Di Francesco, S. Energy dissipation and hydraulics of flow over trapezoidal–triangular labyrinth weirs. Water 2020, 12, 1992. [Google Scholar] [CrossRef]
- Ghaderi, A.; Abbasi, S. CFD simulation of local scouring around airfoil-shaped bridge piers with and without collar. Sādhanā 2019, 44, 216. [Google Scholar] [CrossRef] [Green Version]
- Ghaderi, A.; Dasineh, M.; Abbasi, S.; Abraham, J. Investigation of trapezoidal sharp-crested side weir discharge coefficients under subcritical flow regimes using CFD. Appl. Water Sci. 2019, 10, 31. [Google Scholar] [CrossRef] [Green Version]
- Ghaderi, A.; Abbasi, S.; Abraham, J.; Azamathulla, H.M. Efficiency of Trapezoidal Labyrinth Shaped stepped spillways. Flow Meas. Instrum. 2020, 72, 101711. [Google Scholar] [CrossRef]
- Daneshfaraz, R.; Aminvash, E.; Ghaderi, A.; Abraham, J.; Bagherzadeh, M. SVM Performance for Predicting the Effect of Horizontal Screen Diameters on the Hydraulic Parameters of a Vertical Drop. Appl. Sci. 2021, 11, 4238. [Google Scholar] [CrossRef]
- Daneshfaraz, R.; Bagherzadeh, M.; Esmaeeli, R.; Norouzi, R.; Abraham, J. Study of the performance of support vector machine for predicting vertical drop hydraulic parameters in the presence of dual horizontal screens. Water Supply 2021, 21, 217–231. [Google Scholar] [CrossRef]
- Thakur, B.; Kalra, A.; Ahmad, S.; Lamb, K.W.; Lakshmi, V. Bringing statistical learning machines together for hydro-climatological predictions—Case study for Sacramento San joaquin River Basin, California. J. Hydrol. Reg. Stud. 2020, 27, 100651. [Google Scholar] [CrossRef]
- Roushangar, K.; Koosheh, A. Evaluation of GA-SVR method for modeling bed load transport in gravel-bed rivers. J. Hydrol. 2015, 527, 1142–1152. [Google Scholar] [CrossRef]
- Roushangar, K.; Alami, M.T.; Shiri, J.; Asl, M.M. Determining discharge coefficient of labyrinth and arced labyrinth weirs using support vector machine. Hydrol. Res. 2017, 49, 924–938. [Google Scholar] [CrossRef]
- Ferreira, C. Gene Expression Programming in Problem Solving. In Soft Computing and Industry: Recent Applications; Roy, R., Köppen, M., Ovaska, S., Furuhashi, T., Hoffmann, F., Eds.; Springer: London, UK, 2002; pp. 635–653. [Google Scholar]
- Borrelli, A.; De Falco, I.; Della Cioppa, A.; Nicodemi, M.; Trautteur, G. Performance of genetic programming to extract the trend in noisy data series. Phys. A Stat. Mech. Its Appl. 2006, 370, 104–108. [Google Scholar] [CrossRef]
- Majedi-Asl, M.; Daneshfaraz, R.; Fuladipanah, M.; Abraham, J.; Bagherzadeh, M. Simulation of bridge pier scour depth base on geometric characteristics and field data using support vector machine algorithm. J. Appl. Res. Water Wastewater 2020, 7, 137–143. [Google Scholar]
- Antoniadis, A.; Lambert-Lacroix, S.; Poggi, J.-M. Random forests for global sensitivity analysis: A selective review. Reliab. Eng. Syst. Saf. 2021, 206, 107312. [Google Scholar] [CrossRef]
- Pavlišič, A.; Pohar, A.; Likozar, B. Comparison of computational fluid dynamics (CFD) and pressure drop correlations in laminar flow regime for packed bed reactors and columns. Powder Technol. 2018, 328, 130–139. [Google Scholar] [CrossRef]
- Pavlišič, A.; Huš, M.; Prašnikar, A.; Likozar, B. Multiscale modelling of CO2 reduction to methanol over industrial Cu/ZnO/Al2O3 heterogeneous catalyst: Linking ab initio surface reaction kinetics with reactor fluid dynamics. J. Clean. Prod. 2020, 275, 122958. [Google Scholar] [CrossRef]
- French, R.H. Open-Channel Hydraulics; McGraw-Hill: New York, NY, USA, 1985. [Google Scholar]


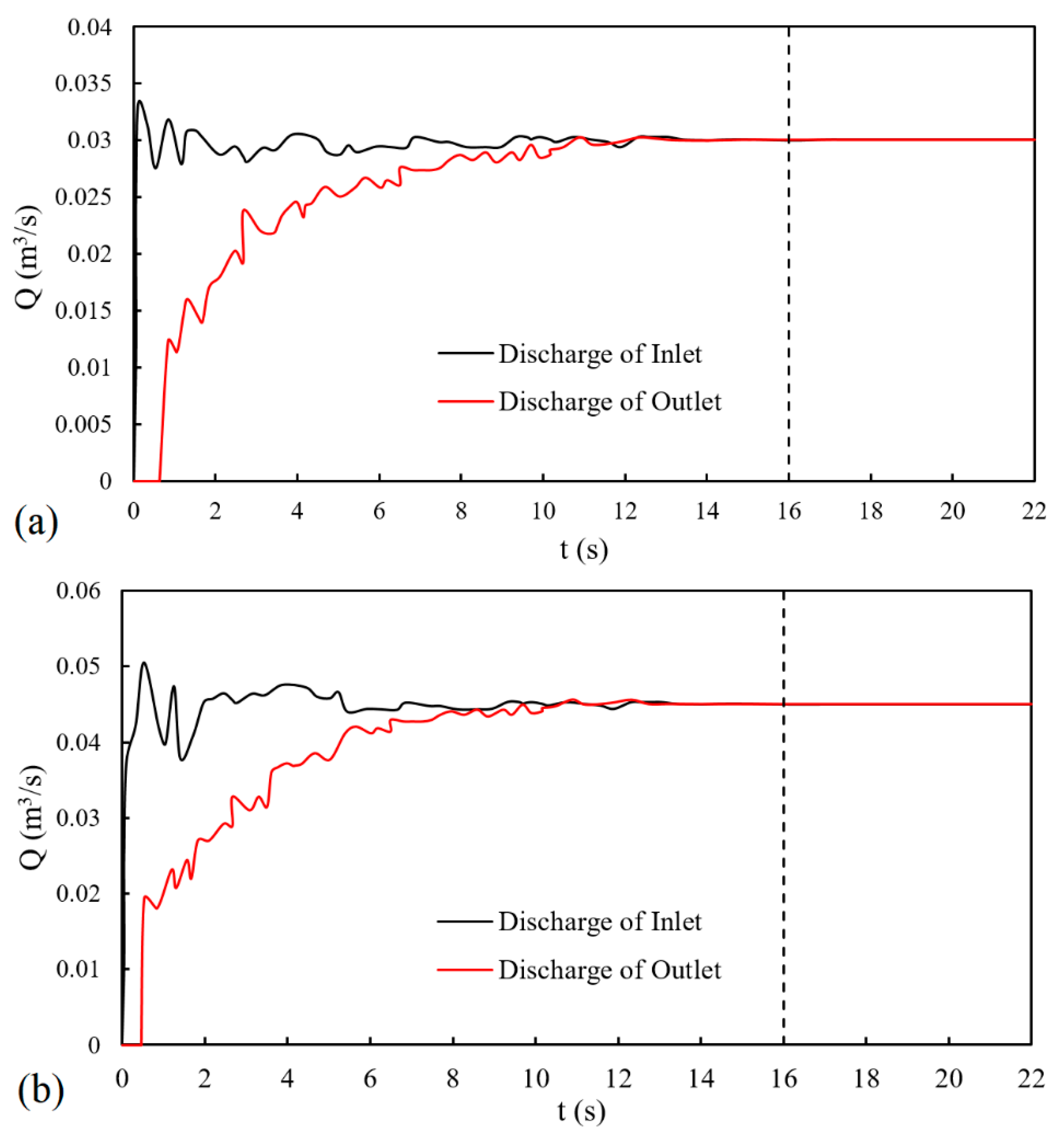





| Bed Type | Q (m3/s) | I (cm) | T (cm) | d (cm) | y1 (cm) | y4 (cm) | Fr1 | SF |
|---|---|---|---|---|---|---|---|---|
| Smooth | 0.03, 0.045 | - | - | 5 | 1.62–3.83 | 9.64–32.10 | 1.7–9.3 | 0.26–0.50 |
| Triangular roughness | 0.03, 0.045 | 4–8–12–16–20 | 4 | 5 | 1.62–3.84 | 6.82–30.08 | 1.7–9.3 | 0.21–0.44 |
| Test No. | Coarser Cells Size (cm) | Finer Cells Size (cm) | Total Cells | (y3/y1)Num | (y3/y1)Exp | (y2/y1)Num | (y2/y1)Exp | MAPE 1-y3/y1 (%) | MAPE-y2/y1 (%) |
|---|---|---|---|---|---|---|---|---|---|
| T1 | 2.00 | 0.95 | 910,358 | 8.55 | 6.88 | 7.43 | 5.88 | 26.36 | 24.27 |
| T2 | 1.70 | 0.85 | 1,285,482 | 7.85 | 6.88 | 6.91 | 5.88 | 17.51 | 14.09 |
| T3 | 1.50 | 0.75 | 1,871,649 | 7.38 | 6.88 | 6.44 | 5.88 | 9.52 | 7.26 |
| T4 | 1.30 | 0.65 | 2,908,596 | 7.17 | 6.88 | 6.20 | 5.88 | 5.44 | 4.21 |
| T5 | 1.15 | 0.60 | 3,812,035 | 7.10 | 6.88 | 6.08 | 5.88 | 3.41 | 3.34 |
| Function | Expression |
|---|---|
| Linear Kernel | |
| Polynomial Kernel | |
| Radial Basis Kernel | |
| Sigmoid Kernel |
| Models | Bed | Q (m3/s) | d (cm) | y1 (cm) | u1 (m/s) | Fr1 |
|---|---|---|---|---|---|---|
| Numerical and physical | Smooth | 0.045 | 5 | 1.62–3.83 | 1.04–3.70 | 1.7–9.3 |
| Training | Testing | |||||||
|---|---|---|---|---|---|---|---|---|
| Model | R2 | RMSE | NRMSE (%) | MAPE (%) | R2 | RMSE | NRMSE (%) | MAPE (%) |
| GEP | 0.9953 | 0.2356 | 4.03 | 5.35 | 0.9933 | 0.3335 | 5.56 | 8.83 |
| RF | 0.9682 | 0.5924 | 10.97 | 11.91 | 0.9275 | 1.0811 | 14.73 | 11.26 |
| SVM | 0.9966 | 0.2075 | 3.5481 | 5.07 | 0.9960 | 0.2990 | 4.98 | 8.46 |
| Training | Testing | |||||||
|---|---|---|---|---|---|---|---|---|
| y3/y1 | R2 | RMSE | NRMSE (%) | MAPE (%) | R2 | RMSE | NRMSE (%) | MAPE (%) |
| GEP | 0.9903 | 0.4016 | 5.96 | 8.63 | 0.9895 | 0.5379 | 7.61 | 9.92 |
| RF | 0.9815 | 0.5679 | 8.43 | 11.97 | 0.9750 | 0.7804 | 11.04 | 23.03 |
| SVM | 0.9978 | 0.2024 | 3.01 | 2.67 | 0.9964 | 0.3391 | 4.80 | 4.93 |
| y4/y1 | R2 | RMSE | NRMSE (%) | MAPE (%) | R2 | RMSE | NRMSE (%) | MAPE (%) |
| GEP | 0.9972 | 0.2811 | 3.41 | 3.34 | 0.9963 | 0.3923 | 4.54 | 6.84 |
| RF | 0.9901 | 0.5157 | 6.26 | 9.68 | 0.9899 | 0.6462 | 7.48 | 10.04 |
| SVM | 0.9991 | 0.1639 | 1.99 | 1.63 | 0.9988 | 0.2806 | 3.25 | 5.08 |
| Training | Testing | |||||||
|---|---|---|---|---|---|---|---|---|
| / | R2 | RMSE | NRMSE (%) | MAPE (%) | R2 | RMSE | NRMSE (%) | MAPE (%) |
| GEP | 0.829 | 0.234 | 4.39 | 3.66 | 0.766 | 0.249 | 4.54 | 4.54 |
| RF | 0.752 | 0.278 | 5.08 | 3.92 | 0.741 | 0.319 | 6.32 | 5.21 |
| SVM | 0.919 | 0.169 | 3.16 | 2.74 | 0.881 | 0.174 | 3.19 | 2.90 |
| / | R2 | RMSE | NRMSE (%) | MAPE% | R2 | RMSE | NRMSE (%) | MAPE (%) |
| GEP | 0.878 | 0.273 | 3.88 | 3.17 | 0.867 | 0.336 | 4.71 | 4.33 |
| RF | 0.787 | 0.316 | 4.37 | 3.51 | 0.764 | 0.425 | 6.50 | 5.46 |
| SVM | 0.961 | 0.154 | 2.19 | 1.93 | 0.940 | 0.212 | 2.97 | 2.37 |
| Training | Testing | |||||||
|---|---|---|---|---|---|---|---|---|
| (ΔE/E1)f | R2 | RMSE | NRMSE (%) | MAPE (%) | R2 | RMSE | NRMSE (%) | MAPE (%) |
| GEP | 0.980 | 0.029 | 6.76 | 6.59 | 0.977 | 0.040 | 10.19 | 16.04 |
| RF | 0.855 | 0.069 | 16.5 | 25.61 | 0.801 | 0.072 | 16.32 | 21.22 |
| SVM | 0.985 | 0.027 | 6.37 | 6.58 | 0.984 | 0.031 | 7.80 | 9.04 |
| (ΔE/E1)S | R2 | RMSE | NRMSE (%) | MAPE (%) | R2 | RMSE | NRMSE (%) | MAPE (%) |
| GEP | 0.980 | 0.025 | 7.22 | 8.85 | 0.969 | 0.033 | 10.07 | 11.63 |
| RF | 0.912 | 0.051 | 12.94 | 13.83 | 0.916 | 0.047 | 13.53 | 13.43 |
| SVM | 0.985 | 0.022 | 6.22 | 6.43 | 0.984 | 0.023 | 7.25 | 9.05 |
| Training | Testing | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Input parameter | Omitted parameter | R2 | RMSE | NRME (%) | MAPE (%) | R2 | RMSE | NRMSE (%) | MAPE (%) |
| Fr1, SF, T/I | - | 0.999 | 0.163 | 1.99 | 1.63 | 0.998 | 0.280 | 3.25 | 5.08 |
| SF, T/I | Fr1 | 0.787 | 1.639 | 24.33 | 34.63 | 0.731 | 2.417 | 34.21 | 36.69 |
| Fr1, T/I | SF | 0.986 | 0.479 | 7.12 | 10.83 | 0.984 | 0.664 | 9.41 | 15.9 |
| Fr1, SF | T/I | 0.989 | 0.415 | 6.17 | 9.85 | 0.988 | 0.548 | 7.76 | 14.66 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dasineh, M.; Ghaderi, A.; Bagherzadeh, M.; Ahmadi, M.; Kuriqi, A. Prediction of Hydraulic Jumps on a Triangular Bed Roughness Using Numerical Modeling and Soft Computing Methods. Mathematics 2021, 9, 3135. https://doi.org/10.3390/math9233135
Dasineh M, Ghaderi A, Bagherzadeh M, Ahmadi M, Kuriqi A. Prediction of Hydraulic Jumps on a Triangular Bed Roughness Using Numerical Modeling and Soft Computing Methods. Mathematics. 2021; 9(23):3135. https://doi.org/10.3390/math9233135
Chicago/Turabian StyleDasineh, Mehdi, Amir Ghaderi, Mohammad Bagherzadeh, Mohammad Ahmadi, and Alban Kuriqi. 2021. "Prediction of Hydraulic Jumps on a Triangular Bed Roughness Using Numerical Modeling and Soft Computing Methods" Mathematics 9, no. 23: 3135. https://doi.org/10.3390/math9233135
APA StyleDasineh, M., Ghaderi, A., Bagherzadeh, M., Ahmadi, M., & Kuriqi, A. (2021). Prediction of Hydraulic Jumps on a Triangular Bed Roughness Using Numerical Modeling and Soft Computing Methods. Mathematics, 9(23), 3135. https://doi.org/10.3390/math9233135









