Reliability Analysis of High Concrete-Face Rockfill Dams and Study of Seismic Performance of Earthquake-Resistant Measures Based on Stochastic Dynamic Analysis
Abstract
:1. Introduction
2. Reliability Analysis Method Based on Stochastic Dynamics
2.1. Non-Stationary Ground Motion Model
2.2. Generalized Probability Density Evolution Theory
2.3. Reliability Calculation Based on GPDEM
2.4. Calculation Indexes of Reliability Analysis of Concrete Face Rockfill Dam
2.4.1. Overall Stability Index
- (1)
- Safety factor
- (2)
- Cumulative time of Fs < 1.0
2.4.2. Local Sliding Failure Index
2.5. Reliability Analysis
3. Example Analysis
3.1. Model Establishment
3.2. Constitutive Model and Material Parameters
3.3. Ground Motions Input
3.4. Seismic Response Analysis
3.5. Reliability Analysis of Dam
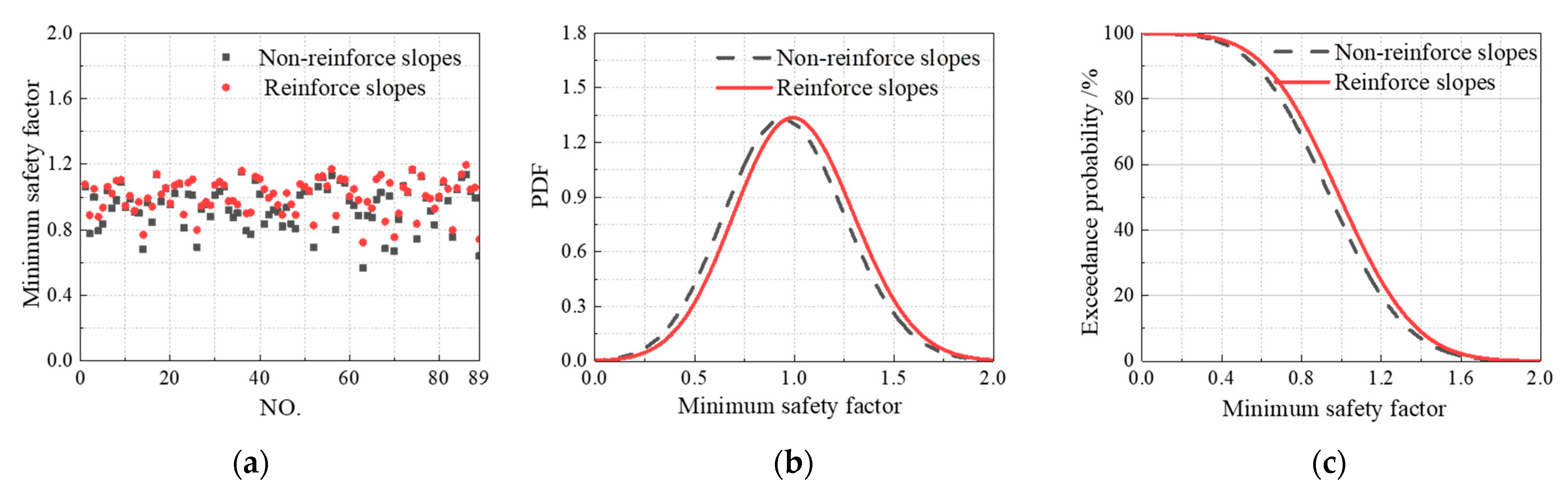
3.5.1. Overall Stability Analysis of Dam Body
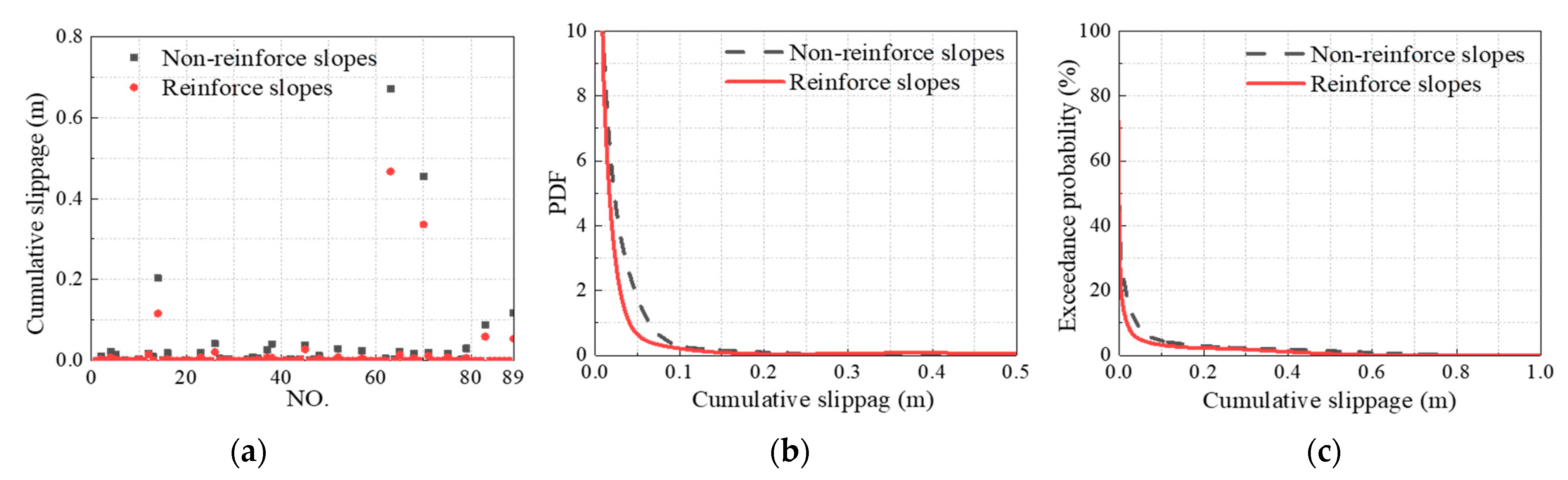
3.5.2. Analysis of Local Sliding Failure of Dam Slope
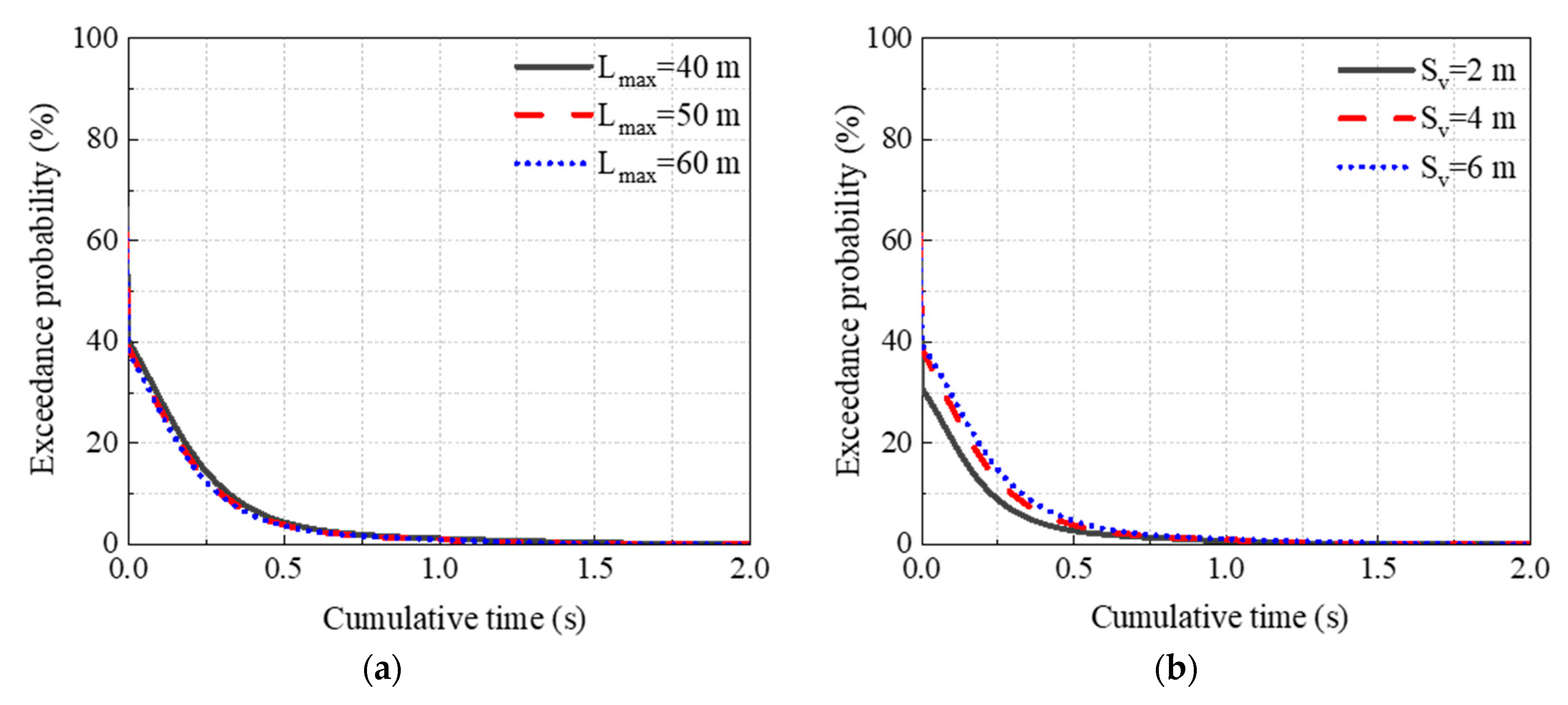
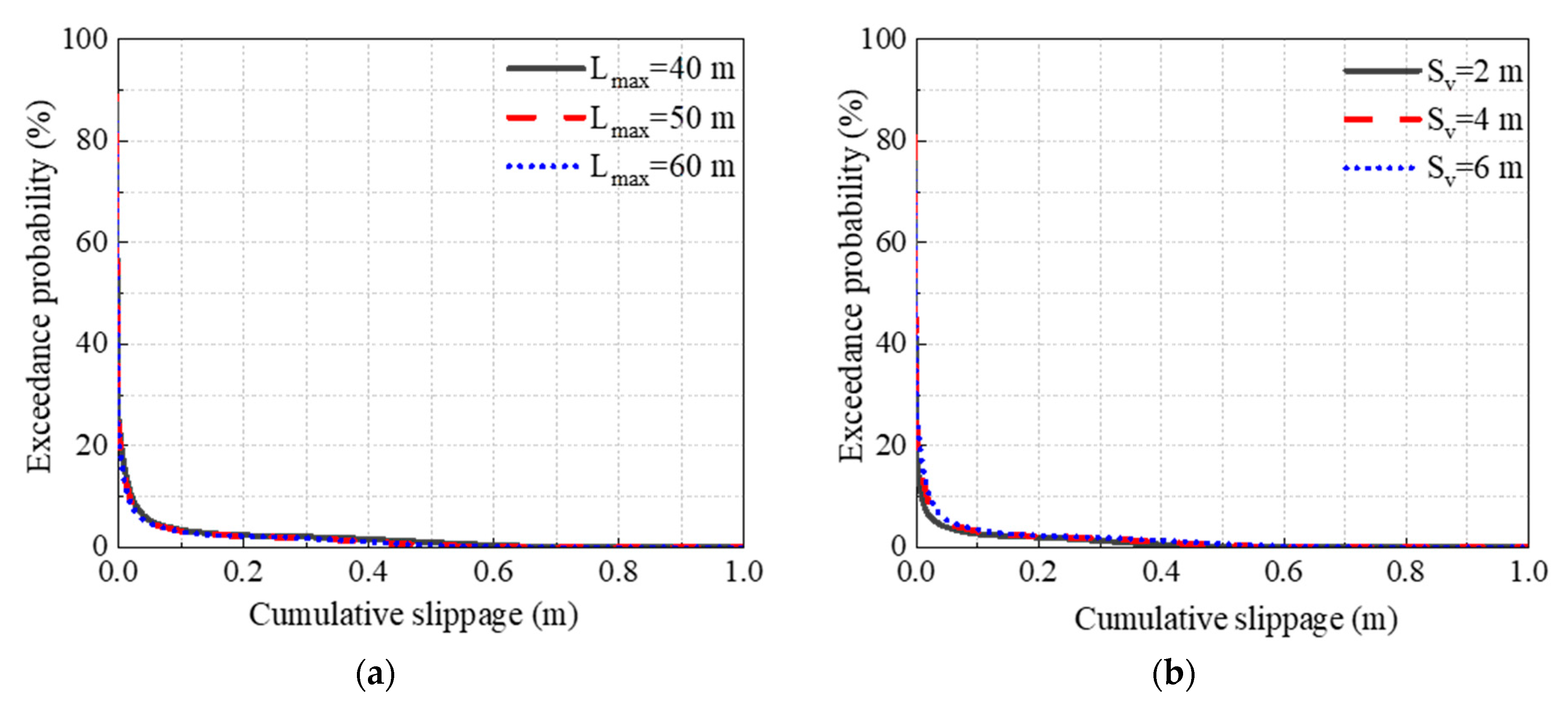
3.6. Analysis on Influenceing Factors of GRSS Performance
3.6.1. Impact on Maintaining Overall Stability
3.6.2. Influence on Restraining Local Sliding Failure
4. Conclusions
- (1)
- A set of reliability analysis systems of high CFRDs was established by combining a non-stationary ground motion model, a generalized probability density evolution theory, and multi-evaluation indicators, providing a method for the evaluation of seismic performance of earthquake-resistant measures.
- (2)
- GRSS can not only maintain the stability of a dam body during an earthquake; it can also improve the stability of the overall response of a dam under different ground motions.
- (3)
- The dam slope of the Gushui CFRD is more susceptible to slight damage under random ground motions with a PGA of 0.340 g, with a certain probability of moderate damage and a lower probability of severe damage. The calculation results showed that the seismic performance of GRSS can inhibit mild damage of 20–30% of ground motion samples and avoid severe damage with a high probability.
- (4)
- With an increase in geogrid reinforcement length and a decrease in vertical spacing, the seismic performance in maintaining dam slope stability increases due to strong constraints. However, the increase in reinforcement length has little influence on the performance of GRSS. When reinforcement vertical spacing is reduced from 4 m to 2 m, the reduction in the earthquake-resistant effect of GRSS is relatively obvious. This is conducive to actual engineering design, considering economics and seismic performance.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Chen, S.; Fu, Z.; Wei, K.; Han, H. Seismic Responses of High Concrete Face Rockfill Dams: A Case Study. Water Sci. Eng. 2016, 9, 195–204. [Google Scholar] [CrossRef] [Green Version]
- Zhou, Y.; Zhang, Y.; Pang, R.; Xu, B. Seismic Fragility Analysis of High Concrete Faced Rockfill Dams Based on Plastic Failure with Support Vector Machine. Soil Dyn. Earthq. Eng. 2021, 144, 106587. [Google Scholar] [CrossRef]
- Zhang, J.M.; Yang, Z.; Gao, X.; Zhang, J. Geotechnical Aspects and Seismic Damage of the 156-m-High Zipingpu Concrete-Faced Rockfill Dam Following the Ms 8.0 Wenchuan Earthquake. Soil Dyn. Earthq. Eng. 2015, 76, 145–156. [Google Scholar] [CrossRef]
- Liu, H.; Chen, Y.; Yu, T.; Yang, G. Seismic Analysis of the Zipingpu Concrete-Faced Rockfill Dam Response to the 2008 Wenchuan, China, Earthquake. J. Perform. Constr. Facil. 2015, 29, 04014129. [Google Scholar] [CrossRef]
- Ling, H.I.; Leshchinsky, D.; Perry, E.B. Seismic Design and Performance of Geosynthetic-Reinforced Soil Structures. Géotechnique 1997, 47, 933–952. [Google Scholar] [CrossRef]
- Ling, H.I.; Leshchinsky, D. Effects of Vertical Acceleration on Seismic Design of Geosynthetic-Reinforced Soil Structures. Géotechnique 1998, 48, 347–373. [Google Scholar] [CrossRef]
- Li, H.J.; Chi, S.C.; Li, G. Seismic Stability Analysis of Reinforced Slope of High Core Rockfill Dam. Chin. J. Geotech. Eng. 2007, 29, 1881–1887. (In Chinese) [Google Scholar] [CrossRef]
- Noorzad, R.; Omidvar, M. Seismic Displacement Analysis of Embankment Dams with Reinforced Cohesive Shell. Soil Dyn. Earthq. Eng. 2010, 30, 1149–1157. [Google Scholar] [CrossRef]
- Zhu, Y.; Kong, X.; Zou, D.; Zhu, S. Dynamic Elastoplastic Analysis of Geogrid Reinforced High Earth Rockfill Dam. J. Hydraul. Eng. 2012, 43, 1478–1486. (In Chinese) [Google Scholar]
- Yang, X.; Chi, S.; Lu, X. Upper Limit Analysis of Seismic Stability of Reinforced Earth Rock Dam Slope. J. Hydraul. Eng. 2014, 45, 304–311. (In Chinese) [Google Scholar] [CrossRef]
- Glovatsky, O.; Hamdamov, B.; Bekchanov, F.; Saparov, A. Strengthening Technology and Modeling of Dams from Reinforced Soil. IOP Conf. Ser. Mater. Sci. Eng. 2021, 1030, 012155. [Google Scholar] [CrossRef]
- Peng, M.; Sun, R.; Chen, J.-F.; Zhang, L.-M.; Yu, S.-B. Stochastic Seismic Analysis of Geosynthetic-Reinforced Soil Slopes Using the Probability Density Evolution Method. Comput. Geotech. 2021, 140, 104485. [Google Scholar] [CrossRef]
- Hariri-Ardebili, M.A. Risk, Reliability, Resilience (R 3) and beyond in Dam Engineering: A State-of-the-Art Review. Int. J. Disaster Risk Reduct. 2018, 31, 806–831. [Google Scholar] [CrossRef]
- Kartal, M.E.; Bayraktar, A.; Başağa, H.B. Seismic Failure Probability of Concrete Slab on CFR Dams with Welded and Friction Contacts by Response Surface Method. Soil Dyn. Earthq. Eng. 2010, 30, 1383–1399. [Google Scholar] [CrossRef]
- Li, Y.; Tang, W.; Wen, L.; Wang, J. Study on Seismic Failure Probability of High Earth-Rock Dam Considering Dam Body Deformation and Slope Stability. Eur. J. Environ. Civ. Eng. 2020, 1–15. [Google Scholar] [CrossRef]
- Zai, D.; Pang, R.; Xu, B.; Fan, Q.; Jing, M. Slope System Stability Reliability Analysis with Multi-Parameters Using Generalized Probability Density Evolution Method. Bull. Eng. Geol. Environ. 2021, 80, 8419–8431. [Google Scholar] [CrossRef]
- Pang, R.; Xu, B.; Zhou, Y.; Song, L. Seismic Time-History Response and System Reliability Analysis of Slopes Considering Uncertainty of Multi-Parameters and Earthquake Excitations. Comput. Geotech. 2021, 136, 104245. [Google Scholar] [CrossRef]
- Pang, R.; Xu, B.; Zou, D.; Kong, X. Stochastic Seismic Performance Assessment of High CFRDs Based on Generalized Probability Density Evolution Method. Comput. Geotech. 2018, 97, 233–245. [Google Scholar] [CrossRef]
- Deodatis, G. Non-Stationary Stochastic Vector Processes: Seismic Ground Motion Applications. Probabilistic Eng. Mech. 1996, 11, 149–167. [Google Scholar] [CrossRef]
- Liu, Z.; Liu, W.; Peng, Y. Random Function Based Spectral Representation of Stationary and Non-Stationary Stochastic Processes. Probabilistic Eng. Mech. 2016, 45, 115–126. [Google Scholar] [CrossRef]
- Zhou, Y.; Xu, B.; Pang, R.; Zou, D.; Kong, X. Stochastic Seismic Response and Stability Reliability Analysis of a Vertical Retaining Wall in Front of the Pumping Station of a Nuclear Power Plant Using the Probability Density Evolution Method. Nuclear Eng. Design 2018, 334, 110–120. [Google Scholar] [CrossRef]
- Jacobson, R.A.; Bracewell, R.N. The Hartley Transform. Math. Comput. 1987, 48, 847. [Google Scholar] [CrossRef]
- Li, J.; Chen, J.B. Probability Density Evolution Method for Dynamic Response Analysis of Structures with Uncertain Parameters. Comput. Mech. 2004, 34, 400–409. [Google Scholar] [CrossRef]
- Li, J.; Chen, J. The Number Theoretical Method in Response Analysis of Nonlinear Stochastic Structures. Comput. Mech. 2007, 39, 693–708. [Google Scholar] [CrossRef]
- Li, J. Probability Density Evolution Method: Background, Significance and Recent Developments. Probabilistic Eng. Mech. 2016, 44, 111–117. [Google Scholar] [CrossRef]
- Li, J.; Chen, J. The Principle of Preservation of Probability and the Generalized Density Evolution Equation. Struct. Saf. 2008, 30, 65–77. [Google Scholar] [CrossRef]
- Pang, R.; Xu, B.; Kong, X.; Zhou, Y.; Zou, D. Seismic Performance Evaluation of High CFRD Slopes Subjected to Near-Fault Ground Motions Based on Generalized Probability Density Evolution Method. Eng. Geol. 2018, 246, 391–401. [Google Scholar] [CrossRef]
- Li, J.; Chen, J.; Fan, W. The Equivalent Extreme-Value Event and Evaluation of the Structural System Reliability. Struct. Saf. 2007, 29, 112–131. [Google Scholar] [CrossRef]
- Newmark, N.M. Effects of Earthquakes on Dams and Embankments. Géotechnique 1965, 15, 139–160. [Google Scholar] [CrossRef] [Green Version]
- Ling, H.I.; Leshchinsky, D.; Mohri, Y. Soil Slopes under Combined Horizontal and Vertical Seismic Accelerations. Earthq. Engng. Struct. Dyn. 1997, 26, 1231–1241. [Google Scholar] [CrossRef]
- Softening of Rockfill Based on Generalized Probability Density Evolution Method. Soil Dyn. Earthq. Eng. 2018, 107, 96–107. [CrossRef]
- Ozkan, M.Y. A Review of Considerations on Seismic Safety of Embankments and Earth and Rock-fill Dams. Soil Dyn. Earthq. Eng. 1998, 17, 439–458. [Google Scholar] [CrossRef]
- Darbre, G.R. Swiss Guidelines for the Earthquake Safety of Dams. In Proceedings of the 13th WCEE 2004, Vancouver, BC, Canada, 1–6 August 2004. [Google Scholar]
- Feng, Y.L.; Chen, Y.; Lei, H.J. Research Results on Safety Index and Design Engineering Measures of Gushui High Face Rockfill Dam. In Technology for Earth-Rockfill Dam; China Electric Power Press: Beijing, China, 2015. (In Chinese) [Google Scholar]
- Kong, X.; Zhou, Y.; Zou, D. Numerical analysis of dislocations of the face slabs of the Zipingpu Concrete Faced Rockfill Dam during the Wenchuan earthquake. Earthq. Eng. Eng. Vib. 2011, 10, 9. [Google Scholar] [CrossRef]
- Zhu, Y.; Peng, N.; Zuo, C.; Dong, Y. Study on Presettlement Control Measures for High Concrete-Faced Rockfill Dams. Eur. J. Environ. Civil Eng. 2021, 1–14. [Google Scholar] [CrossRef]
- Li, Y.; Pang, R.; Xu, B.; Wang, X.; Fan, Q.; Jiang, F. GPDEM-Based Stochastic Seismic Response Analysis of High Concrete-Faced Rockfill Dam with Spatial Variability of Rockfill Properties Based on Plastic Deformation. Comput. Geotech. 2021, 139, 104416. [Google Scholar] [CrossRef]
- Westergaard, H.M. Water Pressures on Dams During Earthquakes. Trans. Asce 1933, 98, 418–432. [Google Scholar] [CrossRef]
- Duncan, J.M.; Byrne, P.; Wong, K.S. Strength, Stress-strain and Bulk Modulus Parameters for Finite Element Analysis of Stress and Movements in Soil Masses. J. Consult. Clin. Psychol. 1981, 49, 67–554. [Google Scholar]
- Clough, G.W.; Duncan, J.M. Finite Element Analyses of Retaining Wall Behavior. Soil Mech. Found. Div. J. 1971, 97, 1657–1673. [Google Scholar] [CrossRef]
- Pang, R.; Xu, B.; Zhou, Y.; Zhang, X.; Wang, X. Fragility Analysis of High CFRDs Subjected to Mainshock-Aftershock Sequences Based on Plastic Failure. Eng. Struct. 2020, 206, 110152. [Google Scholar] [CrossRef]
- Wang, S.; Tang, Y.; Li, X.; Du, K. Analyses and Predictions of Rock Cuttabilities under Different Confining Stresses and Rock Properties Based on Rock Indentation Tests by Conical Pick. Trans. Nonferrous Met. Soc. China 2021, 31, 1766–1783. [Google Scholar] [CrossRef]
- Wang, S.; Tang, Y.; Wang, S. Influence of Brittleness and Confining Stress on Rock Cuttability Based on Rock Indentation Tests. J. Cent. South Univ. 2021, 28, 2786–2800. [Google Scholar] [CrossRef]
- Cai, X.; Cheng, C.; Zhou, Z.; Konietzky, H.; Song, Z.; Wang, S. Rock mass watering for rock-burst prevention: Some thoughts on the mechanisms deduced from laboratory results. Bull. Eng. Geol. Environ. 2021, 80, 8725–8743. [Google Scholar] [CrossRef]
- Xu, B.; Pang, R.; Zhou, Y. Verification of Stochastic Seismic Analysis Method and Seismic Performance Evaluation Based on Multi-Indices for High CFRDs. Eng. Geol. 2020, 264, 105412. [Google Scholar] [CrossRef]
- Jingbo, L.; Yandong, L. A Direct Method for Analysis of Dynamic Soil-Structure Interaction Based on Interface Idea. In Developments in Geotechnical Engineering; Elsevier: Amsterdam, The Netherlands, 1998; Volume 83, pp. 261–276. ISBN 978-0-444-50035-9. [Google Scholar]
- Zou, D.; Han, H.; Liu, J.; Yang, D.; Kong, X. Seismic Failure Analysis for a High Concrete Face Rockfill Dam Subjected to Near-Fault Pulse-like Ground Motions. Soil Dyn. Earthq. Eng. 2017, 98, 235–243. [Google Scholar] [CrossRef]
- Yang, G.; Li, H.; Yu, Y.; Lv, H. Study on Seismic Measures of Nuozhadu High Core Rockfill Dam. J. Hydroelectr. Eng. 2008, 27, 89–93. (In Chinese) [Google Scholar]
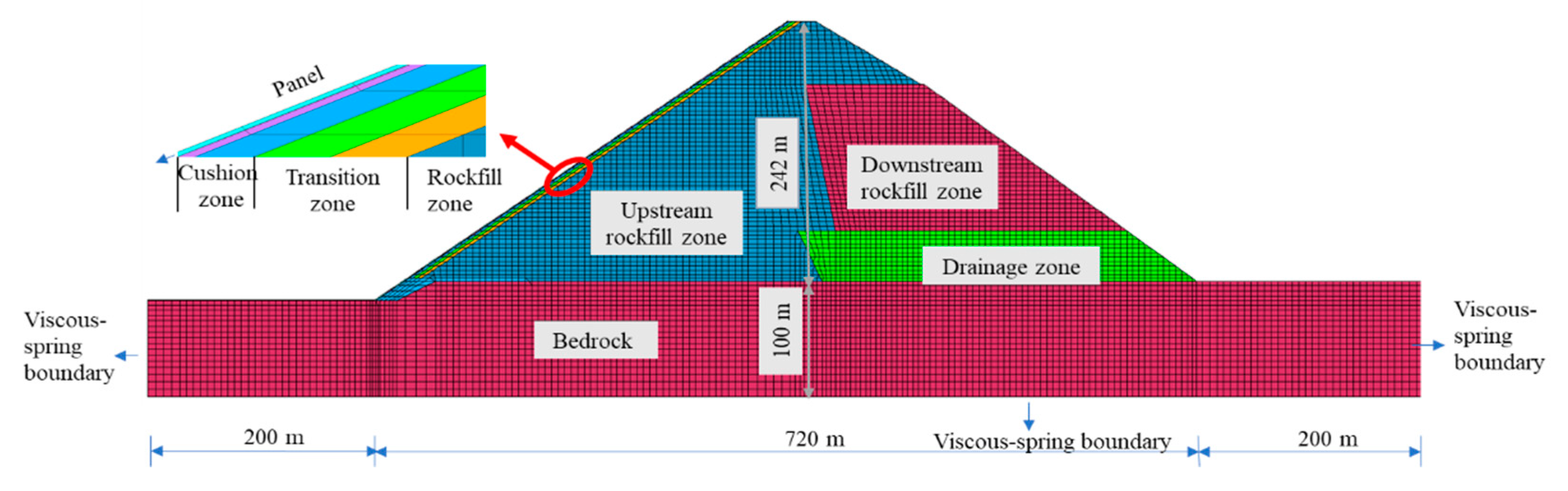

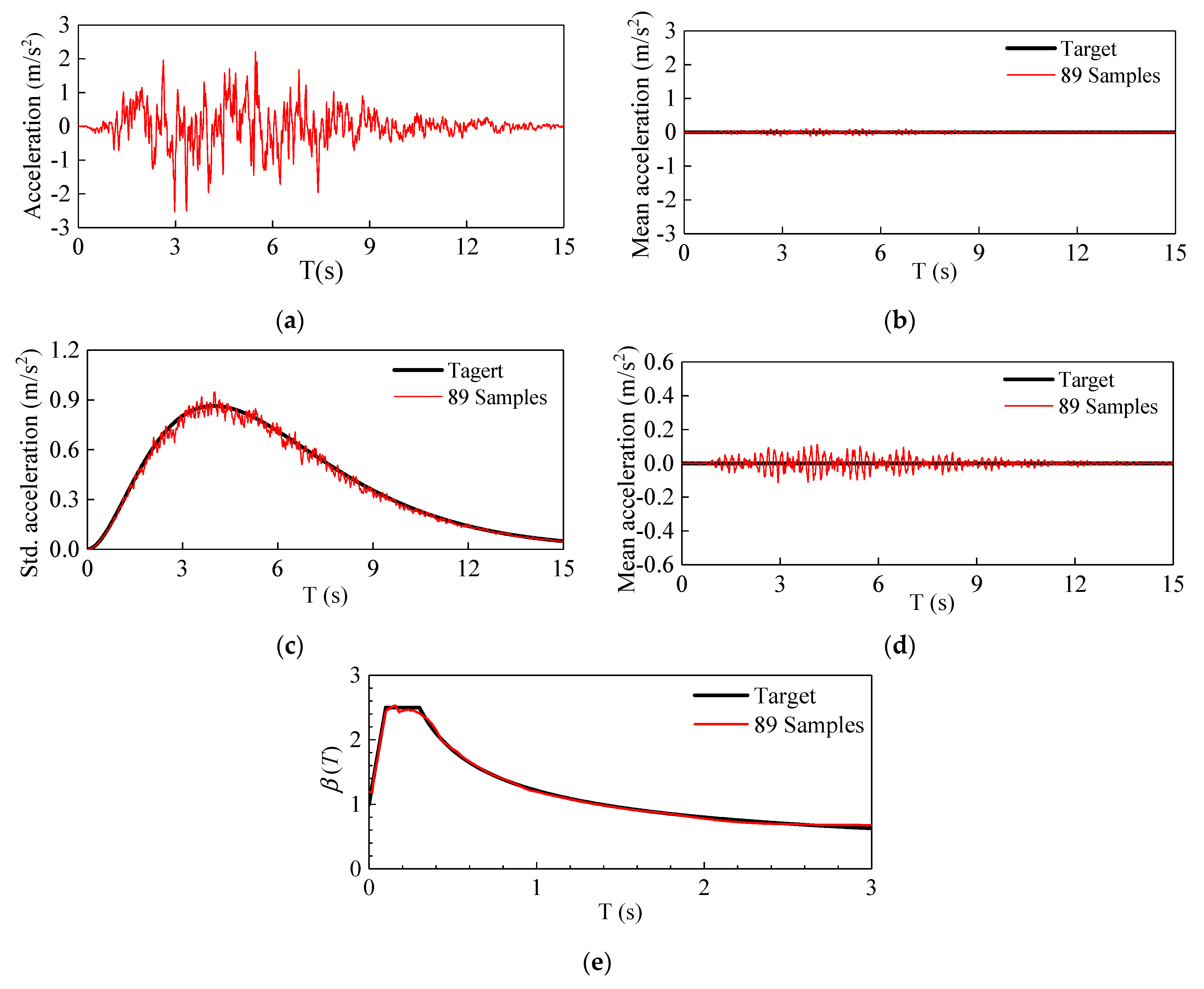
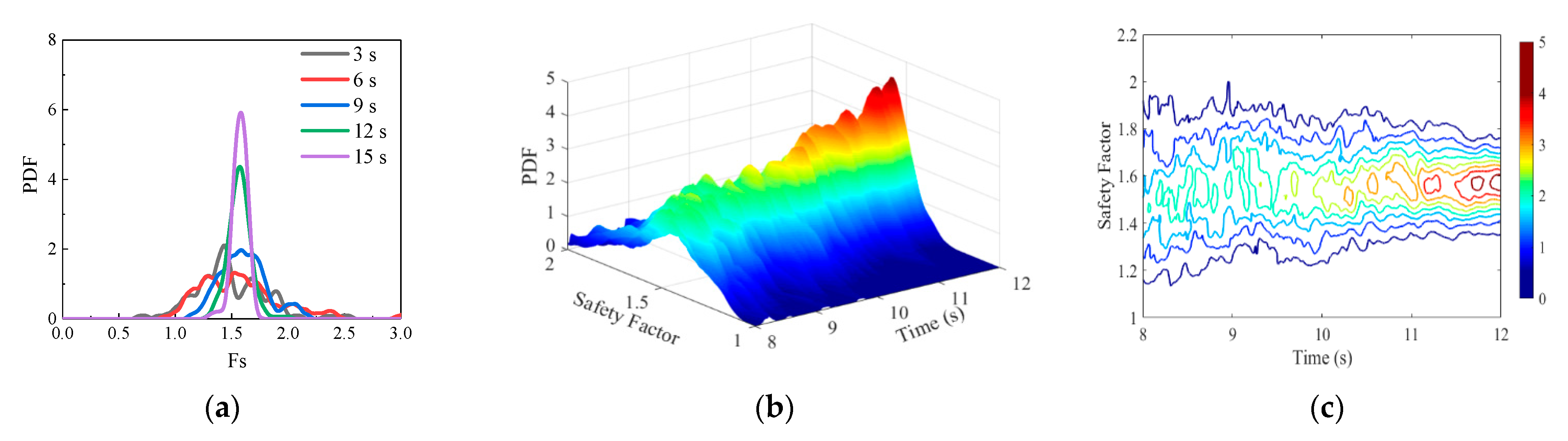
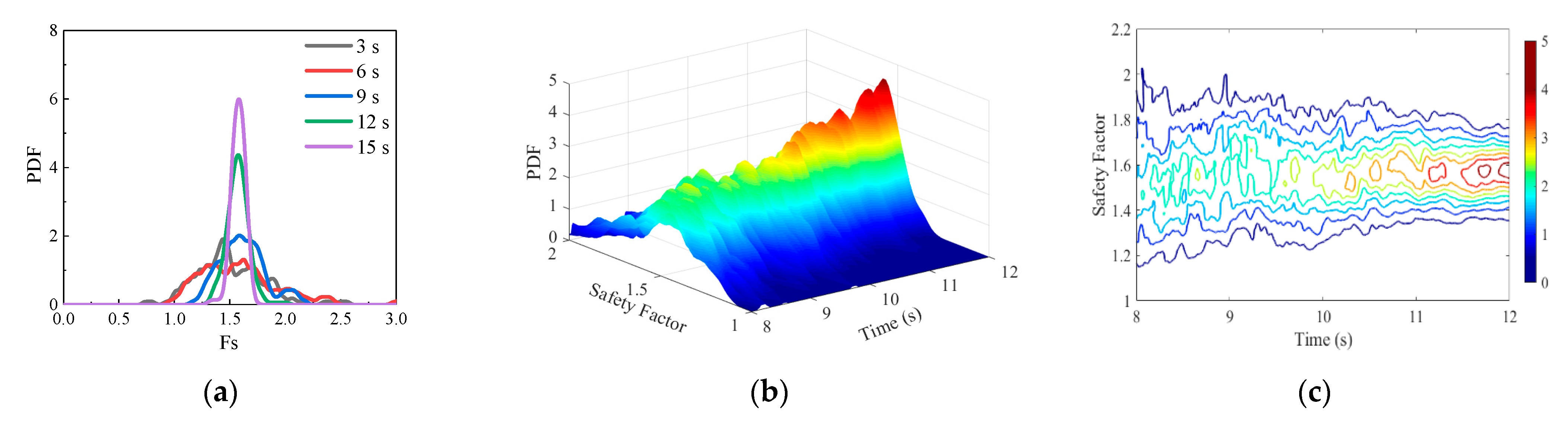

| Material | ρ (kg/m3) | φ0 (°) | Δφ (°) | n | Rf | Kb | m | K |
|---|---|---|---|---|---|---|---|---|
| Upstream rockfill | 2214 | 55.5 | 11.3 | 1350 | 0.28 | 0.80 | 780 | 0.18 |
| Downstream rockfill | 2214 | 53.0 | 11.0 | 1000 | 0.26 | 0.79 | 700 | 0.16 |
| Drainage zone | 2214 | 55.0 | 12.2 | 1300 | 0.31 | 0.79 | 800 | 0.12 |
| Transition material | 2222 | 53.5 | 10.7 | 1250 | 0.31 | 0.78 | 720 | 0.16 |
| Cushion material | 2258 | 54.4 | 10.6 | 1200 | 0.30 | 0.75 | 680 | 0.15 |
| Material | K | n |
|---|---|---|
| Upstream rockfill | 2660 | 0.444 |
| Downstream rockfill | 4997 | 0.298 |
| Drainage zone | 3115 | 0.396 |
| Transition material | 3828 | 0.345 |
| Cushion material | 5297 | 0.33 |
| Exceedance Probability (%) | Non-Reinforce Slopes | Reinforce Slopes | Reduced Value | Relative Reduction Value | |
|---|---|---|---|---|---|
| Cumulative time (s) | 0 | 50.11 | 37.96 | 12.15 | 24.25 |
| 0.2 | 24.92 | 16.55 | 8.37 | 33.59 | |
| 0.5 | 6.86 | 3.77 | 3.09 | 45.04 | |
| 1.0 | 1.36 | 0.94 | 0.42 | 30.88 | |
| 1.5 | 0.47 | 0.16 | 0.31 | 65.96 | |
| 2.0 | 0.06 | - | 0.06 | 100.00 | |
| Exceedance Probability (%) | Non-Reinforce Slopes | Reinforce Slopes | Reduced Value | Relative Reduction Value | |
|---|---|---|---|---|---|
| Cumulative slippage (m) | 0 | 33.79 | 23.63 | 10.16 | 30.07 |
| 0.2 | 2.88 | 2.23 | 0.65 | 22.57 | |
| 0.5 | 1.39 | 0.44 | 0.95 | 68.35 | |
| 1.0 | - | - | - | - | |
| 1.5 | - | - | - | - | |
| Exceedance Probability (%) | Sv (m) | Lmax (m) | Cumulative Time (s) | ||||
|---|---|---|---|---|---|---|---|
| 0 | 0.5 | 1.0 | 1.5 | 2.0 | |||
| Condition 1 | 2 | 50 | 30.73 | 2.69 | 0.69 | 0.06 | - |
| Condition 2 | 4 | 40 | 40.10 | 4.42 | 1.15 | 0.36 | 0.03 |
| Condition 3 | 4 | 50 | 37.96 | 3.77 | 0.94 | 0.16 | - |
| Condition 4 | 4 | 60 | 37.80 | 3.67 | 0.94 | 0.16 | - |
| Condition 5 | 6 | 50 | 39.47 | 4.63 | 1.09 | 0.28 | 0.02 |
| Exceedance Probability (%) | Sv (m) | Lmax (m) | Cumulative Slippage (m) | ||||
|---|---|---|---|---|---|---|---|
| 0 | 0.2 | 0.5 | 1.0 | 1.5 | |||
| Condition 1 | 2 | 50 | 18.05 | 2.01 | 0.12 | - | - |
| Condition 2 | 4 | 40 | 25.41 | 2.38 | 0.99 | - | - |
| Condition 3 | 4 | 50 | 23.63 | 2.23 | 0.44 | - | - |
| Condition 4 | 4 | 60 | 23.07 | 2.20 | 0.42 | - | - |
| Condition 5 | 6 | 50 | 26.52 | 2.37 | 0.71 | - | - |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rong, Z.; Yu, X.; Xu, B.; Du, X. Reliability Analysis of High Concrete-Face Rockfill Dams and Study of Seismic Performance of Earthquake-Resistant Measures Based on Stochastic Dynamic Analysis. Mathematics 2021, 9, 3124. https://doi.org/10.3390/math9233124
Rong Z, Yu X, Xu B, Du X. Reliability Analysis of High Concrete-Face Rockfill Dams and Study of Seismic Performance of Earthquake-Resistant Measures Based on Stochastic Dynamic Analysis. Mathematics. 2021; 9(23):3124. https://doi.org/10.3390/math9233124
Chicago/Turabian StyleRong, Zhuo, Xiang Yu, Bin Xu, and Xueming Du. 2021. "Reliability Analysis of High Concrete-Face Rockfill Dams and Study of Seismic Performance of Earthquake-Resistant Measures Based on Stochastic Dynamic Analysis" Mathematics 9, no. 23: 3124. https://doi.org/10.3390/math9233124
APA StyleRong, Z., Yu, X., Xu, B., & Du, X. (2021). Reliability Analysis of High Concrete-Face Rockfill Dams and Study of Seismic Performance of Earthquake-Resistant Measures Based on Stochastic Dynamic Analysis. Mathematics, 9(23), 3124. https://doi.org/10.3390/math9233124








