Nonstandard Finite Difference Schemes for an SIR Epidemic Model
Abstract
1. Introduction
- •
- In the first-order discrete derivatives, step-size h in the denominator is replaced by a function , such that
- •
- Nonlinear terms in can be approximated non-locally (by a suitable function of several of the mesh points), for instance:
2. Mathematical Model
- •
- : susceptible individuals;
- •
- : infective individuals;
- •
- : recovered individuals.
- •
- : The transmission rate;
- •
- : The death rate;
- •
- : The recovery rate;
- •
- a: The inhibitory rate;
- •
- N: The total population size;
- : the disease-free equilibrium;
- : the endemic equilibrium,
3. Construction of New Schemes
3.1. Scheme 1
3.2. Scheme 2
4. Positivity
5. Elementary Stability
- ,
- ,
- .
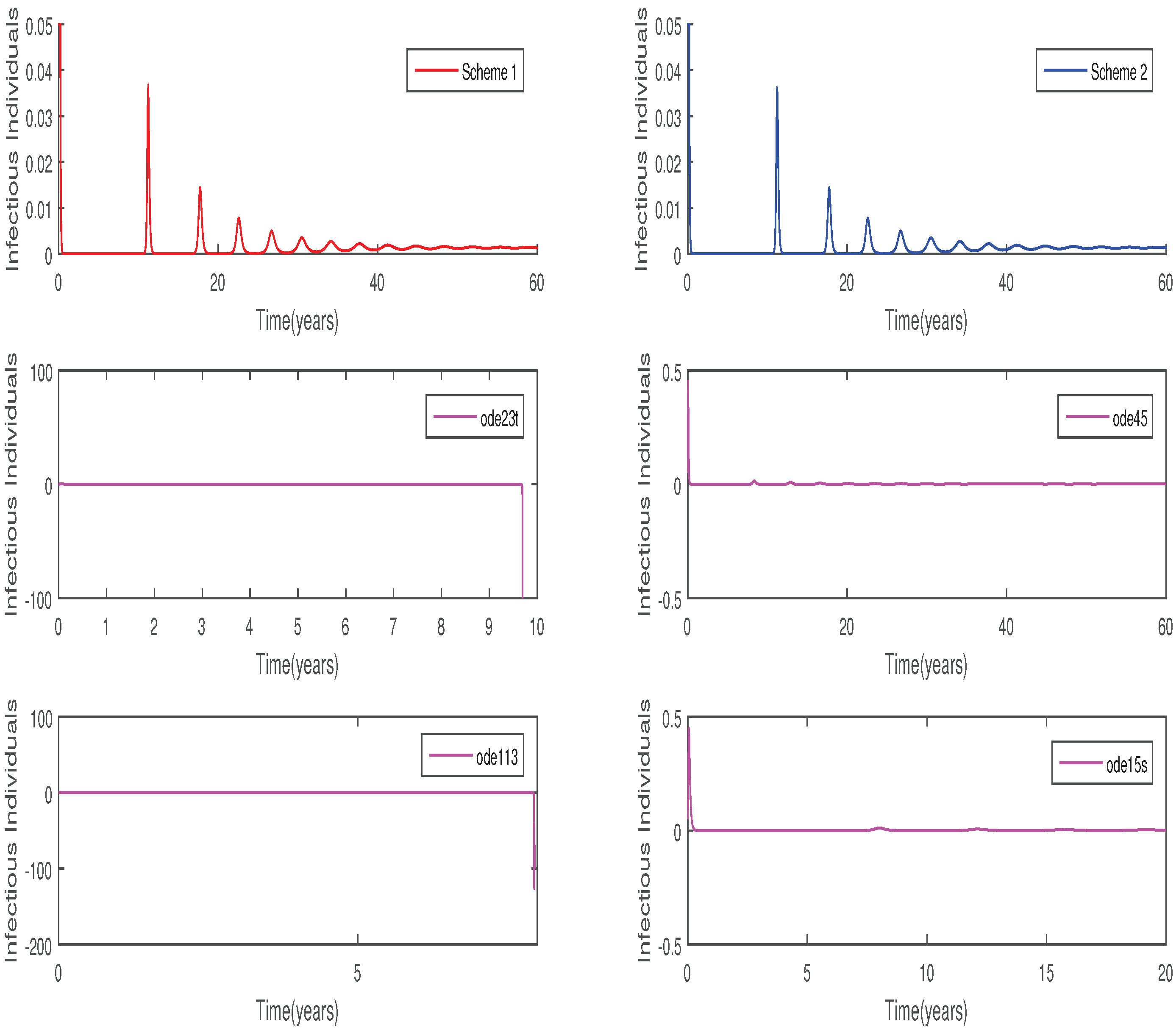
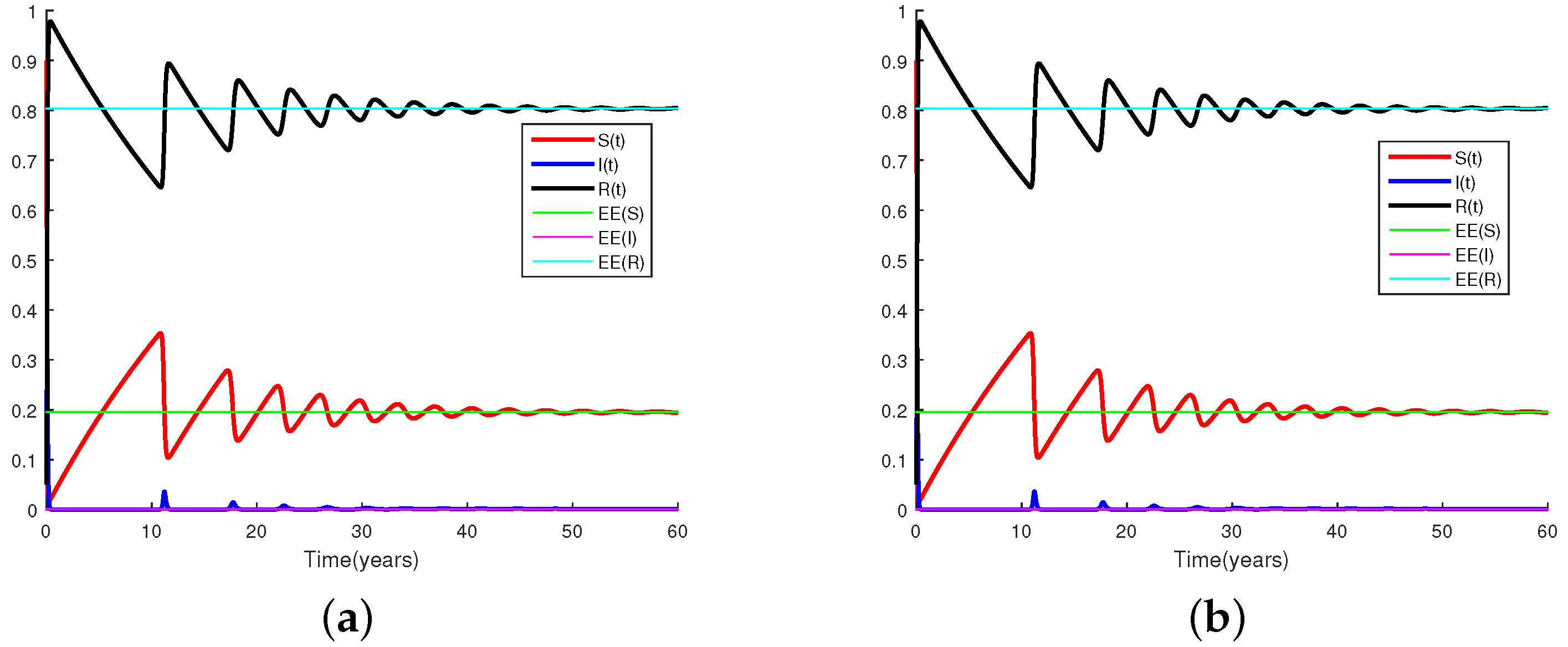
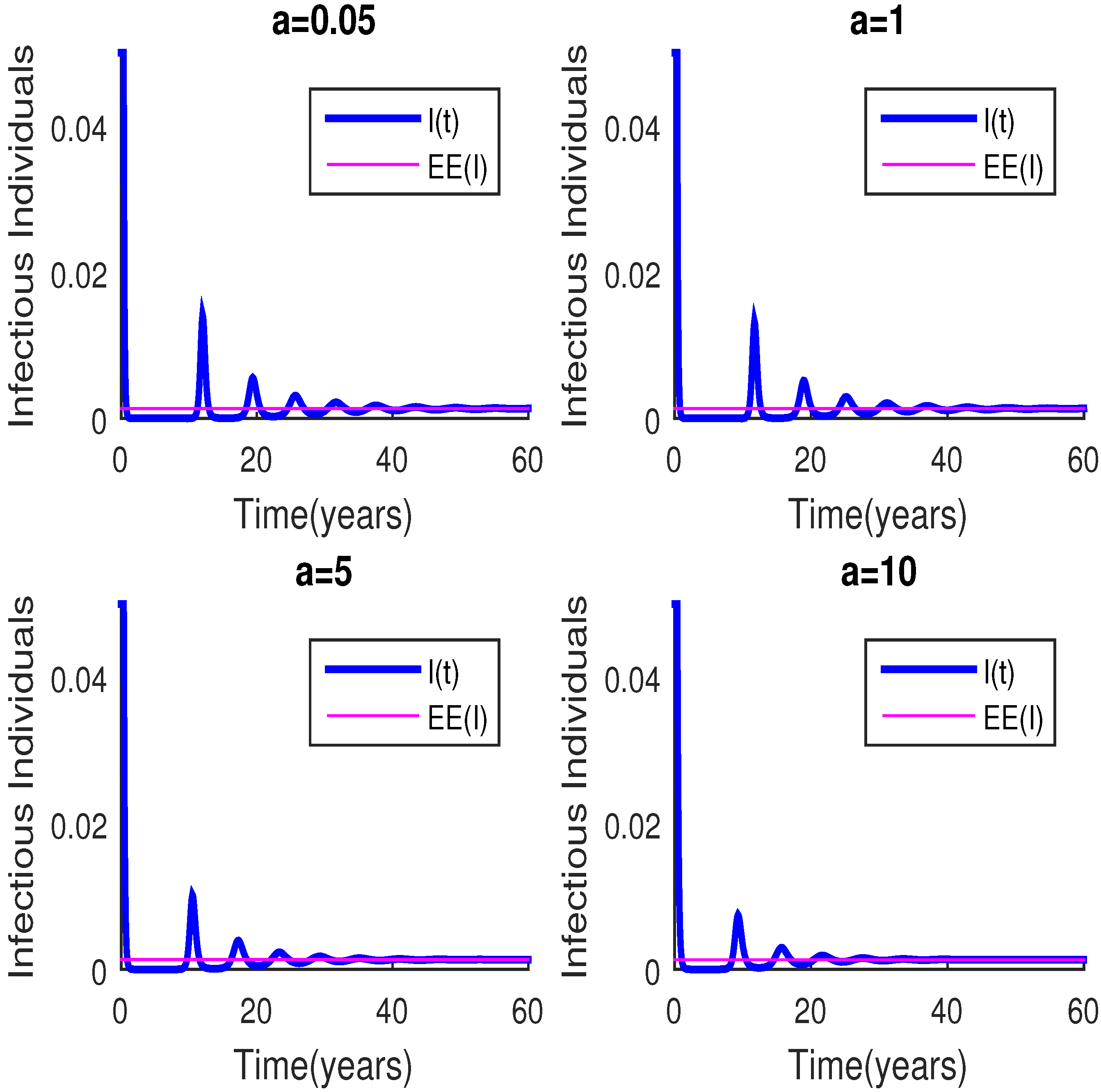
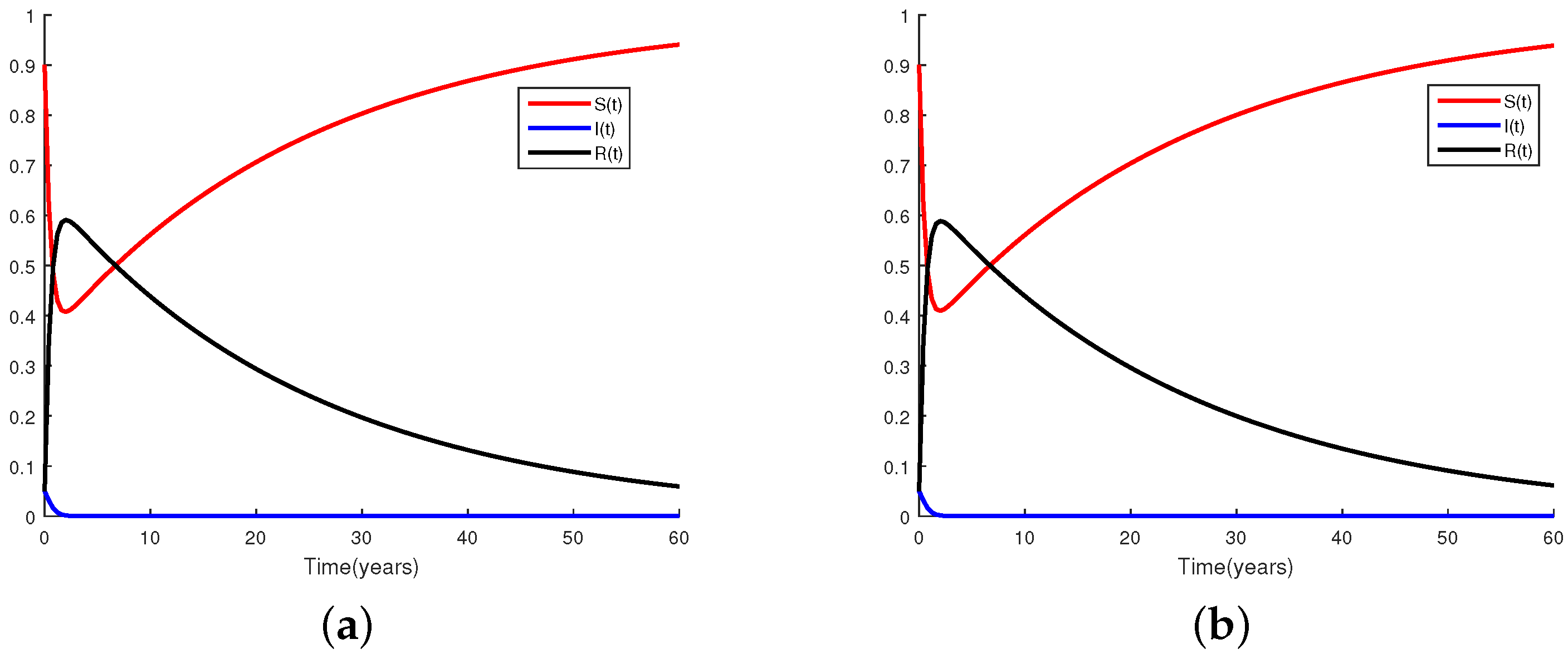
6. Numerical Results
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Arenasa, A.J.; Gonzlez-Parrab, G.; Chen-Charpentier, B.M. An Accurate Nonstandard Scheme of Predictor-Corrector Type for an SIR Epidemic Model, Technical Report 2009-01. Available online: https://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.407.848&rep=rep1&type=pdf (accessed on 27 April 2021).
- Ashyralyev, A.; Agirseven, D.; Agarwal, R.P. Stability estimates for delay parabolic differential and difference equations. Appl. Comput. Math. 2020, 19, 175–204. [Google Scholar]
- Ashyralyev, A.; Erdogan, A.S.; Tekalan, S.N. An investigation on finite difference method for the first order partial differential equation with the nonlocal boundary condition. Appl. Comput. Math. 2019, 18, 247–260. [Google Scholar]
- Lin, C.; Hsu, C.-W.; Simos, T.E.; Tsitouras, C. Explicit, semi-symmetric, hybrid, six-step, eighth order methods for solving y″ = f(x, y). Appl. Comput. Math. 2019, 18, 296–304. [Google Scholar]
- Lambert, J.D. Computational Methods in Ordinary Differential Equations; John Wiley & Sons/Wiley: Hoboken, NJ, USA, 1973. [Google Scholar]
- Osa, A.L.; Olaoluwa, O.E. A Fifth-fourth Continuous Block Implicit Hybrid Method for the Solution of Third Order Initial Value Problems in Ordinary Differential Equations. Appl. Comput. Math. 2019, 8, 50–57. [Google Scholar]
- Magagula, V.M.; Motsa, S.S.; Sibanda, P. A new bivariate spectral collocation method with quadratic convergence for systems of nonlinear coupled differential equations. Appl. Comput. Math. 2019, 18, 113–122. [Google Scholar]
- Khalsaraei, M.M.; Shokri, A.; Ramos, H.; Heydari, S. A positive and elementary stable nonstandard explicit scheme for a mathematical model of the influenza disease. Math. Comput. Simul. 2021, 182, 397–410. [Google Scholar] [CrossRef]
- Khalsaraei, M.M.; Shokri, A. The new classes of high order implicit six-step P-stable multiderivative methods for the numerical solution of Schrödinger equation. Appl. Comput. Math. 2020, 19, 59–86. [Google Scholar]
- Odibat, Z. Fractional power series solutions of fractional differential equations by using generalized Taylor series. Appl. Comput. Math. 2020, 19, 47–58. [Google Scholar]
- Sweilam, N.H.; Nagy, A.M.; El-Sayed, A.A. Sinc-Chebyshev collocation method for time-fractional order telegraph equation. Appl. Comput. Math. 2020, 19, 162–174. [Google Scholar]
- Tadumadze, T.; Dvalishvili, P.; Shavadze, T. On the representation of solution of the perturbed controlled differential equation with delay and continuous initial condition. Appl. Comput. Math. 2019, 18, 305–315. [Google Scholar]
- Mickens, R.E. Nonstandard Finite Difference Models of Differential Equations; World Scientific: Singapore, 1994. [Google Scholar]
- Mickens, R.E. Nonstandard finite difference schemes for differential equations. J. Differ. Appl. 2002, 8, 823–847. [Google Scholar] [CrossRef]
- Abbas, S.; Benchohra, M.; Hamidi, N.; Nieto, J.J. Hilfer and Hadamard fractional differential equations in Frchet spaces. TWMS J. Pure Appl. Math. 2019, 10, 102–116. [Google Scholar]
- Aliev, F.A.; Larin, V.B.; Velieva, N.; Gasimova, K.; Faradjova, S. Algorithm for solving the systems of the generalized Sylvester-transpose matrix equations using LMI. TWMS J. Pure Appl. Math. 2019, 10, 239–245. [Google Scholar]
- Anguelov, R.; Lubuma, J.M.S. Contributions to the mathematics of the nonstandard finite difference method and applications. Numer. Meth. Par. Diff. Equ. 2001, 17, 518–543. [Google Scholar] [CrossRef]
- Chen, C.; Wang, W.; Wang, X.; Wise, S.M. Positivity-preserving, energy stable numerical schemes for the Cahn-Hilliard equation with logarithmic potential. J. Comput. Phys. 2019, X3, 100031. [Google Scholar] [CrossRef]
- Dong, L.; Wang, C.; Zhang, H.A.; Zhang, Z. A positivity-preserving, energy stable and convergent numerical scheme for the cahn-hilliard equation with a flory-huggins-degennes energy. Commun. Math. Sci. 2019, 17, 921–939. [Google Scholar] [CrossRef]
- Fedorov, F.M.; Potapova, S.V. On remarkable relations and the passage to the limit in the theory of infinite systems II. TWMS J. Pure Appl. Math. 2019, 10, 154–174. [Google Scholar]
- Golbabai, A.; Nikan, O.; Molavi-Arabshahi, M. Numerical approximation of time fractional advection-dispersion model arising from solute transport in rivers. TWMS J. Pure Appl. Math. 2019, 10, 117–131. [Google Scholar]
- Harikrishnan, S.; Kanagarajan, K.; Elsayed, E.M. Existence and stability results for differential equations with complex order involving Hilfer fractional derivative. TWMS J. Pure Appl. Math. 2019, 10, 94–101. [Google Scholar]
- Imomkulov, A.N. Classification of a family of three dimensional real evolution algebras. TWMS J. Pure Appl. Math. 2019, 10, 225–238. [Google Scholar]
- Kounchev, O.; Simeonov, G.; Kuncheva, Z. Scenarios for the spread of COVID-19 anallyzed by the TVBG-SEIR spline model. Biomath 2021, 10, 17. [Google Scholar] [CrossRef]
- Kyurkchiev, N.; Kyurkchiev, V.; Iliev, A.; Rahnev, A. A New Modificatins of the SIR/SEIR Models with ”Intervention Polynomial Factor”, Methodological Aspects. Int. J. Differ. Equ. Appl. 2021, 20, 15–30. [Google Scholar]
- Kyurkchiev, N.; Kyurkchiev, V.; Iliev, A.; Rahnev, A. A look at the Modified SIRD Models with ”Intervention Polynomial Factor”, Methodological Aspects. Int. J. Differ. Equ. Appl. 2021, 20, 31–41. [Google Scholar]
- Roeger, L.W.; Barnard, R.W. Preservation of local dynamics when applying central difference methods: Application to SIR model. J. Differ. Equ. Appl. 2007, 13, 333. [Google Scholar] [CrossRef]
- Khalsaraei, M.M. Positivity of an explicit Runge-Kutta method. Ain. Shams. Eng. J. 2015, 6, 1217–1223. [Google Scholar] [CrossRef][Green Version]
- Khalsaraei, M.M.; Khodadoosti, F. Qualitatively stability of nonstandard 2-stage explicit Runge-Kutta methods of order two. Compu. Math. Phys. 2016, 56, 235–242. [Google Scholar] [CrossRef]
- Khalsaraei, M.M.; Jahandizi, R.S. Efficient explicit nonstandard finite difference scheme with positivity- preserving property. GU J. Sci. 2017, 30, 259–268. [Google Scholar]
- Khalsaraei, M.M. An improvement on the positivity results for 2-stage explicit Runge-Kutta methods. J. Comput. Appl. Math. 2010, 235, 137–143. [Google Scholar] [CrossRef]
- Noeiaghdam, S.; Micula, S. Dynamical Strategy to Control the Accuracy of the Nonlinear Bio-mathematical Model of Malaria Infection. Mathematics 2021, 9, 1031. [Google Scholar] [CrossRef]
- Noeiaghdam, S.; Sidorov, D. Caputo-Fabrizio Fractional Derivative to Solve the Fractional Model of Energy Supply-Demand System. Math. Model. Eng. Probl. 2020, 7, 359–367. [Google Scholar] [CrossRef]
- Noeiaghdam, S. A novel technique to solve the modified epidemiological model of computer viruses. SeMA J. 2019, 76, 97–108. [Google Scholar] [CrossRef]
- Panakhov, E.; Ercan, A.; Bas, E.; Ozarslan, R. Hilfer fractional spectral problem via Bessel operator. TWMS J. Pure Appl. Math. 2019, 10, 199–211. [Google Scholar]
- Piyawong, W.; Twizell, E.H.; Gumel, A.B. An unconditionally convergent finite difference scheme for the SIR model. Appl. Math. Comput. 2003, 146, 611–625. [Google Scholar] [CrossRef]
- Qalandarov, A.A.; Khaldjigitov, A.A. Mathematical and numerical modeling of the coupled dynamic thermoelastic problems for isotropic bodies. TWMS J. Pure Appl. Math. 2020, 11, 119–126. [Google Scholar]
- Ramos, H.; Popescu, P. How many k-step linear block methods exist and which of them is the most efficient and simplest one? Appl. Math. Comput. 2018, 316, 296–309. [Google Scholar] [CrossRef]
- Restrepo, J.E.; Chinchane, V.L.; Agarwal, P. Weighted reverse fractional inequalities of Minkowski’s and Holder’s type. TWMS J. Pure Appl. Math. 2019, 10, 188–198. [Google Scholar]
- Tunc, T.; Sarikaya, M.Z.; Yaldiz, H. Fractional hermite Hadamards type inquality for the co-ordinated convex functions. TWMS J. Pure Appl. Math. 2020, 11, 3–29. [Google Scholar]
- Zhang, J.; Shen, Y.; He, J. Some analytical methods for singular boundary value problem in a fractal space: A review. Appl. Comput. Math. 2019, 18, 225–235. [Google Scholar]
- Duncan, C.J.; Duncan, S.R.; Scott, S. Whooping cough epidemic in london, 1701-1812: Infection dynamics seasonal forcing and the effects of malnutrition. Proc. R. Soc. Lond. B 1996, 263, 445–450. [Google Scholar]
- Mickens, R.E.; Jordan, P.M. A positivity-preserving nonstandard finite difference scheme for the Damped Wave Equation. Numer. Meth. Parti. Diff. Equ. 2004, 20, 639–649. [Google Scholar] [CrossRef]
- Bacaer, N.; Ouifki, R.; Pretorius, C.; Wood, R.; Williams, B. Modeling the joint epidemics of TB and HIV in a south African township. J. Math. Biol. 2008, 57, 557–593. [Google Scholar] [CrossRef] [PubMed]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mehdizadeh Khalsaraei, M.; Shokri, A.; Noeiaghdam, S.; Molayi, M. Nonstandard Finite Difference Schemes for an SIR Epidemic Model. Mathematics 2021, 9, 3082. https://doi.org/10.3390/math9233082
Mehdizadeh Khalsaraei M, Shokri A, Noeiaghdam S, Molayi M. Nonstandard Finite Difference Schemes for an SIR Epidemic Model. Mathematics. 2021; 9(23):3082. https://doi.org/10.3390/math9233082
Chicago/Turabian StyleMehdizadeh Khalsaraei, Mohammad, Ali Shokri, Samad Noeiaghdam, and Maryam Molayi. 2021. "Nonstandard Finite Difference Schemes for an SIR Epidemic Model" Mathematics 9, no. 23: 3082. https://doi.org/10.3390/math9233082
APA StyleMehdizadeh Khalsaraei, M., Shokri, A., Noeiaghdam, S., & Molayi, M. (2021). Nonstandard Finite Difference Schemes for an SIR Epidemic Model. Mathematics, 9(23), 3082. https://doi.org/10.3390/math9233082






