Abstract
In this work, we attempted to find a non-linear dependency in the time series of strawberry production in Huelva (Spain) using a procedure based on metric tests measuring chaos. This study aims to develop a novel method for yield prediction. To do this, we study the system’s sensitivity to initial conditions (exponential growth of the errors) using the maximal Lyapunov exponent. To check the soundness of its computation on non-stationary and not excessively long time series, we employed the method of over-embedding, apart from repeating the computation with parts of the transformed time series. We determine the existence of deterministic chaos, and we conclude that non-linear techniques from chaos theory are better suited to describe the data than linear techniques such as the ARIMA (autoregressive integrated moving average) or SARIMA (seasonal autoregressive moving average) models. We proceed to predict short-term strawberry production using Lorenz’s Analog Method.
JEL Classification:
Q11; C15; C22; C53; C65
1. Introduction
The strawberry of Huelva (strawberry from Spain) belongs to the select group of agricultural activities in which Spain is the absolute leader in the European Union [1]. Huelva accounts for 9% of world strawberry production and 25% of that of the European Union; it is the second-largest area of production, technology, and research in the world in this sector behind California [2] and contributes more than 400 million euros to the province in direct total agricultural production value [3].
On the other hand, the evolution of strawberry production is sensitive to price fluctuations [4,5]. Strawberry is a free-market crop with no entry or exit barriers, without intervention prices or production controls. The price of strawberries is determined strictly by the free interaction of supply and demand. Knowing the future productions of these time series could mean a considerable increase in profitability for the strawberry-producing sector [1], since a large distribution usually results in sales programs with heavy penalties for non-compliance.
Yield forecast approaches are basically divided into single-factor time series models and multi-factor models. The former considers time as an independent variable and builds up mathematical models based on the yield time series to produce future predictions; the latter also considers the main influential factors in the system under study. As a first approach to the study of strawberry yield predictions, we considered only single-factor models. Multi-factor models are generally more time consuming and require extensive user intervention. In addition, external factors such as prices, costs, crop characteristics, consumer behavior, or climatic conditions often require data that may be unavailable or difficult to obtain. Finally, to use the forecasting model in the future, predictions for such factors are also required, the quality of which will depend on the accuracy of the forecasts. Thus, it is worth considering whether single-factor models provide acceptable forecasts.
Typically, autoregressive integrated moving average (ARIMA) or seasonal autoregressive moving average (SARIMA) models have been widely used in recent years for modeling and to make predictions in the livestock [6,7] and agricultural [8,9,10] sectors. In this article, we discuss an alternative non-linear method for the cases in which the resulting series is not stationary. Although we find many emerging non-linear techniques that can be used to make both short-term and long-term predictions on non-stationary chaotic data, such as the sparse identification of nonlinear dynamics (SINDy) algorithm [11] widely used to model non-linear dynamic systems and make predictions on them [12,13,14,15], or non-linear systems reconstruction techniques that allow the regeneration of time series subjected to white noise, which would allow a new study of stationarity and eliminate the disturbances associated with the observed variable [16,17], in this work, we focus on maximal Lyapunov exponents.
Deterministic chaos theory has made possible the modeling and forecasting of many time series traditionally considered as the noise of purely random behavior. There are many fields in which the deterministic chaos methodology is being applied successfully, from the climate [18] to COVID-19 [19]. For this reason, the construction and analysis of chaotic predictive models are of special interest. However, the empirical detection of chaotic dynamics is an extremely subtle problem because the strange attractor’s reconstruction that originates the deterministic dynamics is sensitive to the parameters used in non-linear tests [20].
This study focuses on this sector and proposes a novel method for yield prediction in relation to the recent literature on time series predictive models. First, we detected deterministic chaos by computing the maximum Lyapunov exponents of the time-series and observing that they are positive. Secondly, since these cannot be generated by linear models such as ARIMA [21] or SARIMA [22], we used the analog method [23,24,25]—a non-linear forecasting technique consisting of analyzing, for each of the final observations of the series, the possibilities of short-term forecasting. We intended to study whether the reconstructed phase space’s points behave according to the principle of prediction by analogous occurrences; that is, we try to see if nearby points evolve in the short-term with similar trajectories within the phase space.
Since the description of the method of analogs by Lorenz [26], this method has gained popularity for forecasting and has been applied in many studies [27,28,29,30], offering even more accurate results than other approaches that apply machine learning techniques [31,32].
The paper is organized as follows: in Section 2.1, the time series are described; Section 2.2 analyzes stationarity; in Section 2.3, the spectral analysis is performed; in Section 2.4, the maximum Lyapunov exponents are computed; in Section 3, analogous occurrences are used to obtain the predictions; in Section 4, our conclusions are discussed and presented.
2. Materials and Methods
This research uses R and Haskell programming languages, which are applied for time series forecasting.
2.1. Description of the Data
We work with time series of the daily production of three large agri-food cooperatives in the province of Huelva (coop1, coop2, and coop3) during a time interval ranging from 6 to 10 years. The time-series data refer to the total weight of strawberries, in kilograms, picked in one day. The coop1 data were collected over 10 strawberry picking seasons, from January 2011 to June 2020. The coop2 data cover 8 seasons, from January 2013 to June 2020. Finally, the coop3 data cover 6 periods, from January 2015 to June 2020.
Since the fruit picking season begins on a different date each year, we handled the datasets as follows: if for each company, corresponds to the first day of the period that started earlier and to the last day of the period that ended later, then we establish that each period starts at and ends at , filling in the days where there is no fruit picking with zeros. Finally, we join the series of each period in chronological order, obtaining a single time series for each company. The time series of coop1 contains 1642 data points, that of coop2 2130 data points, and that of coop3 1633 data points, as represented in Figure 1, Figure 2 and Figure 3.
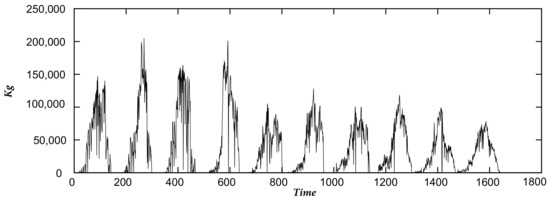
Figure 1.
Coop1 time series.
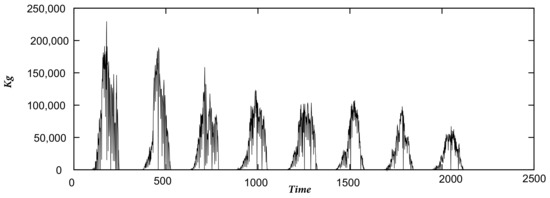
Figure 2.
Coop2 time series.
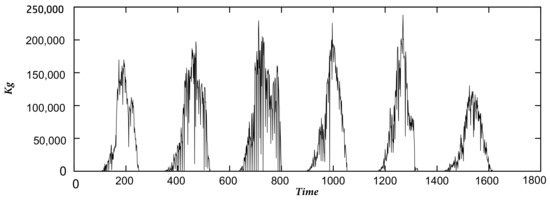
Figure 3.
Coop3 time series.
2.2. Stationarity
One of the characteristics that distinguish time series from other types of statistical data is that, in general, the data at different instants of time can be correlated. The most classical methodology for the analysis of time series is that of Box and Jenkins [21,33,34,35], which allows the identification and estimation of ARMA models (autoregressive and moving averages). These models assume the hypothesis that the series is stationary (or may become stationary from a simple transformation) and follow a linear model.
In this sense, and without carrying out an exhaustive analysis, as can be seen in Table 1, for each period of the time series, the fluctuation of the sample means is greater than the standard error, which shows that the series is not stationary.

Table 1.
Local means and standard errors of production.
It was also not possible to obtain a stationary time series by taking differences or logarithms or using seasonal autoregressive moving average (SARIMA) [36,37,38,39,40] as the sources that manage daily data use a short seasonal component; that is, the seasonal component is not very far from the data to be predicted, unlike in our work, where the seasonal component has a lag of 317 days, which makes its use computationally very expensive.
2.3. Fourier Analysis
To differentiate between random, stochastic, or chaotic non-linear deterministic processes, we used the Fourier transform to compute the time series’ power spectra. Thus, a series with very irregular temporal variability will have a smooth and continuous spectrum, indicating that all frequencies in a certain range or band of frequencies are excited by this process. On the contrary, a purely periodic or quasi-periodic process, or a superposition of them, is described by a single “line” or a finite number of “lines” in the frequency domain. Between these two extremes, chaotic non-linear deterministic processes can have peaks superimposed on a continuous and highly rippled background.
The Fourier transform [21,41,42,43,44,45,46], which is a standard tool for time-series analysis in both stationary and non-stationary series, provides a linear decomposition of the signal into Fourier bases (i.e., sine and cosine functions of different frequencies) and establishes a one-to-one correspondence between the signal at certain times (time domain) and how certain frequencies contribute to the signal, as well as how the phase of each oscillation is related to the phases of the other oscillations (frequency domain).
Figure 4, Figure 5 and Figure 6 show the log–log analysis of the squared amplitude against the frequency in cycles/day, presenting a broad spectrum for each company. Therefore, we can conclude that the data are neither periodic nor quasi-periodic. Furthermore, the data do not correspond to white noise. Wide peaks are observed at different frequencies, showing the influence of the past in both the short and long term, representing a seasonal influence.
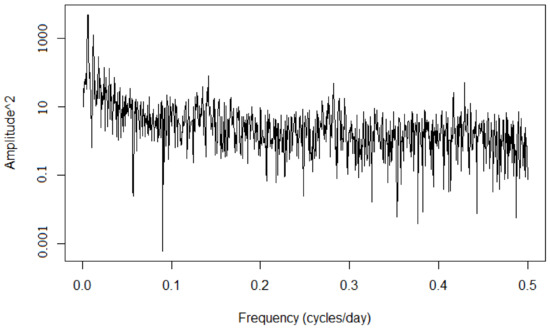
Figure 4.
Power spectrum log–log for coop1.
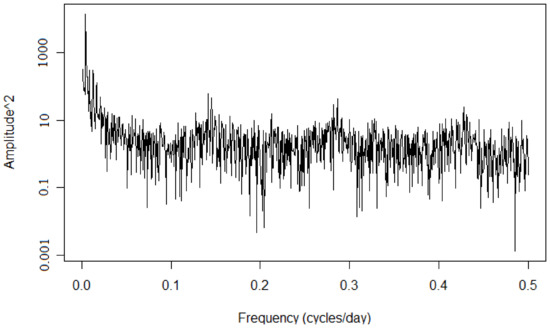
Figure 5.
Power spectrum log–log for coop2.
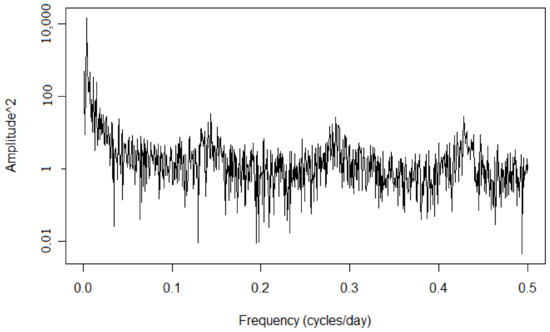
Figure 6.
Power spectrum log–log for coop3.
2.4. Lyapunov Exponents
Now that we know that the time series studied are not stationary, periodic, quasi-periodic, or stochastic, we study the series from the point of view of nonlinear deterministic processes. This section discusses the sensitivity of these dynamic systems to initial conditions by computing the maximal Lyapunov exponent of each series [47,48].
In chaotic systems, the distance between two neighboring points in phase space diverges exponentially, and therefore, even if the system is deterministic, the prediction is only possible for a short period in the future. The exponent that characterizes this exponential divergence is the Lyapunov exponent [49,50]. In this way, only a positive exponent can show sensitivity to initial conditions, so the long-term behavior of any specified initial condition with uncertainty cannot be predicted.
Some non-linear techniques compatible with small data time series, such as the Lyapunov maximal exponent calculation, are only guaranteed to work with stationary data. This problem can be circumvented using over-embedding for sufficiently high embedding dimensions and data that depend to some extent on some (unknown) parameters, and techniques designed for stationary data can be applied [51,52,53]. Furthermore, whether the series is appropriate to compute the exponent (and other non-linear quantities) can be checked by observing how well the computation converges to the overall value when increasingly large parts of the time series are used (for example, exponents for the first and second half of the data must exist and should agree with the value computed for the whole series). Finally, when a “smooth” transformation is applied to the series (such as constructing the series of the differences), these quantities should not vary either.
Since the exact definition of the Lyapunov exponent involves limits of distances (and thus points that are arbitrarily close) and we only have a finite time series, a finite approximation must be used. Several algorithms for the computation of Lyapunov exponents of finite time series have been proposed in the literature ([48,54,55]). We use the algorithm by Rosenstein et al. [56] and by [47], which is presented below.
Given a time series , we use a time-delay embedding to form a series in Euclidean m-dimensional space [51,57,58]. We choose a distance and define the map
where is the ball centered at with radius and d is the Euclidean distance. If the graph of shows a linear increase for some range of values of , then there is a maximal Lyapunov exponent for , and its value is the slope of the graph. This value must be consistent for different choices of the embedding dimension and the radius ; that is, it should not differ for different values of provided it is small enough and for dimensions above some dimension .
In Figure 7, we show the graphs of on a logarithmic scale (which has the same slope as on a linear scale, but the values on the y axis represent distances instead of logarithms of distances) for the series of coop1, for varying between 0 and 90, with embedding dimensions 2 to 13, , and a delay of 1 day [59]. There is a linear increase for between 36 and 60 and dimensions 5 and above. This suggests the existence of an attractor.
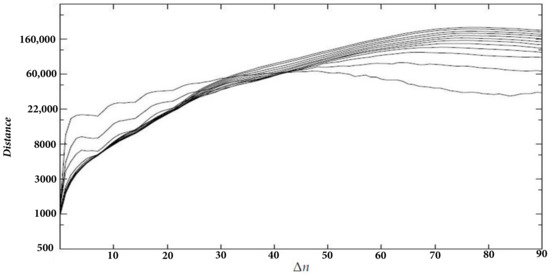
Figure 7.
for coop1 ().
In Figure 8, we conducted the same analysis for coop2. We chose a delay of 2 days, = 2000, a ranging from 0 to 100, and a dimension ranging from 2 to 13. We observe a linear increase between 38 and 52 for dimensions 5 and above.
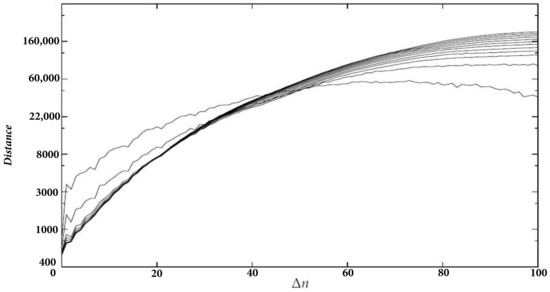
Figure 8.
for coop2 ().
Finally, Figure 9 shows the graphs for coop3. The delay is 1 day, the dimensions range from 2 to 13, = 1000, and is between 0 and 120. There is a linear increase for dimensions above 4 and between 46 and 74.
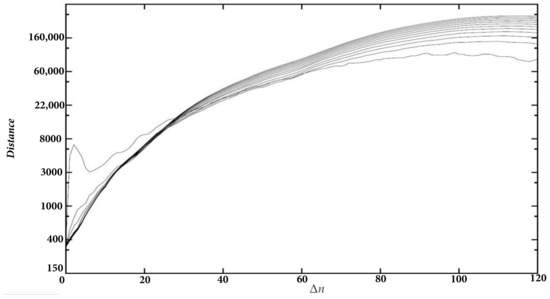
Figure 9.
for coop3 ().
Now, we verify that there are linear increases for other values of the radius and compute the exponent. In Figure 10, we plotted the graphs of coop1 for 2500, 5000, 7000, 9000, and 14,000 and dimensions between 10 and 13, again with a delay of 1 day. Each group of curves corresponds to a value of . For the sake of visibility, we displaced each curve a given amount upwards depending on .
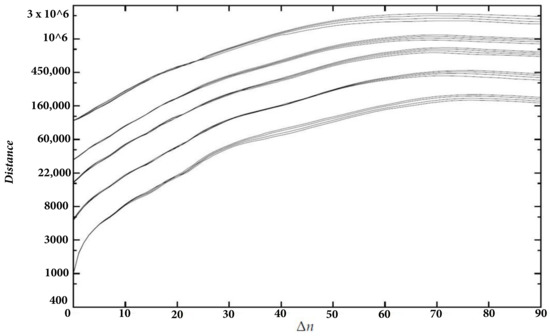
Figure 10.
for coop1 ( 2500, 5000, 7000, 9000, 14,000).
Using the least-squares method, we fitted lines to the five curves corresponding to dimension 10 and obtained Figure 11. Table 2 shows each value of , the interval where the lines were fitted to , the maximal Lyapunov exponent, and the correlation coefficient.
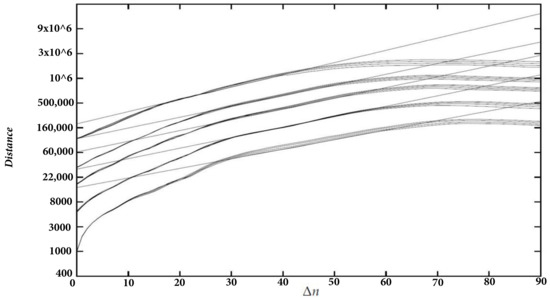
Figure 11.
Regression lines for coop1.

Table 2.
Maximal Lyapunov exponents for coop1.
Table 3 and Table 4 show the exponents for both coop2 and coop3, respectively. We used delays of 2 and 1 day, respectively, and the curves corresponding to dimension 10.

Table 3.
Maximal Lyapunov exponents for coop2.

Table 4.
Maximal Lyapunov exponents for coop3.
Since the series are non-stationary, we performed additional checks to ensure that the exponent was correct. First, we computed the exponent for some parts of each series. We found that the exponents differed to some extent, but there was not a big difference. For coop1, we divided the series into the first four seasons and the last six seasons, which seemed to be stationary. Results are shown in Table 5. For coop2 (Table 6), we chose the first four seasons and the last four seasons. For coop3, we chose seasons 1–3, 4–6, 1–4 y 1–5 (Table 7 and Table 8). Since these series are shorter than the whole series and thus noisier, sometimes we chose a different delay than the whole series to obtain a longer range of linear increase.

Table 5.
Maximal Lyapunov exponents for coop1 subseries.

Table 6.
Maximal Lyapunov exponents for coop2 subseries.

Table 7.
Maximal Lyapunov exponents for coop3 (first and second half).

Table 8.
Maximal Lyapunov exponents for coop3 (seasons 1–4 and 1–5).
Next, we computed the maximal exponent for the series of the differences. The results are shown in Table 9, Table 10 and Table 11. For these series, we fitted the lines to the curves corresponding to dimension 13. In all cases, we used a delay of 2 days.

Table 9.
Maximal Lyapunov exponents for coop1 (differences).

Table 10.
Maximal Lyapunov exponents for coop2 (differences).

Table 11.
Maximal Lyapunov exponents for coop3 (differences).
Finally, we can estimate the noise level from the graphs of . In Figure 10, we observe a sharp increase at the beginning of the curve for that is not present in the other curves. This is probably due to measurement noise. Indeed, when is of the order of the noise level, some points that are inside the balls of radius would be outside the balls if the noise were suppressed. Then, their real distance is larger than , so they seem to diverge faster than the other points in the balls, increasing the slope. After some time steps, an exponential divergence of distances due to chaos dominates over noise, and the slope decreases. Thus, the noise level for coop1 is probably around 1000. Applying the same method to coop2 and coop3, we obtained similar noise levels.
3. Results
In the field of predictability research, the non-linear local Lyapunov theory also involves analogs [23,24,25] to model predictive systems [60,61,62,63,64].
Given a series , we construct a new series in m-dimensional Euclidean space by time-delay embedding, using a delay of d days [51,57,58]. To predict the behavior of the series days ahead of day i, we choose a small and define
where is the set of the points of the sphere of radius centered at such that j is less than (so that we know ) and less than , where q is large enough to prevent temporal correlations between and . The radius should be as small as possible but above the noise level. Furthermore, there should be enough points in to prevent strong statistical fluctuations. Thus, we choose a threshold h and, if there are less than h points in the sphere, we increase the radius for that sphere until it contains at least h points.
We split the series into two parts: the first part is used to obtain appropriate parameters for the forecasting model, and the second part is used for a comparison of the real data to the forecasts obtained from the model. In this case, for each series, we chose the second part to be the last season and the first part to be the rest of the series.
The threshold q can be determined from the autocorrelation function. Thus, we have only four adjustable parameters: the dimension m, the delay d, the radius , and the minimum number of points h. To determine these parameters for each series, we performed predictions from 1 to 14 days in the future for every day in the second-last season and for some ranges of parameters. Next, we determined by least-squares the combination of parameters that produces the smallest errors in the first week, and the same for the second week and the two weeks. Thus, for each series, we obtained three sets of parameters.
The chaotic paradigm states that, despite the noisy appearance of the original series, a correct adjustment of the immersion dimension m will give rise to a complex configuration in phase space known as a strange attractor. These attractors, far from being randomly distributed, have deterministic geometric and dynamic characteristics [65].
For all the series, dimensions [59] were in the range 3–10, the delay ranged from 1 and 14, and the minimum numbers of points were 10, 16, and 22. For coop1, the radiuses were 2000, 3250, 4500, 5750, 7000, 8250, 9500, 10,750, and 12,000. For coop2, the radiuses were 200, 925, 1650, 2375, 3100, 3825, 4550, 5275, and 6000. For coop3, the radiuses were 600, 1525, 2450, 3375, 4300, 5225, 6150, 7075, and 8000. The best parameters for coop1, coop2 and coop3 are listed in the Table 12, Table 13 and Table 14, respectively.

Table 12.
Best parameters for coop1.

Table 13.
Best parameters for coop2.

Table 14.
Best parameters for coop3.
Finally, we used these parameters to perform predictions for each series’ last season and to compute the errors. In detail, for each day in the last season, we forecasted two weeks in the future; that is, for day i and prediction horizon , we made a prediction for day . Then, for each , we computed the root mean squared error , where is the real data from the series, and we divided it by the standard deviation of the last season’s data. We summarize the results in Figure 12, Figure 13 and Figure 14. Lines with circles correspond to the parameters for days 1 to 7, lines with squares correspond to days 8 to 14, and lines with diamonds correspond to days 1 to 14.
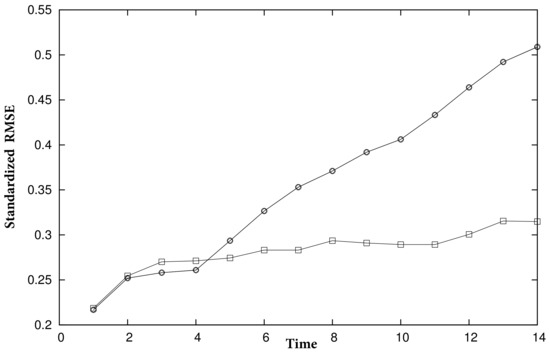
Figure 12.
Prediction errors for coop1 using nonlinear methods.
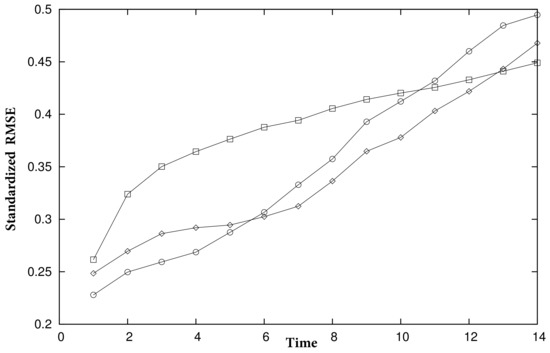
Figure 13.
Prediction errors for coop2 using nonlinear methods.
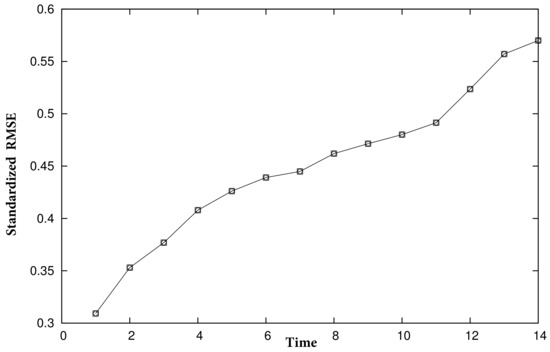
Figure 14.
Prediction errors for coop3 using nonlinear methods.
4. Discussion and Conclusions
We studied three time series of daily strawberry production data for an interval of between 6 and 10 years. We discovered that the system is chaotic and therefore, even if the data were stationary, linear methods such as Box–Jenkins could not have been applied.
First, we detected that the power spectra were all broadband, which is consistent with chaos. Then, we studied the system’s sensitivity to the initial conditions (exponential growth of the errors) using the maximal Lyapunov exponent (a metric model that studies the growth of the distances between points of a strange attractor). To confirm the validity of its calculation in short and non-stationary series, we used over-immersion and repeated the calculation in sections of the series and transformed series.
Applying non-linear methods, such as the maximal Lyapunov exponent computation, we observe ranges of exponential divergence of the distances, with maximal Lyapunov exponents around 0.04. The Fourier analysis also shows the cyclical influences of the weekday and the season. We also tried to compute the correlation dimension. However, we did not obtain clear results, and we conjectured that the quasi-periodic influence of the weekday and the season introduce strong temporal correlations that require longer time series to compute a significant dimension. Finally, we estimate that the non-deterministic noise is around 1000. We made forecasts for the last season of the series and compared the real data results, obtaining an appropriate model for short-term prediction.
The results indicate that power spectra and the maximal Lyapunov exponent can be used as effective methods to judge chaos characteristics [18,19]. We also conclude that non-linear models are more suitable than linear models for the study of strawberry harvest prediction in these companies, and that there is possibly a small-dimension attractor in this dynamic system.
In the methodology described in this work, the existence of predictable structures is also contrasted for each observation, since the unpredictability of an observation of the series from the rest reveals the independence of the random variable that generates it with respect to the rest and hence white noise, and predictability reveals non-linear determinism and therefore chaos. Thus, with the production series, we have made local predictions for analogous occurrences.
This deterministic and non-stochastic chaotic series has the characteristic that short-term prediction is possible, while medium and long-term prediction is not possible with a high degree of reliability. The practical implication from an economic perspective is the impossibility of making long-term predictions that can reorient the company’s productive policy or the sector. However, short-term predictions will support the logistics and commercial operations of a company and therefore the product profitability. The use of machine learning techniques that try to find internal structures with the predictive power of certain characteristics of the series in the long term, instead of a detailed behavior in the short term, thanks to deterministic chaos is perhaps a future objective to be investigated. However, this requires a much longer data series than we currently have.
Another step to study will be to incorporate other variables into the model to verify if the predictive result improves and determine the bifurcation points that will alert us to the risks of catastrophes that may change the dynamics of the model.
Finally, in order to simplify the computational part of the resolution to our problem, we have discarded other recent algorithms that identify implicit non-linearities or non-linear systems reconstruction techniques on non-stationary chaotic data since the main idea of our work was to find a simple solution to the stationarity problems encountered. For example, if we apply the SINDy method [11], we must consider many non-linear functions within the matrix of possible functions, which makes it computationally difficult. On the other hand, we have obtained good results without having to rebuild the time series, such as in [16], making the method lighter, although certainly less successful. However, we leave these objectives as some very interesting future lines of research that can potentially improve upon the typical linear research carried out on the modeling of primary sector activities.
Author Contributions
Conceptualization, J.D.B.; methodology, J.D.B. and J.M.; validation, J.D.B. and J.M.; investigation, J.D.B. and J.M.; resources, J.D.B.; data curation, J.M.; writing—original draft preparation, J.D.B. and J.M.; writing—review and editing, J.D.B.; project administration, J.D.B. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Junta de Andalucía. Consejería de la Presidencia, Administración Pública e Interior. Secretaría General de Acción Exterior grant number G/82A/44103/00 01.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Restrictions apply to the availability of these data. Data were obtained from a third party. The data are not publicly available due to privacy concerns.
Acknowledgments
The authors acknowledge the support provided by the companies by releasing the data used for the experiments.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Cicco, A.D. The Fruit and Vegetable Sector in the EU—A Statistical Overview; EU: Maastricht, The Netherlands, 2020. [Google Scholar]
- De Andalucia, J. El Sector de la Fresa de Huelva; Junta de Andalucia: Sevilla, Spain, 2008. [Google Scholar]
- Hortoinfo. Andalucia Produce el 97 por Ciento de la Fresa Espanola y el 26 de la Europea; Hortoinfo: Almería, Spain, 2018. [Google Scholar]
- Invenire Market Intelligence. Berries in the World, Introduction to the International Markets of Berries; Invenire Market Intelligence: Angelniemi, Finland, 2008. [Google Scholar]
- Willer, H.; Schaak, D.; Lernoud, J. Organic farming and market development in Europe and the European Union. In Organics International: The World of Organic Agriculture; FiBL; IFOAM—Organics International: Frick, Switzerland; Bonn, Germany, 2018; pp. 217–250. Available online: https://orgprints.org/id/eprint/31187/ (accessed on 22 November 2021).
- Selvaraj, J.J.; Arunachalam, V.; Coronado-Franco, K.V.; Romero-Orjuela, L.V.; Ramírez-Yara, Y.N. Time-series modeling of fishery landings in the Colombian Pacific Ocean using an ARIMA model. Reg. Stud. Mar. Sci. 2020, 39, 101477. [Google Scholar] [CrossRef]
- Wang, M. Short-term forecast of pig price index on an agricultural internet platform. Agribusiness 2019, 35, 492–497. [Google Scholar] [CrossRef]
- Mehmood, Q.; Sial, M.; Riaz, M.; Shaheen, N. Forecasting the Production of Sugarcane Crop of Pakistan for the Year 2018–2030, Using Box-Jenkin’s Methodology. J. Anim. Plant Sci. 2019, 5, 1396–1401. [Google Scholar]
- Wu, H.; Wu, H.; Zhu, M.; Chen, W.; Chen, W. A new method of large-scale short-term forecasting of agricultural commodity prices: Illustrated by the case of agricultural markets in Beijing. J. Big Data 2017, 4, 1–22. [Google Scholar] [CrossRef] [Green Version]
- Osman, T.; Chowdhury, A.; Chandra, H.R. A study of auto-regressive integrated moving average (ARIMA) model used for forecasting the production of tomato in Bangladesh. Afr. J. Agron. 2017, 5, 301–309. [Google Scholar]
- Brunton, S.L.; Proctor, J.L.; Kutz, J.N. Discovering governing equations from data by sparse identification of nonlinear dynamical systems. Proc. Natl. Acad. Sci. USA 2016, 113, 3932–3937. [Google Scholar] [CrossRef] [Green Version]
- Leylaz, G.; Wang, S.; Sun, J.Q. Identification of nonlinear dynamical systems with time delay. Int. J. Dyn. Control 2021, 1–12. [Google Scholar] [CrossRef]
- Liang, J.; Zhang, X.; Wang, K.; Tang, M.; Tian, M. Discovering dynamic models of COVID-19 transmission. Transbound. Emerg. Dis. 2021, 1–7. [Google Scholar] [CrossRef]
- Bhadriraju, B.; Bangi, M.S.F.; Narasingam, A.; Kwon, J.S.I. Operable adaptive sparse identification of systems: Application to chemical processes. AIChE J. 2020, 66, e16980. [Google Scholar] [CrossRef]
- Bhadriraju, B.; Narasingam, A.; Kwon, J.S.I. Machine learning-based adaptive model identification of systems: Application to a chemical process. Chem. Eng. Res. Des. 2019, 152, 372–383. [Google Scholar] [CrossRef]
- Karimov, A.; Nepomuceno, E.G.; Tutueva, A.; Butusov, D. Algebraic Method for the Reconstruction of Partially Observed Nonlinear Systems Using Differential and Integral Embedding. Mathematics 2020, 8, 300. [Google Scholar] [CrossRef] [Green Version]
- Wang, W.X.; Lai, Y.C.; Grebogi, C. Data based identification and prediction of nonlinear and complex dynamical systems. Phys. Rep. 2016, 644, 1–76. [Google Scholar] [CrossRef] [Green Version]
- Yuan, Q.Y.; Li, C.; Yang, Y.; Ye, K.H. Nonlinear Characteristics Analysis of Wind Speed Time Series. J. Eng. Therm. Energy Power 2018, 33, 135–143. [Google Scholar]
- Raj, V.; Renjini, A.; Swapna, M.; Sreejyothi, S.; Sankararaman, S. Nonlinear time series and principal component analyses: Potential diagnostic tools for COVID-19 auscultation. Chaos Solitons Fractals 2020, 140, 110246. [Google Scholar] [CrossRef]
- Chen, D. Searching for Economic Chaos: A Challenge to Econometric Practice and Nonlinear Tests. Nonlinear Dyn. Evol. Econ. 1992, 217, 253. [Google Scholar]
- Box, G.E.P.; Jenkins, G.M. Time Series Analysis; Holden-Day: San Francisco, CA, USA, 1976. [Google Scholar]
- Geurts, M.; Ibrahim, I. Comparing the Box-Jenkins approach with the exponentially smoothed forecasting model application to Hawaii tourists. J. Mark. Res. 1975, 12, 182–188. [Google Scholar] [CrossRef]
- Ruelle, D. Chance an Chaos; Princeton University Press: Princeton, NJ, USA, 1991. [Google Scholar]
- Katok, A.; Hasselblatt, B. Introduction to the Modern Theory of Dynamical Systems; Cambridge University Press: Cambridge, UK, 1996. [Google Scholar]
- Ruelle, D. Chaotic Evolution and Strange Attractors: The Statistical Analysis of Time SERIES for Deterministic Nonlinear Systems; Cambridge University Press: Cambridge, UK, 1989. [Google Scholar]
- Lorenz, E.N. Atmospheric predictability as revealed by naturally occurring analogues. J. Atmos. Sci. 1969, 26, 636–646. [Google Scholar] [CrossRef] [Green Version]
- Raynaud, D.; Hingray, B.; Evin, G.; Favre, A.C.; Chardon, J. Assessment of meteorological extremes using a synoptic weather generator and a downscaling model based on analogues. Hydrol. Earth Syst. Sci. 2020, 24, 4339–4352. [Google Scholar] [CrossRef]
- LuValle, M. A simple statistical approach to prediction in open high dimensional chaotic systems. arXiv 2019, arXiv:1902.04727. [Google Scholar]
- Hamill, T.M.; Whitaker, J.S. Probabilistic quantitative precipitation forecasts based on reforecast analogs: Theory and application. Mon. Weather Rev. 2006, 134, 3209–3229. [Google Scholar] [CrossRef]
- Lguensat, R.; Tandeo, P.; Ailliot, P.; Pulido, M.; Fablet, R. The analog data assimilation. Mon. Weather Rev. 2017, 145, 4093–4107. [Google Scholar] [CrossRef] [Green Version]
- Amnatsan, S.; Yoshikawa, S.; Kanae, S. Improved Forecasting of Extreme Monthly Reservoir Inflow Using an Analogue-Based Forecasting Method: A Case Study of the Sirikit Dam in Thailand. Water 2018, 10, 1614. [Google Scholar] [CrossRef] [Green Version]
- Shunya Okuno, K.A.; Hirata, Y. Combining multiple forecasts for multivariate time series via state-dependent weighting. Chaos Interdiscip. J. Nonlinear Sci. 2019, 29, 033128. [Google Scholar] [CrossRef]
- Wold, H. A Study in the Analysis of Stationary Time Series; Almquist and Wiksell: Estocolm, Sweden, 1938. [Google Scholar]
- Yule, G.U. Why do we Sometimes Get Nonsense-correlation between Time Series? A Study in Sampling and the Nature of Times Series. J. R. Stat. Soc. 1926, 89, 1–64. [Google Scholar] [CrossRef]
- Slutsky, E. The Summation of Random Causes as the Source of Cyclic Processes. Econometrica 1937, 5, 105–146. [Google Scholar] [CrossRef]
- Li, D.; Jiang, F.; Chen, M.; Qian, T. Multi-step-ahead wind speed forecasting based on a hybrid decomposition method and temporal convolutional networks. Energy 2022, 238, 121981. [Google Scholar] [CrossRef]
- Sekadakis, M.; Katrakazas, C.; Michelaraki, E.; Kehagia, F.; Yannis, G. Analysis of the impact of COVID-19 on collisions, fatalities and injuries using time series forecasting: The case of Greece. Accid. Anal. Prev. 2021, 162, 106391. [Google Scholar] [CrossRef]
- He, K.; Ji, L.; Wu, C.W.D.; Tso, K.F.G. Using SARIMA-CNN-LSTM approach to forecast daily tourism demand. J. Hosp. Tour. Manag. 2021, 49, 25–33. [Google Scholar] [CrossRef]
- García, J.R.; Pacce, M.; Rodrígo, T.; de Aguirre, P.R.; Ulloa, C.A. Measuring and forecasting retail trade in real time using card transactional data. Int. J. Forecast. 2021, 37, 1235–1246. [Google Scholar] [CrossRef]
- Guizzardi, A.; Pons, F.M.E.; Angelini, G.; Ranieri, E. Big data from dynamic pricing: A smart approach to tourism demand forecasting. Int. J. Forecast. 2021, 37, 1049–1060. [Google Scholar] [CrossRef]
- Priestley, M.B. Spectral Analysis and Time Series; Academic Press: London, UK, 1981; Volumes I and II. [Google Scholar]
- Jenkins, G.M.; Watts, D.G. Spectral Analysis and Its Applications; Holden-Day: San Francisco, CA, USA, 1986. [Google Scholar]
- Brockwell, P.; Davis, R. Time Series: Theory and Methods; Springer Series in Statistics; Springer: New York, NY, USA, 1987. [Google Scholar]
- Meynard, A.; Torrésani, B. Spectral estimation for non-stationary signal classes. In Proceedings of the 2017 International Conference on Sampling Theory and Applications (SampTA), Tallinn, Estonia, 3–7 July 2017; pp. 174–178. [Google Scholar]
- Bruscato, A.; Toloi, C.M.C. Spectral analysis of non-stationary processes using the Fourier transform. Braz. J. Probab. Stat. 2004, 18, 69–102. [Google Scholar]
- Priestley, M. Power spectral analysis of non-stationary random processes. J. Sound Vib. 1967, 6, 86–97. [Google Scholar] [CrossRef]
- Kantz, H. A robust method to estimate the maximal Lyapunov exponent of a time series. Phys. Lett. A 1994, 185, 77–87. [Google Scholar] [CrossRef]
- Wolf, A.; Swift, J.B.; Swinney, H.L.; Vastano, J.A. Determining Lyapunov exponents from a time series. Phys. D Nonlinear Phenom. 1985, 16, 285–317. [Google Scholar] [CrossRef] [Green Version]
- Abarbanel, H. Local and global Lyapunov exponents on a strange attractor. In Nonlinear Modeling and Forecasting; SFI Studies in the Science of Complexity; Casdagli, M., Eubank, S., Eds.; Addison-Wesley: Boston, MA, USA, 1992; Volume XII, pp. 229–247. [Google Scholar]
- Eckmann, J.; Ruelle, D. Ergodic theory of chaos and strange attractors. Rev. Mod. Phys. 1985, 57, 617–656. [Google Scholar] [CrossRef]
- Kantz, H.; Schreiber, T. Nonlinear Time Series Analysis, 2nd ed.; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Hegger, R.; Kantz, H.; Matassini, L.; Schreiber, T. Coping with non-stationarity by overembedding. Phys. Rev. Lett. 2000, 84, 4092–4095. [Google Scholar] [CrossRef]
- Parlitz, U.; Zöller, R.; Holzfuss, J.; Lauterborn, W. Reconstructing physical variables and parameters from dynamical systems. Int. J. Bifurc. Chaos 1994, 4, 1715–1719. [Google Scholar] [CrossRef]
- Sano, M.; Sawada, Y. Measurement of the Lyapunov spectrum from a chaotic time series. Phys. Rev. Lett. 1985, 55, 1082. [Google Scholar] [CrossRef]
- Eckmann, J.P.; Kamphorst, S.O.; Ruelle, D.; Ciliberto, S. Lyapunov exponents from a time series. Phys. Rev. A 1986, 34, 4971. [Google Scholar] [CrossRef]
- Rosenstein, M.T.; Collins, J.J.; Luca, C.J.D. A practical method for calculating largest Lyapunov exponents from small data sets. Phys. D Nonlinear Phenom. 1993, 65, 117–134. [Google Scholar] [CrossRef]
- Takens, F. Detecting Strange Attractors in Turbulence; Lecture Notes in Mathematics; Springer: New York, NY, USA, 1981; Volume 898. [Google Scholar]
- Sauer, T.; Yorke, J.A.; Casdagli, M. Embedology. J. Stat. Phys. 1991, 65, 579–616. [Google Scholar] [CrossRef]
- Takens, F. Estimation of dimension and order of time series. In Nonlinear Dynamical Systems and Chaos; Progress in Nonlinear Differential Equations and Their Applications; Springer: Basel, Switzerland, 1996; Volume 19, pp. 405–422. [Google Scholar] [CrossRef]
- Li, J.P.; Ding, R.Q. Temporal-spatial distribution of atmospheric predictability limit by local dynamical analogs. Mon. Weather Rev. 2011, 139, 3265–3283. [Google Scholar] [CrossRef]
- Li, J.P.; Ding, R.Q. Temporal-spatial distribution of the predictability limit of monthly sea surface temperature in the global oceans. Int. J. Climatol. 2013, 33, 1936–1947. [Google Scholar] [CrossRef]
- Li, J.P.; Ding, R.Q. Weather forecasting: Seasonal and interannual weather prediction. In Encyclopedia of Atmospheric Sciences, 2nd ed.; Elsevier: London, UK, 2015; pp. 303–312. [Google Scholar]
- Li, J.P.; Feng, J.; Ding, R.Q. Attractor radius and global attractor radius and their application to the quantification of predictability limits. Clim. Dyn. 2018, 51, 2359–2374. [Google Scholar] [CrossRef] [Green Version]
- Huai, X.W.; Li, J.P.; Ding, R.Q.; Feng, J.; Liu, D.Q. Quantifying local predictability of the Lorenz system using the nonlinear local Lyapunov exponent. Atmos. Ocean. Sci. Lett. 2017, 10, 372–378. [Google Scholar] [CrossRef] [Green Version]
- Schuster, H. Deterministic Chaos: An Introduction; VCH: Weinheim, Germany, 1988. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).