1. Introduction
In this paper, we consider systems of differential equations with polynomial and rational nonlinearities and with a dependence on a discrete parameter (hybrid systems). Such systems arise in biological and ecological applications, where the discrete parameter allows us to incorporate in the model a genetic regulation by a genetic code. We investigate the stability of attractors of these systems under stress. The attractors define system functioning regimes, while stresses are sudden changes of system parameters (for example, heat shocks). Our aim is to investigate the attractor stability under infinite sequences of shocks. It is inspired by the following idea of M. Gromov and A. Carbone: “Homeostasis of an individual cell cannot be stable for a long time as it would be destroyed by random fluctuations within and out of cell. There is no adequate mathematical formalism to express the intuitively clear idea of replicative stability of dynamical systems” ([
1], p. 40). It is clear that replicative stability is important for the evolution of cancer cells, viruses, for example, such as COVID 19, and bacteria such as
E. coli. There is no doubt that replication helps viruses and bacteria survive in changing environments (see, for example, Lensky’s experiment with
E. coli [
2]). However, there is a non-trivial question: how to estimate chances that such replicative evolution can continue eternally even under action of therapeutic agents? For COVID-19, it is an important question of will we have fourth or fifth pandemic waves, etc., or can the virus vanish? In this paper, however, we consider cancer cells as an example because our analyses are more applicable to this case.
Using a model, proposed in this paper, one can formulate the Gromov–Carbone idea in rigorous mathematical terms and, under some assumptions, to prove this hypothesis. Our model exploits ideas of artificial intelligence theory; namely, we suppose that the response to stress is defined by deep gene networks (DGN), which are similar to deep neural networks (DNNs). It allows us to use estimates obtained recently in DNN theory [
3,
4,
5]. Note that deep networks were recently applied as interpretable models of the gene network regulations in [
6].
To describe replicative stability, we incorporate into our model a regulation by the discrete parameter (for biosystems and ecosystems it is a gene regulation) and consider how the stochastic stability depends on regulation. Our results help us to explain, for example, why cancer cells exhibit a long survival time even under a strong therapy. Indeed, cancer cells give us an example of evolving biosystem affected by a sequence of stresses (for example, immune therapy or chemotherapy). It is worth noting that replicative stability for biochemical systems, introduced in this paper, is a new idea for the theory of stability (robustness) of these systems. Earlier, a number of works (see fundamental papers [
7,
8] and references therein) considered a more usual approach, which investigates reactions of the biochemical system to the small disturbances of kinetic rates or reagent concentrations. We also investigate the stability in the vicinity of small changes in some states (attractors). However, we take into account variations of the system genotype. We suppose that these variations compensate for a significant part of external perturbations that reinforces the system stability. The gene regulation system evolves in such a way that this compensation mechanism becomes more and more effective, which provides stability under fluctuations for large times.
Let us first outline the concept of stochastic stability. We consider organisms as biochemical machines, which can be modeled by a system of ordinary differential equations. A regime of our biosystem functioning is defined by an attractor
. Let us denote by
the probability that the system state lies in a
-neighborhood of the attractor
within the time interval
. The parameter
defines the size of a homeostasis domain, where the system stays viable (here we follow viability theory, see, for example, [
9]). In the framework of that viability approach, the Gromov–Carbone hypothesis reduces to two claims. The first assertion is that for biological systems with fixed parameters and a fixed genetic code,
This means that all biosystem states, sooner or later, will be destroyed by fluctuations. The second assertion is that a sequence of modifications of the system genotype can lead to eternal stability, where the viability probability stays positive for all times:
where
. The constant
can be interpreted as follows: imagine a large population of cancer cells, bacteria or viruses. Let this population be affected by consecutive therapeutic attacks. The constant
describes the relative fraction of cells ( bacteria, viruses) that will survive.
In other words, systems with fixed parameters are unstable under environment fluctuations but the evolution of the genetic code can stabilize them. This replicative stability is considered in [
10] for some network models; see [
11] for an overview. For some classes of hybrid dynamical systems involving a dependence on discrete genotypes
, which can evolve in time, it is shown that inequality (
2) implies
i.e., the genotype length
L has a tendency to increase. Here we assume that the genotype
s is a Boolean string
and the length
L of
s is
N. However, it is well known that the genotype length does not correlate directly with the morphological complexity and that evolution does not always lead to a genotype length increase. For example, Drosophila, nematode and human have numbers of coding genes of the same order (although bacteria genomes are much shorter than the nematode genome). Nonetheless, it is well known that the gene regulation system has become more and more complex throughout evolution. In this paper, we use deep networks (DNs) to describe gene regulation and show that DN network growth makes biosystems stable for long time periods.
Let us outline the model in more detail. In contrast to some earlier works [
12,
13,
14], which used either formidable computations [
12,
13], or sophisticated nonlinear asymptotics [
14], we use deep networks. These networks consist of, in general, many layers. The depth
of a network is the number of hidden layers, and the size
is the total number of units. In practice, networks with depth
can be considered as shallow, while deep networks typically have many layers. Connections between units in these networks depend on coding sequences
,
of Boolean genes, which could be switched off (
) or switched on (
). The inputs of the DN’s are the stress parameter values and the system states. The DN produces an output, which depends on unit interconnections and thus on the genetic code, which determines these interconnections. The main idea behind our model of regulation is that the DN output and the stress impact cancel out each other.
To describe stress impacts, we use a model of subsequent environmental shocks. This idea is consistent with the Gould–Eldredge concept [
15], where evolution is represented as a sequence of intermittent short bursts and longtime stasis periods, the evolution bursts appear in response to stresses induced by environment. Let
be an infinite increasing sequence of time moments
. These moments can be considered as moments of environment shocks (stresses), when the environment suddenly changes. At these moments, some system parameters can change. A well-known example is a heat shock connected with temperature, which affects kinetic rates in biochemical systems and produces mutations [
16]. For cancer cells, these shocks can describe a therapy. Our aim is to estimate the probability that a local attractor
is robust under all those environmental shocks within a large (maybe, infinite) time interval.
Let us outline our results. The first result (Theorem 1) concerns a connection between gene regulation complexity and uncertainty of environment. The important measure of genetic regulation complexity is the number of equilibria of gene regulation network
. This question on the number of the equilibria has received the attention of many works; in particular, it was studied for the famous NK model (pioneered in [
17]). The NK model is a mathematical model describing a “tunably rugged” fitness landscape, depending on two parameters,
N and
K. The parameter
N is the length of a Boolean genotype
s length, and
K defines the topology of fitness landscape via the number of genes involved in the trait control. The NK model has the main applications in evolutionary biology. First, it was supposed that
is a relatively small,
, where an exponent
. In particular, for the Hopfield model with symmetrical interaction [
18], this relation holds with
. However, later it was shown that in the NK model,
can be exponentially large [
19]. A similar result is obtained for another simple model, which describes a special class of Hopfield models with asymmetric interaction and a special interaction topology [
20]. Experimental data [
21,
22] show that in gene interaction networks there are strongly connected nodes that can be named hubs, or centers. The hubs communications go via a number of weakly connected nodes. This centralized connectivity has been found in gene–gene and protein–protein interaction networks [
21,
22], and such networks can support many equilibrium states.
To explain why they have a number of equilibria, we define an entropy
of environment uncertainty, depending on the robustness level
and gene regulation. This quantity is the Kolmogorov
-entropy (see, for example, [
23,
24]) on the metric space of perturbations
with a special metric. We show that if an attractor describing biosystem functioning does not collapse under all perturbations (conserves its topological structure) then there exists a connection between
and the entropy
:
This means that entropy of regulation must be no less than the environment uncertainty.
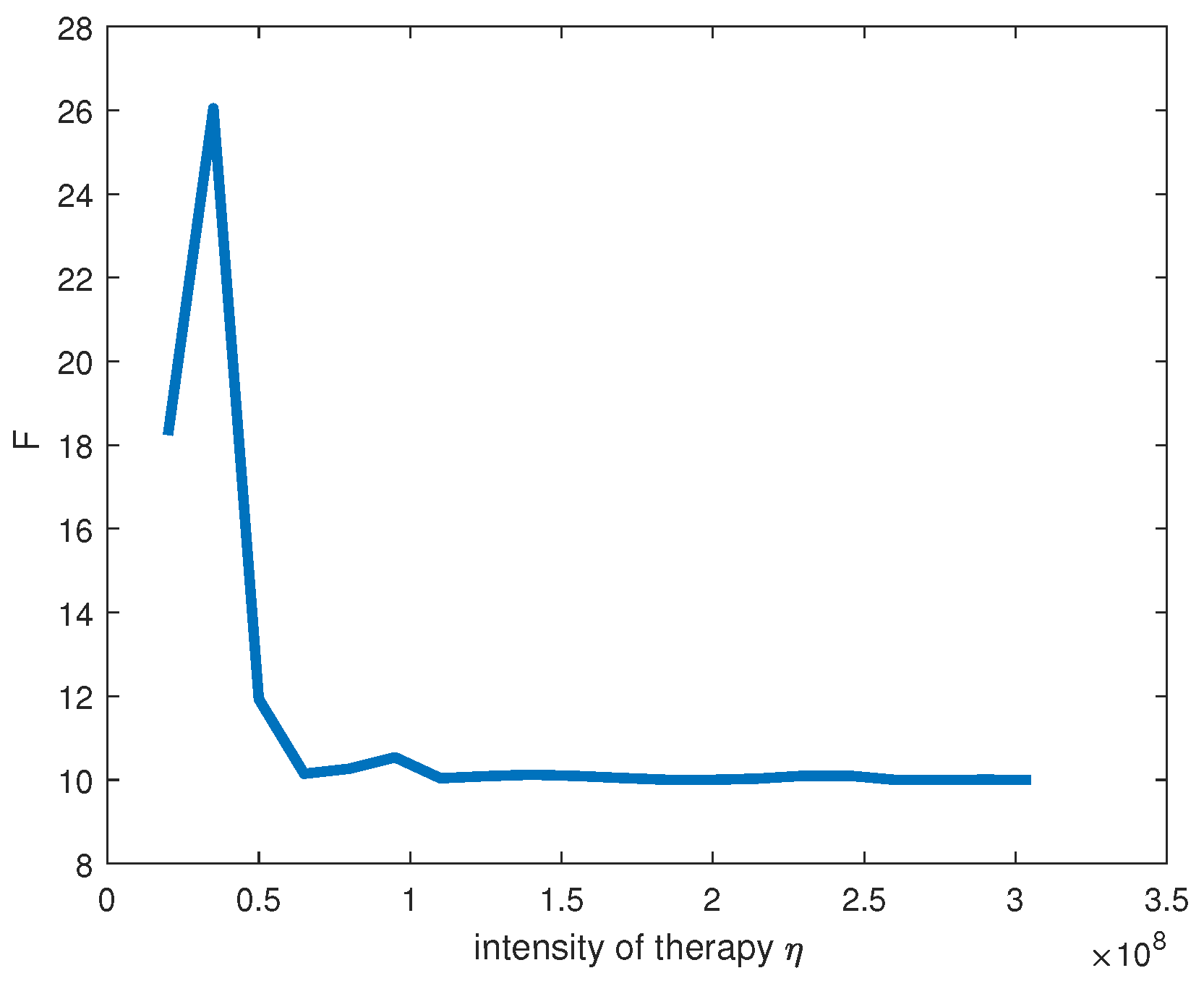
This result, in particular, shows that, to kill cancer cells, we should use a combined therapy (for example, chemotherapy together with a heat therapy). Hyperthermia therapy is heat treatment for cancer that can be a powerful tool when used in combination with chemotherapy or radiation. Chemotherapy resistance develops over time as the tumors adapt (due to replicative stability). Chemoresistance against several anticancer drugs could be reversed by the addition of heat therapy.
Our results show that before all, it is necessary to attack hubs of the gene regulation network. In fact,
critically depends on the gene interaction topology. Even a small increase in the number of hubs in gene regulation networks leads to a sharp increase in
[
20]. These results are consistent with the conclusions of [
25,
26], where it was shown that network hubs buffer environmental variations and also make switches in regulatory networks. Our results are supported by some experimental data, at least qualitatively [
27]. A number of hub genes are identified in cancer cell regulation. According to these results, drugs attacking the hub genes should be especially effective. A list of such candidate drugs targeting hub genes can be found in Table 3 from [
27].
There is also a connection with basic results of hard combinatorial problem theory. Fundamental results [
28] on Boolean functions and the
K-SAT problem assert that to satisfy many constraints, we should use a number of Boolean variables. Our result (
4) can be considered as an analog of these results. If we have a genotype
s of the length
N, then
; thus, for Boolean regulation models, (
4) implies that the genome length
N should be more than the entropy
.
Furthermore, we show that it is possible to provide stochastic attractor robustness by an appropriate genotype choice at each environment shock
. If, in contrast, the genotype is fixed, then the stochastic stability tends to zero as
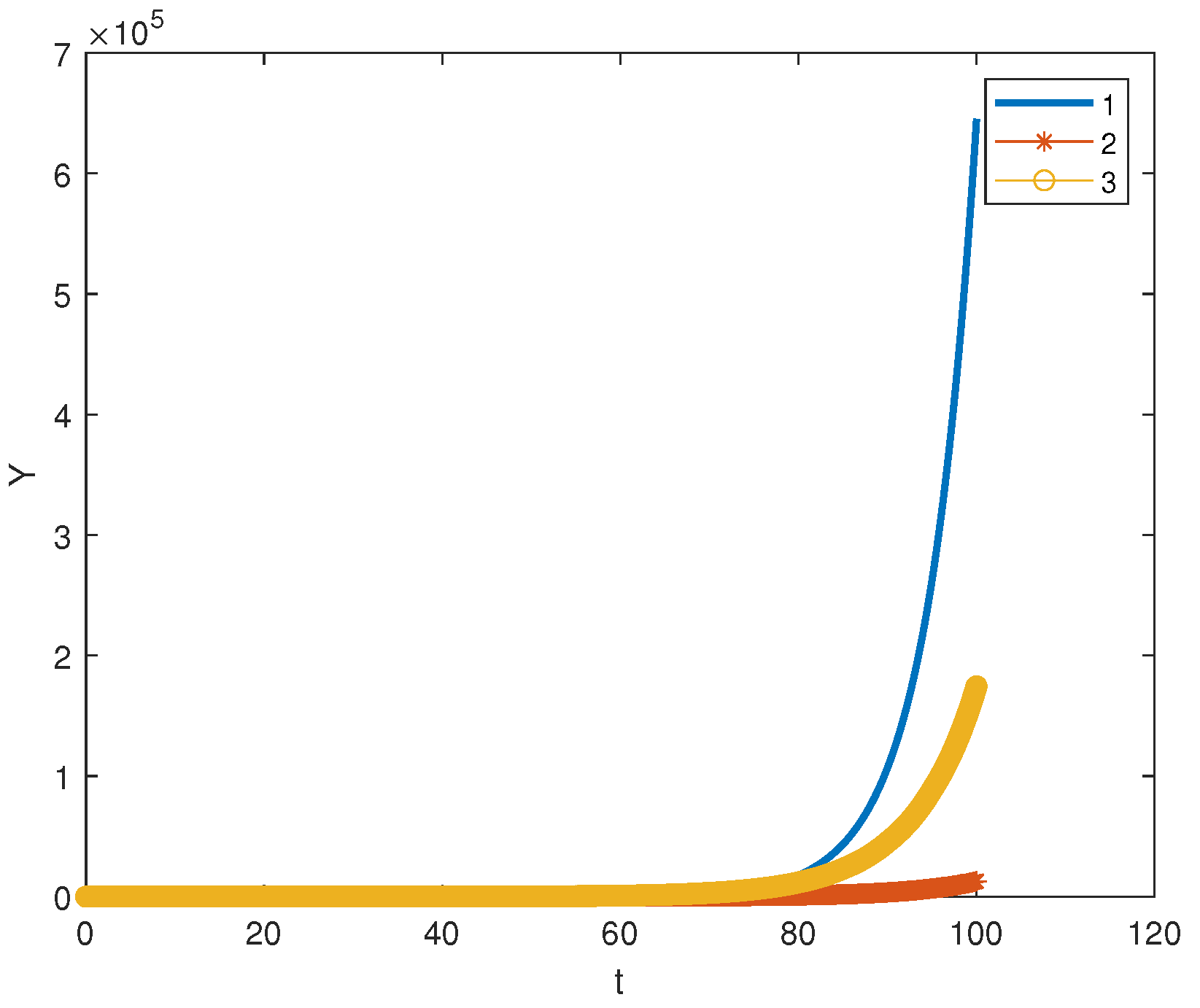
. For cancer these results are confirmed by numerical simulations, where we use a model from [
29] extended to take into account the evolution of cancer cells. If the cancer cells do not evolve, immune therapy may be effective, otherwise cancer wins sooner or later.
To conclude this introduction, let us note that the estimates of stochastic stability, obtained in the paper (see Theorem 3), allows us to find the main factors, which determine the organism fate under the stress stability: the sparsity of reaction network, the stress sensitivity, the stress dimension (the number of perturbed external parameters affecting the rates of biochemical reactions) and the size of gene regulation network.
The paper is organized as follows. In the next section, we describe models with random perturbations and gene regulation. In
Section 4, we state the model of environmental shocks and formulate some assumptions needed for the mathematical tractability of the problem. In
Section 5, we formulate some definitions, and further, we find a necessary condition for the attractor stability.
In
Section 7, we consider attractor robustness under a sequence of environment shocks. In this section, we apply DNN’s that finally give Theorem 3, which states an estimate of replicative stability. The last section contains a discussion and conclusions. To simplify reading, the technical parts of demonstrations are relegated into
Appendix A.
3. Model with Random Parameters
We describe our models in two steps, first we formulate a model without gene regulations and then with regulation.
We consider systems of differential equations with a dependence on a random process
. They have the form
where
, where
D is a compact domain in
with a smooth boundary
,
are biochemical species concentrations,
, the reaction terms
are sufficiently smooth functions of
v, for example, multivariate polynomials in
v, and also smooth functions of
. The functions
are random processes of a trajectory, which are piecewise constant in
t and take values in a compact subset
of
, where the quantity
p is a positive integer (dimension of stress parameter
). These processes
describe multiplicative noise. The source of this noise is an environment of a biosystem. Other assumptions of
will be described later.
We complement the system of stochastic Equation (
5) by initial conditions
To define
f we use the standard models of chemical kinetics and population dynamics. The simplest choice is a polynomial model, which can be derived by the law of mass action:
where
is a multi-index with integers
,
are finite subsets of
and
are coefficients that determine kinetic rates. Note that the well-known Lotka–Volterra and generalized Lotka–Volterra systems (which have ecological and economical applications, see [
31,
32]) are also included in the class of systems defined by (
7).
In real biochemical applications, we are often dealing with binary reactions, where only two exponents
, and sparse
, where, although the reagent number
n may be large, for each
i, the number
of non-zero coefficients
in each row is bounded,
. In a more sophisticated case (which arises when in a slow-fast polynomial system we express fast variables via slow ones) we have rational
v nonlinearities, for example,
where
and
are polynomials. We suppose that
are separated from zero:
for all
and
. Such systems appear in biochemical kinetics, population dynamics and cancer modeling. As an example, let us consider the following model of cancer immunotherapy [
29,
30]:
where
denotes the concentration of cells with antitumor activity in the tumor site (CTL cells), and
is the concentration of tumor cells. This model thus concerns two cell populations: normal cells and cancer ones. Parameters
are positive coefficients, which can be explained as follows. The parameter
is the normal rate of immune cell flow into the tumor site,
is the immune cells death rate due to interaction with tumor cells,
is the fraction of tumor cells killed by immune cells,
is the tumor cells carrying capacity,
r is the tumor cells growth rate,
is a natural death rate of immune cells,
is the steepness coefficient of immune cell recruitment and
is the maximal immune cells recruitment rate [
29]. For
this model and its generalizations are investigated in [
30], the term
describes a therapy by infusion of CTL cells (it is proposed in [
29]).
To provide the existence and uniqueness of solutions to the Cauchy problem (
5) and (
6) for all
, we assume the following. Let
where
is a unit normal vector directed outside
D at the point
. Then solutions of the Cauchy problem (
5) and (
6) exist and are unique for all
.
It is worth noting that polynomial and rational functions
may not satisfy conditions (
12). Since we further investigate a local stability of local attractors, we can restrict ourselves to considering narrow neighborhoods of those attractors
. Therefore, we can truncate nonlinearities in
setting for instance
, where
outside of an open neighborhood
W of
.
3.1. Extended Model with Regulation
Different complicated models of gene regulation were proposed, for example, [
33,
34] for Drosophila morphogenesis, however, we apply another approach using DNN’s and inspired by recent biological works (for example, [
6]).
Let
be a time dependent gene expression vector. We have
N Boolean genes
, which take values in the set
,
. The
i-th gene may be switch on (when
), or switch off (when
). The Boolean string
s encodes interconnections in the networks of gene regulation (see
Section 7.2). We incorporate genes
s into system (
5) using the following
Assumption GRSuppose that coefficients depend on the genetic code s:and they are Lipshitz in ξ for each s. This assumption means that regulation goes via a genetic control of kinetic rates. Moreover, we assume that the network finds a genotype s, which produces an optimal answer to stress, almost instantly. We obtain thus that s is involved in the vector field via kinetic coefficients : .
Let us introduce vector fields describing perturbations. Consider, for example, a heat shock. All kinetic rates depend on the temperature
T:
, sometimes in a complicated manner. However, typically we have a reference value
corresponding to an optimal functioning regime (for example, if
T is the human body temperature, then
is about 36 degrees). Let
, where
is a temperature increment corresponding to a heat shock. Then in the case (
7) one obtains that the perturbations
of the
have the form
where
In the general case, let
be an optimal parameter value corresponding to a normal system functioning. Then we denote by
the perturbation of
f, which appears as a result of a parameter
variation. Let us denote the non-perturbed field
by
. Then we have the two following systems: the non-perturbed one
and the perturbed system:
where, in general case,
and
s can depend on
t.
3.2. Attractors and Semiflows
Let us denote by
a compact invariant locally attracting set (a local attractor) of semiflow
generated by the Cauchy problem for system (
17) for given fixed
s and
. The semiflow generated by the non-perturbed system (
16) will be denoted by
and the corresponding attractors by
. We consider mainly two cases:
is a stable hyperbolic equilibrium
or a stable hyperbolic limit cycle
with a period
. (A reminder that hyperbolicity for an equilibrium means that the spectrum of the corresponding linearized operator does not intersect an imaginary axis, while for cycles it means that the corresponding Floquet multiplicators do not lie on the unit circle of the complex plane. For the general theory of hyperbolic sets, see [
35,
36]). We are going to estimate the probability that a local attractor (or an invariant set) of our system is stable under those shocks. We define that probability in the next subsection.
7. Stability under Many Shocks
In this section, we use the model of gene regulation from
Section 4.1. We are going to prove the Gromov–Carbone hypothesis and show that the complexity growth of the gene regulation network can lead to a successful evolution, where attractors stay robust under all shocks. First, in the coming subsection, we study the case when the gene regulation does not work and the genotype
s is fixed.
7.1. Instability for Systems with Fixed Parameters
Let us prove a claim. Remember that on the set of possible perturbations , a probabilistic measure is defined.
Theorem 2. Let be a hyperbolic equilibrium for system (17) with . Suppose that for each s the range of the map contains a closed ball of radius centered at 0, and the measure μ on is continuous with respect to the Lebesgue measure on . Then for sufficiently small where . Proof. Using the theorem assumptions, we choose such a perturbation
such that
If
is small enough then by implicit function theorem and using that our equilibrium
is hyperbolic, one can show that the equation
has a solution
close to
:
. This solution is a hyperbolic equilibrium attractor for system (
17). If a trajectory
stays inside the
-neighborhood of
for all
, this trajectory converges to
:
Therefore,
. However, according to Proposition 1, one has
which creates a contradiction with (
33) for sufficiently small
. Therefore, we have a non-zero probability
to find a
such that all trajectories
, which start in a
-neighborhood
of
, leave that neighborhood within a sufficiently large interval
. Now we use the fact that the parameters
are i.i.d. random variables. In fact, consider the intervals
. The probability to find
such that the state leaves
within
is not less than
. All these leaving events are independent, because
are independent. Therefore, the probability of leaving
within
is not less than
, and as a result, we obtain (
32). □
This result confirms Gromov–Carbone’s hypothesis on the fundamental instability of biosystems under large parameter variations. However, if we suppose that the gene regulation system can evolve, it is possible that inequality (
2) holds for a
. Then, evolution can continue within a large time frame, with a positive probability. We consider that evolution in the coming subsection.
7.2. Evolution and DNN’s
To investigate the evolution problem in more detail, we apply recent results of the deep networks theory [
4,
24,
38]. Recently, people started to apply ReLU networks to model gene regulation [
3,
6,
39]. The deep networks with ReLU activators allow us to overcome the curse of dimensionality [
38].
Let the gene regulation be defined by deep networks with ReLU activator functions. Remember that the depth of a network is the number of hidden layers, and the size is the total number of units. Let us denote by the maximal number of units in the network layers.
The following estimate follows from results [
4]. Let
be a Lipshitz function defined on a compact set
. Then there is a network
with
layers and
units in each layer such that
where
is the Lipshitz constant of
G.
Note that this approximation is made by a network with real-valued synaptic weights, for example, for a single hidden layer perceptron, we have
where
are real valued coefficients. We however need a network whose parameters depend on a binary string
s. For ReLU sigmoids
, this binary coding problem can be resolved as follows. Consider for simplicity the case (
35) (a multilayered case can be considered in a similar way). We first find values of real valued coefficients
, providing the needed approximation. Each
we approximate by
M bits within a precision
:
where
The ReLU function is Lipshitz with the constant 1. Therefore,
for bounded inputs
and some constants
, and
denotes the network of the same structure as
but with the weights
. The same procedure with the replacement of
to
can be performed for coefficients
.
Remark. If the network has the size , then we use genes to construct the network encoded by a binary string .
7.3. Result on Replicative Stability
We assume that assumption
GR holds and consider the non-perturbed system (
16). Let
be a local attractor of the semiflow
generated by this system. The following theorem describes the probability of stochastic robustness of this attractor with gene regulation under a sequence of shocks
,
. Together with (
16) we consider the same systems with gene regulation terms defined by DNN’s (which are considered in the previous subsection):
Within each interval , the system under an environmental shock is defined by the parameter , , where is the k-th set of external perturbations. The shocks are independent and we choose the set randomly from a countable set . The index k defines a kind of interaction between the organism and its environment. At the k-th step the corresponding gene regulation networks have the size , the depth and units in each layer. The weights of connections in that network are encoded by a genotype as it is explained in the previous subsection. We suppose that this network finds the correct choice instantly. These networks solve the following approximation problem:
Approximation problem APFor a given target functionof v to find a deep network such that the erroris minimal. Further, to formulate the next theorem, let us introduce important parameters permitting to estimate the Lipshitz constants of the target functions
. The first parameter is the sparsity of the reaction network
, which is the number of elements in
. We introduce the sparsity of the whole biochemical system by
. The second parameter is a sensitivity of kinetic rates under the perturbation of
k-th type defined as follows. Let
Then the
k-th stress sensitivity
is
The third parameter is the productivity of the network, or in other words, the maximal (over all components and all reactions) reaction output
Then the Lipshitz constant
of perturbation
g as a function of
can be estimated via the introduced quantities:
An estimate obtained in the next theorem is rough; nonetheless, it allows us to identify the main factors, which determine the organism fate under the stress stability: the sparsity of reaction network, the stress sensitivity, and the size of the gene regulation network.
Theorem 3. Suppose that is either a stable hyperbolic equilibrium or a stable hyperbolic limit cycle for the semiflow defined by non-perturbed system (16), and we have stresses at the moments . Then there is a sequence of networks , , such that for sufficiently small positive the stochastic stability satisfieswhereand is a constant uniform in δ as . Let us make some comments.
(i) The main idea is to provide stability as follows: at each time we choose resolving the approximation problem AP.
(ii) If the attractor is chaotic, the attractor contains unstable trajectories and a priori estimates from the proof fail. The standard ideas connected with hyperbolicity do not work because our perturbation is not autonomous in time and moreover it is not sufficiently smooth ( are Lipshitz functions but they are not ).
(iii) We suppose that the number of coding genes in the layer may depend on the evolution step k: , where is the number of genes in each layer at the k-th evolution step. The dependence on k is very important: it determines the evolution of the regulation network, and according to assertion 2, without that evolution, it is impossible to reach the robustness for all times.
(iv) From the biological point of view, assumptions of the theorem are not quite realistic because we suppose here that the gene regulation system instantly finds an optimal genotype , but it is hard to study a completely realistic model. If the time lag between action of environmental stress and the system adaptive answer is sufficiently small with respect to a characteristic time of biochemical evolution, then one can expect that our results are still valid (although the mathematical analysis becomes more sophisticated). However, if that time lag is not small, our results are not applicable and the biochemical system can lose its adaptivity.
(v) For infinite sequences of perturbations , the stability for all times is possible if the series converges.
(
vi) Due to results of
Section 7.2 (see the remark at the end of that subsection), the number
of genes needed to encode a deep gene regulations network can be estimated as
, i.e., it is more than the network size up to a logarithmic factor. This is roughly consistent with experimental data. For example, for the
E. coli metabolic network includes 744 reactions catalyzed by 607 enzymes and the
E. coli genome contains 4288 protein coding genes [
40].
Note that Theorems 1 and 3 lead to the following interesting corollary: if
, then, to provide eternal robustness (
2), the size
of the gene regulation network cannot be bounded as
:
.
Proof. Note that
are non-smooth (although Lipshitz bounded) functions of
v; therefore, we cannot use ideas connected with
-shadowing, hyperbolicity, etc. Instead of this, we use rough straight forward estimates. Let us consider the Cauchy problems
where
and
. Let
. Then for
one has
where
and
denote the derivative of
with respect to
v.
Lemma 1. Let the errors of approximation problemAPsatisfyfor each k. Then for sufficiently small one haswhere is uniform in . For the proof, which is quite standard, see
Appendix A.
Using the lemma, at
k-th evolution step we solve approximation problem
AP. We use the estimate (
34). This estimate shows that the probability to satisfy condition (
41) for each
k equals
, which according to Lemma 1, gives the estimate of
from below. This proves the theorem. □