Global Dynamics for an Age-Structured Cholera Infection Model with General Infection Rates
Abstract
:1. Introduction
- (II)
- There exists one positive constant satisfying for .
- (III)
- and are Lipschitz-continuous on with , and , for .
2. Preliminaries
2.1. Existence and Uniqueness of Solutions
2.2. Point Dissipativeness
- (i)
- , , ;
- (ii)
- , .
2.3. Asymptotical Smoothness and Global Attractor
3. Existence and Local Stability of Equilibria
3.1. Equilibria and Basic Reproductive Number
3.2. Local Stability of Equilibria
4. Global Stability of Equilibria
4.1. Uniform Persistence
4.2. Global Stability of the Infection-Free Equilibrium
4.3. Global Stability of the Infection Equilibrium
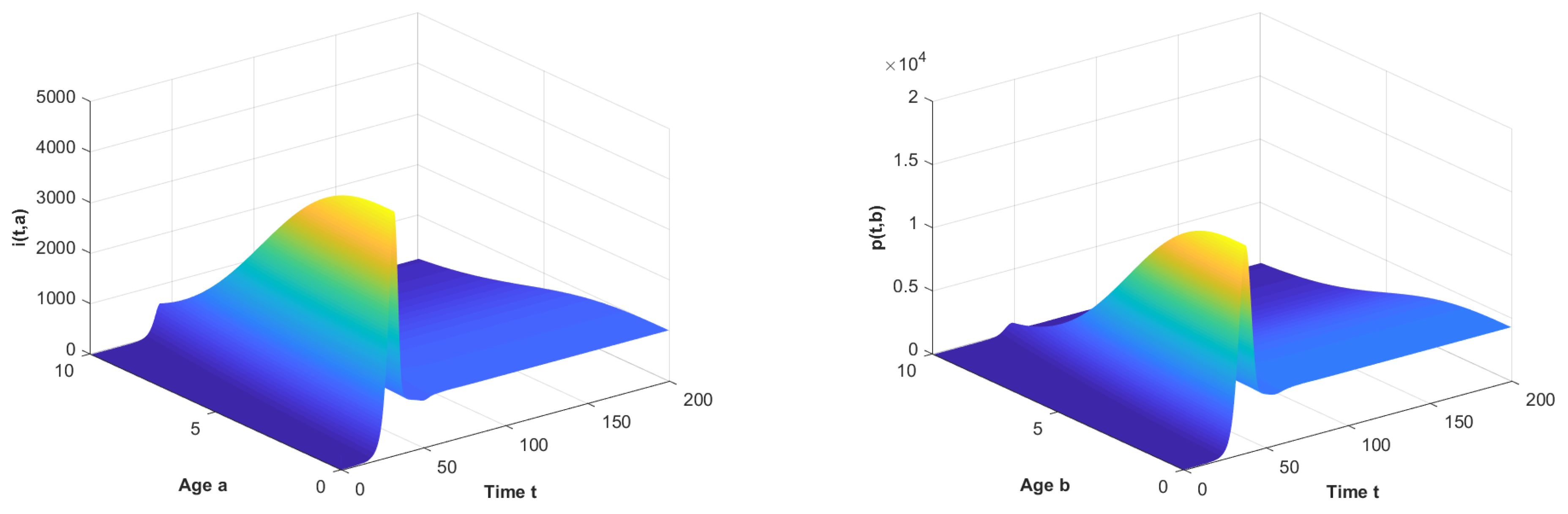
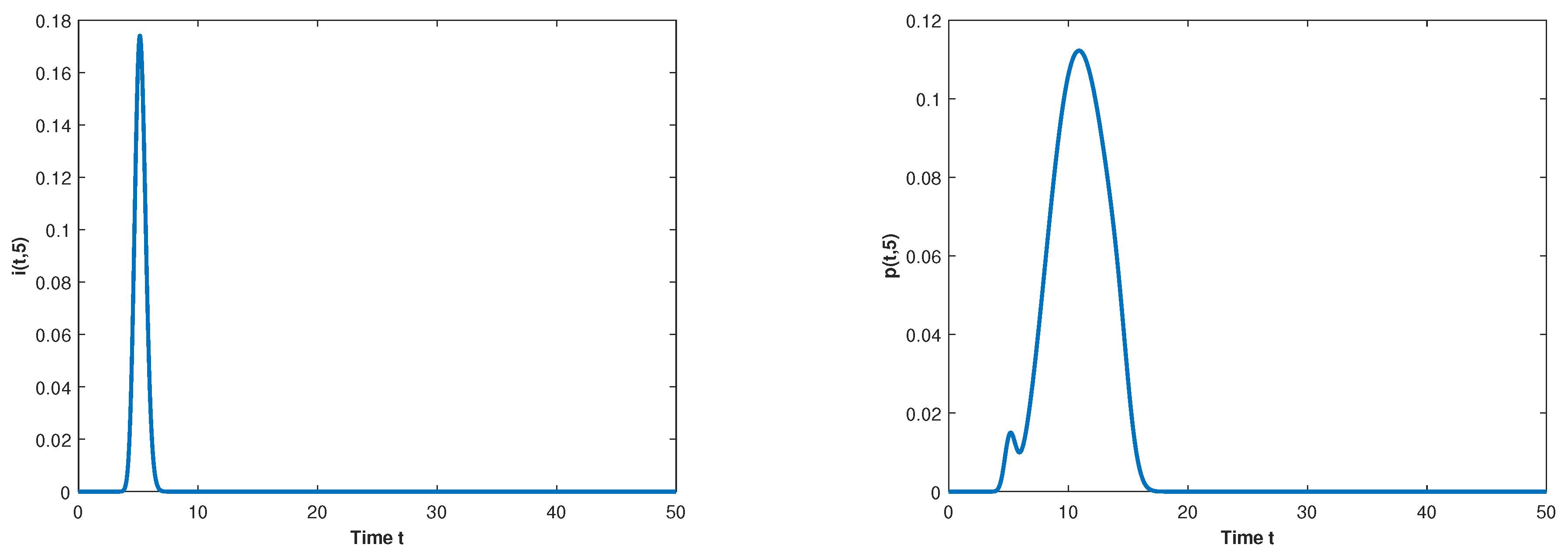
5. Numerical Simulations
6. Conclusions and Discussion
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Hartley, D.M.; Morris, J.G., Jr.; Smith, D.L. Hyperinfectivity: A critical element in the ability of V. cholerae to cause epidemics? PLoS Med. 2006, 3, 63–69. [Google Scholar] [CrossRef]
- Tien, J.H.; Earn, D.J.D. Multiple transmission pathways and disease dynamics in a waterborne pathogen model. Bull. Math. Biol. 2010, 72, 1506–1533. [Google Scholar] [CrossRef] [PubMed]
- World Health Organization. Cholera Prevention and Control, May 2018. Available online: www.who.int (accessed on 16 April 2021).
- Capasso, V.; Paveri-Fontana, S.L. A mathematical model for the 1973 cholera epidemic in the european mediterranean region. Revue d’épidémiologie et de Santé Publiqué 1979, 27, 121. [Google Scholar]
- Posny, D.; Wang, J.; Mukandavire, Z.; Modnak, C. Analyzing transmission dynamics of cholera with public health interventions. Math. Biosci. 2015, 264, 38–53. [Google Scholar] [CrossRef]
- Misra, A.K.; Gupta, A.; Venturino, E. Cholera dynamics with bacteriophage infection: A mathematical study. Chaos Solitons Fractals 2016, 91, 610–621. [Google Scholar] [CrossRef]
- Phan, T.A.; Tian, J.P.; Wang, B. Dynamics of cholera epidemic models in fluctuating environments. Stoch. Dyn. 2021, 21, 2150011. [Google Scholar] [CrossRef]
- Brauer, F.; Driessche, P.v.; Wu, J. (Eds.) Mathematical Epidemiology; Lecture Notes in Mathematics; Springer: Berlin/Heidelberg, Germany, 2008; Volume 1945. [Google Scholar]
- Iannelli, M. Mathematical Theory of Age-Structured Population Dynamics; Appl. Math. Monogr. CNR 7; Giadini Editori e Stampator: Pisa, Italy, 1994. [Google Scholar]
- Kuniya, T. Global stability analysis with a discretization approach for an age-structured multigroup SIR epidemic model. Nonlinear Anal. RWA 2011, 12, 2640–2655. [Google Scholar] [CrossRef]
- Webb, G.F. Theory of Nonlinear Age-Dependent Population Dynamics; Marcel Dekker: New York, NY, USA; Basel, Switzerland, 1985. [Google Scholar]
- Brauer, F.; Shuai, Z.; van den Driessche, P. Dynamics of an age-of-infection cholera model. Math. Biosci. Eng. 2013, 10, 1335–1349. [Google Scholar]
- Wang, J.; Zhang, R.; Kuniya, T. A note on dynamics of an age-of-infection chorela model. Math. Biosci. Eng. 2016, 13, 227–247. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Cai, L.; Fan, G.; Yang, C.; Wang, J. Modeling and analyzing cholera transmission dynamics with vaccination age. J. Frankl. Inst. 2020, 357, 8008–8034. [Google Scholar] [CrossRef]
- Huang, G.; Takeuchi, Y.; Ma, W.; Wei, D. Global stability for delay SIR and SEIR epidemic models with nonlinear incidence rate. Bull. Math. Biol. 2010, 72, 1192–1207. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Huang, G.; Yokoi, H.; Takeuchi, Y.; Kajiwara, T.; Sasaki, T. Impact of intracellular delay, immune activation delay and nonlinear incidence on viral dynamics. Jpn. J. Ind. Appl. Math. 2011, 28, 383–411. [Google Scholar] [CrossRef]
- Korobeinikov, A.; Maini, P.K. Nonlinear incidence and stability of infectious disease models. Math. Med. Biol. 2005, 22, 113–128. [Google Scholar] [CrossRef] [Green Version]
- Xu, S. Global stability of the virus dynamics model with Crowley-Martin functional response. Electron. J. Qual. Theory Differ. Equ. 2012, 9, 1–10. [Google Scholar] [CrossRef]
- Zhou, X.; Cui, J. Global stability of the viral dynamics with Crowley-Martin functional response. Bull. Korean Math. Soc. 2011, 48, 555–574. [Google Scholar] [CrossRef] [Green Version]
- Huang, G.; Liu, X.; Takeuchi, Y. Lyapunov functions and global stability for age-structured HIV infection model. SIAM J. Appl. Math. 2012, 72, 25–38. [Google Scholar] [CrossRef]
- Magal, P.; McCluskey, C.C.; Webb, G.F. Lyapunov functional and global asymptotic stability for an infection-age model. Appl. Anal. 2010, 89, 1109–1140. [Google Scholar] [CrossRef]
- Melnik, A.V.; Korobeinikov, A. Lyapunov functions and global stability for SIR and SEIR models with age-dependent susceptibility. Math. Biosci. Eng. 2013, 10, 369–378. [Google Scholar]
- Magal, P.; Ruan, S. Theory and Applications of Abstract Semilinear Cauchy Problems; Springer: Berlin/Heidelberg, Germany, 2018. [Google Scholar]
- Liu, S.; Zhang, R. On an Age-Structured Hepatitis B Virus Infection Model with HBV DNA-Containing Capsids. Bull. Malays. Math. Sci. Soc. 2021, 44, 1345–1370. [Google Scholar] [CrossRef]
- Zhang, R.; Liu, S. Global dynamics of an age-structured within-host viral infection model with cell-to-cell transmission and general humoral immunity response. Math. Biosci. Eng. 2020, 17, 1450–1478. [Google Scholar] [CrossRef]
- Magal, P.; Thieme, H. Eventual compactness for a semiflow generated by an age-structured models. Commun. Pure Appl. Anal. 2004, 3, 695–727. [Google Scholar] [CrossRef]
- Smith, H.L.; Thieme, H.R. Dynamical Systems and Population Persistence; American Mathematical Society: Providence, RI, USA, 2011. [Google Scholar]
- Hale, J.K. Asymptotic Behavior of Dissipative Systems, Mathematical Surveys and Monographs; American Mathematical Society: Providence, RI, USA, 1988; Volume 25. [Google Scholar]
- Georgescu, P.; Hsieh, Y.H. Global stability for a virus dynamics model with nonlinear incidence of infection and removal. SIAM J. Appl. Math. 2006, 67, 337–353. [Google Scholar] [CrossRef] [Green Version]
- Huang, G.; Ma, W.; Takeuchi, Y. Global properties for virus dynamics model with Beddington-DeAngelis functional response. Appl. Math. Lett. 2009, 22, 1690–1693. [Google Scholar] [CrossRef] [Green Version]
- Korobeinikov, A. Global properties of basic virus dynamics models. Bull. Math. Biol. 2004, 66, 879–883. [Google Scholar] [CrossRef] [PubMed]
- Leenheer, P.D.; Smith, H.L. Virus dynamics: A global analysis. SIAM J. Appl. Math. 2003, 63, 1313–1327. [Google Scholar]
- McCluskey, C.C. Global stability for an SEI model of infectious disease with age structure and immigration of infecteds. Math. Biosci. Eng. 2016, 13, 381–400. [Google Scholar] [CrossRef]
- Shuai, Z.; van den Driessche, P. Global dynamics of cholera models with differential infectivity. Math. Biosci. 2010, 234, 118–126. [Google Scholar] [CrossRef]
- Vargas-De-León, C.; Esteva, L.; Korobeinikov, A. Age-dependency in host-vector models: The global analysis. Appl. Math. Comput. 2014, 243, 969–981. [Google Scholar] [CrossRef]
- Hale, J.; Waltman, P. Persistence in infinite-dimensional systems. SIAM J. Math. Anal. 1989, 20, 388–395. [Google Scholar] [CrossRef]
- Walker, J.A. Dynamical Systems and Evolution Equations; Plenum Press: New York, NY, USA; London, UK, 1980. [Google Scholar]
- Brauer, F.; van den Driessche, P. Models for transmission of disease with immigration of infectives. Math. Biosci. 2001, 171, 143–154. [Google Scholar] [CrossRef]
- Khalsaraei, M.M.; Shokri, A.; Ramos, H.; Heydari, S. A positive and elementary stable nonstandard explicit scheme for a mathematical model of the influenza disease. Math. Comput. Simul. 2021, 182, 397–410. [Google Scholar] [CrossRef]
- Jódar, L.; Villanueva, R.J.; Arenas, A.J.; González, G.C. Nonstandard numerical methods for a mathematical model for influenza disease. Math. Comput. Simul. 2008, 79, 622–633. [Google Scholar] [CrossRef]
- Mickens, R.E. Numerical integration of population models satisfying conservation laws: NSFD methods. Biol. Dyn. 2007, 1, 1751–1766. [Google Scholar] [CrossRef] [PubMed]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiang, X. Global Dynamics for an Age-Structured Cholera Infection Model with General Infection Rates. Mathematics 2021, 9, 2993. https://doi.org/10.3390/math9232993
Jiang X. Global Dynamics for an Age-Structured Cholera Infection Model with General Infection Rates. Mathematics. 2021; 9(23):2993. https://doi.org/10.3390/math9232993
Chicago/Turabian StyleJiang, Xin. 2021. "Global Dynamics for an Age-Structured Cholera Infection Model with General Infection Rates" Mathematics 9, no. 23: 2993. https://doi.org/10.3390/math9232993
APA StyleJiang, X. (2021). Global Dynamics for an Age-Structured Cholera Infection Model with General Infection Rates. Mathematics, 9(23), 2993. https://doi.org/10.3390/math9232993




