A New Inversion-Free Iterative Scheme to Compute Maximal and Minimal Solutions of a Nonlinear Matrix Equation

Abstract

The goal of this article is to investigate a new solver in the form of an iterative method to solve $\mathcal{X}+A^{\ast }{\mathcal{X}}^{-1}A=I$ as an important nonlinear matrix equation (NME), where $A,\mathcal{X},I$ are appropriate matrices. The minimal and maximal solutions of this NME are discussed as Hermitian positive definite (HPD) matrices. The convergence of the scheme is given. Several numerical tests are also provided to support the theoretical discussions.

1. Subject, Literature, Motivation and Progress

1.1. Problem Statement

In this article, we take into account the nonlinear matrix equation (NME) [1]:

$$\mathcal{X}+A^{\ast }{\mathcal{X}}^{-1}A=I,$$

(1)

where $\mathcal{X}\in {\mathbb{C}}^{n\times n}$ is its Hermitian positive definite (HPD) solution, I is an identity matrix of the appropriate size, A is an $n\times n$ invertible real or complex matrix and $A^{\ast }$ is the conjugate transpose of the matrix A. The existence of the solution for this NME was discussed in [2] and it was found that if one HPD solution was available, then all its Hermitian solutions would be positive definite. This problem for any HPD solution $\mathcal{X}$ possesses the minimal solution ${\mathcal{X}}_S$ and the maximal solution ${\mathcal{X}}_L$ such that ${\mathcal{X}}_S\le \mathcal{X}\le {\mathcal{X}}_L$, for more details see [3].

The maximal solution for (1) can be derived via

$${\mathcal{X}}_L=I-{\mathcal{Y}}_S,$$

(2)

where ${\mathcal{Y}}_S$ is the minimal solution of the dual NME as follows:

$$A{\mathcal{Y}}^{-1}{A}^{\ast }+\mathcal{Y}=I.$$

(3)

The NME in (1) is an important member of the general NME of the following form:

$${\mathcal{X}}^{\alpha }+A^{\ast }{\mathcal{X}}^{-\beta }A+B^{\ast }{\mathcal{X}}^{-\gamma }B=I,$$

(4)

where $\alpha ,\beta ,\gamma \ge 1$, $A,B$ are arbitrary $n\times n$ matrices [4,5].

In several disciplines such as control theory, stochastic filtering, queuing theory, etc., this type of nonlinear equation typically appears, see [6,7,8] for further discussions. On the other hand, it is always a daunting task to find a positive definite solution (PDS) to an NME [9,10]. This is because most of the existing methods are computationally expensive due to presence of the inverse part in each loop, see the discussions given in [11,12].

1.2. Literature

One of the pioneer solvers for computing the maximal solutions of (1) is the iterative expression (FPI) below which is based on a fixed-point strategy [13]:

$$\left\{\begin{array}{c}{\mathcal{X}}_0=I,\hfill \\ {\mathcal{X}}_{k+1}=I-A^{\ast }{\mathcal{X}}_k^{-1}A.\hfill \end{array}\right.$$

(5)

Here, for each computing cycle, one matrix inverse must be computed. The authors in [14] presented another iteration scheme (SM) to compute the minimal solution as follows:

$$\left\{\begin{array}{c}{\mathcal{X}}_0=A{A}^{\ast },\hfill \\ {\mathcal{X}}_{k+1}={\mathcal{X}}_k(2I-A^{-\ast }(I-{\mathcal{X}}_k)A^{-1}{\mathcal{X}}_k).\hfill \end{array}\right.$$

(6)

This scheme is categorized as a method without the computation of an inverse for each computing step, since $A^{-1}$ is calculated once only by noticing that $A^{-\ast }=A^{{-1}^{\ast }}$.

The main challenge in employing iterative schemes such as (6) is their slow rate of convergence specially at the initial stage of the process. To overcome this, author in [15] proposed to apply the multiple second-order Newton’s scheme for finding the HPD solution at the initial phase of convergence. This was pursued as follows:

$${\mathcal{X}}_{k+1}={\mathcal{X}}_k\left((t+1)I-t{A}_k{X}_k\right),$$

(7)

for any $1\le t\le 2$.

Another well-known iteration scheme is the method proposed in [16,17], here denoted by EAM, which is as follows:

$$\left\{\begin{array}{c}{\mathcal{X}}_0={\mathcal{Z}}_0=I,\hfill \\ {\mathcal{Z}}_{k+1}=I+(I-{\mathcal{X}}_k){\mathcal{Z}}_k,\hfill \\ {\mathcal{X}}_{k+1}=I-A^{\ast }{\mathcal{Z}}_{k+1}A.\hfill \end{array}\right.$$

(8)

Authors in [18] proposed another iteration scheme as a generalization of the Chebyshev’s method (SOM) to solve (1) as follows:

$$\left\{\begin{array}{c}{\mathcal{X}}_0=A{A}^{\ast },\hfill \\ {\mathcal{X}}_{k+1}={\mathcal{X}}_k[3I-A^{-\ast }(I-{\mathcal{X}}_k)A^{-1}{\mathcal{X}}_k(3I-A^{-\ast }(I-{\mathcal{X}}_k)A^{-1}{\mathcal{X}}_k)].\hfill \end{array}\right.$$

(9)

1.3. Our Result

Our major result is a new iteration scheme similar to the form of SM for extreme solutions of (1). The method needs only the calculation of one inversion at the initial stage of the process and because of this, is categorized under the inversion-free iterative methods. Under mild conditions, the convergence of the scheme as well as some theoretical investigations to show how the method produces HPD solutions are given. In conclusion, we accelerate the long-standing algorithms for an important problem of numerical linear algebra. The experiments considered in this work reconfirm the competitiveness of the proposed iteration scheme compared to known algorithms. These will make this work interesting both practically and theoretically.

1.4. Organization of the Paper

After having a short introductory discussion regarding the issues with iterative methods for NMEs in this section, the remaining parts of this article are structured as follows. In Section 2, the solution of this NME as the zero of a nonlinear operator equation is introduced. In Section 2, several numerical experiments are investigated with implementation details given in Section 3 to confirm its applicability and to compare with several well-known and state-of-the-art methods from the literature. It is shown by way of illustration that the proposed solution method is useful and provides promising results. Lastly, some concluding remarks are made in Section 4.

2. Novel Iteration Method

2.1. An Equivalent NME

Another way to calculate the HPD solutions of (1) is to compute the zero of the NME, $\mathcal{P}\left(\mathcal{X}\right)=0$, where [14]:

$$\mathcal{P}\left(\mathcal{X}\right):=-I+\mathcal{X}+A^{\ast }{\mathcal{X}}^{-1}A=0.$$

(10)

The relation (10) can be re-written as follows [18]:

$$\begin{array}{ccc}\mathcal{P}\left(\mathcal{X}\right)\hfill & =\hfill & A^{\ast }{\mathcal{X}}^{-1}A+\mathcal{X}-I\hfill \\ \hfill & =\hfill & -(I-\mathcal{X})+A^{\ast }{\mathcal{X}}^{-1}A\hfill \\ \hfill & =\hfill & -(A^{-\ast }-\mathcal{X}{A}^{-\ast })A^{\ast }+A^{\ast }{\mathcal{X}}^{-1}A\hfill \\ \hfill & =\hfill & A^{\ast }{\mathcal{X}}^{-1}A-A(A^{-1}{A}^{-\ast }-A^{-1}\mathcal{X}{A}^{-\ast })A^{\ast }\hfill \\ \hfill & =\hfill & {\left(A^{-1}\mathcal{X}{A}^{-\ast }\right)}^{-1}-A(A^{-1}{A}^{-\ast }-A^{-1}\mathcal{X}{A}^{-\ast })A^{\ast }.\hfill \end{array}$$

(11)

Clearly we can now impose a transformation as follows

$$L=A^{-1}\mathcal{X}{A}^{-\ast },$$

(12)

to further simplify the nonlinear operator equation:

$$\mathcal{G}\left(L\right)=L^{-1}-A(A^{-1}{A}^{-\ast }-L)A^{\ast }=0.$$

(13)

To obtain an iteration scheme to find the minimal HPD solutions, now it is necessary to solve the following problem:

$$L^{-1}-B=0,$$

(14)

where

$$B=A(A^{-1}{A}^{-\ast }-L)A^{\ast }.$$

(15)

2.2. Our Method

We employ (14) and (15) and view this NME as an inverse-finding problem via the Schulz-type iterative schemes (see, e.g., [19]), and accordingly we propose the following method:

$$\left\{\begin{array}{c}{\mathcal{X}}_0=A{A}^{\ast },\hfill \\ H_k=A^{-\ast }(I-{\mathcal{X}}_k)A^{-1},\hfill \\ T_k=I-H_k{\mathcal{X}}_k,\hfill \\ {\mathcal{X}}_{k+1}={\mathcal{X}}_k[I+T_k+T_k^2+T_k^3].\hfill \end{array}\right.$$

(16)

The matrix iteration (16) requires to compute $A^{-1}$ once specially at the initial stage of the implementation and it provides the iteration scheme considered an inversion-free method to solve (1).

Moreover, it is straightforward to state that the zeros of the map $\mathcal{G}\left(Z\right)=L^{-1}-B$ are equal to the zeros of the map $\mathcal{P}\left(\mathcal{X}\right)={\mathcal{X}}^{-1}-H$, wherein $H=A^{-\ast }(I-\mathcal{X})A^{-1}$. To discuss further, we find the inverse of H, which corresponds to the minimal HPD solution of (1).

The derivation of (16) can mainly be viewed as a matrix inverse finder. In fact, the last step of (16) is a method that can be used for finding generalized inverses. It is a member of the family of hyperpower iteration schemes employing several matrix products to compute the inverse of a given matrix. The iterative method can be rearranged to be written in its Horner form in order to reduce the rounding and cancellation errors when facing big matrices.

2.3. Theoretical Investigations

Lemma 1.

Employing the Hermitian matrix ${\mathcal{X}}_0=A{A}^{\ast }$, the iteration scheme (16) provides a sequence of Hermitian matrices.

Proof. 

It is obvious that the seed $A{A}^{\ast }$ is Hermitian, and $H_k=A^{-\ast }(I-{\mathcal{X}}_k)A^{-1}$. Therefore, $H_0=A^{-\ast }{A}^{-1}-A^{-\ast }A{A}^{\ast }{A}^{-1}$ is also Hermitian, i.e., $H_0^{\ast }=H_0$. Using an inductive argument, we have:

$$\begin{array}{ccc}{\left({\mathcal{X}}_1\right)}^{\ast }\hfill & =\hfill & {\left({\mathcal{X}}_0[I+T_0+T_0^2+T_0^3]\right)}^{\ast }\hfill \\ \hfill & =\hfill & {[{\mathcal{X}}_0+{\mathcal{X}}_0(I-H_0{\mathcal{X}}_0)+{\mathcal{X}}_0{(I-H_0{\mathcal{X}}_0)}^2+{\mathcal{X}}_0{(I-H_0{\mathcal{X}}_0)}^3]}^{\ast }\hfill \\ \hfill & =\hfill & {\mathcal{X}}_1.\hfill \end{array}$$

(17)

By considering ${\left({\mathcal{X}}_l\right)}^{\ast }={\mathcal{X}}_l$, ($l\ge k$), we then show that:

$$\begin{array}{ccc}{\left({\mathcal{X}}_{l+1}\right)}^{\ast }\hfill & =\hfill & {\left({\mathcal{X}}_l[I+T_l+T_l^2+T_l^3]\right)}^{\ast }\hfill \\ \hfill & =\hfill & {[{\mathcal{X}}_l+{\mathcal{X}}_l(I-H_l{\mathcal{X}}_l)+{\mathcal{X}}_l{(I-H_l{\mathcal{X}}_l)}^2+{\mathcal{X}}_l{(I-H_l{\mathcal{X}}_l)}^3]}^{\ast }\hfill \\ \hfill & =\hfill & {\mathcal{X}}_{l+1}.\hfill \end{array}$$

(18)

Note that $H_l={\left(H_l\right)}^{\ast }$ has been employed in (18). The conclusion is valid for any $l+1$. □

Theorem 1.

Assume that ${\mathcal{X}}_k$ and A are invertible matrices. Then the sequence $\left\{{\mathcal{X}}_k\right\}$ produced by (16) tends to the minimal solution of the NME (1) by having ${\mathcal{X}}_0=A{A}^{\ast }$.

Proof. 

We start by denoting that $H_k=A^{-\ast }(I-{\mathcal{X}}_k)A^{-1}$. Thus, we can write:

$$\begin{array}{ccc}I-H_k{\mathcal{X}}_{k+1}\hfill & =\hfill & I-\left[A^{-\ast }(I-{\mathcal{X}}_k)A^{-1}\right]\left({\mathcal{X}}_k[I+T_k+T_k^2+T_k^3]\right)\hfill \\ \hfill & =\hfill & I-\left[A^{-\ast }(I-{\mathcal{X}}_k)A^{-1}\right]\left({\mathcal{X}}_k\right[I+(I-H_k{X}_k)\hfill \\ \hfill & \hfill & +{(I-H_k{X}_k)}^2+{(I-H_k{X}_k)}^3\left]\right)\hfill \\ \hfill & =\hfill & {(I-H_k{X}_k)}^4.\hfill \end{array}$$

(19)

Then, by using (19) and taking a norm on both sides, one obtains:

$$\parallel I-H_k{\mathcal{X}}_{k+1}\parallel \le \parallel I-H_k{X}_k{\parallel }^4.$$

(20)

Therefore, the inequality (20) can lead to convergence as long as the initial approximation reads $\parallel I-H{X}_0\parallel <1$. This yields to the following condition:

$$\parallel I-\left[A^{-\ast }(I-\mathcal{X})A^{-1}\right]{\mathcal{X}}_0\parallel <1.$$

Then, by employing the HPD initial approximation ${\mathcal{X}}_0=A{A}^{\ast }$, one obtains that

$$\parallel A^{-\ast }X{A}^{\ast }\parallel <1,$$

which holds as long as $\mathcal{X}$ is the minimal HPD solution of (1). Furthermore, due to

$$0<{\mathcal{X}}_S=I-A^{\ast }{\mathcal{X}}_S^{-1}A=A^{\ast }[A^{-\ast }{A}^{-1}-{\mathcal{X}}_S^{-1}]A=A^{\ast }[{\mathcal{X}}_0^{-1}-{\mathcal{X}}_S^{-1}]A,$$

we obtain that ${\mathcal{X}}_0^{-1}>{\mathcal{X}}_S^{-1}$, thus ${\mathcal{X}}_0<{\mathcal{X}}_S$. Hence, by mathematical induction, it is seen that $\left\{{\mathcal{X}}_k\right\}$ converges to ${\mathcal{X}}_S$. □

It is required to discuss the rate of convergence. Although the proposed method (16) converges to the HPD solution under mild conditions, its q order of convergence is just linear. As will be seen later, however, due to its structure and a higher rate for computing matrix inverses, it converges faster because it comes to the convergence phase more quickly. This linear rate of convergence can be improved by employing an accelerator such as (7), in the initial phase of convergence.

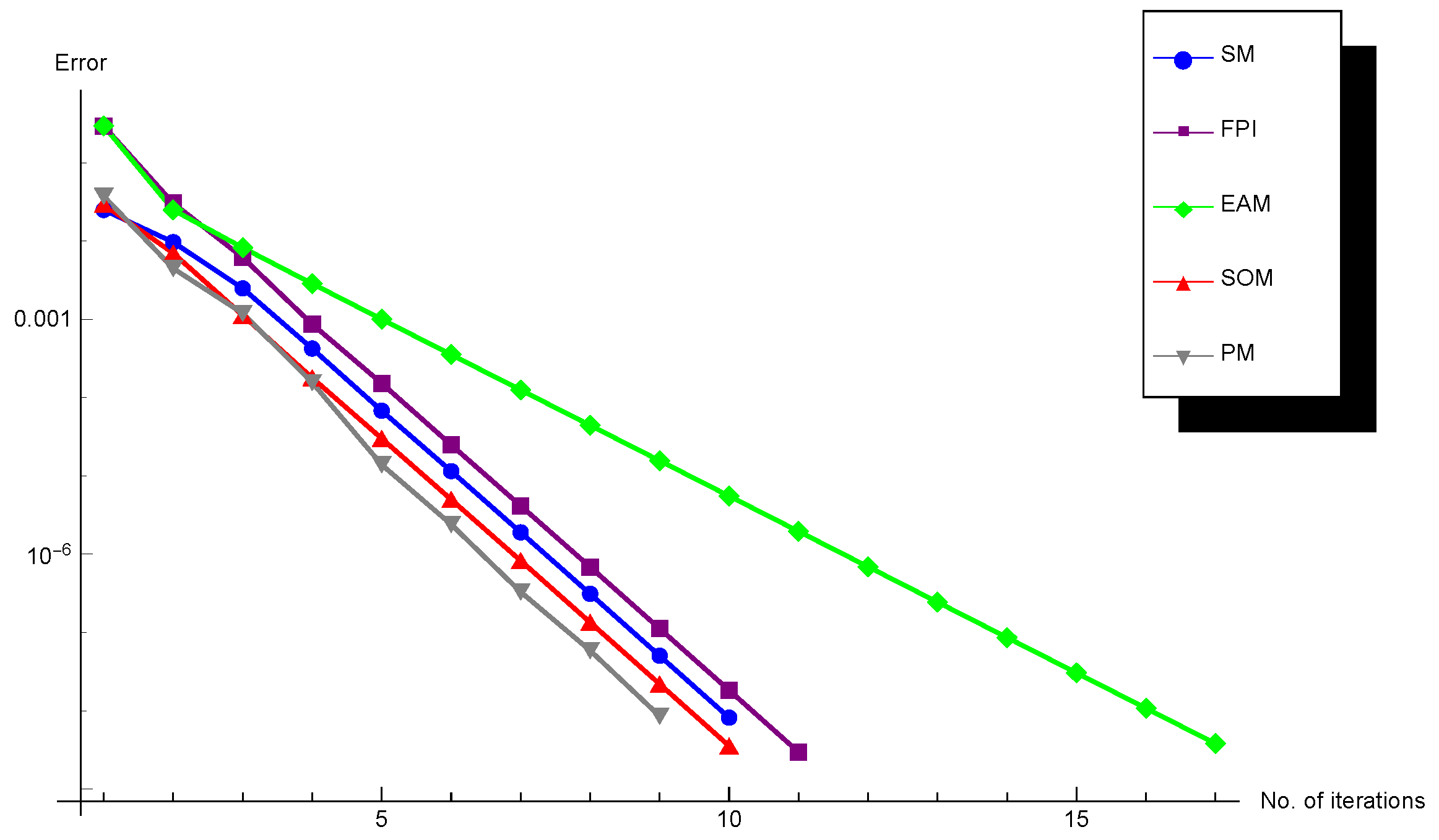
3. Experiments

The computational efficiency and convergence behavior of PM (16) for the NME (1) are hereby illustrated on some numerical problems. All the compared methods were written in the programming package Mathematica 12.0 [20].

All computations were performed in standard floating point arithmetic without applying any compilations. In addition, computations were done on a laptop with 16.0 GB of RAM and Intel^® Core™ i7-9750H. The matrix inversions whenever required were done using Mathematica 12.0 built-in commands. We found the number of iterations required to observe convergence. In the code we wrote to implement different schemes, we stopped all the applied schemes when two successive iterations in the infinity norm was less than a tolerance, as follows:

$$\parallel {\mathcal{X}}_{k+1}-{\mathcal{X}}_k{\parallel }_{\infty }<ϵ.$$

(21)

Here PM and SOM were employed along with (7) with $k=2$ and $t=1.5$ iterations and then (16) was used. Without imposing (7) the iteration schemes PM and SOM were faster than the other competitive ones, but the superiority was not tangible. Because of this, a multiple Newton’s method was imposed at the beginning of the iterations to accelerate the convergence as much as possible. The impact of the multiple Newton’s method is that it is useful when there is a clear smoothness around the zero of the nonlinear operator equation. It helps arrive at the convergence region much faster than simple root finders.

Example 1.

This example tests the effectiveness of PM on a $3\times 3$ real matrix A defined as follows:

$$A=\left(\begin{array}{ccc}0.1& -0.13& 0.32\\ -0.23& 0.02& 0.4\\ 0.31& 0.14& 0.16\end{array}\right),$$

to find the minimal solution of (1) which is given by

$${\mathcal{X}}_S=\left(\begin{array}{ccc}0.168846& 0.133619& 0.0927809\\ 0.133619& 0.244969& 0.00671869\\ 0.0927804& 0.00671813& 0.216639\end{array}\right).$$

The results are given in Figure 1 using $ϵ={10}^{-6}$.

Figure 1. Convergence history for Example 1.

Note that PM converges to ${\mathcal{X}}_S$, therefore we employed other methods to compute the maximal solution of the dual problem $A{X}^{-1}{A}^{\ast }+\mathcal{X}-I=0$ in our written implementations to have fair comparisons.

Numerical evidence of Example 1 reveals that PM converges much faster than existing solvers for the same purpose. Our method requires fewer numbers of iterations to reach the stopping criterion. In fact, under mild conditions, the error analysis, convergence and stability of the scheme were observed based on the expected norm of the error.

Example 2.

Using $ϵ={10}^{-8}$, we compare different iteration schemes to find the minimal solution of (1) when A is a complex matrix as follows:

$$A=\frac{1}{5}\left(\begin{array}{cccc}1.2& -1.1& -0.5& 0.3+0.1i\\ -0.1& 0.6& -0.5& 0.7\\ -0.5& -0.5& 0.1& 0.8\\ 0.1& i& 1.8& 0.5\end{array}\right),$$

and the solution is:

$${\mathcal{X}}_S=\left(\begin{array}{cccc}0.136245\hfill & -0.0143856+0.00708363i\hfill & 0.00451262+0.00795439i\hfill & -0.0249869+0.0539135i\hfill \\ -0.0143856-0.00708363i\hfill & 0.0489688\hfill & 0.0161382-0.000846549i\hfill & -0.0183093-0.0268946i\hfill \\ 0.00451262-0.00795439i\hfill & 0.0161382+0.000846549i\hfill & 0.0563786\hfill & 0.0284051+0.0188581i\hfill \\ -0.0249869-0.0539135i\hfill & -0.0183093+0.0268946i\hfill & 0.0284051-0.0188581i\hfill & 0.197196\hfill \end{array}\right).$$

The numerical evidence is given in Figure 2. It too reveals that the proposed method is efficient in solving NME (1). Note that the CPU time for all methods is low, though PM converges in less than a second for the given examples and performs faster than the other solvers.

Figure 2. Convergence history for Example 2.

4. Concluding Remarks

We have studied the minimal HPD solution of (1). The proposed solver needs the calculation of one matrix inversion at the initial stage of the process and then it is an inversion-free scheme. In this paper, a novel iterative scheme was developed. Several computational tests were given and found in agreement with the theoretical findings. Lastly, based on the computational evidence, we can conclude that the novel scheme is useful and effective in computing the numerical solutions of a broad range of NMEs.