Secondary Teacher Candidates’ Mathematical Modeling Task Design and Revision

Abstract

The purpose of this study is to investigate secondary teacher candidates’ experience of mathematical modeling task design. In the study, 54 teacher candidates in a university-based teacher education program created modeling tasks and scoring rubrics. Next, the participants pilot-tested the tasks with students and had the opportunity to revise the original tasks and rubrics based on student responses. The data included participants’ statements, in which they described and reflected on the design and revision process of modeling tasks. The study describes six didactic revision strategies in revising modeling tasks and identifies five emerging pedagogical ideas from revising tasks and rubrics. The study also discusses the way modeling task design activities have the potential to support teacher candidates’ learning through a bottom-up modeling curriculum in teacher education.

1. Introduction

A mathematical modeling task involves mathematizing a real-life situation, identifying problems in the situation, and solving the problems using mathematical models. From the teacher’s point of view, modeling tasks have the potential to create the opportunity for students to connect with mathematics, and research recommends that teachers use modeling tasks consisting of appropriate and authentic contexts [1,2,3,4]. In particular, Hernández et al. recommended that modeling tasks involve real-life contexts and build on student interests so that students are better “invested in their own learning while seeing the relevance of mathematics in their real lives” (p. 340, [5]).

This study identifies the important role of future teachers as facilitators of students’ mathematical learning. However, teacher candidates have little experience in curriculum design and can benefit from task design activities. In light of the need for designing math modeling tasks in the classroom with contexts in consideration of student thinking and life experiences, this study examines the ways in which teacher candidates revise modeling tasks—we call these didactic revision strategies in this study—on the basis of students’ actual responses. In doing so, the study seeks to answer two research questions: What are teacher candidates’ didactic revision strategies in the process of revising mathematical modeling tasks, and what pedagogical ideas emerge from the participants’ revision of the rubrics?

2. Literature Review

2.1. Modeling Framework

In Maaβ [6] and Staats and Robertson [7], the modeling process framework connects two domains, such as reality and mathematics, and identifies the steps involved in mathematical modeling as simplifying, mathematizing, working within the mathematics, interpreting, and validating. Hernández et al. [5] add more components to the modeling process, such as “identifying the problem” and “iterating”, which has the effect of underscoring mathematical modeling as a human activity. In Alhammouri et al. [8], the modeling process includes making assumptions, defining variables, and creating a mathematical model. In this framework, the modeling process is drawn from a product-oriented perspective rather than a process-oriented perspective.

The modeling strategies in Cavey and Champion [9] at the middle-school level involve solving simpler but related problems, listing reasonable assumptions, gathering necessary information through research, breaking the task into smaller subtasks, interpreting and revising the solution in the context of the task, and combining multiple estimates. At the high-school level, the strategies include posing clarifying questions, gathering necessary information through research, listing reasonable assumptions, building efficient notation, and using technology to do extended calculations. These strategies were useful in this study to categorize the participants’ revision strategies of modeling tasks based on student responses.

2.2. Modeling Task Design in Teacher Education

This study conceptualizes learner-centered mathematical modeling in terms of modeling tasks that seek a balance of mathematics, student motivation, and an interest in modeling. Furthermore, this study adds the pedagogy of modeling to the current framework and aims to clarify the design of mathematical modeling tasks for teacher candidates from a pedagogical point of view. To this end, the study investigates modeling task design in teacher education, which consists of two parts: (1) the modeling task design process and (2) the modeling task design product.

As the study theorizes the modeling task design process and modeling task design product, the constructs of “didactic transposition” and “professional teacher noticing” have guided the study. The theory of didactic transposition helps to reframe our thinking about the modeling task design process in terms of the transition process, involving “knowledge to be taught,” “taught knowledge,” and “learned knowledge,” and the factors involved in the transition process [10]. Examples of such factors include teacher noticing as the social process of didactic transposition [11]. For teacher candidates to develop knowledge and skills in the combined process of didactic transposition and teacher noticing, it is necessary to provide them with opportunities to practice a task design and to reflect on outcomes [12]. To understand the teacher candidates’ experiences in the social process of didactic transposition, this study draws on the work of Jacobs et al. [13], which conceptualizes the “professional noticing of children’s mathematical thinking” as a set of three interrelated skills: (1) attending to children’s strategies, (2) interpreting children’s understanding, and (3) deciding how to respond. This study adapts this skill set so that teacher candidates can practice as follows: (1) attending to student responses to a modeling task, (2) interpreting student works (e.g., problem-solving strategies, misunderstandings, student reasoning), and (3) deciding how to revise the task and the rubric.

2.3. Related Studies

The current literature about the pedagogy of modeling covers a variety of modeling tasks and elements of modeling in student development and cognition. For example, Kelly [14] and Poon et al. [15] use manipulatives in modeling activities for elementary students. For secondary mathematics, Alhammouri et al. [8] illustrate a post-placing activity in algebra, and Lee [16] shows how students engage in conjecturing the modeling of soccer balls. Park et al. [17] used spreadsheets in a modeling task to teach derivatives and integrals. At the post-secondary level, Staats and Robertson [7] introduce a calendar game in teaching college algebra, and Harwood [18] illustrates modeling tasks with multiple themes. These studies document an approach to teaching modeling that features a prescribed cycle of modeling steps generally categorized into a situation, mathematizing, building mathematical models, solving the problems, and validating and interpreting the solutions.

Extending the literature on the modeling cycle and examples in the classroom, Zbiek and Conner elaborate how prospective teachers’ “learning takes place during mathematical modeling” (p. 110, [19]). In doing so, they highlight the benefits of a modeling curriculum in mathematics teacher education, arguing that there is much to be gained from modeling experiences—modeling tasks involve deep mathematics with various contexts and applications in school mathematics. More recently, Guerrero-Oritz et al. [20] in Chile investigated teacher candidates’ knowledge development through modeling.

2.4. Situating the Study

In reviewing the literature on modeling frameworks, sample activities, and recommended pedagogies, as well as on the use of a modeling curriculum in teacher education, we identified a gap in the literature with regard to teacher candidates learning to actively design modeling tasks, which is different from training teacher candidates to facilitate modeling lessons. The active design process of modeling in this study involved the designers using real-life contexts in a modeling task so that students could engage with the modeling; it also used student answers and solutions to the task in order to increase the teachers’ pedagogical ideas about facilitating authentic modeling tasks in their classroom. More importantly, the design process involves not only mathematics and modeling but also a deeper understanding of student interest and motivation to produce a student-centered modeling task.

In this study, the first curricular goal is to support teacher candidates in learning to understand the gap between taught knowledge and learned knowledge in the modeling task design. To be specific, the participants in our study first learn the concept of mathematical modeling and apply it to design their own modeling task (i.e., developing knowledge to be taught). The participants then recruit students, have them solve the modeling task, and collect the students’ works. This enables the teacher participants to experience the gap between knowledge to be taught and learned knowledge. Next, the participants are asked to analyze the student works (which are, in part, the learned knowledge) and to revise the knowledge to be taught on the basis of the analysis—this is what we call in this study the modeling task design product. The participants may discover potential problems in their modeling tasks and revise/refine their tasks on the basis of actual student responses. Thus, the term “didactic” in this study is used to refer to teacher candidates’ didactic transposition, in which they learn the difference between knowledge to be taught and learned knowledge and revise and reflect on the modeling task design product. This study uses the term “revision” to refer to the revision/refinement of both modeling tasks and accompanying rubrics (i.e., knowledge to be taught) through the analysis of students’ products (i.e., taught knowledge). In this way, all revision strategies for didactic transposition experienced by teacher candidates while revising and refining modeling tasks and rubrics based on student responses are referred to as the Didactic Revision Strategy (henceforth, DRS in short).

3. Methods

3.1. Participants

The study was conducted in the period between the fall, 2017 (data collection) and the spring of 2018 (data analysis). Fifty-four teacher candidates (mostly sophomores and juniors) enrolled in a mathematics education course titled “Mathematical Logic and Essay” at a large university in Seoul, Korea participated in this study. The participants had diverse coursework experience with respect to mathematics courses (which includes a course in mathematical modeling) and education courses. In this study, the participants formed 11 groups of four or five members each.

3.2. Curriculum of Modeling Task Design

The curricular goals of the course included understanding the process of mathematical modeling, developing a mathematical modeling task, and accompanying rubrics. Before the midterm exam, the assessment standards [21] and the process standards [22] were covered so that the participants could use the information in designing modeling tasks. The Trends in International Mathematics and Science Study (TIMSS) and Programme for International Student Assessment (PISA) problems were used to help the participants understand how the mathematical processes and contexts were structured as an assessment item. In addition, the participants conducted group assignments in which they analyzed the connection between textbook assessment items and the process standards. In the midterm exam, the participants reviewed the course material about creating math tasks that successfully used mathematical contents, processes, and contexts. The curriculum after the midterm was composed of activities in which the participants were able to recognize the importance of context, understand in depth the mathematical modeling process through various sources (e.g., Illuminations, CMP curriculum, Core-plus curriculum, and other video clips about mathematical modeling), and experience the three stages of the modeling process, that is, relationship mapping, choices and simplification, and situation analysis [23]. The participants also learned the methods of holistic scoring and analytic scoring in order to understand how rubrics are used to evaluate students’ modeling tasks.

3.3. Data Collection

The primary data include modeling tasks and rubrics submitted by the 11 groups (see Supplementary Materials (Appendix 1) for more detail about modeling tasks by 11 groups). Other data include the participants’ written reflections to identify participant perceptions of task development. For the study, the participants eventually submitted a draft of a mathematical modeling task as a group assignment. The instructor provided feedback based on a rubric and discussed improvements (e.g., the need for the following: to provide a title for each task; for a problem statement explaining the learning goal of the modeling task; to state prerequisite knowledge; for an operational definition before introducing new terminology; to explain any new unit systems, and for a gradual increment in difficulty levels).

The participants were asked to pilot their modeling tasks on middle- or high-school students and collect student responses. The participants collected actual responses on their modeling tasks from about 20 to 30 middle- or high-school students (see Supplementary Materials (Appendix 1)). Based on the student responses, the participants revised their modeling tasks and rubrics. The participants were also asked to describe their revision process in detail. In the written reflection, the participants were also asked to explain the goals of the mathematical modeling task, the rationale behind the choice of the task, and the process of revising task items, and why they made such changes based on the student responses.

3.4. Data Analysis

Extending the modeling strategies of Cavey and Champion [9], the DRS framework (

Table 1. Framework for DRS in Analyzing Mathematical Modeling Tasks.

DRS	Operational Definitions
Revising complicated computations for simpler problems (S strategy)	When the students’ solution process involves complicated computations that are in conflict with the learning goal of the task, the task could be simplified.
Breaking the task into smaller subtasks (B strategy)	When one task involves multiple layers of response, the task could be broken down into smaller subtasks.
Revising assumptions in the context of the task for articulation (A strategy)	When student responses demonstrate their confusion in understanding the problem, the assumptions can be revised in the context of the task.
Using wording appropriate for student levels (W strategy)	When wording is too difficult or lacks information, new words or additional information can be added to support the student in understanding the modeling situation.
Revising notations, such as symbols or letters that can cause student misunderstandings or mistakes (N strategy)	When students display difficulty in understanding the problem due to certain notations, the notations can be revised to clarify their meaning.
Using technology to do extended calculations (T strategy)	When the solution process necessitates complex calculations, the task can be revised so that the use of technology is allowed.

) in this study has six strategies. To be specific, the strategy of solving simpler but related problems can be mapped onto the DR-S strategy, in that students may encounter difficulty due to the excessive complexity of calculations, and the task can be revised so that such calculations can be avoided. The strategy of breaking the task into smaller subtasks can be mapped onto the DR-B strategy, in that students may find it challenging to address two or three embedded questions at the same time and the task can be broken down further. The strategy of interpreting and revising the solution in the context of the task maps onto the DR-A strategy, in the sense that when student responses show their confusion about understanding the problem as intended, assumptions about the task can be revised or clarified in the context of the task. The strategy of posing clarifying questions maps onto the DR-W strategy, in that certain wording in the task may not be appropriate for the students’ level and can be clarified to aid students’ understanding of the problem. The strategy of building efficient notation maps onto the DR-N strategy, in the sense that when students misinterpret the meaning of the notation, the notation can be revised to clarify the meaning. Lastly, the strategy of using technology to do extended calculations maps onto the DR-T strategy, in the sense that when student responses indicate complex calculations and such calculations are necessary for the learning goal, the task can be revised so that the use of technology is recommended.

4. Results

The revision process of (1) modeling tasks and (2) rubrics by teacher candidates (e.g., appendices 2 and 3 for original and revised tasks and rubrics by G1) is analyzed and presented on the basis of the six DR strategies.

4.1. DRS in Revising Mathematical Modeling Tasks

4.1.1. G1’s Modeling Task on Public Transportation Vehicle Scheduling Optimization

Group G1 developed a modeling task related to the vehicle scheduling of public transportation. The group reported that a member of the group wanted to improve the bus schedule during commuting. Initially, the group read papers on how bus companies optimize vehicle schedules and decided to develop a modeling task on optimizing vehicle schedules that involved the bus fare and customer satisfaction. G1 constructed a problem statement as the context for their modeling task.

DRS Used in the Revision of a Problem Statement. The teacher candidates in G1 used the W strategy (using words appropriate for student understanding; see

Table 2. W Strategy (Using Words Appropriate for Student Understanding).

DRS	Original Version	Revised Version
W strategy	No explanation of approximation	(a) Suppose a continuous function on an arbitrary do-main, such as a radical function like $\mathrm{y}=4\sqrt{x}$. We know that it could be easier to deal with polyno-mials such as quadratics or cubics than to deal with a radical function, and the method of approximation may be useful to model some situations. For example, an approximation of $\mathrm{y}=4\sqrt{x}$ can be $\mathrm{y}=-x^2+4x+1$ over any particular interval of the domain. Both func-tions have the same y-value, 4, at x = 1, and their func-tion values are close to each other in the neighborhood of x = 1. Hence, both functions share similar properties. In addition, the radical function $\mathrm{y}=4\sqrt{x}$ can be approximated using a cubic function. It is known that the cubic function is even closer to the $\mathrm{y}=4\sqrt{x}$ and shares more similar properties than the quadratic function does.

) and the N strategy (revising notations) as their DRS in revising their problem statement in light of student responses.

First, the teacher candidates in G1 used the W strategy to add an explanation about approximation in their revision of the modeling task. The reason for the addition of this explanation was that one of the students responded as follows: “I thought this task was made for high-school students, but I felt quite unfamiliar with the word ‘approximation.’” In response to the student’s feedback, the teacher candidates in G1 added a detailed explanation about the concept of approximation in the original statement, using examples of a radical function being approximated by a quadratic function and comparing function values at some x values. Furthermore, they explained an improved approximation with a higher degree (in this case, a cubic function), which might be of help with the next step and enable students to recognize the need for the third-degree approximation. In the following paragraphs of the modeling task, they used the N strategy (see

Table 3. N Strategy (Revising Notations).

DRS	Original Version	Revised Version
N strategy	The profit function of the time interval was approximated by $f\left(t\right)=-{\left(t-10\right)}^2+300$ where t stands for the time interval in minutes. The company can maximize its profit to 300 (ten-thousand won) when t = 10, and so they have scheduled vehicles every 10 min for the last three years. … After investigating relevant factors, it is expected that when the time interval de-creases by $t_1(0\le t_1<10)$ from 10 min during rush hours, the profit will change by $-\frac{9}{8}{t}_1^3-\frac{9}{8}{t}_1^2+63t_1$. When the time interval increases by $t_2 \left(0\le t_2\le 170\right)$ from 10 min, the profit will change by g(t2).	(b) The profit function of the time interval was approximated by $f\left(t\right)=-{\left(t-10\right)}^2+300$ where t stands for the time interval in minutes. The company can maximize its profit to 300 (ten-thousand won) when t = 10, and so they have scheduled vehicles every 10 min for the last three years. … After investigating relevant factors, it is expected that when the time interval changes by $x (-10<x\le 0)$ from 10 min during rush hours, the ex-pected profit will change by $\mathrm{g}\left(x\right)=\frac{9}{8}{x}^3-\frac{9}{8}{x}^2-63x$. When the time interval changes by $x (0\le x<170)$ from 10 min, the expected profit will change by h(x).

).

The N strategy was used in response to a student comment: “In the first paragraph, t meant the time interval, but in the third paragraph, it was set up to mean the amount of change. This is confusing.” In the original problem statement, the variable t represented time, and the time variable could mean either the time interval in the function f (t) or later the change in the time interval. The group adopted a new variable, x, in the revised task so that students could clearly discern the interval and the change in the time interval; t indicates an interval, and x indicates the change in the time interval.

DRS Utilized in the Revision of a Mathematical Question. The teacher candidates in G1 set up a context in the problem statements and then asked students mathematical questions related to the context. The DR strategies used to revise the mathematical questions about optimizing vehicle schedules according to student responses include the N strategy (revising notation; see

Table 4. Shows the use of the N strategy.

DRS	Original Version			Revised Version
N strategy	(1) The following table shows a part of a chart that an employee of this company used to find h(t) on a closed interval [0, 170]. Find h(t).			[1–1] The following table shows a part of a chart that an employee of this company used to find h(x) on an interval [0, 170). Find h(x).
	$t$	1	4	$x$	1	4
	$h\left(t\right)$	80	140	$h\left(x\right)$	80	140
	$h^{\prime }\left(t\right)$	80		$h^{\prime }\left(x\right)$	80

), the W strategy (using words appropriate for students), the S strategy (revising complicated computations for simpler problems), and the B strategy (breaking the task into smaller subtasks).

In question (1), which is the first question that connects the problem context and problem solving, the participants changed the variable t to x so that it is consistent with the variable in the problem context. In the next question, they used the W strategy (see

Table 5. W Strategy (Using Words Appropriate for Students).

DRS	Original Version	Revised Version
W strategy	(2) In the table above, what is the meaning of the derivative h′(1)? Explain its meaning in relation to the profit.	[1–2] For any constant $a (0<a<170)$ we have $h^{\prime }\left(a\right)>0$. When the time interval between vehicles has changed by a min from 10 min, what happens to the profit if the time interval gets greater than (10 + a)? Explain what happens, including its mathematical meaning.

).

The reason for the changes in wording that reflect the W strategy was a response from one of the students: “I have no clue as to how to write my response in (1) and (2). For example, is $h\left(t\right)$ the change from the current profit? Is $h^{\prime }\left(t\right)$ then the change in the change of profit, or is it the rate of change in the profit?” In order to ask for the rate of change in profit when the time interval is 11 min, the teacher candidates first phrased the text thus: “What is the meaning of the derivative $h^{\prime }\left(1\right)$? Explain its meaning in relation to the profit.” However, the students provided unexpected responses, which led the participants to revise the question and add the condition $h^{\prime }\left(a\right)>0$ for any specific interval so that the mathematical meaning of the rate of change in profits as the a value changes could be conveyed more clearly to students. In this way, the students were expected to relate the meaning of the derivative to the profit in the context.

In their third question, they used the S strategy (revising complicated computations for simpler problems) for simplification and the W strategy (using words appropriate for students) for the clarity of wording (see

Table 6. S and W Strategies.

DRS	Original Version	Revised Version
S & W Strategies	(3) Draw, by using the table of the increase and decrease in y-values, a sketch of the graphs, y = g(x) defined on the interval (−10, 0) and y = h(x) defined on the interval [0, 170].	[2–1] Construct a table of the increase and decrease in y-values for each of the y = g(x) defined on the interval (−10, 0) and y = h(x) defined on the interval [0, 170). Using the table, graph the two functions y = g(x) and y = h(x). (Note: There is no need to find the second derivative.)

).

The reason for the changes reflecting the S strategy was the response of one student: “When I constructed the table, $g\left(-10\right)$ and $h\left(170\right)$ were too complicated, and so I did not find them, but I guess the calculation should be done no matter what. Can you adjust the interval on which the function $g\left(x\right)$ and $h\left(x\right)$ are defined?” The student’s response indicates that $h\left(170\right)$ could be too complicated to calculate. There is no issue in the overall problem solving even if $h\left(170\right)$ is excluded, and so the teacher candidates changed the interval from $\left[0, 170\right]$ to $\left[0, 170\right)$ so that students did not need to calculate $h\left(170\right)$.

In addition, they used the W strategy to clarify the wording in response to another student comment: “In question (3), I think it would be better to include the wording ‘graphs of the functions $g\left(x\right)$, $h\left(x\right)$’ right after ‘Draw.’” To reflect this student’s opinion and make sure the intended meaning of the question was delivered clearly, the participants revised the wording from “Draw, by using the table of the increase and decrease in y-values, a sketch of the graphs …” to “Construct a table … Using the table, graph the two functions $y=g\left(x\right)$ and $y=h\left(x\right)$.” In this way, the direction of the question became clearer so that the focus was on graphing the two functions.

The modeling task also included a question about finding the optimal time interval in scheduling vehicles. In this question, the participants used the B strategy of breaking the task into smaller subtasks (see

Table 7. B Strategy (Breaking the Task into Smaller Subtasks).

DRS	Original Version	Revised Version
B Strategy	(4) Considering this particular bus line, find the range of time intervals between vehicles during rush hours that would generate more profit than the last three years, and find the time interval between vehicles during rush hours that will maximize profits.	[2–2] Considering this particular bus line, find the range of time intervals between vehicles during rush hours that would generate more profit than the last three years. [2–3] Building on your answer to question [2–2] find the time interval between vehicles during rush hours that will maximize profits.

).

The reason for the use of the B strategy was indicated in the teacher candidates’ reflections: “We realized that students have difficulty understanding a mathematical question that involves a lengthy sentence”. Because the original version had a question that involved two layers of responses, the teacher candidates parsed it into two questions so that students could understand it better and solve the problem step by step.

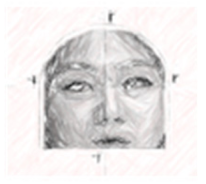
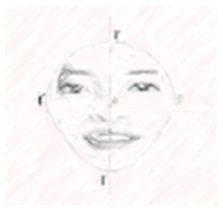
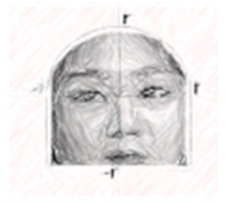
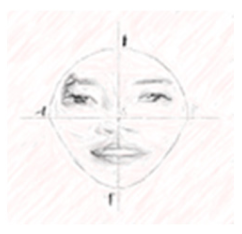
4.1.2. G4’s Modeling Task on the Effective Use of Sunscreen According to Face Shape

Group G4 developed a modeling task (see Supplementary Materials (Appendix 4)) related to the use of sunscreen. Although they initially considered the use of make-up products because some group members showed an interest in the topic, the group felt that this task could be gender-biased and problematic for the fairness of the assessment. The use of sunscreen, by contrast, is quite common regardless of gender, so the group chose a modeling task on the effective use of sunscreen—how long one can use a sunscreen product in relation to the amount of sunscreen per use.

DRS Used in the Revision of a Problem Statement. The teacher candidates in G4 used the W strategy (using words appropriate for student understanding; see

Table 8. W Strategy (Using Words Appropriate for Student Understanding).

DRS	Original Version			Revised Version
W strategy	… The following are the face shapes of Hosung, Naree, and Susan. Suppose the midpoint of the segment between the top of the forehead and the bottom of the chin is point O. Then, the distance from the top of the forehead to point O and the distance from the bottom of the chin to point O are both r. $(\mathrm{Note}: 1 \mathrm{mL}=1 {\mathrm{cm}}^3$) (Note: Please assume that the surface of the face is flat, ignoring all the curvature.)			… The following are the face shapes of Hosung, Naree, and Susan. Suppose the midpoint of the segment between the top of the forehead and the bottom of the chin is point O. Then the distance from the top of the forehead to point O and the distance from the bottom of the chin to point O are both r. $(\mathrm{Note}: 1 \mathrm{mL}=1 {\mathrm{cm}}^3$) (Note: Please assume that the surface of the face is flat, ignoring all the curvature.)
	Hosung (Round shape: Circle)	Naree (Angular: Half-circle + Quadrilateral)	Susan (Egg shape: Half-circle + Quadratic curve)	Hosung (Round shape: Circle)	Naree (Angular: Half-circle + Rectangle)	Susan (Egg shape: Half-circle + Quadratic function)

) as their DRS in revising a problem statement based on student responses.

The changes to the problem statement that reflect the W strategy were made in response to comments from two students: “It would have been better if it said quadratic function instead of the quadratic curve” (Student 1); “Is it the case that the bottom part of Naree’s face shape is rectangular?” (Student 2). As noted in Student 1’s response, the original version stated that Susan’s face shape featured a quadratic curve. Considering the student’s suggestions, the participants changed the wording from “quadratic curve” to “quadratic function” to help the students understand the context. They also developed the modeling task while assuming that Naree’s face shape included a rectangle, but Student 2’s response indicates that the assumption was unclear. To avoid confusion, the participants changed the wording from “quadrilateral” to “rectangle.”

DRS Used in the Revision of a Mathematical Question. The DR strategies used to revise the mathematical questions about sunscreens in response to student comments included the W strategy (using words appropriate for student understanding; see

Table 9. W Strategy.

DRS	Original Version	Revised Version
W strategy	(1) Find an expression for the area of the face shape of Hosung, Naree, and Susan in terms of r and explain the process.	(1) Find an expression for the area of the face of Hosung, Naree, and Susan in terms of r and explain the process.

), the A strategy (revising assumptions in the context of the task for clarification), and the T strategy (using technology to do extended calculations).

In question (1), the first question that connects the problem context and problem solving, the participants used the W strategy. The participants made changes in wording that reflected the W strategy in response to a student comment: “In question (1), wouldn’t it be better to say the area of the face of Hosung, Naree, and Susan rather than the area of the face shape?” The teacher candidates concluded that “area of the face” was more accurate than “area of the face shape” and revised the question accordingly. The second question asked for the maximum number of times that each person could apply a certain amount of sunscreen on their faces, and the teacher candidates used the A strategy (revising assumptions in the context of the task for articulation) and the W strategy in their revision (see

Table 10. A and W Strategies.

DRS	Original Version	Revised Version
A & W strategies	(2) When the sunscreen’s volume is 30 mL, write an expression for the maximum number of times that each person can apply the sunscreen on their faces. In doing so, use the symbol ‘[ ]’ and the variables t and r and explain the solution process. Note that t represents the thickness of the sunscreen layer and [x] represents the greatest integer less than or equal to x.	(2) When the sunscreen’s volume is 30 mL, write an expression for the maximum number of times that each person can apply the sunscreen on their faces, respectively. (Note: Only applying to the entire face is counted.) In doing so, use the symbol ‘[ ]’ and the variables t and r and explain the solution process. Note that t represents the thickness of the sunscreen layer and [x] represents the greatest integer less than or equal to x.

).

The participants made changes to the assumption using the A strategy in response to a student comment: “It is possible to use the leftover sunscreen on Day 25 after applying it entirely on Day 24. (The number of days) = (Usage) = $\frac{30}{{\mathsf{\pi }\mathrm{r}}^2\mathrm{t}}$.” This student’s response demonstrates the confusion about the maximum number of uses. Hence, the teacher candidates revised the definition by adding in the assumption that only apply to the entire face is counted as valid for the maximum number of uses.

They also used the W strategy to revise the question because of the following student response: “It can be said that (the total volume of sunscreen) = (the maximum number of uses) $\times$ (the volume of sunscreen used each time). Now, suppose the surface area is s and the thickness of the sunscreen layer is t (the volume of sunscreen used each time) = $s\times t$. Hence, (the maximum number of uses) =$\left[\frac{30 \mathrm{mL}}{s\times t}\right]$.” This student’s response provides a general expression without providing an individual expression for Hosung, Naree, and Susan, respectively. To make it clear that the students were required to find three different expressions for each of the three people, the teacher candidates added the word “respectively” to the question. After finding the maximum number of uses for each of the three people, the third question asked who (of the three) could use the sunscreen the longest time. The teacher candidates used the T strategy (using technology to do extended calculations) and the W strategy in their revision of the question (see

Table 11. T and W Strategies.

DRS	Original Version	Revised Version
T & W strategies	(3) Use the following conditions and assume that they apply the sunscreen on their faces once per day. Explain who will be able to use the sunscreen the longest time. (Note: Assume π = 3 in your calculation.) Conditions: The thickness of the sunscreen layer is 0.005 cm on Hosung, 0.003 cm on Naree, and 0.004 cm on Susan. Assume r is 9 cm.	(3) Use the following conditions and assume that they apply the sunscreen on their faces once per day and that the volume of the sunscreen is 30 mL. Explain who will be able to use the sunscreen the longest time based on your results in question (2). (Note: Assume π = 3 in your calculation.) Conditions: The thickness of the sunscreen layer is 0.005 cm on Hosung, 0.003 cm on Naree, and 0.004 cm on Susan. Assume r is 9 cm.

).

They used the W strategy in response to two student comments: “It would be great if question (3) made it clear that the volume of the sunscreen is 30 mL” (Student 3); “(Hosung) = $\pi r^{2}t=\frac{243}{200}$, (Naree) = $\left[\frac{\pi }{2}{r}^2+2r^2\right]t=\frac{1701}{2000}$, (Susan) = $\left[\frac{\pi }{2}{r}^2+\frac{4}{3}{r}^2\right]t=\frac{1836}{2000}$; hence Naree, who has the smallest amount to apply each time, would be able to use the sunscreen the longest time” (Student 4).

The teacher candidates reviewed Student 3’s suggestion and added the information that the volume of the sunscreen was 30 mL to make the assumption clear for students. Student 4’s response suggested that s/he had compared the volume of the sunscreen used each time by Hosung, Naree, and Susan without considering the maximum number of uses. To encourage them to use “the expression of the maximum number of times that each person can apply the sunscreen on their faces” from question (2) and make the intention of the problem clear, the teacher candidates added the wording “based on your results in question (2).”

The use of the T strategy in their revision of the question stemmed from the following student response: “The calculation was very complicated, and I was confused about whether we could use a calculator.” Many students said that the calculation was an important part of the solution in question (3) was too complicated. Hence, the participants added the image of the calculator in the problem statement to indicate that the use of the calculator was encouraged.

4.2. Emerging Pedagogical Ideas from Revising Tasks/Rubrics

The participants used various DRSs in the process of modifying the rubrics (e.g., Supplementary Materials (Appendix 5) for used DRS by G1) and the modeling tasks in response to the student comments. They also experienced cognitive changes in relation to the modeling tasks and rubrics in their reflections. On the basis of the teacher candidates’ written data (i.e., reflective writing), this section summarizes the results concerning the various cognitive changes in terms of the emerging pedagogical ideas experienced by teacher candidates through the process of developing and revising modeling tasks and rubrics. In particular, while adopting DRSs in their revision of rubrics, the participants were found to develop new pedagogical ideas. These can be categorized in terms of five cognitive changes.

4.2.1. Need for Developing Modeling Tasks to Pique (Student) Interest

In all groups, the participants started the study course with the goal of developing modeling tasks that are meaningful to students based on the context of their life experiences and that engage students in realistic and worthwhile mathematical activities while still satisfying the mathematics standards [21]. In comments, students from nine of the 11 groups who solved the modeling tasks stated that the task was very interesting. The comments included the following: “It was interesting because it was about armaments, which is currently an issue” (G3); “it was interesting to see celebrities in the problem and to mathematize a daily-life problem” (G4); “the approach was interesting because I can see these in real-life” (G7); “the problem was interesting” (G9); “I like soccer, and so I became interested because it was a subject closely related to everyday life, and the fact that mathematics can be applied to this area was interesting” (G10); and “it would be interesting to think about how it will change depending on the speed of the car” (G11). These results, in line with the existing literature, support the view that authentic modeling tasks can increase student interest.

On the basis of the comments about student interest reported by the participants, it was found that the participants recognized the importance of student interest in modeling tasks: “In the students’ feedback, it was said that the story of the problem was interesting, and I was satisfied that I had made the problem suitable for the goal of the mathematical essay question” (G1); “as much as I invested a lot of time creating the task, I created a fun task and it was a pleasant experience” (G2); and “I was able to see that the students were interested in the problem using modeling, so I could understand why the importance of realistic modeling continues to be emphasized in current mathematics education” (G8).

4.2.2. Need for Assessment That Impacts Student Learning

The participants recognized that there could be a wide range of student ideas and solutions to the same problem (G7). Furthermore, some stated that it was necessary to make the rubrics as detailed as possible to provide students with high-quality feedback (G9).

4.2.3. Need for a Body of Modeling Tasks and Rubrics as an Interactive Process

The participants in all groups recognized that the rubrics had to change as the modeling tasks were revised. In particular, the participants in G2 considered not only the change in the items but also the change in the assigned points. In addition, the participants in G3 concluded that the modeling task and rubrics should interact with each other because the change in the rubric is not a one-directional thinking process (i.e., the change in modeling tasks directs the change in the rubric), but rather an interactive process.

4.2.4. Need for Diverse Thinking by Students in the Design of Modeling Tasks

Through the process of modifying the rubrics based on the student responses, the participants encountered unanticipated (e.g., creative, idiosyncratic) responses in the students’ idiosyncratic strategies or approaches to the problem. In the process of modifying the rubrics in response to the unanticipated solutions, the participants recognized “the difficulty in scoring due to the unexpected various responses” (G4) and that “student responses were surprisingly very diverse” (G1). For example, they reported in their reflections that “there were various solution methods, such as using functions or equations” (G2), “It will be considered correct when the area enclosed by the quadratic function and the x-axis is found using a formula” (G4), and “It was beneficial to be able to see a variety of ideas in the student responses; we could see that the difference between the student’s solution method and the intended solution method was much greater than we expected” (G8). Furthermore, the participants in G10 mentioned in their reflection that “it is absolutely necessary to gather students’ feedback after tasks are developed.”

4.2.5. Need for Developing a Rubric with a Clear Scoring Scheme and a Rich Description of Acceptable Methods and Solutions

The participants noted that a variety of student responses were not effectively graded by the original rubrics, especially when the grading was done in strict adherence to prescribed scoring criteria as opposed to a holistic grading method. Regarding the scoring criteria, the participants concluded that they should improve the rubrics by describing the scoring criteria in more detail (G2, G3), clarifying the language of the scoring criteria (G4, G10), and adding more examples of viable solutions to the scoring criteria (G11).

5. Discussion

The findings indicate that the teacher candidates used the S strategy (revising complicated computations for simpler problems) when excessive calculations were unnecessary; however, they used the T strategy (using technology to do extended calculations) when they found that complicated calculations were an essential aspect of the learning goal, thereby modifying the knowledge to be taught. They also used the B strategy (breaking the task into smaller subtasks) on the basis of the learned knowledge evidenced in student responses when one item required higher thinking skills. In cases where student responses did not correspond to the solution path expected by the question, the teacher candidates revised the knowledge to be taught using the A strategy (revising assumptions in the context of the task for articulation).

Other cases in which the teacher candidates revised knowledge to be taught included their use of the W strategy (using wording appropriate for students) and the N strategy (revising notations such as symbols or letters that cause students’ misunderstandings or mistakes). Specifying a DRS that teacher candidates can implement based on learned knowledge evidenced in student responses has the potential to inform teacher education about the way teacher candidates’ didactic transpositions take place between knowledge to be taught and learned knowledge and how a novice teacher may make instructional decisions based on student responses.

The experience of implementing various DRSs can have a positive impact on teacher candidates’ development of pedagogical ideas in relation to the NCTM assessment standards [21]. More specifically, the participants were found to recognize modeling task design as an interactive process. This suggests that the participants were able to see the need to ensure that various parts of the assessment process form a coherent whole (see the coherence standard of [21]). The participants’ statements also indicated the need for students’ diverse thinking in the design of modeling tasks. These statements echo the openness standard [21,22], in that the participants concluded that the assessment process needs to be open to various forms of student thinking and to improve tasks that incorporate student feedback. In addition, the participants reported that there was a large gap between anticipated solution methods and the various, creative students’ methods, concluding that the original rubrics needed significant revision to include students’ creative strategies. That said, the modeling design by the participants provided a valuable experience for teacher candidates by minimizing teacher bias in making inferences about students’ learning (see the inferences standard in [21]).

The teacher candidates in this study recognized the challenges involved in developing modeling tasks but also realized the importance of mathematical modeling in stimulating student interest and motivation. The participants’ comments in support of the need to develop modeling tasks that engage students to suggest that modeling task design should consider students’ interests from a pedagogical perspective.

Furthermore, the participants’ comments indicate that the modeling task design process led them to reflect on the role of teachers (e.g., “Creating formulas and scoring criteria and participating in all phases of the assessment made me experience the role of a teacher”) and enabled them to argue for the benefits of pedagogical learning opportunities in teacher education (e.g., “It is important to learn college mathematics in college, but I also wanted to engage in an activity that is practically helpful in the future as a teacher, and this class was the right opportunity for me. I think this class will be remembered as a meaningful experience when I become a teacher.”). The benefits of learning opportunities in this study are mostly concerned with assessment skills. For example, the participants’ comments regarding the need for assessments that affect student learning suggest that modeling tasks are useful as assessments that can indicate student understanding and affect student mathematical learning (c.f. Dynamical Continuous Discrete assessment in [24] about teacher feedback and students’ improved competencies). This indicates that the design of modeling tasks can serve as an effective learning activity for teacher candidates in teacher education, enabling teacher candidates to recognize modeling not only as a pedagogical strategy to stimulate student interest but also as a tool for assessment and learning. In addition, the participants also mentioned the need to develop rubrics with a clear scoring scheme and a rich description of acceptable methods and solutions. The participants modified the scoring criteria through elaboration, concretization, and clarification while the rubrics became increasingly inclusive with regard to student responses that were unanticipated but mathematically valid.

In sum, their reflections suggested that the teacher candidates were able to (1) see the need for a cohesive practice of assessment with modeling tasks and rubrics, (2) recognize the gap between teachers’ views of the modeling task and students’ interpretation of it, and (3) identify the need for student feedback and for assessments that could promote students’ individual progress. In particular, analyzing student responses gave them a chance to see that some of the mathematical terminology or facts that are obvious to teachers may be interpreted differently by students, providing a better understanding of the process of didactic transposition.

6. Implications

This study sheds light on one possible use of the design of mathematical modeling tasks as a learning activity in teacher education. Existing frameworks [5,6,7,8] on mathematical modeling mainly highlight the use and process of student learning through modeling activities in the classroom. However, the framework did not say much about how the teacher may facilitate modeling activities and support students. More research is necessary about the pedagogy of modeling. While it is important to understand the properties of modeling tasks and the modeling process, we note that it is just as important to rethink the modeling process from a pedagogical point of view and to appreciate the complicated teaching process of communicating with and supporting students in modeling tasks.

From the viewpoint of a future teacher in teacher education, the study has theorized the mathematical modeling process as a pedagogical context in which mathematics teacher candidates can relate to various didactic transpositions posed by the professional noticing of student answers and solutions to modeling tasks. We note that the student-centered modeling task design may also be framed by different theoretical frameworks such as competency-based approaches [24,25] other than didactic transposition theory. One important result worthy of mentioning here is that the learning activity in this study could be characterized as bottom-up rather than top-down (or didactical) since the participants produced the emergent pedagogical ideas on their own rather than being handed a list of pedagogical ideas. Approaching the modeling process from a pedagogical perspective also helped the teacher candidates to identify a potential gap between the teacher (as a poser of the modeling task) and students (as participants in the modeling task), to minimize the gap actively by implementing DRSs, and to make the modeling task more authentic and accessible. Although there is some literature on mathematical modeling in teacher education, few studies have involved teacher candidates in university-based teacher education programs engaging in the design of mathematical modeling tasks and using actual student responses to revise the tasks. The findings of the current study suggest the effectiveness and possibility of integrating a top-down process (creating modeling tasks and rubrics as part of the course activity) and a bottom-up process (the revision of modeling tasks guided by student answers and solutions only). In the study, the (top-down) process involved teacher candidates learning the mathematical modeling process, NCTM process standards, and the TIMSS framework, as well as creating modeling tasks. The (bottom-up) process involved the teacher candidates implementing the task with students and using the experience to revise the task and reflect on their pedagogical insights from the experience. We recommend that future studies investigate the process of designing various learning tasks, possibly in areas other than mathematical modeling, so that DRS patterns can be tested and improved, just as we asked our teacher candidates to revise their tasks and discuss the lessons learned from the process.