Influence of MHD Hybrid Ferrofluid Flow on Exponentially Stretching/Shrinking Surface with Heat Source/Sink under Stagnation Point Region

Abstract

The numerical investigations of hybrid ferrofluid flow with magnetohydrodynamic (MHD) and heat source/sink effects are examined in this research. The sheet is assumed to stretch or shrink exponentially near the stagnation region. Two dissimilar magnetic nanoparticles, namely cobalt ferrite, CoFe₂O₄ and magnetite, Fe₃O₄, are considered with water as a based fluid. Utilizing the suitable similarity transformation, the governing equations are reduced to an ordinary differential equation (ODE). The converted ODEs are numerically solved with the aid of bvp4c solver from Matlab. The influences of varied parameters on velocity profile, skin friction coefficient, temperature profile and local Nusselt number are demonstrated graphically. The analysis evident the occurrence of non-unique solution for a shrinking sheet and it is confirmed from the analysis of stability that only the first solution is the stable solution. It is also found that for a stronger heat source, heat absorption is likely to happen at the sheet. Further, hybrid ferrofluid intensifies the heat transfer rate compared to ferrofluid. Moreover, the boundary layer separation is bound to happen faster with an increment of magnetic parameter, while it delays when CoFe₂O₄ nanoparticle volume fraction increases.

1. Introduction

Ferrofluids or magnetic colloids are made by disseminating magnetic nanoparticles like cobalt ferrite CoFe₂O₄, hematite Fe₂O₃, magnetite Fe₃O₄ and many other nanometer-sized particles containing iron in the base fluid [1]; as a result, these particles have a dipolar interaction energy and magnetic moment in the base fluid. Ferrofluids have various biomedicine and engineering applications specifically in drug delivery [2], chemical activity monitoring in the human brain in real-time, destruction of tumors and toxin elimination from the body [3], rotary seals in computer hard drives and other rotating shaft motors [4]. For these reasons, many researchers [5,6,7,8] have focused their investigation on ferrofluids. Usually, nanofluid comprises only one nanoparticle whereas the hybrid nanofluid comprises two distinct nanoparticles disseminated in a base fluid [9]. Through the combination of two dissimilar nanomaterials, hybrid nanofluids are created to improve their thermal and rheological properties [10]. Suresh et al. [11] presented an experimental investigation using a two-step method (thermomechanical method) to synthesize hybrid (Al₂O₃-Cu/water) nanofluid. The outcomes demonstrated that the prepared hybrid nanofluid for a concentration of 2% nanoparticle volume fraction increase its thermal conductivity by 12.11%. In another experimental investigation, Madhesh and Kalaiselvam [12] examined the properties of Cu-TiO₂/water nanofluid in a cooling system, while Esfe et al. [13] scrutinized the thermal conductivity of the hybrid (Ag-MgO) nanofluid and discovered that its conductivity rises with augmentation of nanoparticles concentration. Chu et al. [14] examined the thermal performance and flow characteristics of hybridized nanofluid (MWCNT-Fe₃O₂/water) in a cavity. The flow features of hybrid ferrofluids (Fe₃O₄–CoFe₂O₄) with water–ethylene glycol mixture (50–50%) as a based fluid in the thin film flow were investigated by Kumar et al. [15] and they revealed that hybrid ferrofluid offers a higher rate of heat transfer than that of ferrofluid. Researchers from all over the world have been drawn to hybrid nanofluids because of their exceptional heat augmentation behavior, which gives fine control over heat transfer in numerous industries. Due to that, several experimental and theoretical investigations on hybrid nanofluid have been published widely such as in references [16,17,18]. Therefore, the aim of developing hybrid ferrofluid is therefore to manage heat transfer efficiently in the flow field.

It seems that magnetohydrodynamic (MHD), heat source (generation) and heat sink (absorption) effects are crucial in monitoring the heat transfer in the production of quality products as it depends on the heat monitoring factor. This is also mainly due to the reason that MHD terms extremely appeared in various engineering and industrial processes like MHD generator, cancer therapy, MHD power generation, nuclear reactor, etc. [19]. The influences of heat source and sink are also important in cooling problems associated with nuclear reactions, combustion processes, and magnetized utilization in neurobiology to learn brain function [20]. In view of the increasing importance of MHD and heat source/sink, a lot of work has been carried out to investigate these effects in boundary layer flow. For instance, the simultaneous impact of MHD, heat source/sink and suction instigated by a shrinking sheet can be observed in the work of Bhattacharyya [21] and observed that increasing heat sink parameters cause the heat transfer to enhance. Further, Gorla et al. [22] explored the same effects in a hybrid nanofluid-filled porous cavity. Recently, Armaghani et al. [23] scrutinized the generation/absorption of heat and MHD in their investigation of hybrid nanofluid in an L-shaped cavity. They deduced that using the highest number of sink power results in the best heat transfer. Furthermore, the studies on MHD flow and heat source/sink by means of various physical configurations have been conducted by Jamaludin et al. [24] and Reddy et al. [25].

Nowadays, the existence of non-unique solutions has gained the attention of modern researchers. In some boundary layer flow problems, non-unique solutions have generally been found for linear shrinking sheet cases. For instance, non-unique solutions have been observed by Wang [26], Bachok et al. [27], Kamal et al. [28] and Anuar and Bachok [29], among others for the stagnation flow problem. Meanwhile, Bhattacharyya and Vajravelu [30], Bachok et al. [31] and Anuar et al. [32] have observed the occurrence of non-unique solutions in their investigation of stagnation flow when the sheet is shrunk exponentially. They conclude that the domain of similarity solution to existing is larger for the stagnation flow in the exponential case rather than in the linear case. However, there also exist some situations where non-unique solutions happen to exist for both cases, i.e., stretching and shrinking (see for instance the research carried out by Lund et al. [33] and Waini et al. [34]). With regards to the existence of more than one solution, a stability analysis on the solutions obtained has been performed by some researchers. This kind of analysis is important in order to avoid any misleading interpretation of flow. Some important investigations concerning the stability analysis on the solutions of boundary layer flow problem were made by Merkin [35], Weidman et al. [36], Harris et al. [37] and more recently by Anuar et al. [38], Mustafa et al. [39] and Aladdin et al. [40,41], among others. It has been observed that the second solution has always been unstable and therefore unobtainable in practice, while the other solution is stable.

Owing to the nonlinearity of equations that describe most engineering and science phenomena, many authors used numerical methods such as finite element methods [22,23], shooting method [6,15,30] and bvp4c solver [18,24,34,40] to solve the governing equations. For the present problem, in solving the system of nonlinear equations, Matlab bvp4c built-in code is employed. The Matlab bvp4c solver is a residual control-based adaptive mesh solver. The algorithm is based on the Runge–Kutta improved formulas that have interpolation capability [42]. It has been used successfully by many researchers to solve boundary value problems from different models in science and engineering. This method was found to be robust and consistent, showing superiority over the shooting method.

The goal of this investigation is to scrutinize the heat generation/absorption of MHD hybrid ferrofluid (CoFe₂O₄–Fe₃O₄/water) flow instigated by an exponentially deformable sheet. In the light of the previous literature survey, it is worthy to mention that no attempt has been made on this kind of flow problem yet. Here, the similarity variable is used to convert the governing equations into an ODE which later be solved numerically using bvp4c (Matlab’s built-in function). The computed results for relevant parameters concerning local Nusselt number and skin friction coefficient, together with temperature profile and velocity profile, are visualized graphically and elaborated in detail. Further, the occurrence of two solutions motivates us to identify the stable and unstable solutions by performing the stability analysis. In addition, this theoretical study would help engineers who are experimentally working on hybrid ferrofluids, and the findings are expected to reduce the cost of future experiments.

2. Problem Formulation

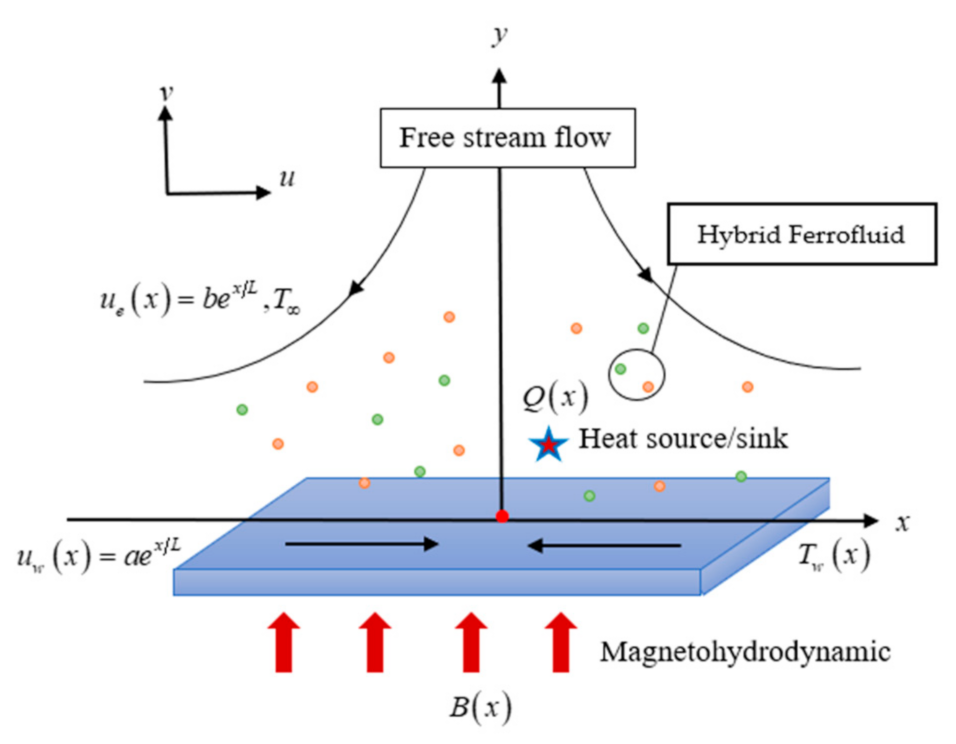
2.1. Mathematical Framework

The two-dimensional and steady flow of MHD hybrid ferrofluid past a deformable sheet are investigated and portrayed in Figure 1. The $x$-axis is selected along the direction of the horizontal surface while $y$-axis is perpendicular to it. The surface of the sheet is shrunk or stretched with exponential velocity $u_w\left(x\right)=a\exp \left(x/L\right)$ given that $a$ and $L$ are the positive constant and characteristic length, respectively. As shown in Figure 1, magnetic $B$ and heat generation/absorption $Q\left(x\right)$ are applied parallel to the $y$-axis and will be defined later. Distant from the horizontal surface, the flow is kept at constant temperature $T_{\infty }$ and free stream velocity $u_e\left(x\right)=b\exp \left(x/L\right)$; here $b$ is the positive constant. Further, the surface temperature is assumed to vary as prescribed exponential function and denoted by $T_w=T_{\infty }+T_0\exp \left(\frac{x}{2L}\right)$ where $T_0$ is the rate at which the temperature rises along the sheet is measured.

Following the mathematical formulation and idea proposed by Kumar et al. [15], Wang [26] and Kamal et al. [28], the governing partial differential equations are denoted as:

$$\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}=0$$

(1)

$$u\frac{\partial u}{\partial x}+v\frac{\partial u}{\partial y}=u_e\frac{d{u}_e}{dx}+\frac{{\mu }_{hf}}{{\rho }_{hf}}\frac{{\partial }^{2}u}{\partial y^2}-\frac{{\sigma }_{hf}}{{\rho }_{hf}}{B}^2\left(u-u_e\right)$$

(2)

$$u\frac{\partial T}{\partial x}+v\frac{\partial T}{\partial y}=\frac{k_{hf}}{{\left(\rho C_p\right)}_{hf}}\frac{{\partial }^{2}T}{\partial y^2}+\frac{Q\left(x\right)}{{\left(\rho C_p\right)}_{hf}}\left(T-T_{\infty }\right)$$

(3)

$\left(u,v\right)$ in the above equation indicates the velocity component in the $\left(x,y\right)$ direction and $T$ refers to the fluid’s temperature. Further, $\mu$ denotes the dynamic viscosity, $\rho$ refers to the density, $\sigma$ and $k$ are the electrical and thermal conductivity, respectively, and $C_p$ is the specific heat where the subscript $‘hf’$ signifies the hybrid ferrofluid.

The relevant boundary conditions are given as (Bachok et al. [27]):

$$T=T_w\left(x\right),v=0,u=u_w\left(x\right)\mathrm{at}y=0;T\to T_{\infty },u\to u_e\left(x\right)\mathrm{as}y\to \infty$$

(4)

2.2. Correlation Used for Hybrid Ferrofluid

The thermophysical properties for the hybrid ferrofluid are employed from the work of Takabi and Salehi [9] and Gorla et al. [22] (see

Table 1. Thermophysical traits of hybrid ferrofluid.

Properties	Hybrid Ferrofluid
Density	${\rho }_{hf}=\left(1-\phi \right){\rho }_f+{\phi }_1{\rho }_1+{\phi }_2{\rho }_2$
Thermal conductivity	$\frac{k_{hf}}{k_f}=\frac{\left(\left({\phi }_1{k}_1+{\phi }_2{k}_2\right)/\phi \right)+2k_f+2\left({\phi }_1{k}_1+{\phi }_2{k}_2\right)-2\phi k_f}{\left(\left({\phi }_1{k}_1+{\phi }_2{k}_2\right)/\phi \right)+2k_f-\left({\phi }_1{k}_1+{\phi }_2{k}_2\right)+\phi k_f}$
Heat capacity	${\left(\rho C_p\right)}_{hf}=\left(1-\phi \right){\left(\rho C_p\right)}_f+{\phi }_1{\left(\rho C_p\right)}_1+{\phi }_2{\left(\rho C_p\right)}_2$
Dynamic viscosity	${\mu }_{hf}={\mu }_f/{\left(1-\phi \right)}^{2.5}$
Electrical conductivity	$\frac{{\sigma }_{hf}}{{\sigma }_f}=1+\frac{3\left(\left(\left({\phi }_1{\sigma }_1+{\phi }_2{\sigma }_2\right)/{\sigma }_f\right)-\phi \right)}{\left(\left(\left({\phi }_1{\sigma }_1+{\phi }_2{\sigma }_2\right)/\left(\phi {\sigma }_f\right)\right)+2\right)-\left(\left(\left({\phi }_1{\sigma }_1+{\phi }_2{\sigma }_2\right)/{\sigma }_f\right)-\phi \right)}$

). The first and second nanoparticles are denoted by subscripts “1” and “2” in the table. Further, $\phi$ is the summation of the volume concentration of two dissimilar kinds of nanoparticles, i.e., $\phi ={\phi }_1+{\phi }_2$.

It should be emphasized that the desired hybrid ferrofluid is formed by suspending 1% of Iron Oxide (Fe₃O₄) nanoparticle into the base fluid (water). Then, Cobalt Iron Oxide (CoFe₂O₄) nanoparticle is added into the Fe₃O₄/water nanofluid and eventually formed a hybrid ferrofluid. In addition, the volume fraction of CoFe₂O₄ nanoparticles is fluctuated from 0 to 2%. Therefore, in this study, the first nanoparticle is denoted by Fe₃O₄ while the second nanoparticle refers to CoFe₂O₄. The physical characteristics of the base fluid and the nanosized particles are shown in

Table 2. Thermophysical properties of nanoparticle and base fluid.

	Physical Properties
	${\mathit{C}}_{\mathit{p}}\left(\mathit{J}\cdot \mathit{k}{\mathit{g}}^{-1}\cdot {\mathit{K}}^{-1}\right)$	$\mathit{\rho }\left(\mathit{k}\mathit{g}\cdot {\mathit{m}}^{-3}\right)$	$\mathit{k}\left(\mathit{W}\cdot {\mathit{m}}^{-1}\cdot {\mathit{K}}^{-1}\right)$	$\mathit{\sigma }\left(\mathit{S}\cdot {\mathit{m}}^{-1}\right)$
water, H2O	4179	997.1	0.613	0.05
Magnetic nanoparticles
Magnetite, Fe3O4	670	5180	9.7	0.74 × 106
Cobalt Ferrite, CoFe2O4	700	4907	3.7	1.1 × 107
Non-magnetic nanoparticles
Copper, Cu	385	8933	401	5.96 × 107
Titania, TiO2	686.2	4250	8.9538	1 × 10−12
Alumina, Al2O3	765	3970	40	1 × 10−10

(Abbas and Sheikh [7], Oztop and Abu-Nada [43], Sheikholeslami et al. [44], Tlili et al. [45]).

2.3. Similarity Solutions

The similarity transformations take the following form (Bhattacharyya and Vajravelu [30]):

$$\eta =y{\left(\frac{b}{2{\nu }_{f}L}\right)}^{1/2}\exp \left(\frac{x}{2L}\right),\theta \left(\eta \right)=\frac{T-T_{\infty }}{T_w\left(x\right)-T_{\infty }},\psi ={\left(2{\nu }_{f}Lb\right)}^{1/2}\exp \left(\frac{x}{2L}\right)f\left(\eta \right)$$

(5)

where ${\nu }_f$, $\eta$ and $\psi$ are the kinematic viscosity, similarity variable and stream function, while $f$ and $\theta$ is the dimensionless functions. Next, we defined $u=\partial \psi /\partial y$ and $v=-\partial \psi /\partial x.$ Accordingly, Equation (1) is automatically satisfied.

We take $Q\left(x\right)=\frac{Q_0}{2L}\exp \left(x/L\right)$ and $B=B_0\exp \left(\frac{x}{2L}\right)$ where $Q_0$ denotes the heat source/sink coefficient and $B_0$ is the constant magnetic field in order for the similarity solutions to exist. Variables (5) are substituted into the governing Equations (2) and (3) to produce the following ODEs:

$$\frac{{\mu }_{hf}/{\mu }_f}{{\rho }_{hf}/{\rho }_f}{f}^{‴}-2{f^{\prime }}^2+f f^{″}-\frac{{\sigma }_{hf}/{\sigma }_f}{{\rho }_{hf}/{\rho }_f}M\left(f^{\prime }-1\right)+2=0$$

(6)

$$\frac{1}{\mathrm{Pr}}\frac{k_{hf}/k_f}{{\left(\rho C_p\right)}_{hf}/{\left(\rho C_p\right)}_f}{\theta }^{″}+f{\theta }^{\prime }-f^{\prime }\theta +\frac{1}{{\left(\rho C_p\right)}_{hf}/{\left(\rho C_p\right)}_f}\beta \theta =0$$

(7)

in which prime denotes the differentiation with respect to $\eta$. Further, $\mathrm{Pr}={\nu }_f{\left(\rho C_p\right)}_f/k_f$ and $M=\frac{2{\sigma }_f{B}_0{}^{2}L}{b{\rho }_f}$ refer to the Prandtl number and magnetic field parameter, while $\beta =\frac{Q_0}{b{\left(\rho C_p\right)}_f}$ denotes the heat source/sink parameter where $\beta >0$ stands for heat generation (source) and $\beta <0$ refers to heat absorption (sink).

Subsequently, Equation (4) becomes:

$$\theta \left(0\right)=1,f^{\prime }\left(0\right)=\lambda ,f\left(0\right)=0;\theta \left(\eta \right)\to 0,f^{\prime }\left(\eta \right)\to 1\mathrm{as}\eta \to \infty$$

(8)

Here, $\lambda =a/b$ is the stretching/shrinking parameter given that $\lambda <0$ and $\lambda >0$ denote the sheet is shrunk and stretch, respectively, $\lambda =0$ refers to a static sheet.

2.4. Physical Quantities

The skin friction $C_f$ and Nusselt number $N{u}_x$ are the physical quantities of interest in this research and can be described as:

$$C_f=\frac{{\mu }_{hf}{\left(\frac{\partial u}{\partial y}\right)}_{y=0}}{{\rho }_f{u}_e^2},N{u}_x=-\frac{2L{k}_{hf}{\left(\frac{\partial T}{\partial y}\right)}_{y=0}}{k_f\left(T_w-T_{\infty }\right)}$$

(9)

By implementing the variables (5) into Equation (9), we have:

$$C_f{\mathrm{Re}}_x^{1/2}=\frac{{\mu }_{hf}}{{\mu }_f}{f}^{″}\left(0\right),N{u}_x{\mathrm{Re}}_x^{-1/2}=-\frac{k_{hf}}{k_f}{\theta }^{\prime }\left(0\right)$$

(10)

where ${\mathrm{Re}}_x=2L{u}_e/{\nu }_f$ is the Reynolds number.

3. Stability Analysis of Solutions

The present investigation admits more than one solution for some range of governing parameters. As a result, a stability analysis is required. The first step is to consider the current problem as an unsteady problem as suggested by Merkin [35]. Therefore, Equation (1) remains the same while the unsteady governing equations is rewritten as:

$$\frac{\partial u}{\partial t}+u\frac{\partial u}{\partial x}+v\frac{\partial u}{\partial y}=u_e\frac{d{u}_e}{dx}+\frac{{\mu }_{hf}}{{\rho }_{hf}}\frac{{\partial }^{2}u}{\partial y^2}-\frac{{\sigma }_{hf}}{{\rho }_{hf}}{B}^2\left(u-u_e\right)$$

(11)

$$\frac{\partial T}{\partial t}+u\frac{\partial T}{\partial x}+v\frac{\partial T}{\partial y}=\frac{k_{hf}}{{\left(\rho C_p\right)}_{hf}}\frac{{\partial }^{2}T}{\partial y^2}+\frac{Q\left(x\right)}{{\left(\rho C_p\right)}_{hf}}\left(T-T_{\infty }\right)$$

(12)

subjected to the conditions (4). Next, a new dimensionless time variable $\tau$ is introduced:

$$\tau =\frac{b}{2L}t\exp \left(\frac{x}{L}\right)$$

(13)

while the new dimensionless transformation can be rewritten as:

$$\eta =y{\left(\frac{b}{2{\nu }_{f}L}\right)}^{1/2}\exp \left(\frac{x}{2L}\right),\psi ={\left(2{\nu }_{f}Lb\right)}^{1/2}\exp \left(\frac{x}{2L}\right)f\left(\eta ,\tau \right),\theta \left(\eta ,\tau \right)=\frac{T-T_{\infty }}{T_w\left(x\right)-T_{\infty }}$$

(14)

When the variables (13) and (14) are substituted into Equations (11) and (12), the obtained equations are:

$$\frac{{\mu }_{hf}/{\mu }_f}{{\rho }_{hf}/{\rho }_f}\frac{{\partial }^{3}f}{\partial {\eta }^3}-2{\left(\frac{\partial f}{\partial \eta }\right)}^2+f\frac{{\partial }^{2}f}{\partial {\eta }^2}+2-\frac{{\sigma }_{hf}/{\sigma }_f}{{\rho }_{hf}/{\rho }_f}M\left(\frac{\partial f}{\partial \eta }-1\right)-\frac{{\partial }^{2}f}{\partial \eta \partial \tau }+2\tau \left(\frac{\partial f}{\partial \tau }\frac{{\partial }^{2}f}{\partial {\eta }^2}-\frac{\partial f}{\partial \eta }\frac{{\partial }^{2}f}{\partial \eta \partial \tau }\right)=0$$

(15)

$$\frac{1}{\mathrm{Pr}}\frac{k_{hf}/k_f}{{\left(\rho C_p\right)}_{hf}/{\left(\rho C_p\right)}_f}\frac{{\partial }^2\theta }{\partial {\eta }^2}-\theta \frac{\partial f}{\partial \eta }+f\frac{\partial \theta }{\partial \eta }+\frac{\beta }{{\left(\rho C_p\right)}_{hf}/{\left(\rho C_p\right)}_f}\theta -\frac{\partial \theta }{\partial \tau }-2\tau \left(\frac{\partial f}{\partial \eta }\frac{\partial \theta }{\partial \tau }-\frac{\partial f}{\partial \tau }\frac{\partial \theta }{\partial \eta }\right)=0$$

(16)

and the transform conditions are:

$$\begin{array}{c}f\left(0,\tau \right)+2\tau \frac{\partial f}{\partial \tau }\left(0,\tau \right)=0,\theta \left(0,\tau \right)=1,\frac{\partial f}{\partial \eta }\left(0,\tau \right)=\lambda ,\\ \theta \left(\eta ,\tau \right)\to 0,\frac{\partial f}{\partial \eta }\left(\eta ,\tau \right)\to 1\mathrm{as}\eta \to \infty \end{array}$$

(17)

Afterwards, we write [36]:

$$f\left(\eta ,\tau \right)=f_0\left(\eta \right)+e^{-\gamma \tau }F\left(\eta ,\tau \right),\theta \left(\eta ,\tau \right)={\theta }_0\left(\eta \right)+e^{-\gamma \tau }H\left(\eta ,\tau \right),$$

(18)

for the purpose to specify the stability of the steady flow solution of $\theta \left(\eta \right)={\theta }_0\left(\eta \right)$ and $f\left(\eta \right)=f_0\left(\eta \right)$. From the above equation, $F\left(\eta ,\tau \right)$ and $H\left(\eta ,\tau \right)$ are relatively smaller than $f_0\left(\eta \right)$ and ${\theta }_0\left(\eta \right)$, while $\gamma$ is the smallest eigenvalues parameter. Substitute Equation (18) into Equations (15)–(17) and setting $\tau =0$, we have $H\left(\eta \right)=H_0\left(\eta \right)$ and $F\left(\eta \right)=F_0\left(\eta \right)$. Therefore, the final linearized equations take the following form:

$$\frac{{\mu }_{hf}/{\mu }_f}{{\rho }_{hf}/{\rho }_f}{F}_0^{‴}-4f_0{}^{\prime }{F}_0{}^{\prime }+f_0{F}_0^{″}+f_0^{″}{F}_0-\frac{{\sigma }_{hf}/{\sigma }_f}{{\rho }_{hf}/{\rho }_f}M{F}_0^{\prime }+\gamma F_0^{\prime }=0$$

(19)

$$\frac{1}{\mathrm{Pr}}\frac{k_{hf}/k_f}{{\left(\rho C_p\right)}_{hf}/{\left(\rho C_p\right)}_f}{H}_0^{″}+f_0{H}_0{}^{\prime }+F_0{\theta }_0{}^{\prime }-F_0{}^{\prime }{\theta }_0-H_0{f}_0{}^{\prime }+\frac{\beta }{{\left(\rho C_p\right)}_{hf}/{\left(\rho C_p\right)}_f}{H}_0+\gamma H_0=0$$

(20)

associated with conditions:

$$H_0\left(0\right)=0,F_0{}^{\prime }\left(0\right)=0,F_0\left(0\right)=0;H_0\left(\eta \right)\to 0,F_0{}^{\prime }\left(\eta \right)\to 0\mathrm{as}\eta \to \infty$$

(21)

To solve the above-linearized equations, we need to relax a boundary condition of $F_0^{\prime }\left(\eta \right)\to 0$ when $\eta \to \infty$ and replace it with a new boundary condition $F_0^{″}\left(0\right)=1$ as advocated by Harris et al. [37]. This set of linearized equations will eventually display an infinite set of eigenvalues ${\gamma }_1<{\gamma }_2<\dots <{\gamma }_n$.

4. Results and Discussion

With the help of Matlab’s in-built function (i.e., bvp4c solver), the self-similar ODEs (6) and (7) associated with its conditions (8) are solved numerically. In this section, the Prandtl number is fixed to 6.2 which denotes water [43], and the nanoparticle volume fraction $\left({\phi }_1,{\phi }_2\right)$ is varied from 0 to 0.2. Further, we take $\beta =-0.2,-0.4,-0.6$ (for a heat sink), $\beta =0$ (without heat source/sink), $\beta =0.2,0.4,0.6$ (for the heat source) and magnetic parameter $M=0.1,0.2,0.3$.

4.1. Validation of Results

To validate the present model, we computed the outcomes as in

Table 3. Comparison values of $C_f{\mathrm{Re}}_x^{1/2}$ for some values of $\lambda$ when ${\phi }_1=0.1, {\phi }_2=0$ and $M=0$.

$\mathit{\lambda }$	Cu-Water		Al2O3-Water		TiO2-Water
	Bachok et al. [31]	Present	Bachok et al. [31]	Present	Bachok et al. [31]	Present
−0.5	3.2381	3.238160	2.7531	2.753091	2.7827	2.782709
0	2.5794	2.579342	2.1929	2.192963	2.2166	2.216555
0.5	1.4682	1.468240	1.2483	1.248302	1.2618	1.261731

and

Table 4. Comparison values of $N{u}_x{\mathrm{Re}}_x^{-1/2}$ for some values of $\lambda$ when ${\phi }_1=0.1, {\phi }_2=0$ and $\beta =0$.

$\mathit{\lambda }$	Cu-Water		Al2O3-Water		TiO2-Water
	Bachok et al. [31]	Present	Bachok et al. [31]	Present	Bachok et al. [31]	Present
−0.5	3.2381	3.238160	2.7531	2.753091	2.7827	2.782709
0	2.5794	2.579342	2.1929	2.192963	2.2166	2.216555
0.5	1.4682	1.468240	1.2483	1.248302	1.2618	1.261731

for the skin friction coefficient $C_f{\mathrm{Re}}_x^{1/2}$ and local Nusselt number $N{u}_x{\mathrm{Re}}_x^{-1/2}$ when $\lambda =-0.5,0,0.5$. The results of our numerical calculation are in a good harmony with the results obtained from the work of Bachok et al. [31] when $M$ and $\beta$ are set to zero. Therefore, we are assured that the present code is true and this problem can be solved using the bvp4c solver.

4.2. Interpretation of Results

In Figure 2 and Figure 3, numerical results for various nanoparticle volume fraction ${\phi }_1$ and ${\phi }_2$ for shrinking sheet $\left(\lambda =-1.2\right)$ are plotted for velocity $f^{\prime }\left(\eta \right)$ and temperature $\theta \left(\eta \right)$ profiles. Both figures are exemplified for 3 sets of nanoparticle volume fraction, i.e., ${\phi }_1={\phi }_2=0$ (Set 1), ${\phi }_1=0.01,{\phi }_2=0$ (Set 2) and ${\phi }_1={\phi }_2=0.01$ (Set 3). Here, set 1 indicates the regular fluid, while sets 2 and 3 refer to ferrofluid (Fe₃O₄/water) and hybrid ferrofluid (CoFe₂O₄–Fe₃O₄/water), respectively. From these graphical results, the second and first solutions are displayed through the dashed line and solid line, respectively. From the figures, we observed that set 3 shows a thinner boundary layer thickness (momentum and thermal) for the first and second solutions than sets 1 and 2. The disparities of skin friction coefficient $C_f{\mathrm{Re}}_x^{1/2}$ and local Nusselt number $N{u}_x{\mathrm{Re}}_x^{-1/2}$ against stretching/shrinking parameter $\lambda$ for some values of CoFe₂O₄ nanoparticle volume fraction ${\phi }_2$ are portrayed in Figure 4 and Figure 5. It is observed from Equation (10) that $C_f{\mathrm{Re}}_x^{1/2}$ and $N{u}_x{\mathrm{Re}}_x^{-1/2}$ are directly associated with the dimensionless velocity gradient $f^{″}\left(0\right)$ and temperature gradient $-{\theta }^{\prime }\left(0\right)$ at the wall, respectively. It is seen that these physical quantities of interest ($C_f{\mathrm{Re}}_x^{1/2}$ and $N{u}_x{\mathrm{Re}}_x^{-1/2}$) enhance with an upsurge in the volume fraction of CoFe₂O₄ nanoparticle ${\phi }_2$ for the first solution. However, we observed that the values of $C_f{\mathrm{Re}}_x^{1/2}$ and $N{u}_x{\mathrm{Re}}_x^{-1/2}$ decrease when stretching/shrinking parameter $\lambda$ near its critical value ${\lambda }_c$. The rise in the $C_f{\mathrm{Re}}_x^{1/2}$ is due to an increment in the nanoparticles colloidal suspension that enhanced the collision of nanoparticle dispersion of ferrofluid. An increase in the nanoparticles volume fraction may physically increase its synergistic effect which, consequently, improves the heat transfer rate. This demonstrates that cooling in hybrid ferrofluid is much faster, whereas cooling in ferrofluid flow may take longer. It can also be seen from Figure 4 and Figure 5 that a non-unique solution (dual solutions) happens to exist for shrinking sheet $\left(\lambda <-1\right)$, unique (one) solution is observed when $-1\le \lambda \le 1$ and no solution when $\lambda <{\lambda }_c$, i.e., boundary layer separation is bound to take place. It should be noted that ${\lambda }_c=-1.53463,-1.53634$ and $-1.53818$ are the respective critical values of $\phi =0,0.01$ and $0.02$. Accordingly, we can deduce that nanoparticle volume fraction acts in postponing the boundary later separation.

Figure 6 and Figure 7 depict the graphical representation of the temperature profile $\theta \left(\eta \right)$ for selected values of heat source/sink parameter $\beta$. The influence of rising values of heat source $\left(\beta >0\right)$ is to increase the boundary layer thickness (thermal) for both solutions. As the heat source is increased, the temperature rises, thereby the sheet’s temperature also increases. On the contrary, heat sink $\left(\beta <0\right)$ leads to decrement of the boundary layer (thermal) in first and second solutions. More heat is removed from the sheet as the heat sink increases, lowering the sheet’s temperature. Furthermore, the temperature overshoot is observed for the second solution. This is in line with the fact that the dashed line which indicates the second solution always has a thicker boundary layer than the solid line, i.e., the first solution. The effect of heat source/sink $\left(\beta =-0.2,0,0.2\right)$ on the local Nusselt number $N{u}_x{\mathrm{Re}}_x^{-1/2}$ versus stretching/shrinking sheet $\lambda$ for hybrid ferrofluid is portrayed in Figure 8. One can see that as $\beta$ is increased, the temperature rises, which consequently lowers $N{u}_x{\mathrm{Re}}_x^{-1/2}$. Again, the appearance of the non-unique solution is discovered for the shrinking sheet $\left(\lambda <-1\right)$ only. In addition, for all heat source/sink parameter values $\beta$, the critical value ${\lambda }_c$ is the same, i.e., ${\lambda }_c=-1.53634$.

The influence of magnetic parameter $M$ in the existence of heat source $\left(\beta =0.2\right)$ on the velocity $f^{\prime }\left(\eta \right)$ profile and temperature $\theta \left(\eta \right)$ profile are depicted in Figure 9 and Figure 10, while skin friction coefficient $C_f{\mathrm{Re}}_x^{1/2}$ and local Nusselt number $N{u}_x{\mathrm{Re}}_x^{-1/2}$ are plotted in Figure 11 and Figure 12, respectively. For accumulating amounts of magnetic parameter $M,$ these profiles ($f^{\prime }\left(\eta \right)$ and $\theta \left(\eta \right)$) significantly decrease and also cause the boundary layer thickness to reduce in the first solution. Nevertheless, an opposite observation is made for the other solution. The upsurge value of $M$ in the flow causes an increase in the Lorentz force or also known as resistive type force and consequently generates much more resistance to the flow and increases the temperature. Figure 11 and Figure 12 for the skin friction coefficient $C_f{\mathrm{Re}}_x^{1/2}$ and local Nusselt number $N{u}_x{\mathrm{Re}}_x^{-1/2}$ demonstrate an increasing behavior for hybrid ferrofluid with an increasing magnetic parameter $M$. The influence of magnetic parameter $M$ on $N{u}_x{\mathrm{Re}}_x^{-1/2}$ is minimal as $M$ is not explicitly occurred in Equation (7). Again, the same observation is observed for the presence of dual solutions (see Figure 4, Figure 5 and Figure 8). It is also clear from these graphs that as the magnetic parameter $M$ intensifies, the domain of the occurrence of dual solutions expands. For instance, the critical values of stretching/shrinking parameter for $M=0.1,0.2$ and $0.3$ are ${\lambda }_c=-1.53634,$ $-1.58568$ and $-1.63506$. This implies that the presence of magnetic parameters can slow down the boundary layer separation to occur.

The linearized Equations (19)–(21) are numerically solved using the same numerical approach as before in order to execute the stability of the solutions. To verify the stability of the solutions, a sign of the smallest eigenvalues $\gamma$ is essential. Hence, Figure 13 is plotted to demonstrate the behavior of the smallest eigenvalues $\gamma$ when $\beta =0.2$ and $M=0.1$ for hybrid ferrofluid $\left({\phi }_1={\phi }_2=0.01\right)$ concerning $\lambda$. Here, the positive eigenvalues indicate the stable solution (i.e., there is only a small disturbance that does not interrupt the flow) while negative eigenvalues convey the unstable solution (which explains the growth of disturbance). Therefore, it can be concluded from Figure 13 that the first solution is a stable solution and the other solution is not. In addition, it can be clearly seen that as stretching/shrinking parameter $\lambda$ near its critical value ${\lambda }_c,$ the value of $\gamma$ also approximate to zero.

5. Concluding Remarks

The steady, stagnation point, MHD of hybrid ferrofluid flow caused by an exponentially deformable surface with heat source/sink effect is studied. The similarity transformation is applied to generate self-similar equations, which are then numerically solved with Matlab’s built-in solver (bvp4c). The impact of governing parameters such as heat source/sink parameter, nanoparticle volume fraction, magnetic parameter and stretching/shrinking parameter are discussed in detail. We can therefore conclude that:

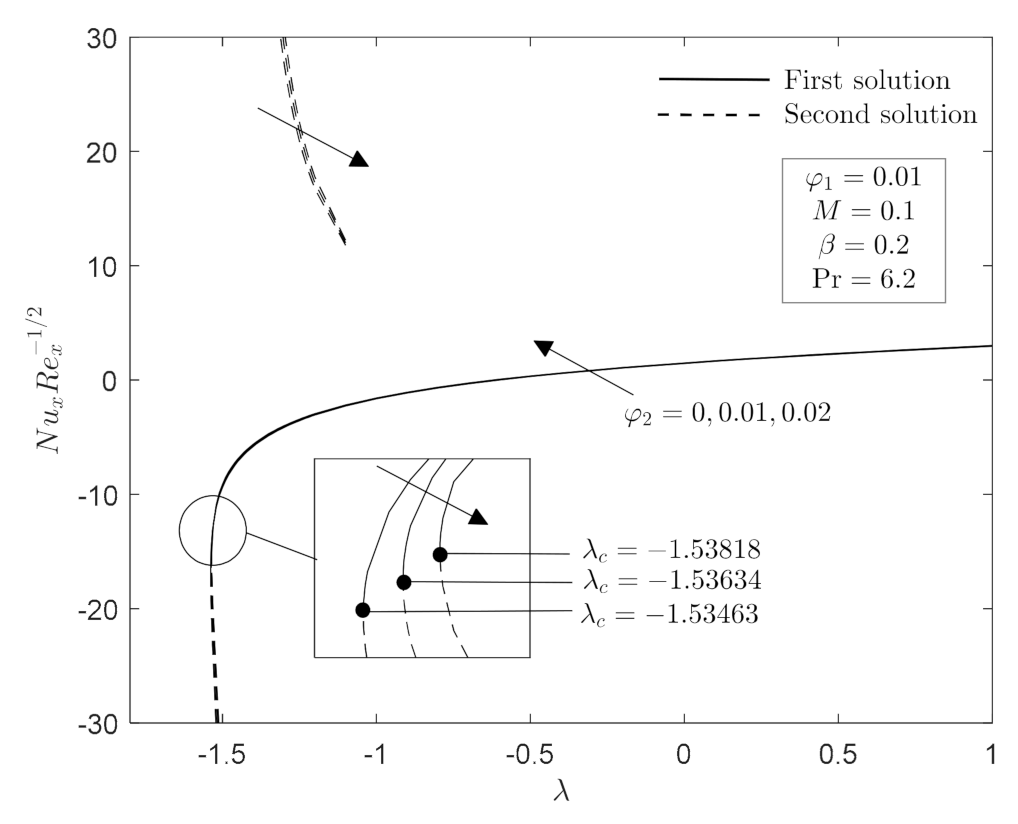
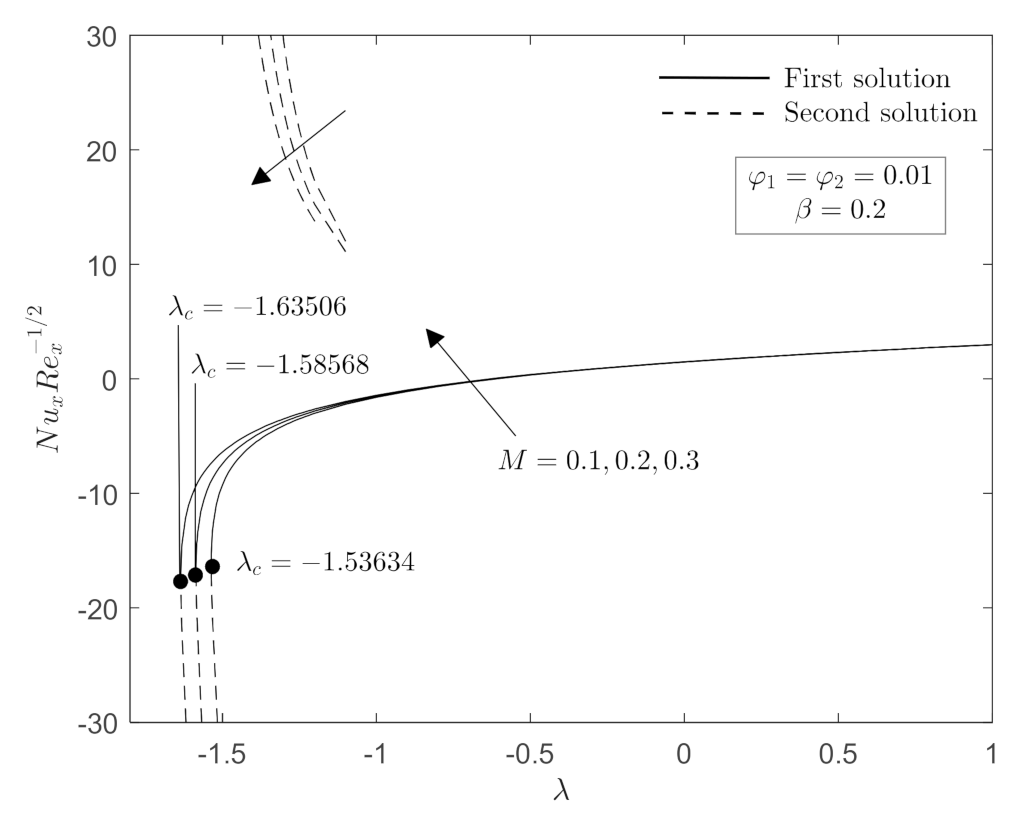
• Non-unique solution (two solutions) occurs for a specific range of shrinking parameter $\left({\lambda }_c<\lambda <-1\right)$, whereas one solution exists when $\lambda \ge -1$.
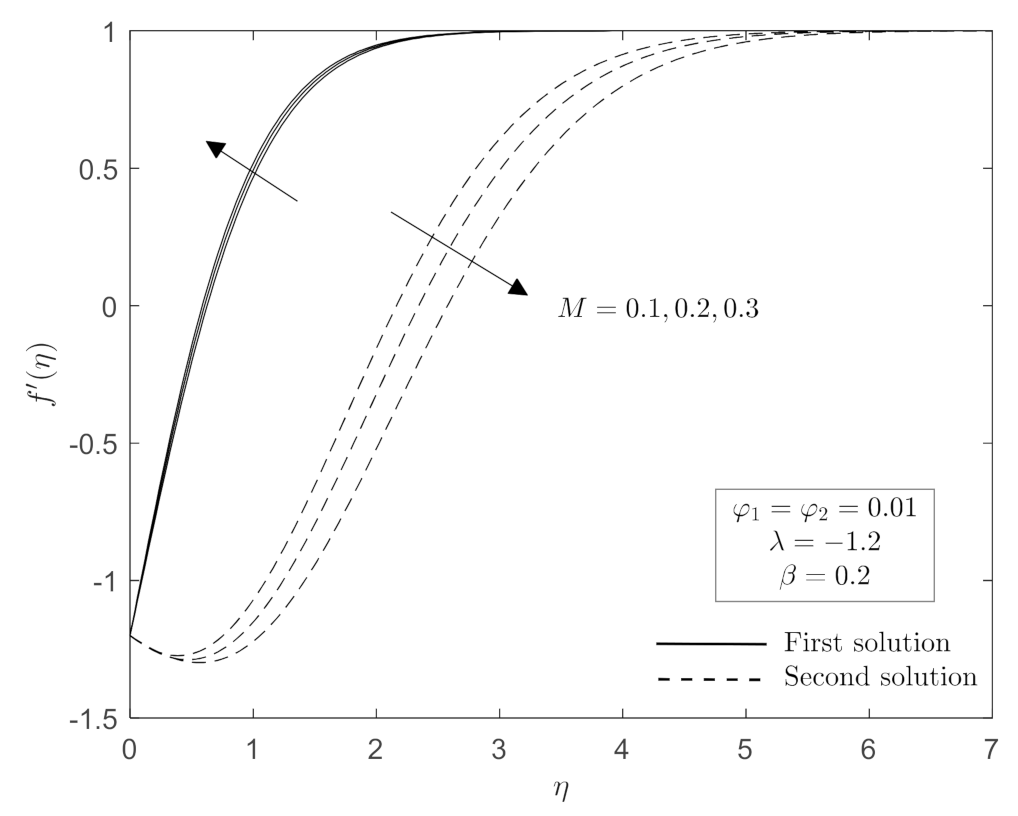
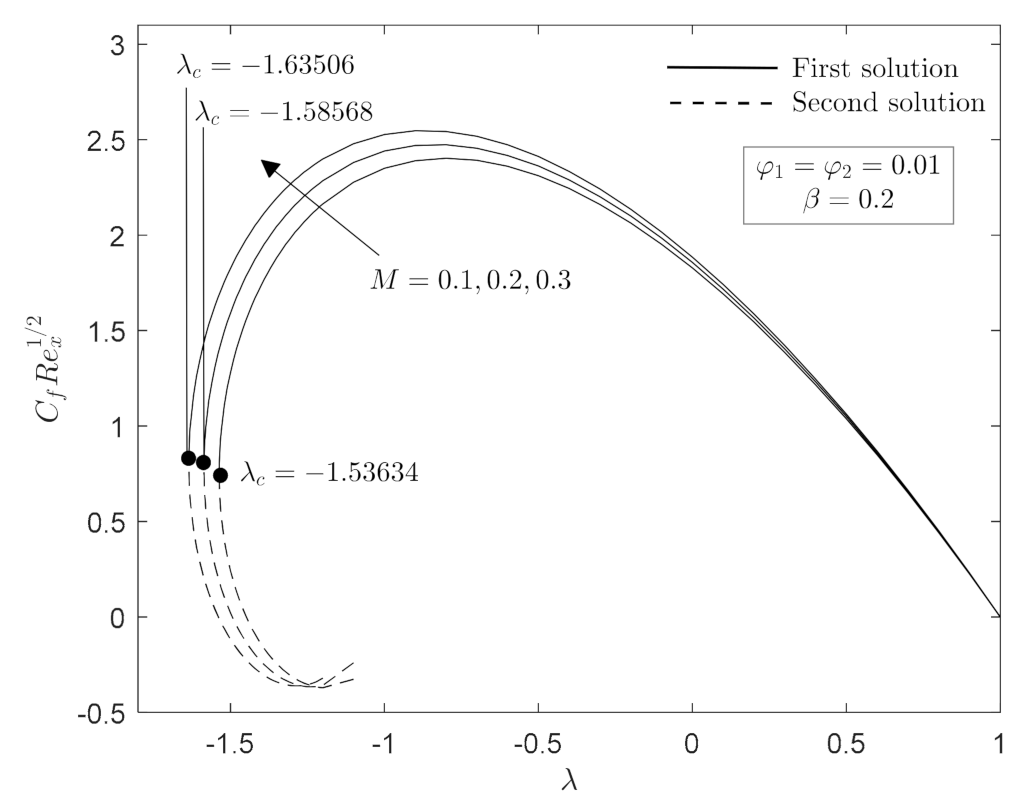
• The range of stretching/shrinking parameter $\lambda$ for which the non-unique solutions are in existence increased as magnetic parameter increase, while it decreased with an increase in CoFe₂O₄ nanoparticle volume fraction.
• The heat transfer and skin friction are escalated for increasing of CoFe₂O₄ nanoparticle volume fraction and magnetic parameter.
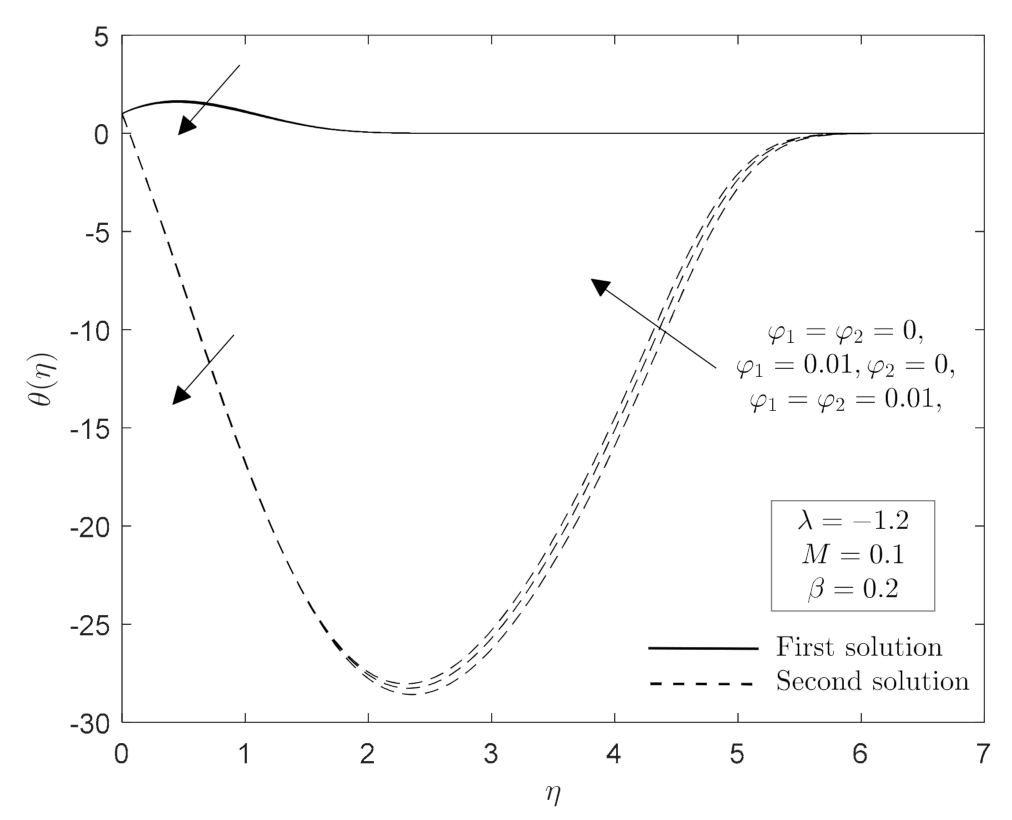
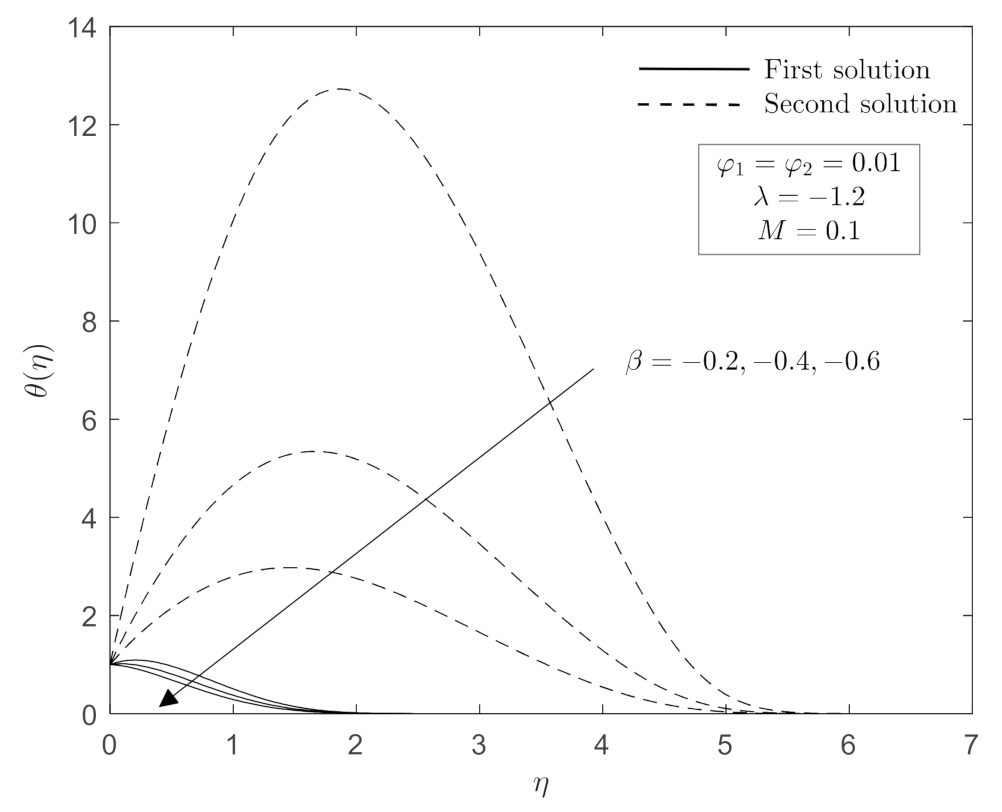
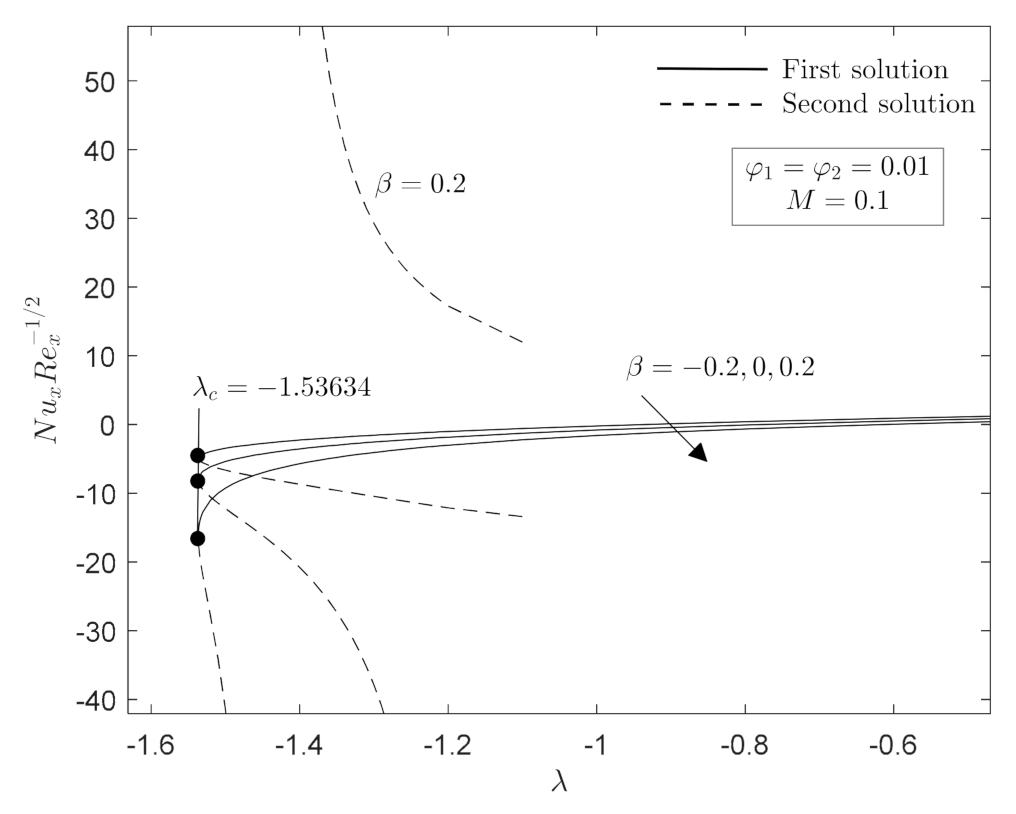
• When the heat source/sink parameter is increased, the surface temperature rises, and the local Nusselt number decreases.
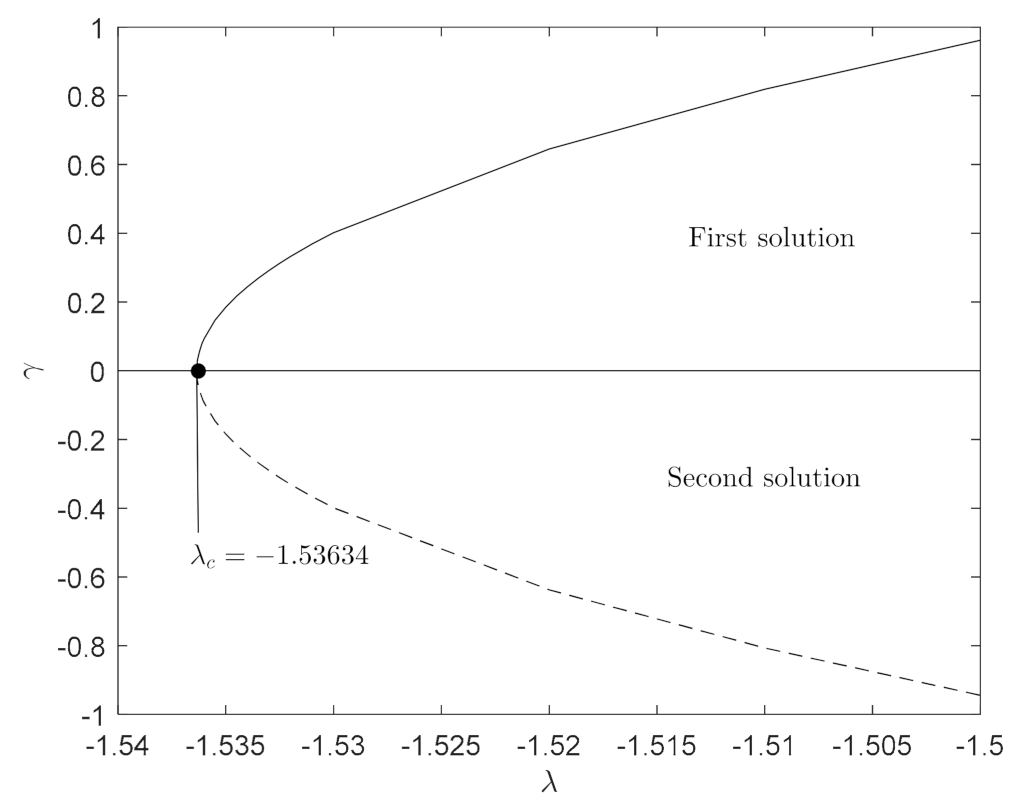
• The first solution is confirmed to be a stable solution from the stability analysis test.