Designing a Solar Photovoltaic System for Generating Renewable Energy of a Hospital: Performance Analysis and Adjustment Based on RSM and ANFIS Approaches
Abstract
:1. Introduction
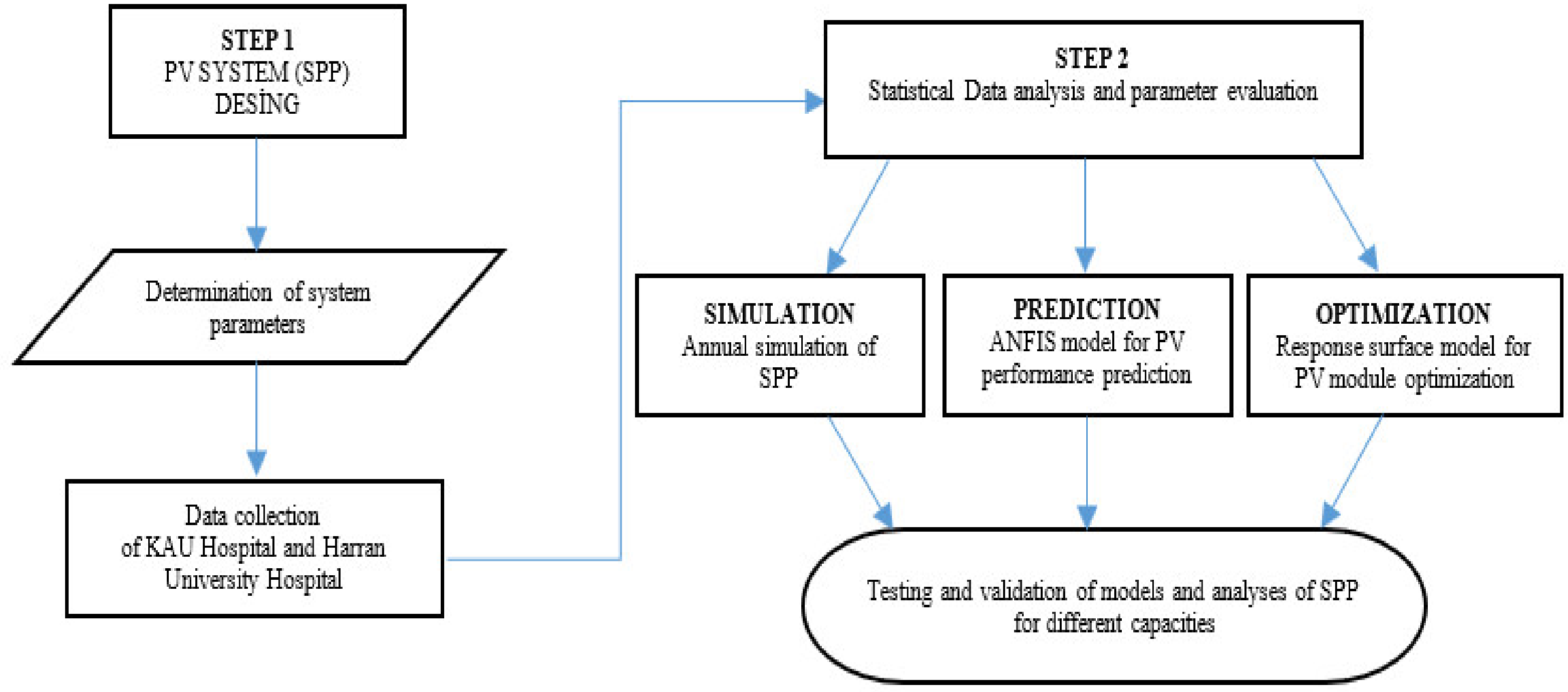
2. Materials and Methods
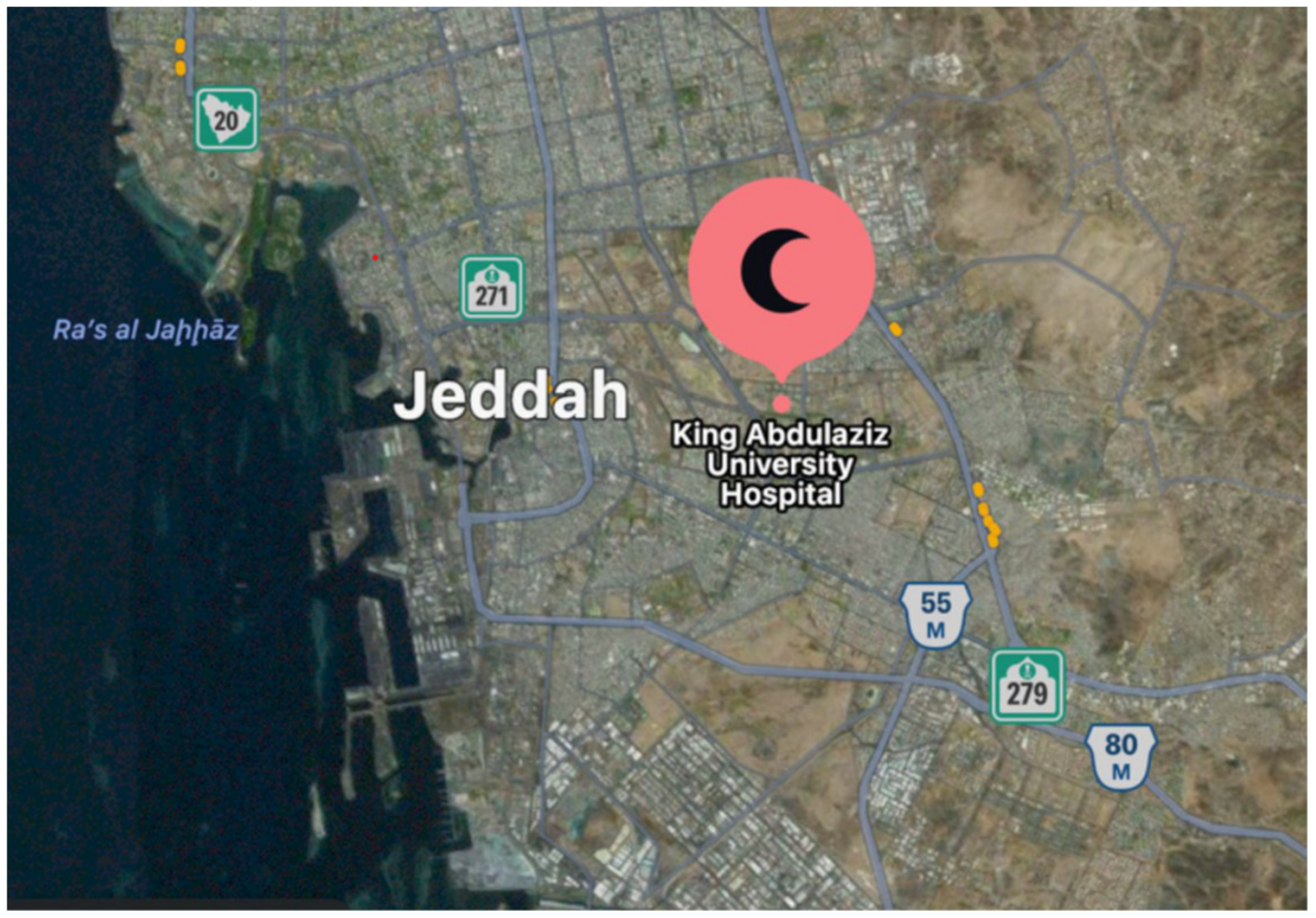
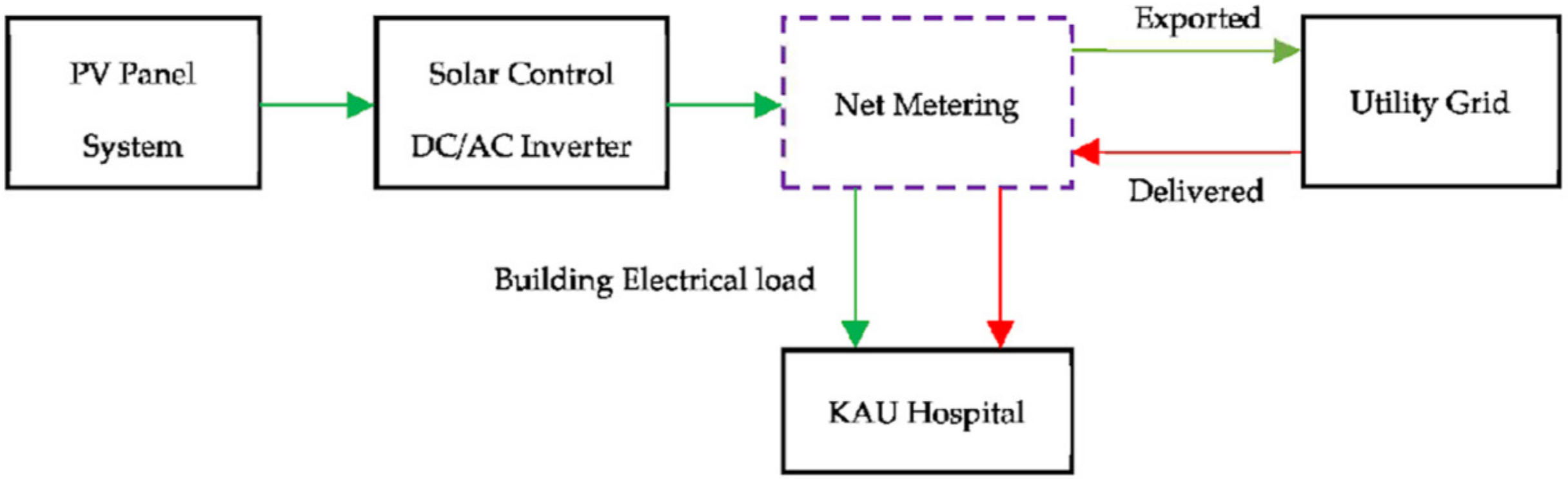
2.1. Solar Energy Generation Design for KAU Hospital
2.2. The Solar Power Plant Types
2.3. PV System Design
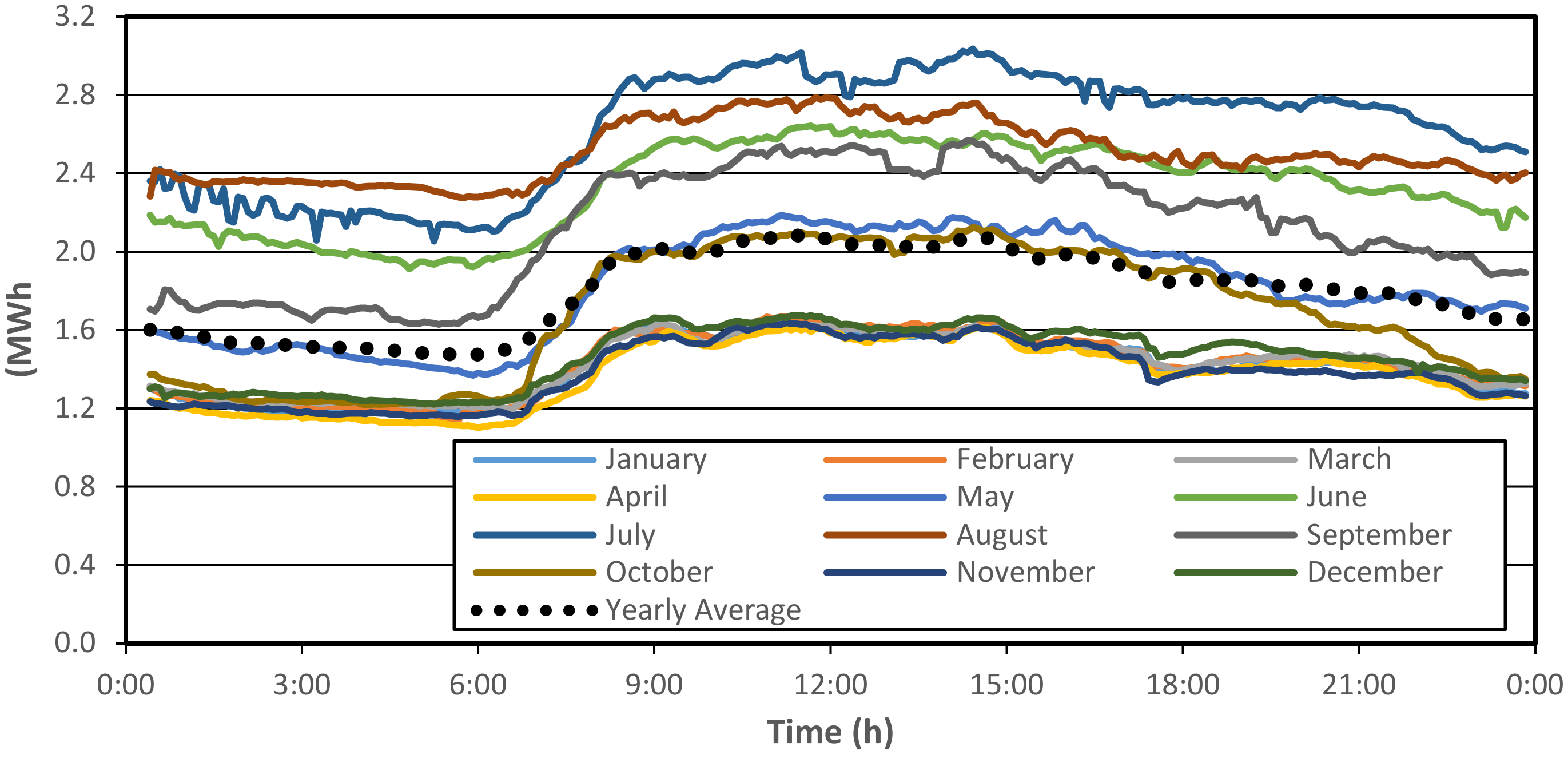
2.3.1. Determining the Hourly Distribution of the Energy Consumption of the Harran University Hospital
- The maximum energy consumption of HUH is in July.
- Electricity consumption is the highest in 4 months (summer period) from June to September,
- Electricity consumption is the lowest in the period of 6 months (winter period) from November to April,
- The electricity consumption profiles of an average day obtained for May and October are similar to the consumption profile obtained for an average day determined according to annual data.
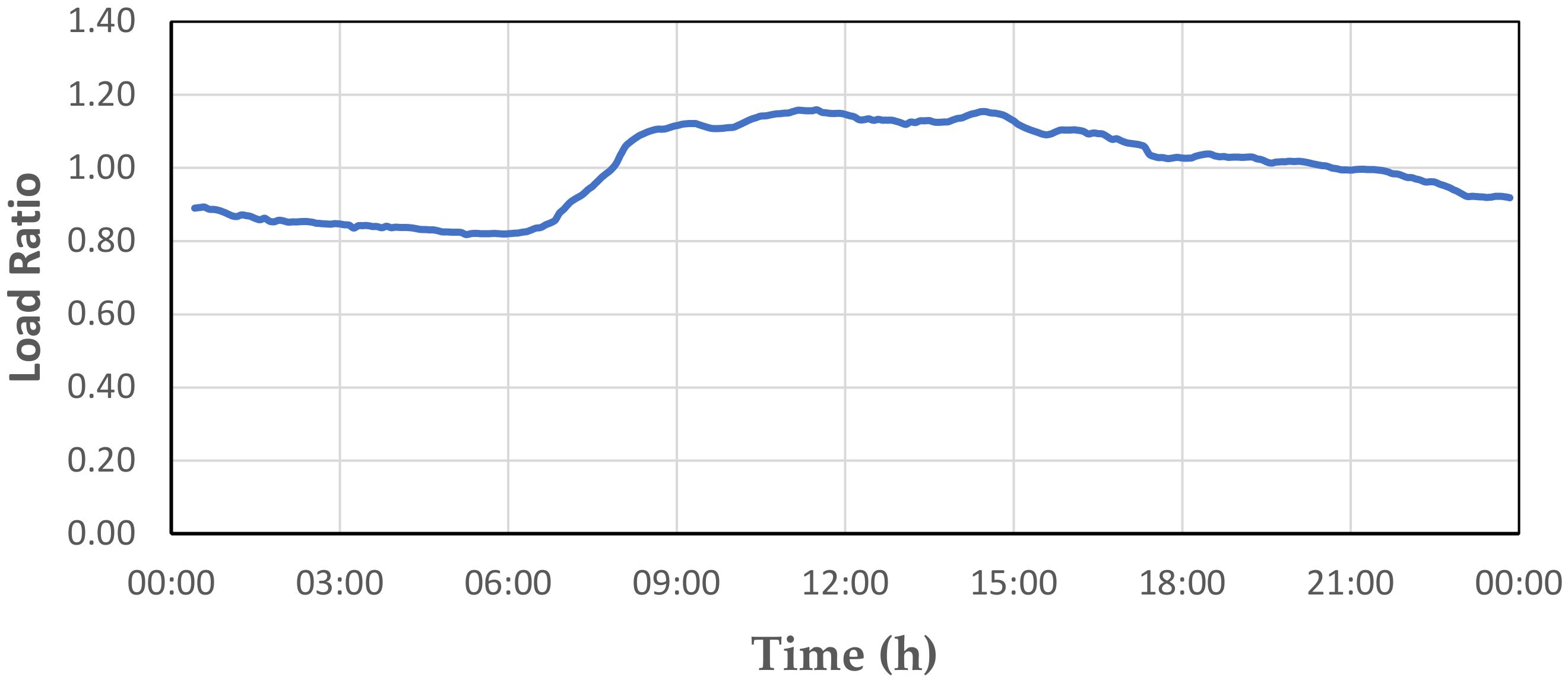
2.3.2. Determining the Load Profile of the Energy Consumption of the Harran University Hospital
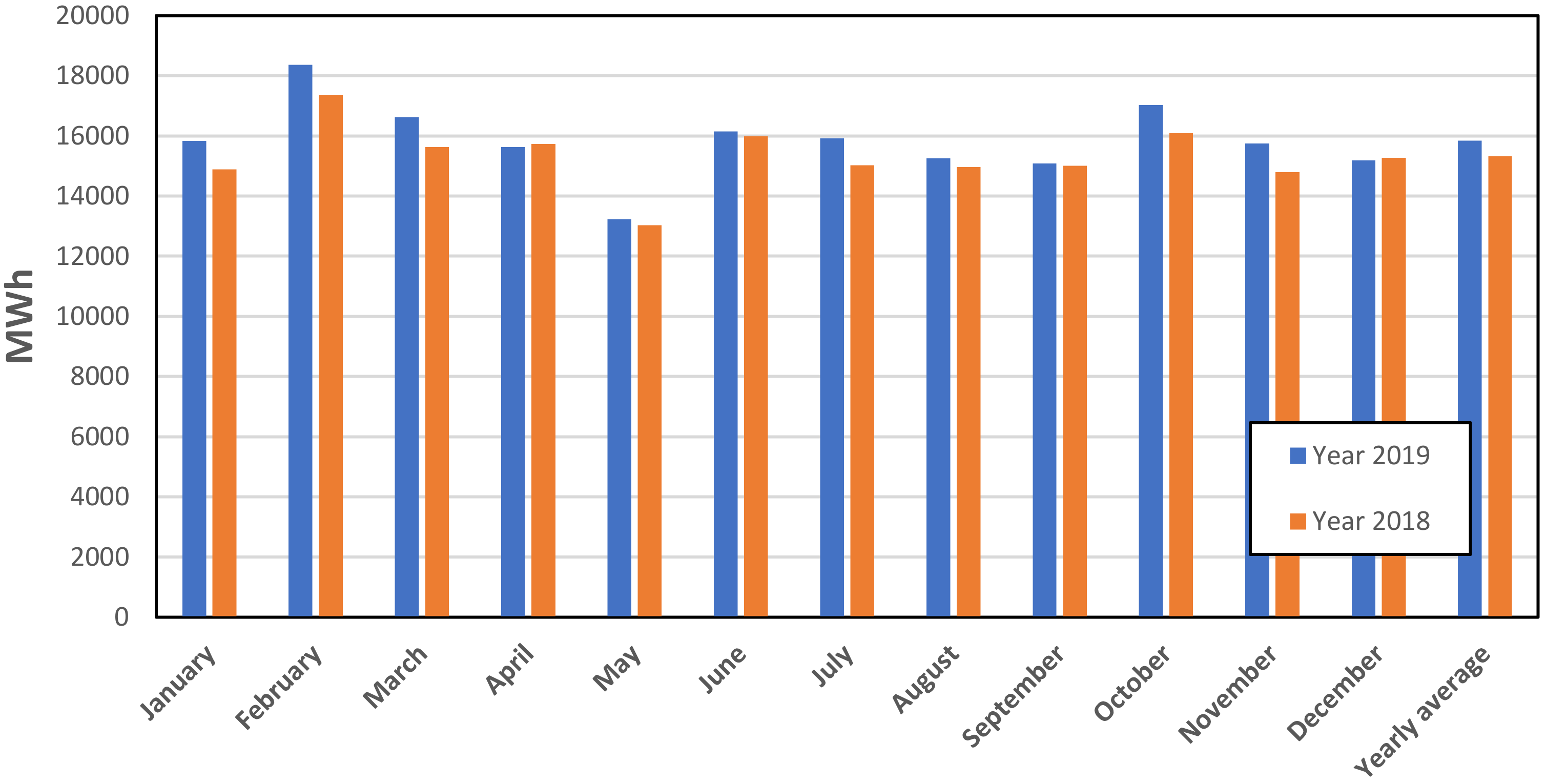
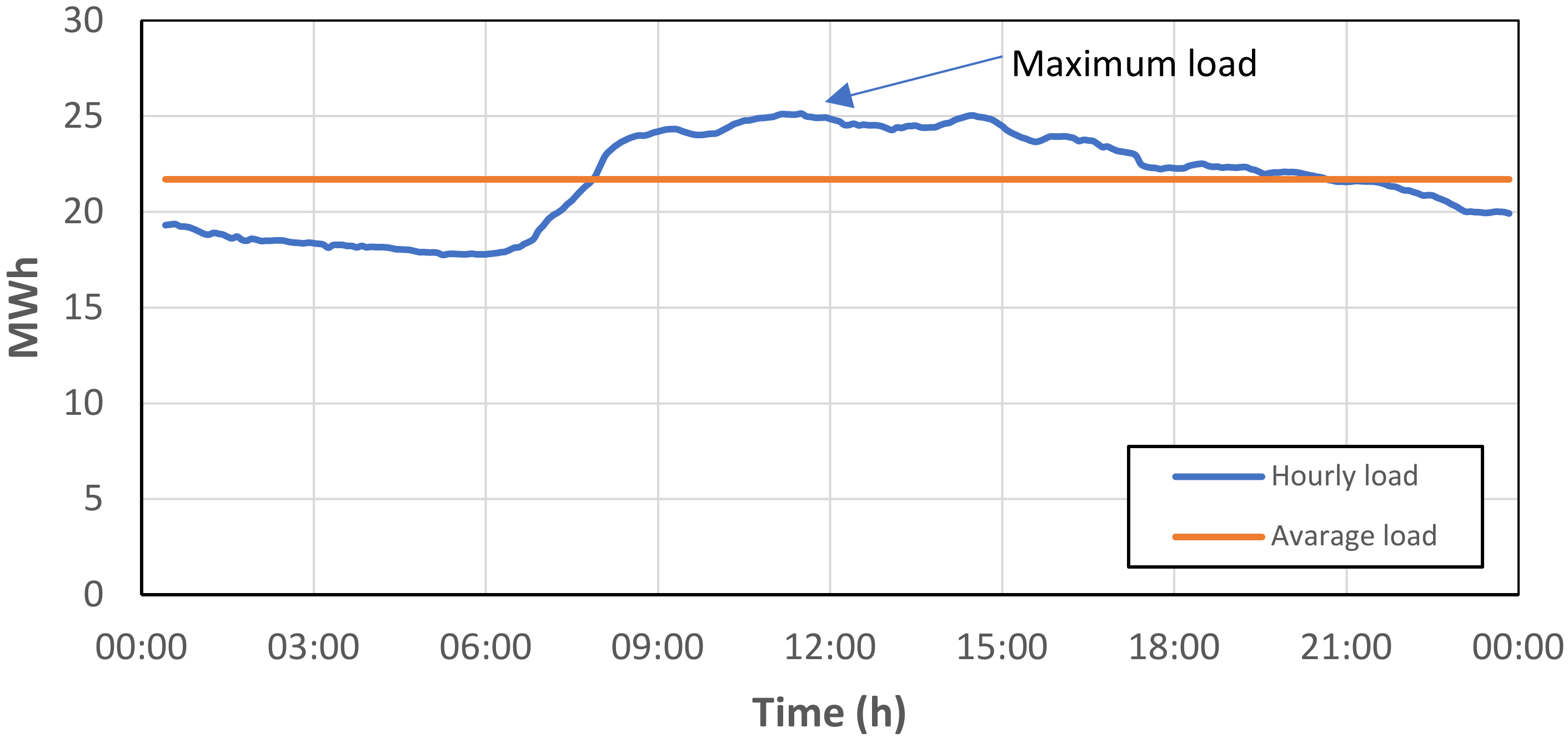
2.3.3. The Hourly Energy Consumption Distribution of the KAU Hospital
3. Solar PV System Analysis and Performance Prediction
3.1. Data Collection and Analysis
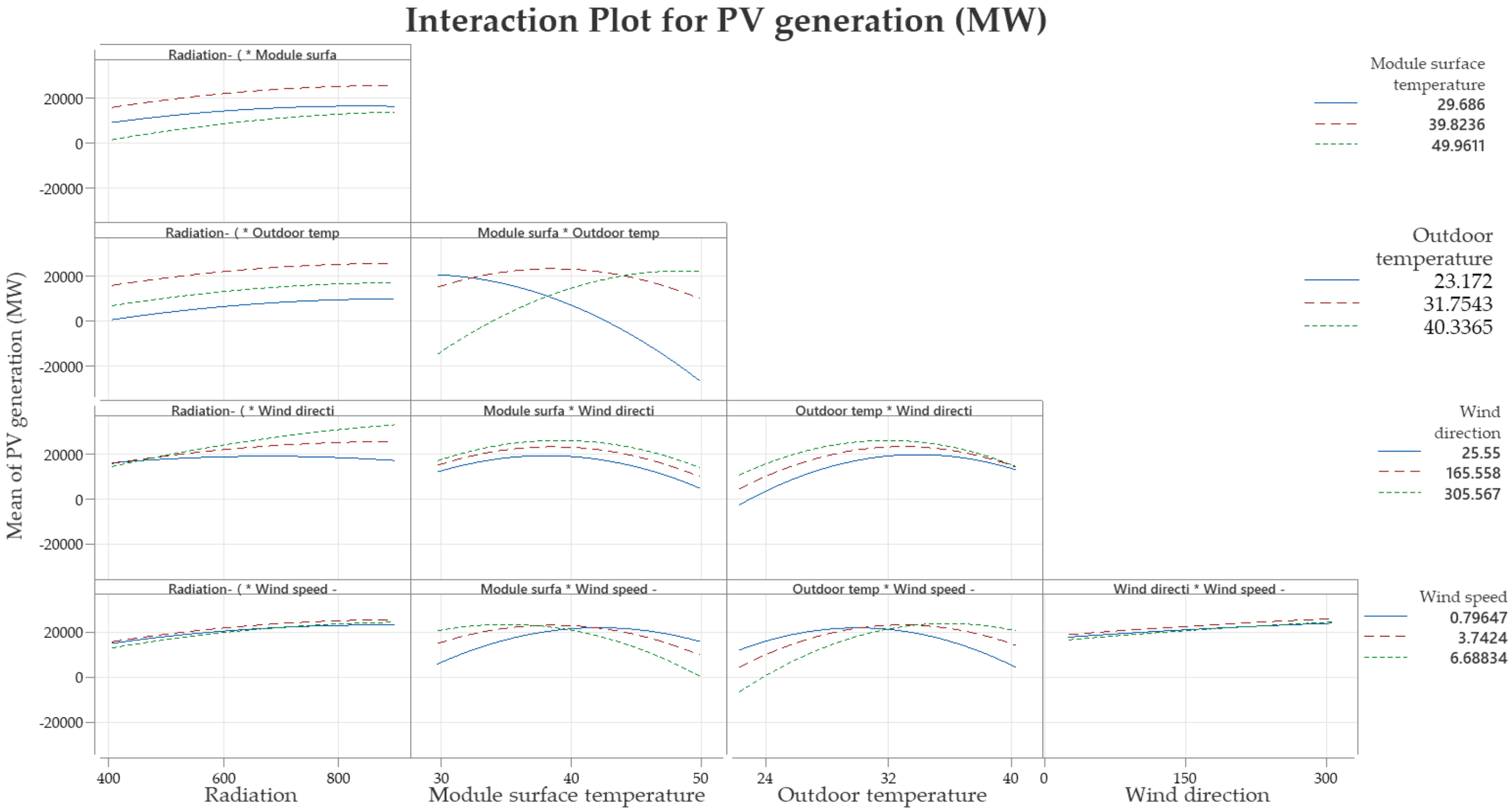
3.2. RSM for Optimization of Solar PV System
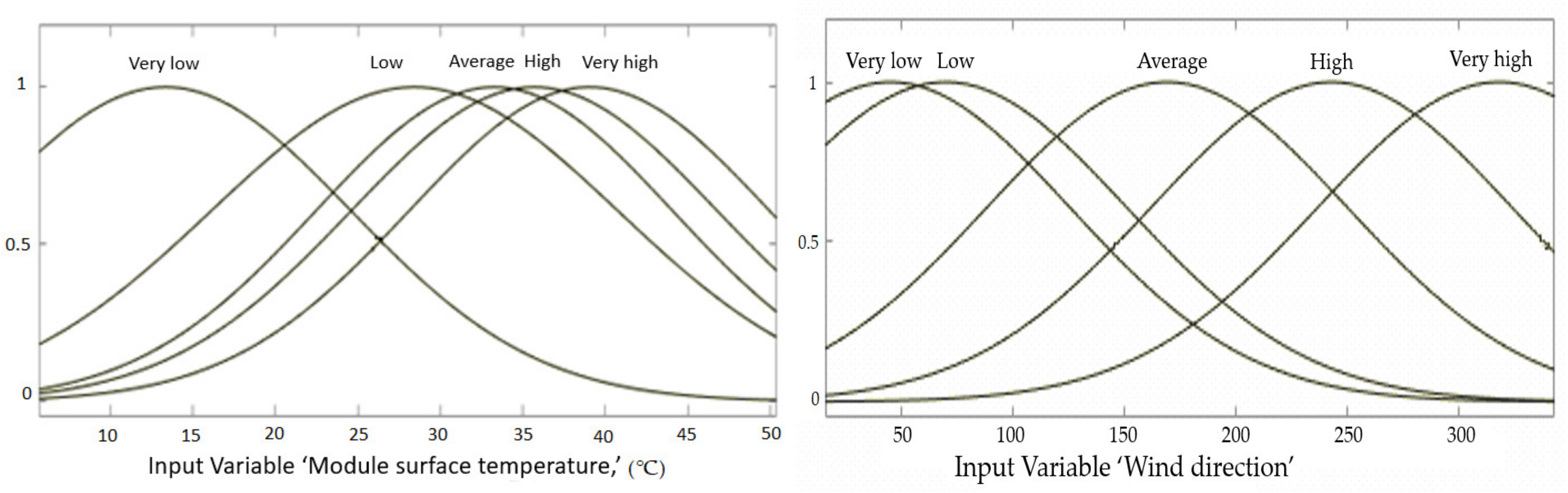
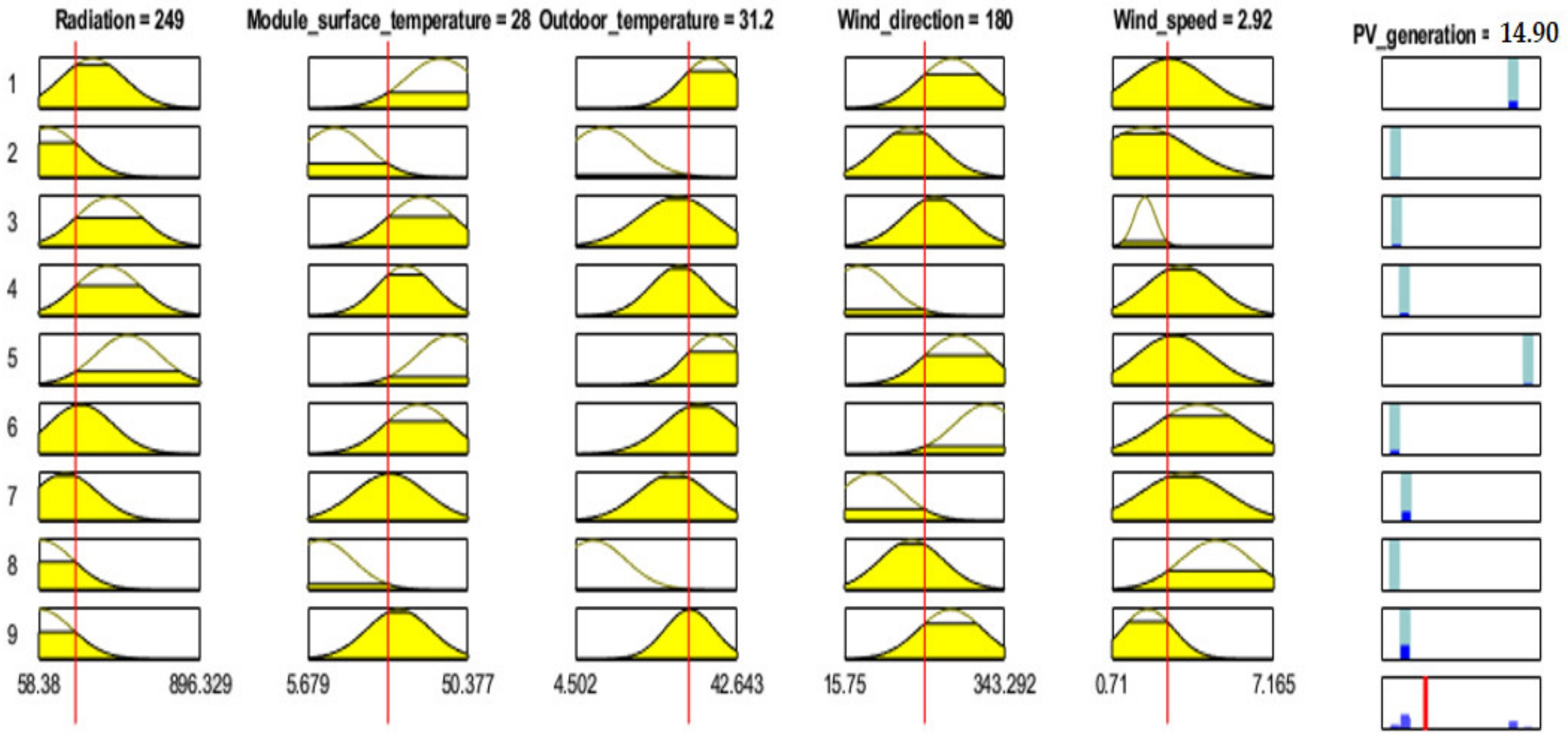
3.3. ANFIS Approach for PV Efficiency Estimation and Analysis
4. Results and Discussions for Solar PV System Findings
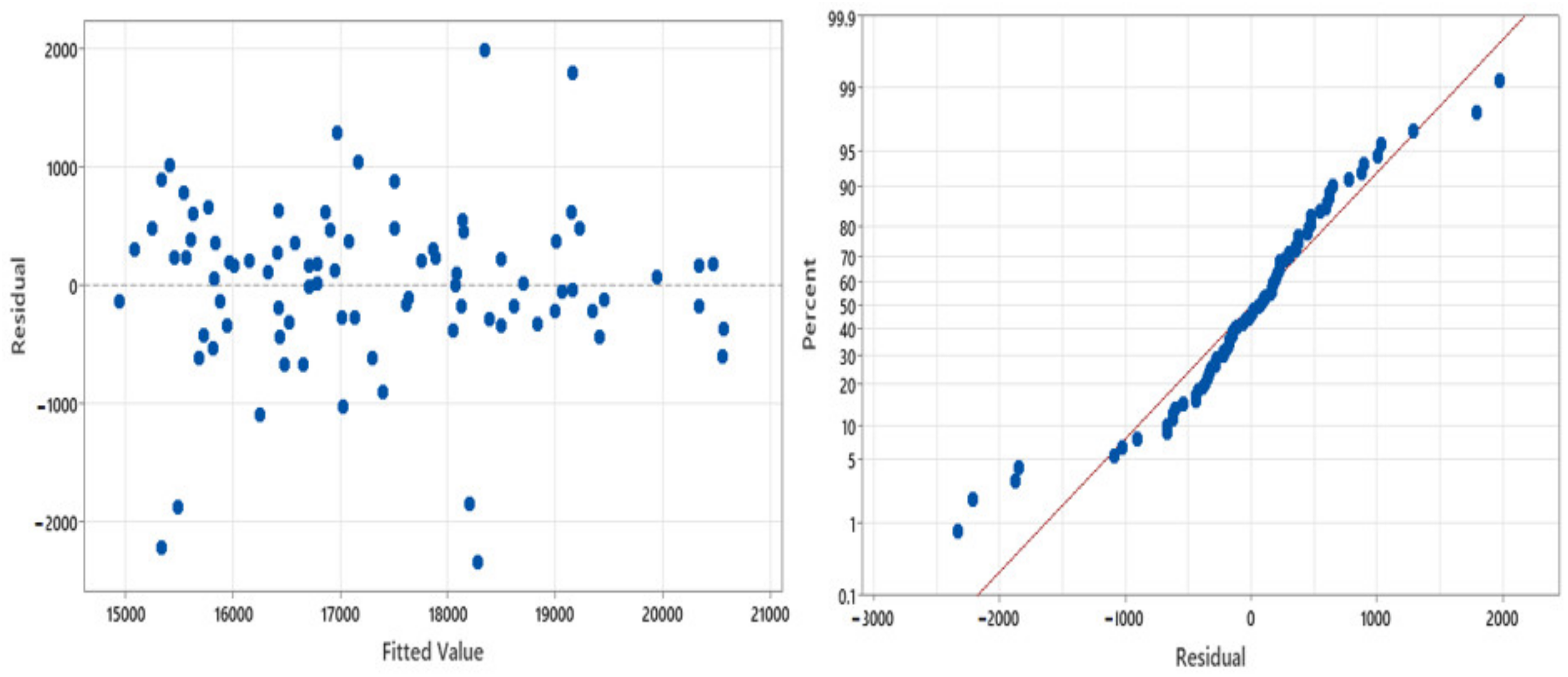
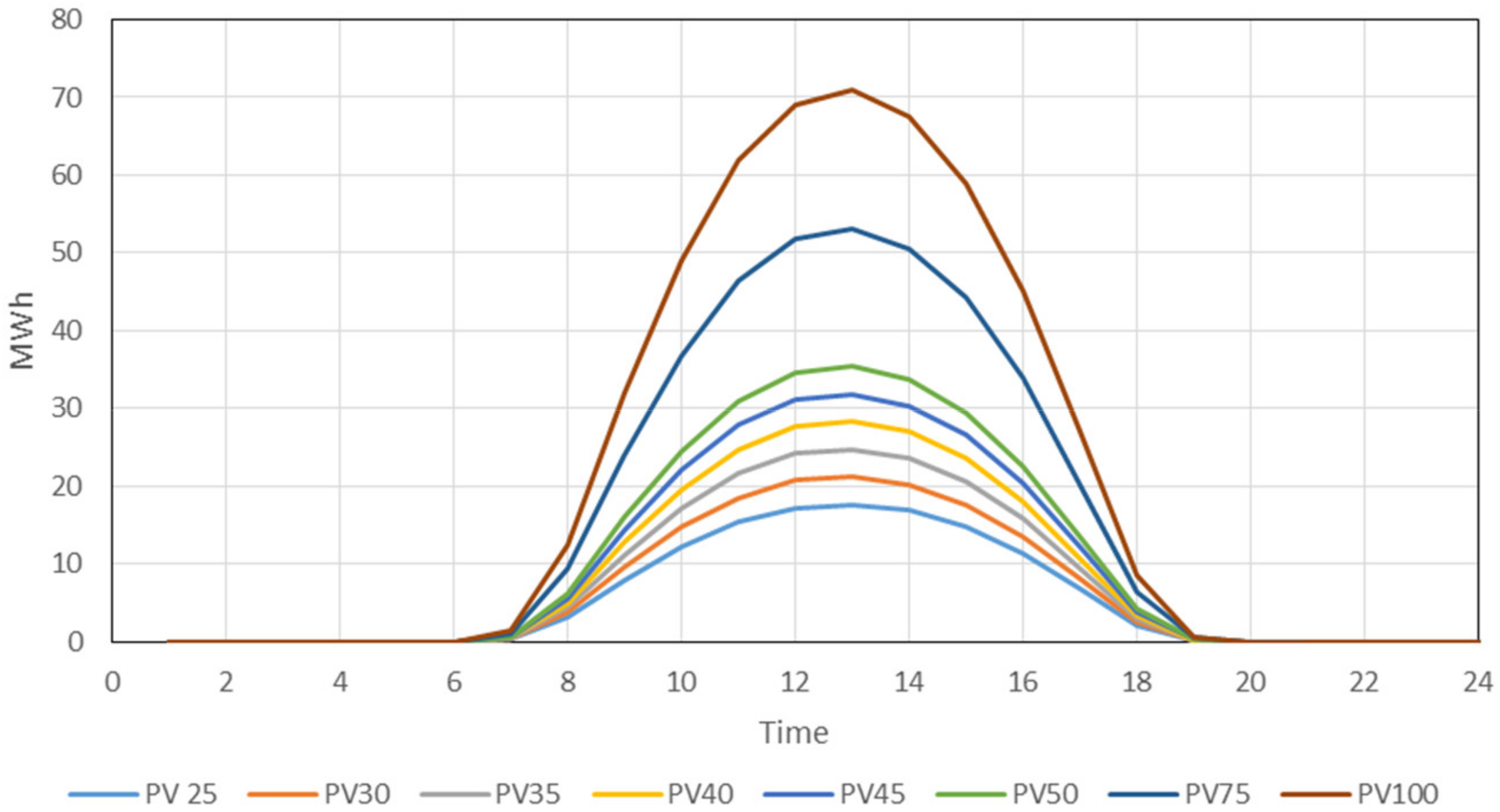
4.1. The Assessment of PV System Simulation
The Assessment of Solar PV Module Using RSM Approach
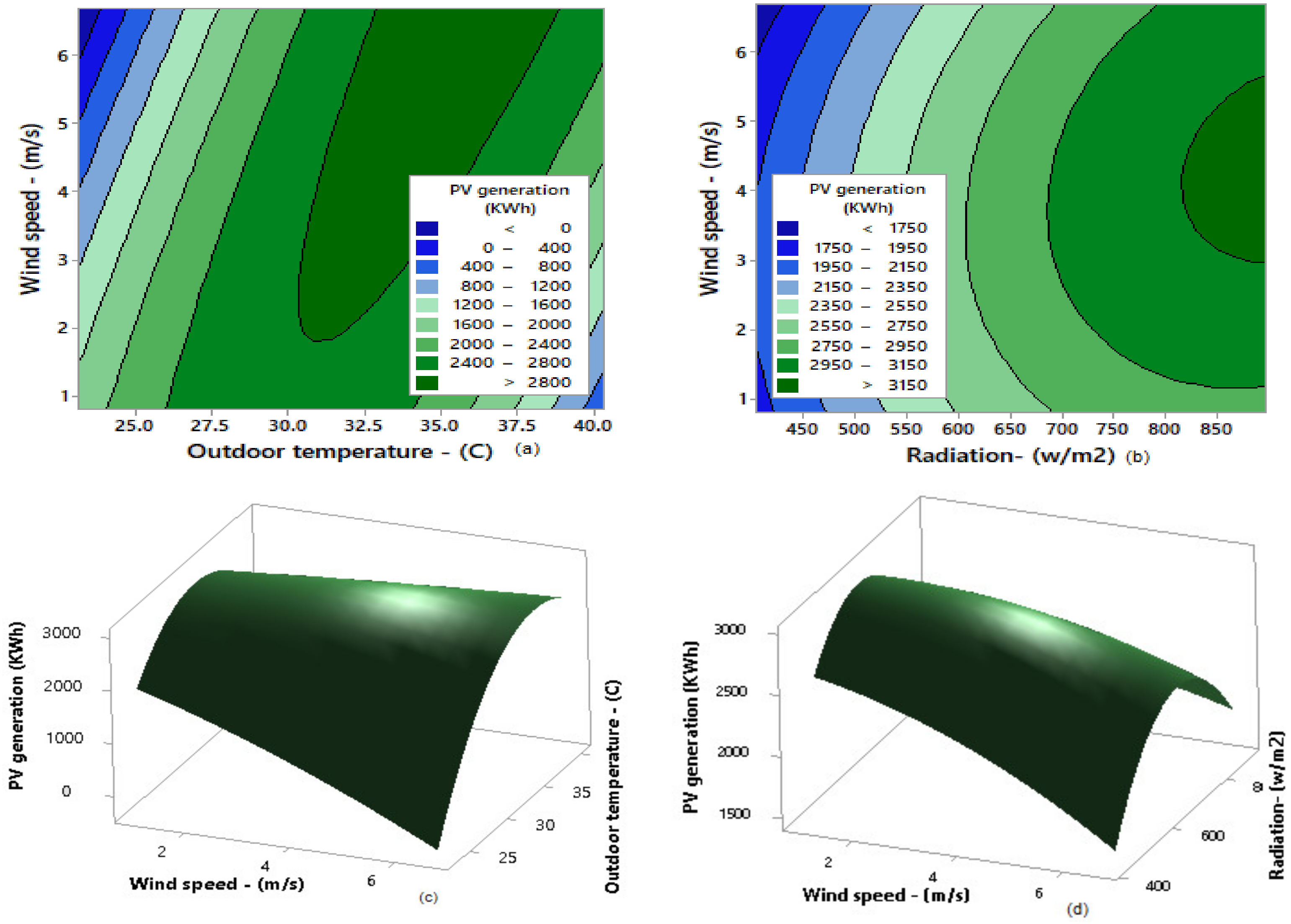
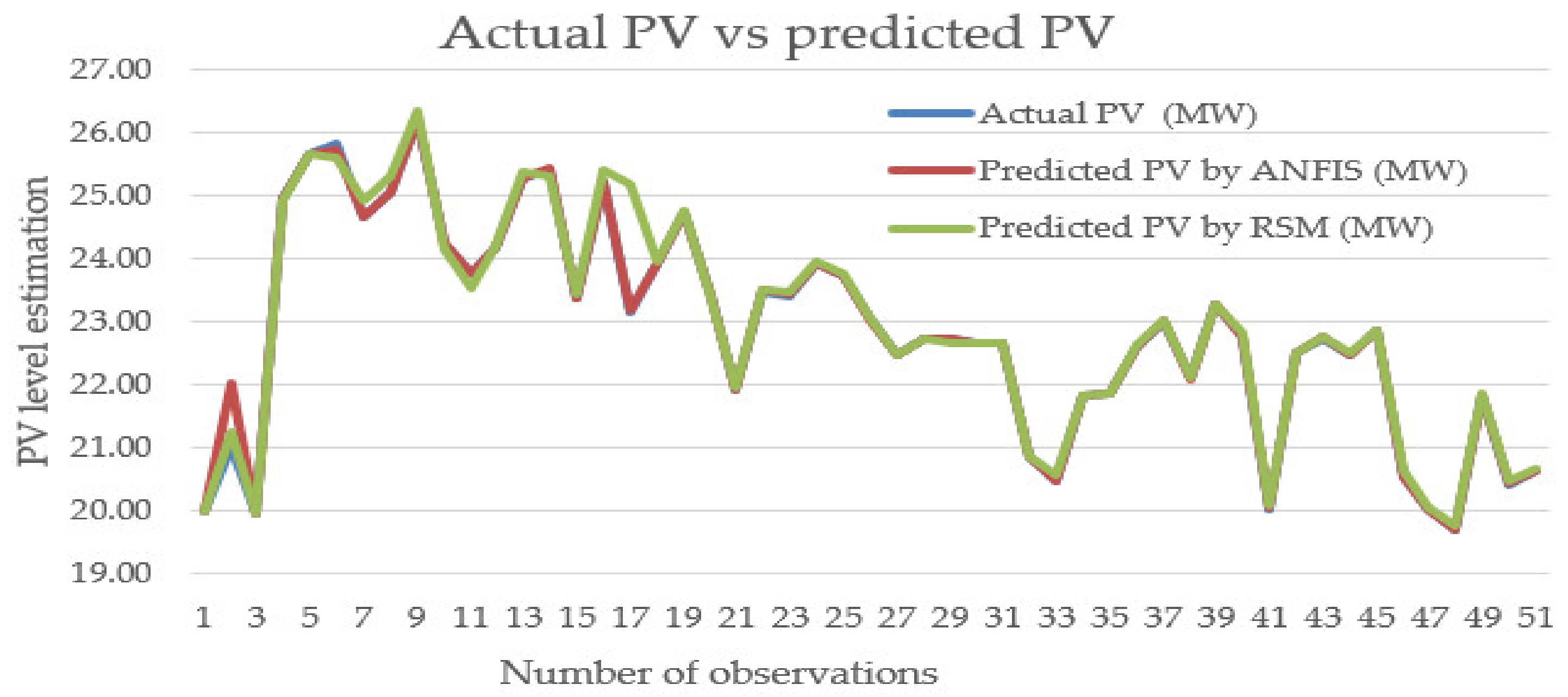
4.2. The Assessment of Performance of Developed Models Using ANFIS Approach
4.3. Comparison of the Results with the Cases Introduced by Other Works
5. Conclusions
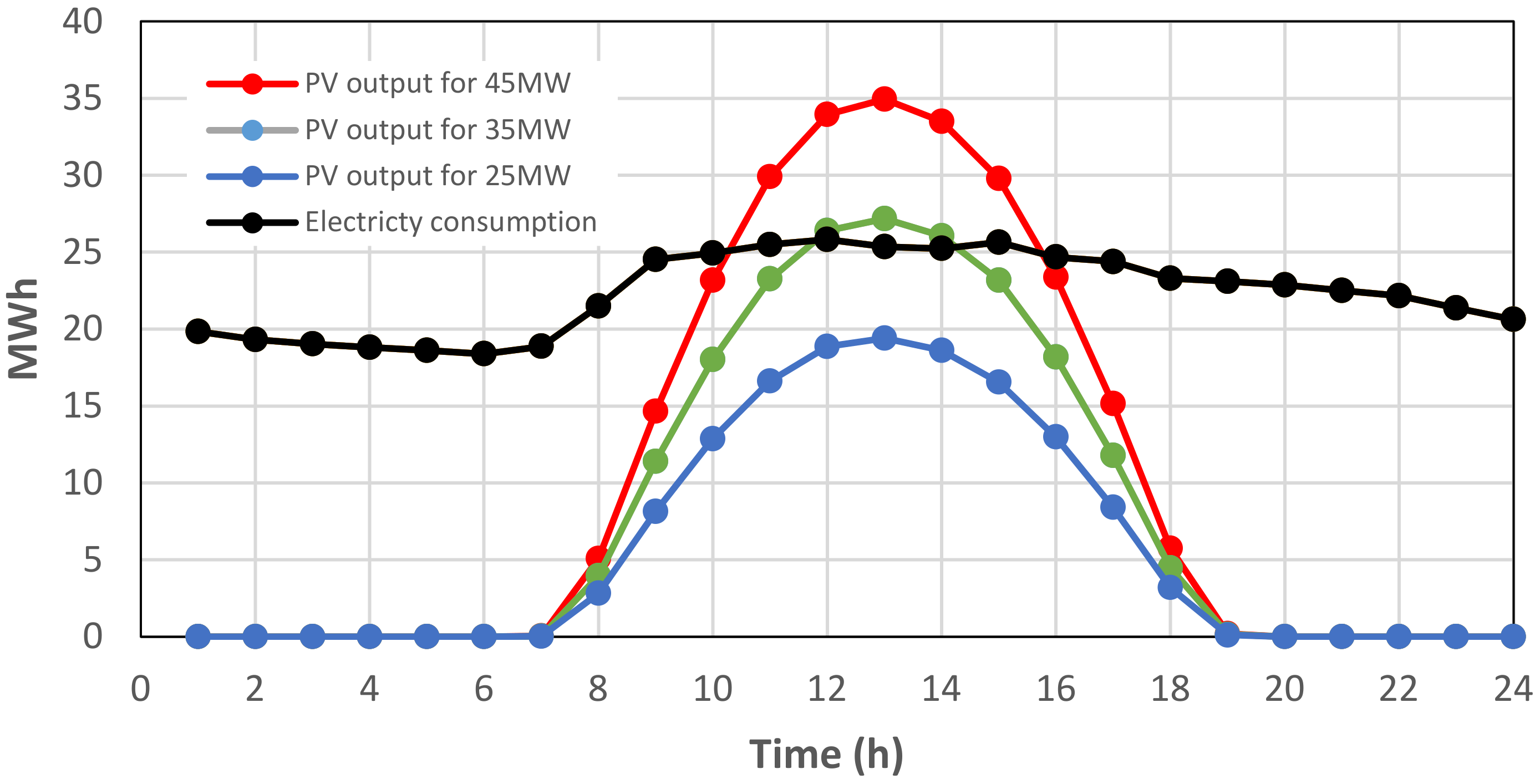
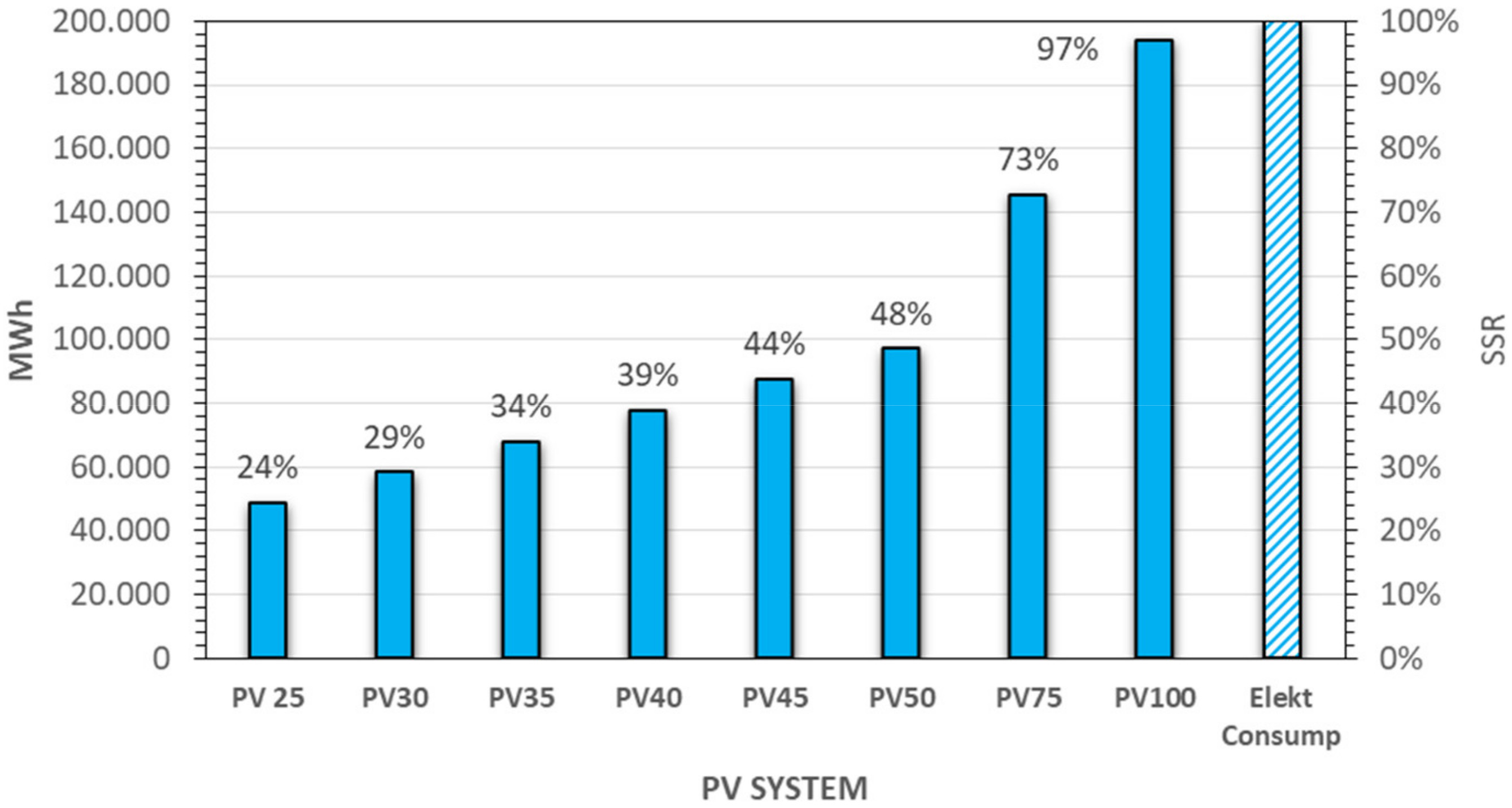
- A solar PV system with a capacity of 35 MW and/or more will be sufficient for the KAU hospital and meet the electrical energy demand of the hospital;
- For a PV system of 40 MW capacity, the maximum electricity generation is approximately between 26 and 31 MWh. Hence, the hourly maximum electrical energy requirement of the hospital between 11:00 and 15:00 h can be met by the PV system during all months;
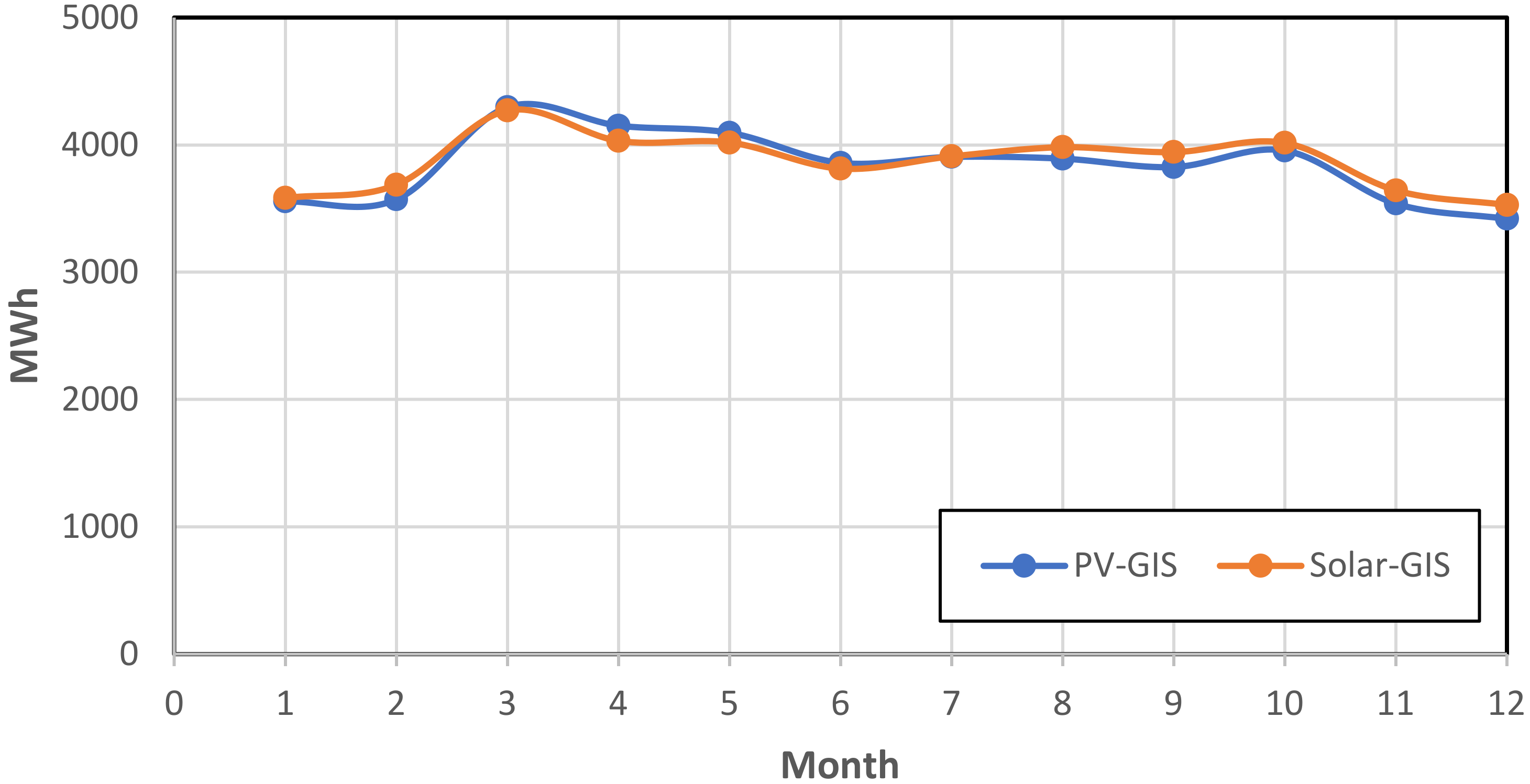
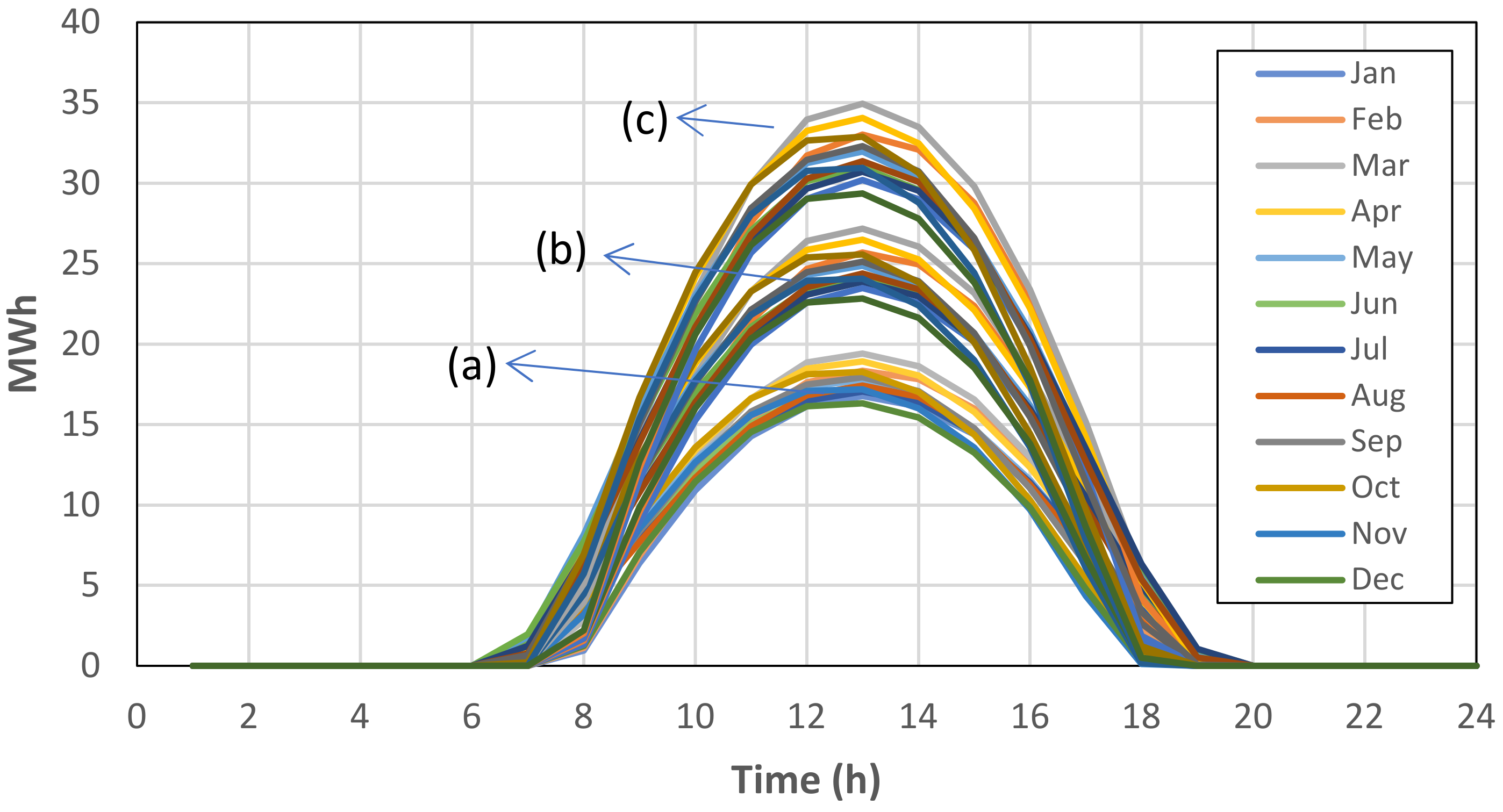
- In all PV designs and simulation tests, the highest electrical energy production during the year was observed in March;
- The self-sufficiency ratio for March was 31% for PV25, 37% for PV30, 43% for PV35, 50% for PV40, 56% for PV45, 62% for PV50, 93% for PV75 and 124% for PV100;
- The self-sufficiency ratio for the yearly period was found as 24% for PV25, 29% for PV30, 34% for PV35, 39% for PV40, 44% for PV45, 48% for PV50, 73% for PV75 and 97% for PV100.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Taylan, O.; Alamoudi, R.; Kabli, M.; AlJifri, A.; Ramzi, F.; Herrera-Viedma, E. Assessment of Energy Systems Using Extended Fuzzy AHP. Fuzzy VIKOR. and TOPSIS Approaches to Manage Non-Cooperative Opinions. Sustainability 2020, 12, 2745. [Google Scholar] [CrossRef] [Green Version]
- Bersano, A.; Segantin, S.; Falcone, N.; Panella, B.; Testoni, R. Evaluation of a potential reintroduction of nuclear energy in Italy to accelerate the energy transition. Electr. J. 2020, 33, 106813. [Google Scholar] [CrossRef]
- Khan, M.M.A.; Asif, M.; Stach, E. Rooftop PV Potential in the Residential Sector of the Kingdom of Saudi Arabia. Buildings 2017, 7, 46. [Google Scholar] [CrossRef]
- Almasoud, A.H.; Gandayh, H.M. Future of solar energy in Saudi Arabia. J. King Saud Univ. Eng. Sci. 2015, 27, 153–157. [Google Scholar] [CrossRef] [Green Version]
- Belloumi, M.; Alshehry, A. Sustainable Energy Development in Saudi Arabia. Sustainability 2015, 7, 5153–5170. [Google Scholar] [CrossRef] [Green Version]
- Alnaser, W.E.; Alnaser, N.W. The status of renewable energy in the GCC countries. Renew. Sustain. Energy Rev. 2011, 15, 3074–3098. [Google Scholar] [CrossRef]
- Yıldırım, E.; Aktacir, M.A. Optimization of PV System and Technology in View of a Load Profile: Case of Public Building in Turkey. Therm. Sci. 2019, 23, 3567–3577. [Google Scholar] [CrossRef] [Green Version]
- Martin, A.G.; Yoshihiro, H.; Wilhelm, W.; Ewan, D.D.; Dean, H.L.; Jochen, H.; Anita, W.H.H.B. Solar cell efficiency tables (version 50). Prog. Photovolt. Res. Appl. 2017, 25, 668–676. [Google Scholar]
- Mehrabankhomartash, M.; Rayati, M.; Sheikhi, A.; Ranjbar, A.M. Practical battery size optimization of a PV system by considering individual customer damage function. Renew. Sustain. Energy Rev. 2017, 67, 36–50. [Google Scholar] [CrossRef]
- Kaldellis, J.K.; Kapsali, M.; Kavadias, K.A. Temperature and wind speed impact on the efficiency of PV installations. Experience obtained from outdoor measurements in Greece. Renew. Energy 2014, 66, 612–624. [Google Scholar] [CrossRef]
- Bai, A.; Popp, J.; Balogh, P.; Gabnai, Z.; Pályi, B.; Farkas, I.; Pintér, G.; Zsiborács, H. Technical and economic effects of cooling of monocrystalline photovoltaic modules under Hungarian conditions. Renew. Sustain. Energy Rev. 2016, 60, 1086–1099. [Google Scholar] [CrossRef] [Green Version]
- Grubisic-Cabo, F.; Sandro, N.; Giuseppe, T. Photovoltaic panels: A review of the cooling techniques. Trans. FAMENA 2016, 40, 63–74. [Google Scholar]
- Makrides, G.; Zinsser, B.; Norton, M.; Georghiou, G.E. Performance of Photovoltaics Under Actual Operating Conditions. In Third Generation Photovoltaics; Springer: Berlin/Heidelberg, Germany, 2012; ISBN 978-953-51-0304-2. [Google Scholar]
- Lee, S.; Lee, H.; Yoon, B. Modeling and analyzing technology innovation in the energy sector: Patent-based HMM approach. Comput. Ind. Eng. 2012, 63, 564–577. [Google Scholar] [CrossRef]
- Fan, Y. Energy Management and Economics. Comput. Ind. Eng. 2012, 63, 539–728. [Google Scholar] [CrossRef]
- Tian, G.; Liu, Y.; Ke, H.; Chu, J. Energy evaluation method and its optimization models for process planning with stochastic characteristics: A case study in disassembly decision-making. Comput. Ind. Eng. 2012, 63, 553–563. [Google Scholar] [CrossRef]
- Akpolat, A.N.; Dursun, E.; Kuzucuoğlu, A.E.; Yang, Y.; Blaabjerg, F.; Baba, A.F. Performance Analysis of a Grid-Connected Rooftop Solar Photovoltaic System. Electronics 2019, 8, 905. [Google Scholar] [CrossRef] [Green Version]
- Muteri, V.; Cellura, M.; Curto, D.; Franzitta, V.; Longo, S.; Mistretta, M.; Parisi, M.L. Review on Life Cycle Assessment of Solar Photovoltaic Panels. Energies 2020, 13, 252. [Google Scholar] [CrossRef] [Green Version]
- Pradhan, A.K.; Kar, S.K.; Mohanty, M.K. Grid Renewable Hybrid Power Generation System for a Public Health Centre in Rural Village. Int. J. Renew. Energy Res. 2016, 6, 282–288. [Google Scholar]
- Almarshoud, A. Performance of solar resources in Saudi Arabia. Renew. Sustain. Energy Rev. 2016, 66, 694–701. [Google Scholar] [CrossRef]
- Mittal, M.; Bora, B.; Saxena, S.; Gaur, A.M. Performance prediction of PV module using electrical equivalent model and artificial neural network. Sol. Energy 2018, 176, 104–117. [Google Scholar] [CrossRef]
- Yahya-Khotbehsara, A.; Shahhoseini, A. A fast modeling of the double-diode model for PV modules using combined analytical and numerical approach. Sol. Energy 2018, 162, 403–409. [Google Scholar] [CrossRef]
- Goverde, H.; Goossens, D.; Govaerts, J.; Catthoor, F.; Baert, K.; Poortmans, J.; Driesen, J. Spatial and temporal analysis of wind effects on PV modules: Consequences for electrical power evaluation. Sol. Energy 2017, 147, 292–299. [Google Scholar] [CrossRef]
- Goossens, D.; Goverde, H.; Catthoor, F. Effect of wind on temperature patterns, electrical characteristics, and performance of building-integrated and building-applied inclined photovoltaic modules. Sol. Energy 2018, 170, 64–75. [Google Scholar] [CrossRef]
- Curto, D.; Favuzza, S.; Franzitta, V.; Musca, R.; Navarro, M.A.N.; Zizz, G. Evaluation of the optimal renewable electricity mix for Lampedusa island: The adoption of a technical and economical methodology. J. Clean. Prod. 2020, 263, 121404. [Google Scholar] [CrossRef]
- Awan, A.B.; Zubair, M.; Praveen, R.P.; Abokhalil, A.G. Solar Energy Resource Analysis and Evaluation of Photovoltaic System Performance in Various Regions of Saudi Arabia. Sustainability 2018, 10, 1129. [Google Scholar] [CrossRef] [Green Version]
- Rani, P.; Mishra, A.R.; Pardasani, K.R.; Mardani, A.; Liao, H.; Streimikienef, D. A novel VIKOR approach based on entropy and divergence measures of Pythagorean fuzzy sets to evaluate renewable energy technologies in India. J. Clean. Prod. 2019, 238, 117936. [Google Scholar] [CrossRef]
- Daus, Y.V.; Yudaev, I.V.; Stepanchuk, G.V. Reducing the Costs of Paying for Consumed Electric Energy by Utilizing Solar Energy. Appl. Sol. Energy 2018, 54, 139–143. [Google Scholar] [CrossRef]
- Yoomak, Y.; Patcharoen, T.; Ngaopitakkul, A. Performance and Economic Evaluation of Solar Rooftop Systems in Different Regions of Thailand. Sustainability 2019, 11, 6647. [Google Scholar] [CrossRef] [Green Version]
- Kassem, Y.; Camur, H.; Alhuoti, S.M.A. Solar Energy Technology for Northern Cyprus: Assessment, Statistical Analysis, and Feasibility Study. Energies 2020, 13, 940. [Google Scholar] [CrossRef] [Green Version]
- Ascencio-Vásquez, J.; Brecl, K.; Topič, M. Methodology of Köppen-Geiger-Photovoltaic climate classification and implications to worldwide mapping of PV system performance. Sol. Energy 2019, 191, 672–685. [Google Scholar] [CrossRef]
- Zell, E.; Gasim, S.; Wilcox, S.; Katamoura, S.; Stoffel, T.; Shibli, H.; Engel-Cox, J.; Al Subie, M. Assessment of solar radiation resources in Saudi Arabia. Sol. Energy 2015, 119, 422–438. [Google Scholar] [CrossRef] [Green Version]
- Roy, P.; Sinha, N.K.; Tiwari, S.; Khare, A. A review on perovskite solar cells: Evolution of architecture, fabrication techniques, commercialization issues and status. Sol. Energy 2020, 198, 665–688. [Google Scholar] [CrossRef]
- Naderloo, L. Prediction of solar radiation on the horizon using NN methods, ANFIS and RSM (Case study-Iran). J. Earth Syst. Sci. 2020, 129, 148. [Google Scholar]
- Benmouiza, K.; Cheknane, A. Clustered ANFIS network using fuzzy c-means, subtractive clustering, and grid partitioning for hourly solar radiation forecasting. Theor. Appl. Climatol. 2019, 137, 31–43. [Google Scholar] [CrossRef]
- Mohammadi, K.; Shamshirband, S.; Kamsin, A.; Lai, P.C.; Mansor, Z. Identifying the most significant input parameters for predicting global solar radiation using an ANFIS selection procedure. Renew. Sustain. Energy Rev. 2016, 63, 423–434. [Google Scholar] [CrossRef]
- Aldair, A.A.; Obed, A.A.; Halihal, A.F. Design and implementation of ANFIS-reference model controller based MPPT using FPGA for photovoltaic system. Renew. Sustain. Energy Rev. 2018, 82, 2202–2217. [Google Scholar] [CrossRef]
- Khosravi, A.; Malekan, M.; Pabon, J.J.G.; Zhao, X.; Assad, M.E.H. Design parameter modelling of solar power tower system using adaptive neuro-fuzzy inference system optimized with a combination of genetic algorithm and teaching learning-based optimization algorithm. J. Clean. Prod. 2020, 244, 118904. [Google Scholar] [CrossRef]
- Solar-GIS. Available online: https://globalsolaratlas.info/map (accessed on 30 May 2020).
- PVGIS. Available online: https://ec.europa.eu/jrc/en/pvgis (accessed on 30 May 2020).
- Colak, N.S.; Sahin, E.; Dertli, E.; Yilmaz, M.T.; Taylan, O. Response surface methodology as optimization strategy for asymmetric bioreduction of acetophenone using whole cell of Lactobacillus senmaizukei. Prep. Biochem. Biotechnol. 2019, 49, 884–890. [Google Scholar] [CrossRef] [PubMed]
- Dirnberger, D.; Kräling, U. Uncertainty in PV Module Measurement—Part I: Calibration of Crystalline and Thin-Film Modules. IEEE J. Photovolt. 2013, 3, 1016–1026. [Google Scholar] [CrossRef]
- Taylan, O.; Darrab, I.A. Fuzzy control charts for process quality improvement and product assessment in tip shear carpet industry. J. Manuf. Technol. Manag. 2012, 23, 402–420. [Google Scholar] [CrossRef]
- Taylan, O.; Taşkın, H. Fuzzy Modelling af A Production System. J. Nav. Sci. Eng. 2003, 1, 1–13. [Google Scholar]
- Taylan, O.; Karagozoglu, B. An Adaptive Neuro-Fuzzy Model for Prediction of Student’s Academic Performance. Comput. Ind. Eng. 2009, 57, 732–741. [Google Scholar] [CrossRef]
- Taylan, O. Neural and fuzzy model performance evaluation of a dynamic production system. Int. J. Prod. Res. 2006, 44, 1093–1105. [Google Scholar] [CrossRef]
- Taylan, O.; Darrab, I.A. Determining optimal quality distribution of latex weight using adaptive neuro-fuzzy modeling and control systems. Comput. Ind. Eng. 2011, 61, 686–696. [Google Scholar] [CrossRef]
- Al-Ghamdi, K.; Taylan, O. A comparative study on modelling material removal rate by ANFIS and polynomial methods in electrical discharge machining process. Comput. Ind. Eng. 2015, 79, 27–41. [Google Scholar] [CrossRef]
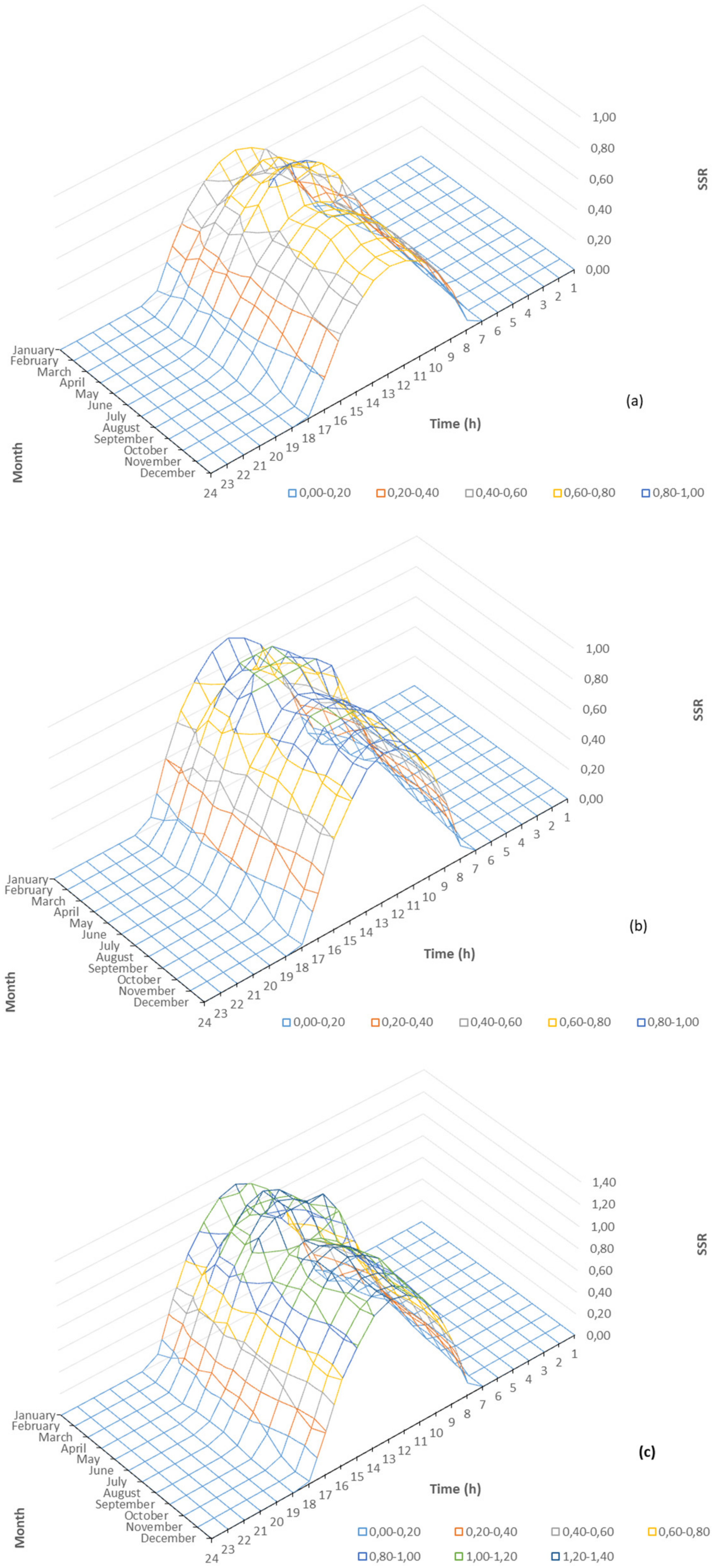

| PV25 | PV30 | PV35 | PV40 | PV45 | PV50 | PV75 | PV100 | |
|---|---|---|---|---|---|---|---|---|
| January | 0.22 | 0.27 | 0.31 | 0.36 | 0.40 | 0.45 | 0.67 | 0.90 |
| February | 0.19 | 0.23 | 0.27 | 0.31 | 0.35 | 0.39 | 0.58 | 0.78 |
| March | 0.26 | 0.31 | 0.36 | 0.41 | 0.47 | 0.52 | 0.78 | 1.03 |
| April | 0.27 | 0.32 | 0.37 | 0.42 | 0.48 | 0.53 | 0.80 | 1.06 |
| May | 0.31 | 0.37 | 0.43 | 0.50 | 0.56 | 0.62 | 0.93 | 1.24 |
| June | 0.24 | 0.29 | 0.33 | 0.38 | 0.43 | 0.48 | 0.72 | 0.96 |
| July | 0.25 | 0.29 | 0.34 | 0.39 | 0.44 | 0.49 | 0.74 | 0.98 |
| August | 0.26 | 0.31 | 0.36 | 0.41 | 0.46 | 0.51 | 0.77 | 1.02 |
| September | 0.25 | 0.30 | 0.36 | 0.41 | 0.46 | 0.51 | 0.76 | 1.01 |
| October | 0.23 | 0.28 | 0.33 | 0.37 | 0.42 | 0.46 | 0.70 | 0.93 |
| November | 0.22 | 0.27 | 0.31 | 0.36 | 0.40 | 0.45 | 0.67 | 0.90 |
| December | 0.23 | 0.27 | 0.32 | 0.36 | 0.41 | 0.45 | 0.68 | 0.90 |
| Yearly | 0.24 | 0.29 | 0.34 | 0.39 | 0.44 | 0.48 | 0.73 | 0.97 |
| Radiation-(W/m2) | Module Surface Temperature-(°C) | Outdoor Temperature-(°C) | Wind Direction | Wind Speed-(m/s) | Actual PV (MW) | Predicted PV by ANFIS (MW) | Predicted PV by RSM (MW) |
|---|---|---|---|---|---|---|---|
| 896.33 | 43.73 | 26.16 | 232.64 | 3.63 | 19.98 | 19.98 | 19.99 |
| 826.38 | 41.64 | 25.05 | 235.65 | 3.33 | 21.01 | 22.00 | 21.22 |
| 658.68 | 37.27 | 28.08 | 59.63 | 3.02 | 19.93 | 19.95 | 19.94 |
| 589.66 | 49.96 | 39.08 | 262.91 | 3.35 | 24.95 | 24.96 | 24.93 |
| 573.58 | 48.56 | 38.70 | 278.39 | 4.42 | 25.64 | 25.64 | 25.65 |
| 570.30 | 46.60 | 36.26 | 218.72 | 3.95 | 25.81 | 25.72 | 25.59 |
| 561.30 | 41.62 | 30.26 | 125.83 | 1.28 | 24.64 | 24.65 | 24.91 |
| 552.27 | 46.25 | 36.21 | 216.56 | 3.97 | 25.03 | 25.05 | 25.29 |
| 548.65 | 38.49 | 32.64 | 63.35 | 3.15 | 26.20 | 26.21 | 26.33 |
| 538.25 | 46.39 | 37.40 | 89.96 | 2.52 | 24.23 | 24.22 | 24.13 |
| 533.89 | 47.18 | 36.54 | 214.12 | 3.25 | 23.76 | 23.79 | 23.51 |
| 530.75 | 37.48 | 33.72 | 182.00 | 5.90 | 25.26 | 25.28 | 25.37 |
| 526.28 | 35.71 | 30.55 | 39.37 | 3.73 | 25.41 | 25.45 | 25.31 |
| 520.78 | 47.59 | 38.69 | 285.97 | 4.44 | 23.36 | 23.37 | 23.42 |
| PV Model Power Output (Aldair et al.) [37] | Our PV Model Power Output | |||
|---|---|---|---|---|
| Radiation | Temperature (°C) | ANFIS (MW) | ANFIS (MW) | RSM (MW) |
| 500 | 0 | 33.36 | 46.14 | 48.50 |
| 500 | 25 | 27.72 | 34.78 | 35.23 |
| 500 | 50 | 22.58 | 32.02 | 30.61 |
| 750 | 0 | 51.4 | 56..12 | 52.98 |
| 750 | 25 | 43.6 | 47.78 | 41.19 |
| 750 | 50 | 35.98 | 36.86 | 34.53 |
| 1000 | 0 | 69.4 | 70.25 | 71.36 |
| 1000 | 25 | 59.1 | 58.17 | 60.88 |
| 1000 | 50 | 48.74 | 43.79 | 39.24 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alamoudi, R.; Taylan, O.; Aktacir, M.A.; Herrera-Viedma, E. Designing a Solar Photovoltaic System for Generating Renewable Energy of a Hospital: Performance Analysis and Adjustment Based on RSM and ANFIS Approaches. Mathematics 2021, 9, 2929. https://doi.org/10.3390/math9222929
Alamoudi R, Taylan O, Aktacir MA, Herrera-Viedma E. Designing a Solar Photovoltaic System for Generating Renewable Energy of a Hospital: Performance Analysis and Adjustment Based on RSM and ANFIS Approaches. Mathematics. 2021; 9(22):2929. https://doi.org/10.3390/math9222929
Chicago/Turabian StyleAlamoudi, Rami, Osman Taylan, Mehmet Azmi Aktacir, and Enrique Herrera-Viedma. 2021. "Designing a Solar Photovoltaic System for Generating Renewable Energy of a Hospital: Performance Analysis and Adjustment Based on RSM and ANFIS Approaches" Mathematics 9, no. 22: 2929. https://doi.org/10.3390/math9222929
APA StyleAlamoudi, R., Taylan, O., Aktacir, M. A., & Herrera-Viedma, E. (2021). Designing a Solar Photovoltaic System for Generating Renewable Energy of a Hospital: Performance Analysis and Adjustment Based on RSM and ANFIS Approaches. Mathematics, 9(22), 2929. https://doi.org/10.3390/math9222929







