Abstract
In recent papers the authors introduce, study and apply a variant of the Eggenberger—Pólya urn, called the “rescaled” Pólya urn, which, for a suitable choice of the model parameters, exhibits a reinforcement mechanism mainly based on the last observations, a random persistent fluctuation of the predictive mean and the almost sure convergence of the empirical mean to a deterministic limit. In this work, motivated by some empirical evidence, we show that the multidimensional Wright—Fisher diffusion with mutation can be obtained as a suitable limit of the predictive means associated to a family of rescaled Pólya urns.
1. Introduction
The well-known standard Eggenberger—Pólya urn [1,2] works as follows. An urn initially contains balls of color i, for , and at each time-step, a ball is drawn from the urn and then it is returned into the urn together with additional balls of the same color (here and in the following, the expression “number of balls” is not to be understood literally, but all the quantities are real numbers, not necessarily integers). Hence, denoting by the number of balls of color i inside the urn at time-step n, we have
where if the drawn ball at time-step n is of color i, and otherwise. The parameter tunes the reinforcement mechanism: the greater the , the greater the dependence of on .
In [3,4,5], the rescaled Pólya (RP) urn has been introduced, studied, generalized and applied. This model differs from the original one by the introduction of a parameter such that
Therefore, at time-step 0, the urn contains balls of color i and the parameters and regulate the reinforcement mechanism. More precisely, the term connects to the “configuration” at time-step n by means of the “scaling” parameter , and the term connects to the outcome of the drawing at time-step by means of the parameter . The case corresponds to the standard Eggenberger—Pólya urn with an initial number of balls of color i. When , the RP urn model shows the following three characteristics:
- (i)
- A reinforcement mechanism mainly based on the last observations;
- (ii)
- A random persistent fluctuation of the predictive mean ;
- (iii)
- The almost sure convergence of the empirical mean to the deterministic limit , and a chi-squared goodness of fit result for the long-term probability distribution .
Regarding point (iii), we specifically have that the chi-squared statistics
where N is the sample size and the number of sampled observations equal to i, is asymptotically distributed as , with . Therefore, the presence of correlation among observations attenuates the effect of N, which multiplies the chi-squared distance between the observed frequencies and the expected probabilities. This is a key feature for statistical applications in the framework of a “big sample”, where a small value of the chi-squared distance might be significant, and hence a correction related to the correlation between observations is required. In [3,5], a possible application in the context of clustered data was described, with independence between clusters and correlation due to a reinforcement mechanism inside each cluster.
In [4], the RP urn was applied as a good model for the evolution of the sentiment associated with Twitter posts. Precisely, we analyzed three data sets: (i) the “COVID-19 epidemic” data set covers the period from 21 February to 20 April to 2020 and includes tweets in Italian about the COVID-19 epidemic; (ii) the “Migration debate” data set refers to the period from 23 January to 22 February 2019 and the collected posts are related to the Italian debate on migration; (iii) the “10 days of traffic” data set collects the entire traffic of posts in Italian in the period from 1 September to 10 September 2019. For every post, the relative sentiment, that is, the positive or negative connotation of the text, was computed using the polyglot python module developed in [6], which provides a numerical value for the sentiment of a post (for a survey on sentiment analysis, also known as opinion mining, we refer to [7] and references therein). We fixed a threshold T so that a tweet with was classified as a tweet with a positive sentiment and one with was classified as a tweet with a negative sentiment. Tweets with a value were discarded. We took the following different values for T: , and . We applied the RP urn model, ordering the tweets according to their creation time and taking each tweet with a positive/negative classification as an extraction in the urn model. More specifically, we applied the RP model with : the time series of the tweets represents the time series of the extractions from the urn, that is, the random variables . The event means that tweet n exhibits a positive sentiment, while means that tweet n exhibits a negative sentiment. For all the considered data sets, the estimated values of were strictly smaller than 1, but very near to 1 (details about the parameters estimation can be found in [4]). Note that the RP urn dynamics with such a value for cannot be approximated by the standard Pólya urn (), because one would lose the fluctuations of the predictive means and the possibility of touching the barriers . In this work, we show that the law of such an RP urn process can be approximated by a Wright—Fisher diffusion with mutation. More precisely, we prove that the multidimensional Wright—Fisher diffusion with mutation can be obtained as a suitable limit of the predictive means associated with a family of RP urns with [0, 1), . As an example, in Figure 1, for the data set “COVID-19 epidemic”, we show the plot of the process , reconstructed from the data (details about the reconstruction process can be found in [4]) and rescaled in time as , the plot of a simulated (by the Euler–Maruyama method) trajectory of the Wright—Fisher process, the plot of the approximation of this trajectory by means of the RP urn and the approximation of the data process by means of the standard Pólya urn.
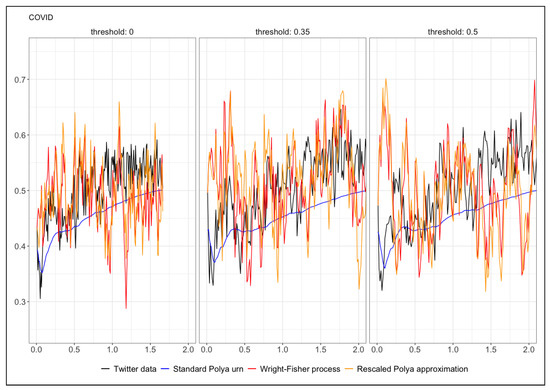
Figure 1.
“COVID-19 epidemic” Twitter data set: the black line is the process , reconstructed from the data and rescaled in time as ; the red line is a simulated trajectory of the Wright—Fisher process; the orange line is the approximation of this trajectory by means of the RP urn and the blue line is the approximation of the data process by means of the standard Pólya urn. The numbers 0, and refer to the values chosen for the threshold T. The corresponding estimated values for are: 0.000776 (), 0.00115 () and 0.00130 ().
The Wright—Fisher (WF) class of diffusion processes models the evolution of the relative frequency of a genetic variant, or allele, in a large randomly mating population with a finite number k of genetic variants. When , the WF diffusion obeys the one-dimensional stochastic differential equation
The drift coefficient, , can include a variety of evolutionary forces such as mutation and selection. For example, describes a process with recurrent mutation between the two alleles, governed by the mutation rates and . The drift vanishes when which is an attracting point for the dynamics. Equation (1) can be generalized to the case . The WF diffusion processes are widely employed in Bayesian statistics, as models for time-evolving priors [8,9,10,11] and as a discrete-time finite-population construction method of the two-parameter Poisson–Dirichlet diffusion [12]. They have been applied in genetics [13,14,15,16,17,18], in biophysics [19,20], in filtering theory [21,22] and in finance [23,24].
The benefit coming from the proven limit result is twofold. First, the known properties of the WF process can give a description of the RP urn when the parameter is strictly smaller than one, but very near to one. Second, the given result might furnish the theoretical base for a new simulation method of the WF process. Indeed, the simulation from Equation (1) is highly nontrivial because there is no known closed form expression for the transition function of the diffusion, even in the simple case with null drift [25].
The rest of the paper is organized as follows. In Section 2, we set up our notation and we formally define the RP urn model. Section 3 provides the main result of this work, that is, the convergence result of a suitable family of predictive means associated with RP urns with . In Section 4, employing the boundary classification of the WF diffusion with mutation and connecting it to the parameters of the RP urn model, we introduce an RP urn with a value of very near to 1 the notion of recessive subsets of colors and the notion of dominant color. These two concepts are related to the possibility of reaching the barriers 0 and 1 by the predictive means of the urn process. Finally, Section 5 summarizes the work and concludes it.
2. The Rescaled Pólya Urn
For a vector , we set and . Moreover we denote by and the vectors with all the components equal to 1 and equal to 0, respectively.
Let and . At time-step 0, the urn contains distinct balls of color i, with . We set and . We suppose and we set . At each time-step , a ball is drawn at random from the urn and we define the random vector as
The number of balls inside the urn is updated as follows:
which gives
Similarly, from the equality
we get, using ,
Setting , that is the total number of balls inside the urn at time-step n, we get the relations
and
Denoting by the trivial -field and setting for , the conditional probabilities of the extraction process, also called predictive means, are
and, from (3) and (4), we have
The dependence of on is regulated by the factor , with . In the case of the standard Eggenberger—Pólya urn (i.e., the case ), each observation has the same “weight” . Instead, when the factor increases with h, and the main contribution is given by the most recent drawings. The case is an extreme case, for which depends only on the last drawing .
Setting and letting and , from (9) we obtain
3. Main Result
Consider the RP urn with parameters , , and such that . Consequently, the total number of balls in the urn along the time-steps is constantly equal to and if we denote by the predictive means corresponding to the fixed value , we have the dynamics
where
and . Note that we have for , with . Finally, we define , where
The following result holds true:
Theorem 1.
Suppose that weakly converges towards some process when . Then, for , the family of stochastic processes weakly converges towards the k-alleles Wright—Fisher diffusion , with type-independent mutation kernel given by and with dynamics
with and , that is,
Proof.
Fix a sequence , with and . The sequence of processes is bounded, hence we have to prove the tightness of the sequence in the space of right-continuous functions with the usual Skorohod topology, and the characterization of the law of the unique limit process.
For any , define
We note that, for any , the partial derivatives in (16) are uniformly bounded, as belongs to the compact simplex . The family is then uniformly integrable. Thus, as a consequence of [26] (Theorem 4) (or [27] (ch. 7.4.3, Theorem 4.3, p. 236)), we have that the sequence of processes is tight in the space of right-continuous functions with the usual Skorohod topology. Since, for any n and t, , then . Moreover, the generator of the limit process is determined by the limit
Hence, the weak limit of the sequence of the bounded processes is the diffusion process
The expression (15) follows from [28] (Corollary 3). □
Remark 1 (Limiting ergodic distribution).
Since the simplex has dimension with respect to the Lebesgue measure, it is convenient to change the notations. Let be the -dimensional simplex defined by
where, with the old definition, we have and . Obviously, there is a one-to-one natural correspondence between and the simplex defined by
The Kolmogorov forward equation for the density of the limiting process is
Therefore, it is not hard to show that the limit invariant ergodic distribution is
because it satisfies (18) (see also [29]). The above distribution is the Dirichlet distribution as a function of .
Remark 2 (Transition density of the limit process).
The transition density is defined by
and it can be represented in terms of series of orthogonal polynomials [30] as shown in [31]. Moreover, we refer to [9,32,33] for the explicit form of the reproducing kernel orthogonal polynomials.
4. Recessive and Dominant Colors in an RP Urn with near to 1
Let be a partition of , in that , , and . Here denotes the cardinality of . Define the -dimensional objects , and as
and . With these definitions, from (11), we immediately get that is a -dimensional RP urn following the dynamics
and that Theorem 1 holds for . Consequently, the convergence to the Wright—Fisher diffusion still holds if we group together some components of the process. For instance, when we consider two groups of components, we have the following result:
Corollary 1.
Let with , . Under the hypothesis of Theorem 1, each component of the sequence of processes converges, for , to the one-dimensional diffusion process with values in that satisfies the SDE
In addition, and .
Now, if we further specialize the grouping choice to , we get:
Corollary 2.
Under the conditions of Theorem 1 the i-th component of the sequence of processes converges, for , to the one-dimensional diffusion with values in satisfying the SDE
For instance, the above two results are useful in order to translate the well-known classification of the boundaries of the WF process with mutation [34] (p. 239, Example 8) (see also [35]) to the RP urn model when the parameter is strictly smaller than 1, but very near to 1. Indeed, Corollary 1 implies that satisfies the SDE
Setting and and noting that , we obtain:
- (1)
- , i.e., , if and only if ;
- (2)
- , i.e., , if and only if .
With the same spirit, Corollary 2 states that satisfies the SDE
Setting and , we get:
- (3)
- , i.e., , if and only if ;
- (4)
- , i.e., , if and only if .
Therefore, for an RP urn with , but very near to 1, we can give the following definition:
Definition 1.
We call recessive a non-empty subset of colors such that . We call dominant a color such that is recessive.
Obviously, every subset of a recessive set is recessive. Moreover, when , every set is recessive. The terms “recessive” and “dominant” are justified by the fact that, recalling properties (1)–(4) of the WF process, if a set of colors is recessive, then we can observe that at some times the corresponding predictive means of the urn process are very near to zero. On the contrary, when a color is dominant, we can observe that at some times the corresponding predictive mean of the urn process is very near to one. In Figure 2, we plot the process related to the simulation of an RP urn with , and , where it is possible to observe the excursions near the barrier 1.
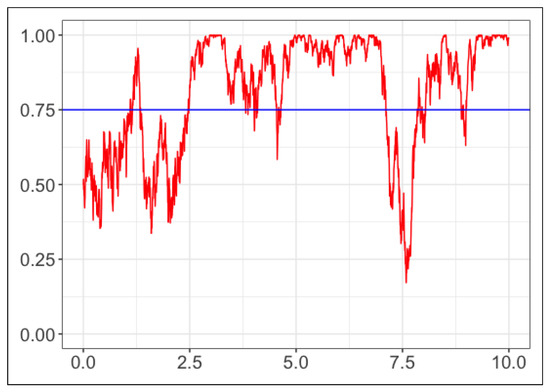
Figure 2.
Simulation: plot of the process related to the simulation of an RP urn with , and .
5. Conclusions
We have proven that the multidimensional WF diffusion with mutation can be obtained as the limit of the predictive means associated with a family of RP urns with , . As a consequence, the known properties of the WF process can give a description of the RP urn when the parameter is strictly smaller than 1, but very near to 1. For instance, starting from the known classification of the boundaries for the WF process and connecting it to the model parameters of the RP urn, we have obtained for an RP urn with a value of very near to one, the notion of recessive subsets of colors and the notion of a dominant color. These two concepts are related to the possibility of reaching the barriers 0 and 1 by the predictive means of the urn process. Other classical problems, together with the corresponding known results for the WF process, can be found in [31]. These results can be used in order to give an approximated answer to the considered problems in the case of an RP urn with a value of near 1.
Author Contributions
Both authors contributed equally to this work. All authors have read and agreed to the published version of the manuscript.
Funding
Irene Crimaldi is partially supported by the Italian “Programma di Attività Integrata” (PAI), project “TOol for Fighting FakEs” (TOFFE) funded by the IMT School for Advanced Studies Lucca. This research received funding from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme under grant agreement No 817257.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Acknowledgments
Both authors sincerely thank the organizers of the present special issue for their invitation to contribute and Fabio Saracco for having collected and shared with them the analyzed Twitter data sets. Giacomo Aletti is a member of the Italian group “Gruppo Nazionale per il Calcolo Scientifico” of the Italian Institute “Istituto Nazionale di Alta Matematica”. Irene Crimaldi is a member of the Italian group “Gruppo Nazionale per l’Analisi Matematica, la Probabilità e le loro Applicazioni” of the Italian Institute “Istituto Nazionale di Alta Matematica”.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Eggenberger, F.; Pólya, G. Über die Statistik verketteter Vorgänge. ZAMM-J. Appl. Math. Mech./Z. Angew. Math. Mech. 1923, 3, 279–289. [Google Scholar] [CrossRef]
- Mahmoud, H.M. Pólya Urn Models; Texts in Statistical Science Series; CRC Press: Boca Raton, FL, USA, 2009. [Google Scholar]
- Aletti, G.; Crimaldi, I. The Rescaled Pólya Urn: Local reinforcement and chi-squared goodness of fit test. Adv. Appl. Probab. Available online: https://iris.imtlucca.it/handle/20.500.11771/19197#.YZNznboRVPZ (accessed on 1 November 2021).
- Aletti, G.; Crimaldi, I.; Saracco, F. A model for the Twitter sentiment curve. PLoS ONE 2021, 16, e0249634. [Google Scholar] [CrossRef]
- Aletti, G.; Crimaldi, I. Generalized Rescaled Pólya urn and its statistical applications. arXiv 2021, arXiv:2010.06373. [Google Scholar]
- Chen, Y.; Skiena, S. Building sentiment lexicons for all major languages. In Proceedings of the 52nd Annual Meeting of the Association for Computational Linguistics (Short Papers), Baltimore, MD, USA, 22–27 June 2014; pp. 383–389. [Google Scholar]
- Chakraborty, K.; Bhattacharyya, S.; Bag, R. A Survey of Sentiment Analysis from Social Media Data. IEEE Trans. Comput. Soc. Syst. 2020, 7, 450–464. [Google Scholar] [CrossRef]
- Favaro, S.; Ruggiero, M.; Walker, S.G. On a Gibbs sampler based random process in Bayesian nonparametrics. Electron. J. Stat. 2009, 3, 1556–1566. [Google Scholar] [CrossRef]
- Griffiths, R.C.; Spanò, D. Diffusion processes and coalescent trees. In Probability and Mathematical Genetics, Papers in Honour of Sir John Kingman; Bingham, N.H., Goldie, C.M., Eds.; LMS Lecture Note Series; Cambridge University Press: Cambridge, UK, 2010; Volume 378, pp. 358–375. [Google Scholar]
- Mena, R.; Ruggiero, M. Dynamic density estimation with diffusive Dirichlet mixtures. Bernoulli 2016, 22, 901–926. [Google Scholar] [CrossRef]
- Walker, S.G.; Hatjispyros, S.J.; Nicoleris, T. A Fleming-Viot process and Bayesian nonparametrics. Ann. Appl. Probab. 2007, 17, 67–80. [Google Scholar] [CrossRef][Green Version]
- Costantini, C.; De Blasi, P.; Ethier, S.; Ruggiero, M.; Spanò, D. Wright-Fisher construction of the two-parameter Poisson-Dirichlet diffusion. Ann. Appl. Probab. 2017, 27, 1923–1950. [Google Scholar] [CrossRef]
- Bollback, J.P.; York, T.L.; Nielsen, R. Estimation of 2Nes from temporal allele frequency data. Genetics 2008, 179, 497–502. [Google Scholar] [CrossRef]
- Gutenkunst, R.N.; Hernandez, R.D.; Williamson, S.H.; Bustamante, C.D. Inferring the Joint Demographic History of Multiple Populations from Multidimensional SNP Frequency Data. PLoS Genet. 2009, 5, e1000695. [Google Scholar] [CrossRef] [PubMed]
- Malaspinas, A.S.; Malaspinas, O.; Evans, S.N.; Slatkin, M. Estimating allele age and selection coefficient from time-serial data. Genetics 2012, 192, 599–607. [Google Scholar] [CrossRef]
- Schraiber, J.; Griffiths, R.C.; Evans, S.N. Analysis and rejection sampling of Wright-Fisher diffusion bridges. Theor. Popul. Biol. 2013, 89, 64–74. [Google Scholar] [CrossRef] [PubMed]
- Williamson, S.H.; Hernandez, R.; Fledel-Alon, A.; Zhu, L.; Bustamante, C.D. Simultaneous inference of selection and population growth from patterns of variation in the human genome. Proc. Natl. Acad. Sci. USA 2005, 102, 7882–7887. [Google Scholar] [CrossRef]
- Zhao, L.; Lascoux, M.; Overall, A.D.J.; Waxman, D. The characteristic trajectory of a fixing allele: A consequence of fictitious selection that arises from conditioning. Genetics 2013, 195, 993–1006. [Google Scholar] [CrossRef]
- Dangerfield, C.; Kay, D.; Burrage, K. Stochastic models and simulation of ion channel dynamics. Procedia Comput. Sci. 2010, 1, 1587–1596. [Google Scholar] [CrossRef]
- Dangerfield, C.E.; Kay, D.; MacNamara, S.; Burrage, K. A boundary preserving numerical algorithm for the Wright—Fisher model with mutation. BIT Numer. Math. 2012, 5, 283–304. [Google Scholar] [CrossRef]
- Chaleyat-Maurel, M.; Genon-Catalot, V. Filtering the Wright–Fisher diffusion. ESAIM Probab. Stat. 2009, 13, 197–217. [Google Scholar] [CrossRef][Green Version]
- Papaspiliopoulos, O.; Ruggiero, M. Optimal filtering and the dual process. Bernoulli 2014, 20, 1999–2019. [Google Scholar] [CrossRef]
- Delbaen, F.; Shirakawa, H. An interest rate model with upper and lower bounds. Asia-Pac. Financ. Mark. 2002, 9, 191–209. [Google Scholar] [CrossRef]
- Gourieroux, C.; Jasiak, J. Multivariate Jacobi process with application to smooth transitions. J. Econom. 2006, 131, 475–505. [Google Scholar] [CrossRef]
- Jenkins, P.A.; Spanò, D. Exact simulation of the Wright-Fisher diffusion. Ann. Appl. Probab. 2017, 27, 1478–1509. [Google Scholar] [CrossRef]
- Kushner, H.J. Approximation and Weak Convergence Methods for Random Processes, with Applications to Stochastic Systems Theory; MIT Press Series in Signal Processing, Optimization, and Control; MIT Press: Cambridge, MA, USA, 1984; Volume 6. [Google Scholar]
- Kushner, H.J.; Yin, G.G. Stochastic Approximation and Recursive Algorithms and Applications, 2nd ed.; Applications of Mathematics; Springer: New York, NY, USA, 2003; Volume 35. [Google Scholar]
- Tanabe, K.; Sagae, M. An Exact Cholesky Decomposition and the Generalized Inverse of the Variance-Covariance Matrix of the Multinomial Distribution, with Applications. J. R. Stat. Soc. Ser. B (Methodol.) 1992, 54, 211–219. [Google Scholar] [CrossRef]
- Wright, S. Evolution and the Genetics of Populations, Volume 2: Theory of Gene Frequencies; Evolution and the Genetics of Populations; University of Chicago Press: Chicago, IL, USA, 1984. [Google Scholar]
- Dunkl, C.F.; Xu, Y. Orthogonal Polynomials of Several Variables, 2nd ed.; Encyclopedia of Mathematics and Its Applications; Cambridge University Press: Cambridge, UK, 2014; Volume 155. [Google Scholar] [CrossRef]
- Aletti, G.; Crimaldi, I. The rescaled Pólya urn and the Wright—Fisher process with mutation. arXiv 2021, arXiv:2110.01853. [Google Scholar]
- Griffiths, R.C.; Spanò, D. Orthogonal polynomial kernels and canonical correlations for Dirichlet measures. Bernoulli 2013, 19, 548–598. [Google Scholar] [CrossRef]
- Griffiths, R.C.; Spanò, D. Multivariate Jacobi and Laguerre polynomials, infinite-dimensional extensions, and their probabilistic connections with multivariate Hahn and Meixner polynomials. Bernoulli 2011, 17, 1095–1125. [Google Scholar] [CrossRef]
- Karlin, S.; Taylor, H.M. A Second Course in Stochastic Processes; Subsidiary of Harcourt Brace Jovanovich; Academic Press, Inc.: New York, NY, USA; London, UK, 1981. [Google Scholar]
- Huillet, T. On Wright–Fisher diffusion and its relatives. J. Stat. Mech. Theory Exp. 2007, 2007, P11006. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).