A Note on a Meshless Method for Fractional Laplacian at Arbitrary Irregular Meshes

Abstract

The existence and uniqueness of the discrete solutions of a porous medium equation with diffusion are demonstrated. The Cauchy problem contains a fractional Laplacian and it is equivalent to the extension formulation in the sense of trace and harmonic extension operators. By using the generalized finite difference method, we obtain the convergence of the numerical solution to the classical/theoretical solution of the equation for nonnegative initial data sufficiently smooth and bounded. This procedure allows us to use meshes with complicated geometry (more realistic) or with an irregular distribution of nodes (providing more accurate solutions where needed). Some numerical results are presented in arbitrary irregular meshes to illustrate the potential of the method.

1. Introduction

The well-known porous medium equation appears in the description of different phenomena. There are a number of physical applications where this simple model appear in a natural way, mainly to describe processes involving fluid flow, heat transfer or diffusion. Moreover, applications have been found in mathematical biology, spread of viscous fluids, boundary layer theory and other fields (see [1]). In this paper, we consider the porous medium equation with fractional Laplacian, which represents processes with anomalous diffusion. This kind of diffusion is observed in continuum mechanics, phase transition phenomena, population dynamics, optimal control, image processing, game theory, finance and others (see [2] and the references therein).

This paper deals with a numerical scheme given by the generalized finite difference method (GFDM) in order to solve the one dimensional porous medium equation with fractional diffusion

$$\left\{\begin{array}{ccc}\hfill & w_t+{(-\mathsf{\Delta })}^{1/2}{w}^m=0,\hfill & \hfill x\in {\mathbb{R}}^N,t\in (0,\infty ),\\ \hfill & w(x,0)=f\left(x\right),\hfill & \hfill x\in {\mathbb{R}}^N,\end{array}\right.$$

(1)

for $m,N\ge 1$ and nonnegative initial data in $L^1\left({\mathbb{R}}^N\right)\cap L^{\infty }\left({\mathbb{R}}^N\right)$. The existence, uniqueness and regularity of solutions to (1) are well known [3]. In order to remove the nonlocality induced by the fractional Laplacian ${(-\mathsf{\Delta })}^{1/2}$, Caffarelli and Silvestre showed that any power of the fractional Laplacian in ${\mathbb{R}}^N$ could be realized as an operator that mapped a Dirichlet boundary condition to a Neumann-type condition via an extension on the upper half-space ${\mathbb{R}}^N\times {\mathbb{R}}^{+}$. In [3], the authors stated that (1) is equivalent to the so-called extension formulation (see [4,5]):

$$\left\{\begin{array}{ccc}\hfill & \mathsf{\Delta }u(x,y,t)=0,\hfill & \hfill x\in {\mathbb{R}}^N,y>0,t>0,\\ \hfill & \frac{\partial u^{1/m}}{\partial t}(x,0,t)=\frac{\partial u}{\partial y}(x,0,t),\hfill & \hfill x\in {\mathbb{R}}^N,y=0,t>0,\\ \hfill & u(x,0,0)=f^m\left(x\right),\hfill & \hfill x\in {\mathbb{R}}^N.\end{array}\right.$$

(2)

The equivalence of both problems holds in the sense of trace and harmonic extension operators, that is,

$$w(x,t)=Tr(u^{1/m}(x,y,t)),u(x,y,t)=E\left(w^m(x,t)\right).$$

See [3,6,7] for more details about the Silvestre–Caffarelli extension. The reader can also see [8,9] for more information about the method.

Numerical results for the discrete problem have been obtained using the finite difference method in [6]. In [7], authors used the standart finite difference method to solve a Caputo-type parabolic equation with a fractional laplacian. Furthermore, recently, Chen and Shen have solved numerically Poisson-type problems with the diagonalization matrix method and the enriched spectral method [10]. Padgett dealt with the same problem numerically in [11]. In addition, different numerical methods have been applied for approximating the fractional powers of the laplacian operator, see [12,13,14].

We approximate the solutions to (2) in the whole space by the solutions of the problem posed a bounded domain. In the sequel, we study the problem with $N=1$, because the numerous indices in the formulas and to further simplify the notation but all the arguments are also valid for $N>1$. Consider the problem in a bounded domain $\mathsf{\Omega }$ with boundary $\Gamma =\partial \mathsf{\Omega }$.

The generalized finite difference method is a meshless procedure based on the Taylor series and moving least squares (see [15]). The main advantage of the meshless methods is the possibility of using completely irregular meshes. In this way, one can concentrate a higher number of nodes in certain parts of the domain and use the previous information of the problem. In this paper, we consider the porous medium phenomena, which is of a diffusive nature; therefore, the known information about the problem such as the Barenblatt profiles [16] can be used for placing a higher number of nodes in the centre of the profiles and less in the tails. Despite this fact, the explicit formulae remain in a simple form, even for nonlinear equations. Several applications of the GFDM have been implemented in the recent years such as modelling of chemotaxis models [17] and recently, for solving fractional differential equations [18]. For completeness, let us state the basics of the method, which can be found in the above cited references. Let $M={\{{\mathit{x}}_i=(x_i,y_i)\}}_{i=1}^P$ be a set of data points in the computational domain. For each ${\mathit{x}}_i\in M$, call $u(x_i,y_i,t_j)=u_i^j$ the solution of (2) in the point of the mesh and $u(x_i,y_i,t_j)\approx U_i^j$ the solution of the numerical method. Let $S_0$ be a localized star centered at ${\mathit{x}}_0\in M$ with s neighbors. Call $h_i=x_i-x_0$ and $k_i=y_i-y_0$. Then, the Taylor’s expansions around ${\mathit{x}}_i$ each data point of the $S_0$ star are

$$u\left({\mathit{x}}_i\right)=u\left({\mathit{x}}_0\right)+h_i\frac{\partial u}{\partial x}{|}_{{\mathit{x}}_0}+k_i\frac{\partial u}{\partial y}{|}_{{\mathit{x}}_0}+\frac{1}{2}{\left[h_i^2\frac{{\partial }^{2}u}{\partial x^2}\right|}_{{\mathit{x}}_0}+2h_i{k}_i\frac{{\partial }^{2}u}{\partial x\partial y}{|}_{{\mathit{x}}_0}+k_i^2\frac{{\partial }^{2}u}{\partial y^2}{|}_{{\mathit{x}}_0}]+R^i.$$

Here, $R^i$ is the remainder term. Consider the weighted sum of squares of these remainder terms based on Moving Least Squares (MLS) and then the residual function is defined as

$$Re\left(u\right)=\sum _{i=1}^s{\left[{\left(u\left({\mathit{x}}_0\right)-u\left({\mathit{x}}_i\right)+h_i\frac{\partial u}{\partial x}\right|}_{{\mathit{x}}_0}+k_i\frac{\partial u}{\partial y}\right|}_{{\mathit{x}}_0}+\frac{1}{2}{\left[h_i^2\frac{{\partial }^{2}u}{\partial x^2}\right|}_{{\mathit{x}}_0}+2h_i{k}_i\frac{{\partial }^{2}u}{\partial x\partial y}{|}_{{\mathit{x}}_0}+k_i^2\frac{{\partial }^{2}u}{\partial y^2}{|}_{{\mathit{x}}_0}){\delta }_{0,i}{]}^2,$$

(3)

where ${\delta }_i:=\delta (\parallel {\mathit{x}}_0-{\mathit{x}}_i\parallel )$ is some weighting function defined in MLS theory (see [19]). Examples of $\delta$ can be found in [15]. By minimizing expression (3) with respect to the partial derivatives, the linear system $\mathit{AD}=\mathit{b}$ is obtained (see [15]), where

$$\mathit{A}=\left(\begin{array}{cccc}{h}_1& h_2& \dots & h_s\\ k_1& k_2& \dots & k_s\\ ⋮& ⋮& ⋮& ⋮\\ h_1{k}_1& h_2{k}_2& \dots & h_s{k}_s\end{array}\right)\left(\begin{array}{cccc}{\delta }_1^2& & & \\ & {\delta }_2^2& & \\ & & \dots & \\ & & & {\delta }_s^2\end{array}\right)\left(\begin{array}{cccc}{h}_1& k_1& \dots & h_1{k}_1\\ h_2& k_2& \dots & h_2{k}_2\\ ⋮& ⋮& ⋮& ⋮\\ h_s& k_s& \dots & h_s{k}_s\end{array}\right),$$

$${\mathit{D}}^T=\left(\frac{\partial u_0}{\partial x},\frac{\partial u_0}{\partial y},\frac{{\partial }^2{u}_0}{\partial x^2},\frac{{\partial }^2{u}_0}{\partial y^2},\frac{{\partial }^2{u}_0}{\partial x\partial y}\right).$$

and

$$\begin{array}{cc}{\mathit{b}}^T=\hfill & {\displaystyle \left(\sum _{i=1}^s(-u_0+u_i)h_i{\delta }_i^2,\sum _{i=1}^s(-u_0+u_i)k_i{\delta }_i^2,\sum _{i=1}^s(-u_0+u_i)\frac{h_i^2{\delta }_i^2}{2},\right.}\hfill \\ \hfill & {\displaystyle \left.\sum _{i=1}^s(-u_0+u_i)\frac{k_i^2{\delta }_i^2}{2},\sum _{i=1}^s(-u_0+u_i)h_i{k}_i{\delta }_i^2\right).}\hfill \end{array}$$

By solving the above system, the GFD formulae are deduced

$$\begin{array}{cc}\hfill \frac{\partial u}{\partial x}{|}_{{\mathit{x}}_0}=-{\lambda }_{01}& u\left({\mathit{x}}_0\right)+\sum _{i=1}^s{\lambda }_{i1}u\left({\mathit{x}}_i\right),\frac{\partial u}{\partial y}{|}_{{\mathit{x}}_0}=-{\lambda }_{02}u\left({\mathit{x}}_0\right)+\sum _{i=1}^s{\lambda }_{i2}u\left({\mathit{x}}_i\right),\hfill \\ & \mathsf{\Delta }u\left({\mathit{x}}_0\right)=-{\lambda }_{00}u\left({\mathit{x}}_0\right)+\sum _{i=1}^s{\lambda }_{i0}u\left({\mathit{x}}_i\right).\hfill \end{array}$$

(4)

Using the above GFDM formulae, the discretized version of (2) for each time step $j=1,...,J$ is as follows:

$$\left\{\begin{array}{ccc}\hfill & -{\lambda }_{00}{U}_0^j+\sum _{i=1}^s{\lambda }_{i0}{U}_i^j=0,\hfill & \hfill (x_0,y_0)\in \mathsf{\Omega },\\ \hfill & \frac{{\left(U_0^j\right)}^{1/m}-{\left(U_0^{j-1}\right)}^{1/m}}{\mathsf{\Delta }t}=-{\lambda }_{02}{U}_0^{j-1}+\sum _{i=1}^s{\lambda }_{i2}{U}_i^{j-1},\hfill & \hfill (x_0,y_0)\in {\Gamma }_1,\\ \hfill & U_0^j=0,\hfill & \hfill (x_0,y_0)\in {\Gamma }_2.\end{array}\right.$$

(5)

Here, ${\Gamma }_1$ denotes the border $\{y=0,t>0\}$ and ${\Gamma }_2=\partial \mathsf{\Omega }\backslash {\Gamma }_1$. For our computational examples, the domains of Figure 1 are considered, where the distribution of the nodes is irregular. More precisely, ${\Gamma }_1=[-2,2]$ and $\mathsf{\Omega }=[-2,2]\times {\Gamma }_2$. The first mesh is generated in such a way that the number of nodes is higher in the centre, so the numerical solution is more accurate. The second mesh has a very irregular distribution of nodes near the border ${\Gamma }_2.$ The second equation in system (5) is explicit in the time variable, i.e., it only depends on the solution of the numerical method in the previous time step. Therefore, to initialize the numerical method, one uses the solution of

$$\left\{\begin{array}{ccc}\hfill & -{\lambda }_{00}{U}_0^0+\sum _{i=1}^s{\lambda }_{i0}{U}_i^0=0,\hfill & \hfill (x_0,y_0)\in \mathsf{\Omega },\\ \hfill & U_0^0=f^m\left(x_0\right),\hfill & \hfill (x_0,y_0)\in {\Gamma }_1,\\ \hfill & U_0^0=0,\hfill & \hfill (x_0,y_0)\in {\Gamma }_2.\end{array}\right.$$

(6)

For the sake of simplicity, we introduce the following notation: $d_i=\sqrt{h_i^2+k_i^2}$ (with $i\in \{1,\dots ,s\}$) and ${\displaystyle d=\underset{i}{max}\left\{d_i\right\}}$ for each star.

The paper is organized as follows: in Section 2 the order of the local truncation error and the consistency are proved. Using this together with a discrete maximum principle, the existence and uniqueness of solutions to the problem is shown. Section 3 is devoted to the proof of our convergence result. Finally, in Section 4, numerical examples are shown to validate the theoretical results.

2. Local Truncation Error and Consistency

Now, we substitute the solution u of the continuous problem (2) to be solved in the bounded domain $\mathsf{\Omega }$ into the numerical scheme (5) and denote the local truncation error obtained by ${\tau }_i^j$. Let us define

$$A=\underset{i,j}{max}\left|{\tau }_i^j\right|.$$

The next theorem gives the order of the truncation error.

Theorem 1.

Assume that there exist two constants $C_1,C_2>0$ such that $C_1{d}^2<\mathsf{\Delta }t<C_2{d}^2$. The order of the local truncation error is $A=O\left(\mathsf{\Delta }t(d^2+\mathsf{\Delta }t)\right)$.

Proof. 

In all the following the fact that the theoretical solution is smooth enough is taken into consideration.

It is easy to observe that, in the boundary nodes on ${\Gamma }_2$, the local truncation error vanishes due to the imposed hypothesis on the solution. For the interior nodes, it is

$${\tau }_0^j=-{\lambda }_{00}{u}_0^0+\sum _{i=1}^s{\lambda }_{i0}{u}_i^0=\mathsf{\Delta }u(x_0,y_0,t_j)+O\left(d^2\right)=O\left(\mathsf{\Delta }t(d^2+\mathsf{\Delta }t)\right)$$

and for the ${\Gamma }_1$ nodes, it yields

$$\begin{array}{cc}\hfill {\tau }_0^j& =\mathsf{\Delta }t\left(-{\lambda }_{02}{u}_0^j+\sum _{i=1}^s{\lambda }_{i2}{u}_i^j\right)+{\left(u_0^j\right)}^{1/m}-{\left(u_0^{j+1}\right)}^{1/m}\hfill \\ \hfill & =\mathsf{\Delta }t\left(\frac{\partial u}{\partial y}(x_0,y_0,t_j)+O\left(d^2\right)\right)-\mathsf{\Delta }t\left(\frac{\partial u^{1/m}}{\partial t}(x_0,y_0,t_j)+O\left(\mathsf{\Delta }t\right)\right)\hfill \\ \hfill & =O\left(\mathsf{\Delta }t{d}^2\right)+O\left(\mathsf{\Delta }{t}^2\right)=O\left(\mathsf{\Delta }t(d^2+\mathsf{\Delta }t)\right).\hfill \end{array}$$

(7)

□

Define the following variable ${\displaystyle \rho =\underset{x}{max}\left\{f^m\left(x\right)\right\}}$ and denote by $\psi \left(x\right)=x^m$. In order to obtain the existence and uniqueness of the numerical solution $U_i^j$ of (5) we need a discrete maximum principle given by the next theorem.

Theorem 2.

Let $U_i^j$ be a solution of (5) with $m\ge 1$. Define $C(m,f)={\left[m{\left(\rho \right)}^{m-1}\right]}^{-1}$ and assume the following relation $\mathsf{\Delta }t\le C(m,f)d^2$. Then, for every i and j, one has $0\le U_i^j\le \rho .$

Proof. 

A maximum principle can be derived at the boundary nodes because at each time step we have a discrete harmonic extension problem. That is why the interior nodes are automatically smaller than they are. At each time step we proceed by induction. Observe that $0\le U_0^0\le \rho .$ By assuming $0\le U_0^j\le \rho$, we obtain

$${\left(U_0^{j+1}\right)}^{1/m}=\mathsf{\Delta }t\left(-{\lambda }_{02}{U}_0^j+\sum _{i=1}^s{\lambda }_{i2}{U}_i^j\right)+{\left(U_0^j\right)}^{1/m},$$

(8)

and for the new variable $z_i^j={\left(U_0^j\right)}^{1/m},$ it can be obtained

$$z_0^{j+1}=\mathsf{\Delta }t\left(-{\lambda }_{02}{\left(z_0^j\right)}^m+\sum _{i=1}^s{\lambda }_{i2}{\left(z_i^j\right)}^m\right)+z_0^j=\mathsf{\Delta }t\left(-\sum _{i=1}^s{\lambda }_{i2}{\left(z_0^j\right)}^m+\sum _{i=1}^s{\lambda }_{i2}{\left(z_i^j\right)}^m\right)+z_0^j.$$

(9)

By the Mean Value Theorem, ${(z_i^j)}^m-{(z_0^j)}^m=(z_i^j-z_0^j){\psi }^{\prime }\left(\xi \right)$, for some $\xi \in (z_i^j,z_0^j)$, rewrite (9) as

$$z_0^{j+1}={\psi }^{\prime }\left(\xi \right)\mathsf{\Delta }t\sum _{i=1}^s{\lambda }_{i2}{z}_i^j+\left(1-{\psi }^{\prime }\left(\xi \right)\mathsf{\Delta }t\sum _{i=1}^s{\lambda }_{i2}\right)z_0^j.$$

(10)

Thanks to the induction hypothesis and the value of the constant $C(m,f)$, we obtain ${\psi }^{\prime }\left(\xi \right)\mathsf{\Delta }t{\lambda }_{02}\le 1$ and the following estimate holds

$$\begin{array}{cc}\hfill |z_0^{j+1}|& \le {\psi }^{\prime }\left(\xi \right)\mathsf{\Delta }t\sum _{i=1}^s{\lambda }_{i2}|z_i^j|+\left(1-{\psi }^{\prime }\left(\xi \right)\mathsf{\Delta }t\sum _{i=1}^s{\lambda }_{i2}\right)\left|z_0^j\right|\hfill \\ \hfill & \le {\psi }^{\prime }\left(\xi \right)\mathsf{\Delta }t\sum _{i=1}^s{\lambda }_{i2}{\rho }^{1/m}+\left(1-{\psi }^{\prime }\left(\xi \right)\mathsf{\Delta }t\sum _{i=1}^s{\lambda }_{i2}\right){\rho }^{1/m}={\rho }^{1/m}.\hfill \end{array}$$

For $z_0^j\ge 0$ the same result is obtained by performing similar steps. □

At this stage, the result of existence and uniqueness of solution can be presented.

Theorem 3.

Under the restriction $\mathsf{\Delta }t\le C(m,f)d^2,$ the discrete scheme (5) has a unique solution.

Proof. 

Proving the uniqueness of solutions is enough due to the linearity of the system of equations, the existence and the uniqueness are equivalent.

Suppose that there exist two different solutions $U_0^j$ and $V_0^j$ of (5) and we denote with $W_0^j=U_0^j-V_0^j$ the difference between them, which, in principle, is non-zero. It is easy to see that $W_0^0$ satisfies (5) with $f\equiv 0$ and so, by the discrete maximum principle, we obtain $0\le W_0^0\le 0$. Proceeding by induction we obtain $W_0^j=0$; thus, $U_0^j$ and $V_0^j$ coincide and the uniqueness is obtain. □

3. Convergence of the Numerical Solution

With the above results we hereby provide the main result of the article, the convergence of the numerical solution of (5) to the theoretical solution of the Equation (2). The error of the numerical method is given by

$$e_i^j=u(x_i,y_i,t_j)-U_i^j,e^j=\underset{i}{max}\left|e_i^j\right|.$$

Theorem 4.

Let u be the solution to (2) and $U_0^j$ be the solution to system (5) with $m\ge 1$. Assume that there exist two constants $C(m,f)$, $D>0$ such that $D{d}^2\le \mathsf{\Delta }t\le C(m,f)d^2.$ Then,

$$e^j=O(d^2+\mathsf{\Delta }t).$$

Proof. 

The selection for the boundary conditions in ${\Gamma }_2$ in the numerical method produces a zero error as in the local truncation error.

In addition,

$$e^j\le max\{e_{{\Gamma }_1}^j,O\left(d^2\right)\}\le e_{{\Gamma }_1}^j+O\left(d^2\right)$$

because of the approximation for the Laplacian of second order. To compute $e_{{\Gamma }_1}^j$, one has the Equations (7) (the first identity) and (8). Rewriting them in terms of z and $Z_0^j$ and subtracting them the following is obtained

$$\begin{array}{cc}\hfill e_0^{j+1}& =\mathsf{\Delta }t\left[-{\lambda }_{02}\left({(z_0^j)}^m-{(Z_0^j)}^m\right)+\sum _{i=1}^s{\lambda }_{i2}\left({(z_i^j)}^m-{(Z_i^j)}^m\right)\right]+e_0^j-{\tau }_0^n\hfill \\ \hfill & =\mathsf{\Delta }t\left[-{\lambda }_{02}{\psi }^{\prime }\left({\xi }_0\right)e_0^j+\sum _{i=1}^s{\lambda }_{i2}{\psi }^{\prime }\left(x{i}_i\right)e_i^j\right]+e_0^j-{\tau }_0^n,\hfill \end{array}$$

(11)

for some ${\xi }_0\in (z_0^j,Z_0^j)$ and ${\xi }_i\in (z_i^j,Z_i^j)$. Then,

$$e^{j+1}\le e^j(1-\mathsf{\Delta }t{\lambda }_{02}{\psi }^{\prime }\left({\xi }_0\right))+\mathsf{\Delta }t\sum _{i=1}^s{\lambda }_{i2}{\psi }^{\prime }\left({\xi }_i\right)·e^j+A.$$

(12)

There exists a constant (assuming enough regularity of the solution z) $K\ge 0$ such that $|z_0^j-z_i^j|\le Kd$ and $|Z_0^j-Z_i^j|\le Kd$, then since

$$\begin{array}{cc}\hfill {\psi }^{\prime }\left({\xi }_i\right)& =\sum _{l=1}^m{\left[z_i^j\right]}^{m-l}{\left[Z_i^j\right]}^{l-1}\le \sum _{l=1}^m{[z_0^j+Kd]}^{m-l}{[Z_0^j+Kd]}^{l-1}\hfill \\ \hfill & \sum _{l=1}^m{\left[z_0^j\right]}^{m-l}{\left[Z_0^j\right]}^{l-1}+Ld={\psi }^{\prime }\left({\xi }_0\right)+Ld,\hfill \end{array}$$

(13)

we have

$$e^{j+1}\le e^j\left(1-\mathsf{\Delta }t\sum _{i=1}^s{\lambda }_{i2}{\psi }^{\prime }\left({\xi }_0\right)+\sum _{i=1}^s{\lambda }_{i2}{\psi }^{\prime }\left({\xi }_0\right)+\sum _{i=1}^s{\lambda }_{i2}Ld\right)+A=e^j[1+{\lambda }_{02}Ld]+A.$$

(14)

Remember that $(N+1)\mathsf{\Delta }t=T$, where T was the final time and $N+1$ the number of elements in the time discretization. Then, the last expression can be rewritten, since $A=O\left(\mathsf{\Delta }{t}^2\right)$, as

$$\begin{array}{cc}\hfill e^{N+1}& \le e^N\left[1+C\frac{1}{N+1}\right]+R\mathsf{\Delta }{t}^2\le \left[1+C\frac{1}{N+1}\right]\left[e^N+R\mathsf{\Delta }{t}^2\right]\hfill \\ \hfill & \le \left[1+C\frac{1}{N+1}\right]\left[e^{N-1}+R\mathsf{\Delta }{t}^2+R\mathsf{\Delta }{t}^2\right]\hfill \\ \hfill & \le {\left[1+C\frac{1}{N+1}\right]}^2\left[e^{N-1}+2R\mathsf{\Delta }{t}^2\right]\hfill \\ \hfill & \le \dots \le {\left[1+C\frac{1}{N+1}\right]}^{N+1}[e^0+R\mathsf{\Delta }{t}^2].\hfill \end{array}$$

(15)

However, ${(1+C\frac{1}{N+1})}^{N+1}\le e^C$ and $e^0\le D\mathsf{\Delta }{t}^2,$ for some $D>0,$ so $e^{N+1}\le e^C[D\mathsf{\Delta }{t}^2+T\mathsf{\Delta }t]$, and finally $e^{N+1}=O\left(\mathsf{\Delta }t\right)=O(d^2+\mathsf{\Delta }t).$ □

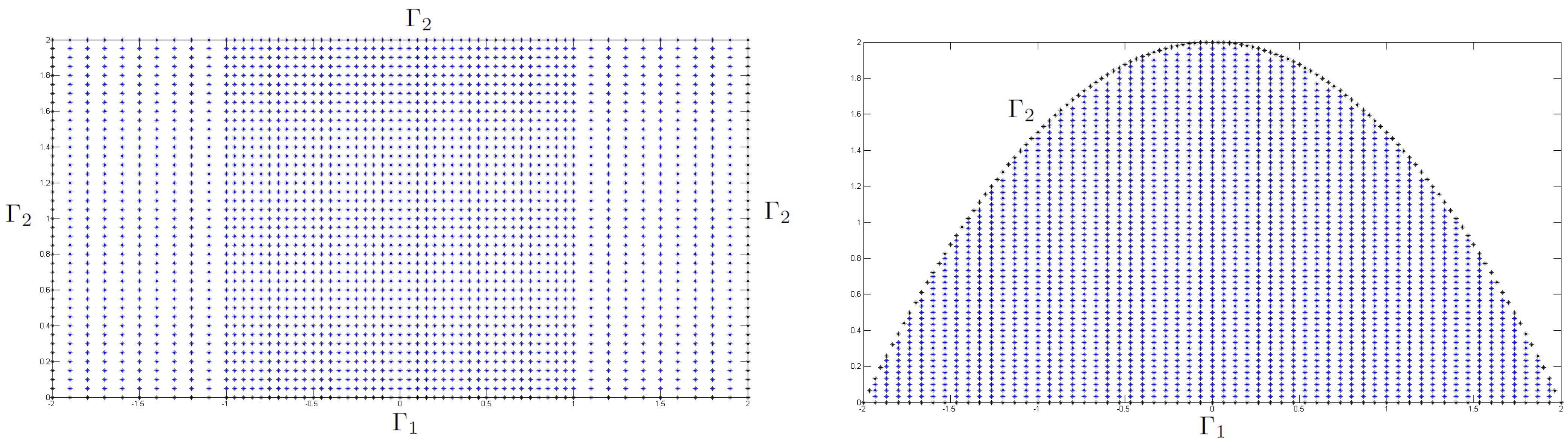
4. Numerical Examples

Two numerical examples using the meshes of Figure 1 are performed in this section. The first one shows that the numerical solution given by the GFDM presents the well-known Barenblatt profiles. In the second, the error is computed using the two formulas:

$$l_2=\sqrt{{\displaystyle \frac{{\displaystyle \sum _{i=1}^P{(W_i-w_i)}^2}}{P}}},l_{\infty }=\underset{i}{max}\left\{\right|W_i-w_i\left|\right\}.$$

Sensitivity analysis for the GFDM were performed in [19], where the authors considered different factors such as number of nodes of the stars, time step and weighting functions $\delta$.

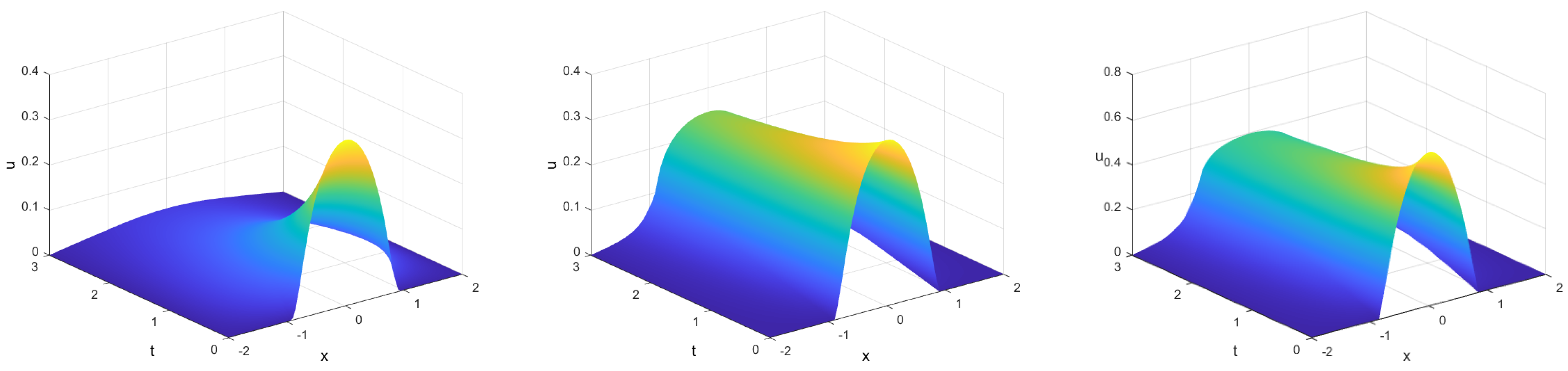
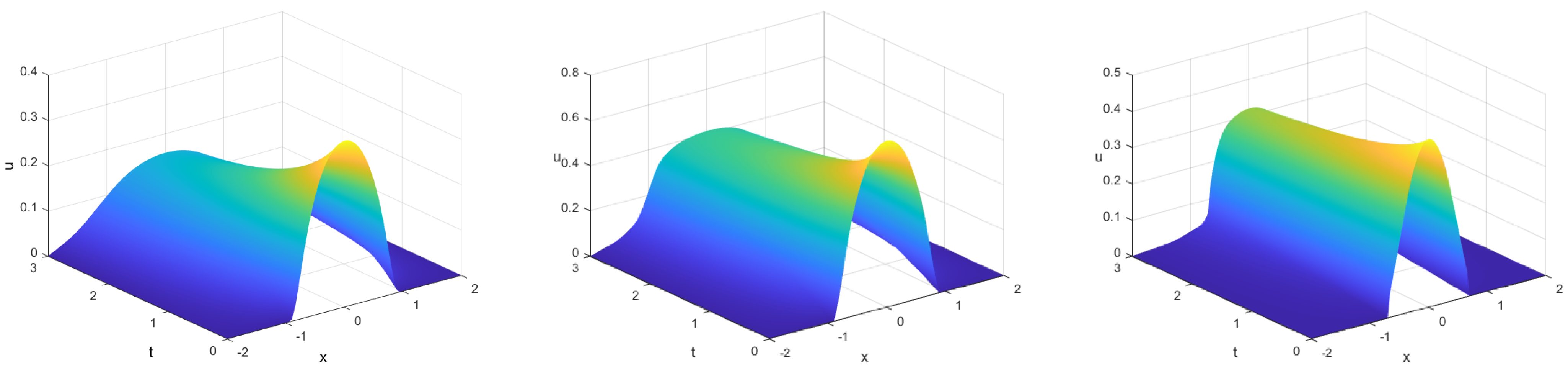
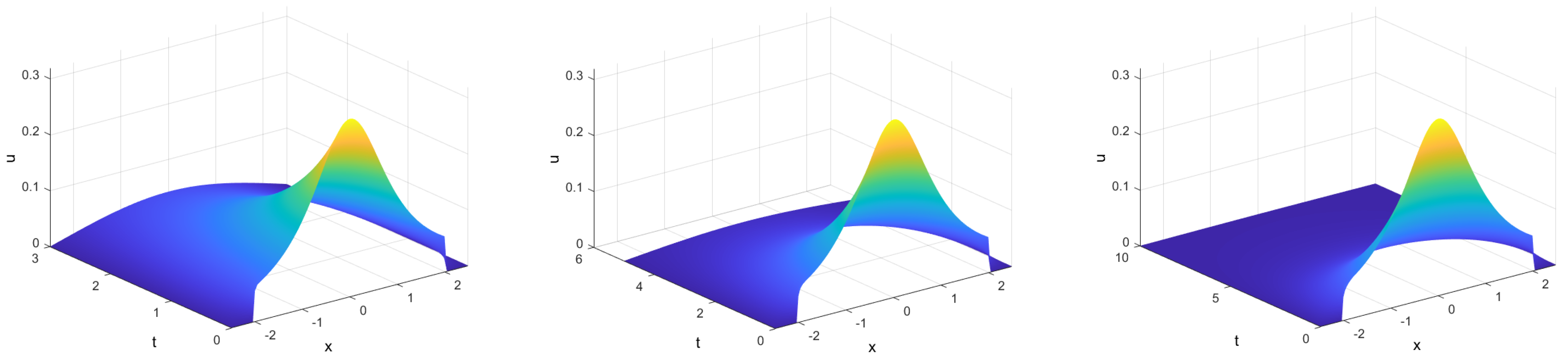
4.1. Example 1: Barenblatt Profiles

In this section we perform several examples showing the application of the described method over the domain given in Figure 1. For our computations we use the initial data

$$w(x,0)=f\left(x\right)=e^{-\frac{1}{(1-x)(1+x)}}{\chi }_{[-1,1]}\left(x\right),$$

where

$${\chi }_{[-1,1]}\left(x\right)=\left\{\begin{array}{ccc}\hfill & 1,\hfill & \hfill x\in [-1,1],\\ & 0,\hfill & \hfill \mathrm{otherwise}.\end{array}\right.$$

Based on the cited reference [6] some Barenblatt profiles as in Vázquez [16] are expected.

In Figure 2 we show the numerical solutions for three different values of m ($m=1,3$ and 5) for the rectangular domain of Figure 1. As expected, the slow diffusion occurs when m increases. Similarly, Figure 3 contains the cases $m=2,4$ and 10 for the parabolic domain of Figure 1.

4.2. Example 2

For the following example we consider $m=1$ and $f\left(x\right)=\frac{1}{\pi }\frac{1}{{\left|x\right|}^2+1}$ in $[-2,2]$. The exact solution is

$$w(x,t)=\frac{1}{\pi }\frac{t+1}{{\left|x\right|}^2+{(t+1)}^2},$$

(see [6,20]). The errors of the numerical method are shown in

Table 1. $l^2$ and $l^{\infty }$ norms of the errors in Example 2.

$\mathit{t}\left(\mathit{s}\right)$	3	5	10
$l_2$	$3.7489\times {10}^{-2}$	$3.9929\times {10}^{-2}$	$3.7068\times {10}^{-2}$
$l_{\infty }$	$6.2268\times {10}^{-2}$	$6.2268\times {10}^{-2}$	$6.2268\times {10}^{-2}$

for times $t=3,5$ and 10 s.

In order to obtain a general idea of the performance of the scheme, in [6] the author obtained an error of order $4.329\times {10}^{-4}$ in our second example. In [7], the authors solved a similar equation with a forcing term and a time Caputo fractional derivative obtaining $5.28\times {10}^{-2}$ and $1.50\times {10}^{-2}$ errors for small space steps $\mathsf{\Delta }x=\mathsf{\Delta }y$. The numerical solution given the GFDM are plotted in Figure 4 for times $t=3,5$ and 10.

5. Conclusions and Future Work

The aim of this paper is to study the main properties of the discrete solution given by the generalized finite difference method of the porous media problem (1) with fractional laplacian. To do so, the Silvestre–Caffarelli extension is used. The numerical solution given by the GFDM allows us to discretize the new computational domain with an irregular distribution of nodes.

The order of the truncation error is obtained as well as a discrete maximum principle. Under some conditions in the time step, the convergence of the GFDM scheme is proved. Finally, some numerical examples are given, showing the application of the proposed scheme for solving this fractional porous media equation.

Some possible lines of future work are the following:

• The extension of the proposed method for higher dimensional settings.
• The application of the above procedure for solving the fractional laplacian equation.