Abstract
Given a connected graph , a set is said to be a k-metric generator for G if any pair of different vertices in is distinguished by at least k elements of S. A metric generator of minimum cardinality among all k-metric generators is called a k-metric basis and its cardinality is the k-metric dimension of G. We initially present a linear programming problem that describes the problem of finding the k-metric dimension and a k-metric basis of a graph G. Then we conducted a study on the k-metric dimension of a unicyclic graph.
1. Introduction
Given a graph , we say that a vertex distinguishes two different vertices , if , where denotes the length of a shortest path. A set is said to be a k-metric generator for G if and only if for any pair of different vertices , there exist at least k vertices such that
In other words, a set is a k-metric generator for G if and only if for any pair of vertices of G there exist at least k vertices in S that distinguish it. The k-metric dimension of G, denoted by , is the minimum cardinality among all k-metric generator for G. Any k-metric generator with cardinality is called a k-metric basis of G.
These concepts were introduced, in the context of graph theory, by Estrada-Moreno et al. in [1], as a generalization of the well-known concept of metric dimension in graphs. In particular, for is when these concepts correspond to the original theory of metric dimension introduced independently by Harary and Melter in [2] and Slater in [3]. However, the particular case of had also been previously defined in [4]. Recent studies on the k-metric dimension of a graph can be consulted in [1,5,6,7,8,9]. Independently of the aforementioned articles, k-metric dimension was studied in [10,11,12] with a computer science oriented approach. More recently, based on the generalization given for k-metric dimension, k-partition dimension was introduced in [13] as a generalization of partition dimension previously defined in [14].
The theory of the metric dimension of a space general metric space was introduced in 1953 in [15] and it was not until 20 years later that it attracted attention in the context of graph theory. Recently, the theory of metric dimension was developed further for general metric spaces in [16]. However, it was also generalized for the k-metric dimension in the context of general metric spaces in [17]. Again, in the context of graph theory, the concept of k-metric dimension was generalized for a more general metric than the standard distance in graphs in [18]. A particular case of this general metric, known as the adjacency distance, had already been studied previously in [19].
Metric generators for a graph, for the particular case of , were shown to have a high number of applications in real life. In particular, in those problems that can be represented as graphs and it is also necessary that each vertex be uniquely identified with respect to the rest of the vertices of the graph. Example of this kind of applications is the navigation of robots in networks [20]. However, it was shown in [1] that the metric generators, in their primary version, have a weakness for the case where some of the sensors located in the network, used to guide the robots, fail. Therefore, in order to guarantee that the robots are not lost within the network when one of their sensors fails, it is necessary to place the sensors on vertices that belong to k-metric generators, for some . The higher the value of k, the more security we provide to the network, but we may also incur additional costs. The k-metric generators, for , have also been shown to have application in theory of error correcting codes which was presented in [21]. As k-metric generators are studied in depth, new applications of this concept of graph theory may emerge.
The problem of finding the k-metric dimension and a k-metric basis for a graph can be given in terms of an integer programming problem. Let G be a connected graph with and let be the distance matrix of G, where . Given a binary variable for , we define the objective function F by
The integer programming problem would then be minimizing F subject to the following constraints
Please note that the set , for any given assignment A to the n binary variables , is a k-metric generator for G if and only if the constraints are satisfied by A. Since and F is minimum, we conclude that S is also k-metric basis of G and F is the k-metric dimension.
The previous integer programming problem has been proven to be NP-hard in [9,22]. Even for a more general metric than standard distance in graphs, it has been proven in [18] that the problem is also NP-hard, for any odd k. Therefore, it would be convenient in order to solve the problem either to use approximate methods, such as heuristics or metaheuristics, or to determine closed formulae, or bounds, for the k-metric dimension of certain families of graphs. In this article, we work on the second of the research lines. However, presenting the original problem in terms of an integer programming problem can motivate researchers in the area of operations research to work on the first of the research lines in order to solve this problem mainly in graphs with a complex structure.
We present now some additional terminology and notation. If two vertices are adjacent in , then we write or we say that . Given we define to be the (open) neighbourhood of x in G, i.e., . The closed neighbourhood, denoted by , equals . If there is no ambiguity, we will simply write or . Two vertices are called false twin if and are called true twin if . Two vertices are twin if they are false twin vertices or true twin vertices. In this work, the remainder definitions will be introduced whenever a concept is needed.
A unicyclic graph is a connected graph containing exactly one cycle. This article is dedicated to the study of the k-metric dimension of unicyclic graphs. The paper is organised in the following way: Section 2 is devoted to the study of the values of k for which there is a k-metric basis for some unicyclic graphs while in Section 3, we obtain closed formulae for the k-metric dimension of some unicyclic graphs.
2. k-Metric Dimensional Graphs
In this section, we tackle the problem of finding the largest integer k such that there exists a k-metric generator for some unicyclic graphs. We say that a graph G is k-metric dimensional if k is the largest integer such that there exists a k-metric basis of G. Notice that if G is a k-metric dimensional graph, then for each positive integer , there exists at least one r-metric basis of G.
Next, we give a characterization of k-metric dimensional graphs. To do so, we need some additional terminology. Given two vertices , we say that the set of distinctive vertices of is
Theorem 1
([1]).A connected graph G is k-metric dimensional if and only if
In particular, the case of cycles was analysed in the following result.
Proposition 1
([1]).Let be a cycle graph of order n. If n is odd, then is -metric dimensional and if n is even, then is -metric dimensional.
Although it has been shown in [9] that can be computed in polynomial time for any graph, it is sometimes interesting to consider this value for some particular cases of graphs.
k-Metric Dimensional Unicyclic Graphs
From now on, we consider some notations for a unicyclic graph G. Let C be the cycle of G, that is, the subgraph of G induced by the vertices that form the single cycle of G. Let be the vertex set of C. In this context, we shall assume that for every , where the subscripts are taken modulo s. Given , we define as the tree rooted in , obtained by removing from G the two neighbours of belonging to C. Please note that a rooted tree, such as the one defined, may be trivial. A unicyclic graph G is said to be type 1 if the following conditions are satisfied:
- (a)
- For every we have .
- (b)
- For every such that , we have is a path.
- (c)
- There exists at least such that .
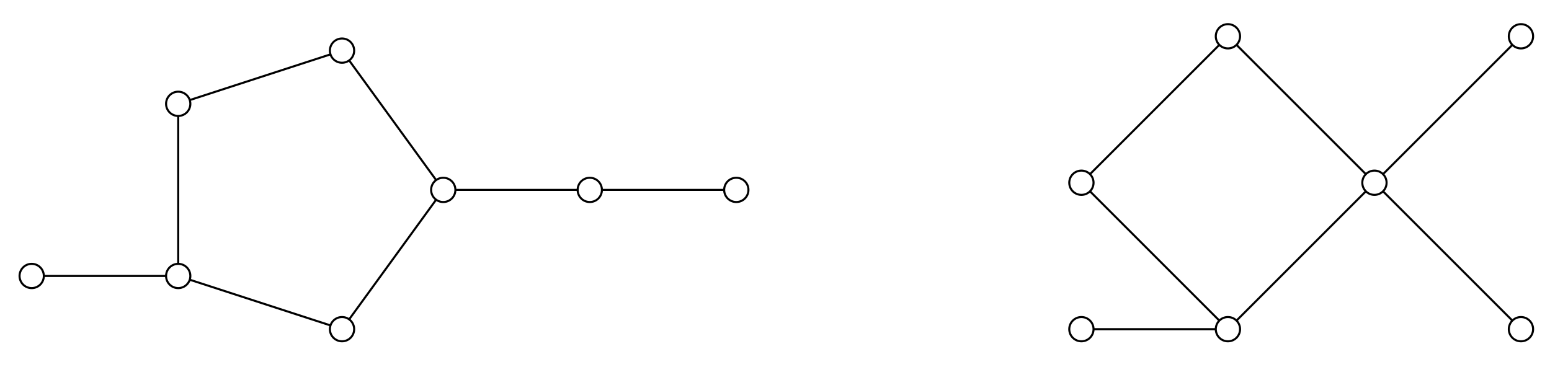
We said that G is type 2 if G is not a cycle and it is not type 1. In Figure 1, we show an example of each type of unicyclic graph.
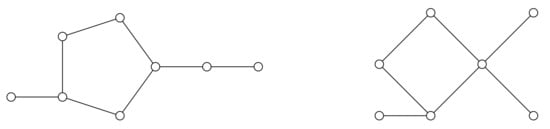
Figure 1.
The graph on the left is type 1, and the one on the right is type 2.
Let G be a unicyclic graph of type 1 with odd cycle C. We define the following parameter for G
Let and be the order of the tree rooted in . Let j be an integer such that . We define the following sets for every :
From the previous sets we define the parameters
Let be two subsets of U. A vertex belong to if there exists another vertex such that and . A vertex belong to if there exists another vertex such that and . If , then we define , otherwise, . Analogously, if , then we define , otherwise, . From these two parameters, we introduce
Finally, we define
Proposition 2.
Any unicyclic graph of type 1 with odd cycle is-metric dimensional.
Proof.
Let G be a unicyclic graph of type 1 with odd cycle and order n. Given we consider , where and for . In this context, the subscripts that refer to the vertices of cycle C, as well as their respective rooted paths, will be taken modulo s. We now consider four cases:
- Case 1.
- , with . These vertices are distinguished by the elements of with at most one exception. This exception happens when , where considering . Hence, either or .
- Case 2.
- . If , then , otherwise, . Thus, if , then .
- Case 3.
- and , with and . Recall that diameter of odd cycle C is . We consider two subcases for :
- Subcase 3.1.
- . In this case and . If , then , and considering for any , it follows that . Analogously, if , then . Thus, if , then either or , and as a consequence, .
- Subcase 3.2.
- . Now . Please note that . If , then are distinguished by elements of with at most one exception. This exception is when , where . Thus, if , then . Suppose now that . If , then and, if , then the vertices . Thus, .
- Case 4.
- and , with . In this case and . Without loss of generality we assume that . We analyse the next subcases:
- Subcase 4.1.
- . If , then , otherwise, . Hence, in this case .
- Subcase 4.2.
- . If , then any vertex in distinguishes with at most one exception given when , which implies that . If , then any vertex in distinguishes with the exception of vertices in , where is the only vertex in such that , and as a consequence, . If , then for we have that , while if it follows that . In this case , which implies .
Since by Theorem 1, we conclude that G is -metric dimensional. □
We next discuss the case when G is a unicyclic graph of type 1 such that whose cycle C is even. To this end, we will introduce some parameters as we did with the case where C was odd:
Please note that in this case and are antipodal vertices of C. Given we define
and
Proposition 3.
Any unicyclic graph of type 1 with even cycle is -metric dimensional.
Proof.
Let G be a unicyclic graph of type 1 with even cycle and order n. Given we consider , where and for . We now consider three cases:
- Case 1.
- . This case is analogous to Case 1 of Proposition 2.
- Case 2.
- . If , then , otherwise, . If , then since , we have that .
- Case 3.
- and . Notice that diameter of cycle C is . Given we consider two subcases for the pairs of the form :
- Subcase 3.1.
- . In this case . Notice that . If , then . Please note that for any which implies . Analogously, if , then and . Thus, , where or.
- Subcase 3.2.
- . Now . Please note that . If , then are distinguished by elements of with at most the exception when . Thus, if , then either or . If , then for and for . Thus, .
- Case 4.
- and , with . In this case and . Without loss of generality we assume that . We analyse the next subcases:
- Subcase 4.1.
- . If , then , otherwise, . Hence, in this case .
- Subcase 4.2.
- If , then any vertex in distinguishes with at most one exception given when , which implies that . If , then any vertex in distinguishes with at most the exception, when , of vertices in , where are the only vertices in such that and , and as a consequence, . If , then for we have that , while if it follows that . In this case , which implies .
Since by Theorem 1, we conclude that G is -metric dimensional. □
3. The k-Metric Dimension of Unicyclic Graphs
To begin this section, we present some results and definitions that were given previously in [1]. Later, in Section 3, we give some closed formulae for the unicyclic graphs that fulfil certain properties.
From the fact that every pair of vertices is distinguished only by the elements of , we deduce the following Lemma given in [1].
Lemma 1
([1]).If, then for any k-metric basis B we have that.
Next we give an important bound given in [1].
Theorem 2
([1]).Let G be a k-metric dimensional graph different from a path. Then for any,
Now we introduce some definitions that will be useful to us to prove our next results. A vertex of degree at least three in a graph G will be called a major vertex of G. Any end-vertex (a vertex of degree one) u of G is said to be a terminal vertex of a major vertex v of G if for every other major vertex w of G. The terminal degree of a major vertex v is the number of terminal vertices of v. A major vertex v of G is an exterior major vertex of G if its terminal degree is positive. Let be the set of exterior major vertices of G whose terminal degree is greater than one.
Given and a terminal vertex of w, we denote by the shortest path that starts at and ends at w. Let be the length of . Now, given and the set of terminal vertices of w, we define . Please note that by definition of exterior major vertex, is obtained by concatenating the paths and , where w is the only vertex of degree greater than two lying on these paths.
Now we present a lower bound for the r-metric dimension of any k-metric dimensional graph. To do so, we first define the following function for any exterior major vertex and any .
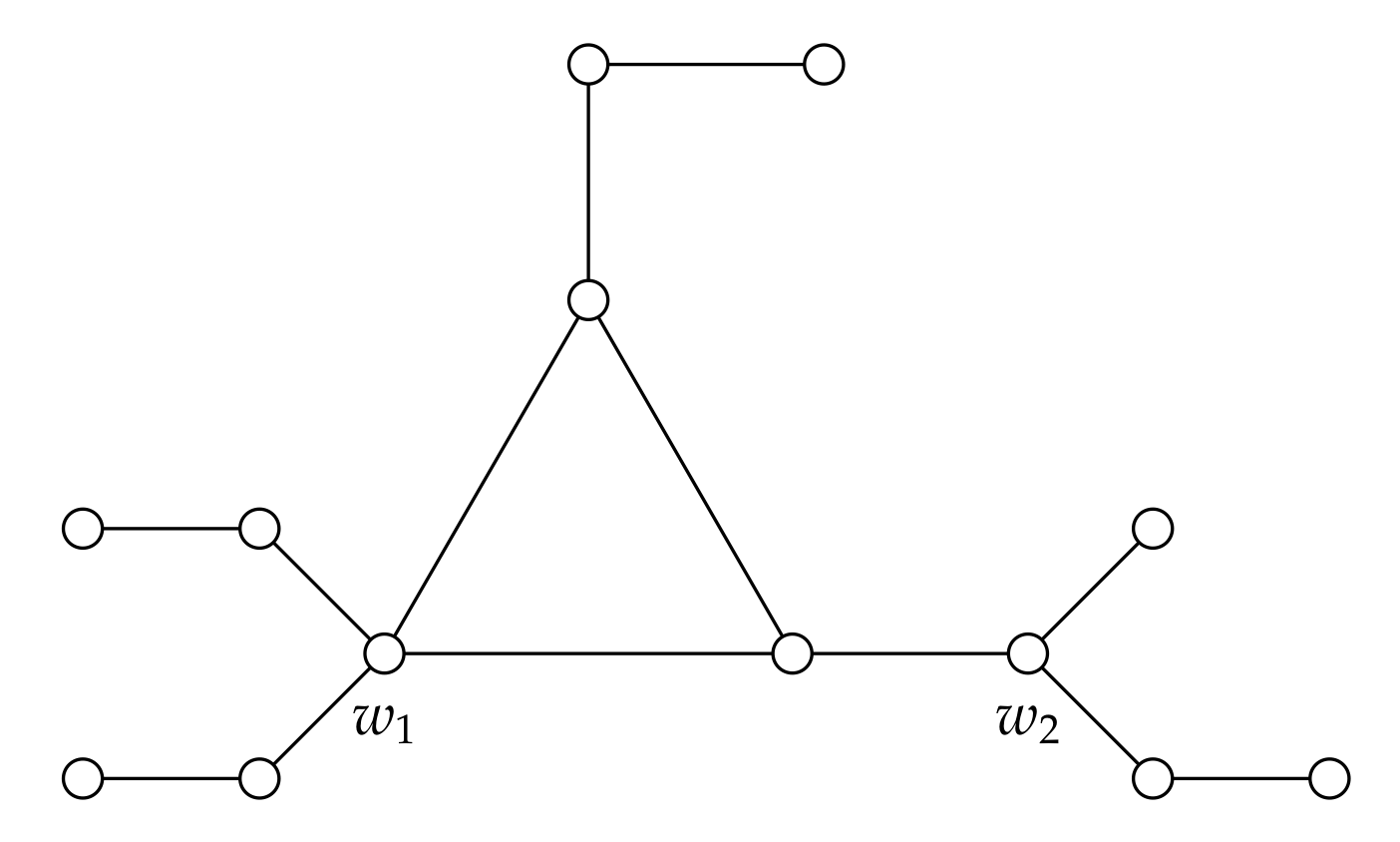
In order to clarify the previous formula for the vertices that belong to the set , we will use the graph G given in Figure 2. In this case, are the only exterior major vertices with terminal degree at least two, and as a consequence, . In both cases these vertices have terminal degree 2, and . Hence, , , and . Analogously, .
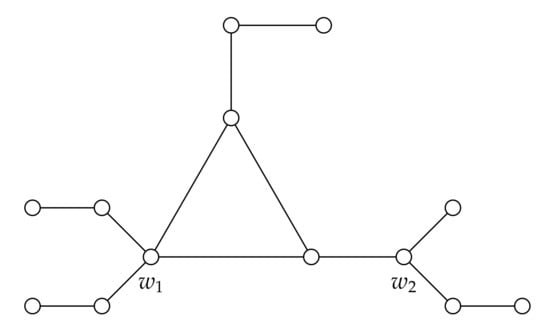
Figure 2.
A unicyclic graph G where , , , and .
Theorem 3
([1]).If G is a k-metric dimensional graph such that , then for every ,
The tightness of the previous bound is shown in [1] for the case of the tree different from path. We present, in Theorem 6, that this bound is reached for some unicyclic graphs.
Closed Formulae for the k-Metric Dimension of Some Unicyclic Graphs
Proposition 4.
Let be cycle graph of order n.
- (i)
- If n is even, then
- for every .
- for every .
- (ii)
- If n is odd, then
- for every .
Proof.
By Proposition 1, we have that if n is odd is -metric dimensional, otherwise is -metric dimensional. Thus, if n is odd, then exists for and, if n is even, then exists for . On the other hand, by Theorem 2, we have that . We now consider two cases for computing :
- Case 1.
- n is odd. For any pair of vertices there exist only one vertex such that w does not distinguish u and v. Hence, for every such that and every pair there exists at least k element of S which distinguish . Thus, S is a k-metric generator for and, consequently, . Therefore, .
- Case 2.
- n is even. In this case, is 2-antipodal (The diameter of is defined as ). We say that u and v are antipodal vertices or mutually antipodal if . We recall that is 2-antipodal if for each vertex there exists exactly one vertex such that ). For any pair of vertices , such that , we can take a vertex x such that . Therefore, , where x and y are antipodal vertices. On the other hand, if is odd, then . Now, we analyse two subcases:
- Subcase 2.1.
- . Let be a path in . Since there are no two antipodal vertices on P. Thus, for any pair of vertices there exists at most only one vertex such that w does not distinguish u and v. Therefore, P is k-metric generator for and, consequently, . Therefore, .
- Subcase 2.2.
- . Since , for any such that , there exist at least two antipodal vertices , which leads there exist at least two vertices which are not distinguish by . Hence, if , then , and as consequence, . On the other hand, since each pair of vertices of is distinguished by with at most the exception of two vertices, every such that , is a k-metric generator for . Therefore, , which implies .
□
Theorem 4.
Let G be a unicyclic graph of type 1 whose cycle C is of odd order s. If there exists only one vertex such that whose rooted tree T is the order r, then for any
Proof.
By Proposition 2, we have that G is -metric dimensional graph for , and as a consequence, exists. Let be the vertex set of C such that . We consider, without loss of generality, and , where and for . Since by Theorem 2, we have and , and also considering that and are a metric generator and a 2-metric generator for G, respectively, we deduce and .
From now on, we assume that . Keep the following facts in mind
- .
- .
- .
Let be a k-metric basis of G. First, suppose that k is odd. Since , there exists such that and . Given , and , if , then as we need to take at least vertices of for distinguishing at least k times the pairs and , we conclude that . If , then at least I have to choose the vertices in , and at least vertices of to distinguish at least k times the pairs and , and consequently, . Now, suppose k is even. By an analysis analogous to the previous one, and considering , if , then , otherwise .
We now define the following sets for each case considered in our result:
- (a)
- For k odd and , we consider. Please note that .
- (b)
- For k odd and , we consider . Please note that .
- (c)
- For k even and , we consider . Please note that .
- (d)
- For k even and , we consider .
We claim, in the cases (a)–(d), that the respective sets previously defined are k-metric generator for G. In this context, we will consider and we only make distinctions where necessary. We now analyse three cases:
- Case 1.
- . These vertices are distinguished by the elements of with at most one exception. Assume that . If , then . Since , we deduce are distinguished by at least k elements of S.
- Case 2.
- . If , then and, if , then . Since for any pair of vertices such that does not distinguish it, we have distinguish it, and also considering , in this case we are done. The rest of the pairs of vertices are distinguished by the vertices of with the exception of one vertex of . Thus, in this case which implies each pair in is distinguished by at least k elements of S.
- Case 3.
- and . Recall that diameter of cycle C is . We consider two subcases for the pairs of the form :
- Subcase 3.1.
- . In this case . Notice that . If , then . Please note that for any j. Analogously, if , thenand for any j. Since and , we conclude, each pair is distinguished by k elements of S.
- Subcase 3.2.
- . In this case , and . If we suppose , then are distinguished by elements of with at most one exception. This exception happens when , where we have . Thus, if , then . Suppose now that . If , then and, if , then . Hence, again . In any case are distinguished by at least k elements of S.
Therefore, S, in each case, is a k-metric generator for G, and as a consequence, . □
Theorem 5.
Let G be a unicyclic graph of type 1 whose cycle C is of even order s. If there exists only one vertex such that whose rooted tree T is the order r, then for any
Proof.
By Proposition 3, we have that G is -metric dimensional graph for , and as a consequence, exists. Let be the vertex set of C such that . We consider, without loss of generality, and , where and for . Let be a k-metric basis of G.
First, suppose that and . Since are twin vertices, by Lemma 1, we have that . Since the pair is not distinguished by , there exist two vertices in which belonging to and, consequently, . Since is a 2-metric generator for G, we conclude that and, consequently, .
From now on, we consider or . Keep the following facts in mind
- .
- .
- .
First, suppose that k is odd. Since , there exists such that and . Given , and , if , then as we need to take at least vertices of for distinguishing at least k times the pairs and , we conclude that . If , then at least I have to choose the r vertices in , and at least vertices of to distinguish at least k times the pairs and , and consequently, . Now, suppose k is even. By an analysis analogous to the previous one, and considering , if , then , otherwise . We now define the following sets for each case considered in our result:
- (a)
- For k odd and , we consider. Please note that .
- (b)
- For k odd and , we consider . Please note that .
- (c)
- For k even and , we consider . Please note that .
- (d)
- For k even and , we consider .
We claim, in the cases (a)–(d), that the respective sets previously defined are k-metric generator for G. In this context, we will consider and we only make distinctions where necessary. We now analyse three cases:
- Case 1.
- . These vertices are distinguished by the elements of with at most one exception. This exception happens when , where assuming . Since , each pair in is distinguished by at least k elements of S.
- Case 2.
- . These vertices are distinguished by the elements of with at most two exceptions. These exceptions happen when , where . Since for any pair of vertices such that does not distinguish it, we have distinguish it, and also considering , in this case we are done. The rest of the pairs of vertices are distinguished by the vertices of with the exception of two vertices of . Please note that only if . However, if , then . Otherwise, since , we deduce each pair in is distinguished by at least k elements of S.
- Case 3.
- and . Recall that diameter of cycle C is . We consider two subcases for the pairs of the form :
- Subcase 3.1.
- . In this case . Notice that . If , then . Please note that for any j. Analogously, if , then and for any j. Since and , we conclude, each pair is distinguished by k elements of S.
- Subcase 3.2.
- . Now . Please note that . If then, are distinguished by elements of with at most one exception. This exception happens when , where . Hence, . Now, suppose that . If , then . If , then , and as a consequence, . In any other case, .
Therefore, S, in each case, is a k-metric generator for G, and as a consequence, . □
We say a vertex v of a unicyclic graph G is transcendental if and only if or the tree T rooted in v is not a path. We will denote by the set of transcendental vertices of G.
Theorem 6.
Let G be a k-metric dimensional unicyclic graph such that . If for any vertex such that and its rooted tree is a path we have and , where and , then for every ,
Proof.
By Theorem 3 it follows that . Since , we deduce . For every , we assume is a terminal vertex of w such that . Let be the set of terminal vertices of w. Now, for every , let the path and we consider the set given by:
and for ,
Let and . Since for every it follows that and , we obtain that . Furthermore, notice that for every , such that we have and, if , then we have . On the other hand, for any vertex , the tree T rooted in v holds . We claim that S is an r-metric generator for G. For any two distinct vertices we consider the following cases.
- Case 1.
- , where . If is a tree different from a path, then , and it was proved in [1], are distinguished by r vertices of . If is a path and is not a leaf of this path, then , and as a consequence, are distinguished by at least r vertices of . Suppose that is a path and is a leaf of this path. In this case are distinguished by the elements of with at most the exception of one vertex of which happens when . Since , for any vertex with tree rooted in a, we have every vertex in distinguishes which implies that they are distinguished by r vertices of S.
- Case 2.
- . Since there exists at most two vertices do not distinguish and , we have there exists a vertex that distinguishes . Hence, are distinguished by at least r vertices , where is the tree rooted in a.
- Case 3.
- and , where . In this case we consider two subcases:
- Subcase 3.1.
- . If is not a path or , then any vertex distinguishes . Thus, are distinguished by r elements of S. Suppose now that is a path and . By premise we have and , where and . Since or , there exists a vertex that distinguishes . Hence, they are distinguished by at least r vertices , where is the tree rooted in a.
- Subcase 3.2.
- . If , then are distinguished by elements of with at most the exception of when . Thus, are distinguished by at least r vertices , where is the tree rooted in any vertex . If , then at most two vertices of do not distinguish . Since , we have there exists a vertex that distinguishes , which implies they are distinguished by at least r vertices , where is the tree rooted in a.
- Case 4.
- and , where and are not trivial graphs. In this case, at most two vertices of do not distinguish . Since , we have there exists a vertex that distinguishes , which implies they are distinguished by at least r vertices , where is the tree rooted in a.
Therefore, , and the result follows. □
4. Conclusions and Open Problems
This article is a contribution to the theory k-metric dimension in graph. In particular, we study this invariant for unicyclic graph. In our study, we obtain closed formulae to determine the largest value of k for which there is a k-metric generator of a unicyclic graph of type 1. Finally, we give closed formulae for k-metric dimension of unicycle graphs of type 1 with a single vertex of degree three and for unicycle graphs of type 2 with at least three transcendental vertices and that satisfy a specific property for those vertices of the cycle with degree 3 and whose rooted tree is a path.
Some open problems have emerged from the study carried out. For instance, we highlight the following.
- (a)
- It would be interesting to characterize all graphs that satisfy the formula given in Theorem 6. For instance, the graph in Figure 2 satisfies this formula, however it does not satisfy the premises given in Theorem 6.
- (b)
- We gave a closed formula for the k-metric dimension of a particular family of unicyclic graphs of type 1. Therefore, it would be convenient to see if it is possible to obtain closed formulae or to be able to bound the k-metric dimension of the rest of the unicyclic graphs of type 1.
- (c)
- Since the optimization problem of finding k-metric dimension is NP-hard, it would be interesting to devise polynomial-time algorithm for families of unicyclic graphs or to develop heuristics that allow estimating as accurately as possible this parameter for these families.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The author declares no conflict of interest.
References
- Estrada-Moreno, A.; Rodríguez-Velázquez, J.A.; Yero, I.G. The k-metric dimension of a graph. Appl. Math. Inf. Sci. 2015, 9, 2829–2840. [Google Scholar]
- Harary, F.; Melter, R.A. On the metric dimension of a graph. Ars Comb. 1976, 2, 191–195. [Google Scholar]
- Slater, P.J. Leaves of trees. Congr. Numer. 1975, 14, 549–559. [Google Scholar]
- Hernando, C.; Mora, M.; Slater, P.J.; Wood, D.R. Fault-tolerant metric dimension of graphs. In Convexity in Discrete Structures; Changat, M., Klavzar, S., Mulder, H.M., Vijayakumar, A., Eds.; Number 5 in RMS Lecture Notes Series; Ramanujan Mathematical Society, National College: Tiruchirappalli, India, 2008; pp. 81–85. [Google Scholar]
- Estrada-Moreno, A.; Yero, I.; Rodríguez-Velázquez, J.A. The k-metric dimension of the lexicographic product of graphs. Discret. Math. 2016, 339, 1924–1934. [Google Scholar] [CrossRef]
- Estrada-Moreno, A.; Yero, I.G.; Rodríguez-Velázquez, J.A. k-metric resolvability in graphs. Electron. Notes Discret. Math. 2014, 46, 121–128. [Google Scholar] [CrossRef]
- Estrada-Moreno, A.; Yero, I.G.; Rodríguez-Velázquez, J.A. The k-Metric Dimension of Corona Product Graphs. Bull. Malays. Math. Sci. Soc. 2016, 39, 135–156. [Google Scholar] [CrossRef][Green Version]
- Corregidor, S.G.; Martínez-Pérez, Á. A note on k-metric dimensional graphs. Discret. Appl. Math. 2021, 289, 523–533. [Google Scholar] [CrossRef]
- Yero, I.G.; Estrada-Moreno, A.; Rodríguez-Velázquez, J.A. Computing the k-metric dimension of graphs. Appl. Math. Comput. 2017, 300, 60–69. [Google Scholar] [CrossRef]
- Adar, R.; Epstein, L. Models for the k-metric dimension. arXiv 2014, arXiv:1410.4209. [Google Scholar]
- Adar, R.; Epstein, L. The weighted 2-metric dimension of trees in the non-landmarks model. Discret. Optim. 2015, 17, 123–135. [Google Scholar] [CrossRef]
- Adar, R.; Epstein, L. The k-metric dimension. J. Comb. Optim. 2017, 34, 1–30. [Google Scholar] [CrossRef]
- Estrada-Moreno, A. On the k-partition dimension of graphs. Theor. Comput. Sci. 2020, 806, 42–52. [Google Scholar] [CrossRef]
- Chartrand, G.; Salehi, E.; Zhang, P. The partition dimension of a graph. Aequationes Math. 2000, 59, 45–54. [Google Scholar] [CrossRef]
- Blumenthal, L.M. Theory and Applications of Distance Geometry; Oxford University Press: Oxford, UK, 1953; p. 347. [Google Scholar]
- Bau, S.; Beardon, A.F. The Metric Dimension of Metric Spaces. Comput. Methods Funct. Theory 2013, 13, 295–305. [Google Scholar] [CrossRef]
- Beardon, A.F.; Rodríguez-Velázquez, J.A. The k-Metric Dimension of Metric Spaces. Ars Math. Contemp. 2019, 16, 25–38. [Google Scholar] [CrossRef]
- Estrada-Moreno, A.; Yero, I.; Rodríguez-Velázquez, J. On The (k,t)-Metric Dimension Of Graphs. Comput. J. 2021, 64, 707–720. [Google Scholar] [CrossRef]
- Estrada-Moreno, A.; Ramírez-Cruz, Y.; Rodríguez-Velázquez, J.A. On the adjacency dimension of graphs. Appl. Anal. Discret. Math. 2016, 10, 102–127. [Google Scholar] [CrossRef]
- Khuller, S.; Raghavachari, B.; Rosenfeld, A. Landmarks in graphs. Discret. Appl. Math. 1996, 70, 217–229. [Google Scholar] [CrossRef]
- Bailey, R.F.; Yero, I.G. Error-correcting codes from k-resolving sets. Discuss. Math. 2019, 39, 341–355. [Google Scholar] [CrossRef]
- Schmitz, Y.; Vietz, D.; Wanke, E. A note on the complexity of k-Metric Dimension. arXiv 2021, arXiv:2101.12018. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).