A Fractional-Order Chaotic Sparrow Search Algorithm for Enhancement of Long Distance Iris Image

Abstract

At present, iris recognition has been widely used as a biometrics-based security enhancement technology. However, in some application scenarios where a long-distance camera is used, due to the limitations of equipment and environment, the collected iris images cannot achieve the ideal image quality for recognition. To solve this problem, we proposed a modified sparrow search algorithm (SSA) called chaotic pareto sparrow search algorithm (CPSSA) in this paper. First, fractional-order chaos is introduced to enhance the diversity of the population of sparrows. Second, we introduce the Pareto distribution to modify the positions of finders and scroungers in the SSA. These can not only ensure global convergence, but also effectively avoid the local optimum issue. Third, based on the traditional contrast limited adaptive histogram equalization (CLAHE) method, CPSSA is used to find the best clipping limit value to limit the contrast. The standard deviation, edge content, and entropy are introduced into the fitness function to evaluate the enhancement effect of the iris image. The clipping values vary with the pictures, which can produce a better enhancement effect. The simulation results based on the 12 benchmark functions show that the proposed CPSSA is superior to the traditional SSA, particle swarm optimization algorithm (PSO), and artificial bee colony algorithm (ABC). Finally, CPSSA is applied to enhance the long-distance iris images to demonstrate its robustness. Experiment results show that CPSSA is more efficient for practical engineering applications. It can significantly improve the image contrast, enrich the image details, and improve the accuracy of iris recognition.

1. Introduction

1.1. Research Background

Biometric identification has became an important approach to protect information security. It uses the human body’s biologic characteristics such as iris, face, vein, and fingerprint recognition. Among these, iris images offer some excellent characteristics for identity recognition, such as uniqueness, stability, contactless, and anti-counterfeiting. At present, iris authentication and recognition is one of the most secure and reliable biometric technologies [1].

In the applications of long-distance iris recognition, the quality of iris image is generally lower than that of traditional cooperative iris image due to the constraints of acquisition environment and human cooperation [2]. Low-quality iris images have low contrast, unclear details, and some noise. These are inferior for identity recognition due to the loss of some texture information [3]. On the other hand, the iris edge and pupil center may not be accurately located. This will lead to iris segmentation errors, bring difficulties to subsequent image analysis and affect the accuracy of iris recognition [4]. Therefore, the enhancement of iris image is necessary to provide more effective features for feature detection and recognition. However, the iris image enhancement is quite different from the traditional image enhancement. It not only needs to enhance the visual clarity, but also requires the enhanced image to have good performance in detection and recognition [5].

Generally, the process of biometric recognition is generally divided in four steps, i.e., image acquisition, image preprocessing, feature extraction, and feature matching. Image enhancement is a critical part of image preprocessing and plays an important role in computer vision, pattern recognition, and other fields. The purpose of image enhancement is to enhance the appearance of the image by correcting the image in order to produce an intuitive, vivid, and suitable image for further image analysis [6].

Among the existing methods, histogram equalization (HE) is one of the most widely used algorithm in image enhancement [7]. It can improve the appearance of the image by stretching the histogram for satisfying the image contrast [8]. Histogram stretching is designed based on the gray grouping method, which can be applied to images with low contrast and low brightness. It has advantages with respect to the high efficiency and simplicity. Although it is an effective method in iris image enhancement technology [9], if there is a high peak in the histogram, it may unfortunately over-enhance the image [10]. In order to overcome the above problems, many researchers have developed some local enhancement methods. For instance, the adaptive histogram equalization (AHE) [11] and the contrast-limited adaptive histogram equalization algorithm (CLAHE) [12] are two classical and most recent advances in this field. In AHE, the local information is considered while enhancing the image. Thus, it can enhance textures and details of the image. Then, the image could have contained sharper edges. However, this method produces a lot of noise and needs long computation time. On the basis of AHE, the histogram of each sub-image is limited by CLAHE. The noise generated by AHE is reduced so that the image contrast will be more vivid. However, the clipping value in the CLAHE cannot be selected adaptively. In [13], Vidya et al. proposed a novel triangular fuzzy membership (TFM) function-based CLAHE (TFM-CLAHE) to solve this problem. The algorithm has good effect on the iris, face, fingerprint, and other biological images. However, the work in [13] only uses some objective indicators such as Peak Signal Noise Ratio (PSNR), Mean Square Error (MSE), and Average Information Content (AIC) to evaluate the effect of TFM-CLAHE.

1.2. Related Works

In order to solve the above problems, in recent years, many researchers have developed different swarm intelligence (SI) optimization algorithms for image enhancement, such as particle swarm optimization algorithm [14], and immune algorithm [15]. Table 1 summarizes several newly published related works.

Table 1. Swarm intelligence optimization algorithms for image enhancement.

Authors	Algorithms	Strategy
Maurya et al. [16]	Cuckoo search (CS) algorithm	CSA is used to balance the contrast and brightness
Nickfarjam et al. [17]	Modified PSO algorithm	Consists of the standard deviation and edge content
Sathiyabhama, B et al. [18]	Gray wolf optimizer algorithm	Improve with rough set theory
Qin et al. X [19]	Modified PSO algorithm	A modified inertia weight function used in the PSO
Acharya et al. [20]	Modified genetic (GA) algorithm	Adaptive histogram equalization technique used in the GA
Muniyappan et al. [21]	Adaptive genetic algorithm	Introduce adaptive crossover and mutation operations in GA
Bhandari et al. [22]	CS algorithm	Improve the contrast of low-contrast image using CSA
Kamoona et al. [23]	Modified CS algorithm	Image transform enhancement functions and objective function
Prasath et al. [24]	Modified CS algorithm	Distance-Oriented Cuckoo Search (DOCS) algorithm
Sridevi et al. [25]	Modified genetic algorithm	Fractional Genetic Algorithm
Chen et al. [26]	Artificial bee colony algorithm	A new fitness function and new image transformation function
Banharnsakun et al. [27]	Artificial bee colony algorithm	Image edge detection enhancement using ABC algorithm

As can be seen from Table 1, for this hot research field, many SI optimization algorithms have been used to enhance various types of images. This type of algorithm has advantages such as simple implementation and easy expansion. They have attracted increasing attention from the related research community. Among them, a sparrow search algorithm (SSA) proposed by Xue and Shen in 2020 is a novel SI optimization algorithm [28]. Compared with other SI optimization algorithms, SSA has higher search accuracy, faster convergence speed, better stability, and stronger robustness. However, like other swarm intelligence optimization algorithms, SSA is also prone to fall into a local optimum. At present, there are some other efforts trying to improve the SSA. For example, Liu et al. [29] used the chaos to strengthen the diversity of the population and use Cauchy–Gaussian mutation to avoid obvious local optimization. Zhou et al. [30] modified the location update of scrounger by introducing GA strategy to achieve a higher convergence rate than the traditional SSA. Therefore, using a modified SSA to enhance the long-distance iris image so as to improve its recognition accuracy has a potential application value.

1.3. Contributions

In this paper, we further propose an innovative modified sparrow search algorithm named chaotic pareto sparrow search algorithm (CPSSA) to enhance the long-distance iris image. The algorithm includes the following steps:

(1)

The population is initialized by fractional chaotic mapping to make the initial individual sparrows distributed as evenly as possible.

(2)

The locations of the finder and scroungers are updated with the Pareto distribution to speed up its global convergence and to avoid falling into a local optimum.

(3)

The standard deviation, edge content, and entropy are integrated into the evaluation function to assess the enhancement effect of the obtained iris image.

Through the simulation experiments based on 12 benchmark test functions, we have validated and verified that the performance of accuracy and stability of CPSSA are much better than the original SSA, PSO, and ABC. Furthermore, the CPSSA algorithm is successfully applied to long-distance iris image enhancement, where our experimental results show that among all the algorithms tested in this paper, the CPSSA has the best performance. The recognition rate of the enhanced iris image has been significantly improved. The rest of this paper is organized as follows. Section 2 represents details of the modified SSA. Section 3 shows the results of the CPSSA based on the benchmark function, and the experimental results for enhancing the long-distance iris image are carried out. Section 4 summarizes the complete analysis and concludes the paper.

2. Methods

2.1. The Sparrow Search Algorithm

In nature, as social birds, sparrows have three roles for the division of labor in the population: finders, scroungers, and scouts. Finders are sparrows who are looking for food. Scroungers are other sparrows who use the position of finders to get food. Scouts are sparrows who are watching for danger. Among them, the finders and the scroungers can convert roles between each other. However, the proportion remains constant. Finders generally account for 10–20% of the population. As the guide of foraging, finders search a wide range and constantly update their position to obtain the foods while the scroungers continue to forage with the finders to attain a status of a higher fitness. However, due to the threats of predators at any time, 10–20% sparrows in the population will be selected randomly as scouts. Scouts will give off a warning signal to the population immediately when a danger occurs. Then, the whole population will be in an anti-predator state. In the SSA, the sparrow foraging process is simulated to obtain the solution of the optimization problem. Assuming that there are N sparrows in a D-dimensional search space, the position of the ith sparrow in the D-dimensional search space is $X_i=\left[x_{i1},\dots ,x_{ij},\dots ,x_{iD}\right]$, where $i=1,2,\cdots ,N$.

The position of the finders is updated with

$$x_{ij}^{t+1}=\left\{\begin{array}{c}{x}_{ij}^{t}exp\left(\frac{-i}{\alpha MaxCycle}\right),R_2<ST\hfill \\ x_{ij}^t+QL,R_2\ge ST\hfill \end{array}\right.$$

(1)

where t indicates the current iteration, $j=1,2,\cdots ,D$. $MaxCycle$ represents the maximum number of iterations. $\alpha \in (0,1]$ is a random number, and $R_2\in \left[0,1\right]$ and $ST\in \left[0.5,1\right]$ indicates the alarm value and the safety threshold, respectively. Q is a random number subject to standard normal distribution. L is a matrix of $1\times D$ and the elements are initialized to 1.

The position update formula for the scrounger is described as

$$X_{i,j}^{t+1}=\left\{\begin{array}{c}Qexp\left(\frac{x_{\mathrm{worst}}^t-x_{ij}^t}{i^2}\right),if,i>N/2\hfill \\ X_P^{t+1}+\left|X_{i,j}^t-X_P^{t+1}\right|A^{+}L,otherwise\hfill \end{array}\right.$$

(2)

where $X_P^{t+1}$ represents the best position of the finders at iteration $t+1$ and $x_{\mathrm{worst}}^t$ represents the current global worst location. A is a matrix of $1\times D$. All the elements inside matrix A are assigned 1 or $-1$, randomly. $A^{+}=A^T{\left(A{A}^T\right)}^{-1}$.

Moreover, the location of the scouts is updated by

$$X_{i,j}^{t+1}=\left\{\begin{array}{c}{X}_{\mathrm{best}}^t+\beta ·\left|X_{i,j}^t-X_{\mathrm{best}}^t\right|,\mathrm{if}{f}_i>f_g\hfill \\ X_{i,j}^t+K·\left(\frac{\left|X_{i,j}^t-X_{\mathrm{worst}}^t\right|}{\left(f_i-f_w\right)+\epsilon }\right),\mathrm{if}{f}_i=f_g\hfill \end{array}\right.$$

(3)

where $X_{best}$ is the best position at iteration t. $\beta$ is a random number with a normal distribution, for which an average value is 0 and a variance is 1. It works as a step size control parameter. $f_i$, $f_g$, and $f_w$ represent the current sparrow fitness value, the best fitness value, and the worst fitness value, respectively. K is a random number between $-1$ and 1. $ϵ$ is a very small constant to avoid zero-division-error.

2.2. Chaotic Pareto Sparrow Search Algorithm

2.2.1. Initializing Population with Fractional Chaotic Sequence

Chaos, as a universal nonlinear phenomenon in nature, is widely applied to the optimization search problem because the chaotic variables have the characteristics of randomness, ergodicity, and regularity. It can not only effectively maintain the diversity of the population, but also help the algorithm jump out of the local optimization and improve the global search ability [31]. Fractional order chaos can produce chaotic sequences with more uniform ergodicity and faster convergence speed [32]. He et al. [32] proposed a fractional-order 2D-SIMM chaotic system, which is given by Equation (4):

$$\left\{\begin{array}{c}{}^C{\Delta }_{t_0}^q{x}_1\left(t\right)=asin\left(\omega x_2(t+q-1)\right)sin(b/x_1(t+q-1))-x_1(t+q-1)\hfill \\ {}^C{\Delta }_{t_0}^q{x}_2\left(t\right)=asin\left(\omega x_1(t+q)\right)sin(b/x_2(t+q-1))-x_2(t+q-1)\hfill \end{array}\right.$$

(4)

where a, b, and $\omega$ are the system parameters; $a,b,\omega \in (0,+\infty )$, $t\in \mathbb{R}$; and ${}^C{\Delta }_{t_0}^q$ is the Caputo-like fractional difference. Definitions regarding ${}^C{\Delta }_{t_0}^q$ are presented in Definitions 1 and 2.

Definition 1

([33]). Suppose that $u:{\mathbb{N}}_{t_0}\to \mathbb{R}$, the discrete fractional-order integral with order q ($q>0$) is defined as

$${\Delta }_{t_0}^{-q}u\left(t\right):=\frac{1}{\Gamma \left(q\right)}\sum _{s=t_0}^{t-q}{(t-\sigma \left(s\right))}^{(q-1)}u\left(s\right),$$

(5)

where $t\in \mathbb{R}$ and $t_0$ is the start time, $\Gamma \left(q\right)$ is the Gamma function, and $t^{\left(q\right)}$ is the falling factoria.

For the Gamma function, it is defined by $\Gamma \left(q\right)={\int }_0^{+\infty }{e}^{q-1}{e}^{-t}dt$. When $\sigma \left(s\right)=s+1$, the falling factoria is given by

$$t^{\left(q\right)}=\frac{\Gamma (t+1)}{\Gamma (t+1-q)}.$$

(6)

Definition 2

([33]). For $q>0,q\notin \mathbb{N}$ and $u\left(t\right)$ defined on ${\mathbb{N}}_{t_0}$, the fractional-order Caputo-like delta difference is defined as

$$\begin{array}{c}\hfill \begin{array}{cc}{}^C{\Delta }_{t_0}^{q}u\left(t\right)\hfill & :={\Delta }_{t_0}^{-(m-q)}{\Delta }^{m}u\left(t\right)\hfill \\ & =\frac{1}{\Gamma (m-q)}{\displaystyle \sum _{s=t_0}^{t-(m-q)}}{(t-\sigma (s\left)\right)}^{(m-q-1)}{\Delta }^{m}u\left(s\right)\hfill \end{array},\end{array}$$

(7)

where $t\in {\mathbb{N}}_{t_0+m-q}$, q is the fractional difference order, and $m=\lceil q\rceil$.

As a result, the numerical solution of this system is given as [32]

$$\left\{\begin{array}{c}{x}_1\left(i+1\right)=x_1\left(0\right)+\frac{1}{\Gamma \left(q\right)}{\displaystyle \sum _{j=1}^{i+1}}\frac{\Gamma \left(i-j+q\right)}{\Gamma \left(i-j+1\right)}\left[asin\left(\omega x_2\left(j-1\right)\right)sin\left(\frac{b}{x_1\left(j-1\right)}\right)-x_1\left(j-1\right)\right]\hfill \\ x_2\left(i+1\right)=x_2\left(0\right)+\frac{1}{\Gamma \left(q\right)}{\displaystyle \sum _{j=1}^{i+1}}\frac{\Gamma \left(i-j+q\right)}{\Gamma \left(i-j+1\right)}\left[asin\left(\omega x_1\left(j-1\right)\right)sin\left(\frac{b}{x_2\left(j-1\right)}\right)-x_2\left(j-1\right)\right]\hfill \end{array}\right.,$$

(8)

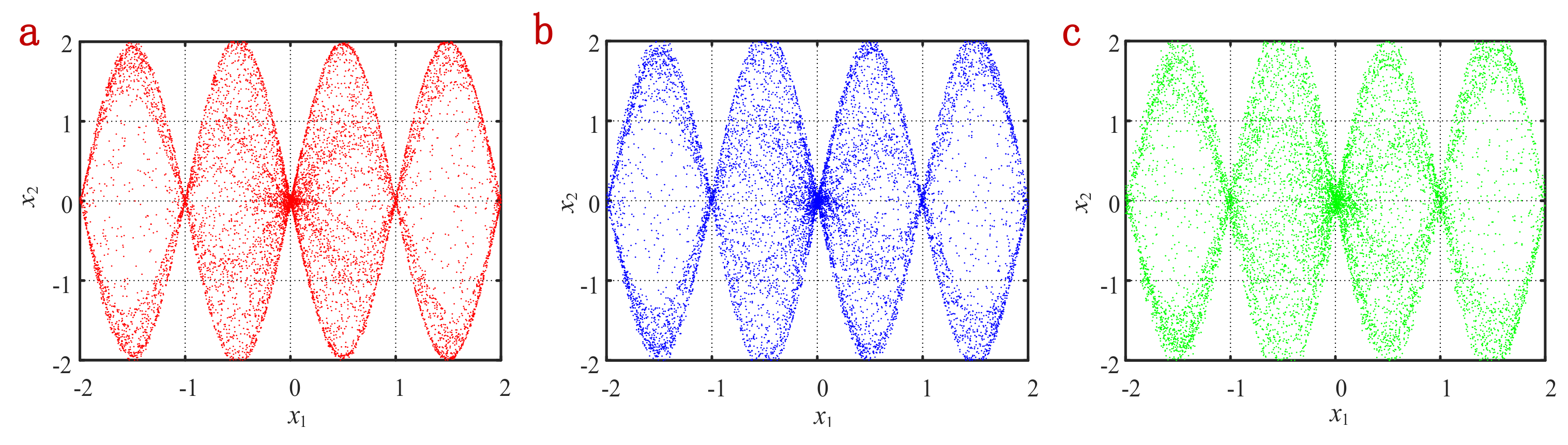
where $q\in (0,1]$, and $\Gamma \left(·\right)$ is the gamma function. Let $a=2$, $b=3$, and $\omega =\pi$, the  phase diagrams are shown in Figure 1.

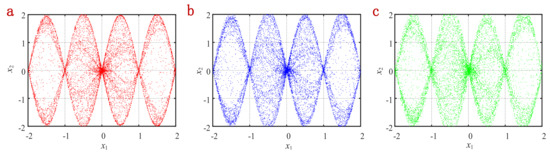
Figure 1. Phase diagrams of the fractional 2D-SIMM with different derivative orders. (a) $q=0.98$. (b) $q=0.95$. (c) $q=0.9$.

The process of initializing population with fractional chaotic sequence is as follows:

(1)

Let $a=2$, $b=3$, $\omega =\pi$, and $q=0.9$.

(2)

Two chaotic sequences $x_1$ or $x_2$ are generated by Equation (8).

(3)

Take one of the chaotic sequences in step 2, for instance, $x_1$, and map it to the solution space of the problem to be solved.

Thus, the newly generated chaotic sequence Z is used as the initial value of sparrow population, which is given by

$$Z=lb+\left(ub-lb\right)x_1$$

(9)

where $ub$ and $lb$ are the maximum and minimum value of the problem to be solved, respectively.

2.2.2. Updating Finders’ and Scroungers’ Locations

In the classical sparrow algorithm, when $R_2<ST$, the location update of the finder is related to the maximum number of iterations. The more iteration it runs, the better the results it yields. However, it certainly needs more computation time. According to the optimization method proposed in [34], the Pareto distribution is very useful for finders’ location. If the cumulative distribution function of a random variable has the following expression, it is said to obey the Pareto distribution [34].

$$F\left(x_3\right)=\left\{\begin{array}{c}1-{\left(\frac{k}{x_3}\right)}^h,x_3\ge k\hfill \\ 0,x_3<k\hfill \end{array}\right.$$

(10)

where $k>0$ is the scale parameter and $h>0$ is the shape parameter which indicates the Pareto’s index of inequality.

We can use Pareto distribution to improve the position of the finders in the SSA when $R_2<ST$. The formula is given by

$$x_{ij}^{t+1}=\left\{{}_{x_{ij}^t+QL,R_2\ge ST}^{x_{ij}^t+\alpha \otimes Pareto(k,h)\otimes (x_i^t-x_{best}),R_2<ST}\right.$$

(11)

where $Pareto\left(k,h\right)$ represents a random number drawn from the Pareto distribution.

When scroungers in SSA are close to the optimal position, the algorithm can converge rapidly. However, this will reduce the variety of the sparrow community, and the algorithm result is more likely to sink into a local optimum. The Pareto distribution is helpful for the algorithm to escape the local optimum [35]. Therefore, the updating position formula of the scroungers in SSA is modified, which is given by

$$x_{ij}^{t+1}=\left\{\begin{array}{c}Q·exp\left(\frac{x_{wj}^t-x_{ij}^t}{i^2}\right),i>n/2\hfill \\ x_{ij}^t+\alpha \otimes Pareto(k,h)\otimes (x_i^t-x_{best}),\mathrm{otherwise}\hfill \end{array}\right..$$

(12)

2.3. Overview of CLAHE

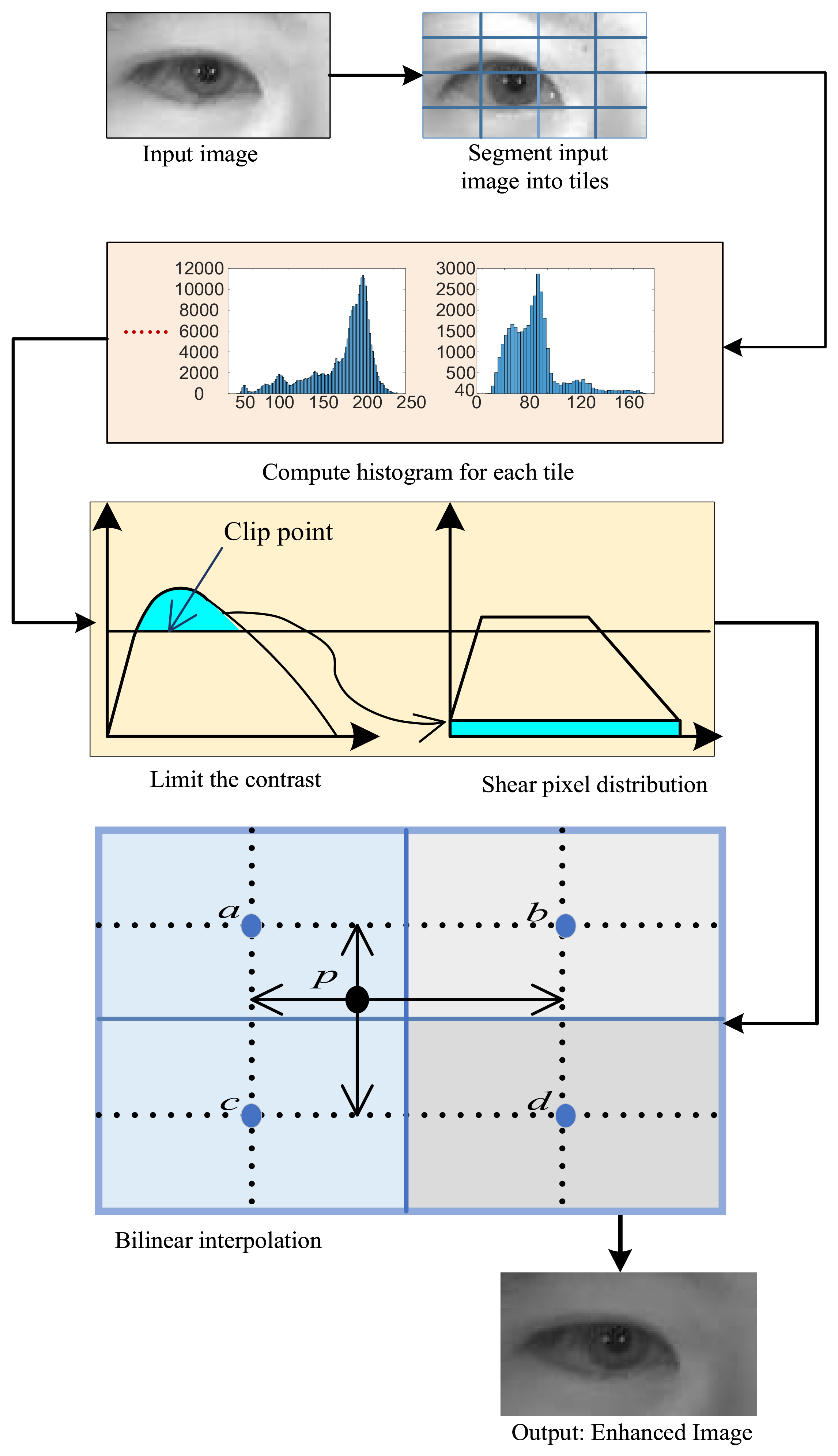
The contrast constrained adaptive histogram equalization (CLAHE) is an algorithm based on limited contrast enhancement range technology and local histogram equalization. Compared with the HE, CLAHE can restraint picture distortion and reduce the noise. CLAHE clips the pixels higher than a certain threshold L in the local histogram. As a result, the clipped parts are evenly distributed into the histogram to limit the amplitude of the histogram [34]. The first step of the local histogram equalization indicates that the image is divided into subimages. Then, histogram equalization is performed for each subimage. There are three ways to divide the image into subimages: non-overlapping, overlapping, and partial overlapping. Considering the computation speed and the difficulty of implementation, this paper selects the non-overlapping method. Because the non-overlapping subimages will produce a block effect in image reconstruction, bilinear interpolation technology can be used to solve the block effect problem in CLAHE. The flow chart of CLAHE is simply represented in Figure 2.

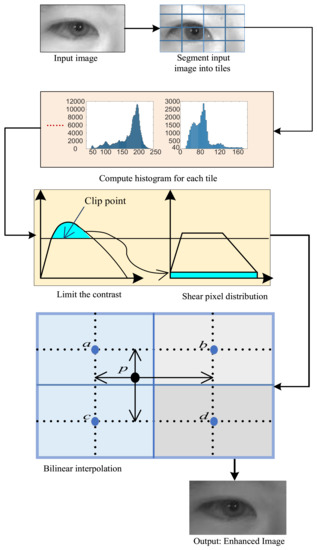
Figure 2. Flow chart of CLAHE.

In this paper, we use the modified sparrow search algorithm to search for the best clip limit value. Then, we cut the histogram and limited the contrast to realize the detail enhancement of the iris image. The clipping limit values vary with the images, which can produce a better enhancement effect.

2.4. CPSSA-CLAHE

The main novelty of our algorithm is to use the CPSSA to adaptively select the optimal clipping limit value of the CLAHE algorithm so that we can improve and enhance the details of the iris image.

2.4.1. The Pseudocode

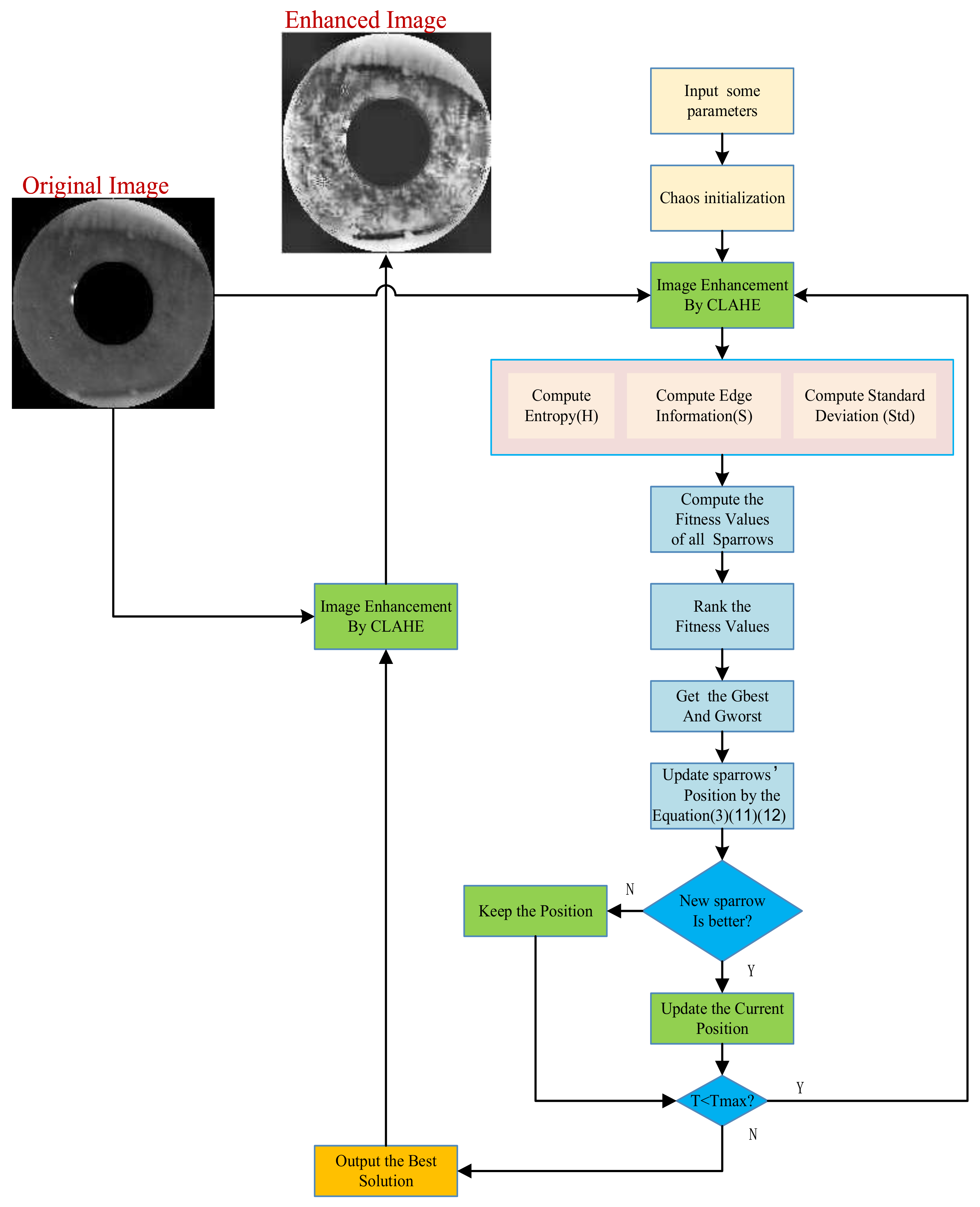
The pseudocode for enhancing long-distance iris images by using the CPSSA-CLAHE technique is presented in Algorithm 1.

The flowchart of the Algorithm 1 is shown in Figure 3.

Algorithm 1 CPSSA-CLAHE

Input: Biometric images, number of subimages, range of clip limit, the alarm value $ST$, the maximum iterations $T_{max}$, the number of sparrows n, the number of finders $Fd$, number of threatened sparrows $Sd$

Output: A CPSSA-CLAHE enhanced biometric image

1: Initializing population with fractional chaotic sequence

2: while $t<T_{max}$ do

3:        According to the location of each sparrow, that is, the clip limit, enhance the image using CLAHE

4:        Compute Entropy(H), Edge Content(S), and Standard Deviation (Std) of the enhanced image

5:        Get the fitness values of all sparrows.

6:        Sort the fitness values.

7:        Get the current best location (Gbest) and the current worst location (Gworst).

8:        Update the location of sparrow by using Equations (3), (11) and (12)

9:        Get the current new location;

10:       If the new location is better than before, update it;

11:       $t=t+1$

12: Get the best clip limit.

13: Output the enhanced image using CLAHE

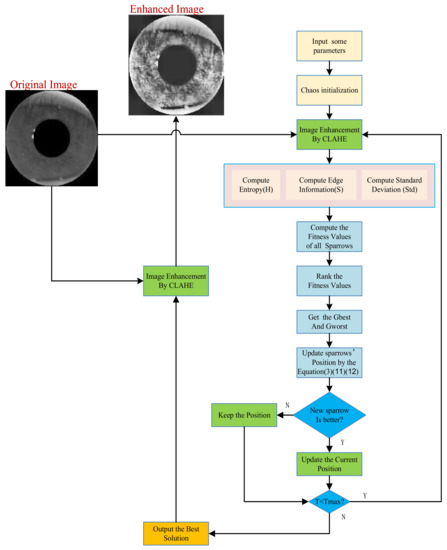
Figure 3. The flowchart of CPSSA-CLAHE.

2.4.2. The Fitness Function

In Algorithm 1, the fitness function value of each sparrow is used to assess the enhancement effect of the image. Long-distance iris images have some features about obscure texture details and low contrast. Therefore, after enhancement by the CPSSA, the enhanced iris image should contain a large amount of information, clear texture, and high contrast. Therefore, we use a multi-objective maximization Equation (10) in the fitness function of CPSSA:

$$Obj=W_{1}H+W_{2}S+W_{3}Std,$$

(13)

where $W_1$, $W_2$, and $W_3$ are constants representing the relative importance weightings of the objective function. Herein, to obtain a more balanced enhancement result, these three performance indexes have equal weights, that is, $W_1=W_2=W_3=1/3$.

In Equation (13), H is the entropy value. The greater the entropy H of the image is, the greater the amount of information contained in the image will be. It is defined as

$$H=-\sum _{i=0}^{255}p\left(i\right){log}_2\left[p\left(i\right)\right],$$

(14)

where $p\left(i\right)$ represents the proportion of pixels with the gray value i.

S is edge content. It represents the amount of edge detail information. A Sobel operator is used to extract the edge pixels from the image [22]. The evaluation function of the amount of edge detail information can be expressed as

$$S=log\left(log\left(E\left(I_s\right)\right)\right)\times \frac{n_e}{r\times c},$$

(15)

where $I_s$ represents the edge graph extracted by Sobel operator, $E\left(I_s\right)$ represents the sum of the intensities of all edge pixels, $n_e$ represents the total number of image edge pixels, and $r\times c$ represents the image size. $Std$ is the gray standard variance of the test image. Usually, the bigger Std value is, the better the contrast of the enhanced picture holds and the more suitable for people would be to examine.

3. Experiments and Discussion

In order to verify the performance of CPSSA, we have carried out the benchmark function comparison experiments, long-distance iris image enhancement experiments, and the respective comparison experiments. The benchmark function comparison experiment aims to verify the general performance improvement of CPSSA. The iris image enhancement experiment aims to test the feasibility of applying CPSSA to long-distance iris image enhancement. The comparative experiment aims to verify the superiority of the CPSSA compared with the traditional image enhancement schemes, such as histogram equalization (HE), AHE, CLAHE, etc. The experiments are run on a desktop PC with 3.20 GHz CPU and 16GB memory.The software used include Windows 10 and MATLAB 2021a.

3.1. Benchmark Function Comparison Experiment

In order to verify the performance of the CPSSA algorithm, we conducted the independent experiments 30 times based on 12 different types of benchmark test functions [36]. There are 4 high-dimensional unimodal functions F1–F4, 3 high-dimensional multimodal functions F5–F7, and 5 low-dimensional multimodal functions F8–F12. They are presented in Table 2, where ‘Type 1’ means unimodal benchmark functions, ‘Type 2’ means Multimodal benchmark functions, and ‘Type 3’ means fixed dimension multimodal functions.

Table 2. Benchmark test functions.

Type	Benchmark Functions	Dim	Range	${\mathit{F}}_{\mathit{min}}$
Type 1	$F_1\left(x\right)={\displaystyle \sum _{i=1}^n}{x}_i^2$	30	[−100, 100]	0
Type 1	$F_2\left(x\right)={\displaystyle \sum _{i=1}^n}\left|x_i\right|+{\displaystyle \prod _{i=1}^n}\left|x_i\right|$	30	[−10, 10]	0
Type 1	$F_3\left(x\right)={\displaystyle \sum _{i=1}^n}{\left({\displaystyle \sum _{j-1}^i}{x}_j\right)}^2$	30	[−100, 100]	0
Type 1	$F_4\left(x\right)={\displaystyle \sum _{i=1}^n}{\left(\left[x_i+0.5\right]\right)}^2$	30	[−100, 100]	0
Type 2	$F_5\left(x\right)={\displaystyle \sum _{i=1}^n}-x_{i}sin\left(\sqrt{\left|x_i\right|}\right)$	30	[−500, 500]	$-418.9829\times n$
Type 2	$\begin{array}{c}{F}_6\left(x\right)=\frac{\pi }{n}\left\{10sin\left(\pi y_1\right)\right.+{\left(y_n-1\right)}^2\hfill \\ +\left.{\displaystyle \sum _{i=1}^{n-1}}{\left(y_i-1\right)}^2\left[1+10{sin}^2\left(\pi y_{i+1}\right)\right]\right\}\hfill \\ +{\displaystyle \sum _{i=1}^n}u\left(x_i,10,100,4\right)\hfill \\ y_i=1+\frac{x_i+1}{4}\hfill \\ u\left(x_i,a,k,m\right)=\left\{\begin{array}{cc}k{\left(x_i-a\right)}^m\hfill & x_i>a\\ 0\hfill & -a<x_i<a\\ k{\left(-x_i-a\right)}^m\hfill & x_i<-a\end{array}\right.\hfill \end{array}$	30	[−50, 50]	0
Type 2	$\begin{array}{c}{F}_7\left(x\right)=0.1\left\{{sin}^2\left(3\pi x_1\right)\right.\hfill \\ +{\left(x_n-1\right)}^2\left[1+{sin}^2\left(2\pi x_n\right)\right]\hfill \\ +\left.{\displaystyle \sum _{i=1}^n}{\left(x_i-1\right)}^2\left[1+{sin}^2\left(3\pi x_i+1\right)\right]\right\}\hfill \\ +{\displaystyle \sum _{i=1}^n}u\left(x_i,5,100,4\right)\hfill \end{array}$	30	[−50, 50]	0
Type 3	$F_8\left(x\right)={\left(\frac{1}{500}+{\displaystyle \sum _{j=1}^{25}}\frac{1}{j+{\displaystyle \sum _{i=1}^2}{\left(x_i-a_{ij}\right)}^6}\right)}^{-1}$	2	[−65, 65]	1
Type 3	$F_9\left(x\right)=4x_1^2-2.1x_1^4+\frac{1}{3}{x}_1^6+x_1{x}_2-4x_2^2+4x_2^4$	2	[−5, 5]	−1.0316
Type 3	$F_{10}\left(x\right)=-{\displaystyle \sum _{i=1}^5}{\left[\left(X-a_i\right){\left(X-a_i\right)}^T+c_i\right]}^{-1}$	4	[0, 10]	−10.1532
Type 3	$F_{11}\left(x\right)=-{\displaystyle \sum _{i=1}^7}{\left[\left(X-a_i\right){\left(X-a_i\right)}^T+c_i\right]}^{-1}$	4	[0, 10]	−10.4028
Type 3	$F_{12}\left(x\right)=-{\displaystyle \sum _{i=1}^{10}}{\left[\left(X-a_i\right){\left(X-a_i\right)}^T+c_i\right]}^{-1}$	4	[0, 10]	−10.5363

The optimization ability of CPSSA can be fully investigated through a variety of category benchmark functions. In the experiment, we set the population size $N=30$, the maximum number of iterations $T_{max}$ = 500, the dimension D of the objective function, and the upper and lower bounds ub and lb are selected according to the benchmark functions in Table 2. The number of finders FD and threatened sparrows SD are taken as 20% of the population size. We run the independent experiments thirty times on each benchmark test function. The best and average value, standard deviation, and the computation time of each algorithm are recorded in Table 3. Under the identical benchmark test function, the best value denotes the exploration ability, the average value represents the convergence accuracy, and the standard variance represents the stability of the CPSSA [29].

Table 3. Experiment results of test functions.

F	SI	Best	Ave	Std	Computation Time (s)
F1	PSO	7.134288 $\times {10}^1$	1.959255 $\times {10}^2$	60.0022	1.157395
F1	ABC	4.574426	8.274577	2.3966	15.104270
F1	SSA	0	1.874825 $\times {10}^{-140}$	1.02688 $\times {10}^{-139}$	4.107282
F1	CPSSA	0	0	0	12.062264
F2	PSO	8.160150	3.057447 $\times {10}^1$	20.0995	1.23973
F2	ABC	2.483748	3.248522 $\times {10}^1$	23.3522	15.511821
F2	SSA	9.537863 $\times {10}^{-299}$	7.955561 $\times {10}^{-68}$	4.34102 $\times {10}^{-67}$	4.154662
F2	CPSSA	0	0	0	11.906737
F3	PSO	2.908686 $\times {10}^3$	8.612808 $\times {10}^3$	5414.9	6.260316
F3	ABC	3.853256 $\times {10}^4$	6.251440 $\times {10}^4$	10,947.1	26.059873
F3	SSA	1.063104 $\times {10}^{-8}$	4.102431 $\times {10}^{-78}$	2.24699 $\times {10}^{-77}$	11.141056
F3	CPSSA	0	0	0	17.316412
F4	PSO	5.852877 $\times {10}^1$	1.591048 $\times {10}^2$	75.627	1.182
F4	ABC	3.448549	1.015906 $\times {10}^1$	4.00236	15.4631
F4	SSA	2.680141 $\times {10}^{-15}$	5.880191 $\times {10}^{-11}$	2.10753 $\times {10}^{-10}$	4.12826
F4	CPSSA	0	0	0	11.9581
F5	PSO	−9.476918 $\times {10}^3$	−7.601357 $\times {10}^3$	1069.6	1.9245
F5	ABC	−1.453578 $\times {10}^{63}$	−8.408056 $\times {10}^{61}$	2.94628 $\times {10}^{62}$	21.44868
F5	SSA	−9.937985 $\times {10}^3$	−8.648037 $\times {10}^3$	656.408	5.2218
F5	CPSSA	−1.256949 $\times {10}^4$	−1.252106 $\times {10}^4$	159.05	12.4857
F6	PSO	1.101431	4.680629	2.56227	8.91828
F6	ABC	1.108390 $\times {10}^4$	4.299645 $\times {10}^5$	423892	32.38175
F6	SSA	6.197603 $\times {10}^{-18}$	2.995160 $\times {10}^{-12}$	9.32387 $\times {10}^{-12}$	15.1853
F6	CPSSA	1.570545 $\times {10}^{-32}$	1.570545 $\times {10}^{-32}$	5.5674 $\times {10}^{-48}$	19.40687
F7	PSO	4.333554	15.26170	9.07786	9.031767
F7	ABC	1.039235 $\times {10}^5$	1.084383 $\times {10}^6$	1.07069 $\times {10}^6$	32.5297
F7	SSA	6.609665 $\times {10}^{-15}$	1.112171$\times {10}^{-11}$	1.86574 $\times {10}^{-11}$	15.10169
F7	CPSSA	1.349784 $\times {10}^{-32}$	1.349784 $\times {10}^{-32}$	5.5674 $\times {10}^{-48}$	19.5371
F8	PSO	9.980038 $\times {10}^{-1}$	9.980038 $\times {10}^{-1}$	2.4774 $\times {10}^{-10}$	14.990997
F8	ABC	9.980038 $\times {10}^{-1}$	9.980069 $\times {10}^{-1}$	5.79252 $\times {10}^{-6}$	47.77464
F8	SSA	9.980038 $\times {10}^{-1}$	4.184485	4.83682	23.997373
F8	CPSSA	9.980038 $\times {10}^{-1}$	1.387087	2.1311	15.59964
F9	PSO	−1.031628	−1.031608	3.10204 $\times {10}^{-5}$	1.094425
F9	ABC	−1.031628	−1.031628	3.47478 $\times {10}^{-10}$	15.420527
F9	SSA	−1.031628	−1.031628	6.25324 $\times {10}^{-16}$	3.8147
F9	CPSSA	−1.031628	−1.031628	6.14542 $\times {10}^{-12}$	1.82324
F10	PSO	−10.1532	−9.399145	2.06047	1.598298
F10	ABC	−10.1532	−10.1532	1.20822 $\times {10}^{-9}$	16.5355
F10	SSA	−10.1532	−9.303533	1.93239	4.5498
F10	CPSSA	−10.1532	−10.15228	4.10674 $\times {10}^{-15}$	2.72803
F11	PSO	−10.40248	−10.20967	0.967761	1.85183
F11	ABC	−10.40294	−10.40294	6.41315 $\times {10}^{-13}$	17.505625
F11	SSA	−10.40294	−10.04859	1.34853	4.859621
F11	CPSSA	−10.40282	−10.40282	7.49301 $\times {10}^{-15}$	3.028603
F12	PSO	−10.53628	−10.51372	0.0370912	2.2475
F12	ABC	−10.53641	−10.53641	1.75039 $\times {10}^{-12}$	18.31669
F12	SSA	−10.53641	−10.17588	1.37204	5.470448
F12	CPSSA	−10.53629	−10.53629	5.21556 $\times {10}^{-15}$	3.381584

As can be seen from Table 3, for unimodal benchmark functions, the optimal value and the average value of CPSSA are identical. They can accurately converge to the minimum value of the function. This shows that CPSSA has the highest convergence accuracy. In addition, the standard deviation of CPSSA is 0, indicating that CPSSA has the best stability. Although PSO is the fastest, its accuracy and stability are the worst. For multimodal benchmark function F5, only CPSSA converges to the minimum value of the function. For the other two multimodal functions, CPSSA is much better than the other three functions in terms of minimum or average value. It shows its good accuracy. In the meantime, its variance is also the smallest of the four functions. Therefore, it also shows the algorithm’s good stability. For fixed dimension multimodal benchmark functions, the best values obtained by the four functions are nearly identical to the average value. However, the CPSSA has the fastest speed. Except for the case using F9, its variance is the smallest of all four algorithms, showing the best stability.

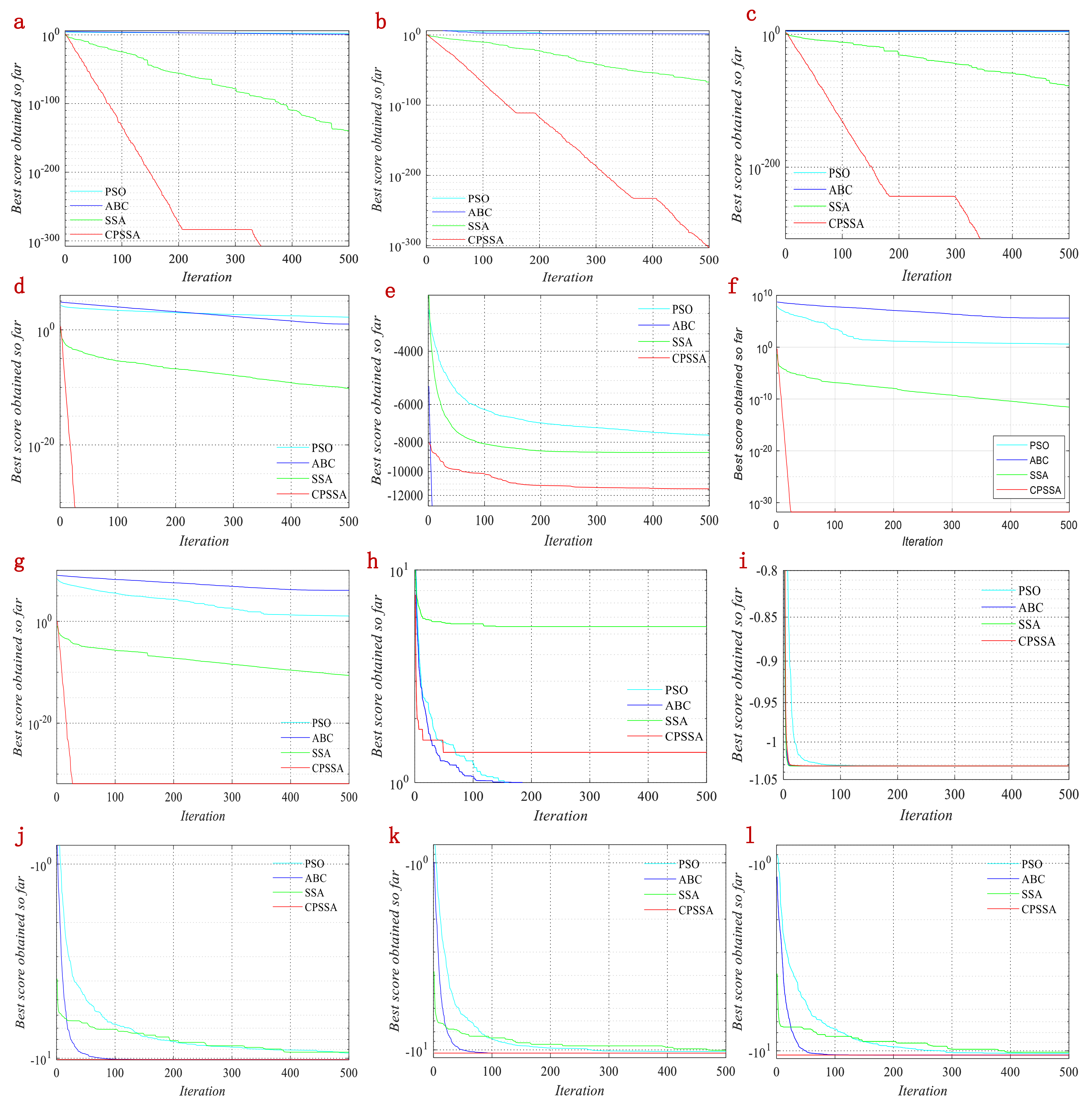
In order to verify the dynamic convergence features of CPSSA, Figure 4 shows the convergence curves of 12 benchmark functions under four optimization algorithms.

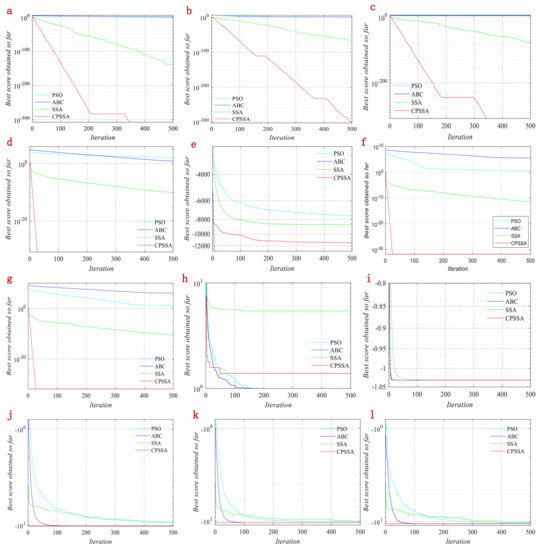
Figure 4. Convergence curves of four algorithms on twelve test functions. (a) F1; (b) F2; (c) F3; (d) F4; (e) F5; (f) F6; (g) F7; (h) F8; (i) F9; (j) F10; (k) F11; (l) F12.

It can be seen from Figure 4 that for high-dimensional functions F1–F7, CPSSA is much better than the other three algorithms in convergence speed and optimization accuracy. The search performance at the early stage of iterations and the exploration ability at the end of iterations are also better than the other three algorithms. This indicates that the CPSSA can fully achieve the search and exploration without losing population diversity and optimization stability. For low-dimensional functions F9–F12, all four algorithms can converge to the optimal value, but the CPSSA is the fastest. To sum up, the CPSSA significantly improves the optimization performance of the 12 benchmark functions. It has excellent stability and strong robustness, especially for F1–F4. Although the speed of the program is slower than SSA, it can effectively avoid the local optimums. This further demonstrates its high optimization accuracy, strong search ability, and obvious advantages. For fixed dimension multimodal benchmark functions, the running speed of CPSSA is significantly better than the other three algorithms, and the real-time performance is the best. It also verifies the feasibility and superiority of CPSSA.

3.2. Long Distance Iris Image Enhancement

In this experiment, we select the iris distance dataset of the Chinese Academy of Sciences (CASIA-Iris-Distance) [31]. It used an advanced biometric sensor, which can actively search iris and facial patterns in the field of vision 3 meters away.

The dataset images were captured by a high resolution camera, so both dual-eye iris and face patterns are included in the image region of interest [31]. This dataset contains 142 subjects and a total number of 2567 images. Each image has 2352 × 1728 pixels. Figure 5 shows three example images from CASIA-Iris-Distance database.

Figure 5. Example images from CASIA-Iris-Distance database.

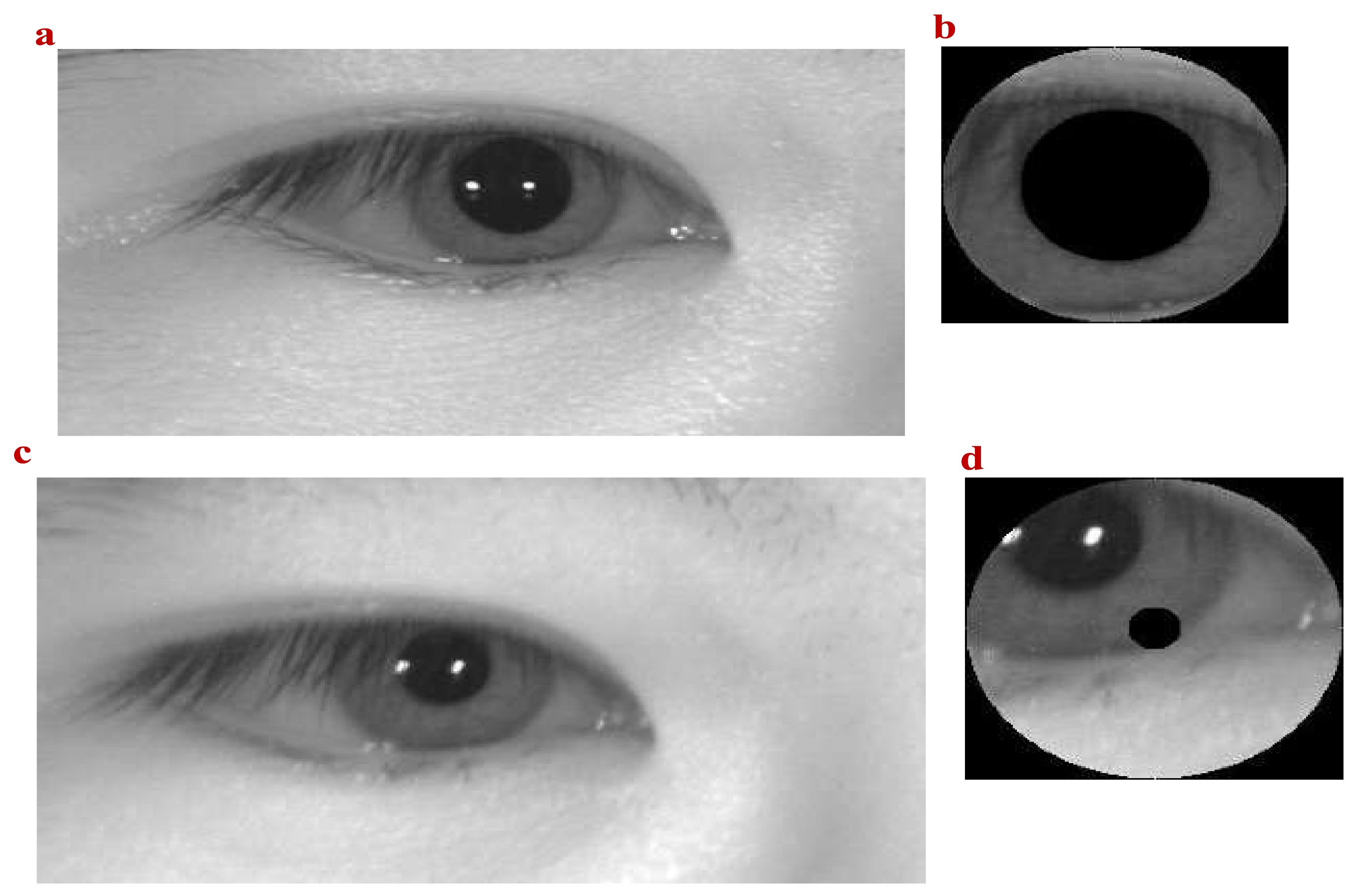
For the above data sets, the process of iris image recognition is generally divided into four steps: locate and segment human eye region, iris location and segmentation, iris feature extraction, and feature matching [37]. The enhancement of iris image can be used before iris location because the blurred image may affect iris location, as shown in Figure 6.

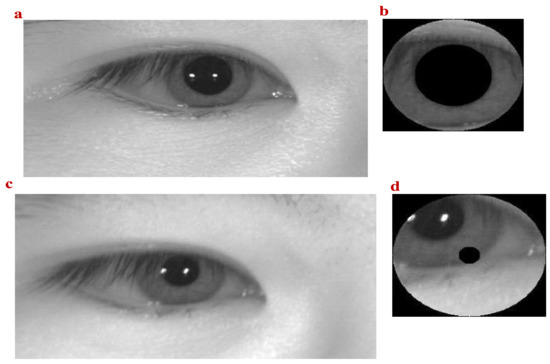
Figure 6. Influence of blurred eye image on iris segmentation (a) Clear eye area with $701\times 401$; (b) Correct iris segmentation; (c) Blurred eye area; (d) Wrong iris segmentation.

Figure 6a,c shows eye regions segmented from different face photos of the same person. As shown from Figure 6, Figure 6a is clearer than Figure 6c. Because the eye region in Figure 6c is unclear, the iris region cannot be correctly segmented by the iris location algorithm, as shown in Figure 6d.

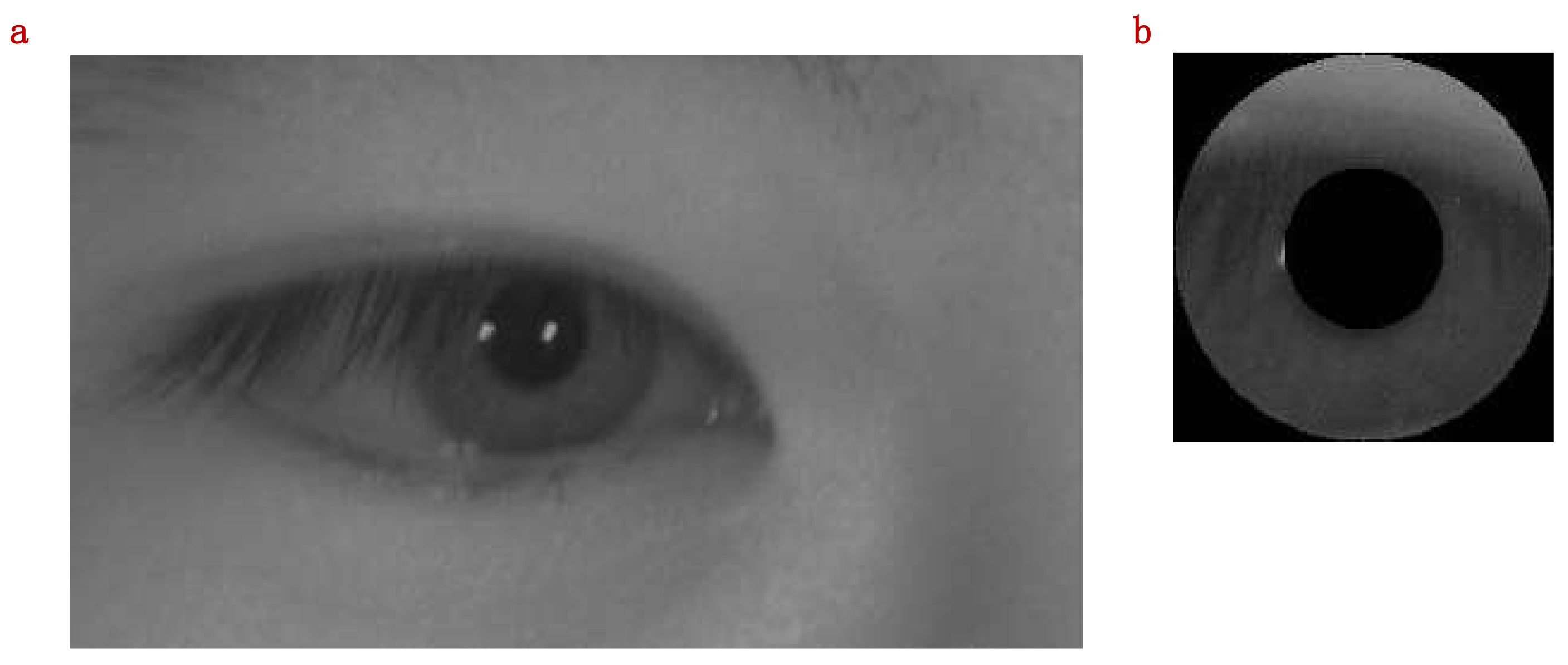
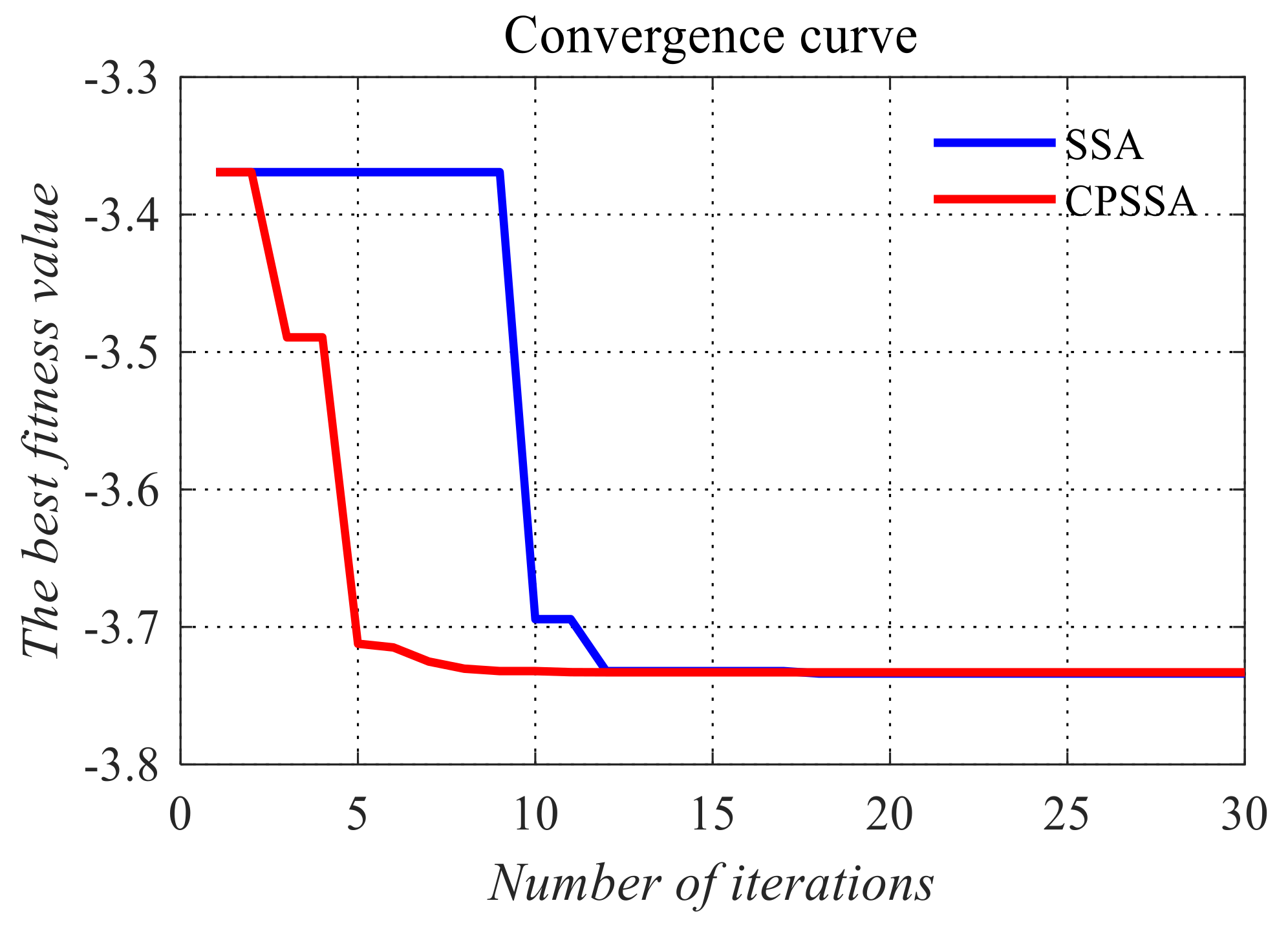
In order to solve this problem, we chose the CLAHE to enhance the image of the eye area in Figure 6c. The CPSSA algorithm is used to select the optimal clipping limit. The experimental parameters of the CPSSA are set as follows: population size $NP=30$, the maximum number of iterations $MaxCycle=30$, individual upper and lower bounds [0, 100], dimension dim is set to 1, and the number of sub images is $10\times 10$. The number of finders $FD$ and number of threatened sparrows $SD$ are taken as 20% of the population size. After the experiment, the enhanced pattern of the eye area is shown in Figure 7a. After iris positioning, the correct iris segmentation pattern is obtained, which is shown in Figure 7b. The fitness curves of CPSSA-CLAHE and SSA for image enhancement of blurred eye areas are shown in Figure 8. Obviously, the convergence speed of the CPSSA algorithm is better than that of the traditional SSA algorithm. The CPSSA can complete the convergence around the 7th iteration. The SSA needs 15th iterations to complete the convergence.

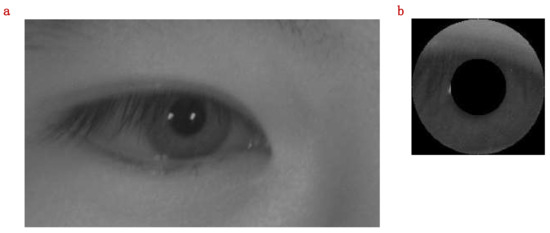
Figure 7. Eye area enhanced with CPSSA-CLAHE. (a) Eye region after image enhancement. (b) Correct iris segmentation.

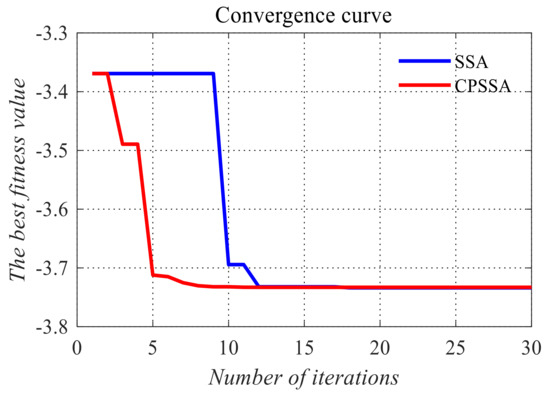
Figure 8. The best results of CPSSA and SSA.

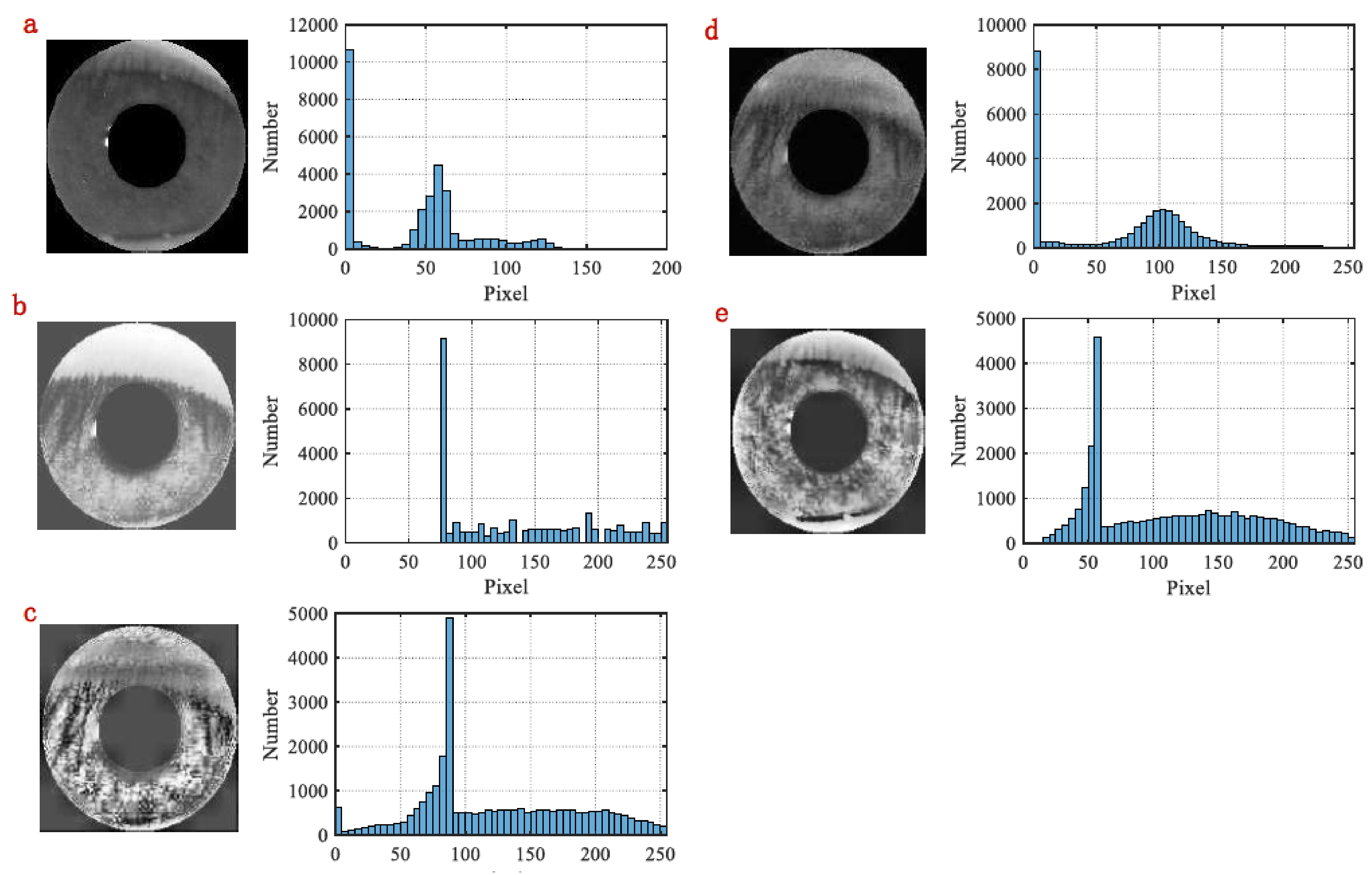
We can also enhance the segmented iris image. Figure 9 shows the gray image and its corresponding histogram after iris image enhancement by different methods.

Figure 9. Comparison of iris image and histograms. (a) Original iris image; (b) iris enhanced by HE; (c) iris enhanced by AHE; (d) iris enhanced by CLAHE; (e) iris enhanced by proposed CPSSA-CLAHE.

From the results of comparative experiments, we can see that HE, AHE, CLAHE, and CPSSA-CLAHE can enhance iris images. However, the purpose of biometric image enhancement is to improve the recognition rate, so we need to check recognition rate of different image enhancement methods.

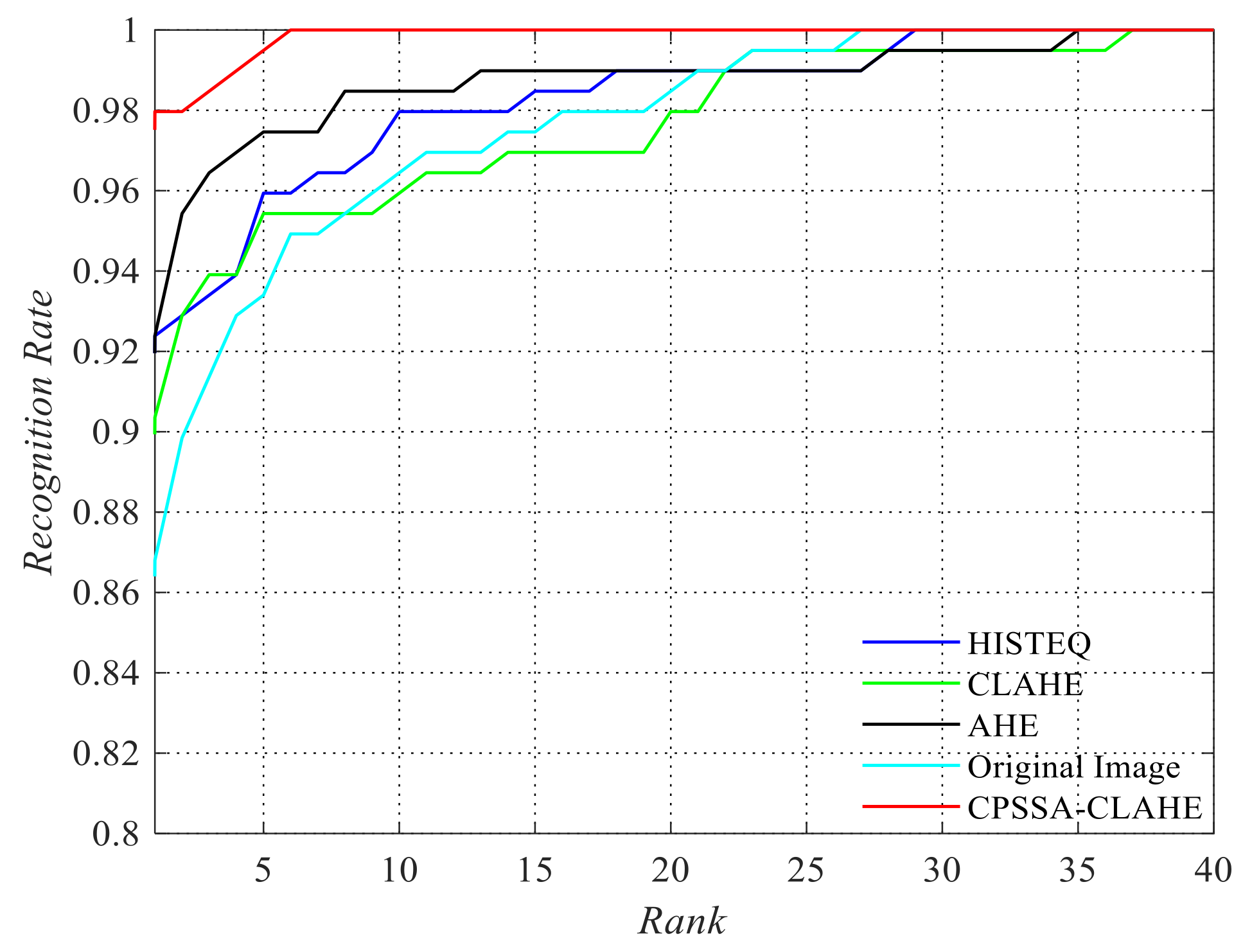
In order to verify whether the proposed method can improve the recognition rate, we selected 400 iris images with correct segmentation from the data set. These 400 pictures belong to 40 people, 10 for each person. The curvlet transform [38] is used to extract the iris features, and the kernel extreme learning machine (KELM) [39] is used as the classifier. The number of training sets is 5. A comparison between the CPSSA-CLAHE with the traditional methods is carried out, and the experimental results are shown in Figure 10.

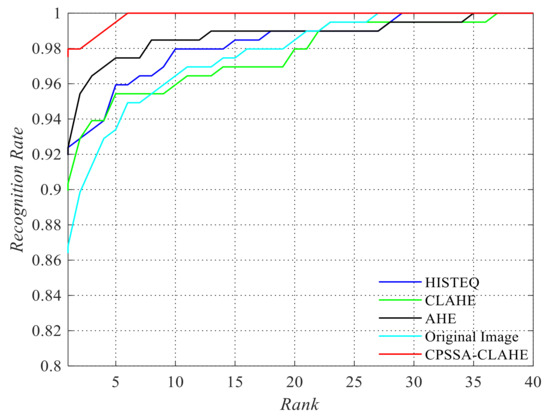
Figure 10. Recognition rate of different image enhancement methods.

According to Figure 10, we can see that the recognition rate is about 86% without image enhancement. HE, AHE, and CLAHE can improve the recognition rate, but the improvement rate is limited, whereas the image enhancement algorithm using CPSSA-CLAHE improves the recognition rate to nearly 98%.

4. Conclusions

In this paper, a modified sparrow search algorithm CPSSA is proposed and successfully applied to the problem of the low recognition rate of long-distance iris images. The algorithm uses fractional-order chaos to initialize the population and Pareto distribution to update the location of finders and scroungers to speed up its global convergence. This paper improves the traditional CLAHE, uses the CPSSA to find the optimal clipping value, and realizes the detail enhancement of the iris image. The clip limit value parameter changes according to different images, which can produce a better enhancement effect. Experimental results show that this method has obvious advantages over the traditional algorithms of HE, AHE, and CLAHE. It can not only improve the appearance of the image, but also effectively improve the recognition rate.

However, because of the hidden position of the iris, except for the image blur, there are many factors that affecting the location and recognition of the iris, for example, the reflection of glasses. These remain as challenges for the future research work.