Abstract
The research evaluates the vehicular routing problem for distributing refrigerated products. The mathematical model corresponds to the vehicle routing problem with hard time windows and a stochastic service time (VRPTW-ST) model applied in Santiago de Chile. For model optimization, we used tabu search, chaotic search and general algebraic modeling. The model’s objective function is to minimize the total distance traveled and the number of vehicles using stochastic waiting restrictions at the customers’ facilities. The experiments were implemented in ten scenarios by modifying the number of customers. Experiments were established with several customers that can be solved using the general algebraic modeling technique in order to validate the tabu search and the chaotic search methods. The study considered two algorithms modified with Monte Carlo (tabu search and chaotic search). Additionally, two modified algorithms, TSv2 and CSv2, were proposed to reduce execution time. These algorithms were modified by delaying the Monte Carlo procedure until the first set of sub-optimal routes were found. The results validate the metaheuristic chaotic search to solve the VRPTW-ST. The chaotic search method obtained a superior performance than the tabu search method when solving a real problem in a large city. Finally, the experiments demonstrated a direct relationship between the percentage of customers with stochastic waiting time and the model resolution time.
1. Introduction
The cold chain is the key element in the transport and logistics of perishables. The cold chain consists of steps that are part of the refrigeration and freezing process that perishable products need in order to reach their final consumer in optimal conditions [1]. Food products often go bad due to long travel times and frequent stops to serve customers during the delivery process. Therefore, it is difficult to effectively manage cold chain distribution and ensure maximum freshness [2].
Logistics operators must have vehicles with temperature control, which are generally more expensive and consume more fuel than normal vehicles. The late delivery of perishable food significantly affects the costs of the logistics operator and retailers [3,4]. Some contracts with retailers involve penalties for delays within the established delivery times. Additionally, energy is required to maintain adequate temperature during distribution, and traffic conditions are different throughout the day [5]. Therefore, the impact of delays on delivering perishable food is more critical than general goods [6].
Requirements to serve customers within specific delivery time windows can increase the complexity of vehicle scheduling and routing problems for logistics operators. Therefore, vehicle routing problems (VRP) related to the delivery of goods have been studied extensively. VRPs are combinatorial optimization problems of high complexity; these problems are categorized as NP-hard [7]. NP-hard models are widely used to solve optimization models in supply chains [8,9], transportation [10,11], telecommunications [12,13], cost optimization [14,15,16], manufacturing [17,18], service production [19], electrical networks [20], and social networks [21], among others. In the NP-hard class, processing time and capacity increase exponentially as the number of customers increases. The need to make decisions on real route assignment problems restricts processing times, and investigations focus on finding the best feasible solution. According to Toth and Vigo [22], heuristics have been designed to narrow down search space, reducing processing times to find feasible solutions.
Other solution methods are metaheuristics. Authors such as Gendreau and Potvin [23] define metaheuristics as solutions which orchestrate an interaction between local improvement procedures and high-level strategies, with processes that avoid local optimum by performing a robust search for a solution space. The main challenge of these metaheuristics is to solve large combinatorial optimization problems in an adequate time period. Different authors have used metaheuristic algorithms to solve VRP: local search [24], simulated annealing [25], greedy randomized adaptive search procedure (GRASP) [26], swarm intelligence [27], tabu search (TS) [28,29], genetic algorithms [30], colony optimization [31], reactive search [32], and maximum coverage [33].
The problem analysis requires that each vehicle delivers the merchandise to the customers within a specific time interval, known as a vehicle routing problem with time windows (VRPTW). Considering Hsu et al. [34] and the randomness of the perishable food delivery process, we propose using VRPTW-ST to generate delivery routes by minimizing the total distance traveled and complying with client demand. This study aims to validate the TS and chaotic search (CS) methods to minimize the total distance traveled and the number of vehicles using stochastic waiting restrictions at the client’s facilities. The second objective is to demonstrate the capacity of these techniques to reduce the execution times of the computational model when establishing daily capacities and to generate new routes.
VRPTW-ST sets new restrictions on the VRP model; time windows limits (TW) are constraints, and the service times (ST) are random variables. Other features of the general VRPTW-ST model are that the vehicles can arrive early; however, the goods will still be received within the time window at a random reception time. The complexity of the VRPTW-ST model lies within the probability of vehicle arrival generated by the TW restrictions and the ST variables [35].
This study uses VRPTW-SW in a frozen products distribution center of a transnational food company located in the Quilicura commune in the Metropolitan Region of Santiago. The distribution routes are planned daily to meet the demand of customers located in the same region. For this case study, two customer segments are considered: (1) supermarkets and (2) road customers. The former establishes a deadline for receiving orders, where the truck is not serviced when it arrives after the scheduled time. Another restriction of the supermarkets is the random waiting time of the trucks before being served. In the case of road customers, they can receive the order at any time, and once the trucks arrive, they immediately begin receiving the merchandise.
1.1. Literature Review
This section analyzes studies on VRP with stochastic service and/or travel times and studies evaluating different sources of uncertainty. VRP is a classic combinatorial optimization problem originally introduced by Dantzig and Ramser [36]. Taş et al. [37] proposed a VRP model with a weak time window and stochastic travel time, comparing the results with TS and an adaptive large neighborhood search. These solutions are useful for large-scale problems, susceptible to rush hour.
Ehmke et al. [38] proposed using programming with probability restrictions in VRP to guarantee a certain level of service for all customers. Stochastic programming must be used to solve this vehicle routing problem. Xu et al. [39] used an improved hybrid ant colony optimization algorithm, K-means, 2-Opt, and crossover. The experimental results showed that the ant colony optimization algorithm is capable of finding high-quality solutions. Furthermore, Tao et al. [32] proposed a metaheuristic based on the hybrid topological graph, genetic algorithm, and TS to minimize travel and waiting times. The algorithm considers time windows, load capacity, and the origin of tasks. The results showed the efficiency and effectiveness of the proposed algorithm, while Urzúa-Morales et al. [33] used a VRP model for a merchandise distribution system in the historic center of the city of Santiago de Chile. The last mile modeling considered a maximum coverage optimization model, k-nearest neighbors, and the analytic hierarchy process. The results reduced 53 tons of carbon dioxide within the square kilometer and reduced 1103 h of interruptions per year in vehicle congestion.
Yu et al. [40] proposed two lower limit models that determine optimal quantity for the bottleneck process in production and distribution logistics. The distribution problem is modeled as a VRPTW. A Lagrangian relaxation model was designed to optimize the lower limit, and an improved subgradient algorithm was proposed. The results show that the suggested algorithm can calculate an adjusted lower limit. Laporte et al. [41] used programming with probability restrictions to assign a certain probability of failure or several restrictions to VRP problems.
Taking into account the third type of uncertainty (service times), Errico et al. [35] developed a VRPTW-ST model for route planning. The model includes a branch and cut-price algorithm and an adaptation of the dynamic programming algorithm to determine the probabilistic consumption of resources. Han et al. [42] presented a single-depot vehicle-routing problem with the time windows (SDVRPTW) model for attended home delivery. This study considers two types of behaviors: customer unavailability and random response time. The solution method proposes a hybrid algorithm which connects dynamic programming and TS heuristics. The proposed approach generates high-quality solutions within a reasonable execution time.
Zhang et al. [43] consider a stochastic VRP problem with uncertain deadlines (VRPD) to find profitable routes complying with the service level, subject to the uncertainty of the distribution. They considered a robust distribution optimization framework. The computational difficulties caused by the probability constraints are approximated using value-at-risk constraints. The results show that the routing policies developed from this framework are robust in all the scenarios considered. Authors such as Shukla et al. [44] use a portfolio of evolutionary algorithms to reduce computer time when searching for local solutions to resolve a vehicle routing problem with stochastic demand (VRPSD). Furthermore, Hand and Chu [45] proposed a multi-start variable neighborhood search approach for solving the split-delivery vehicle routing problem with minimum delivery amounts (SDVRP-MDA), in which the demand of a customer can be split and delivered to the customer by several vehicles on different routes, but the customers each require a minimum delivery amount every time they are visited. The results suggest that a relatively simple multi-start heuristic with good search operators can be as effective as sophisticated metaheuristics. Braaten et al. [46] considered a robust vehicle routing problem with time windows (RVRPTW) with applications in maritime transportation. Computational results show a considerable benefit from the main novel heuristic components.
1.2. Research Gap and Contribution of This Study
The random nature of the variables implicit in route planning (demand, travel times, service times, and physical availability of the client) makes decision making difficult. According to Ehmke et al. [38], there are two main problems in the planning of routes that cause a loss of customers and cost overruns: (1) dissatisfaction in service due to non-compliance with time windows and (2) cost overruns in the final sale price of the product due to overtime pay to drivers. Since 1992, random variables have been incorporated into the VRP models, giving rise to the stochastic vehicle routing problem (SVRP) incorporating random elements.
The main variants studied in recent years are the stochastic demand, when there is no certainty of the demand of each client [47], stochastic travel time [37], and stochastic clients with probability p that the client is found and a probability of 1 − p that the client is not found [37]. Other jobs that incorporate stochastic service time are referenced in [48].
The literature considers two types of time windows: (1) strict time window—if the vehicle arrives before the time window it must wait, in general, without an associated cost; (2) flexible time window, which allows violating the restriction assuming a penalty [22]. For Li et al. [49], high-value penalties greatly limit the probability of violating the restriction and result in adapting behaviors similar to the strict time window. If there is only an upper limit in the time window, the model is called a vehicle routing problem with a deadline (VRPD).
Finally, hybrid methods solve VRPTW-ST. The two-phase method solves a model without the probability of failure to obtain a preliminary result and subsequently resolves a second model that considers the costs associated with the failure of any of the restrictions.
The main contributions of this work are:
- In studies [34,35], a waiting time is established for vehicles only when they arrive before the time window. Our research generalizes random wait times for all delivery vehicles arriving before or during the time window.
- In the article, we develop an extension of the CS and TS method for the VRPTW-ST problem. This extension solves problems with reduced calculation times for the resolution of the model.
- The proposed model is made up of clients with and without reception restrictions. The study presents different combinations of the confidence level (), maintaining the percentage of clients with restrictions. The different variations of the confidence levels modify the best value of . Very high confidence levels decrease the solution quality.
1.3. Problem Statement and Insights from This Study
In this section, the problem described above was represented as a VRP with a deadline and stochastic waiting time (VRPTW-ST) for a real distribution problem of frozen food for a transnational company in the city of Santiago. The vehicle is serviced within the attention intervals defined by the client, and the waiting time is defined. Based on previous works [50], we propose a mathematical model with probabilistic restrictions that considers the random nature of the problem when establishing a level of service for each customer [38].
To address the complexity of the VRPTW-ST, Li et al. [49] developed a metaheuristic TS-based model, and Ikeguchi et al. [50] used a CS method, obtaining better results than the TS method.
To validate the proposed methodology, models were constructed to compare both methods with the empirical results of the industry. The solution methods were programmed in the Python language.
The data used were (i) customer demand, (ii) average travel times and distances between customers, and (iii) average and variance of waiting time for each customer. The proposed modifications to the TSv2 and CSv2 algorithms free up memory and reduce numerical computation. These new algorithms do not use the Monte Carlo (MC) method to choose the new best move. Subsequently, the algorithm recalculates the best value of using the MC method. These modifications allow an efficient optimization design of the vehicle route graph. The program configuration was designed to run all four codes (TS, CS, TSv2, and CSv2). For each code, we created ten experiments, and the results per code correspond to the average of these ten experiments.
The novelty of this research is the development of a metaheuristic that solves real VRPTW-ST to distribute merchandise in large cities. These problems cannot be solved quickly by the general algebraic modeling systems (GAMS) technique. Here, we proposed the use of CS and TS heuristics to solve the problem of time and computational capacity.
The insights of the study correspond (1) to the design of an optimization strategy to solve VRPTW-ST problems associated with the supply chain of frozen products, (2) the techniques TS and CS modified with MC reduce execution times and program the new vehicle routing daily, (3) the optimization strategy can adapt to new VRPTW problems associated with large cities, (4) the modified CS technique provides adequate resolution times for customer volumes higher than 80, and (5) the implementation of the algorithms reduces overtime for drivers, reducing costs. This reduction in labor costs and the reduced processing times of the different scenarios allows commercial implementation of the solution.
The development of this study is divided into four sections. Section 1 reviews the literature concerning the main concepts and heuristics that have served as solution methods to different VRPs with time windows and stochastic service. Section 2 describes the methodology. Section 3 presents the results of the proposed VRPTW-ST. Finally, Section 4 exposes the main conclusions of the proposed investigation.
2. Materials and Methods
2.1. Previous Mathematical Approach
The VRP is defined according to the graph theory as a unidirectional graph represented by G = . Where V = is the set of vertices with n + 1 representing a depot, E = is the set of arcs, denotes the set of customers, 0 represents the depot where a fleet of vehicles with identical capacity Q to serve customers. Each customer i has a fixed demand , which is delivered from the depot in a service time . Each arc is associated with a travel distance or a cost . In general, it is assumed that C = satisfies the triangular inequality, that is, for every .
The VRPTW-ST model probability restrictions are based on the author’s work [51] and assign service levels to comply with the probability restrictions.
2.2. Set, Parameters and Variable
The model is composed of the following sets, parameters, and variables:
| m | : number of vehicles used, can be a constant or a decision variable. |
| : number of customers served by the vehicle . | |
| K | : set of vehicles, which is defined as . |
| Q | : vehicle capacity; assumed that all the vehicles are homogeneous and each one has limited capacity Q = 3000. |
| B | : established working time of the driver. In this case, 480 min. The value of B is composed of travel time, service time, and waiting time. |
| W | : the maximum time that can be spent waiting by every vehicle. |
| : customer demand . | |
| : distance between vertex and with . | |
| : travel time between vertex and . | |
| : customer service time . | |
| : customer timeout ; in this work, is assumed as continuous random variable with normal distribution . | |
| : time for vehicle to visit the customer ; is a continuous random variable because it depends on customer timeout. | |
| A | : maximum waiting time for vehicle k. |
Model variables:
2.3. Objective Function
The probability constrained programming model of the vehicle routing problem with stochastic lead time, and the delivery deadline is shown below.
Subject to:
| (2) | |||
| (3) | |||
| (4) | |||
| (5) | |||
| (6) | |||
| (7) | |||
| (8) | |||
| (9) | |||
| (10) | |||
| (11) | |||
| (12) |
Equation (1) represents the objective function, where parameter M is a large value to minimize the number of vehicles and the total distance traveled. Equation (2) represents how each customer can only be visited once by a vehicle. Equations (3) and (4) indicate that vehicle k must leave and return to the depot. Restriction (5) forces each vehicle k to leave the node. Equation (6) represents the capacity constraint. Equations (7) and (8) are the stochastic restrictions of driving time and waiting time of vehicles using the decision variable . Equation (9) represents the probability of arriving before the deadline ) with a level of confidence α. Equation (10) represents the maximum waiting time of each vehicle. The model prioritized the customer to reduce the difficulty of finding a solution. Finally, constraint (11) does not allow partial services and ensures non-negativity of variables.
2.4. Stochastic Restrictions
Equation (8) establishes the duration of a driver’s route with a B value under a probability P and a confidence level β. Excess in driver hours has a probability of 1 − . For very low β values the probability of overtime is increased.
Equation (9) establishes the probability P with confidence level α of the vehicle arriving before the deadline. The random variable depends on the travel time, the service time, the random waiting time, and the deadline. The confidence level α adjusts the problem’s difficulty level; no feasible solutions may be found for very high values.
Given the high randomness of the waiting time, this constricts the decision-maker to select adequate confidence levels. Therefore, it is often an unnecessary or high cost to hold all restrictions. Firms can establish lower values for the constraint with less relevance than a higher significance value for the limitations.
2.5. Improvement Stochastic Restrictions
Equation (10) is a new restriction to the original model proposed by [49]. It restricts the extra times of each vehicle by adding all the waiting times of each vehicle W under a γ probability.
Equation (8) is transformed into several restrictions where a certain number of possible scenarios are evaluated. The purpose of the transformation is to meet these restrictions a minimum number of times, and the compliance number will depend on the level of trust in the original restriction.
The set of scenarios is defined as s = (, …), where is the number of scenarios. The variable must be redefined by to represent the customer’s wait time i. The variable is a binary variable with a value of 1 when the constraint (8) is satisfied and 0 otherwise. Meanwhile, πs is the probability of occurrence of the scenarios; it is assumed that all the scenarios have the same probability. Finally, is the probability of failure of the constraint (8), which must be greater than zero and less than probability P.
Equation (8) can be written as the following set of restrictions.
| (13) | |||
| (14) | |||
| (15) | |||
| (16) | |||
| (17) |
Finally, the model plans a set of routes subject to probability restrictions. Such scenarios allow routes not satisfied under a certain threshold. However, it does not consider the costs associated with the failure of routes. In this case, the objective is to minimize the number of vehicles and the total distance traveled; for Sawik [52], solutions with fewer vehicles are better than solutions with less total distance traveled.
2.6. Programming of Tabu Search
An initial solution for VRPWT-ST must be available for TS programming. The shortest path from each node must be adapted: the minimum distance between the customers and depot. This solution is built considering a greedy algorithm. Initially, we searched the minimum distance between the depot and customer, which was then repeated with each node until violating any restrictions. To build the solution, we used the upper wait time confidence interval with an await time probability of 0.9999. This level of confidence guarantees a workable initial solution.
The restrictions are addressed as follows: (1) when the next customer exceeds the maximum tuck capacity, then a new route is generated; (2) when the truck arrives after the deadline for delivery, then the delivery is postponed until the next route is generated and another node is analyzed, and (3) if the route time exceeds the working time B (=480) then a new route is generated.
Each visited customer is assigned a large-value datum point to avoid being reassigned, eliminating the probability of partial deliveries. Subsequently, the possible violations of the restrictions of the original problem are checked, penalizing the objective function F(x) of the model. This generates a new F(x) represented in the following way (Equation (18)):
where F(x) is the original objective function defined in Equation (1). represents the feasibility of the capacity constraint. , , and represent the feasibility of the probability constraint: deadline, overtime and total wait time, respectively. , , , and take a value of 1 in case the respective restriction is violated and 0 in the other case. We carried out three movements to build a new neighbor (i) exchange, (ii) relocation, and (iii) the 2-opt movement in each iteration. The first movement (i) switches the position between two random clients, the second movement (ii) transfers a random client to another route, and the third 2-opt movement fixes two random clients of the same route and reverses the order of the intermediate customers. Algorithm 1 summarizes the proposed TS heuristic.
| Algorithm 1. TS heuristic. |
| Set x as the given initial solution Update statistical data: set : and update and . Allow that every neuron shot in the first iteration while and Set n = 0 while |
| Set Z( Randomly relocated, exchange or two-opt operator, and two random customers such constraints for each operator (e.g., the route must differ for relocated customers). Move current solution to its neighboring , Set and . If and and does not tabu then , otherwise if is feasible and ) then , Update list tabu: add for random value iterations, and reduce the rest in one. If and then and If then , Set and If is feasible and , , and . Set and If and if x* is not updated for iterations then and If then |
2.7. Programming of Chaotic Search
Based on the research of Kato et al. [53], the algorithm uses two local searches: (1) customer change and (2) customer relocation. The method requires neurons to solve a problem with n customers. When a neuron is triggered, the effect over the search is a change of customer or customer relocation. The variables and the parameters to use in the method are the following:
| : scalar parameter of tabu effect. | |
| : scalar parameter of the effect gained. | |
| : bias positive. | |
| : number of customers. | |
| : number of local searches. In this case, there are only 2. | |
| : decay parameters for tabu effects, . | |
| : internal state of the -th neuron in the period t corresponding to the effect gained, where and . | |
| : internal state of the -th neuron in the period t corresponding to the refractory effect. |
Each local search previously selects the best possible movement, that is, the movement which decreases the value of F(x). The movement is performed when the most efficient neuron is fired. Each neuron has a gained effect and a refractory effect described below:
| Effect gained: | (19) |
The effect gained refers to the profit obtained when performing the local search; in this case, it corresponds to the greatest savings. Variable is obtained by the change or relocation of the customer i with the customer s due to the local search j.
| Refractory effect: | (20) |
The refractory effect is used to avoid falling into local optimum. This element performs a job similar to memory in the TS method. The last shot is memorized as a previous state when the intensity of the refractory effect of the current state is decided. The value increases only after the neuron is fired and recovers exponentially over time, depending on the value of and θ. This does not escape possible local minimums.
The trigger functions used in the CS are Equations (21)–(23). Equation (22) is f(y) with sigmoid function and ε is a very small value. The sigmoid function generates more complex shots.
For the condition , the ij-th neuron is triggered in the time t, and the corresponding local search is performed; that is, if the n1-ith neuron is fired, the n-nth customer is changed, and if the n2-ith neuron is fired, then the nn-ith neuron is relocated.
Neurons update asynchronously, and the iteration ends when all neurons are updated. As in the TS, if iterations do not improve the solution, we propose intensifying the search by returning to the best solution found so far. Algorithm 2 summarizes the proposed CS heuristic.
| Algorithm 2. CS heuristic. |
| Set x as the given initial solution Update statistical data: set : and update and . Allow every neuron shot in the first iteration while and |
| for (i,k) in neuron: Move current solution to its neighboring , Set and for CS calculate used MC. Calculate Refractory and Gain. Set . Update If shot the neuron and then and (for CS v2 update with MC). If then Else If is feasible and , , and . Set and Else and . Update of values of If x* is not updated for iterations then and If mod(t,15) = 0, is updated as follows: , set |
2.8. Monte Carlo and Penalization Procedure
Both TS and CS were initially built for VRP deterministic cases. The authors of [49] adapted the TS to apply in stochastic cases. They implemented an MC simulation to validate the feasibility of chance constraints, providing a maximum number of runs (), any chance constraint (e.g., (10)), and confidence level (e.g., ). In each simulation, waiting time w is set randomly from a normal distribution where and are the mean and standard deviation of the waiting time, respectively. Later, it is verified whether it holds the constraint. If the percentage of simulation it is greater or equal to the level of confidence, then the constraint is not violated; otherwise, a penalty is added to Z. Additionally, we updated the penalty value after a certain number of the iteration (in this case 15) to allow for diversification. Hence, the is multiplied for , where is the number of instances that satisfy the constraint . Notice that if the is small (the constraint has been violated in the last iterations), then the penalty increases with the proposed force to satisfy the successive 15 iterations, otherwise it is reduced to acceded new solutions. These procedures were considered for both TS and CS. It embeds these procedures into CS, extending its usefulness to stochastic problems. However, notice that CS for every neuron must search the best move possible, which impacts its performance. For this reason, we considered only two operator exchanges for CS, and relocated.
Two modifications of the TS shown in [49] were proposed. They proposed MC to prove the feasibility of the chance constraints, calculate the value of , and repeat it for every neighboring candidate generated. However, the runtime depended drastically on the number of candidates and the number of simulations established. Therefore, we proposed an alternative not to run MC proceedings while generating the candidates, but after selecting the best move to reduce the runtime. We used the average to random variable to calculate the best value of , and we updated its value using MC when finalizing this procedure. Additionally, for the neighborhood structure, we chose a pair of customers randomly to generate an admissible solution. After, we selected an operator randomly to relocate the customers in a different route. The heuristics with this consideration are called TSv2 and CSv2.
3. Results
3.1. Results of the Previous Mathematical Approach
The investigation corresponds to the resolution of a real VRPTW-ST product transport problem in the City of Santiago. To validate the implementation of the TS and CS methods, they were compared with the authors’ works [51]. The problem with probability restrictions could only be resolved by a small number with the GAMS mathematical programming module using exact methods. The programming with probability restrictions is resolved by evaluating the same model in different scenarios for computational downtime of 6 h, obtaining a maximum resolved size of 20 nodes.
Table 1 shows the results obtained for the instances with parameters α, β, of 0.75. The effectiveness of the TS method for the solution of the proposed problem was evaluated. The results obtained in the instances that could be resolved through GAMS were compared with those obtained by TS. Table 1 shows the comparative results between GAMS-TS and GAMS-CS.

Table 1.
Results GAMS and TS-CS.
The results have the expected behavior, the increase in customers, and/or an increase in the stochastic elements of the problem increases the objective function F(x). The results of the GAMS module failed to obtain the optimal solution; however, the difference concerning the optimal value is negligible. The resolution model is validated to solve this problem.
The difference obtained between both solutions GAMS and TS is similar. With TS, feasible results are obtained from the mathematical model proposed in Section 2.
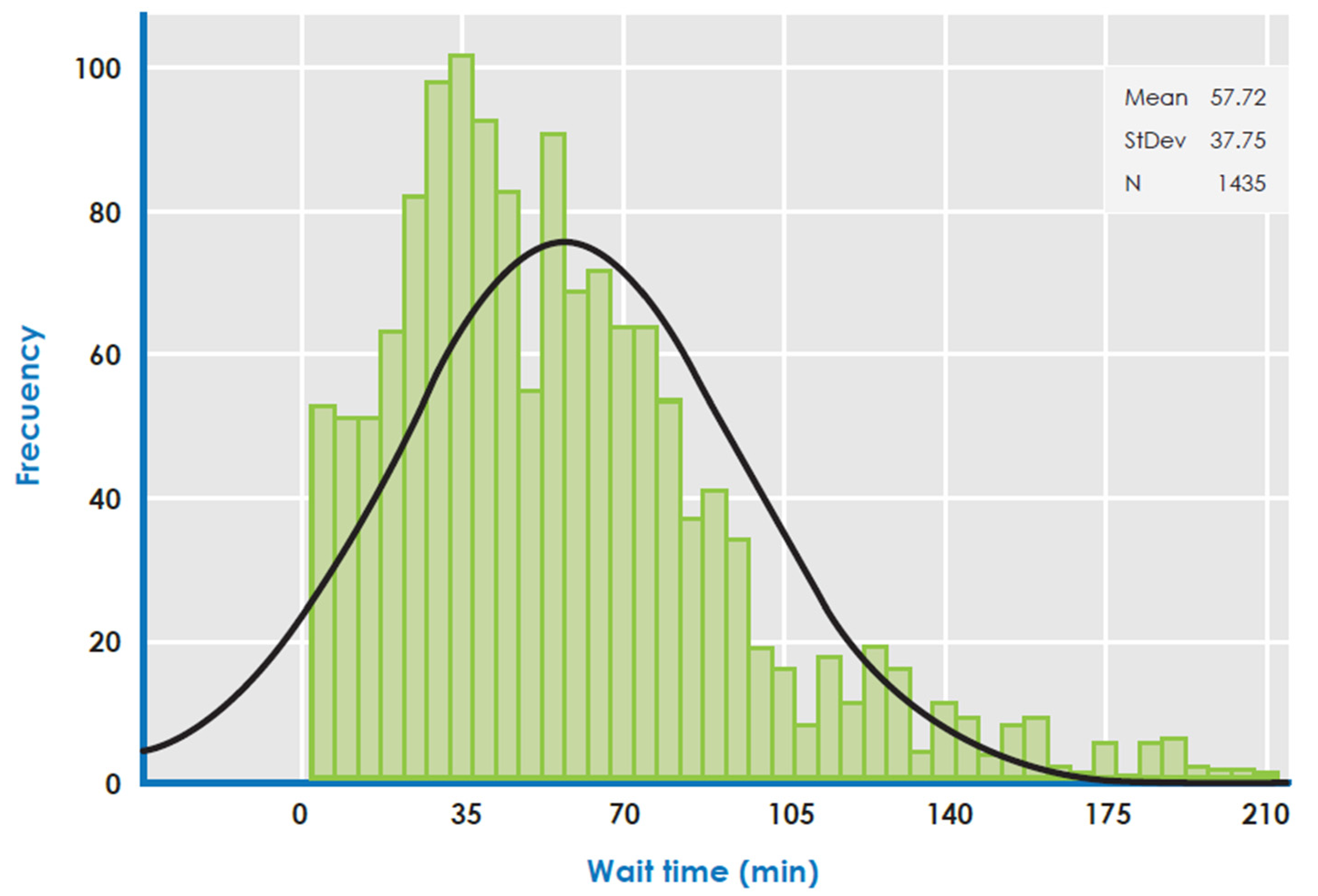
The results of the metaheuristic CS confirm the validity of the technique by comparing the results with the GAMS technique for the problem posed in Section 2. In this case study, the main challenge was delivery to supermarkets because they only received orders until midday. Additionally, Table 1 shows that the mean waiting time was between 52 and 63 min, with a standard deviation of 33 and 53 min, depending on the brand.
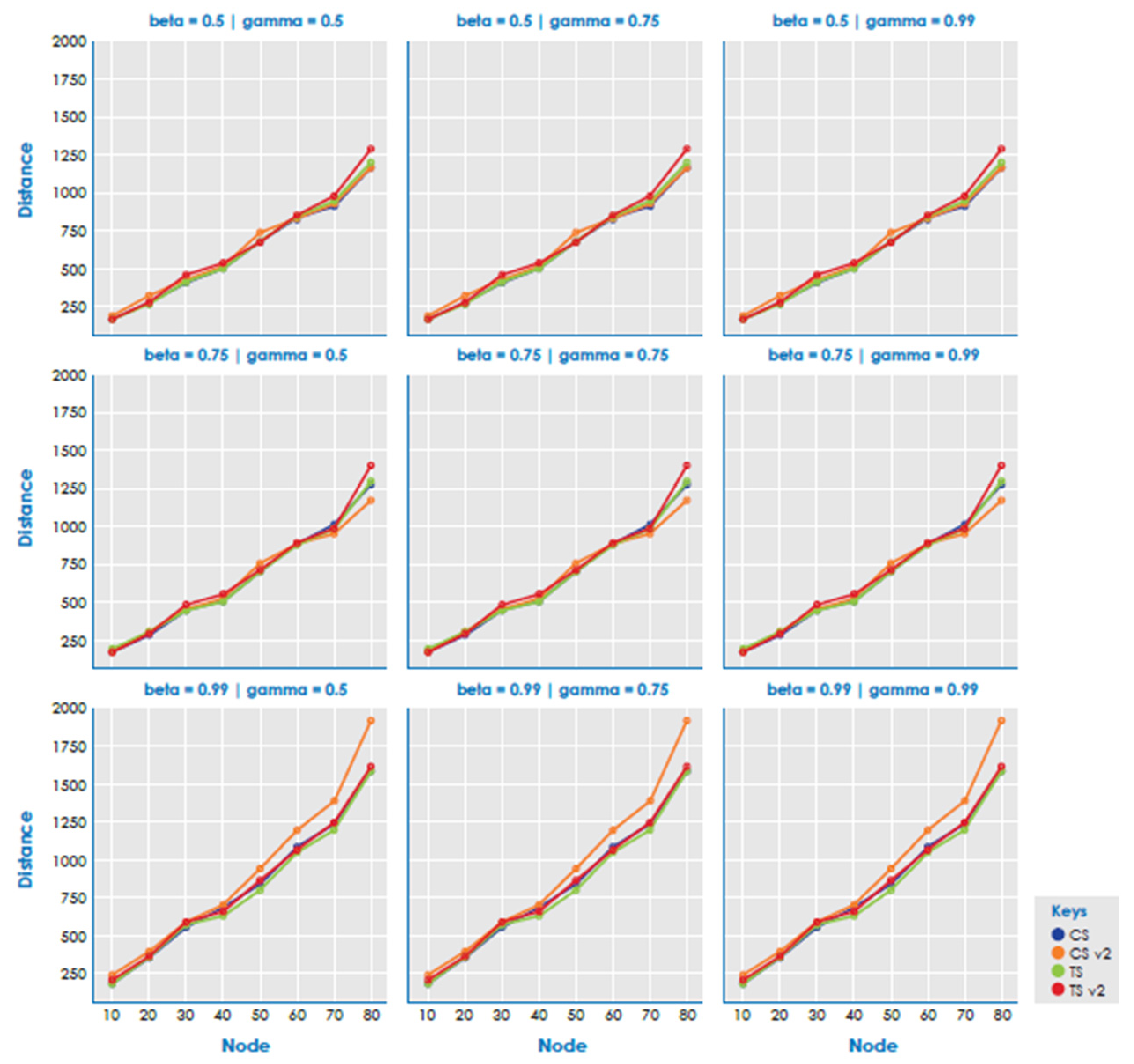
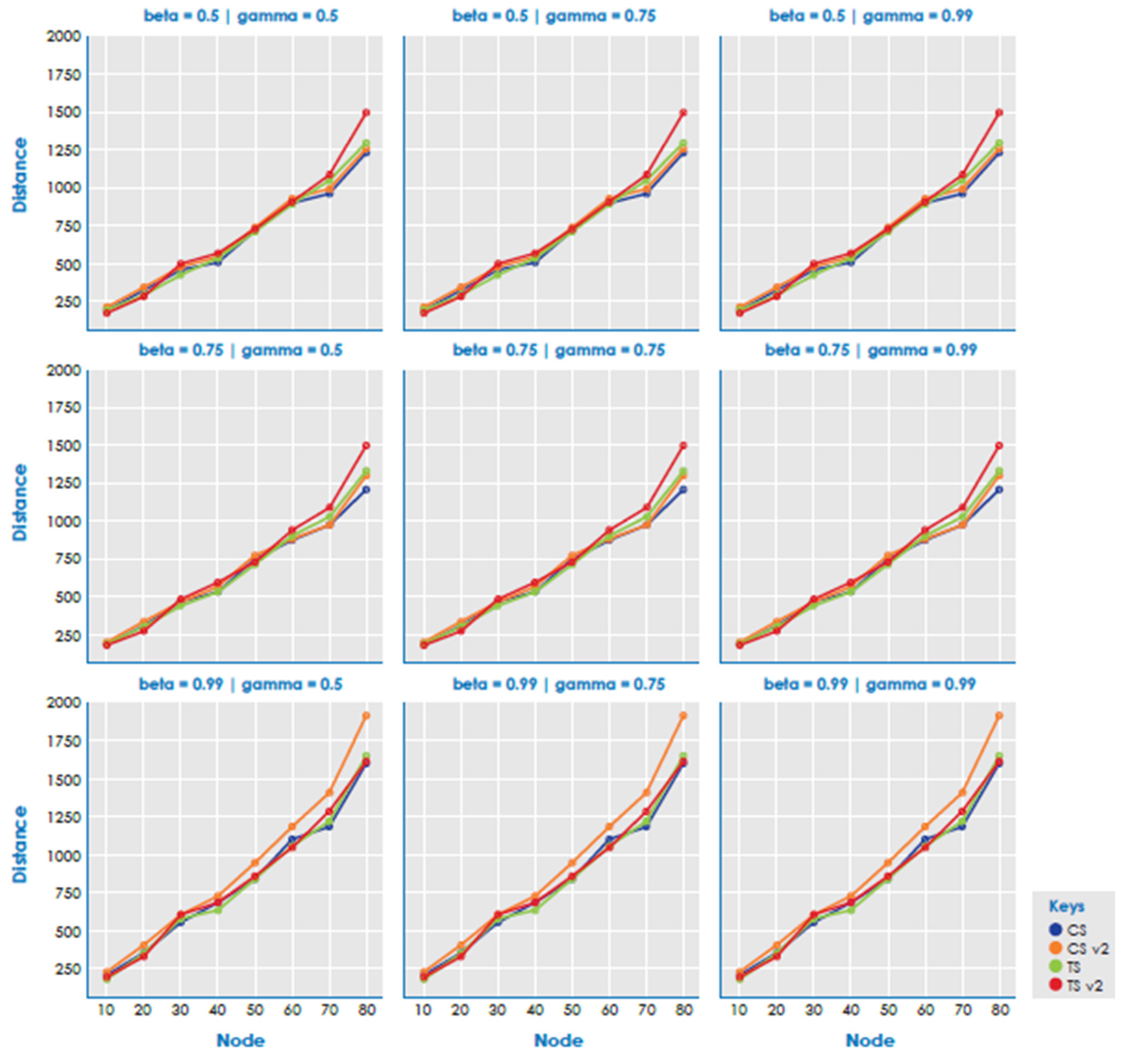
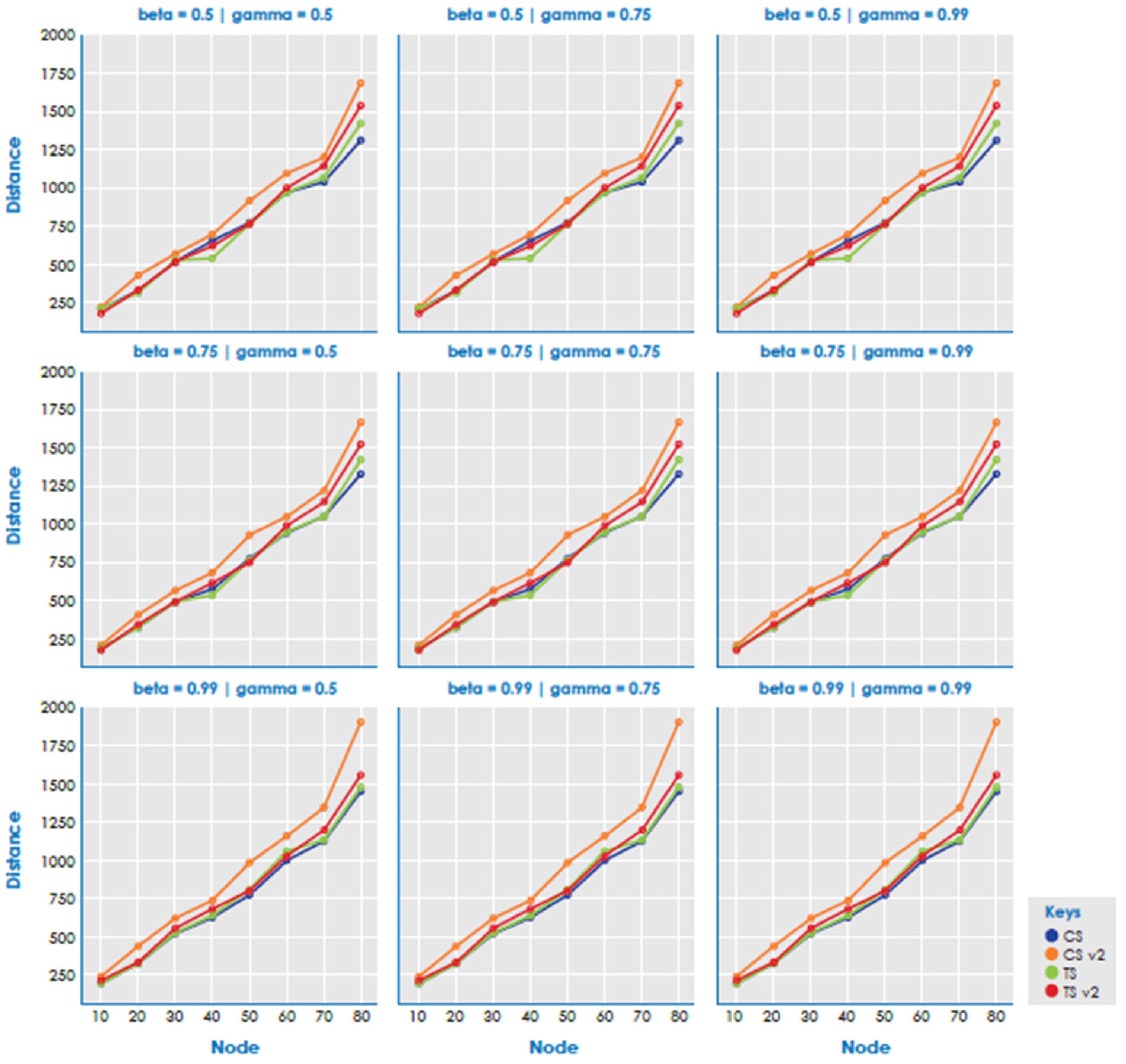
Figure 1, Figure 2 and Figure 3 show the average methods. The results showed that there is no clear advantage between heuristics. For instance, CSv2 obtained better results when alpha, beta, and gamma values were lower and worse when they were higher. CS and TS are the best results, with CS being the best in most instances.
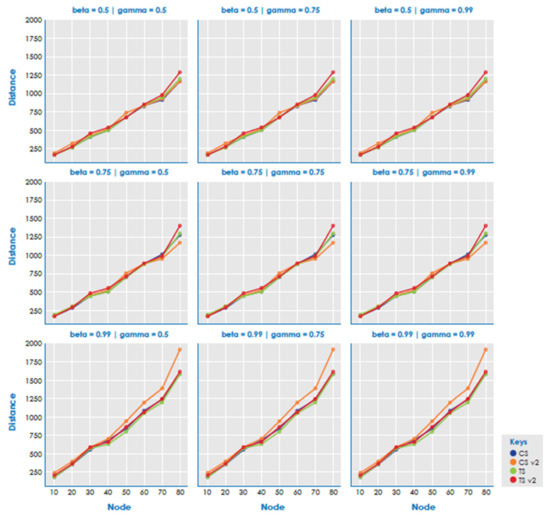
Figure 1.
Total distance by methods. α = 0.5 and supermarket = 60%.
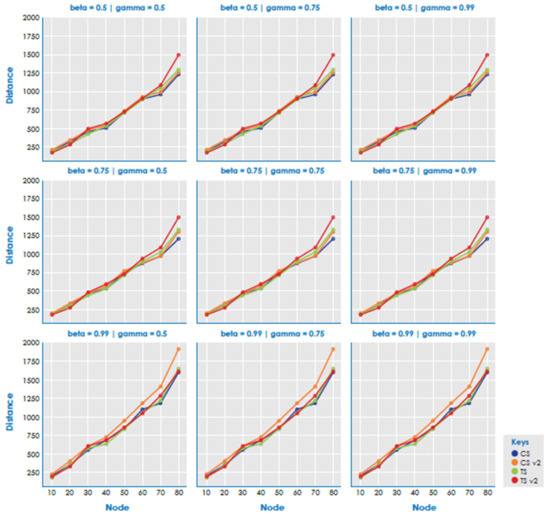
Figure 2.
Total distance by methods. α = 0.75 and supermarket = 60%.
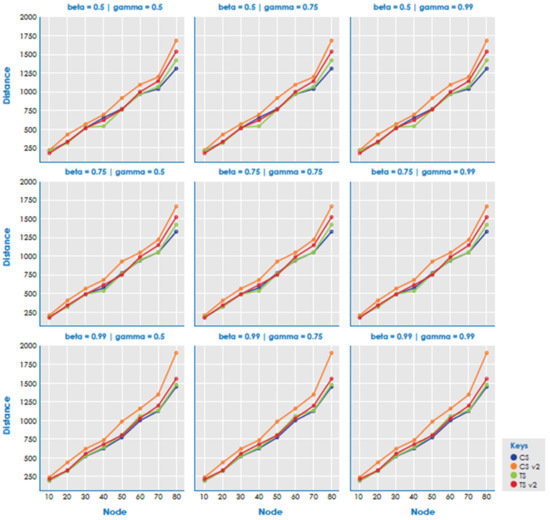
Figure 3.
Total distance by methods. A = 0.99 and supermarket = 60%.
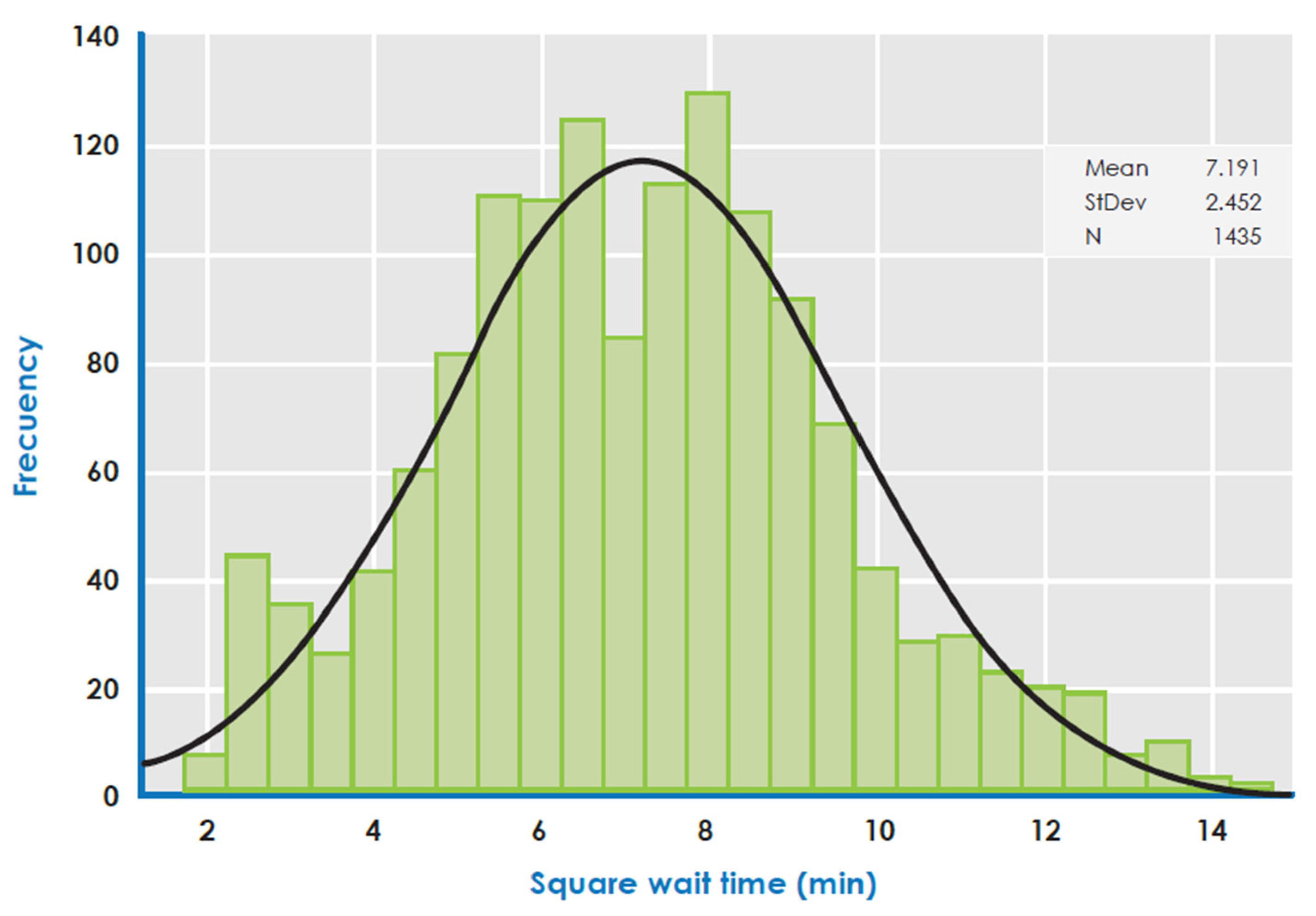
Figure 4 shows the waiting time distribution for all brands (Table 2). Figure 5 shows the waiting time distribution as a function of . The waiting time distribution is almost normally distributed, validating the probability distribution suggested in Section 2. Historically, 10% to 60% of a supermarket’s total customers visit every day. We recommend a deterministic mean service time between 15 and 25 min for road customers and supermarkets, respectively.
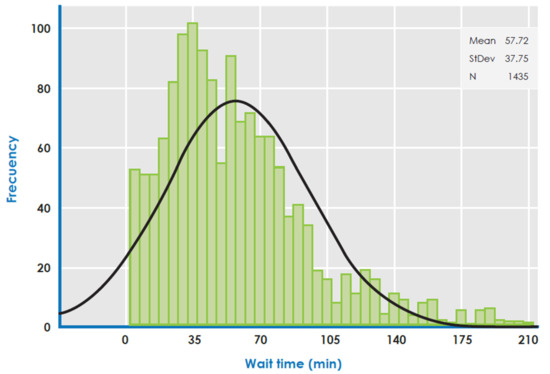
Figure 4.
Histogram of supermarket waiting time.

Table 2.
Statistical data of supermarket-type customers.
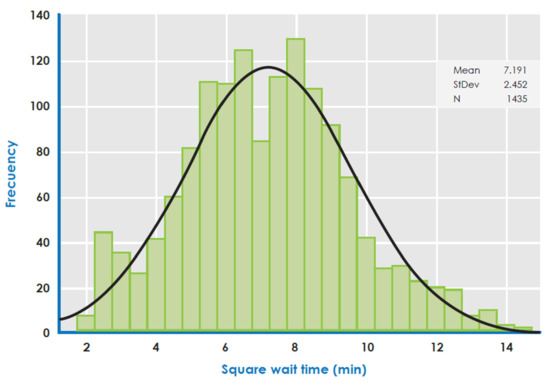
Figure 5.
Histogram applying transformation to supermarket waiting time.
Meanwhile, we used historical data to establish the 80 customers’ demand, mean wait time, travel times, and distances randomly selected, 10, 20, 30, … 80, and then set the supermarket variable at 20%, 40% and 60% and randomly selected them again. We only selected supermarkets with random waiting times and set a deadline of half the working time (). We only used the average waiting time for road customers. To study how the confidence level () influenced chance constraints, we used instances of 0.5, 0.75, and 0.99 for each confidence level, i.e., = 0.5, 0.75 and 0.99, = 0.5, 075, and 0.99, and = 0.5, 0.75, and 0.99. Additionally, we used the highest value for the standard deviation of the random variable . We set the rest of the parameters as , , and . We set the parameters of the TS , , the CS to , , and established 100 simulations for every iteration of the MC proceedings. We ran 10 instances with different seeds for each set of parameters. Likewise, we incorporated the maximum runtime as a stop criterion set in 3600 min.
The resolution was made with TS and CS with their respective version 2. Table 3, Table 4 and Tables S1–S4 show the result for the average distance, vehicles, and execution time; the results establish a direct relationship between the increase in the percentage of stochastic customers and the number of customers with the increased distances. Likewise, the number of trucks and distances increased with higher confidence levels, alpha (associated with the deadline constraint) being the one which harms the objective function the most.

Table 3.
Summary of the results obtained by the company data using GAMS.

Table 4.
TS and CS results for the real case.
The results show that version 2 (i.e., when the feasibility of only the best candidate is tested) has reduced runtime; however, the average distances and amount of trucks are not necessarily reduced.
The above is explained because CS and TS test the feasibility of each candidate and select the best of them; in contrast, the best candidate selected for version 2 could have worse values after testing the feasibility. However, version 2 reduces the runtime by increasing the accuracy (i.e., increasing the number of MC simulations) and the number of candidates of each iteration. Meanwhile, CS is executed in a greater time than TS because each candidate is chosen from the best move; in contrast, in TS, the candidates are selected randomly, performing fewer calculations in each iteration.
3.2. Case Ice Cream Industry Results
The city of Santiago, Chile is in a valley of 15,000 . The big customers of the Ice Cream Industry are 157 establishments with 43 customers with hard time windows and stochastic service divided into five zones: center, north, east, west and south. Table 3 shows the distance, the number of trucks, deadline exceed, working time exceed, and runtime obtained by GAMS. The large number of customers generates a low-quality solution using the GAMS method. GAMS programming was carried out by creating subgroups throughout the different areas of Santiago. The total post-resolution time exceeds 20 h. A daily excess of a 22 h deadline is incurred with the truck fleet, and it is possible not to exceed the normal working hours of the drivers.
The results obtained with the TS and CS algorithms for the ice cream industry problem show a (1) clear decrease in processing time, (2) reduction in the distance traveled, (3) do not exceed the deadline, and (4) do not they generate extra work. The results delivered by TS and CS increase the overall quality of service by reducing the deadlines (Table 4).
4. Conclusions
In this work, the VRPTW-ST model is used to solve a routing problem in Santiago de Chile, specifically in the distribution center of the ice cream area of the company Unilever. The TS and CS optimization methods were validated by comparison with the GAMS algorithm. The results validated the use of CS for VRPTW-ST, and the resolution capacity of the CS algorithm for problems with stochastic time-out variables was established. The CS algorithm obtained better results compared with TS.
This study demonstrates that CS and TS can solve stochastic variables using MC simulations at each stage.
A greater number of MC simulations in each algorithm iteration increases the robustness of the results but increases computation time. The effect of using the MC simulation is not similar for both heuristics; CS is subjected to more candidates than TS in each interaction.
The best candidate is selected to improve the model, and then the MC simulation is run. These modifications (TSv2 and CSv2) reduce the processing time without increasing the total distance traveled.
There is a slight advantage in the CS2 vs. TS2, showing the efficiency of incorporating chaotic neurons when choosing candidates. Chaotic neurons generate greater diversification in the search space for possible solutions.
A model with probability restrictions concerning a model with deterministic variables (i) requires more time for resolution, (ii) reduces the maximum number of customers in the model, and (iii) increases the distances and vehicles required for resolution. The uncertainty of the waiting times generates an increase in the calculation times of the optimal solution; if the number of customers increases with stochastic waiting times, the complexity of the model increases. This model uncertainty must be controlled using different levels of services in F(x) to categorize each customer.
To validate the implementation of TS and CS methods, the results were compared with the authors’ works [32,39]. The adjustment of the TS and CS parameters improved convergence and achieved better results compared with the GAMS algorithm. The improved performance in the distribution of refrigerated elements of the Unilever Company is achieved by the best search features of the CS method for VRPTW-ST models, (i) compliance with restrictions without decreasing service levels; (ii) the ability to plan routes in shorter times; (iii) shorter total routes, and (iv) reducing cost overruns by controlling overtime.
The experiments were performed comparing real models with a size limit of 20 customers for the three optimization techniques. Using the GAMS technique with sizes greater than 20 customers, the optimization model developed in the research cannot be solved quickly enough for operational decision making. The applicability limits of the experiment were restricted to 80 customers using the CS optimization techniques. The growth of processing times and computer memory generates operating restrictions for the model with a client size equal to or less than 100.
The high randomness of the waiting time generates a very costly restriction. The decision-maker must select the product delivery policy with the confidence levels that best suit their needs by modifying the constraint values of the proposed model.
The use of efficient mathematical models positively influences the correct daily decision making of a company. This type of optimization tool facilitates the work of administrators, reducing costs and above all, time, allowing adjustments to be quickly made before possible eventualities that huddle in the logistic chain.
For future work, we propose to consider (i) the randomness of travel times. This random time variable would allow us to adjust the model’s results to the real conditions in a city with high traffic flow.
The model presented considers deterministic customer demand. Therefore, another extension of the model corresponds (ii) to the uncertain customer demand. Finally, (iii) the randomness presented in the future extended model requires a study on execution times. This study will allow us to establish the real computational cost of each random variable.
Supplementary Materials
The following are available online at https://www.mdpi.com/article/10.3390/math9212750/s1, Table S1: Averages of the execution time, amount of trucks, and distance obtained for the TS method with α = 0.5 according to the confidence levels β and γ, and percentage of supermarkets., Table S2: Averages of the execution time, amount of trucks, and distance obtained for the TSv2 method with α = 0.75 according to the confidence levels β and γ. and percentage of supermarkets, Table S3: Averages of the execution time, amount of trucks, and distance obtained for the CS method with α = 0.5 according to the confidence levels β and γ, and percentage of supermarkets, Table S4: Averages of the execution time, amount of trucks, and distance obtained for the CSv2 method with α = 0.5 according to the confidence levels β and γ, and percentage of supermarkets.
Author Contributions
Conceptualization, S.D., M.A. and G.F.; methodology, M.V., G.F. and S.D.; validation, M.A. and M.C.; formal analysis, M.C. and M.A.; Investigation, S.D., M.A. and M.V.; writing—original draft preparation, M.C. and M.V.; writing—review and editing, G.F., S.D. and M.V.; project administration, M.A., M.C. and G.F.; funding acquisition, S.D., M.C. and M.A. All authors have read and agreed to the published version of the manuscript.
Funding
This research has been supported by DICYT (Scientific and Technological Research Bureau) of the University of Santiago of Chile (USACH) and Department of Industrial Engineering. This work was supported in part by Fondecyt (Chile) Grant No. 11200993 (M.V.).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are available on request from the corresponding author.
Acknowledgments
This research has been supported by DICYT (Scientific and Technological Research Bureau) of the University of Santiago of Chile (USACH) and Department of Industrial Engineering.
Conflicts of Interest
The authors declare no conflict of interest.
Notations
| TS | Tabu search |
| CS | Chaotic search |
| TW | Time windows |
| ST | Service times |
| MC | Monte Carlo |
| TSv2 | Modified tabu search algorithm |
| CSv2 | Modified chaotic search algorithm |
| VRP | Vehicle routing problems |
| SVRP | Stochastic vehicle routing problem |
| VRPD | Vehicle routing problem with deadline |
| VRPSD | Vehicle routing problem with stochastic demand |
| GAMS | General algebraic modeling systems |
| VRPTW | Vehicle routing problem with time windows |
| GRASP | Greedy randomized adaptive search procedure |
| RVRPTW | Robust vehicle routing problem with time windows |
| SDVRPTW | Single-depot vehicle-routing problem with time windows |
| VRPTW-ST | Vehicle routing problem with hard time windows and stochastic service time |
| SDVRP-MDA | Split-delivery vehicle routing problem with minimum delivery amounts |
References
- Theophilus, O.; Dulebenets, M.A.; Pasha, J.; Lau, Y.Y.; Fathollahi-Fard, A.M.; Mazaheri, A. Truck scheduling optimization at a cold-chain cross-docking terminal with product perishability considerations. Comput. Ind. Eng. 2021, 156, 107240. [Google Scholar] [CrossRef]
- Yu, Y.; Xiao, T. Analysis of cold-chain service outsourcing modes in a fresh agri-product supply chain. Transp. Res. Part E Logist. Transp. Rev. 2021, 148, 102264. [Google Scholar] [CrossRef]
- Zhang, S.; Chen, N.; She, N.; Li, K. Location optimization of a competitive distribution center for urban cold chain logistics in terms of low-carbon emissions. Comput. Ind. Eng. 2021, 154, 107120. [Google Scholar] [CrossRef]
- He, B.; Yin, L. Prediction Modelling of Cold Chain Logistics Demand Based on Data Mining Algorithm. Math. Probl. Eng. 2021, 2021, 3421478. [Google Scholar] [CrossRef]
- Hu, B.; Huang, B.; Liu, Z.; Guo, H.; Chen, Z.; Shi, L. Optimization Model of Carbon Footprint of Fresh Products in Cold Chain from the Energy Conservation and Emission Reduction Perspective. Math. Probl. Eng. 2021, 2021, 5559021. [Google Scholar] [CrossRef]
- Li, X.; Zhou, K. Multi-objective cold chain logistic distribution center location based on carbon emission. Environ. Sci. Pollut. Res. 2021, 28, 32396–32404. [Google Scholar] [CrossRef]
- Papadimitriou, C.H.; Steiglitz, K. Combinatorial Optimization: Algorithms and Complexity; Prentice-Hall: Hoboken, NJ, USA, 1982. [Google Scholar]
- Demirel, E.; Demirel, N.; Gökçen, H. A mixed integer linear programming model to optimize reverse logistics activities of end-of-life vehicles in Turkey. J. Clean. Prod. 2016, 112, 2101–2113. [Google Scholar] [CrossRef]
- Gupta, S.; Haq, A.; Ali, I.; Sarkar, B. Significance of multi-objective optimization in logistics problem for multi-product supply chain network under the intuitionistic fuzzy environment. Complex Intell. Syst. 2021, 7, 2119–2139. [Google Scholar] [CrossRef]
- López-Ospina, H.; Cortés, C.E.; Pérez, J.; Peña, R.; Figueroa-García, J.C.; Urrutia-Mosquera, J. A maximum entropy optimization model for origin-destination trip matrix estimation with fuzzy entropic parameters. Transp. A Transp. Sci. 2021, 1–39. [Google Scholar] [CrossRef]
- Gmira, M.; Gendreau, M.; Lodi, A.; Potvin, J.Y. Tabu search for the time-dependent vehicle routing problem with time windows on a road network. Eur. J. Oper. Res. 2021, 288, 129–140. [Google Scholar] [CrossRef]
- Heidari, A.; Dong, Z.Y.; Zhang, D.; Siano, P.; Aghaei, J. Mixed-integer nonlinear programming formulation for distribution networks reliability optimization. IEEE Trans. Ind. Inform. 2018, 14, 1952–1961. [Google Scholar] [CrossRef]
- Fuertes, G.; Navarrete, R.; Alfaro, M.; Millan, G.; Vargas, M.; Lagos, C. Adaptive equalization using artificial neural networks for a visible light communication system. In Proceedings of the IEEE International Conference on Automation, Concepcion, Chile, 17–19 October 2018; pp. 1–6. [Google Scholar]
- Kumar, R.; Chandrawat, R.K.; Sarkar, B.; Joshi, V.; Majumder, A. An advanced optimization technique for smart production using α-cut based quadrilateral fuzzy number. Int. J. Fuzzy Syst. 2021, 23, 107–127. [Google Scholar] [CrossRef]
- Garai, A.; Chowdhury, S.; Sarkar, B.; Roy, T.K. Cost-effective subsidy policy for growers and biofuels-plants in closed-loop supply chain of herbs and herbal medicines: An interactive bi-objective optimization in T-environment. Appl. Soft Comput. 2021, 100, 106949. [Google Scholar] [CrossRef]
- Sarkar, B.; Mondal, S.P.; Hur, S.; Ahmadian, A.; Salahshour, S.; Guchhait, R.; Iqbal, M.W. An optimization technique for national income determination model with stability analysis of differential equation in discrete and continuous process under the uncertain environment. RAIRO Oper. Res. 2019, 53, 1649–1674. [Google Scholar] [CrossRef] [Green Version]
- Kłosowski, G.; Kozłowski, E.; Gola, A. Integer linear programming in optimization of waste after cutting in the furniture manufacturing. In Intelligent Systems in Production Engineering and Maintenance; Springer International Publishing: Wroclaw, Poland, 2018; pp. 260–270. [Google Scholar]
- Güiza, J.; Luque, R.; Murillo, J.; Romero, R.; Barrera, D.; López-Ospina, H. Integrating pricing and coordinated inventory decisions between one warehouse and multiple retailers. J. Ind. Prod. Eng. 2021, 38, 1–11. [Google Scholar] [CrossRef]
- Kang, C.W.; Imran, M.; Omair, M.; Ahmed, W.; Ullah, M.; Sarkar, B. Stochastic-petri net modeling and optimization for outdoor patients in building sustainable healthcare system considering staff absenteeism. Mathematics 2019, 7, 499. [Google Scholar] [CrossRef] [Green Version]
- Sabattin, J.; Fuertes, G.; Alfaro, M.; Quezada, L.; Vargas, M. Optimization of large electric power distribution using a parallel genetic algorithm with dandelion strategy. Turk. J. Electr. Eng. Comput. Sci. 2018, 26, 1–13. [Google Scholar] [CrossRef]
- Samanta, S.; Dubey, V.K.; Sarkar, B. Measure of influences in social networks. Appl. Soft Comput. 2021, 99, 106858. [Google Scholar] [CrossRef]
- Toth, P.; Vigo, D. Vehicle Routing: Problems, Methods, and Applications; SIAM: Philadelphia, PA, USA, 2014; ISBN 1611973589. [Google Scholar]
- Gendreau, M.; Potvin, J.-Y. Handbook of Metaheuristics; Springer: Melbourne, Australia, 2010; ISBN 9781441916655. [Google Scholar]
- Linfati, R.; Escobar, J.W. Reoptimization heuristic for the capacitated vehicle routing problem. J. Adv. Transp. 2018, 2018, 8. [Google Scholar] [CrossRef]
- Feng, Y.; Zhang, R.-Q.; Jia, G. Vehicle routing problems with fuel consumption and stochastic travel speeds. Math. Probl. Eng. 2017, 2017, 16. [Google Scholar] [CrossRef]
- Zeng, Z.; Xu, W.; Xu, Z.; Shao, W. A hybrid GRASP+VND heuristic for the two-echelon vehicle routing problem arising in city logistics. Math. Probl. Eng. 2014, 2014, 517467. [Google Scholar] [CrossRef] [Green Version]
- Kaiwartya, O.; Kumar, S.; Lobiyal, D.K.; Tiwari, P.K.; Abdullah, A.H.; Hassan, A.N. Multiobjective dynamic vehicle routing problem and time seed based solution using particle swarm optimization. J. Sens. 2015, 2015, 14. [Google Scholar] [CrossRef]
- Wang, Q.; Ji, Q.; Chiu, C.-H. Optimal routing for heterogeneous fixed fleets of multicompartment vehicles. Math. Probl. Eng. 2014, 2014, 847630. [Google Scholar] [CrossRef] [Green Version]
- Zhang, X.; Zhong, S.; Liu, Y.; Wang, X. A framing link based tabu search algorithm for large-scale multidepot vehicle routing problems. Math. Probl. Eng. 2014, 2014, 13. [Google Scholar] [CrossRef] [Green Version]
- Yue, Y.; Zhang, T.; Yue, Q. Improved fractal space filling curves hybrid optimization algorithm for vehicle routing problem. Comput. Intell. Neurosci. 2015, 2015, 9. [Google Scholar] [CrossRef]
- Xu, H.; Pu, P.; Duan, F. A hybrid ant colony optimization for dynamic multidepot vehicle routing problem. Discret. Dyn. Nat. Soc. 2018, 2018, 3624728. [Google Scholar] [CrossRef] [Green Version]
- Tao, N.-R.; Jiang, Z.-H.; Liu, J.-F.; Xia, B.-X.; Li, B.-H. A metaheuristic algorithm to transporter scheduling for assembly blocks in a shipyard considering precedence and cooperating constraints. Discret. Dyn. Nat. Soc. 2019, 2019, 14. [Google Scholar] [CrossRef]
- Urzúa-Morales, J.G.; Sepulveda-Rojas, J.P.; Alfaro, M.; Fuertes, G.; Ternero, R.; Vargas, M. Logistic modeling of the last mile: Case study Santiago, Chile. Sustainability 2020, 12, 648. [Google Scholar] [CrossRef] [Green Version]
- Hsu, C.I.; Hung, S.F.; Li, H.C. Vehicle routing problem with time-windows for perishable food delivery. J. Food Eng. 2007, 80, 465–475. [Google Scholar] [CrossRef]
- Errico, F.; Desaulniers, G.; Gendreau, M.; Rei, W.; Rousseau, L.M. The vehicle routing problem with hard time windows and stochastic service times. EURO J. Transp. Logist. 2018, 7, 223–251. [Google Scholar] [CrossRef]
- Dantzig, G.B.; Ramser, J.H. The truck dispatching problem. Manag. Sci. 1959, 6, 80–91. [Google Scholar] [CrossRef]
- Taş, D.; Dellaert, N.; van Woensel, T.; de Kok, T. Vehicle routing problem with stochastic travel times including soft time windows and service costs. Comput. Oper. Res. 2013, 40, 214–224. [Google Scholar] [CrossRef] [Green Version]
- Ehmke, J.F.; Campbell, A.M.; Urban, T.L. Ensuring service levels in routing problems with time windows and stochastic travel times. Eur. J. Oper. Res. 2015, 240, 539–550. [Google Scholar] [CrossRef]
- Xu, H.; Pu, P.; Duan, F. Dynamic vehicle routing problems with enhanced ant colony optimization. Discret. Dyn. Nat. Soc. 2018, 2018, 1295485. [Google Scholar] [CrossRef] [Green Version]
- Yu, N.-K.; Hu, R.; Qian, B.; Wang, L. An improved lagrangian relaxation algorithm for solving the lower bound of production logistics. In Proceedings of the International Conference Intelligent Computing Theories and Application, Shenzhen, China, 12–15 August 2021; Springer: Shenzhen, China, 2021; pp. 652–662. [Google Scholar]
- Laporte, G.; Louveaux, F.; Mercure, H. The vehicle routing problem with stochastic travel times. Transp. Sci. 1992, 26, 161–170. [Google Scholar] [CrossRef]
- Han, S.; Zhao, L.; Chen, K.; Luo, Z.W.; Mishra, D. Appointment scheduling and routing optimization of attended home delivery system with random customer behavior. Eur. J. Oper. Res. 2017, 262, 966–980. [Google Scholar] [CrossRef]
- Zhang, D.; Li, D.; Sun, H.; Hou, L. A vehicle routing problem with distribution uncertainty in deadlines. Eur. J. Oper. Res. 2021, 292, 311–326. [Google Scholar] [CrossRef]
- Shukla, N.; Choudhary, A.K.; Prakash, P.K.S.; Fernandes, K.J.; Tiwari, M.K. Algorithm portfolios for logistics optimization considering stochastic demands and mobility allowance. Int. J. Prod. Econ. 2013, 141, 146–166. [Google Scholar] [CrossRef] [Green Version]
- Han, A.F.W.; Chu, Y.C. A multi-start heuristic approach for the split-delivery vehicle routing problem with minimum delivery amounts. Transp. Res. Part E Logist. Transp. Rev. 2016, 88, 11–31. [Google Scholar] [CrossRef]
- Braaten, S.; Gjønnes, O.; Hvattum, L.M.; Tirado, G. Heuristics for the robust vehicle routing problem with time windows. Expert Syst. Appl. 2017, 77, 136–147. [Google Scholar] [CrossRef]
- Marinakis, Y.; Marinaki, M.; Migdalas, A. A hybrid clonal selection algorithm for the location routing problem with stochastic demands. Ann. Math. Artif. Intell. 2016, 76, 121–142. [Google Scholar] [CrossRef]
- Binart, S.; Dejax, P.; Gendreau, M.; Semet, F. A 2-stage method for a field service routing problem with stochastic travel and service times. Comput. Oper. Res. 2016, 65, 64–75. [Google Scholar] [CrossRef]
- Li, X.; Tian, P.; Leung, S.C.H. Vehicle routing problems with time windows and stochastic travel and service times: Models and algorithm. Int. J. Prod. Econ. 2010, 125, 137–145. [Google Scholar] [CrossRef]
- Ikeguchi, T.; Hasegawa, M.; Kimura, T.; Matsuura, T.; Aihara, K. Theory and applications of chaotic optimization methods. In Innovative Computing Methods and Their Applications to Engineering Problems; Springer: Berlin/Heidelberg, Germany, 2011; pp. 131–161. [Google Scholar]
- Berhan, E.; Beshah, B.; Kitaw, D.; Abraham, A. Stochastic vehicle routing problem: A literature survey. J. Inf. Knowl. Manag. 2014, 13, 1450022. [Google Scholar] [CrossRef]
- Sawik, B. Weighted-sum approach for bi-objective optimization of fleet size with environmental aspects. In Applications of Management Science; Emerald Publishing Limited: Bingley, UK, 2018; pp. 101–116. [Google Scholar]
- Kato, H.; Kimura, T.; Ikeguchi, T. Self-organized neural network structure depending on the STDP learning rules. In Applications of Nonlinear Dynamics; Springer: Berlin/Heidelberg, Germany, 2009; pp. 413–416. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).