Abstract
Manufacturing process optimization is an ever-actual goal. Within this goal, machining parameters optimization is a very important task. Machining parameters strongly influence the manufacturing costs, process productivity and piece quality. Literature presents a series of optimization methods. The results supplied by these methods are comparable and it is difficult to establish which method is the best. For machining parameters optimization, this paper proposes a novel, simple and efficient method, without additional costs related to new software packages. This approach is based on linear mathematical programming. The optimization mathematical models are, however, nonlinear. Therefore, mathematical model linearization is required. The major and difficult problem is the linearization of the objective function. This represents the key element of the proposed optimization method. In this respect, the paper proposes an original mathematical procedure for calculating the part of the objective function that refers to the analytical integration of the tool life into the model. This calculus procedure was transposed into an original software tool. For demonstrating the validity of the method, a comparison is presented among the results obtained by certain optimization techniques. It results that the proposed method is simple and as good as those presented by the literature.
Keywords:
optimization; linear objective function; linear solving method; machining parameters; comparative results MSC:
90XX; 90C05
1. Introduction
For machining parameters optimization, the relationships among machining parameters, piece accuracy, process cost/productivity and technological resources must be mathematically modelled. These relationships concern the restrictive technical conditions, as well as the chosen optimization criterion. Among the first scientific studies focused on technological process optimization papers [1,2] must be mentioned. Most of the relations of the optimization mathematical models are nonlinear. The particularities of the models for machining parameters optimization should recommend the use of nonlinear mathematical programming [3]. In nonlinear mathematical programming, certain methods could be used in accordance with the particularities of the mathematical models, but there is no general valid method. It must also be mentioned that the methods of nonlinear mathematical programming (for example convex programming) use algorithms of linear mathematical programming. In addition, the efficiency of these methods depends on choosing a starting solution. These particularities and the nonlinearity of the mathematical models have determined seeking certain solutions outside the mathematical programming field, as well. As a consequence, literature presents numerous optimization techniques combined with mathematical programming elements. Linear mathematical programming supplies certain efficient algorithms that can be successfully used for solving the discussed issue. These algorithms impose that the optimization mathematical models be linear. For example, in linear programming, the Simplex algorithm is one of the most efficient [3,4,5]. The fundamentals of this algorithm were set up by the American mathematician G.B. Dantzig [4]. Due to the advantages of this algorithm, the present paper proposes to present the method for using linear mathematical programming in solving nonlinear mathematical models, regarding machining parameters optimization. The problem that must be solved is the mathematical model’s linearization. The cutting constraints of the mathematical models related to machining parameters optimization might be easily linearized by a calculus trick. Objective function linearization is the major problem. The present paper approaches this issue, presenting an original solving method. The difficulty of linearizing the optimization is due to a mathematical function, which is a component of the objective function that integrates the tool life. The tool life is also a function that controls the variables , , /, , . The convenient solution is finding a replacement function that facilitates the linearization of the objective function. The new problem is the calculus of this function. For automation of this calculus, the authors have conceived a software tool with a view to the industrial use of the method.
2. Materials and Methods
2.1. Literature Review
Literature supplies a series of optimization techniques for machining parameters optimization. The optimization techniques use differential calculus, Lagrange multipliers, geometric programming, goal-programming, linear programming, dynamic programming, simulated annealing, genetic algorithm, particle swarm optimization, and a certain combination of those. Shin and Joo [6] approach the optimization for a multi-pass turning operation. The paper proposes a mathematical model for optimization of the tool passes of rough cutting and finishing cutting. The objective function refers to cost minimization. The dynamic programming method (DPM) is used for optimization. The mathematical model proposed by Shin and Joo is also used by many other papers. Wang [7] uses a neural network (NN) for multiple-objective optimization of machining parameters. Gupta et al. [8] approach the optimal subdivision of the total depth of cut and has in mind the total production cost minimization. For solving it is used an integer programming model (IPM). Chen and Tsai [9] have been developed a method centered on the simulated annealing algorithm and the Hooke-Jeeves pattern search (SA/PS) for unit production cost minimization in case of multi-pass turning. Chen and Tsai extended the Shin and Joo model by adding other constraints. The optimization model proposed by Chen and Tsai is also used in other papers. Onwubolu and Kumalo [10] propose an optimization method based on a genetic algorithm (GA) for the determination of the cutting parameters in multi-pass machining operations aimed at unit production cost minimization. Chen [11] is based on the application of scatter search (SS) for turning operations optimization. Kumar et al. [12] also use a genetic algorithm (GA) for the unit production cost optimization. Sardinas et al. [13] approach a multi-objective optimization technique, based on genetic algorithms (GA) to optimize the machining parameters in turning processes. Satishkumar et al. [14] develop a comparative study regarding the use of genetic algorithms (GA), simulated annealing (SA), and ant colony optimization (ACO), with respect to optimization of multi-pass turning. The considered objective function refers to minimizing total production cost. Wang and Chen [15] approach an evolutionary-strategy (ES)-based optimization technique to optimize machining conditions for the multi-pass dry turning. The method aims at the minimization of unit production cost. Srinivas et al. [16] approach an optimization technique of machining parameters using particle swarm optimization (PSO) to minimize unit production cost. Bharathi Raja and Baskar [17] make a retrospection regarding simulated annealing (SA), genetic algorithm (GA), and particle swarm optimization (PSO) in various mathematical models. The considered objective functions were: to minimize the total production cost for multi-pass turning, to maximize the material removal rate, and to minimize the combined objective functions (the production time and the production cost). Costa et al. [18] propose a hybrid particle swarm optimization technique (HPSO) for production cost optimization in the case of multi-pass turning. Xie and Guo [19] approach an optimization technique based on ant colony optimizations (ACO) combined with a pass enumerating method to minimize the unit production cost for multi-pass turning operations. Belloufi et al. [20] present a hybrid genetic algorithm by using sequential quadratic programming (HGASQP) in order to determine the cutting conditions in case of multi-pass turning. Lu et al. [21] approach a hybrid method to minimize the production cost per unit piece. The used method combines genetic algorithm (GA), sequential quadratic programming (SQP), and dynamic programming (DP) technique for optimizing the sequence of cutting pass and the machining parameters. In paper [22] Lu et al. continue the ideas from [20] to minimize production time per unit piece. Yildiz [23] develops a hybrid optimization algorithm entitled hybrid robust differential evolution (HRDE) by adding ideas of Taguchi’s method for minimizing the production cost regarding multi-pass turning operation. Homami et al. [24] used an artificial neural network (ANN) for modelling certain experimental results, that have been then optimized through a genetic algorithm (GA). Gayatri and Baskar [25] have analysed three non-traditional algorithms for minimizing unit production cost in the case of multi-pass turning: genetic algorithm (GA), simulated annealing (SA) and particle swarm optimization (PSO). Mellal and Williams [26] use a method, called the cuckoo optimization algorithm (COA) for machining parameters optimization. The aim of the optimization is the minimization of the unit production cost. Jabri et al. [27] propose a hybrid genetic simulated annealing algorithm (HSAGA) to find minimum unit production cost, for multi-pass turning operation. Rana and Lalwani [28] approach turning process optimization using an amended differential evolution algorithm (ADEA), to optimize unit production cost and production time. Xu et al. [29] propose an improved flower pollination algorithm (FPA) for optimization of multi-pass machining parameters-turning. The optimization aims to minimize the unit production cost. Abbas et al. [30] approach machining of AZ61 Magnesium Alloy in a different way: they consider that is important to assure minimum machining times of unit volume and minimum surfaces roughness, Ra, simultaneously. Paper [30] aims to establish the turning conditions that are capable to supply the minimum unit-volume machining time, the minimum surface roughness, and the minimum cost of machining one part, using a Pareto optimization (PO) of an artificial neural network (ANN). Abbas et al. [31] use genetic programming (GP) for optimization of machining of AISI 1045 steel, taking into consideration different cooling and blurbification techniques. Mia et al. [32] approach machining parameters optimization in case of turning using intelligent evolutionary algorithms. The optimization is made for the lowest surface roughness and cutting temperature and there are used two methods: teaching-learning-based optimization and bacterial foraging optimization. Miodragovic et al. [33] propose the use of a subpopulation firefly algorithm (SP-FA) for the optimization of multi-pass turning. The objective function refers to minimizing unit production costs. Rana et al. [34] presented a review of research related to the optimization of machining using evolutionary optimization techniques (years 2000–2006). Sofuoglu et al. [35] propose a method for solving heuristic optimization problems to determine optimum parameters while minimizing cost functions. Sun et al. [36] propose the use of linear mathematical programming for feed rate scheduling of five-axis machining. Sun et al. present a method where the nonlinear multi-constrained feed rate scheduling problem is transformed into a manageable linear programming problem. The overview of the literature shows that many methods have been developed for machining parameters optimization. But the question: which method is the best? has not a clear answer yet. The analysed papers use similar mathematical models for machining parameters optimization. Many methods are based on the mathematical models overtaken from Shin and Joo [6], Gupta et al. [8], Chen and Tsai [9], Chen [11], Mellal and Williams [26]. There are also presented certain comparative results [14,15,20,25,27,28,29,33,35]. From the searched literature it results that machining parameters optimization can be done in three modalities: (a) into two separate phases, one for the roughing machining and the second for the finishing machining; (b) global approach, into a single phase; (c) pass optimization. The potential of linear mathematical programming should be even more turned to advantage in the case of machining parameters optimization. For this, the mathematical models should be linear. From this viewpoint, the way of integrating the tool life equation into the mathematical models is very important. This equation is essential for machining parameters optimization. For this reason, starting with Taylor, this subject permanently came to the attention of researchers from the field [1,37,38,39,40,41,42,43,44,45]. One of the commonly used tool life equations is the extended Taylor’s tool life equation, as follows:
2.2. Proposed Method
The main aim of the work is to present a mathematical procedure of linearization of the mathematical models for machining parameters optimization for a single tool pass. This procedure connected to the use of certain existing, efficient and cheap algorithms (for example Simplex) represents the novel proposed method for machining parameters optimization. This procedure involves a novel modality of integrating the tool life into the mathematical models. For demonstrating the validity of the method, the obtained results are compared to those from the analyzed papers in Section 2.1. The comparison is based on the mathematical model proposed by Shin and Joo [6]. The mathematical model for a machining parameters optimization issue must express the objective function under practical cutting constraints.
2.3. A Novel Expression of the Objective Function
The machining cost per single-pass can be expressed as:
where, is machining idle cost due to loading and unloading operations and tool idle motion time ($/piece) and represents the part of the machining cost per single-pass that varies with the machining parameters ($/pass). represents the weight for the pass related to machine idle cost. As objective function we have in mind the minimization of the part of the machining cost per single-pass that varies with the machining parameters (min ). This part is composed of the following cost elements:
Parameters D and L refer to the machined surface at every pass. Thus, becomes:
where:
The Equation (8) is further processed with a view to integrating it into a mathematical model of linear programming. For this purpose, the substitution procedure from the paper [46] and developed in [47] will be customized for the specific conditions of the present paper and we will use the following notation:
For the values of , and T met in industrial experience, Equation (10) might be approximated by , as follows:
The mathematical procedure (11) allows the linearization of the objective function.
Considering Equations (1) and (11), the objective function can be expressed in a new form:
2.4. AlphaBeta Software Module
The AlphaBeta is a software module for calculating and parameters. AlphaBeta was conceived by means of the Delphi environment and is presented as a flow chart in Figure 1 and Table 1, with the following remark: if the rough pass and finishing pass are made by the same tool, the tool life from Equation (10) must be considered as a combination between the rough tool life and finishing tool life.
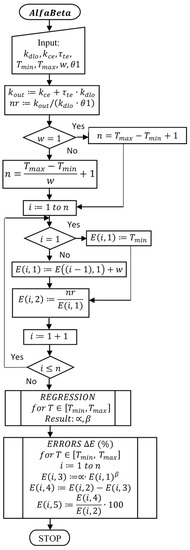
Figure 1.
Flow chart of the and β calculus.

In accordance with Figure 1, the calculus is made in four stages: (a) the calculus of the elements that depend on the concrete cutting conditions (; (b) the calculus of the data series that must be mathematically modeled with a view to determining the concrete form of the function (11). It is about the first two columns of Table 1; (c) the concrete calculus of functions (11), meaning the determination of α and β parameters (regression analysis); (d) the errors calculus. The use of this software tool is simple: the users have just to introduce the values of the seven required variables (Figure 1 and Table 2).

Table 2.
Input data and results (AlphaBeta software).
Thus:
2.5. Cutting Constraints
Cutting parameters bounds:
Tool life constraint:
Cutting force constraint:
Machine power constraint:
Stable cutting region constraint:
Chip-tool interface temperature constraint:
Surface finish constraint:
Practical relation between rough and finish parameters:
The mathematical model given by relations (12) and (14)–(25) might be linearized using the following substitutions:
Variables and refer to or to .
Consequently, the new form of the objective function becomes:
where is:
The cutting constraints become:
where is:
where is:
where is:
where is:
where is:
where is:
For finishing:
3. Results and Discussion
To demonstrate the validity of the proposed method, the obtained results are compared with those presented by the papers mentioned in Section 2.1. The numerical data used for the comparison are mentioned in Table 3 [14,20,21,22,23,25,27,29,33,35], and the results are presented in Table 4.

Table 3.
Input data for the comparison of different methods.

Table 4.
Comparison of various optimization methods.
The problem to be solved by the proposed method refers to the optimization of a turning process. The input data are: the diameter D = 50 mm, the length L = 300 mm, maximum allowable surface SR = 10 and nose radius of the cutting tool r = 1.2 mm. Tool material is carbide and work piece material is carbon steel.
The analyzed methods, including the proposed method, are based on the use of the tool life function . In case rough machining as well as finish machining are made by the same tool, the tool life T must be considered . Literature presents the relations [18,26,27,28,29,33,35]:
The Equations (50) and (51) were used by the methods from Table 4, less by the proposed method (ObOFL). For the proposed method Equation (13) was used. In this case or are obtained by convenient establishment of the parameter . For making the comparison of the results the same must be used. For the case of Equation (50) this is possible, meaning that can be determined. For the case of Equation (51) a correlation between and cannot be done. For this reason, the evaluation of the validity of the proposed method must consider only the case when considering given by Equation (50). Comparing the unit costs, as well as the machining parameters from Table 4, it might be considered that the proposed method is as good as the analyzed methods (Figure 2, Figure 3, Figure 4 and Figure 5).
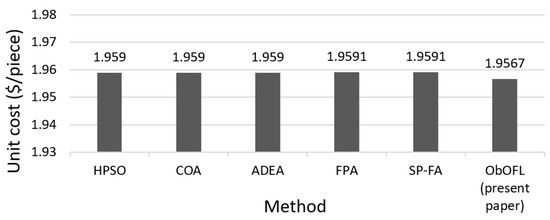
Figure 2.
Comparison of the unit costs.
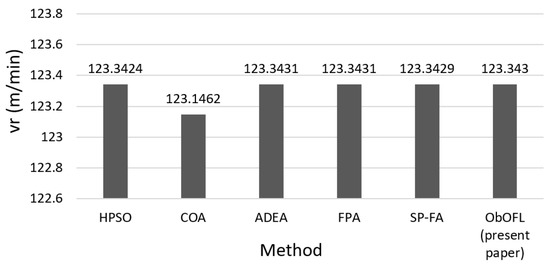
Figure 3.
Comparison of the cutting speeds.
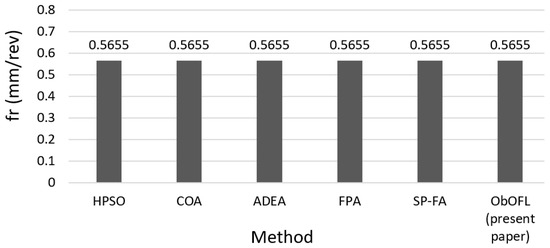
Figure 4.
Comparison of the feed rates.
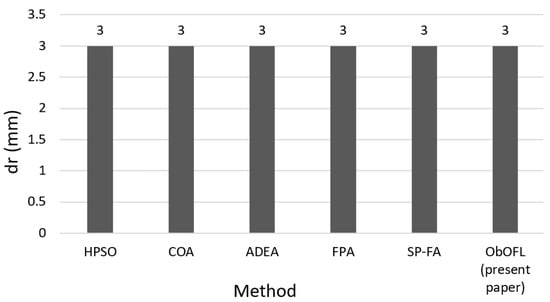
Figure 5.
Comparison of the depths of cut.
The present paper approaches the machining parameters optimization in the case of single-pass turning. Rough pass and finish pass could be done by the same tool or by different tools. The novel optimization mathematical model is given by relations (29)–(49). The proposed method is accurate, efficient, and cheap because the linear programming software usually exists in the software platforms of the companies. For linearizing the objective function, it is proposed the mathematical procedure in accordance with Equation (11). The curves and are overlapped (the error is very low, Figure 6).
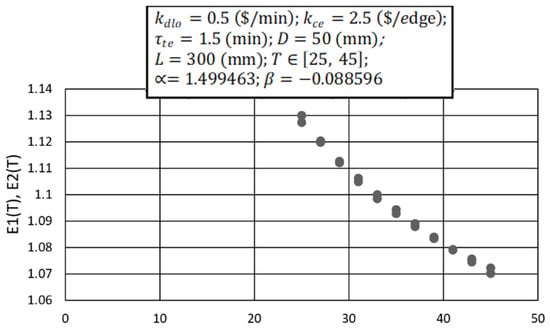
Figure 6.
Approximation E1(T) ≅ E2(T).
AlphaBeta software tool allows the calculus of the errors, as well. The minimum and maximum errors at are: = 0.0002, meaning 0.01839%; 0.00258, meaning 0.22875%. The minimum and maximum errors for the tool life are: = −0.1029 (min), meaning 0.25098%; = 1.29176 (min), meaning 2.875058%. Parameter for , and for . For a single pass, or . The proposed method was applied under the conditions specified in the papers that have been used for the comparisons (Table 3). Machining idle cost, , was also calculated in accordance with the same papers.
4. Conclusions
The present paper addresses the issue of machining parameters optimization. The novelty of the present paper is represented by the proposed mathematical procedure for the use of linear solving methods in solving nonlinear mathematical models, related to machining parameters optimization. The purpose is the use of certain existing and widely used efficient and cheap algorithms, aiming at cost reduction in respect to machining parameters optimization.
This mathematical procedure aims to express the objective function (nonlinear) into a form that allows the linearization. Thus, the part of the objective function that does not allow the linearization is replaced by a convenient function (11), that can be calculated by the original algorithm described in Figure 1.
The key to linearizing the mathematical model is linearizing the objective function.
For automation of the calculus of α and β parameters the proposed algorithm was transposed into the AlphaBeta software tool, conceived by the authors.
The tool life Equation (1) is fundamental for the method described in the present paper.
The proposed optimization method is based on the use of an existing linear programming algorithm (for example Simplex) applied to linearizing the mathematical model (29)–(49). The method does not involve additional costs because the software (linear programming) exists.
The mathematical model (29)–(49) is generally valid, the quantitative data (Table 3) are varying in accordance with the used materials.
Linearization of the constraints was ensured by the substitutions (26)–(28).
The proposed mathematical procedure is good because the calculated errors are low (Figure 6). Lower the interval considered for the tool life , lower the errors for .
The comparative study from Section 3 has confirmed the validity of the proposed method. The results obtained by the proposed method are as good as the results obtained by the analysed methods (Figure 2, Figure 3, Figure 4 and Figure 5). The statement is valid for the case of equalizing of the Equations (13) and (50). In case Equations (13) and (51) must be equalized must be further studied with a view to finding a correlation . Without this correlation the comparison of the results is difficult. For a correct design of optimization mathematical models, it is required that the parameters and are correctly determined, not empiric.
From a mathematical point of view, the proposed procedure might be applied to the mathematical functions expressed by multiplications of sub-functions of (10) type, or similar, and that can be expressed by functions of (11) type. The limit is imposed by the accepted errors.
In future research, the authors intend to apply the proposed method for those industrial cases where the data for developing the optimization mathematical models are poorer. For a correct design of mathematical models, the authors are further studying the correlation between the parameters 1 and .
Author Contributions
Conceptualization, C.G. and N.-V.I.; methodology, C.G.; software, N.-V.I. and G.O.; validation, C.G., N.-V.I. and G.O.; formal analysis, C.G. and N.-V.I.; investigation, C.G., N.-V.I. and G.O.; resources, C.G. and G.O.; writing—original draft preparation, N.-V.I.; writing—review and editing, C.G. and N.-V.I.; supervision, N.-V.I. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data sharing is not applied.
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
| Constants of the tool life equation | |
| Feed rates in rough and finish turning, respectively (mm/rev) | |
| Depths of cut in rough and finish turning, respectively (mm) | |
| Machining cost per single-pass ($/pass) | |
| UC | Unit production cost, excluding material cost ($/piece) |
| Machining idle cost duet to loading and unloading operations and tool idle motion time ($/piece) | |
| Weight for pass related to machine idle cost | |
| The part of the machining cost per single pass that varies with the machining parameters ($/pass) | |
| ,, | Cutting cost by actual time, tool cost and tool exchange cost, respectively ($/pass) |
| Actual cutting time per single-pass (min) | |
| Direct labour cost and overheads ($/min) | |
| Cutting edge cost ($/edge) | |
| Tool exchange time (min) | |
| Global using tool cost per single pass ($/pass) | |
| Diameter and length of work surface, respectively (mm) | |
| Depths of cut for each pass and total depth of cut to be removed, respectively (mm) | |
| , | Cutting speed, cutting speed in rough and finish turning, respectively (m/min) |
| Feed rate (mm/rev) | |
| Tool life (min) | |
| Coefficient and exponent calculated for making the mathematical model linear | |
| Tool life of weighted combination of and (min) | |
| Expected tool life for rough and finish turning, respectively (min) | |
| Weight for , in accordance with the present paper | |
| Weight for , in accordance with papers analysed in Section 2.1 | |
| Regression | Regression subprogram |
| Errors | Subprogram for errors calculation |
| Lower and upper bounds for cutting speed, respectively (m/min) | |
| Lower and upper bounds for feed rate, respectively (mm/rev) | |
| Lower and upper bounds for depth of cut (mm) | |
| Lower and upper bounds for tool-life, respectively (min) | |
| n | Number of points for regression analysis |
| Constants of the cutting force equation | |
| Maximum allowable cutting force (N) | |
| r | Nose radius of the cutting tool (mm) |
| Power efficiency (%) | |
| Maximum allowable cutting power (kW) | |
| Maximum allowable chip-tool interface temperature (°C) | |
| Constants for the equation of chip-tool interface temperature | |
| SCR | Limit of stable cutting region |
| SR | Maximum allowable surface roughness (mm) |
| Constants related to formula of the stable cutting region | |
| Preparation time (as loading and unloading time), idle tool motion time (as tool travel and tool approach/depart time), and total machine idle time, respectively (min) | |
| Constants related to tool travel and approach/depart time, respectively (min) | |
| Increment of tool life increasing with a view to the regression analysis | |
| Constants for roughing and finishing parameter relations |
References
- Taylor, F.W. On the Art of Cutting Metals; The American Society of Mechanical Engineers: New York, NY, USA, 1907. [Google Scholar]
- Gilbert, W.W. Economics of Machining, Machining-Theory and Practice; American Society of Metals: Cleveland, OH, USA, 1950; pp. 465–485. [Google Scholar]
- Cottle, R.W.; Thapa, M.N. Linear and Nonlinear Optimization; Springer: New York, NY, USA, 2017; pp. 61–228. [Google Scholar] [CrossRef]
- Dantzig, G.B. Linear Programming and Extension; Princeton University Press: New York, NY, USA, 1963. [Google Scholar]
- Disser, Y.; Skutella, M. The Simplex Algorithm Is NP-Mighty. ACM Trans. Algorithms 2019, 15, 5. [Google Scholar] [CrossRef] [Green Version]
- Shin, Y.C.; Joo, Y.S. Optimization of machining conditions with practical constraints. Int. J. Prod. Res. 1992, 30, 2907–2919. [Google Scholar] [CrossRef]
- Wang, J. Multiple-objective optimization of machining operations based on neural networks. Int. J. Adv. Manuf. Technol. 1993, 8, 235–243. [Google Scholar] [CrossRef]
- Gupta, R.; Batra, J.L.; Lal, G.K. Determination of optimal subdivision of depth of cut in multipass turning with constraints. Int. J. Prod. Res. 1995, 33, 2555–2565. [Google Scholar] [CrossRef]
- Chen, M.C.; Tsai, D.M. A simulated annealing approach for optimization of multi-pass turning operations. Int. J. Prod. Res. 1996, 34, 2803–2825. [Google Scholar] [CrossRef]
- Onwubolu, G.C.; Kumalo, T. Optimization of multipass turning operations with genetic algorithms. Int. J. Prod. Res. 2001, 39, 3727–3745. [Google Scholar] [CrossRef]
- Chen, M.C. Optimizing machining economics models of turning operations using the scatter search approach. Int. J. Prod. Res. 2004, 42, 2611–2625. [Google Scholar] [CrossRef]
- Kumar, A.S.; Khan, M.A.; Thiraviam, R. Machining parameters optimization for alumina based ceramic cutting tools using genetic algorithm. Mach. Sci. Technol. 2006, 10, 471–489. [Google Scholar] [CrossRef]
- Sardinas, R.Q.; Santana, M.R.; Brindis, E.A. Genetic algorithm-based multi-objective optimization of cutting parameters in turning processes. Eng. Appl. Art. Intell. 2006, 19, 127–133. [Google Scholar] [CrossRef]
- Satishkumar, S.; Asokan, P.; Kumanan, S. Optimization of depth of cut in multi-pass turning using nontraditional optimization techniques. Int. J. Adv. Manuf. Technol. 2006, 29, 230–238. [Google Scholar] [CrossRef]
- Wang, Y.C.; Chen, T. Modelling and optimization of machining conditions for the multi-pass dry turning process. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2008, 222, 1387–1394. [Google Scholar] [CrossRef]
- Srinivas, J.; Giri, R.; Yang, S.H. Optimization of multi-pass turning using particle swarm intelligence. Int. J. Adv. Manuf. Technol. 2009, 40, 56–66. [Google Scholar] [CrossRef]
- Bharathi Raja, S.; Baskar, N. Optimization techniques for machining operations: A retrospective research based on various mathematical models. Int. J. Adv. Manuf. Technol. 2010, 48, 1075–1090. [Google Scholar] [CrossRef]
- Costa, A.; Celano, G.; Fichera, S. Optimization of multi-pass turning economies through a hybrid particle swarm optimization technique. Int. J. Adv. Manuf. Technol. 2011, 53, 421–433. [Google Scholar] [CrossRef]
- Xie, S.; Guo, Y. Optimisation of machining parameters in multi-pass turnings using ant colony optimisations. Int. J. Mach. Mach. Mater. 2012, 11, 204–220. [Google Scholar] [CrossRef]
- Belloufi, A.; Assas, M.; Rezgui, I. Optimization of Turning Operations by Using a Hybrid Genetic Algorithm with Sequential Quadratic Programming. J. Appl. Res. Technol. 2013, 11, 88–94. [Google Scholar] [CrossRef]
- Lu, K.; Jing, M.; Zhang, X.; Liu, H. Optimization of sequential subdivision of depth of cut in turning operations using dynamic programming. Int. J. Adv. Manuf. Technol. 2013, 68, 1733–1744. [Google Scholar] [CrossRef]
- Lu, K.; Jing, M.; Zhang, X.; Dong, G.; Liu, H. An effective optimization algorithm for multipass turning of flexible workpieces. J. Intell. Manuf. 2015, 26, 831–840. [Google Scholar] [CrossRef]
- Yildiz, A.R. Hybrid Taguchi-differential evolution algorithm for optimization of multipass turning operations. Appl. Soft Comput. 2013, 13, 1433–1439. [Google Scholar] [CrossRef]
- Mokhtari Homami, R.; Fadaei Tehrani, A.; Mirzadeh, H.; Movahedi, B.; Azimifar, F. Optimization of turning process using artificial intelligence technology. Int. J. Adv. Manuf. Technol. 2014, 70, 1205–1217. [Google Scholar] [CrossRef]
- Gayatri, R.; Baskar, N. Performance analysis of non-traditional algorithmic parameters in machining operation. Int. J. Adv. Manuf. Technol. 2015, 77, 443–460. [Google Scholar] [CrossRef]
- Mellal, M.A.; Williams, E.J. Cuckoo optimization algorithm for unit production cost in multi-pass turning operations. Int. J. Adv. Manuf. Technol. 2017, 76, 647–656, Erratum in Int. J. Adv. Manuf. Technol. 2017, 91, 4385. [Google Scholar] [CrossRef]
- Jabri, A.; Barcany, A.E.; Khalfi, A.E.I. Multipass Turning Operation Process Optimization Using Hybrid Genetic Simulated Annealing Algorithm. Model. Simul. Eng. 2017, 2017, 1940635. [Google Scholar] [CrossRef] [Green Version]
- Rana, P.B.; Lalwani, D.L. Optimization of turning process using Amended Differential Evolution Algorithm. Eng. Sci. Technol. Int. J. 2017, 20, 1285–1301. [Google Scholar] [CrossRef]
- Xu, S.; Wang, Y.; Huang, F. Optimization of multi-pass turning parameters through an improved flower pollination algorithm. Int. J. Adv. Manuf. Technol. 2017, 89, 503–514. [Google Scholar] [CrossRef]
- Abbas, A.T.; Pimenov, D.Y.; Erdakov, I.N.; Taha, M.A.; Soliman, M.S.; Rayes, M.M.E. ANN Surface Roughness Optimization of AZ61 Magnesium Alloy Finish Turning: Minimum Machining Times at Prime Machining Costs. Materials 2018, 11, 808. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Abbas, A.T.; Benyahia, F.; Rayes, M.M.E.; Pruncu, C.; Taha, M.A.; Hegab, H. Towards Optimization of Machining Performance and Sustainability Aspects when Turning AISI 1045 Steel under Different Cooling and Lubrication Strategies. Materials 2019, 12, 3023. [Google Scholar] [CrossRef] [Green Version]
- Mia, M.; Krolczyk, G.; Maruda, R.; Wojciechowski, S. Intelligent Optimization of Hard-Turning Parameters Using Evolutionary Algorithms for Smart Manufacturing. Materials 2019, 12, 879. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Miodragovic, G.R.; Dordevic, V.; Bulatovic, R.R.; Petrovic, A. Optimization of multi-pass turning and multi-pass face milling using subpopulation firefly algorithm. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2019, 233, 1520–1540. [Google Scholar] [CrossRef]
- Rana, P.B.; Patel, J.L.; Lalwani, D.I. Parametric Optimization of Turning Process Using Evolutionary Optimization Techniques—A Review (2000–2016). In Soft Computing for Problem Solving. Advances in Intelligent Systems and Computing; Bansal, J., Das, K., Nagar, A., Deep, K., Ojha, A., Eds.; Springer: Singapore, 2019; Volume 817. [Google Scholar] [CrossRef]
- Sofuoğlu, M.A.; Çakır, F.H.; Gürgen, S. An efficient approach by adjusting bounds for heuristic optimization algorithms. Soft Comput. 2019, 23, 5199–5212. [Google Scholar] [CrossRef]
- Sun, Y.; Chen, M.; Jia, J.; Lee, Y.; Guo, D. Jerk-limited feedrate scheduling and optimization for five-axis machining using new piecewise linear programming approach. Sci. China Technol. Sci. 2019, 62, 1067–1081. [Google Scholar] [CrossRef]
- Da Silva, R.B.; Sales, W.F.; Costa, E.S.; Ezugwu, E.O.; Bonney, J.; Da Silva, M.B.; Machado, A.R. Surface integrity and tool life when turning of Ti-6Al-4V with coolant applied by different methods. Int. J. Adv. Manuf. Technol. 2017, 93, 1893–1902. [Google Scholar] [CrossRef]
- Bonfa, M.M.; Costa, E.S.; Sales, W.F.; Amorim, F.L.; Maia, L.H.A.; Machado, A.R. Evaluation of tool life and workpiece surface roughness in turning of AISI D6 hardened steel using PCBN tools and minimum quantity of lubricant (MQL) applied at different directions. Int. J. Adv. Manuf. Technol. 2019, 103, 971–984. [Google Scholar] [CrossRef]
- Kumar, R.; Sahoo, A.K.; Mishra, P.C.; Das, R.K. Investigation on Tool Wear and Surface Characteristics in Hard Turning Under Air-Water Jet Spray Impingement Cooling Environment. Tribol. Ind. 2019, 41, 172–187. [Google Scholar] [CrossRef]
- Kronenberg, M. Replacing the Taylor Formula by a New Tool Life Equation. Int. J. Mach. Tool Des. Res. 1970, 10, 193–202. [Google Scholar] [CrossRef]
- Mamalis, A.G.; Kundrak, J.; Horvath, M. Wear and Tool Life of CBN Cutting Tools. Int. J. Adv. Manuf. Technol. 2002, 20, 475–479. [Google Scholar] [CrossRef]
- Koning, W.; Depiereux, W.R. Wie lassen sich Vorschub und Schnittgeshwindigkeit optimieren? Ind. Anz. 1969, 91, 1481–1484. [Google Scholar]
- Johansson, D.; Hägglund, S.; Bushlya, V.; Stahl, J.E. Assessment of Commonly Used Tool Life Models in Metal Cutting. Procedia Manuf. 2017, 11, 602–609. [Google Scholar] [CrossRef]
- Johansson, D.; Akujärvi, V.; Hägglund, S.; Bushlya, V.; Stahl, J.E. Selecting Cutting Data Tests for Cutting Data Modeling Using the Colding Tool Life Model. Procedia CIRP 2018, 72, 197–201. [Google Scholar] [CrossRef]
- Ojolo, S.J.; Ogunkomaiya, O. A study of effects of machining parameters on tool life. Int. J. Mater. Sci. Appl. 2014, 3, 183–199. [Google Scholar] [CrossRef] [Green Version]
- Draghici, G.; Chiriacescu, S.T. Calculul durabilității sculei și regimului de așchiere folosind programarea matematică (Calculus of tool life and cutting parameters using mathematical programming). Stud. Cercet. Mech. Appl. (Stud. Res. Appl. Mech.) 1971, 30, 975–999. [Google Scholar]
- Draghici, G.; Ivan, N.V. Programarea liniara mai buna ca programarea convexa in unele cazuri de determinare a parametrilor optimi de exploatare a sculelor (Linear programming-better than the convex one-in some cases of optimal determination of the parameters in tool exploitation). Constr. Mas. (Mach. Build.) 1977, XXIX, 598–601. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).