Abstract
In this work, we introduce and theoretically analyze a relatively simple numerical algorithm to solve a double-fractional condensate model. The mathematical system is a generalization of the famous Gross–Pitaevskii equation, which is a model consisting of two nonlinear complex-valued diffusive differential equations. The continuous model studied in this manuscript is a multidimensional system that includes Riesz-type spatial fractional derivatives. We prove here the relevant features of the numerical algorithm, and illustrative simulations will be shown to verify the quadratic order of convergence in both the space and time variables.
Dataset License: CC-BY-NC.
Keywords:
fractional Bose–Einstein model; double-fractional system; fully discrete model; stability and convergence analysis MSC:
65Mxx; 65Qxx
1. Introduction
There have been dramatic developments in the area of fractional calculus in recent decades [1], and many areas in applied and theoretical mathematics have benefited from these developments [2,3]. In particular, there have been substantial developments in the theory and application of numerical methods for fractional partial differential equations. For example, from a theoretical point of view, theoretical analyses of conservative finite-difference schemes to solve the Riesz space-fractional Gross–Pitaevskii system have been proposed in the literature [4], along with convergent three-step numerical methods to solve double-fractional condensates, explicit dissipation-preserving methods for Riesz space-fractional nonlinear wave equations in multiple dimensions [5], energy conservative difference schemes for nonlinear fractional Schrödinger equations [6], conservative difference schemes for the Riesz space-fractional sine-Gordon equation [7], high-order central difference schemes for Caputo fractional derivatives [8], among other examples.
It is important to point out that most of the methods mentioned above refer to discretizations for partial differential equations with fractional derivatives in space. In particular, those models consider fractional partial derivatives of the Riesz type. It is worth noting that the Riesz derivatives are linear combinations of the left and right Riemann–Liouville operators. other approaches strive to provide discretizations of systems of partial differential equations with Caputo-type derivatives in time. As mentioned above, there are reports on high-order central difference schemes for Caputo fractional derivatives [8], modified integral discretization schemes for two-point boundary value problems with Caputo fractional derivatives [9], predictor–corrector schemes for solving nonlinear delay differential equations of fractional order [10], numerical integrators for Caputo fractional differential equations with infinity memory effect at initial conditions [11], second-order schemes for the fast evaluation of the Caputo fractional derivatives [12], and homotopy perturbation methods for solving the Caputo-type fractional-order Volterra–Fredholm integro-differential equations [13].
Various systems mentioned above are capable of preserving some physical quantities, such as mass and energy; the development of numerical schemes that preserve these features is an important area of research. Historically, there have been many reports in this area, including systems of integer-order partial differential equations. For example, there are reports on the numerical solutions of conservative nonlinear Klein-Gordon [14] and sine-Gordon [15,16] equations, symplectic methods for the Schrödinger equation [17], fast and structure-preserving schemes for partial differential equations based on the discrete variational derivative method [18], structure-preserving numerical methods for partial differential equations [19], dissipative or conservative Galerkin methods using discrete partial derivatives for nonlinear evolution equations [20], among other reports [21]. These approaches have been extended to the fractional-case scenario, and have been helpful in designing numerical models that are able to preserve the mass and the energy of nonlinear systems [22,23,24].
Motivated by these developments, the present paper presents an efficient discrete model to approximate the solutions of a nonlinear double-fractional two-component Gross–Pitaevskii system. The system consists of two coupled complex-valued functions, whose dynamics are described by parabolic partial differential equations with nonlinear reactions. We consider here spatial derivatives of fractional order in the Riesz sense. The mathematical model is a complicated system, and the need to approximate its solutions is an interesting task. We propose here an easy-to-implement scheme to approximate the solutions and fully analyze them theoretically. We establish the properties of stability and convergence using a discrete form of Grönwall’s inequality. Some simulations will be provided to illustrate the performance of the scheme, and a numerical test of the convergence is provided. Here, it is worth noting that the main advantage of the present discretization is that the computer implementation is easy. Moreover, the scheme is quadratically convergent, and the experiments show that such is the case. Other discretizations [4,25] are more difficult to implement computationally, in view that a fixed point technique should be coded along with the computational algorithm. Moreover, those schemes provide more complicated conditions in order to guarantee the convergence. Finally, one of the limitations of the present methodology is that, to the best of our knowledge, it is not capable of preserving the energy of the system.
Let and . Define , denote by , for each , and let be such that , for all . Define and , and let . Agree that and , and define . Functions defined on will be extended to all of by letting them be equal to zero outside .
Definition 1
(Podlubny [1]). Let Γ be the Gamma function, let be a function, and assume that and are such that . We define
Definition 2.
Let , and fix . Let and n be as in the definition above. For each , we define
Agree also that
For the remainder, D, , , and are real parameters, and . Let and satisfy and , and assume that and . Here, we study the following problem, for each (see [26,27])
Definition 3
(Ortigueira [28]). Suppose that and assume that . We define the discrete operator
where
It is important to note that, if f is sufficiently smooth, and , then
for almost all (see [29]).
2. Numerical Algorithm
For the remainder, we will let N and be natural numbers, with . Define and . Let us introduce
Let , where . If , we define as . For each , we use to denote a computational approximation to . Finally, let represent the collection of all with the property that .
Definition 4.
If and , we define the averages
and the differences
Moreover, we agree that
With this nomenclature, we introduce the following numerical algorithm to approximate the solution of (4) on , for each :
It is clear that, if , , and are known for some , then the resulting iterative formulas wield expressions where the only unknowns are and . On the other hand, and are prescribed by the initial data.
In order to determine the approximations when the time is equal to , we employ the initial conditions and , for all . The initial conditions yield then
As a consequence, we obtain
and
For the sake of convenience, we let , and denote with the complex-valued functions whose domains are . Moreover, set .
Theorem 1.
For all initial conditions, the system (17) has a unique solution.
Proof.
We provide the proof for the one-dimensional case only, the higher dimensional scenario being similar. Beforehand, notice that and are defined by the initial conditions, and so are and , as shown by the identities (20) and (21), respectively. Suppose that , , and are obtained. The first numerical model is expressed alternatively in the following form:
for each . Here,
As a consequence, the first equation of the system is rewritten as
where
For the existence of , it suffices show that A is invertible [30]. Observe that
Also, the following hold:
By the previous lemma, A is non-singular, which means that there exists a unique solution of (25). The existence of is proved similarly, noting that the second recursive equation of (17) is rewritten by
where
Moreover, B is the square complex matrix defined by
which is also strictly diagonally dominant. The conclusion follows now by induction. □
The discretization proposed in this work is similar to a linear implicit discretization of (4) in various senses. Indeed, notice that our approach hinges on approximating the nonlinear term at the time , while the linear terms are approximated at the time . The difference is that the linear term of the numerical model (17) is approximated by the average of the numerical solutions at the levels and through and . In that sense, the present discretization would seem computationally more complex than the linear implicit scheme. In this point, we would like to clarify that the linear implicit scheme has the advantage of being a two-step method, but the computational implementation would require solving systems of linear equations similar to those associated to the discrete model (17). On the other hand, as we will see in the following section, our current discretization has convergence of the second order in space, while the corresponding order of the linear implicit scheme is known to be linear.
3. Computational Properties
To prove the consistency, let us define the continuous operators
for each . Define the operators
Finally, for each and , we let
Theorem 2.
Proof.
Suppose that the functions u, v, and V are sufficiently smooth. Then there exist real numbers , , and , such that
The conclusion follows from the triangle inequality and Taylor’s theorem. □
In the following, it is worth recalling that the square-root operator of is the discrete fractional operator , for each .
It is easy to check that, if and , then
These identities will be employed in the proofs of Theorems 3 and 4. Similarly, the following result will be crucial in those proofs.
Lemma 1.
If and belong to , then
Proof.
It is easy to check that
which is what we wanted to prove. □
Next, we consider initial data of the form and . Here, and are both complex functions, and the numerical approximations associated to each of these pars is represented as and , respectively.
Lemma 2.
For each , let and . Agree that
for each . Then there exists a constant , which dependents on τ and h, such that , for each .□
Theorem 3.
Let and be as before. For some , whenever holds, then
Proof.
Beforehand, using the notation above, we observe that
Thus, there is some , such that
Algebraic calculations establish that
These identities and bounding, showing that there exists , with the property that
Subtract then the term from both ends of this chain of inequalities, regroup and observe that . Therefore,
The theorem follows employing a suitable discrete Grönwall inequality (see [31]) with and . □
Theorem 4.
Proof.
The proof is similar to that of the stability property of (17). □
Proof.
The proof of this result is similar to that of Theorem 3 and, for that reason, we provide here a shortened proof only. Beforehand, let and , for each . It is obvious then that the pair satisfies the discrete problem
where
for each . Proceeding now as in the proof of Theorem 3, there exists a constant , such that (50) is satisfied. Following the same steps used to obtain (51) and (52), we may readily obtain the following identities, valid for each :
Again, as in the proof of Theorem 3, we add these last two equations and take the sum on both sides over all , for some . Using telescoping sums, rearranging terms, taking then absolute values, using Young’s inequality and (50), and applying the inequality of the hypotheses, it follows that there is a constant , such that
for sufficiently small values of . In this expression, is the constant used in the proof of Theorem 3, for each . Moreover, in this case,
Letting now , using the discrete Grönwall inequality [31] for sufficiently small values of and substituting the initial conditions of (55), we readily reach that
For the remainder of this work, use , , , , , , , and . Set , and . For illustration purposes, Figure 1, Figure 2 and Figure 3 depicts the approximations to the solutions of (4) for various values of and . Finally, we study numerically the convergence of the scheme (17) using and . Table 1a,b summarize the computational results on the temporal and spatial convergence, and they show that (17) is quadratically convergent.
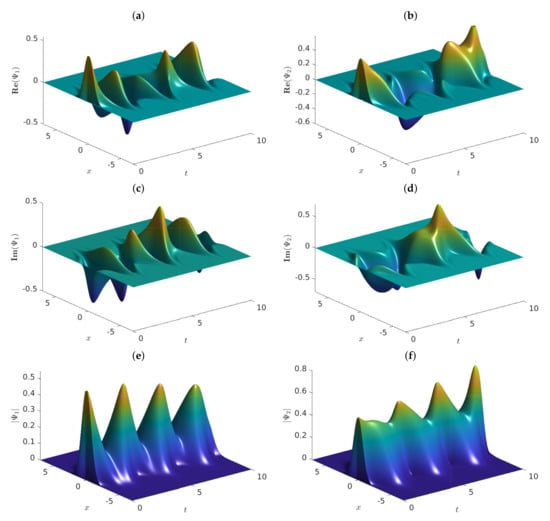
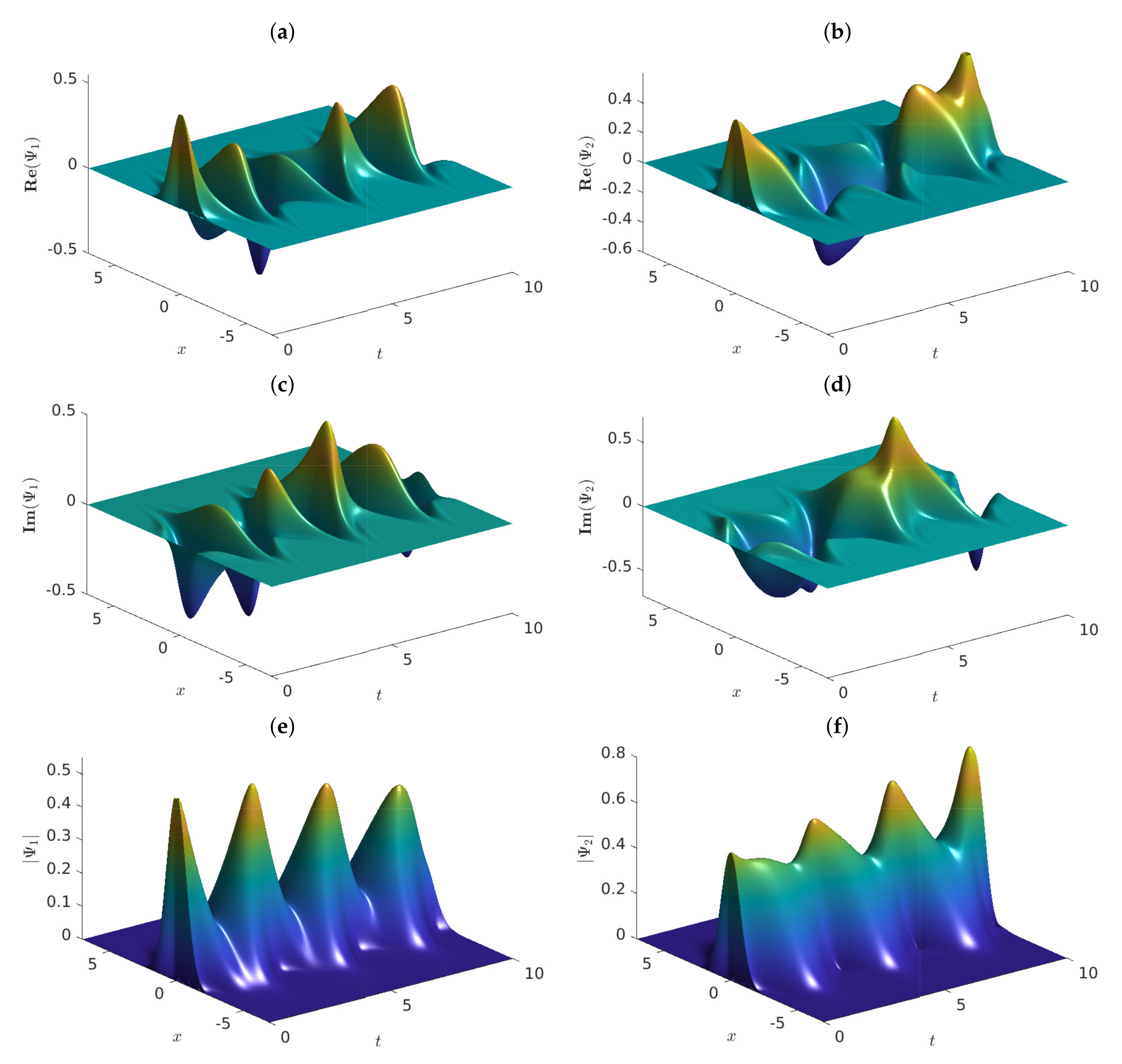
Figure 1.
Graphs of the approximate solutions of problem (4) vs. , employing , and . The graphs show (a) , (b) , (c) , (d) , (e) and (f) .
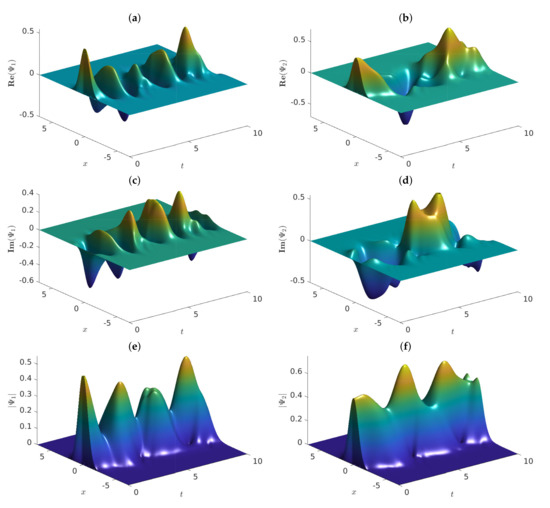
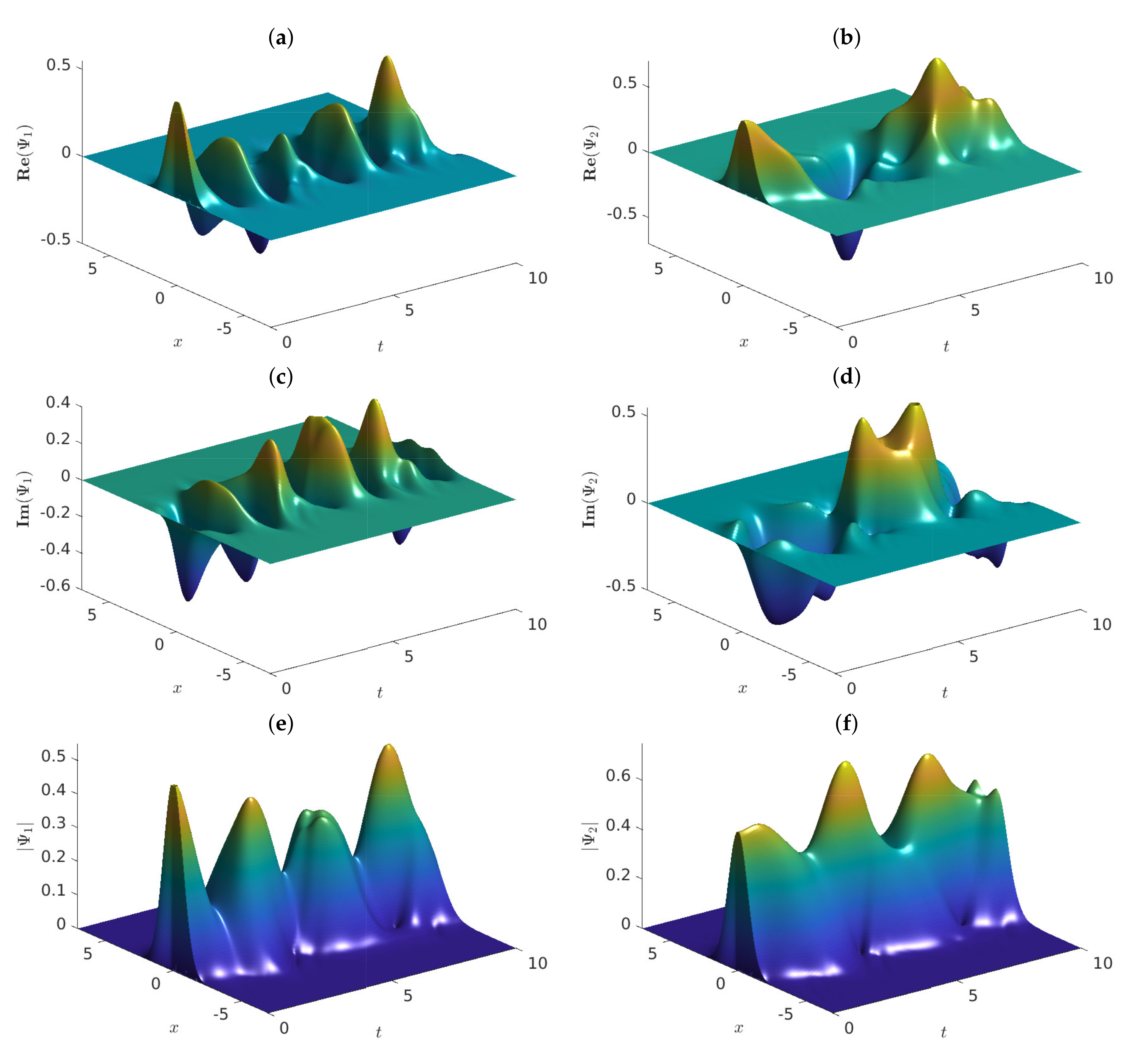
Figure 2.
Graphs of the approximate solutions of problem (4) vs. , employing , and . The graphs show (a) , (b) , (c) , (d) , (e) and (f) .
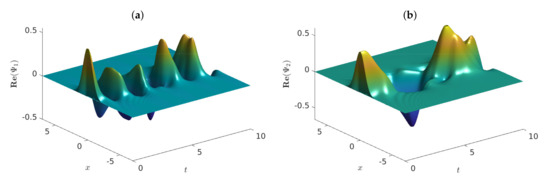
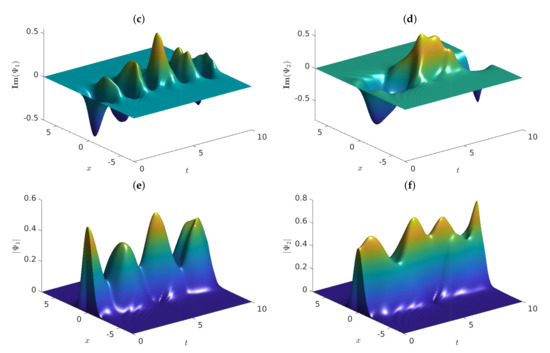
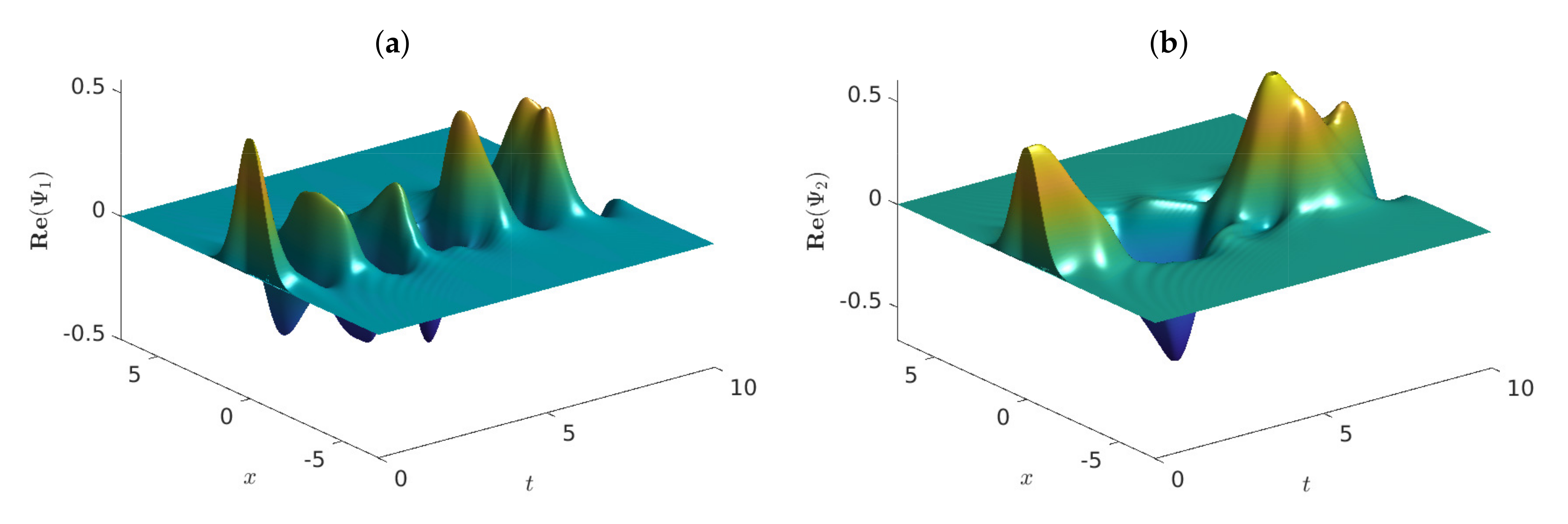
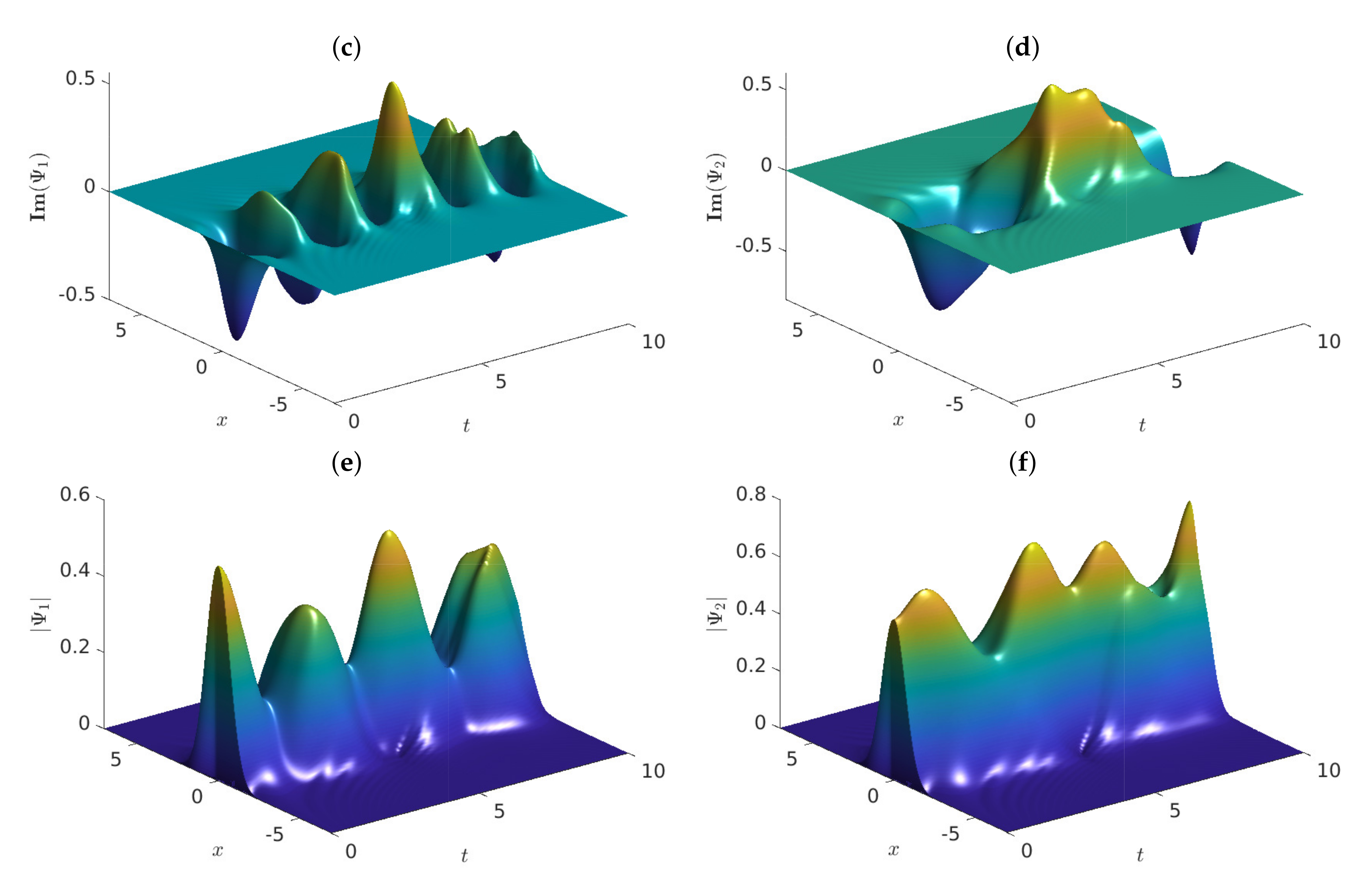
Figure 3.
Graphs of the approximate solutions of problem (4) vs. , employing , and . The graphs show (a) , (b) , (c) , (d) , (e) and (f) .

Table 1.
Computational study of convergence.
4. Conclusions
Before concluding this paper, we must note that our discretization of the double fractional Gross–Pitaevskii system follows a standard approach [4,25]. In particular, this means that the numerical discretization uses local approximations, estimating each of the terms of the mathematical model. A natural question would be whether a non-standard approach could be used to discretize our mathematical model. Here, we understand the adjective ’non-standard’ in the sense of R.E. Mickens [32]. Such topic of investigation is outside the scope of this work, but it is an interesting avenue of research for a future study. On the other hand, the constant in Lemma 2 are not necessarily independent of h and . This is due to the fact that the nonlinear terms in (4) are not globally Lipschitz continuous. This is one of the limitations of our study, and it remains an open problem of research. To solve this shortcoming, it would be desirable to establish the uniform boundedness of the numerical approximations obtained through (4). Following recent reports available in the literature [24], the determination of conserved positive quantities for the finite-difference method (17) would be helpful in bounding the numerical solutions [7]. The authors have attempted to employ the discrete energy method to derive such quantities [33,34]. Unfortunately, their efforts have not yielded conserved positive quantities to this day.
Author Contributions
Conceptualization, J.E.M.-D.; methodology, J.E.M.-D.; software, J.E.M.-D., N.R. and A.J.S.-R.; validation, J.E.M.-D., N.R. and A.J.S.-R.; formal analysis, J.E.M.-D. and A.J.S.-R.; investigation, J.E.M.-D.; resources, J.E.M.-D. and N.R.; data curation, J.E.M.-D. and N.R.; writing—original draft preparation, J.E.M.-D. and A.J.S.-R.; writing—review and editing, J.E.M.-D. and N.R.; visualization, J.E.M.-D.; supervision, J.E.M.-D. and N.R.; project administration, J.E.M.-D. and N.R.; funding acquisition, J.E.M.-D. and N.R. All authors have read and agreed to the published version of the manuscript.
Funding
J.E.M.-D. thanks the National Council of Science and Technology of Mexico for financially supporting him via grant A1-S-45928. Ministerio de Ciencia e Innovación and Regional Development European Funds through project PGC2018-101443-B-I00.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data that support the findings of this study are available from the corresponding author, J.E.M.-D., upon reasonable request.
Acknowledgments
The authors would like to thank the anonymous reviewers and the associate editor for their time and comments. All of their suggestions were strictly followed, and the result was a substantial improvement in the final quality of this work.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Podlubny, I. Fractional Differential Equations: An Introduction to Fractional Derivatives, Fractional Differential Equations, to Methods of Their Solution and Some of Their Applications; Elsevier: Amsterdam, The Netherlands, 1998; Volume 198. [Google Scholar]
- Saeed, A.; Bilal, M.; Gul, T.; Kumam, P.; Khan, A.; Sohail, M.M. Fractional Order Stagnation Point Flow of the Hybrid Nanofluid towards a Stretching Sheet. Sci. Rep. 2021, 11, 20429. [Google Scholar] [CrossRef] [PubMed]
- Gul, T.; Alghamdi, W.; Khan, I.; Ali, I. New similarity variable to transform the fluid flow from PDEs into fractional-order ODEs: Numerical study. Phys. Scr. 2021, 96, 084009. [Google Scholar] [CrossRef]
- Serna-Reyes, A.J.; Macías-Díaz, J. Theoretical analysis of a conservative finite-difference scheme to solve a Riesz space-fractional Gross–Pitaevskii system. J. Comput. Appl. Math. 2021, 113413. [Google Scholar] [CrossRef]
- Macías-Díaz, J. An explicit dissipation-preserving method for Riesz space-fractional nonlinear wave equations in multiple dimensions. Commun. Nonlinear Sci. Numer. Simul. 2018, 59, 67–87. [Google Scholar] [CrossRef]
- Wang, P.; Huang, C. An energy conservative difference scheme for the nonlinear fractional Schrödinger equations. J. Comput. Phys. 2015, 293, 238–251. [Google Scholar] [CrossRef]
- Xing, Z.; Wen, L. A conservative difference scheme for the Riesz space-fractional sine-Gordon equation. Adv. Differ. Equ. 2018, 2018, 238. [Google Scholar] [CrossRef] [Green Version]
- Ying, Y.; Lian, Y.; Tang, S.; Liu, W.K. High-order central difference scheme for Caputo fractional derivative. Comput. Methods Appl. Mech. Eng. 2017, 317, 42–54. [Google Scholar] [CrossRef]
- Cen, Z.; Huang, J.; Xu, A.; Le, A. A modified integral discretization scheme for a two-point boundary value problem with a Caputo fractional derivative. J. Comput. Appl. Math. 2020, 367, 112465. [Google Scholar] [CrossRef]
- Bhalekar, S.; Daftardar-Gejji, V. A predictor-corrector scheme for solving nonlinear delay differential equations of fractional order. J. Fract. Calc. Appl. 2011, 1, 1–9. [Google Scholar]
- Mendes, E.M.; Salgado, G.H.; Aguirre, L.A. Numerical solution of Caputo fractional differential equations with infinity memory effect at initial condition. Commun. Nonlinear Sci. Numer. Simul. 2019, 69, 237–247. [Google Scholar] [CrossRef]
- Yan, Y.; Sun, Z.Z.; Zhang, J. Fast evaluation of the Caputo fractional derivative and its applications to fractional diffusion equations: A second-order scheme. Commun. Comput. Phys. 2017, 22, 1028–1048. [Google Scholar] [CrossRef]
- Das, P.; Rana, S.; Ramos, H. Homotopy perturbation method for solving Caputo-type fractional-order Volterra–Fredholm integro-differential equations. Comput. Math. Methods 2019, 1, e1047. [Google Scholar] [CrossRef] [Green Version]
- Strauss, W.; Vazquez, L. Numerical solution of a nonlinear Klein-Gordon equation. J. Comput. Phys. 1978, 28, 271–278. [Google Scholar] [CrossRef]
- Ben-Yu, G.; Pascual, P.J.; Rodriguez, M.J.; Vázquez, L. Numerical solution of the sine-Gordon equation. Appl. Math. Comput. 1986, 18, 1–14. [Google Scholar] [CrossRef]
- Fei, Z.; Vázquez, L. Two energy conserving numerical schemes for the sine-Gordon equation. Appl. Math. Comput. 1991, 45, 17–30. [Google Scholar] [CrossRef]
- Tang, Y.F.; Vázquez, L.; Zhang, F.; Pérez-García, V. Symplectic methods for the nonlinear Schrödinger equation. Comput. Math. Appl. 1996, 32, 73–83. [Google Scholar] [CrossRef] [Green Version]
- Furihata, D. Fast and structure-preserving schemes for PDEs based on discrete variational derivative method. Geom. Numer. Integr. Its Appl. 2017, 74, 19–22. [Google Scholar]
- Furihata, D.; Matsuo, T. Discrete Variational Derivative Method: A Structure-Preserving Numerical Method for Partial Differential Equations; CRC Press: New York, NY, USA, 2010. [Google Scholar]
- Matsuo, T. Dissipative/conservative Galerkin method using discrete partial derivatives for nonlinear evolution equations. J. Comput. Appl. Math. 2008, 218, 506–521. [Google Scholar] [CrossRef]
- Li, X.G.; Li, S.C. High-order numerical methods with mass and energy conservation for spin–orbit-coupled Bose–Einstein condensates. Int. J. Comput. Math. 2021, 98, 738–757. [Google Scholar] [CrossRef]
- Zhai, L.; Wang, J. High-order conservative scheme for the coupled space fractional nonlinear Schrödinger equations. Int. J. Comput. Math. 2021, 1–22. [Google Scholar] [CrossRef]
- Fu, Y.; Shi, Y.; Zhao, Y. Explicit high-order structure-preserving algorithms for the two-dimensional fractional nonlinear Schrödinger equation. Int. J. Comput. Math. 2021, 1–28. [Google Scholar] [CrossRef]
- Macías-Díaz, J.E. On the solution of a Riesz space-fractional nonlinear wave equation through an efficient and energy-invariant scheme. Int. J. Comput. Math. 2019, 96, 337–361. [Google Scholar] [CrossRef]
- Serna-Reyes, A.J.; Macías-Díaz, J.E.; Reguera, N. A Convergent Three-Step Numerical Method to Solve a Double-Fractional Two-Component Bose–Einstein Condensate. Mathematics 2021, 9, 1412. [Google Scholar] [CrossRef]
- Ertik, H.; Şirin, H.; Demirhan, D.; Büyükkiliç, F. Fractional mathematical investigation of Bose–Einstein condensation in dilute 87Rb, 23Na and 7Li atomic gases. Int. J. Mod. Phys. B 2012, 26, 1250096. [Google Scholar] [CrossRef]
- Perez-Garcia, V.M.; Michinel, H.; Cirac, J.; Lewenstein, M.; Zoller, P. Dynamics of Bose-Einstein condensates: Variational solutions of the Gross–Pitaevskii equations. Phys. Rev. A 1997, 56, 1424. [Google Scholar] [CrossRef]
- Ortigueira, M.D. Riesz potential operators and inverses via fractional centred derivatives. Int. J. Math. Math. Sci. 2006, 2006, 048391. [Google Scholar] [CrossRef]
- Wang, X.; Liu, F.; Chen, X. Novel second-order accurate implicit numerical methods for the Riesz space distributed-order advection-dispersion equations. Adv. Math. Phys. 2015, 2015, 590435. [Google Scholar] [CrossRef]
- Desplanques, J. Théoreme d’algébre. J. Math. Spec. 1887, 9, 12–13. [Google Scholar]
- Pen-Yu, K. Numerical methods for incompressible viscous flow. Sci. Sin. 1977, 20, 287–304. [Google Scholar]
- Mickens, R.E. Nonstandard Finite Difference Schemes: Methodology And Applications, 1st ed.; World Scientific: New York, NY, USA, 2020. [Google Scholar]
- Xiao, A.; Wang, C.; Wang, J. Conservative linearly-implicit difference scheme for a class of modified Zakharov systems with high-order space fractional quantum correction. Appl. Numer. Math. 2019, 146, 379–399. [Google Scholar] [CrossRef]
- Wang, Y.; Li, Q.; Mei, L. A linear, symmetric and energy-conservative scheme for the space-fractional Klein–Gordon–Schrödinger equations. Appl. Math. Lett. 2019, 95, 104–113. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).