Rosenbrock Type Methods for Solving Non-Linear Second-Order in Time Problems

Abstract

In this work, we develop a new class of methods which have been created in order to numerically solve non-linear second-order in time problems in an efficient way. These methods are of the Rosenbrock type, and they can be seen as a generalization of these methods when they are applied to second-order in time problems which have been previously transformed into first-order in time problems. As they also follow the ideas of Runge–Kutta–Nyström methods when solving second-order in time problems, we have called them Rosenbrock–Nyström methods. When solving non-linear problems, Rosenbrock–Nyström methods present less computational cost than implicit Runge–Kutta–Nyström ones, as the non-linear systems which arise at every intermediate stage when Runge–Kutta–Nyström methods are used are replaced with sequences of linear ones.

1. Introduction

In the literature, there are many non-linear second-order in time problems which must be numerically solved by means of appropriate methods. It is usual to use numerical methods that have been designed to numerically solve first-order in time problems by transforming the initial problem into a first-order one. In this way, we have several options to choose from, such as Runge–Kutta methods (RK methods), fractional step Runge–Kutta methods (FSRK methods) or exponential integrators. These methods are a good option if the problem we have is a linear one but they present a high computational cost when the problem we are solving is a non-linear one, as we have to solve non-linear problems at every intermediate stage (see [1,2,3,4]). In this case, a good option is to use Rosenbrock methods or exponential Rosenbrock type methods [5,6,7], for example. However, in this case, when converting the original problem to a first-order one, the dimension of the problem doubles, so the computational cost increases.

Another possibility is to use numerical integrators specially derived to numerically solve second-order in time problems. In this way, we can use, for example, Runge–Kutta–Nyström methods (RKN methods) or fractional step Runge–Kutta–Nyström methods (FSRKN methods) [2,8,9]. When we use this type of method, we have to choose whether to use explicit or implicit methods. When we use explicit methods, there may be stability problems when the problem we are solving is a stiff one. On the other hand, if we choose an implicit method, we can select a method with an infinite stability interval, but with a high computational cost [8] when the problem is non-linear or/and multidimensional in space. In order to avoid the high computational cost that implicit RKN methods present when multidimensional problems in space are solved, FSRKN methods were developed and studied in [9]. The idea of these methods is to split the spatial operator in a suitable way so that at every intermediate stage the problem to be solved is simpler in a certain way than the original one.

In order to avoid all the previous drawbacks when solving a non-linear second-order in time problem, in this paper, we present a new class of methods, which we call Rosenbrock–Nyström methods. These methods avoid the non-linear systems which arise when RKN methods are used by replacing them with sequences of linear ones. Rosenbrock–Nyström methods arise in a natural way as a generalization of Rosenbrock ones when they are applied to second-order in time equations that have been previously transformed into first-order in time problems.

In the literature, the construction of methods of the Rosenbrock type to numerically solve second-order non-linear systems of ordinary differential equations has already been studied [10]. However, the methods presented in that paper differ from the ones presented here. We remark here on three of the most important differences between the methods in [10] and our methods when solving a problem such as $y^{″}(t)=f(t,y)$, $y(0)=y_0$, $y^{\prime }(0)=v_0$, with $0\le t\le T<\infty$. The first one is that to use the methods presented in [10], we have to define $u={(y,v,t)}^T$, with $v=y^{\prime }(t)$ and then we have to convert the problem to a first-order one in the following way: $u^{\prime }=g(y)={(v,f(t,y),1)}^T$, $u(0)={(y_0,v_0,t_0)}^T$, while with our methods we do not need to convert the problem to a first-order one. The second difference is that in [10], we have to solve two linear systems at each intermediate step, instead of the one linear system we have to solve at each intermediate step when using the methods presented here. The last one is that in the mentioned paper, operator $g(y)$ and its Jacobian have to be evaluated at every intermediate stage. When using our method, we evaluate operator $f(t,y)$ at every intermediate stage, but we use fixed values of $f_t(t,y)$ and $f_y(t,y)$ at every time step, so the number of function evaluations per intermediate stage is smaller with our methods.

In this article, we show the development of Rosenbrock–Nyström methods, as well as the conditions that must be satisfied to obtain the desired classical order (up to order four) and the main ideas in order to have stability when linear problems are solved. In addition, we show some numerical experiments that prove the good behavior of these new methods.

This paper is structured as follows: in the next section, we give a brief description of Rosenbrock–Nyström methods, together with their development. In Section 3, we describe the stability requirements that these methods should satisfy when integrating linear problems. In Section 4, we deal with the conditions that the coefficients of the method should satisfy in order to have up to classical order four. The construction of such methods is studied in [11]. Finally, in Section 5, we present some numerical experiments in order to test such methods.

2. Development of Rosenbrock–Nyström Methods

Non-linear second-order in time problems can be written in an abstract form as follows:

“Find $y:[0,T]\to \mathcal{H}$ solution of

$$\begin{array}{c}\hfill \left\{\begin{array}{cccc}\hfill y^{″}(t)& =& f(t,y(t)),\hfill & 0\le t\le T<\infty ,\hfill \\ \hfill y(0)& =& y_0,\hfill \\ \hfill y^{\prime }(0)& =& v_0,"\hfill \end{array}\right.\end{array}$$

(1)

where, typically, $\mathcal{H}$ is a Hilbert space of functions defined in a certain bounded domain $\Omega \subseteq {\mathbb{R}}^M$, integer $M\ge 1$ with smooth boundary $\Gamma$. This formulation involves lots of different problems: partial differential equations, ordinary differential equations, etc.

Example 1.

Let us show here two problems that will be solved in the numerical experiments (Section 5) and can be solved by using Rosenbrock–Nyström methods.

The first problem is a modification of the non-linear wave propagation suggested in [12]

$$\begin{array}{ccc}\hfill u_j^{″}(t)& =& F(u_{j+1}-u_j)-F(u_j-u_{j-1})+g_j(t),j=1,\cdots ,N,\hfill \\ \hfill u_j(0)& =& sin\left(\frac{2\pi j}{N+1}\right),j=1,\cdots ,N,\hfill \\ \hfill u_j^{\prime }(t)& =& 0j=1,\cdots ,N,\hfill \end{array}$$

(2)

with

$$\begin{array}{ccc}\hfill F(u)& =& \lambda u+\alpha u^p,\hfill \\ \hfill u_0(t)& =& u_{N+1}(t)=0,\hfill \end{array}$$

$g_j(t)$ is such that the exact solution is given by $u_j(t)=sin\left(\frac{2\pi j}{N+1}\right)cos(t)$. Parameter λ controls the stiffness of the problem.

Example 2.

The second example is the following non-linear Euler–Bernoulli equation:

$$\begin{array}{c}\hfill \left\{\begin{array}{ccc}{u}_{tt}=-A{u}^2+h(t,x),\hfill & x\in [-1,1]\hfill & 0\le t\le T=1,\hfill \\ u(0,x)={(x^2-1)}^{3}cos(x),\hfill & x\in [-1,1],\hfill \\ u_t(0,x)=-{(x^2-1)}^{3}sin(x),\hfill & x\in [-1,1],\hfill \\ u(t,-1)=u(t,1)=0,\hfill & 0\le t\le T=1\hfill \\ u_x(t,-1)=u_x(t,1)=0,\hfill & 0\le t\le T=1\hfill \end{array}\right.\end{array}$$

(3)

with $h(t,x)$ such that the exact solution is $u(t,x)={(x^2-1)}^{3}cos(t+x)$. Operator A is such that $Au=u_{xxxx}$. This problem can be discretized in space by taking, for example, a pseudo-spectral discretization.

When solving this problem with an explicit Runge–Kutta–Nyström method, we have to impose very restrictive hypotheses over the time step size in order to guarantee stability.

When we solve a problem such as (1) with a Rosenbrock–Nyström method, the numerical approximation to the exact solution and its derivative, $(y(t_n),v(t_n))$ is given by $(y_n,v_n)$, where $t_n=t_0+n\tau$, with $\tau$ as the time step size. The numerical approximation $(y_n,v_n)$ proposed by us is calculated as

$$\begin{array}{ccc}\hfill v_{n+1}& =& v_n+\tau \sum _{i=1}^s{b}_{i}f(t_n+{\alpha }_i\tau ,y_n+\sum _{j=1}^{i-1}{\alpha }_{ij}{K}_{n,j})\hfill \\ & & +{\tau }^2({\beta }^T·e)f_t(t_n,y_n)+\tau f_y(t_n,y_n)\sum _{i=1}^s{\beta }_i{K}_{n,i},\hfill \\ \hfill y_{n+1}& =& y_n+\sum _{i=1}^s{b}_i{K}_{n,i},\hfill \end{array}$$

where $K_{n,i}$, $i=1,\cdots ,s$ are the intermediate stages and $e={(1,\cdots ,1)}^T$. These intermediate stages are given by

$$\begin{array}{ccc}\hfill K_{n,i}& =& \tau v_n+{\tau }^2\sum _{j=1}^i{\delta }_{ij}f(t_n+{\alpha }_j\tau ,y_n+\sum _{l=1}^{j-1}{\alpha }_{jl}{K}_{n,l})\hfill \\ & & +{\tau }^2\sum _{j=1}^i{\gamma }_{ij}(\tau f_t(t_n,y_n)+f_y(t_n,y_n)K_{n,j})\hfill \end{array}$$

(4)

We use notation $f_t(t,y)$ and $f_y(t,y)$ to refer to $\frac{\partial f}{\partial t}(t,y)$ and $\frac{\partial f}{\partial y}(t,y)$, respectively. When the problem we are solving is autonomous, that is, of the form

$$\begin{array}{c}\hfill \left\{\begin{array}{ccc}\hfill y^{″}(t)& =& f(y),\hfill \\ \hfill y(0)& =& y_0,\hfill \\ \hfill y^{\prime }(0)& =& v_0,\hfill \end{array}\right.\end{array}$$

the equations which determine the method are

$$\begin{array}{ccc}\hfill K_{n,i}& =& \tau v_n+{\tau }^2\sum _{j=1}^i{\delta }_{ij}f(y_n+\sum _{l=1}^{j-1}{\alpha }_{jl}{K}_{n,l})+{\tau }^2{f}_y(y_n)\sum _{j=1}^i{\gamma }_{ij}{K}_{n,j},\hfill \\ \hfill v_{n+1}& =& v_n+\tau \sum _{i=1}^s{b}_{i}f(y_n+\sum _{j=1}^{i-1}{\alpha }_{ij}{K}_{n,j})+\tau f_y(y_n)\sum _{i=1}^s{\beta }_i{K}_{n,i},\hfill \\ \hfill y_{n+1}& =& y_n+\sum _{i=1}^s{b}_i{K}_{n,i}.\hfill \end{array}$$

(5)

Notice that in this case, we have a simplification of the main problem (1) and the equations can be obtained by considering that $f_t(y)=0$.

Similarly, as happens with other classical methods such as RK methods, RKN methods, Rosenbrock methods, etc., the coefficients of these methods can be written in a tableau as follows:

(6)

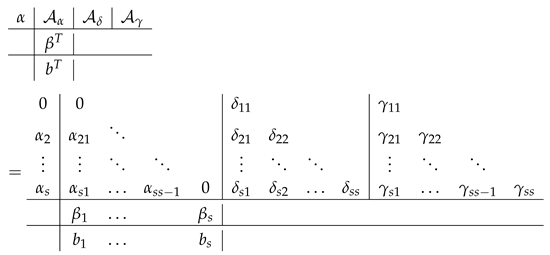
where we will assume that ${\alpha }_i={\sum }_{j=1}^{i-1}{\alpha }_{ij}$.

Notice that at every intermediate stage, the problem to be solved is a linear one, so the computational cost is reduced compared with the equations that implicit RKN methods provide when solving this type of problem. When we select the values ${\gamma }_{ii}=\gamma$, $i=1,\cdots ,s$, then, at every intermediate stage $K_{n,i}$, we have to solve a linear problem such as

$$\begin{array}{c}\hfill (I-{\tau }^2\gamma f_y(t_n,y_n))K_{n,i}=T_i,\end{array}$$

where I denotes the identity operator and $T_i$ is the term in (4) that does not depend on $K_{n,i}$, $i=1,\cdots ,s$. Therefore, the computational cost reduces as $I-{\tau }^2\gamma f_y(t_n,y_n)$ remains constant for all the intermediate stages.

In order to guarantee the solvability of the intermediate stages, we will assume that, for every $t>0$, $f_y(t,y(t))$ is such that ${(I-\mu f_y(t,y(t)))}^{-1}$ exists and is bounded for every $\mu$ with $\mu \ge 0$.

Remark 1.

When we have that for every $t>0$, $f_y(t,y(t))$ is self-adjoint and negative semi-definite, the solvability and boundedness of the intermediate stages are guaranteed because of the following:

• In the case of $f(t,u(t))$ being a space differential operator, $f_y(t,y(t))$ is the infinitesimal generator of a $C_0$-semigroup of type $\tilde{\omega }\le 0$, so ${(\mu I-f_y(t,y(t)))}^{-1}$ exists and is bounded for every μ with $\mu \ge \tilde{\omega }$ [13].
• In the case of $f(t,u(t)):{\mathbb{R}}^{n+1}\to {\mathbb{R}}^n$ being a regular function, then, for every $t>0$, we have that $f_y(t,y(t))$ is a symmetric negative semi-definite matrix, so ${(I-\mu f_y(t,y(t)))}^{-1}$ exists for every $\mu \ge 0$.

Let us see now the way in which these methods have been developed. The way of defining these new methods is the natural one since they can be obtained from Rosenbrock methods applied to problem (1) when it is transformed to a first-order in time problem. Let us remember that the coefficients of Rosenbrock methods are given by an array of the form

and the equations that these methods give when solving a problem such as

$$\begin{array}{c}\hfill \left\{\begin{array}{ccc}\hfill u^{\prime }(t)& =& F(t,u),\hfill \\ \hfill u(0)& =& u_0,\hfill \end{array}\right.\end{array}$$

(7)

are

$$\begin{array}{ccc}\hfill Q_{n,i}& =& \tau F(t_n+{\tilde{\alpha }}_i\tau ,u_n+\sum _{j=1}^{i-1}{\tilde{\alpha }}_{ij}{Q}_{n,j})+{\tau }^2{\tilde{\gamma }}_i{F}_t(t_n,u_n)+\tau F_y(t_n,u_n)\sum _{j=1}^i{\tilde{\gamma }}_{ij}{Q}_{n,j},\hfill \\ \hfill u_{n+1}& =& u_n+\sum _{j=1}^s{\tilde{b}}_j{Q}_{n,j},\hfill \end{array}$$

where $t_n=t_0+n\tau$, with $\tau$ as the time step size and $u_n$ as the numerical approximation to $u(t_n)$. $Q_{n,i}$, $i=1,\cdots ,s$, are the intermediate stages.

To solve problem (1) with a Rosenbrock method, we first write it as a first-order one, by defining $v(t)=y^{\prime }(t)$. In this way, we define $u(t)={(y(t),v(t))}^T$ and, therefore, we have a problem like (7), being $F(t,u)={(v(t),f(t,y))}^T$. The initial condition is $u(0)=u_0$ with $u_0={(y_0,v_0)}^T$. We apply a Rosenbrock method to this problem, by using notation $Q_{n,i}=(Q_{n,i}^y,Q_{n,i}^v)$.

We operate in the equations that give the intermediate stages, replacing $Q_{n,j}^v$ with its expression in the equations for $Q_{n,j}^y$. From this, we obtain

$$\begin{array}{ccc}\hfill Q_{n,i}^y& =& \tau v_n+{\tau }^2\sum _{j=1}^i(\widetilde{{\alpha }_{ij}}+\widetilde{{\gamma }_{ij}})f(t_n+\widetilde{{\alpha }_j}\tau ,y_n+\sum _{j=1}^{i-1}{\tilde{\alpha }}_{ij}{Q}_{n,j}^y)+{\tau }^3\sum _{j=1}^i(\widetilde{{\alpha }_{ij}}+\widetilde{{\gamma }_{ij}})\widetilde{{\gamma }_j}{f}_t(t_n,y_n)\hfill \\ & & +{\tau }^2\sum _{j=1}^i(\widetilde{{\alpha }_{ij}}+\widetilde{{\gamma }_{ij}})\sum _{l=1}^j\widetilde{{\gamma }_{lj}}{Q}_{n,l}^y,\hfill \\ \hfill v_{n+1}& =& v_n+\tau \sum _{j=1}^s{\tilde{b}}_{j}f(t_n+{\tilde{\alpha }}_j\tau ,y_n+\sum _{l=1}^{j-1}{\tilde{\alpha }}_{jl}{Q}_{n,l}^y)\hfill \\ & & +{\tau }^2\sum _{j=1}^s{\tilde{b}}_j{\tilde{\gamma }}_j{f}_t(t_n,y_n)+\tau f_y(t_n,y_n)\sum _{j=1}^s{\tilde{b}}_j\sum _{l=1}^j{\tilde{\gamma }}_{jl},\hfill \\ \hfill y_{n+1}& =& y_n+\sum _{j=1}^s{\tilde{b}}_j{Q}_{n,j}^y\hfill \end{array}$$

Now, lets us assume that the Rosenbrock method satisfies

$$\begin{array}{c}\hfill {\tilde{\alpha }}_i=\sum _{j=1}^{i-1}{\tilde{\alpha }}_{ij},{\tilde{\gamma }}_i=\sum _{j=1}^i{\tilde{\gamma }}_{ij},\sum _{j=1}^s{\tilde{b}}_j=1.\end{array}$$

The first two conditions are usual restrictions satisfied for many Rosenbrock methods and the third one is the condition to have classical order 1. Then, if we denote $K_{n,i}=Q_{n,i}^y$, $i=1,\cdots ,s$ and if we define

$$\begin{array}{ccc}\hfill \alpha & =& \tilde{\alpha },\hfill \\ \hfill {\mathcal{A}}_{\alpha }& =& {\tilde{\mathcal{A}}}_{\alpha }\hfill \\ \hfill {\mathcal{A}}_{\gamma }& =& ({\tilde{\mathcal{A}}}_{\alpha }+\widetilde{{\mathcal{A}}_{\gamma }}){\tilde{\mathcal{A}}}_{\gamma },\hfill \\ \hfill {\mathcal{A}}_{\delta }& =& {\tilde{\mathcal{A}}}_{\alpha }+\widetilde{{\mathcal{A}}_{\gamma }},\hfill \\ \hfill b^T& =& {\tilde{b}}^T,\hfill \\ \hfill {\beta }^T& =& {\tilde{b}}^T{\tilde{\mathcal{A}}}_{\gamma },\hfill \end{array}$$

(8)

what we obtain is precisely Equation (4). Furthermore, we can construct Rosenbrock–Nyström methods that do not come from Rosenbrock ones. This fact gives much more freedom to obtain the coefficients of the desired methods. The proposed methods with classical order 3 and 4 that are used in the numerical experiments have been obtained without using existing Rosenbrock ones.

3. Stability When Solving Linear Ordinary Differential Equations

Following the ideas given for Rosenbrock methods in [6], in this part we deal with the stability of Rosenbrock–Nyström methods when they are applied to a simplified problem such as

$$\begin{array}{ccc}\hfill U^{″}(t)& =& -B^{2}U(t),\hfill \\ \hfill U(0)& =& U_0,\hfill \\ \hfill U^{\prime }(0)& =& V_0,\hfill \end{array}$$

(9)

where B is a given symmetric positive defined matrix of order $m\ge 1$ and $U(t)$, $U_0$ and $V_0\in {\mathbb{R}}^m$.

Here, we study the stability in the energy norm, which is the natural norm for the study of the well-posedness of problem (9). This norm is given by

$$\begin{array}{c}\hfill \parallel {(U(t),U^{\prime }(t))}^T{\parallel }_B^2={\parallel BU(t)\parallel }_2^2+{\parallel U^{\prime }(t)\parallel }_2^2,\end{array}$$

with $\parallel ·\parallel$ being the Euclidean norm in ${\mathbb{R}}^m$.

When solving problem (9) with a Rosenbrock–Nyström method, we obtain

$$\left[\begin{array}{c}{U}_{n+1}\\ V_{n+1}\end{array}\right]=\left[\begin{array}{cc}{r}_{11}(\tau B)& B^{-1}{r}_{12}(\tau B)\\ B{r}_{21}(\tau B)& r_{22}(\tau B)\end{array}\right]\left[\begin{array}{c}{U}_0\\ V_0\end{array}\right],$$

(10)

where terms $r_{ij}(kB)$, $1\le i,j\le 2$ are given, in tensorial form, by

$$\begin{array}{ccc}\hfill r_{11}(\tau B)& =& I-(b^T\otimes {\tau }^2{B}^2)M{({\mathcal{A}}_{\delta },{\mathcal{A}}_{\alpha },{\mathcal{A}}_{\gamma },B)}^{-1}({\mathcal{A}}_{\delta }e\otimes I),\hfill \\ \hfill r_{12}(\tau B)& =& (b^T\otimes \tau B)M{({\mathcal{A}}_{\delta },{\mathcal{A}}_{\alpha },{\mathcal{A}}_{\gamma },B)}^{-1}(e\otimes I)\hfill \\ \hfill r_{21}(\tau B)& =& -\tau B[(b^{T}e\otimes I)-((b^T{\mathcal{A}}_{\alpha }+{\beta }^T)\otimes {\tau }^2{B}^2)M{({\mathcal{A}}_{\delta },{\mathcal{A}}_{\alpha },{\mathcal{A}}_{\gamma },B)}^{-1}({\mathcal{A}}_{\delta }e\otimes I)],\hfill \\ \hfill r_{22}(\tau B)& =& I-((b^T{\mathcal{A}}_{\alpha }+{\beta }^T)\otimes {\tau }^2{B}^2)M{({\mathcal{A}}_{\delta },{\mathcal{A}}_{\alpha },{\mathcal{A}}_{\gamma },B)}^{-1}(e\otimes I).\hfill \end{array}$$

with $M({\mathcal{A}}_{\delta },{\mathcal{A}}_{\alpha },{\mathcal{A}}_{\gamma },B)=\mathcal{I}\otimes I+({\mathcal{A}}_{\delta }{\mathcal{A}}_{\alpha }+{\mathcal{A}}_{\gamma })\otimes {\tau }^2{B}^2$. These elements form matrix $R(\tau B)$,

$$\begin{array}{c}\hfill R(\tau B)=\left[\begin{array}{cc}{r}_{11}(\tau B)& r_{12}(\tau B)\\ r_{21}(\tau B)& r_{22}(\tau B)\end{array}\right].\end{array}$$

By bounding (10) in the energy norm, we obtain that the proof of stability is related to the boundedness of the powers of matrix $R(\tau B)$. As matrix B is assumed to be symmetric and positive definite, then B is normal and we can use the following spectral result:

$$\begin{array}{c}\hfill {\parallel R(\tau B)}^n{\parallel }_2\le {\sup }_{\theta \in \sigma (\tau B)}{\parallel R{(\theta )}^n\parallel }_2,\end{array}$$

(11)

with $\sigma (\tau B)$ being the spectrum of $\tau B$. Then, the boundedness of the powers of matrix $R(\tau B)$ is reduced to the study of the boundedness of matrix $R(\theta )$. (Note: if we assume that B is not normal, we can use a similar result to (11), but considering the numerical range instead of the spectrum [14].)

Following the results in [15], the following definitions and theorem can be stated.

Definition 1.

The interval $\mathcal{C}=[0,{\beta }_{stab})$ is the interval of stability of the Rosenbrock–Nyström method if ${\beta }_{stab}\in {\mathbb{R}}^{+}$ is the highest value, such that

$$\begin{array}{c}\hfill \mathcal{C}\subset \{\theta \in {\mathbb{R}}^{+}\cup \left\{0\right\}/\rho (R(\theta ))\le 1\mathrm{and}R(\theta )\mathrm{is}\mathrm{simple}\mathrm{when}\rho (R(\theta ))=1\}.\end{array}$$

The Rosenbrock–Nyström method is said to be R-stable if $\mathcal{C}={\mathbb{R}}^{+}\cup \left\{0\right\}$.

Definition 2.

The interval ${\mathcal{C}}^{*}=[0,{\beta }_{per})$ is the interval of periodicity of the Rosenbrock–Nyström method if ${\beta }_{per}\in {\mathbb{R}}^{+}$ is the highest value, such that

$$\begin{array}{c}\hfill {\mathcal{C}}^{*}\subset \{\theta \in {\mathbb{R}}^{+}\cup \left\{0\right\}/R(\theta )\mathrm{is}\mathrm{simple}\mathrm{and}\mathrm{for}\mathrm{all}\lambda \in \sigma (R(\theta )),|\lambda |=1\}.\end{array}$$

We can say that the Rosenbrock–Nyström method is P-stable if ${\mathcal{C}}^{*}={\mathbb{R}}^{+}\cup \left\{0\right\}$.

Theorem 1.

Under assumptions that

(i) 

The method is R-stable.

(ii) 

$\sigma ({\mathcal{A}}_{\delta }{\mathcal{A}}_{\alpha }+{\mathcal{A}}_{\gamma })\cap (-\infty ,0]=⌀$.

(iii) 

There exists a value $\overline{\theta }\in \mathbb{R}$ such that $R(\overline{\theta })$ does not have double eigenvalues.

(iv) 

$(b^T{\mathcal{A}}_{\alpha }+{\beta }^T){({\mathcal{A}}_{\delta }{\mathcal{A}}_{\alpha }+{\mathcal{A}}_{\gamma })}^{-1}({\mathcal{A}}_{\delta }e)=1$.

Then,

$$\begin{array}{c}\hfill {\parallel R(kB)}^n{\parallel }_2\le C,n\in \mathbb{N}.\end{array}$$

where C is independent of the size of $\sigma (kB)$.

This result cannot be obtained if assumption (iv) is not satisfied.

Proof. 

The proof of this theorem is straightforward by using the results of Theorems 5 and 7 in [15]. □

Corollary 1.

When the Rosenbrock–Nyström method comes from a Rosenbrock one with classical order greater than or equal to one, the condition

$$(b^T{\mathcal{A}}_{\alpha }+{\beta }^T){({\mathcal{A}}_{\delta }{\mathcal{A}}_{\alpha }+{\mathcal{A}}_{\gamma })}^{-1}({\mathcal{A}}_{\delta }e)=1$$

is always satisfied.

Proof. 

Let us assume that the Rosenbrock–Nyström method comes from a Rosenbrock one with Butcher array

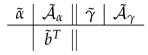and that the coefficients of the Rosenbrock–Nyström method satisfy relations (8). Then,

$$\begin{array}{ccc}\hfill (b^T{\mathcal{A}}_{\alpha }& +& {\beta }^T){({\mathcal{A}}_{\delta }{\mathcal{A}}_{\alpha }+{\mathcal{A}}_{\gamma })}^{-1}({\mathcal{A}}_{\delta }e)\hfill \\ & =& ({\tilde{b}}^T{\tilde{\mathcal{A}}}_{\alpha }+{\tilde{b}}^T{\tilde{\mathcal{A}}}_{\gamma }){(({\tilde{\mathcal{A}}}_{\alpha }+{\tilde{\mathcal{A}}}_{\gamma }){\tilde{\mathcal{A}}}_{\alpha }+({\tilde{\mathcal{A}}}_{\alpha }+{\tilde{\mathcal{A}}}_{\gamma }){\tilde{\mathcal{A}}}_{\gamma })}^{-1}({\tilde{\mathcal{A}}}_{\alpha }+{\tilde{\mathcal{A}}}_{\gamma })e\hfill \\ & =& {\tilde{b}}^T({\tilde{\mathcal{A}}}_{\alpha }+{\tilde{\mathcal{A}}}_{\gamma }){(({\tilde{\mathcal{A}}}_{\alpha }+{\tilde{\mathcal{A}}}_{\gamma })({\tilde{\mathcal{A}}}_{\alpha }+{\tilde{\mathcal{A}}}_{\gamma }))}^{-1}({\tilde{\mathcal{A}}}_{\alpha }+{\tilde{\mathcal{A}}}_{\gamma })e\hfill \\ & =& {\tilde{b}}^T({\tilde{\mathcal{A}}}_{\alpha }+{\tilde{\mathcal{A}}}_{\gamma }){({({\tilde{\mathcal{A}}}_{\alpha }+{\tilde{\mathcal{A}}}_{\gamma })}^2)}^{-1}({\tilde{\mathcal{A}}}_{\alpha }+{\tilde{\mathcal{A}}}_{\gamma })e\hfill \\ & =& {\tilde{b}}^{T}e=1\hfill \end{array}$$

□

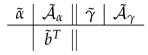
4. Order Conditions for Rosenbrock–Nyström Methods

Let us see the conditions that Rosenbrock–Nyström methods should satisfy to obtain the highest possible order when integrating a problem such as (1). In a similar way as with Runge–Kutta–Nyström methods, a Rosenbrock–Nyström method is said to have classical order p if

$$\begin{array}{ccc}\hfill {\rho }_{n+1}& =& y(t_{n+1})-{\widehat{y}}_{n+1}=O({\tau }^{p+1}),\hfill \\ \hfill {\xi }_{n+1}& =& y^{\prime }(t_{n+1})-{\widehat{v}}_{n+1}=O({\tau }^{p+1}),\hfill \end{array}$$

where ${({\widehat{y}}_{n+1},{\widehat{v}}_{n+1})}^T$ is the numerical solution obtained from the exact solution ${(y(t_n),y^{\prime }(t_n))}^T$$={({\tilde{y}}_{n+1},{\tilde{v}}_{n+1})}^T$ with time step size $\tau$.

In order to study the order conditions, it is useful to write the equations as in the autonomous case, given by (5), in the following way,

$$\begin{array}{ccc}\hfill g_{n,i}^J& =& y_n^J+\sum _{j=1}^{i-1}{\alpha }_{ij}{K}_{n,j}^J,\hfill \\ \hfill K_{n,i}^J& =& \tau v_n^J+{\tau }^2\sum _{j=1}^i{\delta }_{ij}{f}^J(g_j)+{\tau }^2\sum _K{f}_K^J(y_n)\sum _{j=1}^i{\gamma }_{ij}{K}_{n,j}^K,\hfill \\ \hfill v_{n+1}^J& =& v_n^J+\tau \sum _{i=1}^s{b}_i{f}^J(g_i)+\tau \sum _K{f}_K^J(y_n)\sum _{i=1}^s{\beta }_i{K}_{n,i}^K,\hfill \\ \hfill y_{n+1}^J& =& y_n^J+\sum _{i=1}^s{b}_i{K}_{n,i}^J,\hfill \end{array}$$

where the superscript indices in capital letters indicate the component of the vector we are using (in this part, the notation is similar to that used in [6]). In the following, $\partial f^J/\partial y^K$ will be denoted by $f_K^J$, ${\partial }^2{f}^J/\partial y^K\partial y^L$ by $f_{KL}^J$, etc.

To obtain the order conditions, we compare the Taylor series of ${\widehat{y}}_{n+1}$ and ${\widehat{v}}_{n+1}$ obtained from the exact solution ${({\tilde{y}}_n,{\tilde{v}}_n)}^T$ with the Taylor series of the exact solution.

In this part, the following formulae are used:

$$\begin{array}{ccc}\hfill {(\tau \phi (\tau ))}^{(q)}{|}_{\tau =0}& =& q{\phi }^{(q-1)}{(\tau )|}_{\tau =0},q\ge 1,\hfill \\ \hfill {({\tau }^2\phi (\tau ))}^{(q)}{|}_{\tau =0}& =& q(q-1){\phi }^{(q-2)}{(\tau )|}_{\tau =0},q\ge 2.\hfill \end{array}$$

These formulae, which can be proved in a recursive manner, are obtained by using that

$$\begin{array}{ccc}\hfill {(\tau \phi (\tau ))}^{(q)}& =& q{\phi }^{(q-1)}(\tau )+\tau {\phi }^{(q)}(\tau ),q\ge 1,\hfill \\ \hfill {({\tau }^2\phi (\tau ))}^{(q)}& =& q(q-1){\phi }^{(q-2)}(\tau )+2q\tau {\phi }^{(q-1)}(\tau )+{\tau }^2{\phi }^{(q)}(\tau ),q\ge 2.\hfill \end{array}$$

We differentiate by using the notation $\phi (\tau )={\sum }_{j=1}^i({\delta }_{ij}{f}^J(g_j)+{\gamma }_{ij}{\sum }_K{f}_K^J({\tilde{y}}_n)K_{n,j}^K)$ together with the previous formulae. Then, we obtain

$$\begin{array}{ccc}\hfill {(K_{n,i}^J)}^{(0)}{|}_{\tau =0}& =& 0,\hfill \\ \hfill {(K_{n,i}^J)}^{(1)}{|}_{\tau =0}& =& {\tilde{v}}_n^J{{|}_{\tau =0}+\left(2\tau \sum _{j=1}^i({\delta }_{ij}{f}^J(g_j)+{\gamma }_{ij}\sum _K{f}_K^J({\tilde{y}}_n)K_{n,j}^K)\right)|}_{\tau =0}\hfill \\ & & +\left(({\tau }^2\sum _{j=1}^i{({\delta }_{ij}{f}^J(g_j)+{\gamma }_{ij}\sum _K{f}_K^J({\tilde{y}}_n)K_{n,j}^K)}^{(1)}\right){|}_{\tau =0}\hfill \\ & =& {\tilde{v}}_n^J,\hfill \\ \hfill {(K_{n,i}^J)}^{(2)}{|}_{\tau =0}& =& 2\sum _{j=1}^i({\delta }_{ij}{f}^J(g_j)+{\gamma }_{ij}\sum _K{f}_K^J({\tilde{y}}_n)K_{n,j}^K){|}_{\tau =0}\hfill \\ & =& 2\sum _{j=1}^i{\delta }_{ij}{f}^J({\tilde{y}}_n)\hfill \\ \hfill {(K_{n,i}^J)}^{(3)}{|}_{\tau =0}& =& 6\sum _{j=1}^i({\delta }_{ij}{f}^J{(g_j)}^{(1)}+{\gamma }_{ij}\sum _K{f}_K^J({\tilde{y}}_n){(K_{n,j}^K)}^{(1)}){|}_{\tau =0}\hfill \\ & =& 6\sum _{j=1}^i({\delta }_{ij}{\alpha }_j\sum _K{f}_K^J({\tilde{y}}_n){\tilde{v}}_n^K+{\gamma }_{ij}\sum _K{f}_K^J({\tilde{y}}_n){\tilde{v}}_n^K)\hfill \\ & =& 6\sum _{j=1}^i({\delta }_{ij}{\alpha }_j+{\gamma }_{ij})\sum _K{f}_K^J({\tilde{y}}_n){\tilde{v}}_n^K,\hfill \\ \hfill {(K_{n,i}^J)}^{(4)}{|}_{\tau =0}& =& 12\sum _{j=1}^i({\delta }_{ij}{(f^J(g_j))}^{(2)}+{\gamma }_{ij}\sum _K{f}_K^J({\tilde{y}}_n){(K_{n,j}^K)}^{(2)}){|}_{\tau =0}\hfill \\ & =& 12\sum _{j=1}^i{\delta }_{ij}{\alpha }_j^2\sum _{K,L}{f}_{KL}^J({\tilde{y}}_n){\tilde{v}}_n^K{\tilde{v}}_n^L+24\sum _{j=1}^i\sum _{l=1}^{i-1}\sum _{m=1}^l{\delta }_{ij}{\alpha }_{jl}{\delta }_{lm}\sum _K{f}_K^J({\tilde{y}}_n)f^K({\tilde{y}}_n)\hfill \\ & & +24\sum _{j=1}^i\sum _{l=1}^j{\gamma }_{ij}{\delta }_{jl}\sum _K{f}_K^j({\tilde{y}}_n)f^K({\tilde{y}}_n),\hfill \end{array}$$

where we have used that

$$\begin{array}{ccc}\hfill f^J(g_i){|}_{\tau =0}& =& f^J({\tilde{y}}_n),\hfill \\ \hfill {(f^J(g_i))}^{(1)}{|}_{\tau =0}& =& \sum _K{\alpha }_i{f}_K^J({\tilde{y}}_n){\tilde{v}}_n^K,\hfill \\ \hfill {(f^J(g_i))}^{(2)}{|}_{\tau =0}& =& \sum _{K,L}{\alpha }_i^2{f}_{K,L}^J({\tilde{y}}_n){\tilde{v}}_n^K{\tilde{v}}_n^L+2\sum _K{f}_K^J({\tilde{y}}_n))f^K({\tilde{y}}_n)\sum _{j=1}^{i-1}\sum _{l=1}^j{\alpha }_{ij}{\delta }_{jl},\hfill \end{array}$$

together with

$$\begin{array}{ccc}\hfill {(g_i^K)}^{(0)}{|}_{\tau =0}& =& {\tilde{y}}_n^K,\hfill \\ \hfill {(g_i^K)}^{(1)}{|}_{\tau =0}& =& \sum _{j=1}^{i-1}{\alpha }_{ij}{(K_{n,j}^J)}_{\tau =0}^{(1)}\hfill \\ & =& \sum _{j=1}^{i-1}{\alpha }_{ij}{\tilde{v}}_n^J\hfill \\ & =& {\alpha }_i{\tilde{v}}_n^J,\hfill \\ \hfill {(g_i^K)}^{(2)}{|}_{\tau =0}& =& \sum _{j=1}^{i-1}{\alpha }_{ij}{(K_{n,j}^J)}_{\tau =0}^{(2)}\hfill \\ & =& 2\sum _{j=1}^{i-1}\sum _{l=1}^j{\alpha }_{ij}{\delta }_{jl}{f}^J({\tilde{y}}_n),\hfill \\ \hfill {(g_i^K)}^{(3)}{|}_{\tau =0}& =& \sum _{j=1}^{i-1}{\alpha }_{ij}{(K_{n,j}^J)}_{\tau =0}^{(3)}\hfill \\ & =& 6\sum _{j=1}^{i-1}\sum _{l=1}^j{\alpha }_{ij}({\delta }_{jl}{\alpha }_l+{\gamma }_{jl})\sum _K{f}_K^J({\tilde{y}}_n){\tilde{v}}_n^K.\hfill \end{array}$$

Then, by using the expressions obtained for ${(K_{n,i}^J)}^{(l)}$, $l=1,\cdots ,4$, we have

$$\begin{array}{ccc}\hfill {({\widehat{v}}_{n+1}^J)}^{(1)}{|}_{\tau =0}& =& \sum _{i=1}^s{b}_i{f}^J(g_i){{|}_{\tau =0}+\sum _K{f}_K^J({\tilde{y}}_n)\sum _{i=1}^s{\beta }_i{(K_{n,i}^K)}^{(0)}|}_{\tau =0}\hfill \\ & =& f^J({\tilde{y}}_n)\sum _{i=1}^s{b}_i,\hfill \\ \hfill {({\widehat{v}}_{n+1}^J)}^{(2)}{|}_{\tau =0}& =& 2\sum _{i=1}^s{b}_i{(f^J(g_i))}^{(1)}{{|}_{\tau =0}+2\sum _K{f}_K^J({\tilde{y}}_n)\sum _{i=1}^s{\beta }_i{(K_{n,i}^K)}^{(1)}|}_{\tau =0}\hfill \\ & =& 2\sum _{i=1}^s{b}_i\sum _K{f}_K^J({\tilde{y}}_n){\alpha }_i{\tilde{v}}_n^K+2\sum _K{f}_K^J({\tilde{y}}_n)\sum _{i=1}^s{\beta }_i{\tilde{v}}_n^K\hfill \\ & =& 2\sum _{i=1}^s(b_i{\alpha }_i+{\beta }_i)\sum _K{f}_K^J({\tilde{y}}_n){\tilde{v}}_n^K,\hfill \\ \hfill {({\widehat{v}}_{n+1}^J)}^{(3)}{|}_{\tau =0}& =& 3\sum _{i=1}^s{b}_i{(f^J(g_i))}^{(2)}{{|}_{\tau =0}+3\sum _K{f}_K^J({\tilde{y}}_n)\sum _{i=1}^s{\beta }_i{(K_i^K)}^{(2)}|}_{\tau =0}\hfill \\ & =& 3\sum _{i=1}^s{b}_i\sum _{K,L}{f}_{K,L}^J({\tilde{y}}_n){\alpha }_i^2{\tilde{v}}_n^K{\tilde{v}}_n^L\hfill \\ & & +6\sum _{i=1}^s{b}_i\sum _K{f}_K^J({\tilde{y}}_n)f^K({\tilde{y}}_n)\sum _{j=1}^{i-1}\sum _{l=1}^j{\alpha }_{ij}{\delta }_{jl}\hfill \\ & & +6\sum _K{f}_K^J({\tilde{y}}_n)\sum _{i=1}^s\sum _{j=1}^i{\beta }_i{\delta }_{ij}{f}^K({\tilde{y}}_n)\hfill \\ & =& 3\sum _{i=1}^s{b}_i{\alpha }_i^2\sum _{K,L}{f}_{K,L}^J({\tilde{y}}_n){\tilde{v}}_n^K{\tilde{v}}_n^L\hfill \\ & & +6\sum _{i=1}^s\sum _K{f}_K^J({\tilde{y}}_n)f^K({\tilde{y}}_n)\left(\sum _{j=1}^{i-1}\sum _{l=1}^j{b}_i{\alpha }_{ij}{\delta }_{jl}+\sum _{j=1}^i{\beta }_i{\delta }_{ij}\right),\hfill \\ \hfill {({\widehat{v}}_{n+1}^J)}^{(4)}{|}_{\tau =0}& =& 4\sum _{i=1}^s{b}_i{(f^J(g_i))}^{(3)}{{|}_{\tau =0}+4\sum _K{f}_K^J({\tilde{y}}_n)\sum _{i=1}^s{\beta }_i{(K_{n,i}^K)}^{(3)}|}_{\tau =0}\hfill \\ & =& 4\sum _{i=1}^s{b}_i{\alpha }_i^3\sum _{K,L,M}{f}_{K,L,M}^J({\tilde{y}}_n){\tilde{v}}_n^K{\tilde{v}}_n^L{\tilde{v}}_n^M\hfill \\ & & +16\sum _{i=1}^s{b}_i{\alpha }_i\sum _{j=1}^{i-1}\sum _{l=1}^j{\alpha }_{ij}{\delta }_{jl}\sum _{K,L}{f}_{K,L}^J({\tilde{y}}_n)f^K({\tilde{y}}_n){\tilde{v}}_n^L\hfill \\ & & +8\sum _{i=1}^s{b}_i{\alpha }_i\sum _{j=1}^{i-1}\sum _{l=1}^j{\alpha }_{ij}{\delta }_{jl}\sum _{K,L}{f}_{K,L}^J({\tilde{y}}_n)f^L({\tilde{y}}_n){\tilde{v}}_n^K\hfill \\ & & +24\sum _{i=1}^s{b}_i\sum _{j=1}^{i-1}\sum _{l=1}^j{\alpha }_{ij}({\delta }_{jl}{\alpha }_l+{\gamma }_{jl})\sum _{K,L}{f}_K^J({\tilde{y}}_n)f_L^K({\tilde{y}}_n){\tilde{v}}_n^L\hfill \\ & & +24\sum _{i=1}^s\sum _{j=1}^i{\beta }_i({\delta }_{ij}{\alpha }_j+{\gamma }_{ij})\sum _{K,L}{f}_K^J({\tilde{y}}_n)f_L^K({\tilde{y}}_n){\tilde{v}}_n^L\hfill \\ & =& \sum _{K,L,M}{f}_{K,L,M}^J({\tilde{y}}_n){\tilde{v}}_n^K{\tilde{v}}_n^L{\tilde{v}}_n^M\sum _{i^1}^{s}4b_i{\alpha }_i^3\hfill \\ & & +\sum _{K,L}{f}_{K,L}^J({\tilde{y}}_n)f^K({\tilde{y}}_n){\tilde{v}}_n^L\sum _{i=1}^s\sum _{j=1}^{i-1}\sum _{l=1}^{j}24b_i{\alpha }_i{\alpha }_{ij}{\delta }_{jl}\hfill \\ & & +24\sum _{K,L}{f}_K^J({\tilde{y}}_n)f_L^K({\tilde{y}}_n){\tilde{v}}_n^L\sum _{i=1}^s\left(\sum _{j=1}^{i-1}\sum _{l=1}^j{b}_i{\alpha }_{ij}({\delta }_{jl}{\alpha }_l+{\gamma }_{jl})+\sum _{j=1}^i{\beta }_i({\delta }_{ij}{\alpha }_j+{\gamma }_{ij})\right)\hfill \end{array}$$

(12)

where we have used that

$$\begin{array}{ccc}\hfill {(f^J(g_i))}^{(3)}& =& \sum _{K,L,M}{f}_{K,L,M}^J(g_i){(g_i^K)}^{(1)}{(g_i^L)}^{(1)}{(g_i^M)}^{(1)}+2\sum _{K,L}{f}_{K,L}^J(g_i){(g_i^K)}^{(2)}{(g_i^L)}^{(1)}\hfill \\ & & +\sum _{K,L}{f}_{K,L}^J(g_i){(g_i^K)}^{(1)}{(g_i^L)}^{(2)}+\sum _K{f}_K^J(g_i){(g_i^K)}^{(3)}\hfill \end{array}$$

and therefore

$$\begin{array}{ccc}\hfill {(f^J(g_i))}^{(3)}{|}_{\tau =0}& =& \sum _{K,L,M}{f}_{K,L,M}^J({\tilde{y}}_n){\tilde{v}}_n^K{\tilde{v}}_n^L{\tilde{v}}_n^L{\alpha }_i^3+4\sum _{K,L}{f}_{K,L}^J({\tilde{y}}_n)\sum _{j=1}^{i-1}\sum _{l=1}^j{\alpha }_i{\alpha }_{ij}{\delta }_{jl}{f}^K({\tilde{y}}_n){\tilde{v}}_n^L\hfill \\ & & +2\sum _{K,L}{f}_{K,L}^J({\tilde{y}}_n)\sum _{j=1}^{i-1}\sum _{l=1}^j{\alpha }_i{\alpha }_{ij}{\delta }_{jl}{f}^L({\tilde{y}}_n){\tilde{v}}_n^K\hfill \\ & & +6\sum _{K,L}{f}_K^J({\tilde{y}}_n)\sum _{j=1}^{i-1}\sum _{l=1}^j{\alpha }_{ij}({\delta }_{jl}{\alpha }_l+{\gamma }_{jl})f_L^K({\tilde{y}}_n){\tilde{v}}_n^L.\hfill \end{array}$$

For ${({\widehat{y}}_{n+1}^J)}^{(l)}$, $l=1,\cdots ,4$, we have

$$\begin{array}{ccc}\hfill {({\widehat{y}}_{n+1}^J)}^{(0)}{|}_{\tau =0}& =& {\tilde{y}}_n^J,\hfill \\ \hfill {({\widehat{y}}_{n+1}^J)}^{(1)}{|}_{\tau =0}& =& \sum _{i=1}^s{b}_i{(K_{n,i}^J)}^{(1)}{|}_{\tau =0}\hfill \\ & =& {\tilde{v}}_n^J\sum _{i=1}^s{b}_i,\hfill \\ \hfill {({\widehat{y}}_{n+1}^J)}^{(2)}{|}_{\tau =0}& =& \sum _{i=1}^s{b}_i{(K_{n,i}^J)}^{(2)}{|}_{\tau =0}\hfill \\ & =& 2f^J({\tilde{y}}_n)\sum _{i=1}^s\sum _{j=1}^i{b}_i{\delta }_{ij},\hfill \\ \hfill {({\widehat{y}}_{n+1}^J)}^{(3)}{|}_{\tau =0}& =& \sum _{i=1}^s{b}_i{(K_{n,i}^J)}^{(3)}{|}_{\tau =0}\hfill \\ & =& 6\sum _{i=1}^s{b}_i\sum _{j=1}^i({\delta }_{ij}{\alpha }_j+{\gamma }_{ij})\sum _K{f}_K^J({\tilde{y}}_n){\tilde{v}}_n^K\hfill \\ & =& 6\sum _K{f}_K^J({\tilde{y}}_n){\tilde{v}}_n^K\sum _{i=1}^s\sum _{j=1}^i{b}_i({\delta }_{ij}{\alpha }_j+{\gamma }_{ij}),\hfill \\ \hfill {({\widehat{y}}_{n+1}^J)}^{(4)}{|}_{\tau =0}& =& \sum _{i=1}^s{b}_i{(K_{n,i}^J)}^{(4)}{|}_{\tau =0}\hfill \\ & =& 12\sum _{i=1}^s{b}_i\sum _{j=1}^i{\delta }_{ij}{\alpha }_j^2\sum _{K,L}{f}_{K,L}^J({\tilde{y}}_n){\tilde{v}}_n^K{\tilde{v}}_n^L\hfill \\ & & +24\sum _{i=1}^s{b}_i\sum _{j=1}^i\sum _{l=1}^{j-1}\sum _{m=1}^l{\delta }_{ij}{\alpha }_{jl}{\delta }_{lm}\sum _K{f}_K^J({\tilde{y}}_n)f^K({\tilde{y}}_n)\hfill \\ & & +24\sum _{i=1}^s{b}_i\sum _{j=1}^i\sum _{l=1}^j{\gamma }_{ij}{\delta }_{jl}\sum _K{f}_K^J({\tilde{y}}_n)f^K({\tilde{y}}_n)\hfill \\ & =& 12\sum _{K,L}{f}_{K,L}^J({\tilde{y}}_n){\tilde{v}}_n^K{\tilde{v}}_n^L\sum _{i=1}^s\sum _{j=1}^i{b}_i{\delta }_{ij}{\alpha }_j^2\hfill \\ & & +24\sum _K{f}_K^J({\tilde{y}}_n)f^K({\tilde{y}}_n)\sum _{i=1}^s\sum _{j=1}^i\sum _{l=1}^j{b}_i({\gamma }_{ij}{\delta }_{jl}+{\delta }_{ij}{\alpha }_{jl}\sum _{m=1}^l{\delta }_{lm}).\hfill \end{array}$$

(13)

Now, we calculate the derivatives of the exact solution, by taking into account that $y^{″}=f(y)$,

$$\begin{array}{ccc}\hfill {({\tilde{y}}_n^J)}^{(1)}& =& {\tilde{v}}_n^J,\hfill \\ \hfill {({\tilde{y}}_n^J)}^{(2)}& =& {({\tilde{v}}_n^J)}^{(1)}=f^J({\tilde{y}}_n),\hfill \\ \hfill {({\tilde{y}}_n^J)}^{(3)}& =& {({\tilde{v}}_n^J)}^{(2)}={(f^J({\tilde{y}}_n))}^{(1)}=\sum _K{f}_K^J({\tilde{y}}_n){\tilde{v}}_n^K,\hfill \\ \hfill {({\tilde{y}}_n^J)}^{(4)}& =& {({\tilde{v}}_n^J)}^{(3)}={(f^J({\tilde{y}}_n))}^{(2)}\hfill \\ & =& \sum _{K,L}{f}_{KL}^J({\tilde{y}}_n){\tilde{v}}_n^K{({\tilde{y}}_n^L)}^{(1)}+\sum _K{f}_K^J({\tilde{y}}_n){({\tilde{v}}_n^K)}^{(1)}\hfill \\ & =& \sum _{K,L}{f}_{KL}^J({\tilde{y}}_n){\tilde{v}}_n^K{\tilde{v}}_n^L+\sum _K{f}_K^J({\tilde{y}}_n)f^K({\tilde{y}}_n),\hfill \\ \hfill {({\tilde{y}}_n^J)}^{(5)}& =& {({\tilde{v}}_n^J)}^{(4)}={(f^J({\tilde{y}}_n))}^{(3)}\hfill \\ & =& \sum _{K,L,M}{f}_{K,L,M}^J({\tilde{y}}_n){\tilde{v}}_n^K{\tilde{v}}_n^L{({\tilde{y}}_n^M)}^{(1)}+\sum _{K,L}{f}_{K,L}^J({\tilde{y}}_n){({\tilde{v}}_n^K)}^{(1)}{\tilde{v}}_n^L\hfill \\ & & +\sum _{K,L}{f}_{K,L}^J({\tilde{y}}_n){\tilde{v}}_n^K{({\tilde{v}}_n^L)}^{(1)}+\sum _{K,L}{f}_{K,L}^J({\tilde{y}}_n){({\tilde{y}}_n^L)}^{(1)}{f}^K({\tilde{y}}_n)\hfill \\ & & +\sum _{K,L}{f}_K^J({\tilde{y}}_n)f_L^K({\tilde{y}}_n){({\tilde{y}}_n^L)}^{(1)}\hfill \\ & =& \sum _{K,L,M}{f}_{K,L,M}^J({\tilde{y}}_n){\tilde{v}}_n^K{\tilde{v}}_n^L{\tilde{v}}_n^M+\sum _{K,L}{f}_{K,L}^J({\tilde{y}}_n)f^K({\tilde{y}}_n){\tilde{v}}_n^L\hfill \\ & & +\sum _{K,L}{f}_{K,L}^J({\tilde{y}}_n){\tilde{v}}_n^K{f}^L({\tilde{y}}_n)+\sum _{K,L}{f}_{K,L}^J({\tilde{y}}_n)f^K({\tilde{y}}_n){\tilde{v}}_n^L\hfill \\ & & +\sum _{K,L}{f}_K^J({\tilde{y}}_n)f_L^K({\tilde{y}}_n){\tilde{v}}_n^L\hfill \\ & =& \sum _{K,L,M}{f}_{K,L,M}^J({\tilde{y}}_n){\tilde{v}}_n^K{\tilde{v}}_n^L{\tilde{v}}_n^M+3\sum _{K,L}{f}_{K,L}^J({\tilde{y}}_n)f^K({\tilde{y}}_n){\tilde{v}}_n^L\hfill \\ & & +\sum _{K,L}{f}_K^J({\tilde{y}}_n)f_L^K({\tilde{y}}_n){\tilde{v}}_n^L.\hfill \end{array}$$

(14)

To obtain the order conditions up to order four, we compare the results in (12) and (13) with the results in (14). Then, these order conditions are:

Order 1: We compare ${({\widehat{v}}_n^J)}^{(1)}$ with ${({\tilde{v}}_n^J)}^{(1)}$ and ${({\widehat{y}}_n^J)}^{(1)}$ with ${({\tilde{y}}_n^J)}^{(1)}$

$$\begin{array}{c}\hfill \sum _{i=1}^s{b}_i=1.\end{array}$$

Order 2: We compare ${({\widehat{v}}_n^J)}^{(2)}$ with ${({\tilde{v}}_n^J)}^{(2)}$ and ${({\widehat{y}}_n^J)}^{(2)}$ with ${({\tilde{y}}_n^J)}^{(2)}$

$$\begin{array}{ccc}\hfill \sum _{i=1}^s(b_i{\alpha }_i+{\beta }_i)& =& \frac{1}{2},\hfill \\ \hfill \sum _{i=1}^s\sum _{j=1}^i{b}_i{\delta }_{ij}& =& \frac{1}{2}.\hfill \end{array}$$

Order 3: We compare ${({\widehat{v}}_n^J)}^{(3)}$ with ${({\tilde{v}}_n^J)}^{(3)}$ and ${({\widehat{y}}_n^J)}^{(3)}$ with ${({\tilde{y}}_n^J)}^{(3)}$

$$\begin{array}{ccc}\hfill \sum _{i=1}^s{b}_i{\alpha }_i^2& =& \frac{1}{3},\hfill \\ \hfill \sum _{i=1}^s\sum _{j=1}^{i-1}\sum _{l=1}^j{b}_i{\alpha }_{ij}{\delta }_{jl}+\sum _{i=1}^s\sum _{j=1}^i{\beta }_i{\delta }_{ij}& =& \frac{1}{6},\hfill \\ \hfill \sum _{i=1}^s\sum _{j=1}^i{b}_i({\delta }_{ij}{\alpha }_j+{\gamma }_{ij})& =& \frac{1}{6}.\hfill \end{array}$$

Order 4: We compare ${({\widehat{v}}_n^J)}^{(4)}$ with ${({\tilde{v}}_n^J)}^{(4)}$ and ${({\widehat{y}}_n^J)}^{(4)}$ with ${({\tilde{y}}_n^J)}^{(4)}$

$$\begin{array}{ccc}\hfill \sum _{i=1}^s{b}_i{\alpha }_i^3& =& \frac{1}{4},\hfill \\ \hfill \sum _{i=1}^s\sum _{j=1}^{i-1}\sum _{l=1}^j{b}_i{\alpha }_i{\alpha }_{ij}{\delta }_{jl}& =& \frac{1}{8},\hfill \\ \hfill \sum _{i=1}^s\sum _{j=1}^{i-1}\sum _{l=1}^j{b}_i{\alpha }_{ij}({\delta }_{jl}{\alpha }_l+{\gamma }_{jl})+\sum _{i=1}^s\sum _{j=1}^i{\beta }_i({\delta }_{ij}{\alpha }_j+{\gamma }_{ij})& =& \frac{1}{24},\hfill \\ \hfill \sum _{i=1}^s\sum _{j=1}^i{b}_i{\delta }_{ij}{\alpha }_j^2& =& \frac{1}{12},\hfill \\ \hfill \sum _{i=1}^s\sum _{j=1}^i\sum _{l=1}^{j-1}\sum _{m=1}^l{b}_i{\delta }_{ij}{\alpha }_{jl}{\delta }_{lm}+\sum _{i=1}^s\sum _{j=1}^i\sum _{l=1}^j{b}_i{\gamma }_{ij}{\delta }_{jl}& =& \frac{1}{24}.\hfill \end{array}$$

By using notation ${\alpha }^j={({\alpha }_1^j,\cdots ,{\alpha }_s^j)}^T$ and ${(b\alpha )}^T=(b_1{\alpha }_1,\cdots ,b_s{\alpha }_s)$, these order conditions can be written as follows:

Order 1:

$$\begin{array}{c}\hfill b^{T}e=1.\end{array}$$

Order 2:

$$\begin{array}{c}\hfill b^T\alpha +{\beta }^{T}e=\frac{1}{2},b^T{\mathcal{A}}_{\delta }e=\frac{1}{2}.\end{array}$$

Order 3:

$$\begin{array}{c}\hfill b^T{\alpha }^2=\frac{1}{3},(b^T{\mathcal{A}}_{\alpha }+{\beta }^T){\mathcal{A}}_{\delta }e=\frac{1}{6},b^T({\mathcal{A}}_{\delta }{\mathcal{A}}_{\alpha }+{\mathcal{A}}_{\gamma })e=\frac{1}{6}.\end{array}$$

Order 4:

$$\begin{array}{ccc}\hfill b^T{\alpha }^3& =& \frac{1}{4},{(b\alpha )}^T{\mathcal{A}}_{\alpha }{\mathcal{A}}_{\delta }e=\frac{1}{8},(b^T{\mathcal{A}}_{\alpha }+{\beta }^T)({\mathcal{A}}_{\delta }\alpha +{\mathcal{A}}_{\gamma })e=\frac{1}{24},\hfill \\ \hfill b^T{\mathcal{A}}_{\delta }{\alpha }^2& =& \frac{1}{12},b^T({\mathcal{A}}_{\delta }{\mathcal{A}}_{\alpha }+{\mathcal{A}}_{\gamma }){\mathcal{A}}_{\delta }e=\frac{1}{24}.\hfill \end{array}$$

5. Numerical Experiments

This section is devoted to the numerical experiments we have carried out in order to prove the advantages of these methods when solving a non-linear equation.

The Rosenbrock–Nyström methods we have chosen are the ones that are developed and studied in [11]. The first one is the one-stage method given by:

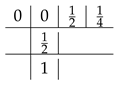This method can be obtained from the well-known Rosenbrock method with

$$\begin{array}{c}\hfill \tilde{\alpha }=0,{\tilde{\mathcal{A}}}_{\alpha }=0,{\tilde{\mathcal{A}}}_{\gamma }=\frac{1}{2},{\tilde{b}}^T=1,\end{array}$$

Therefore, the equations that this Rosenbrock–Nyström method provides are the same that we have with the Rosenbrock method when converting the second order problem in a first order one.

This Rosenbrock method is A-stable, but not L-stable [6]. The method presented here is the only Rosenbrock–Nyström method with one stage and classical order 2 that is stable. In fact, it can be proved that this method is P-stable as the eigenvalues of its stability matrix are $\frac{4-{\theta }^2}{4+{\theta }^2}\pm \frac{4\theta }{4+{\theta }^2}i$, for $\theta \in \mathbb{R}$. They are complex conjugate with modulus 1 except for $\theta =0$ and $\theta \to \infty$, where they are double and equal to 1. There are no one-stage Rosenbrock–Nyström methods with classical order 2 that are just R-stable but not P-stable, so in order to obtain methods of this type, we should use at least two stages. Another possibility is to construct one-stage Rosenbrock–Nyström methods with complex coefficients, following the ideas given in [16] for Rosenbrock methods. This will be the idea of future works.

The second one is an R-stable method with two stages and classical order 3, which we will call $RN3$. The coefficients of this method are given by the following array:

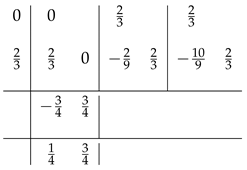
The third one is a method with three stages and classical order 4. This method is called $RN4$. The coefficients of this method are given by the following array:

In the tables, the local and global orders are given. The global error has been calculated as the difference between the exact solution at $T=1$ and the numerical one obtained with our method.

Example 3.

The first problem we have solved is the first problem presented in Example 1, that is, problem (2). Here, the parameters we have selected are

$$\begin{array}{c}\hfill N=20,\lambda =1000,\alpha =2,p=3.\end{array}$$

We present the results obtained for the method with classical order 2 in

Table 1. Local and global errors and orders for problem (2) with RN2.

$\mathit{\tau }$	1/80	1/160	1/320	1/640	1/1280	1/2560
Loc. err. $u(t)$	8.7268 $\times {10}^{-7}$	5.4684 $\times {10}^{-8}$	3.4200 $\times {10}^{-9}$	2.1379 $\times {10}^{-10}$	1.3362 $\times {10}^{-11}$	8.3524 $\times {10}^{-13}$
Order		3.9962	3.9991	3.9998	3.9999	3.9998
Loc. err. $u^{\prime }(t)$	1.3910 $\times {10}^{-4}$	1.7433 $\times {10}^{-5}$	2.1806 $\times {10}^{-6}$	2.7262 $\times {10}^{-7}$	3.4079 $\times {10}^{-8}$	4.2599 $\times {10}^{-9}$
Order		2.9962	2.9991	2.9998	2.9999	3.0000
Glob. err. $u(t)$	1.9668 $\times {10}^{-4}$	4.9142 $\times {10}^{-5}$	1.2282 $\times {10}^{-5}$	3.0700 $\times {10}^{-6}$	7.6745 $\times {10}^{-7}$	1.9186 $\times {10}^{-7}$
Order		2.0008	2.0004	2.0002	2.0001	2.0001
Glob. err. $u^{\prime }(t)$	1.3275 $\times {10}^{-4}$	3.5692 $\times {10}^{-5}$	9.0829 $\times {10}^{-6}$	2.2811 $\times {10}^{-6}$	5.7098 $\times {10}^{-7}$	1.4279 $\times {10}^{-7}$
Order		1.8951	1.9744	1.9934	1.9982	1.9994

, where we can see that the expected orders are obtained for the solution as well as for the derivative. For the local error in the solution, we obtain one order more than the one expected since the odd derivatives vanish.

The results for the method with classical order 3 are given in

Table 2. Local and global errors and orders for problem (2) with RN3.

$\mathit{\tau }$	1/80	1/160	1/320	1/640	1/1280	1/2560
Loc. err. $u(t)$	7.4745 $\times {10}^{-7}$	4.8042 $\times {10}^{-8}$	3.0236 $\times {10}^{-9}$	1.8931 $\times {10}^{-10}$	1.1837 $\times {10}^{-11}$	7.3971 $\times {10}^{-13}$
Order		3.9596	3.9899	3.9975	3.9994	4.0002
Loc. err. $u^{\prime }(t)$	2.5478 $\times {10}^{-6}$	8.0729 $\times {10}^{-8}$	2.5316 $\times {10}^{-9}$	7.9180 $\times {10}^{-11}$	2.4749 $\times {10}^{-12}$	7.7275 $\times {10}^{-14}$
Order		4.9800	4.9950	4.9988	4.9997	5.0012
Glob. err. $u(t)$	4.6594 $\times {10}^{-6}$	4.0170 $\times {10}^{-7}$	3.8542 $\times {10}^{-8}$	4.0814 $\times {10}^{-9}$	4.6400 $\times {10}^{-10}$	5.5107 $\times {10}^{-11}$
Order		3.5360	3.3816	3.2393	3.1369	3.0738
Glob. err. $u^{\prime }(t)$	9.4688 $\times {10}^{-5}$	1.2141 $\times {10}^{-5}$	1.5315 $\times {10}^{-6}$	1.9215 $\times {10}^{-7}$	2.4058 $\times {10}^{-8}$	3.0095 $\times {10}^{-9}$
Order		2.9633	2.9869	2.9947	2.9977	2.9989

where we can see that the expected orders are obtained for the solution as well as for the derivative. For the local error in the derivative, we obtain one order more than the one expected since the odd derivatives vanish.

The results for the method with classical order 4 are presented in

Table 3. Local and global errors and orders for problem (2) with RN4.

$\mathit{\tau }$	1/80	1/160	1/320	1/640	1/1280	1/2560
Loc. err. $u(t)$	6.1363 $\times {10}^{-7}$	9.9822 $\times {10}^{-9}$	1.5757 $\times {10}^{-10}$	2.4682 $\times {10}^{-12}$	3.8384 $\times {10}^{-14}$	4.5776 $\times {10}^{-16}$
Order		5.9419	5.9853	5.9964	6.0068	6.3898
Loc. err. $u^{\prime }(t)$	1.8146 $\times {10}^{-6}$	6.9583 $\times {10}^{-8}$	2.2799 $\times {10}^{-9}$	7.2081 $\times {10}^{-11}$	2.2592 $\times {10}^{-12}$	7.0702 $\times {10}^{-14}$
Order		4.7048	4.9317	4.9832	4.9958	4.9979
Glob. err. $u(t)$	2.6326 $\times {10}^{-6}$	1.9208 $\times {10}^{-7}$	1.2682 $\times {10}^{-8}$	8.1048 $\times {10}^{-10}$	5.1163 $\times {10}^{-11}$	3.2167 $\times {10}^{-12}$
Order		3.7767	3.9209	3.9678	3.9856	3.9914
Glob. err. $u^{\prime }(t)$	7.9785 $\times {10}^{-5}$	2.7301 $\times {10}^{-6}$	9.5300 $\times {10}^{-8}$	3.5643 $\times {10}^{-9}$	1.4775 $\times {10}^{-10}$	6.9183 $\times {10}^{-12}$
Order		4.8691	4.8403	4.7408	4.5924	4.4166

, where again we can see that the expected results are obtained. The local order in the solution is one unit higher than the expected one as the odd derivatives vanish.

Example 4.

The second problem is the equation of motion of a soliton in an exponential lattice. This problem was first proposed in [17] and it is a highly non-linear system.

$$\begin{array}{ccc}\hfill u_j^{″}(t)& =& 2e^{-u_j}-e^{-u_{j-1}}-e^{-u_{j+1}},j=1,\cdots ,N,\hfill \\ \hfill u_j(0)& =& -ln(1+{\beta }^{2}sec{h}^2(\alpha j)),\hfill \\ \hfill u_j^{\prime }(0)& =& \frac{2{\beta }^{3}sec{h}^2(\alpha j)tanh(\alpha j)}{1+{\beta }^{2}sec{h}^2(\alpha j)},\hfill \end{array}$$

(15)

with $\alpha =2$, $\beta =sinh(\alpha )$ and $N=20$. The solution of this problem is $u_j(t)=-ln(1+{\beta }^{2}sec{h}^2(\alpha j+\beta t))$.

The results for method RN2 can be seen in

Table 4. Local and global errors and orders for problem (15) with RN2.

$\mathit{\tau }$	1/80	1/160	1/320	1/640	1/1280	1/2560
Loc. err. $u(t)$	2.6003 $\times {10}^{-6}$	3.0800 $\times {10}^{-7}$	3.7439 $\times {10}^{-8}$	4.6137 $\times {10}^{-9}$	5.7258 $\times {10}^{-10}$	7.1314 $\times {10}^{-11}$
Order		3.0777	3.0403	3.0206	3.0104	3.0052
Loc. err. $u^{\prime }(t)$	1.1920 $\times {10}^{-4}$	1.4952 $\times {10}^{-5}$	1.8721 $\times {10}^{-6}$	2.3420 $\times {10}^{-7}$	2.9286 $\times {10}^{-8}$	3.6615 $\times {10}^{-9}$
Order		2.9949	2.9976	2.9989	2.9994	2.9997
Glob. err. $u(t)$	1.1100 $\times {10}^{-4}$	2.5216 $\times {10}^{-5}$	5.9894 $\times {10}^{-6}$	1.4582 $\times {10}^{-6}$	3.5965 $\times {10}^{-7}$	8.9303 $\times {10}^{-8}$
Order		2.1381	2.0739	2.0383	2.0195	2.0098
Glob. err. $u^{\prime }(t)$	2.6457 $\times {10}^{-4}$	6.6306 $\times {10}^{-5}$	1.6598 $\times {10}^{-5}$	4.1520 $\times {10}^{-6}$	1.0383 $\times {10}^{-6}$	2.5963 $\times {10}^{-7}$
Order		1.9964	1.9982	1.9991	1.9995	1.9998

. There, we can observe that we also obtain the expected local and global order for the solution and the derivative.

The results for the second method, RN3, can be seen in

Table 5. Local and global errors and orders for problem (15) with RN3.

$\mathit{\tau }$	1/80	1/160	1/320	1/640	1/1280	1/2560
Loc. err. $u(t)$	6.0678 $\times {10}^{-7}$	3.8272 $\times {10}^{-8}$	2.4025 $\times {10}^{-9}$	1.5048 $\times {10}^{-10}$	9.4150 $\times {10}^{-12}$	5.8841 $\times {10}^{-13}$
Order		3.9868	3.9937	3.9969	3.9985	4.0001
Loc. err. $u^{\prime }(t)$	7.2800 $\times {10}^{-7}$	4.5052 $\times {10}^{-8}$	2.8007 $\times {10}^{-9}$	1.7456 $\times {10}^{-10}$	1.0895 $\times {10}^{-11}$	6.7900 $\times {10}^{-13}$
Order		4.0143	4.0078	4.0040	4.0020	4.0041
Glob. err. $u(t)$	3.6685 $\times {10}^{-6}$	4.6022 $\times {10}^{-7}$	5.7584 $\times {10}^{-8}$	7.2002 $\times {10}^{-9}$	9.0011 $\times {10}^{-10}$	1.1252 $\times {10}^{-10}$
Order		2.9948	2.9986	2.9996	2.9999	2.9999
Glob. err. $u^{\prime }(t)$	3.2844 $\times {10}^{-6}$	4.1504 $\times {10}^{-7}$	5.2155 $\times {10}^{-8}$	6.5363 $\times {10}^{-9}$	8.1810 $\times {10}^{-10}$	1.0233 $\times {10}^{-10}$
Order		2.9843	2.9924	2.9962	2.9981	2.9991

, for which the expected results have been obtained.

Finally, the results for method RN4 are presented in

Table 6. Local and global errors and orders for problem (15) with RN4.

$\mathit{\tau }$	1/80	1/160	1/320	1/640	1/1280	1/2560
Loc. err. $u(t)$	1.3797 $\times {10}^{-7}$	2.4952 $\times {10}^{-9}$	4.8387 $\times {10}^{-11}$	1.0514 $\times {10}^{-12}$	2.5920 $\times {10}^{-14}$	4.6849 $\times {10}^{-16}$
Order		5.7891	5.6884	5.5242	5.3421	5.7899
Loc. err. $u^{\prime }(t)$	1.6797 $\times {10}^{-6}$	5.3774 $\times {10}^{-8}$	1.6885 $\times {10}^{-9}$	5.2794 $\times {10}^{-11}$	1.6491 $\times {10}^{-12}$	5.2897 $\times {10}^{-14}$
Order		4.9652	4.9931	4.9992	5.0006	4.9624
Glob. err. $u(t)$	1.4563 $\times {10}^{-6}$	5.7019 $\times {10}^{-8}$	3.4328 $\times {10}^{-9}$	2.3119 $\times {10}^{-10}$	1.5242 $\times {10}^{-11}$	9.8139 $\times {10}^{-13}$
Order		4.6748	4.0540	3.8922	3.9229	3.9571
Glob. err. $u^{\prime }(t)$	4.0638 $\times {10}^{-6}$	2.5938 $\times {10}^{-7}$	1.6313 $\times {10}^{-8}$	1.0216 $\times {10}^{-9}$	6.3895 $\times {10}^{-11}$	3.9944 $\times {10}^{-12}$
Order		3.9697	3.9909	3.9971	3.9990	3.9997

.

Example 5.

The last problem we have solved is the non-linear Euler–Bernoulli Equation (3) presented in Example 2.

We first discretized in space, by using a spectral method suggested in [18] and deeply studied in [8]. This spectral method has been derived to discretize in space a problem such as

$$\begin{array}{c}\hfill \left\{\begin{array}{cccc}\hfill -Au& =& F,\hfill & x\in \Omega ,\hfill \\ \hfill \partial u& =& G,\hfill & x\in \Gamma \hfill \end{array}\right.\end{array}$$

with $Au=u_{xxxx}$, $F\in X$, $G\in Y$, and $u\in D(A)$, with X being a Hilbert space of functions and Y being a suitable space of functions defined on the boundary. In particular, for the problem we have, we take $\Omega =(-1,1)$ with boundary $\Gamma =\{-1,1\}$ and boundary conditions $u(-1)=g_{-1}$$u(1)=g_1$, $u_x(-1)=h_{-1}$, $u_x(1)=h_1$. For the spatial discretization of this problem, we consider a grid ${\Omega }_J$, $\Omega \cup \Gamma$ associated with a natural parameter J (related to the number of nodes on it). Then, we take $X_J$ as the space of polynomials of a degree less than or equal to J, integer $J\ge 4$, and $X_{J,0}$ as the subspace of $X_J$ such that they and their derivatives vanish on the boundary. We will consider in $X_J$ an approximation of the $L^2$-norm in $X=L^2(\Omega )$, which will be denoted by ${\parallel ·\parallel }_J$. Then, the spatial discretization is given by

$$\begin{array}{c}\hfill -A_{J,0}{U}_J+C_J\partial u=P_{J}F\end{array}$$

with $A_{J,0}$ being the matrix that discretizes $A_0$ and $C_J$ and $P_J$ being the operators associated with the discretization of A which take into account the information on the boundary of u and F, respectively. The interior nodes are denoted by ${\mu }_j$, $j=1,\cdots ,J$. They are the zeros of the second derivative of the Legendre polynomial of degree $J+2$.

In this way, after the spatial discretization, our problem reads

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}{U}_J^{{}^{″}}=-A_{J,0}{U}_J+C_J\partial u+U_J^2+P_{J}H(t),\hfill & 0\le t\le T=1,\hfill \\ U_J(0)=U_{J,0}\hfill \\ U_J^{\prime }(0)=V_{J,0}\hfill \end{array}\right.\end{array}$$

with $P_{J}H{(t)}_j=h(t,{\mu }_j)$, ${(U_{J,0})}_j=u(0,{\mu }_j)$ and ${(V_{J,0})}_j=u_t(0,{\mu }_j)$.

In the numerical experiments, we have taken $J=40$.

In this part, we present the results that have been obtained with method RN2 in

Table 7. Local and global errors and orders for problem (3) with RN2.

$\mathit{\tau }$	1/80	1/160	1/320	1/640	1/1280
Loc. err. $u(t)$	3.5093 $\times {10}^{-7}$	2.3204 $\times {10}^{-8}$	1.5422 $\times {10}^{-9}$	1.1241 $\times {10}^{-10}$	1.0014 $\times {10}^{-11}$
Order		3.9187	3.9114	3.7781	3.4887
Loc. err. $u^{\prime }(t)$	5.5860 $\times {10}^{-5}$	7.2984 $\times {10}^{-6}$	9.2722 $\times {10}^{-7}$	1.1657 $\times {10}^{-7}$	1.4601 $\times {10}^{-8}$
Order		2.9361	2.9766	2.9917	2.9972
Glob. err. $u(t)$	1.1780 $\times {10}^{-5}$	2.9189 $\times {10}^{-6}$	7.2957 $\times {10}^{-7}$	1.8249 $\times {10}^{-7}$	4.5639 $\times {10}^{-8}$
Order		2.0129	2.0003	1.9993	1.9994
Glob. err. $u^{\prime }(t)$	1.9962 $\times {10}^{-4}$	4.8801 $\times {10}^{-5}$	1.2060 $\times {10}^{-5}$	2.9991 $\times {10}^{-6}$	7.4888 $\times {10}^{-7}$
Order		2.0322	2.0167	2.0076	2.0017

, the results obtained with method RN3 in

Table 8. Local and global errors and orders for problem (3) with RN3.

$\mathit{\tau }$	1/80	1/160	1/320	1/640	1/1280
Loc. err. $u(t)$	2.1291 $\times {10}^{-7}$	1.7820 $\times {10}^{-8}$	1.2296 $\times {10}^{-9}$	7.9634 $\times {10}^{-11}$	5.0414 $\times {10}^{-12}$
Order		3.5786	3.8572	3.9487	3.9815
Loc. err. $u^{\prime }(t)$	1.3417 $\times {10}^{-5}$	9.5553 $\times {10}^{-7}$	6.8098 $\times {10}^{-8}$	4.8287 $\times {10}^{-9}$	3.3715 $\times {10}^{-10}$
Order		3.8117	3.8106	3.8179	3.8402
Glob. err. $u(t)$	1.2456 $\times {10}^{-6}$	1.6021 $\times {10}^{-7}$	2.0110 $\times {10}^{-8}$	2.5093 $\times {10}^{-9}$	3.1001 $\times {10}^{-10}$
Order		2.9587	2.9940	3.0026	3.0169
Glob. err. $u^{\prime }(t)$	1.7959 $\times {10}^{-5}$	2.4474 $\times {10}^{-6}$	3.5574 $\times {10}^{-7}$	5.0192 $\times {10}^{-8}$	6.8569 $\times {10}^{-9}$
Order		2.8754	2.7824	2.8253	2.8718

, and the results that have been obtained with method RN4 in

Table 9. Local and global errors and orders for problem (3) with RN4.

$\mathit{\tau }$	1/80	1/160	1/320	1/640	1/1280
Loc. err. $u(t)$	1.7070 $\times {10}^{-6}$	6.1236 $\times {10}^{-8}$	2.1793 $\times {10}^{-9}$	7.7642 $\times {10}^{-11}$	2.7480 $\times {10}^{-12}$
Order		4.8010	4.8125	4.8109	4.8204
Loc. err. $u^{\prime }(t)$	4.8165 $\times {10}^{-5}$	3.4176 $\times {10}^{-6}$	2.4071 $\times {10}^{-7}$	1.6643 $\times {10}^{-8}$	1.1149 $\times {10}^{-9}$
Order		3.8170	3.8276	3.8543	3.8999
Glob. err. $u(t)$	3.0516 $\times {10}^{-6}$	1.6639 $\times {10}^{-7}$	6.6974 $\times {10}^{-9}$	2.8418 $\times {10}^{-10}$	1.4797 $\times {10}^{-11}$
Order		4.1969	4.6348	4.5587	4.2634
Glob. err. $u^{\prime }(t)$	2.1788 $\times {10}^{-4}$	2.5549 $\times {10}^{-5}$	2.8936 $\times {10}^{-6}$	3.1875 $\times {10}^{-7}$	3.4444 $\times {10}^{-8}$
Order		3.0922	3.1423	3.1824	3.2101

. In this case, with RN4, we do not obtain order 4 in the global error in the derivative because of the order reduction phenomenon, which has been deeply studied for other numerical integrators such as Runge–Kutta methods, Rosenbrock methods, or RKN methods [19,20,21]. The way to avoid this order reduction is the objective of a forthcoming paper.

Finally, we present the comparison in terms of computational cost between RN2, RN3, RN4, and the RKN method with two stages and classical order 3 which is given in [22]:

We will denote this method by the abbreviation RKN3.

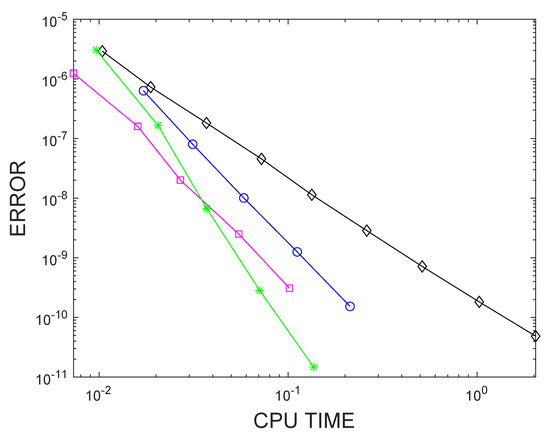
The results can be seen in Figure 1 and

Table 10. Computational cost for problem (3) with RNRN2, RN3, RN4, and RKN3 4.

$\mathit{\tau }$	CPU	Error	CPU	Error	CPU	Error	CPU	Error
	RN2	RN2	RN3	RN3	RN4	RN4	RKN3	RKN3
1/80			7.32 $\times {10}^{-3}$	1.24 $\times {10}^{-6}$	9.66 $\times {10}^{-3}$	3.05 $\times {10}^{-6}$	1.72 $\times {10}^{-2}$	6.34 $\times {10}^{-7}$
1/160	1.04 $\times {10}^{-2}$	2.92 $\times {10}^{-6}$	1.60 $\times {10}^{-2}$	1.60 $\times {10}^{-7}$	2.05 $\times {10}^{-2}$	1.66 $\times {10}^{-7}$	3.13 $\times {10}^{-2}$	8.04 $\times {10}^{-8}$
1/320	1.88 $\times {10}^{-2}$	7.30 $\times {10}^{-7}$	2.70 $\times {10}^{-2}$	2.01 $\times {10}^{-8}$	3.72 $\times {10}^{-2}$	6.70 $\times {10}^{-9}$	5.83 $\times {10}^{-2}$	1.01 $\times {10}^{-8}$
1/640	3.70 $\times {10}^{-2}$	1.82 $\times {10}^{-7}$	5.49 $\times {10}^{-2}$	2.51 $\times {10}^{-9}$	7.07 $\times {10}^{-2}$	2.84 $\times {10}^{-10}$	1.12 $\times {10}^{-1}$	1.26 $\times {10}^{-9}$
1/1280	7.23 $\times {10}^{-2}$	4.56 $\times {10}^{-8}$	1.02 $\times {10}^{-1}$	3.10 $\times {10}^{-10}$	1.36 $\times {10}^{-1}$	1.48 $\times {10}^{-11}$	2.13 $\times {10}^{-1}$	1.53 $\times {10}^{-10}$
1/2560	1.34 $\times {10}^{-1}$	1.14 $\times {10}^{-8}$
1/5120	2.61 $\times {10}^{-1}$	2.86 $\times {10}^{-9}$
1/10240	5.12 $\times {10}^{-1}$	7.17 $\times {10}^{-10}$
1/20480	1.03 $\times {10}^0$	1.82 $\times {10}^{-10}$
1/40960	2.04 $\times {10}^0$	4.86 $\times {10}^{-11}$

, where we have written the values of τ and the value of the computational cost to obtain global errors in the solution in the range $[{10}^{-12},{10}^{-6}]$. In the graph, the error has been plotted as a function of τ in double logarithmic scale. In this graph and this table, we can see that the method which generates more computational cost to achieve the desired error is RN2. Given a fixed value of τ, this method presents a lower computational cost than the other three, but as its classical order is only two, it needs a lower value of τ to obtain the same error than the other three methods, and in this way, it needs more time steps. For example, if we take $\tau =\frac{1}{320}$, we can see that RN2 takes $1.8751\times {10}^{-2}$ seconds to obtain the result, but RN4 needs $3.7180\times {10}^{-2}$ seconds, nearly double. However, for this value, the error that is found with RN2 is $7.2957\times {10}^{-7}$, but with RN4 it is $6.6974\times {10}^{-9}$. To obtain this error with the RN2 method, we need a value of τ between $\frac{1}{2560}$ and $\frac{1}{5120}$, so the number of steps is much greater and so is the computational cost.

As we can also see, both RN3 and RN4 are better in terms of the computational cost than RKN3. As RN4 has more stages than RN3, for bigger values of τ, RN3 needs fewer steps to obtain the desired error, but when τ is smaller, because of the classical order of the RN4 method, it requires fewer time steps and the computational cost of this method is lower.

6. Conclusions and Future Work

As we have seen in this work, these new methods are a good choice when we have a second-order in time problem to solve. By using these methods, we avoid the drawback that other integrators ike Runge–Kutta–Nyström ones present when the problem we are solving is a non-linear one.

This work is an introductory work about these methods and there is more work to do in the near future. For example, we have the problem of the order reduction that this type of method presents when we solve a second-order in time PDE with non-vanishing order conditions. This problem has already been studied for other existing methods such as Runge–Kutta, Rosenbrock, and Runge–Kutta–Nyström.

Another piece of work to be done is the construction and study of Rosenbrock–Nyström methods with complex coefficients. As we have seen, the only stable method that exists with only one stage is a P-stable one. To obtain R-stable methods (not P-stable) with classical order two, we should have two intermediate stages. Rosenbrock methods with complex coefficients have been proven to be very efficient when solving stiff problems [16,23]. In this way, one piece of future work is to use this idea of complex coefficients to obtain efficient Rosenbrock–Nyström methods to solve second-order in time problems.

To conclude the work to be done, we are also interested in the comparison between different Rosenbrock–Nyström methods, in order to study the best method to be used in practice. One high-stage scheme could be worse in practice than one method with fewer stages because of machine round-off errors.