Abstract
We consider the predictor-corrector numerical methods for solving Caputo–Hadamard fractional differential equations with the graded meshes with and , where is a partition of . We also consider the rectangular and trapezoidal methods for solving Caputo–Hadamard fractional differential equations with the non-uniform meshes . Under the weak smoothness assumptions of the Caputo–Hadamard fractional derivative, e.g., with , the optimal convergence orders of the proposed numerical methods are obtained by choosing the suitable graded mesh ratio . The numerical examples are given to show that the numerical results are consistent with the theoretical findings.
1. Introduction
Recently, fractional differential equations have become an active research area due to their applications in a wide range of fields including mechanics, computer science, and biology [1,2,3,4]. There are different kinds of fractional derivatives, e.g., Caputo, Riemman–Liouville, Riesz, which have been studied extensively in the literature. However, the Hadamard fractional derivative is also very important and used to model the different physical problems [5,6,7,8,9,10,11].
The Hadamard fractional derivative was suggested in early 1892 [12]. More recently, a new derivative which involved a Caputo-type modification on the Hadamard derivative known as the Caputo–Hadamard derivative was suggested [8]. The aim of this paper is to study and analyze some useful numerical methods for solving Caputo–Hadamard fractional differential equations with graded and non-uniform meshes under the weak smoothness assumptions of the Caputo–Hadamard fractional derivative, e.g., with .
We thus consider the following Caputo–Hadamard fractional differential equation, with , [8]
where is a nonlinear function with respect to , and the initial values are given and . Here the fractional derivative denotes the Caputo–Hadamard derivative defined by
with and where denotes the smallest integer greater than or equal to [8].
To make sure that (1) has a unique solution, we assume that the function f is continuous and satisfies the following Lipschitz condition with respect to the second variable y [7,13]
For some recent existence and uniqueness results for Caputo–Hadamard fractional differential equations, the readers can refer to [14,15,16] and the references therein.
It is well known that the Equation (1) is equivalent to the following Volterra integral equation, with , [5]
Let us review some numerical methods for solving (1). Gohar et al. [7] studied the existence and uniqueness of the solution of (1) and Euler and predictor-corrector methods were considered. Gohar et al. [13] further considered the rectangular, trapezoidal, and predictor-corrector methods for solving (1) with uniform meshes under the smooth assumption of the fractional derivative, e.g., with . There are also some numerical methods for solving Caputo–Hadamard time fractional partial differential equations [7,17]. In this paper, we shall assume that with and assume that behaves as with which implies that the derivatives of have the singularities at . In such case, we can not expect the numerical methods with uniform meshes have the optimal convergence orders. To obtain the optimal convergence orders, we shall use the graded and non-uniform meshes as in Liu et al. [18,19] for solving Caputo fractional differential equations. We shall show that the predictor-corrector method has the optimal convergence orders with the graded meshes for some suitable . We also show that the rectangular, trapezoidal methods also have the optimal convergence orders with some non-uniform meshes .
For some recent works for the numerical methods for solving fractional differential equations with graded and non-uniform meshes, we refer to [17,20,21,22]. In particular, Stynes et al. [23,24] applied a graded mesh on a finite difference method for solving subdiffusion equations when the solutions of the equations are not sufficiently smooth. Liu et al. [18,19] applied a graded mesh for solving Caputo fractional differential equation by using a fractional Adams method with the assumption that the solution was not sufficiently smooth. The aim of this work is to extend the ideas in Liu et al. [18,19] for solving Caputo fractional differential equations to solve the Caputo–Hadamard fractional differential equations.
The paper is organized as follows. In Section 2 we consider the error estimates of the predictor-corrector method for solving (1) with the graded meshes. In Section 3 we consider the error estimates of the rectangular, trapezoidal methods for solving (1) with non-uniform meshes. In Section 4 we will provide several numerical examples which support the theoretical conclusions made in Section 2 and Section 3.
Throughout this paper, we denote by C a generic constant depending on , but independent of and N, which could be different at different occurrences.
2. Predictor-Corrector Method with Graded Meshes
In this section, we shall consider the error estimates of the predictor-corrector method for solving (1) with graded meshes. We first recall the following smoothness properties of the solutions to (1).
Theorem 1
([25]). Let . Assume that where G is a suitable set. Define . Then there exists a function and some constants such that the solution y of (1) can be expressed in the following form
An example of this would be when . We would have and
This implies that the solution y of (1) would behave as . As such the solution .
Theorem 2
([25]). If for some and , then
where and with .
With the above two theorems, we can see that if one of y and is sufficiently smooth then the other will not be sufficiently smooth unless some special conditions have been met.
Therefore it is natural to introduce the following smoothness assumptions for the fractional derivative in (1).
Assumption 1.
Let and . Let y be the solution of (1). Assume that can be expressed as a function of , that is, there exists a smooth function such that
Further we assume that satisfies the following smooth assumptions, with ,
where and denote the first and second order derivatives of , respectively.
Denote
We then have
Hence the assumptions (6) is equivalent to, with ,
which are similar to the smoothness assumptions given in Liu et al. [18] for the Caputo fractional derivative .
Remark 1.
Assumption 1 gives the behavior of near and implies that has the singularity near . It is obvious that . For example, we may choose with .
Let N be a positive integer and let be the partition on . We define the following graded mesh on with
such that, with ,
which implies that
When we have . Further we have
Denote the approximation of . Let us introduce the different numerical methods for solving (3) with below. Similarly we may define the numerical methods for solving (3) with . The fractional rectangular method for solving (3) is defined as
where the weights are defined as
The fractional trapezoidal method for solving (3) is defined as
where the weights for are defined as
The predictor-corrector Adams method for solving (3) is defined as, with ,
where the weights and are defined as above.
If we assume that satisfies Assumption 1, we shall prove the following error estimate.
Theorem 3.
Assume that satisfies Assumption 1. Further assume that and are the solutions of (3) and (13), respectively.
- If , then we have
- If , then we have
Proof of Theorem 3
In this subsection, we shall prove Theorem 3. To help with this we will start by proving some preliminary Lemmas. In Lemma 1 we will be finding the error estimate between and the piecewise linear function for both and . This will be used to estimate one of the terms in our main proof.
Lemma 1.
Assume that satisfies Assumption 1
- If , then we have
- If , then we havewhere is the piecewise linear function defined by,
Proof.
Note that, with ,
For , we have
Note that, with ,
which implies that, by Assumption 1,
Thus we have, by (14),
Note that there exists a constant such that
which follows from
Thus we have, for ,
For , we have
For we have, with and ,
where we have used the following fact, with ,
which can be seen easily by noting and (7).
By Assumption 1 and by using [24] (Section 5.2), we have, with ,
where defines the ceiling function defined as before. For each of these integrals we shall consider the cases when and when .
For , when , we have, with ,
Note that, with ,
and
Thus, with ,
Case 1, If , we have
Case 2, If , we have
Case 3, If , we have
Thus, we have that for
Next we will take the case for when , we have, with ,
Thus, we have that for ,
For , we have, noting that with ,
which implies that
Note that
we get, with and ,
For , we have, with ,
By Assumption 1, we then have, with ,
Obviously the bound for is stronger than the bound for . Together these estimates complete the proof of this lemma. □
In Lemma 2 below, we state that the weights and are positive for all values of j.
Lemma 2.
Let . We have
Proof.
The proof is obvious, we omit the proof here. □
For Lemma 3, we are attempting to find an upper bound for . This will be used in the main proof when addressing the term.
Lemma 3.
Proof.
We have, by (12), with ,
□
In Lemma 4 we will be finding the error estimate between and the piecewise constant function for both and . This will be used to estimate one of the terms in our main proof.
Lemma 4.
Assume that satisfies Assumption 1.
- If , then we have
- If , then we have
where is the piecewise constant function defined as below, with
Proof.
The proof is similar to the proof of Lemma 1. Note that
For , by Assumption 1, we have
Hence we get
If , we have
If , we have
For , we have, with ,
Hence, by Assumption 1,
For , if , then we have, with ,
If , we have
Note that for any . Hence, we have
For , we have
Noting that, with ,
we have, with ,
For , we have, with ,
Further we have
Together these estimates complete the proof of this Lemma. □
For Lemma 5, we are attempting to find an upper bound for the sum of our weights. This will be used in the main proof when simplifying several terms.
Lemma 5.
Proof.
We only prove (21). The proof of (22) is similar. Note that
where is the remainder term. Let , we have
Thus, (21) follows by the fact in Lemma 2. □
We will now use the above lemmas to prove the error estimates of Theorem 3.
Proof of Theorem 3.
The term I is estimated by Lemma 1. For II, we have, by Lemma 2 and the Lipschitz condition of f,
For , we have, by Lemma 2 and the Lipschitz condition for f,
Note that
Thus,
The term is estimated by Lemma 4. For , we have, by Lemma 2,
Hence, we obtain
The rest of the proof is exactly the same as the proof of [18] (Theorem 1.4). The proof of Theorem 3 is complete. □
3. Rectangular and Trapezoidal Methods with Non-Uniform Meshes
In this section, we will consider the error estimates for the fractional rectangular and trapezoidal methods for solving (1). These results are based on the error estimates proposed by Liu et al. [19]. First, we will introduce the non-uniform meshes for solving (1).
Let N be a positive integer and let be the partition on . We define the following non-uniform mesh on with
such that
which implies that
Now we see when , we have . When we have . Further we have
3.1. Rectangular Method
In this subsection, we prove the following error estimate for the rectangular method over the given non-uniform mesh.
Theorem 4.
Assume that satisfies Assumption 1. Further assume that and are the solutions of (3) and (9), respectively.
- If , then we have
- If , then we have
To prove Theorem 4, we need some preliminary lemmas. Here we only state the lemmas without proofs since the proofs are similar as in Liu et al. [19]. In Lemma 6 we will be defining a key estimate which we will be using in our main proof.
Lemma 6.
Assume that satisfies Assumption 1.
- If , then we have, with , ,
- If , then we have
In Lemma 7 we will find some upper bounds for our weights and .
Lemma 7.
In Lemma 8 we will give an adapted Gronwall inequality to be used in the main results.
Lemma 8.
Assume that and for where N is a positive integer and . Let be positive and the sequence meet
then
Proof of Theorem 4.
For , we have
The first term I can be estimated by Lemma 6. For , we can apply Lemma 2 and the Lipschitz condition of f,
Substituting into the original we get
By applying Lemma 8, we will get
This completes the proof of Theorem 4. □
3.2. Trapezoid Formula
In this subsection we will consider the error estimates of the trapezoid method over the non-uniform mesh. We shall prove the following theorem
Theorem 5.
Assume that satisfies Assumption 1. Further assume that and are the solutions of (3) and (11), respectively.
- If , then we have
- If , then we have
To prove Theorem 5, we need the following lemma. In Lemma 9 we will be defining a key estimate which we will be using in our main proof.
Lemma 9.
Assume that satisfies Assumption 1.
- If , then we have, with ,
- If , then we have
Proof of Theorem 5.
For , we have
The term I is estimated by Lemma 9. For II we can apply Lemma 7 and the Lipschitz condition of f,
Thus we obtain
By using the corresponding Gronwall Lemma 8 we have . This completes the proof of Theorem 5. □
4. Numerical Examples
In this section, we will consider some numerical examples to confirm the theoretical results obtained in the previous sections. For simplicity, all the examples below will take . All the following results may be adapted for all .
Example 1.
Consider the following nonlinear fractional differential equation, with and ,
where
The exact solution of this equation is . We will be solving Example 1 over the interval . Let N be a positive integer and let be the graded mesh on the interval . This mesh is defines as for with . Therefore, we have by Theorem 3,
In Table 1 we can see the maximum absolute error and experimental order of convergence (EOC) for the predictor-corrector method at varying and N values. For our different , we have chosen N values as . For this example we have taken . The maximum absolute errors were obtained as shown above with respect to N and we calculate the experimental order of convergence or EOC as

Table 1.
Table showing the maximum absolute error and EOC for solving (23) using the predictor-corrector method.
As we can see, the EOCs for this example are almost which was predicted by Theorem 3. Due to the solution of the FODE being sufficiently smooth, any value of r will give the optimal convergence order given above. As we are using , this means that we are using a uniform mesh and so can compare these results with the methods introduced by Gohar et al. [13]. We can see, we have obtained a similar result.
In Figure 1, we have plotted the order of convergence for Example 1. From Equation (24) we have, with ,
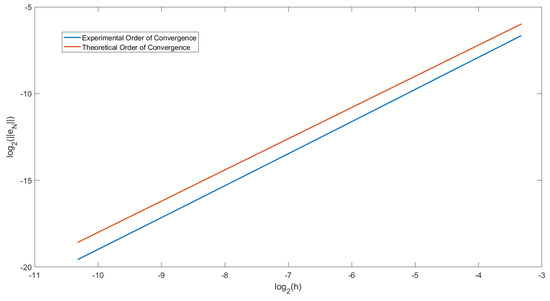
Figure 1.
Graph showing the experimental order of convergence (EOC) at T = 2 in Example 1 with .
Let and let . We then plotted a graph for y against x for . Doing this, we get that the gradient of the graph would equal the EOC. To compare this to the theoretical order of convergence, we have also plotted the straight line . For Figure 1 we choose . We can observe that the two lines drawn are parallel. Therefore we can conclude that the order of convergence of this predictor-corrector method is .
Example 2.
Consider the following nonlinear fractional differential equation, with and ,
where
We will be solving Example 2 over the interval . The exact solution of this equation is and . This implies that the regularity of behaves as . This means that satisfies Assumption 1. We will be using the same graded mesh as in Example 1. Therefore, we have by Theorem 3, with ,
In Table 2, Table 3 and Table 4 we can see the EOC for the predictor-corrector method with varying values of and with r values at and . With a fixed we have obtain the EOC and maximum absolute error for increasing values of N. By doing so we can see that the EOC are almost when and the EOC are almost when .

Table 2.
Table showing the maximum absolute error and EOC for solving (25) using the predictor-corrector method for .

Table 3.
Table showing the maximum absolute error and EOC for solving (25) using the predictor-corrector scheme for .

Table 4.
Table showing the maximum absolute error and EOC for solving (25) using the predictor-corrector method for .
When , we are using a uniform mesh and we can see that the EOC obtained is the same as those obtained by Gohar et al. [13]. Comparing these to the results of the graded mesh when we can see that a higher EOC has been obtained and an optimal order of convergence is recovered.
In Figure 2, we have plotted the order of convergence for Example 2 when and . This plot is the same as for Figure 1. We have also plotted the straight line . We can observe that the two lines drawn are parallel. Therefore we can conclude that the order of convergence of this predictor-corrector method is .
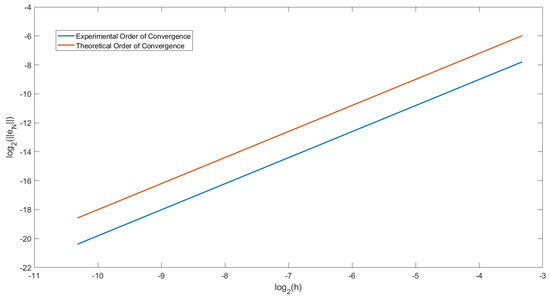
Figure 2.
Graph showing the experimental order of convergence (EOC) at T = 2 in Example 2 with and .
Example 3.
Consider the following nonlinear fractional differential equation, with and ,
The exact solution of this FODE is . Therefore , where is defined as the Mittag–Leffler function
Therefore
This shows that behaves as This means that satisfies Assumption 1. Therefore, with , we have by Theorem 3,
We will be solving this equation over the same graded mesh as in Example 1 with varying r values. In Table 5, Table 6 and Table 7, we have calculated the EOC and maximum absolute error with respect to increasing N values and with r values at and . The experimental orders of convergence are shown to be almost if we choose and almost if we choose . Once again it is shown when we use a graded mesh at the optimal r value, we get a higher order of convergence to that obtained by the uniform mesh at .

Table 5.
Table showing the maximum absolute error and EOC for solving (27) using the predictor-corrector method for .

Table 6.
Table showing the maximum absolute error and EOC for solving (27) using the predictor-corrector method for .

Table 7.
Table showing the maximum absolute error and EOC for solving (27) using the predictor-corrector method for .
In Figure 3, we have plotted the order of convergence for Example 3 when and . This plot is the same as for Figure 1. We have also plotted the straight line . We can observe that the two lines drawn are parallel. Therefore we can conclude that the order of convergence of this predictor-corrector method is for choosing the suitable graded mesh ratio r.
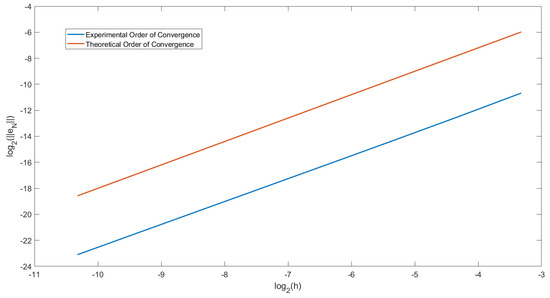
Figure 3.
Graph showing the experimental order of convergence (EOC) at T = 2 in Example 3 with and .
Example 4.
In this example we will be applying the rectangular and trapezoidal methods for solving (27). Let N be a positive integer and let be the graded mesh on the interval for . We will be using and .
In Table 8, we have calculated the EOC and maximum absolute error with respect to increasing N values and with for the rectangular method. By once again using the fact that and applying Theorem 4 we can say

Table 8.
Table showing the maximum absolute error and EOC for solving (27) using the rectangular method on a graded mesh.
The experimental orders of convergence are shown to be almost if we choose and almost if we choose . This confirms the theoretical error estimates calculated in Section 4. In Table 9, we have used the same method to solve (27) but using the uniform mesh. This shows how a larger EOC is achieved when using non-uniform mesh over a uniform mesh.

Table 9.
Table showing the maximum absolute error and EOC for solving (27) using the rectangular method on a uniform mesh.
In Table 10, we have calculated the EOC and maximum absolute error with respect to increasing N values and with for the trapezoidal method. By once again using the fact that and applying Theorem 4 we can say

Table 10.
Table showing the maximum absolute error and EOC for solving (27) using the trapezoidal method on a graded mesh.
The experimental orders of convergence are shown to be almost if we choose and almost if we choose . This confirms the theoretical error estimates calculated in Section 4. In Table 11, we have used the same method to solve (27) but using the uniform mesh. This shows how a larger EOC is achieved when using graded mesh over a uniform mesh.

Table 11.
Table showing the maximum absolute error and EOC for solving (27) using the trapezoidal method on a uniform mesh.
5. Conclusions
In this paper we propose several numerical methods for solving Caputo–Hadamard fractional differential equations with graded and non-uniform meshes. We first introduce a predictor-corrector method and calculate the convergence and error estimates over a graded mesh so to show that the optimal convergence orders can be recovered when the solutions are not sufficiently smooth. We then introduce the error estimates on the fractional rectangle and fractional trapezoidal methods with some non-uniform meshes. Finally, we consider several numerical simulations to support the theoretical results made for the above methods on the convergence orders and error estimates.
Author Contributions
We have equal contributions to this work. C.W.H.G. considered the theoretical analysis and wrote the original version of the work. Y.L. considered the theoretical analysis and performed the numerical simulation. Y.Y. introduced and guided this research topic. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Diethelm, K. The Analysis of Fractional Differential Equations; Lecture Notes in Mathematics; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Kilbas, A.A.; Srivastava, H.M.; Trujillo, J.J. Theory and Applications of Fractional Differential Equations; North-Holland Mathematics Studies; Elsevier: Amsterdam, The Netherlands, 2006; Volume 204. [Google Scholar]
- Oldman, B.K.; Spanier, J. The Fractional Calculus; Academic Press: New York, NY, USA, 1974. [Google Scholar]
- Podlubny, I. Fractional Differential Equations; Math, Science and Engineering; Academic Press: San Diego, CA, USA, 1999. [Google Scholar]
- Adjabi, Y.; Jarad, F.; Baleanu, D.; Abdeljawad, T. On Cauchy problems with Caputo Hadamard fractional derivatives. J. Comput. Anal. Appl. 2016, 21, 661–681. [Google Scholar]
- Garra, R.; Mainardi, F.; Spada, G. A generalization of the Lomnitz logarithmic creep law via Hadamard fractional calculus. Chaos Solitons Fractals 2017, 102, 333–338. [Google Scholar] [CrossRef] [Green Version]
- Gohar, M.; Li, C.; Yin, C. On Caputo Hadamard fractional differential equations. Int. J. Comput. Math. 2020, 97, 1459–1483. [Google Scholar] [CrossRef]
- Jarad, F.; Abdeljawad, T.; Baleanu, D. Caputo-type modification of the Hadamard fractional derivatives. Adv. Differ. Equ. 2012, 2012, 142. [Google Scholar] [CrossRef] [Green Version]
- Kilbas, A.A. Hadamard-type fractional calculus. J. Korean Math. Soc. 2001, 38, 1191–1204. [Google Scholar]
- Li, C.; Cai, M. Theory and Numerical Approximations of Fractional Integrals and Derivatives; SIAM: Philadelphia, PA, USA, 2019. [Google Scholar]
- Ma, L. On the kinetics of Hadamard-type fractional differential systems. Fract. Calc. Appl. Anal. 2020, 23, 553–570. [Google Scholar] [CrossRef]
- Hadamard, J. Essai sur létude des fonctions donnes par leur developpment de Taylor. J. Pure Appl. Math. 1892, 4, 101–186. [Google Scholar]
- Gohar, M.; Li, C.; Li, Z. Finite Difference Methods for Caputo-Hadamard Fractional Differential Equations. Mediterr. J. Math. 2020, 17, 194. [Google Scholar] [CrossRef]
- Abbas, S.; Benchohra, M.; Hamidi, N.; Henderson, J. Caputo-Hadamard fractional differential equations in Banach spaces. Fract. Calc. Appl. Anal. 2018, 21, 1027–1045. [Google Scholar] [CrossRef]
- Samei, M.E.; Hedayati, V.; Rezapour, S. Existence results for a fraction hybrid differential inclusion with Caputo–Hadamard type fractional derivative. Adv. Differ. Equ. 2019, 2019, 163. [Google Scholar] [CrossRef]
- Ardjouni, A. Existence and uniqueness of positive solutions for nonlinear Caputo-Hadamard fractional differential equations. Proyecciones 2021, 40, 139–152. [Google Scholar] [CrossRef]
- Li, C.; Li, Z.; Wang, Z. Mathematical Analysis and the Local Discontinuous Galerkin Method for Caputo-Hadamard Fractional Partial Differential Equation. J. Sci. Comput. 2020, 85, 41. [Google Scholar] [CrossRef]
- Liu, Y.; Roberts, J.; Yan, Y. Detailed error analysis for a fractional Adams method with graded meshes. Numer. Algorithms 2018, 78, 1195–1216. [Google Scholar] [CrossRef] [Green Version]
- Liu, Y.; Roberts, J.; Yan, Y. A note on finite difference methods for nonlinear fractional differential equations with non-uniform meshes. Int. J. Comput. Math. 2018, 95, 1151–1169. [Google Scholar] [CrossRef]
- Li, C.; Yi, Q.; Chen, A. Finite difference methods with non-uniform meshes for nonlinear fractional differential equations. J. Comput. Phys. 2016, 316, 614–631. [Google Scholar] [CrossRef]
- Diethelm, K. Generalized compound quadrature formulae for finite-part integrals. IMA J. Numer. Anal. 1997, 17, 479–493. [Google Scholar] [CrossRef]
- Zhang, Y.; Sun, Z.; Liao, H. Finite difference methods for the time fractional diffusion equation on non-uniform meshes. Int. J. Comput. Math. 2014, 265, 195–210. [Google Scholar] [CrossRef]
- Stynes, M. Too much regularity may force too much uniqueness. Fract. Calc. Appl. Anal. 2016, 19, 1554–1562. [Google Scholar] [CrossRef] [Green Version]
- Stynes, M.; Oriordan, E.; Gracia, J.L. Error analysis of a finite difference method on graded meshes for a time-fractional diffusion equation. SIAM J. Numer. Anal. 2017, 55, 1057–1079. [Google Scholar] [CrossRef]
- Lubich, C. Runge-Kutta theory for Volterra and Abel integral equations of the second kind. Math. Comput. 1983, 41, 87–102. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).