Feasible Optimal Solutions of Electromagnetic Cloaking Problems by Chaotic Accelerated Particle Swarm Optimization

Abstract

The optimization problem of cloaking a perfectly electric conducting or dielectric spherical core is investigated. The primary excitation is due to an external magnetic dipole. The chaotic accelerated particle swarm optimization (CAPSO) algorithm is adjusted and applied to this optimization problem. The optimization variables are the radii, the permittivities and the permeabilities of a small number of spherical shells covering the core. Several feasible optimal designs are obtained, which exhibit perfect or almost perfect cloaking performance for all angles of observation. These optimal designs correspond to two, three or four spherical coating layers composed of ordinary materials. Detailed parametric investigations of the cloaking mechanism with respect to the type and radius of the core and the location of the primary dipole are carried out. The presented optimization procedure and the reported results are expected to be useful in applications like scattering and characterization of optical particles as well as in designing low-profile receiving antennas.

1. Introduction

Optimization-based approaches constitute the foundations for the modeling and analysis of state-of-the-art applications concerning the design of electromagnetic, optical, and metamaterial devices, renewable energy sources’ components as well as antenna elements; see [1] for a recent survey. Particularly, particle swarm optimization (PSO) algorithms, which are bio-inspired and population-based evolutionary algorithms, have been proven to provide efficient and flexible tools for the treatment of the aforementioned applications [2,3,4,5] as well as several other applications in diverse fields [6,7]. The original PSO algorithm, as a concept, was first introduced in 1995 [8,9], and it was directly inspired by simulations mimicking the behavior observed in biological swarms of birds targeting food locations [10]. It was conceptually placed between genetic algorithms and evolutionary computing [8]. The swarm is designed in compliance with the basic principles of swarm intelligence [8,11]. Since its original appearance, many variants and versions of the algorithm have been developed, utilizing different tools and techniques and excelling at different types of problems. For instance, PSO methods are very popular for non-convex optimization problems. Presently, the variety of PSO algorithms constitute a versatile and efficient family of optimization methods.

The development and implementation of PSO algorithms in computational electromagnetics and related engineering and antenna design applications were presented for the first time in [12,13]. Moreover, a quantum PSO algorithm was developed in [14] and applied for finding a set of dipoles producing the same fields as a circular dielectric resonator antenna; this algorithm relied on quantum mechanics rather than the Newton’s laws considered in the original PSO versions. A PSO algorithm based on molecular dynamics and leading to a physical theory for the swarm environment was presented in [15] and applied to the synthesis of antennas arrays. Variants of PSO algorithms with relevant applications in microwave absorbers and base-station antenna optimization for mobile communications were developed in [16].

In this paper, we apply the chaotic APSO (CAPSO) algorithm [17], which is a suggested variant and improvement of the accelerated particle swarm optimization (APSO) algorithm [18]. Both the APSO and the CAPSO algorithms follow the approach of a single-step update regarding the position of the particles of the swarm in contrast to the original PSO, which first updates the velocity of the particles and then the position. There exist parameters to fine tune the algorithm, and to insert necessary randomness. Specifically, in CAPSO, the global attraction parameter is decided to be non-constant; it updates through chaotic maps. The descriptions and definitions regarding the APSO/CAPSO algorithms are presented in the following section, accompanied by necessary specifications and adjustments.

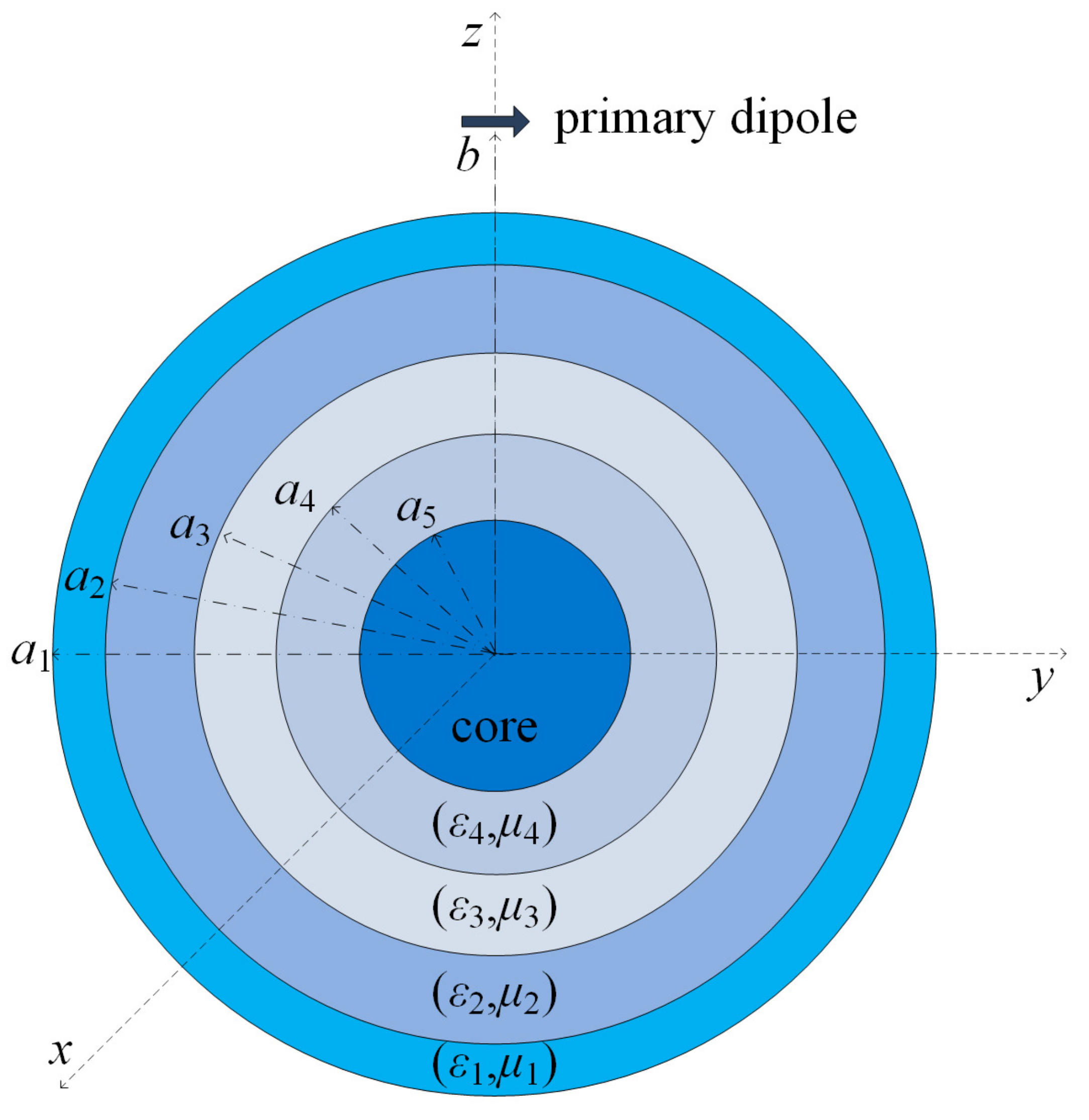
The optimization problem we are considering concerns the electromagnetic cloaking of a perfect electric conducting (PEC) or dielectric spherical core by covering it with a small number of spherical shells (layers). The primary excitation of the spherical medium is due to a magnetic dipole lying either in close proximity to the medium or far from it; in the latter situation, the plane-wave incidence case is fairly approximated. We adjust the CAPSO algorithm to the considered optimization problem and apply it to determine optimal values of the radii as well as the permittivities and the permeabilities of the spherical shells, yielding significantly reduced bistatic scattering cross section values with respect to the bare PEC or dielectric sphere. It is demonstrated by means of several numerical experiments that perfect or almost perfect cloaking performance is achieved for all observation angles. The coating shells yielding this robust cloaking performance are composed of ordinary materials, while only two, three or four shells are sufficient; the number of shells depends on the type and radius of the core, as well as on the location of the primary dipole. Moreover, the fast convergence of the CAPSO algorithm for the examined optimization problem is exhibited by presenting representative convergence plots.

Finding such optimal designs for the considered cloaking problem is an outcome of the effectiveness and versatility of the applied CAPSO algorithm; exhibiting these findings for a variety of scattering configurations is a main goal of this work. In a previous paper [19], the classic version of the PSO algorithm was applied for cloaking a PEC core, and some preliminary numerical investigations were performed. However, the obtained results showed efficient cloaking only for a range of observation angles, while a dielectric core or different radii of the core were not considered. Besides, the cloaking behavior of layered media and related optimization problems were investigated in [20,21,22,23,24,25,26,27,28] by means of different techniques and by employing other types of materials not always easily realizable, such as epsilon-near-zero, mu-near-zero, single-negative, double-negative or plasmonic metamaterials.

This paper is organized as follows. Section 2 includes some background material on PSO and APSO and provides a description of the CAPSO algorithm with specific adjustments needed for the examined cloaking problem. The optimization problem is presented in Section 3, where the exact solution of the scattering problem is derived, and then the optimization strategy is detailed. Several numerical results are given in Section 4 for different parameters of the examined scattering geometry. In all cases, feasible optimal solutions are determined and the efficient cloaking performance is shown. Conclusions are summarized in Section 5.

2. Chaotic Accelerated Particle Swarm Optimization

The CAPSO algorithm was proposed by Gandomi et al. in [17]. APSO stands for Accelerated Particle Swarm Optimization and is an algorithm developed by Yang in [18]; it was also presented in [29]. Thus, CAPSO was introduced as a variant and possible improvement of the APSO.

In this section, we first describe as a background some fundamentals of the PSO and the APSO algorithms. Then, we present mathematical descriptions of the swarm’s movement in CAPSO as well as the pseudo-code and the implementation of the algorithm in the form that proved to be very efficient with respect to obtaining optimal solutions for the electromagnetic cloaking problem we are investigating (details on this optimization problem are given in the next section).

2.1. Particle Swarm Optimization Fundamentals

In PSO algorithms, the swarm consists of “particles”, which are points in the n-dimensional search space of the optimization problem. There exist nature-inspired swarm optimization methods, in which the particles have additional properties or societal structures. For example, the Fish School Search algorithm’s swarm is modeled after fish swarms, and the members have feeding mechanisms resulting to weight [30], while in the Grey Wolf Optimizer [31], hierarchy and hunting behaviors are utilized. PSO particles can also follow topologies and form clans with leaders, such as in [32,33,34]. In this work, we only refer to swarms of particles with no weight and size that follow a global topology.

It is worthwhile to briefly mention that said swarms in PSO algorithms are built with respect to the following principles of swarm intelligence (SI) [11]:

• Proximity: The swarm has the ability to complete simple/elementary computations. We mostly refer to time and space computations, since they concern the swarm’s “natural” environment;
• Quality: The swarm considers quality factors as well (e.g., safety);
• Diverse response: The swarm does not narrow down its strategies regarding the environment to an extreme degree, causing limitations. It ensures the ability to follow alternatives;
• Stability: The swarm does not alter its mode of behavior for every single change observed in its environment;
• Adaptability: The swarm alters its mode of behavior in response to environmental changes when this decision is ensured to be a beneficial one (the swarms are designed to have means of knowing so).

In general, PSO algorithms can be described by the following model. It should be noted that depending on the algorithm, a variety of parameters and/or mechanisms accompany this model.

• Candidate solutions are represented by the particles’ positions $\mathbf{x}\in {\mathbb{R}}^n$;
• The particles move in the search space possessing velocity $\mathbf{u}\in {\mathbb{R}}^n$;
• There is shared knowledge in the swarm regarding the top solution(s) discovered by the swarm. The best solution of the whole swarm per iteration is usually referred to as the global best ${\mathbf{g}}^{*}$. There can be multiples if the algorithm follows such a topology;
• The velocity update formula is certainly affected by the global best solution and by other parameters. For example, the particle’s individual best position so far, ${\mathbf{x}}^{*}$, which is known as the local best;
• Some randomness is necessary to establish better solutions. It is very common to insert some randomness factors in the velocity update formula.
• The position updates after the velocity, commonly with respect to laws of the Newtonian (classical) mechanics;
• The algorithm converges when the particles have agreed to an optimal position. Additionally, there is a stopping criterion when the maximum number of iterations is met.

2.2. Accelerated Particle Swarm Optimization (APSO)

The APSO algorithm follows a minimalist approach regarding the position updates for the swarm. Thus, in this algorithm, we only use the global best ${\mathbf{g}}^{*}$, as well as introduce necessary randomness, to generate the velocity vector $\mathbf{u}$, resulting in the use of a simpler mathematical formula than that of the original PSO algorithm. In one of the formulae proposed in [29], a standard normal distribution $\alpha r_i$ is used, where r is drawn from $N(0,1)$. For a specific particle during the i-th iteration, we have the following updates for the velocity and position:

$${\mathbf{u}}_i={\mathbf{u}}_{i-1}+\beta ({\mathbf{g}}^{*}-{\mathbf{x}}_{i-1})+\alpha r_{i-1},$$

(1)

$${\mathbf{x}}_i={\mathbf{x}}_{i-1}+{\mathbf{u}}_i.$$

(2)

We can draw $r_{i-1}$ from suitable distributions (e.g., a Gaussian one).

It is also suggested to use an even more simplified formula in order to have particle location updates in a single step:

$${\mathbf{x}}_i=(1-\beta ){\mathbf{x}}_{i-1}+\beta {\mathbf{g}}^{*}+\alpha r_{i-1}.$$

(3)

The parameters $\alpha$ and $\beta$ do have a suggested range of suitable values, which are: $\alpha \in [0.1,0.4]$ and $\beta \in [0.2,0.7]$ [17,29]. However, these parameters should scale with respect to the scales of the problem variables and need to be fine-tuned, especially for complicated optimization problems. It should be noted that $\beta$ is a very important parameter, since it characterizes the variations of the global best ${\mathbf{g}}^{*}$ attraction. The parameter $\alpha$ is usually described as $\alpha \left(t\right)$, since a non-increasing, or monotonically decreasing function can be chosen in order to reduce the randomness as the iterations proceed. This is considered to be advantageous for the algorithm’s convergence.

Using a single step simplifies the process and allows us to avoid initializing and updating particle velocity vectors. It reduces the computational burden of the swarm. Thus, it is suggested to apply (Equation (3)) when using this algorithm.

2.3. The Chaotic Accelerated Particle Swarm Optimization (CAPSO) Algorithm

In the CAPSO algorithm [17], it is pointed out that a non-constant parameter $\beta$ can improve the algorithm’s convergence and general behavior. In this variant of APSO, the method suggested for calculating and fine-tuning $\beta$ is chaotic maps. Chaotic maps are evolutionary functions that exhibit some type of chaotic behavior [35]. They are quite well known for their use and application for fractal generation. They are usually (but not necessarily) discrete. Therefore, they take the form of iterated functions, and this is also how they are utilized in CAPSO. As chaotic maps are normalized, their output is always between $[0,1]$, so they can safely be used for tuning parameter $\beta$.

We have chosen to work with the two most effective suggested chaotic maps, which, according to [17], are the sinusoidal map and the singer map.

For a sinusoidal map:

$$x_{k+1}=a{x_k}^{2}sin\left(\pi x_k\right).$$

(4)

For $a=2.3$ and $x_0=0.7$, the following simplified alternative form has been also proposed [17]:

$$x_{k+1}=sin\left(\pi x_k\right).$$

(5)

Hence, the value of a for the sinusoidal map was chosen fixed at 2.3 to provide flexibility regarding the use of either (Equation (4)) or (Equation (5)).

For a Singer map:

$$x_{k+1}=\mu (7.86x_k-23.31{x_k}^2+28.75{x_k}^3-13.302875{x_k}^4),$$

(6)

where $\mu \in [0.9,1.08]$ [17]. After extensive experimentation for our considered cloaking problem, we selected $\mu =0.9$; in general, we noticed that smaller values of $\mu$ yielded slightly more beneficial optimization results.

Both of the above maps have a unimode centered around their middle, and experimentation has dictated that this is advantageous [17].

One can find Matlab code for the original APSO algorithm in [18,29] and their following editions, or at the MathWorks website [36]. In this work, we utilized this code and updated it into the CAPSO algorithm. Additionaly, we adjusted it to the restrictions and requirements of the optimization problem at hand. The chaotic maps applied are as described in (Equations (4) and (6)). The pseudo-code of the CAPSO algorithm is presented in Algorithm 1 below; it was also tested versus the classic PSO variant [8,9] in [37].

Algorithm 1: Chaotic APSO (CAPSO)

As can be seen in Algorithm 1, there are two stopping criteria applied to the algorithm. The first one is the maximum number of iterations, and the second is convergence. Convergence means that the particles of the swarm have agreed to a solution [38]. Thus, in order to check for convergence we need to check for similarity amongst the solutions (particle locations). The method chosen is a minSTD criterion (also pointed out in [12]). The similarity of the solutions is measured by standard deviation with respect to each dimension of the problem, and the algorithm stops when the current STD is smaller than a selected minSTD threshold. When this happens, the PSO is considered to have stagnated around the global best $g^{*}$, which has been chosen as the best solution.

The CAPSO algorithm was chosen for two main reasons: (i) it is an APSO variant; thus, it updates in a single step and spares some computational cost, and (ii) the chaotic maps provide a lot of randomness, which could be very advantageous for the exploration part of the algorithm regarding our problem. The optimization problem is described in detail in the following sections, but it is worthwhile to stress that the above reasons were deemed beneficial for handling its complexity and accumulating several feasible optimized solutions. Regarding CAPSO’s efficiency and evaluation, extensive metrics and benchmark testing were provided in the original work [17].

MATLAB code for the above CAPSO algorithm, adjusted to the considered cloaking problem, is available at a GitHub repository online, https://github.com/alcmenem/Chaotic-APSO (accessed on 21 July 2021), where further information is also available.

3. Optimization Problem

In this section, we describe the optimization problem to be solved concerning the electromagnetic cloaking of a perfect electric conducting (PEC) or dielectric spherical core covered by a fixed number of spherical shells with determinable physical and geometrical parameters. This particular spherical model was chosen mainly because: (i) layered spherical particles can be easily fabricated and (ii) the scattering problem by a layered spherical medium admits an analytic solution in the form of a Mie series, which can be fast and accurately simulated by a computer program. For these reasons, it is a scattering model adopted in cloaking investigations, e.g., in [20,21,22,23,24,25,26,27,28]. First, we determine the exact solution of the scattering problem, and then we describe the optimization strategy that we follow in order to determine the parameters of the structure offering efficient cloaking performance.

3.1. Exact Solution of the Scattering Problem

The scattering geometry is depicted in Figure 1. A spherical core of radius $a_5$ is covered by four concentric spherical shells with radii $a_j$, real relative dielectric permittivities ${ϵ}_j$, and magnetic permeabilities ${\mu }_j$ ($j=1,2,3,4$). The core is either PEC or dielectric with relative permittivity ${ϵ}_5$ and permeability ${\mu }_5$. The layered medium is excited by an external y-polarized magnetic dipole located at $(0,0,b)$ of the z-axis (with $b>a_1$). The limiting case of a plane incident wave is also considered when the distance b becomes suitably large.

The above-described scattering problem is solved analytically (and even for the general case of an arbitrary number of layers) by applying a generalized separation of variables scheme involving suitable expansions of the fields in every region in eigenfunctions of the Helmholtz partial differential operator [39]. Specifically, the scattered field in the exterior of the layered medium is expressed as

$$\begin{array}{c}\hfill {\mathbf{E}}^{\mathrm{sc}}\left(\mathbf{r}\right)=\frac{\mathrm{i}}{{\widehat{h}}_0\left(k_{0}b\right)}\sum _{n=1}^{\infty }\frac{2n+1}{n(n+1)}\left[{\alpha }_n{\widehat{h}}_n\left(k_{0}b\right){\mathbf{N}}_{e1n}^3(\mathbf{r},k_0)-{\beta }_n{\widehat{h}}_n^{\prime }\left(k_{0}b\right){\mathbf{M}}_{o1n}^3(\mathbf{r},k_0)\right],r>a_1,\end{array}$$

(7)

where ${\alpha }_n$ and ${\beta }_n$ are under determination coefficients, $h_n$ is the first-kind spherical Hankel function of order n, ${\widehat{h}}_n\left(z\right)=z{h}_n\left(z\right)$, $k_0=2\pi /{\mathsf{\lambda }}_0$ is the wavenumber of the external region $r>a_1$ (with ${\mathsf{\lambda }}_0$ the corresponding wavelength), while ${\mathbf{M}}_{o1n}^3$ and ${\mathbf{N}}_{e1n}^3$ are the third-kind spherical vector wave functions (Equations (13.3.68)–(13.3.70) of [40]).

By imposing the transmission boundary conditions on the interfaces of the spherical shells and applying a T-matrix method, we obtain the explicit expressions of coefficients ${\alpha }_n$ and ${\beta }_n$. In the case of a dielectric core, these expressions are as follows [39]:

$$\begin{array}{c}\hfill {\alpha }_n=-\frac{{\left(A_n^5{\mathcal{A}}_n\right)}_{12}}{{\left(A_n^5{\mathcal{A}}_n\right)}_{11}},{\beta }_n=-\frac{{\left(B_n^5{\mathcal{B}}_n\right)}_{12}}{{\left(B_n^5{\mathcal{B}}_n\right)}_{11}},\end{array}$$

(8)

where

$$\begin{array}{cc}\hfill {\mathbf{A}}_n^j& =-\mathrm{i}{x}_j\left[\begin{array}{cc}{w}_j{j}_n\left(x_j\right){\widehat{h}}_n^{\prime }\left(y_j\right)-{\xi }_j{\widehat{j}}_n^{\prime }\left(x_j\right)h_n\left(y_j\right)& w_j{j}_n\left(x_j\right){\widehat{j}}_n^{\prime }\left(y_j\right)-{\xi }_j{\widehat{j}}_n^{\prime }\left(x_j\right)j_n\left(y_j\right)\\ {\xi }_j{\widehat{h}}_n^{\prime }\left(x_j\right)h_n\left(y_j\right)-w_j{h}_n\left(x_j\right){\widehat{h}}_n^{\prime }\left(y_j\right)& {\xi }_j{\widehat{h}}_n^{\prime }\left(x_j\right)j_n\left(y_j\right)-w_j{h}_n\left(x_j\right){\widehat{j}}_n^{\prime }\left(y_j\right)\end{array}\right]\hfill \\ \hfill {\mathbf{B}}_n^j& =-\mathrm{i}{x}_j\left[\begin{array}{cc}{\sigma }_j{j}_n\left(x_j\right){\widehat{h}}_n^{\prime }\left(y_j\right)-{\widehat{j}}_n^{\prime }\left(x_j\right)h_n\left(y_j\right)& {\sigma }_j{j}_n\left(x_j\right){\widehat{j}}_n^{\prime }\left(y_j\right)-{\widehat{j}}_n^{\prime }\left(x_j\right)j_n\left(y_j\right)\\ {\widehat{h}}_n^{\prime }\left(x_j\right)h_n\left(y_j\right)-{\sigma }_j{h}_n\left(x_j\right){\widehat{h}}_n^{\prime }\left(y_j\right)& {\widehat{h}}_n^{\prime }\left(x_j\right)j_n\left(y_j\right)-{\sigma }_j{h}_n\left(x_j\right){\widehat{j}}_n^{\prime }\left(y_j\right)\end{array}\right],\hfill \end{array}$$

with $x_j=k_j{a}_j$, $y_j=k_{j-1}{a}_j$, $w_j=k_j/k_{j-1}$, ${\xi }_j={\left({\mu }_j{ϵ}_{j-1}/{\mu }_{j-1}{ϵ}_j\right)}^{1/2}$, ${\sigma }_j={\mu }_j/{\mu }_{j-1}$, while $j_n$ is the spherical Bessel function of order n, and ${\widehat{j}}_n\left(z\right)=z{j}_n\left(z\right)$. Matrices ${\mathcal{A}}_n$ and ${\mathcal{B}}_n$, participating in (8), are defined by

$${\mathcal{A}}_n={\mathbf{A}}_n^4{\mathbf{A}}_n^3{\mathbf{A}}_n^2{\mathbf{A}}_n^1,{\mathcal{B}}_n={\mathbf{B}}_n^4{\mathbf{B}}_n^3{\mathbf{B}}_n^2{\mathbf{B}}_n^1.$$

(9)

Besides, in the case of a PEC core, the corresponding expressions of the scattered field’s coefficients ${\alpha }_n$ and ${\beta }_n$ are given by

$$\begin{array}{c}\hfill {\alpha }_n=-\frac{{\widehat{h}}_n^{\prime }\left(y_5\right){\left({\mathcal{A}}_n\right)}_{12}+{\widehat{j}}_n^{\prime }\left(y_5\right){\left({\mathcal{A}}_n\right)}_{22}}{{\widehat{h}}_n^{\prime }\left(y_5\right){\left({\mathcal{A}}_n\right)}_{11}+{\widehat{j}}_n^{\prime }\left(y_5\right){\left({\mathcal{A}}_n\right)}_{21}},{\beta }_n=-\frac{h_n\left(y_5\right){\left({\mathcal{B}}_n\right)}_{12}+j_n\left(y_5\right){\left({\mathcal{B}}_n\right)}_{22}}{h_n\left(y_5\right){\left({\mathcal{B}}_n\right)}_{11}+j_n\left(y_5\right){\left({\mathcal{B}}_n\right)}_{21}}.\end{array}$$

(10)

We are interested in the variations of the scattered field in the far zone (i.e., as $r\to \infty$) with respect to the physical and geometrical parameters of the scattering problem. To this end, we consider the following asymptotic expression (see, e.g., Corollary 4.9 of [41]):

$$\begin{array}{c}\hfill {\mathbf{E}}^{\mathrm{sc}}\left(\mathbf{r}\right)=\mathbf{F}\left(\widehat{\mathbf{r}}\right)h_0\left(k_{0}r\right)+\mathcal{O}\left(r^{-2}\right),r\to \infty ,\end{array}$$

(11)

where the function $\mathbf{F}\left(\widehat{\mathbf{r}}\right)$ is the so-called far-field pattern and describes the far-field response of the scatterer in the direction of observation $\widehat{\mathbf{r}}=\mathbf{r}/r$ due to the excitation by the considered primary magnetic dipole. The explicit expression of the far-field pattern for the considered scattering problem is found to be [39]

$$\begin{array}{c}\hfill \mathbf{F}\left(\widehat{\mathbf{r}}\right)=S_{\theta }\left(\theta \right)cos\varphi \widehat{\theta }+S_{\varphi }\left(\theta \right)sin\varphi \widehat{\varphi },\end{array}$$

(12)

where

$$\begin{array}{cc}\hfill & S_{\theta }\left(\theta \right)=\sum _{n=1}^{\infty }\frac{{(-1)}^n(2n+1)}{\sqrt{n(n+1)}}\left[{\delta }_n\frac{P_n^1(cos\theta )}{sin\theta }-{\gamma }_n\frac{\partial P_n^1(cos\theta )}{\partial \theta }\right],\hfill \end{array}$$

(13)

$$\begin{array}{cc}\hfill & S_{\varphi }\left(\theta \right)=\sum _{n=1}^{\infty }\frac{{(-1)}^n(2n+1)}{\sqrt{n(n+1)}}\left[{\gamma }_n\frac{P_n^1(cos\theta )}{sin\theta }-{\delta }_n\frac{\partial P_n^1(cos\theta )}{\partial \theta }\right],\hfill \end{array}$$

(14)

where $P_n^1$ is the first-order Legendre function of degree n, and

$${\gamma }_n=\frac{h_n\left(k_{0}b\right)}{h_0\left(k_{0}b\right)}{\mathrm{i}}^n{\alpha }_n,{\delta }_n=\frac{{\widehat{h}}_n^{\prime }\left(k_{0}b\right)}{{\widehat{h}}_0\left(k_{0}b\right)}{\mathrm{i}}^{n-1}{\beta }_n,$$

(15)

with the scattered field’s coefficients ${\alpha }_n$ and ${\beta }_n$ given by (8) and (10) for the cases of a dielectric and a PEC core, respectively.

Having determined the far-field pattern, we provide the definitions and subsequently calculate the two basic scattering cross sections (SCS) of interest. The differential SCS or bistatic radar SCS

$$\sigma \left(\widehat{\mathbf{r}}\right)=\frac{4\pi }{k_0^2}{\left|\mathbf{F}\left(\widehat{\mathbf{r}}\right)\right|}^2$$

(16)

specifies the amount of the field’s power scattered in the direction $\widehat{\mathbf{r}}$. The total SCS can be represented by:

$$\begin{array}{cc}\hfill {\sigma }^{\mathrm{t}}& =\frac{1}{k_0^2}{\int }_{S^2}{\left|\mathbf{F}\left(\widehat{\mathbf{r}}\right)\right|}^2\mathrm{d}s\left(\widehat{\mathbf{r}}\right)\hfill \\ \hfill & =\frac{1}{4\pi }{\int }_{S^2}\sigma \left(\widehat{\mathbf{r}}\right)\mathrm{d}s\left(\widehat{\mathbf{r}}\right),\hfill \end{array}$$

(17)

where $S^2$ denotes the unit sphere in ${\mathbb{R}}^3$ and is defined as the average of $\sigma \left(\widehat{\mathbf{r}}\right)$ over all directions.

Combining (12) with (13) and (16), as well as () with (17), we find that the differential SCS and the total SCS for the considered problem of excitation of the spherically-layered medium by an external magnetic dipole, are, respectively, given by

$$\sigma (\theta ,\varphi )=\frac{4\pi }{k_0^2}\left[|S_{\theta }{\left(\theta \right)|}^2{cos}^2\varphi +{\left|S_{\varphi }\left(\theta \right)\right|}^2{sin}^2\varphi \right]$$

(18)

and

$$\begin{array}{c}\hfill {\sigma }^{\mathrm{t}}=\frac{2\pi }{k_0^2}\sum _{n=1}^{\infty }(2n+1)\left[|{\gamma }_n{|}^2+{\left|{\delta }_n\right|}^2\right].\end{array}$$

(19)

All fields’ expressions derived above in this section correspond to a primary magnetic dipole excitation, but can be converted to the respective ones due to an electric dipole excitation by using the well-known interchanges between the fields and material parameters (see, e.g., Section II of [42]).

3.2. Strategy

Our goal is to determine geometrical and physical parameters of the four spherical shells covering the core such that the entire layered structure cloaks the presence of the core (of fixed radius $k_0{a}_c$). In other words, the far field generated by the core covered by the optimized shells is required to be significantly reduced with respect to the far field generated by the bare sphere of radius $k_0{a}_c$. To this end, we consider as the objective function of the optimization problem the normalized total SCS ${\sigma }^{\mathrm{t}}/\left(\pi a_c^2\right)$. Small values of this objective function assure that the overall response of the scatterer in the far field is substantially reduced. Another option is to consider the backscattering cross section $\sigma (0,\varphi )$ as the problem’s objective function. This was performed in [43], where it was shown that very small values can be attained in the vicinity of the backscattering direction $\theta =0$; however, the cloaking behavior for other observation angles was not so efficient in the examined cases. Hence, $\sigma (0,\varphi )$ is better suited for traditional monostatic applications, while reducing ${\sigma }^{\mathrm{t}}$ serves well the purpose of achieving enhanced cloaking performance.

The optimization variables considered are the radii $a_j$, the relative dielectric permittivities ${ϵ}_j$ and the relative magnetic permeabilities ${\mu }_j$ ($j=1,2,3,4$) of the coating layers. Importantly, we note that $N=4$ is the maximum number N of coating layers sought for in the optimization schemes. Precisely, for a chosen core’s type (PEC or dielectric) and radius, and a chosen dipole’s location, we initiate optimizations with $N=1$ (a single magneto-dielectric coating layer), and then proceed subsequently to $N=$ 2, 3, and 4 (two, three, and four magneto-dielectric coating layers) and report in the next section the best attained results for each N. Regarding the location of the dipole, different cases are considered both close to the boundary $r=a_1$ of the layered medium as well as relatively far from it. In the former case, a genuinely spherical wave impinges on the layered medium, while in the latter case the generated far field is expected to be sufficiently close to that resulting by a plane incident wave propagating along the $-\widehat{\mathbf{z}}$-direction [39]. Besides, dipoles lying at arbitrary locations (inside or outside the layered medium) and possessing arbitrary dipole moments can also be considered; exact solutions for the associated scattering problems were derived in [44,45].

It is worthwhile to emphasize that the exact solution of the scattering problem, which is obtained here in the form of a Mie series [cf. Equation (7)], is highly advantageous for the efficient implementation of an optimization algorithm. Specifically, the objective function, given by the explicit expression (19), is computed fast and accurately without resulting in any numerical approximations. Additionally, results from commercial software simulation packages are not required at any stage of the optimization procedure; it is customary to rely on such packages in many related optimization problems in electromagnetics when an analytic method for solving the underlying boundary-value problem has not been developed.

4. Numerical Results and Discussion

The CAPSO algorithm, described in Section 2, as well as the objective function of the cloaking problem, given by (19), were both implemented in MATLAB R2019a${}^{\circledR }$. The employed swarms were MATLAB structures or arrays constructed according to the steps of Algorithm 1. The components of the CAPSO position vector consisted of the optimization variables $a_j$ of the radii, ${ϵ}_j$ of the relative dielectric permittivities, and ${\mu }_j$ of the relative magnetic permeabilities of the $N=4$ magneto-dielectric layers covering the spherical core. Hence, we considered $3N=12$ optimization variables for the particles’ position. However, as noted above, we also tested the cases of $N=$ 1, 2, and 3 coating layers, for which the numbers of the optimization variables are $3N=$ 3, 6, and 9, respectively. For $N=1$ (a single coating layer), it was found that no substantial cloaking effect is observed. To this end, in the sequel, we report the results obtained for efficient cloaking by using $N=$ 2, 3, and 4 coating layers. The optimization variables were considered in the following ranges: the differences $k_0(a_{j+1}-a_j)$ between two consecutive layers’ radii varied in $(\frac{\pi }{10},\pi )$ or $(\frac{\pi }{10},\frac{\pi }{2})$, while the permittivities ${ϵ}_j$ and permeabilities ${\mu }_j$ varied in (0.4,5). These specific intervals were chosen such that each covering layer is sufficiently thin; more precisely, the width $a_{j+1}-a_j$ is smaller than ${\mathsf{\lambda }}_0/2$, and the physical parameters ${ϵ}_j$ and ${\mu }_j$ of the layers correspond to realizable materials, particularly excluding the cases of epsilon-near-zero, mu-near-zero, single-negative, double-negative or plasmonic metamaterials.

Besides, regarding the characteristics of the core, both cases of PEC and dielectric cores were considered with the radius being either $k_0{a}_c=2\pi$ (one free-space wavelength) or $k_0{a}_c=\pi$ (half of the free-space wavelength). For the distance of the dipole from the scatterer, two cases were simulated: $b=10a_c$ when the dipole lies sufficiently far from the layered medium and hence the plane-wave incidence situation is approximated, and $b=1.3a_1$ when the dipole is in the vicinity of the medium and hence the incident wave impinging on the medium is spherical.

The CAPSO algorithm was applied to minimize the total SCS ${\sigma }^{\mathrm{t}}$. In the experimentation phase, we set a maximum number of iterations equal to 500. This is what we refer to as $i{t}_{max}$ in Algorithm 1, which constitutes the maximum allowed number of swarm updates, and ensures that the while loop is terminated if the algorithm does not converge. Such a maximum iteration limit is widely used in related algorithms to guarantee that the algorithm does not run infinitely (for example in cases of wrong parameter values or failed simulations). Regarding the minSTD criterion, we have chosen a threshold of ${10}^{-7}$. As will become evident by the numerical results presented below, the number of iterations that the algorithm converges will be, at most, 100 for all examined scattering problems, since the minSTD criterion always takes effect when the algorithm agrees around an optimal solution. The plateaus representing the solutions’ agreement are observable in the corresponding graphs.

The procedure we follow is to consider a fixed number of coating layers (we start from $N=2$) and, from all the numerical experiments performed, to retain only the solutions corresponding to values of the objective function ${\sigma }^{\mathrm{t}}/\left(\pi a_c^2\right)$ smaller than −1 in the dB scale. From all the solutions satisfying this criterion, we then select the two giving the smallest values of the objective function. This procedure is then repeated for $N=3$ and $N=4$. In all the numerical results presented below, by “optimized design A/B”, we refer to the optimized solutions achieving the two best scores (the two smallest values of the objective function) for each examined constant value of N. To demonstrate the actual reduction in the generated far field with respect to the spherical observation angles, we compute and depict the normalized bistatic SCS $\sigma (\theta ,\varphi )/\left(\pi a_c^2\right)$ versus the angle $\theta$ in the $xOz$ and $yOz$ planes.

The examined optimization problem is complex and open-ended. Furthermore, there exists no definite prior knowledge on whether the objective function is unimodal or multimodal. Additionally, each added layer further complicates the objective function, since it is accompanied by corresponding permittivity and permeability options, which themselves are strictly limited by the imposed physical boundaries. Nevertheless, in our experiments, the CAPSO algorithm managed to provide feasible optimal solutions. The results are as follows.

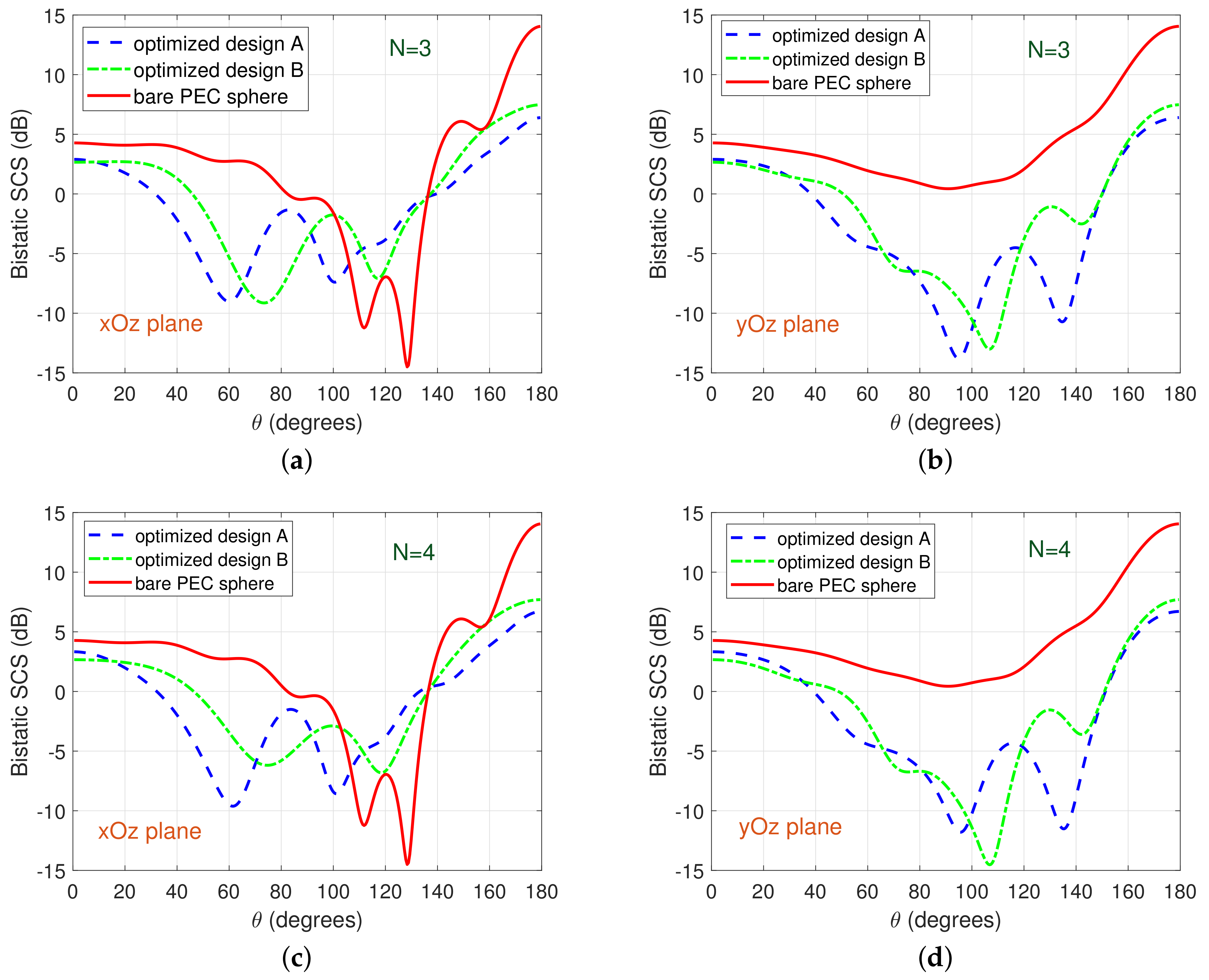
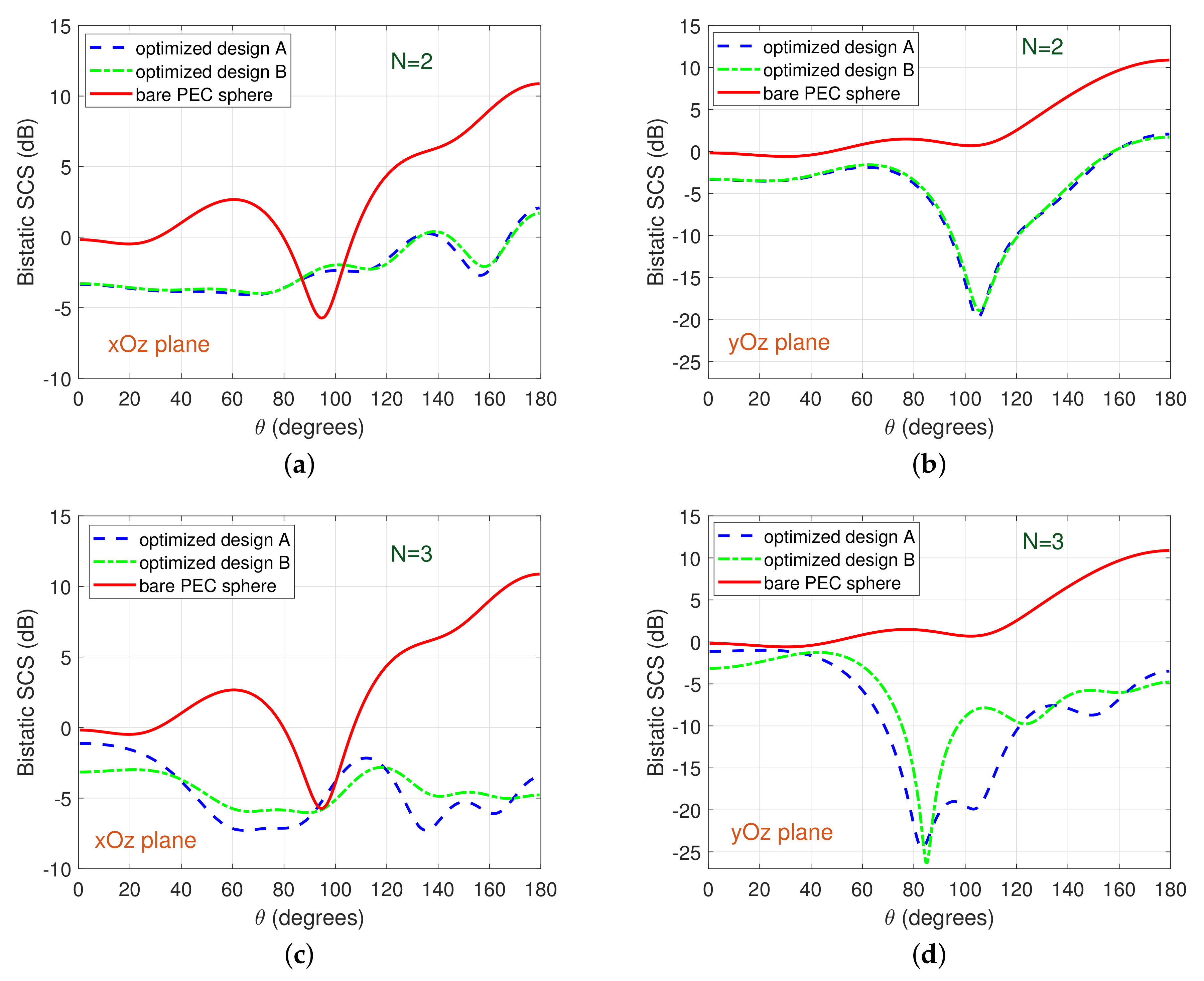
First, we present the results of the numerical experiments for a PEC core with $k_0{a}_c=2\pi$ excited by a dipole at $b=10a_c$. Figure 2 depicts the normalized bistatic SCS in the $xOz$ and $yOz$ planes for the obtained optimized designs A and B with $N=3$ and $N=4$ coating layers covering the PEC core; for this case, $N=2$ did not give results satisfying the above-described criterion for the objective function’s values. The parameters of the optimization variables for optimized designs A and B are detailed in the two first (for $N=3$) and the two last (for $N=4$) columns of

Table A1. Values of the optimization variables for optimized designs A and B of Figure 2.

	A ($\mathit{N}=3$)	B ($\mathit{N}=3$)	A ($\mathit{N}=4$)	B ($\mathit{N}=4$)
$k_0{a}_1$	8.12	8.09	8.24	8.66
$k_0{a}_2$	7.36	7.30	7.86	7.70
$k_0{a}_3$	6.65	6.60	7.30	6.89
$k_0{a}_4$	–	–	6.67	6.75
${ϵ}_1$	0.40	0.40	0.60	0.50
${ϵ}_2$	3.87	4.15	0.40	2.93
${ϵ}_3$	0.40	0.40	5.00	0.50
${ϵ}_4$	–	–	0.60	0.53
${\mu }_1$	1.92	1.88	2.59	1.62
${\mu }_2$	0.40	0.40	0.86	0.50
${\mu }_3$	1.73	1.79	0.40	2.62
${\mu }_4$	–	–	1.25	0.97

of the Appendix A. Besides, in Figure 2, the corresponding SCS curves for a bare PEC sphere of $k_0{a}_c=2\pi$ are also shown for comparison purposes. It is observed that significant reductions in the bistatic SCS of the layered medium with optimally-determined layers compared to the bistatic SCS of a bare PEC spherical core are exhibited. These reductions occur for all observation angles in the $yOz$ plane and for nearly all angles in the $xOz$ plane, apart from a resonance regime of the bare PEC SCS centered $\theta ={140}^{\mathrm{o}}$. Another characteristic—not initially expected—is that the optimal coating layers for $N=3$ perform generally slightly better in both observation planes than the ones for $N=4$. This means that—at least in the present case—the addition of an extra coating layer does not improve the overall cloaking performance of the layered medium; therefore, it is better to choose the simpler coating cover with $N=3$, which would be also potentially easier to be realized.

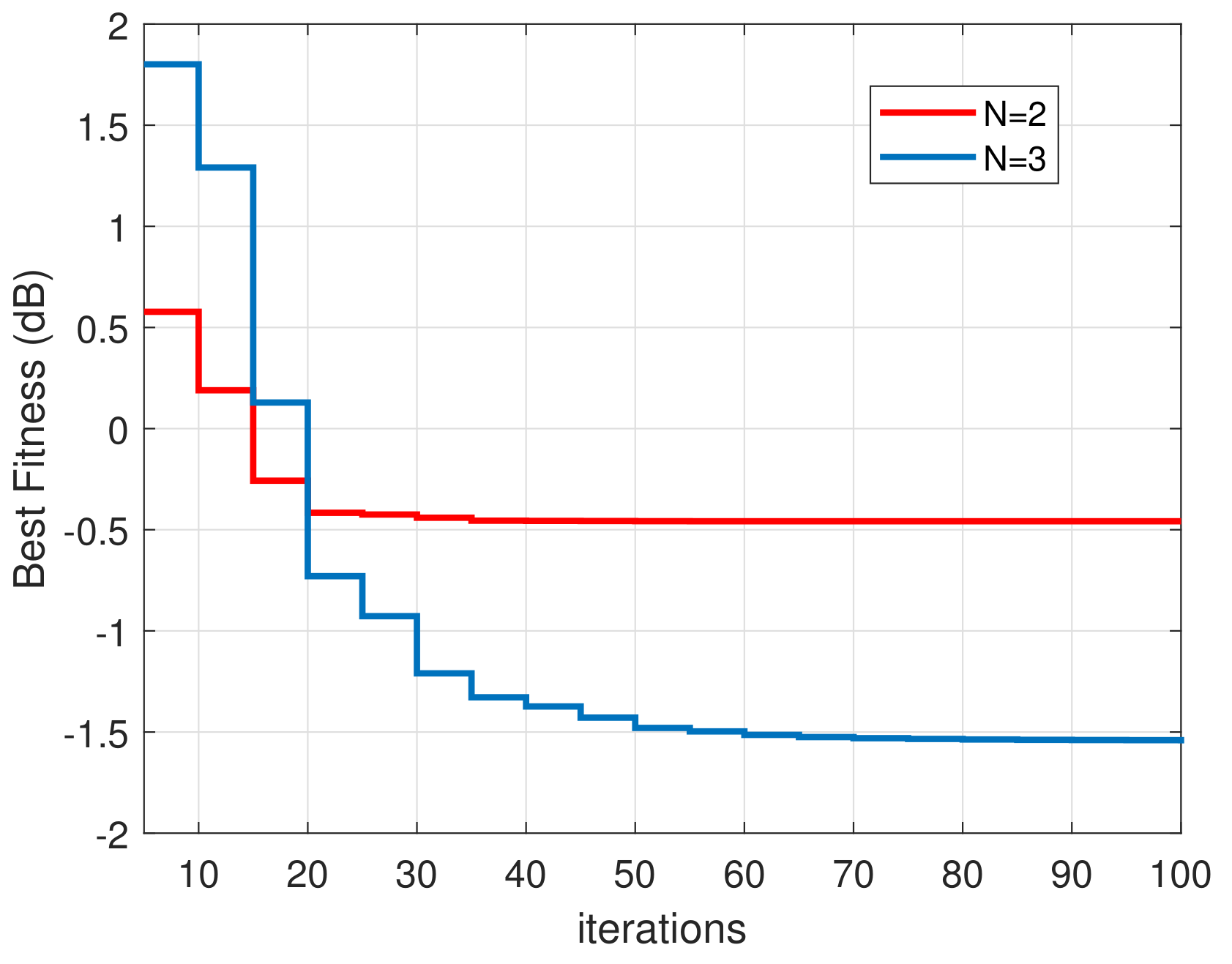
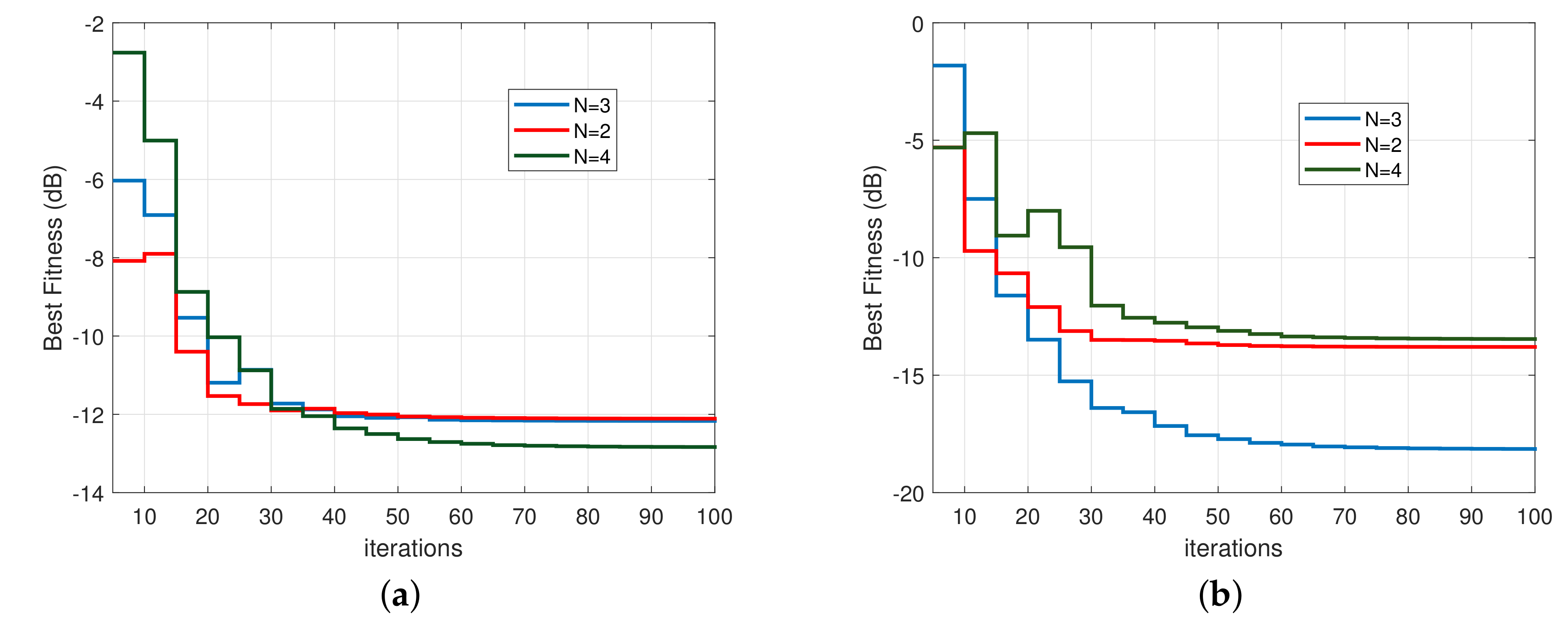
A representative convergence plot of the CAPSO algorithm, when applied to the scattering problem of Figure 2, is shown in Figure 3. This convergence plot is presented in the form of a stairstep graph, in which the values of the objective function are sampled per five iterations, i.e., the best swarm values with a five-iteration step are depicted. PSO algorithms and variants exhibiting similar convergence performances, which are presented in the form of stairstep graphs, are included, e.g., in Figure 10a in [12] and Figure 4a in [46]. Additionally, similar convergence diagrams appear in the curves for the global best depicted in Figures 4 and 7 of [13]. In these figures, convergence regarding the solution similarity can also be observed. From Figure 3, it is evident that the CAPSO algorithm shows very fast convergence requiring, at most, 100 iterations.

Next, we consider the same PEC core of radius $k_0{a}_c=2\pi$, but now excited by a dipole in close proximity to the spherical medium, located at $b=1.3a_1$; thus, a genuinely spherical wave excites the spherical medium. Compared to the previous case of (effectively) plane-wave incidence, now the interaction of the dipole and the medium is definitely stronger, and hence, in this case, the problem is much more difficult to optimize. For this reason, the minimum values of the total SCS obtained by applying the CAPSO algorithm were larger in this examined case of spherical-wave incidence. The bistatic SCS plots for the two best cases found in the numerical experiments are depicted in Figure 4. Evidently, the designed cloaking performs remarkably well in the $yOz$ plane, and quite satisfactorily in the $xOz$ plane, except for the interval $[{105}^{\mathrm{o}},{135}^{\mathrm{o}}]$, where the bistatic SCS of the bare PEC sphere has two minima.

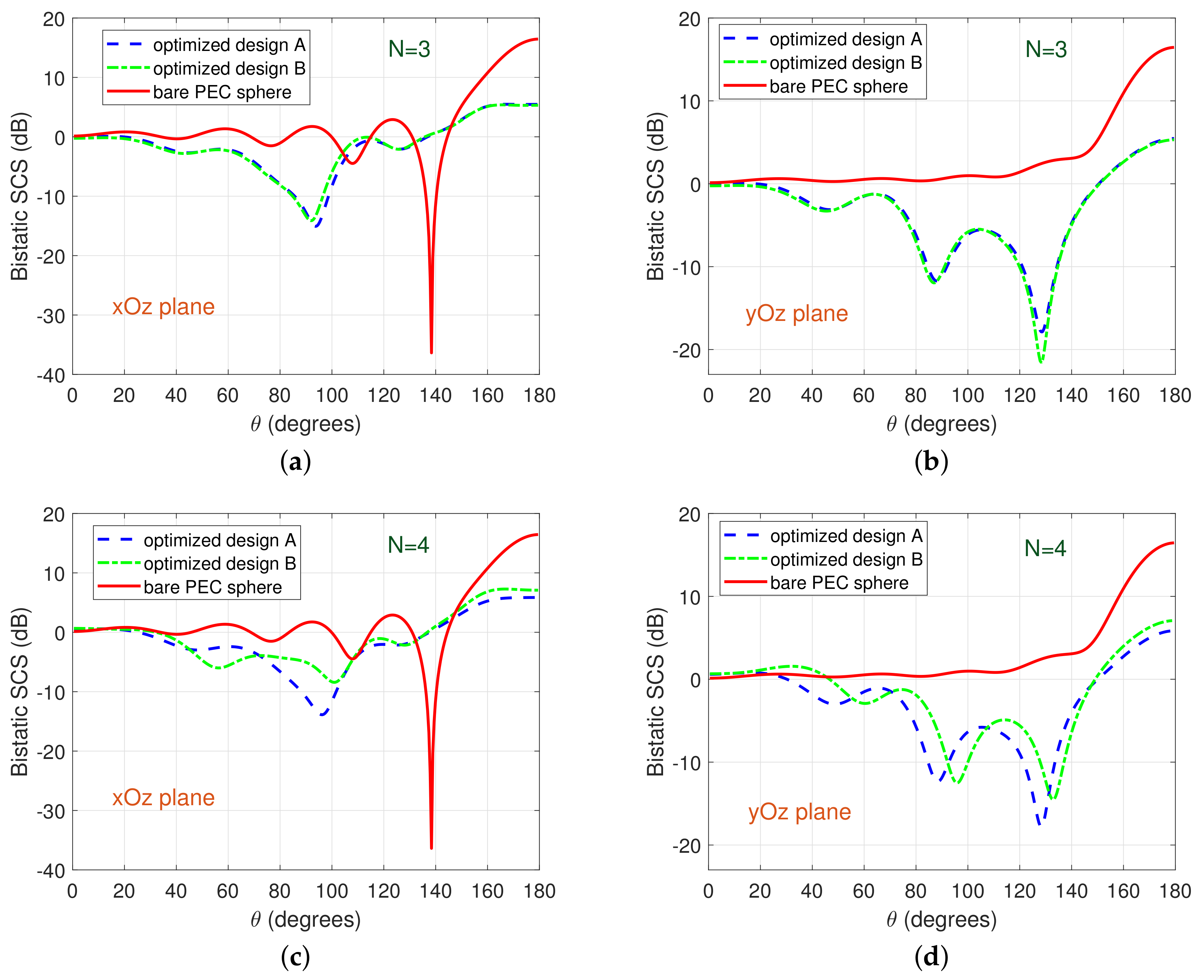
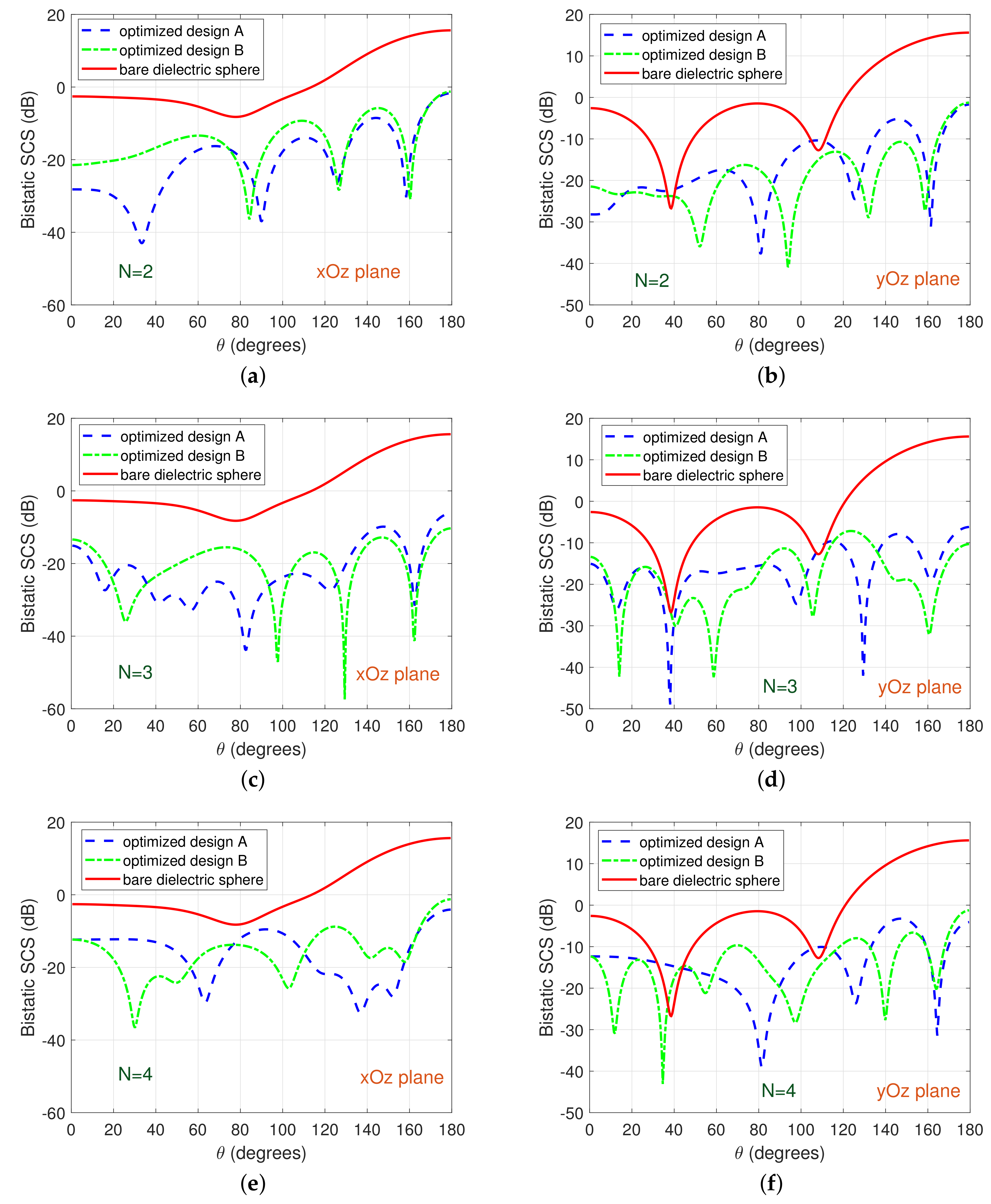
Furthermore, we change the PEC core’s radius to $k_0{a}_c=\pi$. Figure 5 and Figure 6 depict the normalized bistatic SCS for the primary dipole located at $b=10a_c$ (nearly plane-wave incidence case) and $b=1.3a_1$ (spherical-wave incidence case), respectively. The main difference in this scenario of $k_0{a}_c=\pi$ with respect to the previous scenario of $k_0{a}_c=2\pi$ (depicted in Figure 2 and Figure 4) is that now, since the radius of the core is half the previous radius, efficient cloaking performance can be achieved by using a smaller number of coating layers (i.e., $N=2$ or $N=3$ for $k_0{a}_c=\pi$ versus $N=3$ or $N=4$ for $k_0{a}_c=2\pi$). On top of that, it is worthwhile to point out that almost perfect cloaking is obtained when using the optimized $N=3$ coating layers with their parameters determined by the CAPSO algorithm (cf. optimized design B for $N=3$ in Figure 5c,d). As in the case of $k_0{a}_c=2\pi$, also in this case of $k_0{a}_c=\pi$, cloaking is more challenging for a spherical incident than a plane incident wave; still, significant bistatic SCS reductions are obtained, particularly in the $yOz$ plane.

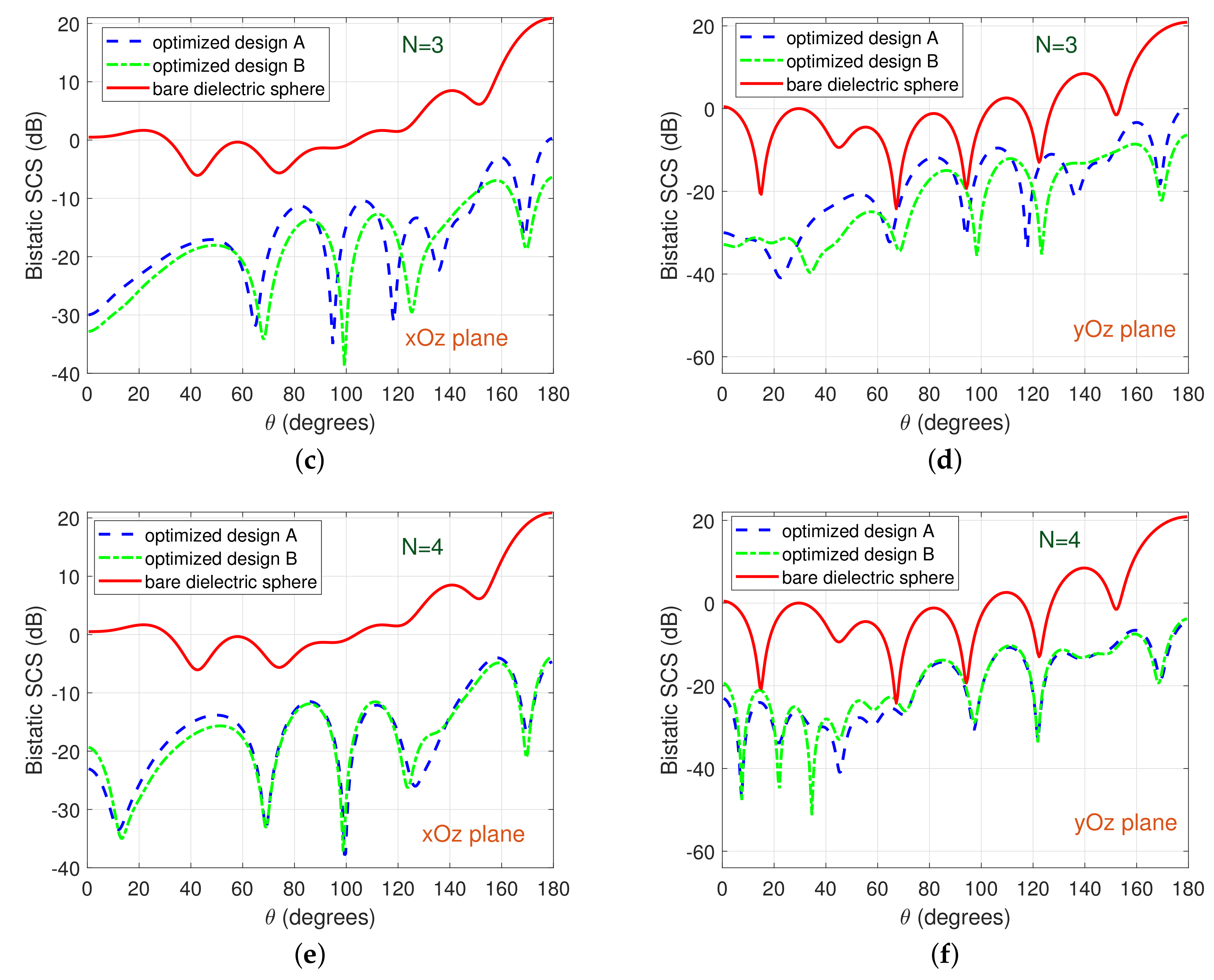
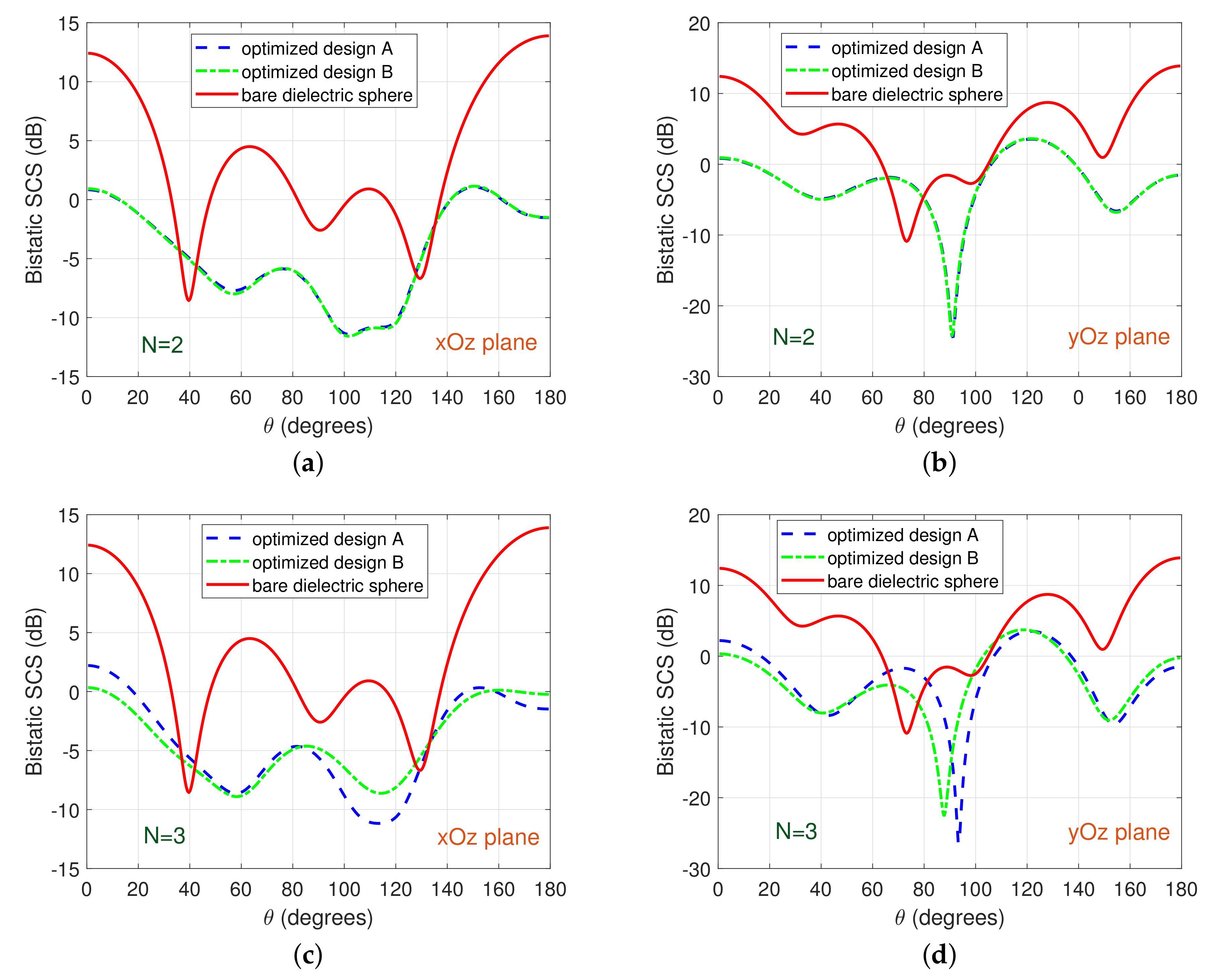
Now, we move to the case of a dielectric core. Its material is considered to be magnetically inert (i.e., ${\mu }_c=1$) with dielectric permittivity initially selected as ${ϵ}_c=2.1$; the latter corresponds to the permittivity of fused silica (a pure form of glass) in the infrared range of the electromagnetic spectrum. Figure 7 depicts the bistatic SCS results (stemming from the best scores of the corresponding total SCS) obtained for $N=$ 2, 3, and 4 optimal layers covering a dielectric core of radius $k_0{a}_c=2\pi$. Importantly, perfect cloaking performance for all angles is observed. Even $N=2$ coating layers are sufficient for rendering the considered dielectric sphere electromagnetically invisible.

Cloaking results for a dielectric sphere of the same material but with radius $k_0{a}_c=\pi$ are shown in Figure 8. The cloaking behavior is again nearly perfect with the best performance attained for $N=3$, covering layers with optimally-determined parameters. Notice also in Figure 8d that the layered medium (for the optimized design A) has a sharp minimum in its bistatic SCS at exactly the same angle ($\theta ={38}^{\mathrm{o}}$) as the bistatic SCS of the bare dielectric sphere.

Representative convergence plots of the CAPSO algorithm when applied to the scattering problems of Figure 7 and Figure 8 are shown in Figure 9. Here, as well, the CAPSO algorithm converges quickly, in 100 iterations. It is observed that for the examined case of a dielectric core, the objective function’s values for which the algorithm converges are significantly smaller than those for the corresponding case of a PEC core; cf. Figure 3 and Figure 9a.

Next, we change the relative dielectric permittivity of the core to ${ϵ}_c=18.7$; this corresponds to the permittivity of amorphous silicon in the infrared range. Now, the optimization problem is more difficult due to the large value of the core’s permittivity. However, as shown in Figure 10, efficient cloaking performance can still be obtained for all angles except two small intervals in the $xOz$ and the $yOz$ planes, where the bistatic SCS of the bare dielectric sphere exhibits global minima. A convergence plot for the scattering problem of Figure 10 is shown in Figure 11. The objective function’s values for which the algorithm converges are notably larger in this case with respect to the previous one, corresponding to a much smaller core permittivity; cf. Figure 9b and Figure 11.

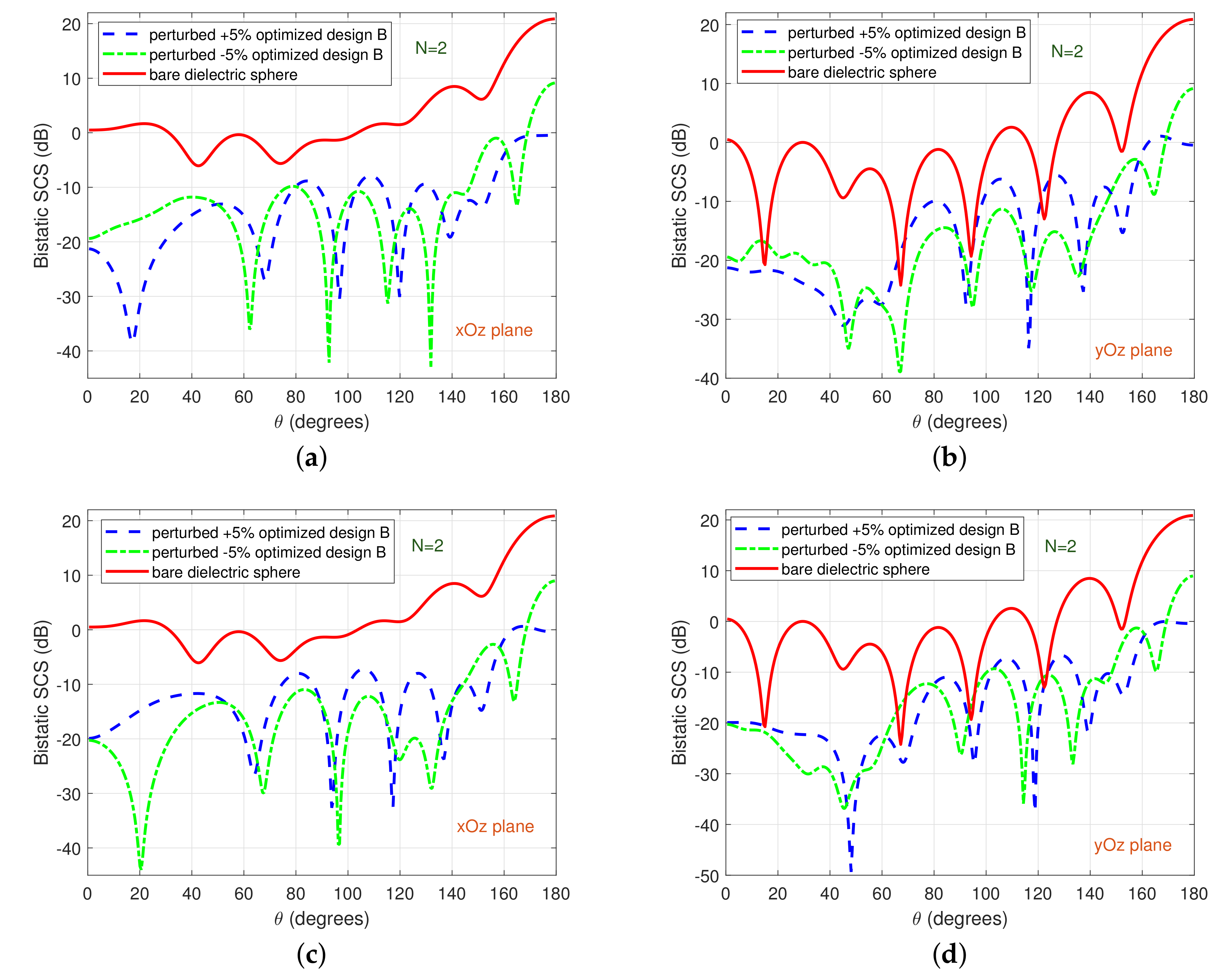
Finally, it is important to examine for practical reasons the sensitivity of the obtained results to the variations of the optimization variables (resulting, e.g., from fabrication imperfections). To this end, we consider the scattering problem analyzed in Figure 7a,b, i.e., a dielectric core with $k_0{a}_c=2\pi$ and ${ϵ}_c=2.1$ and covered by $N=2$ coating layers, and test the effectiveness of the cloaking performance when the permittivity ${ϵ}_1$ or the permeability ${\mu }_1$ of the first coating layer is perturbed. Figure 12 depicts the variations of the bistatic SCS when ${ϵ}_1$ or ${\mu }_1$ are perturbed by $\pm 5\%$ from their optimally determined values (cf.

Table A5. Values of the optimization variables for optimized designs A and B of Figure .

	A ($\mathit{N}=2$)	B ($\mathit{N}=2$)	A ($\mathit{N}=3$)	B ($\mathit{N}=3$)	A ($\mathit{N}=4$)	B ($\mathit{N}=4$)
$k_0{a}_1$	9.68	9.67	9.69	10.23	9.82	9.98
$k_0{a}_2$	7.40	9.00	9.07	9.35	9.03	9.20
$k_0{a}_3$	–	–	7.52	7.46	8.19	9.10
$k_0{a}_4$	–	–	–	–	6.95	7.60
${ϵ}_1$	3.57	2.91	2.56	1.26	1.69	1.54
${ϵ}_2$	5.00	5.00	4.42	4.17	4.73	4.42
${ϵ}_3$	–	–	4.91	4.97	4.82	4.52
${ϵ}_4$	–	–	–	–	4.98	4.39
${\mu }_1$	3.81	2.81	2.41	1.26	1.76	1.63
${\mu }_2$	3.76	3.46	4.31	4.09	4.78	4.17
${\mu }_3$	–	–	3.27	3.42	3.49	4.86
${\mu }_4$	–	–	–	–	3.91	3.11

). It is evident that, although a small deterioration in the performance is observed, the cloaking still performs well in both observation planes.

Closing the numerical results section, we make a comparison of the optimal solutions derived for the examined problem by applying the CAPSO algorithm with those derived in [19] by applying the conventional PSO algorithm. In this work, we derive feasible optimal solutions for cloaking PEC and dielectric cores with different radii and different permittivities (for the dielectric cores). In [19], only the problem of a single-radius PEC core was examined. Besides, the obtained results in [19] yielded efficient cloaking performance only for a range of the observation angles, while the results presented here achieved almost perfect cloaking performance for nearly all observation angles. This means that the application of the CAPSO algorithm for the cloaking problem resulted in solutions with significantly higher scores (i.e., significantly reduced values of the total SCS) than the respective ones determined by the conventional PSO.

5. Conclusions

The scattering problem of a layered spherical medium excited by an external magnetic dipole was considered. Its analytic solution in terms of the Mie series was exploited for formulating a suitable optimization problem concerning the cloaking of a perfectly electric conducting or dielectric core by a small number of spherical shells. The objective function of the problem was the total scattering cross section, while the optimization variables were the geometrical and material parameters of the spherical shells composing the coating. Applying the chaotic accelerated particle swarm optimization algorithm, several feasible optimal solutions were determined, leading to efficient cloaking performances. The coatings were composed of realizable materials, although in certain cases materials with permittivities or permeabilities smaller than one may be required. The total number of coating shells was only two, three or four, hence assisting in fabrication. These facts constitute an advancement to cloaking design because existing methods mainly investigated coatings composed of extraordinary materials. The effects of the core’s type and radius and the location of the dipole on the cloaking mechanism were studied. Significantly reduced objective function values were obtained for all cases examined and for almost the entire range of observation angles.