Irregularity and Modular Irregularity Strength of Wheels

Abstract

It is easily observed that the vertices of a simple graph cannot have pairwise distinct degrees. This means that no simple graph of the order of at least two is, in this way, irregular. However, a multigraph can be irregular. Chartrand et al., in 1988, posed the following problem: in a loopless multigraph, how can one determine the fewest parallel edges required to ensure that all vertices have distinct degrees? This problem is known as the graph labeling problem and, for its solution, Chartrand et al. introduced irregular assignments. The irregularity strength of a graph G is known as the maximal edge label used in an irregular assignment, minimized over all irregular assignments. Thus, the irregularity strength of a simple graph G is equal to the smallest maximum multiplicity of an edge of G in order to create an irregular multigraph from G. In the present paper, we show the existence of a required irregular labeling scheme that proves the exact value of the irregularity strength of wheels. Then, we modify this irregular mapping in six cases and obtain labelings that determine the exact value of the modular irregularity strength of wheels as a natural modification of the irregularity strength.

1. Introduction

Let G be a simple graph. Given a function $\psi :E\left(G\right)\to \{1,2,\dots ,k\}$, the weight of a vertex x is $w{t}_{\psi }\left(x\right)={\sum }_{y\in N\left(x\right)}\psi \left(xy\right)$, where $N\left(x\right)$ denotes the set of neighbors of x in G. Such a function $\psi$ we call an irregular assignment if $w{t}_{\psi }\left(x\right)\ne w{t}_{\psi }\left(y\right)$ for all vertices $x,y\in V\left(G\right)$ with $x\ne y$. The irregularity strength $\mathrm{s}\left(G\right)$ of a graph G is known as the maximal integer k, minimized over all irregular assignments, and is set to ∞ if no such function is possible. Clearly, $\mathrm{s}\left(G\right)<\infty$ if and only if G contains no isolated edge and has, at most, one isolated vertex.

The notion of the irregularity strength was first introduced by Chartrand et al. in [1]. There is also given a lower bound of this graph invariant in the form

$$\begin{array}{c}\hfill \mathrm{s}\left(G\right)\ge max\left\{\frac{n_i+i-1}{i}:1\le i\le \Delta \right\},\end{array}$$

(1)

where $n_i$ denotes the number of vertices of degree i and $\Delta$ is the maximum degree of the graph G.

Faudree and Lehel in [2] studied the irregularity strength of regular graphs and showed that $\mathrm{s}\left(G\right)\le ⌈\frac{n}{2}⌉+9$ for d-regular graphs G of order n, $d\ge 2$. They conjectured that there exists an absolute constant C such that $\mathrm{s}\left(G\right)\le \frac{n}{d}+C$. This upper bound was sequentially improved in [3,4,5] and recently in [6].

For several families of graphs, the exact value of the irregularity strength has been determined, namely for paths and complete graphs [1], for cycles and Turán graphs [7], for generalized Petersen graphs [8], for trees [9] and for circulant graphs [10]. The most complete recent survey of graph labelings is [11].

In [12], the authors introduced a modification of an irregular assignment known as a modular irregular assignment. A function $\psi :E\left(G\right)\to \{1,2,\dots ,k\}$ of a graph G of order n is called a modular irregular assignment if the weight function $\lambda :V\left(G\right)\to {\mathbb{Z}}_n$ defined by $\lambda \left(x\right)=w{t}_{\psi }\left(x\right)={\sum }_{y\in N\left(x\right)}\psi \left(xy\right)$ is bijective and is called the modular weight of the vertex x, where ${\mathbb{Z}}_n$ is the group of integers modulo n. The modular irregularity strength, $\mathrm{ms}\left(G\right)$, is defined as the minimum k for which G has a modular irregular assignment. If there is no such labeling for the graph G, then the value of $\mathrm{ms}\left(G\right)$ is defined as ∞.

Clearly, every modular irregular labeling of a graph with no component of the order of, at most, two is also its irregular assignment. This gives a lower bound of the modular irregularity strength, i.e., if G is a graph with no component of the order of, at most, two, then

$$\begin{array}{c}\hfill \mathrm{s}\left(G\right)\le \mathrm{ms}\left(G\right).\end{array}$$

(2)

We have already mentioned that if a graph G contains an isolated edge or at least two isolated vertices, then $\mathrm{s}\left(G\right)=\infty$. The next theorem gives an infinity condition for the modular irregularity strength of a graph.

Theorem 1.

([12]). If G is a graph of order n, $n\equiv 2(mod4)$, then G has no modular irregular labeling, i.e., $\mathrm{ms}\left(G\right)=\infty$.

The exact values of the modular irregularity strength for certain families of graphs, namely paths, cycles, stars, triangular graphs and gear graphs, are determined in [12]. A fan graph $F_n$, $n\ge 2$, is a graph obtained by joining all vertices of a path $P_n$ on n vertices to a further vertex, called the center. For fan graphs $F_n$ of order $n+1$, $n\ge 2$, in [13], it is proven that

$$\begin{array}{c}\hfill \mathrm{ms}\left(F_n\right)=\left\{\begin{array}{cc}3,\hfill & \mathrm{if}n=2,\hfill \\ 4,\hfill & \mathrm{if}n=8,\hfill \\ \infty ,\hfill & \mathrm{if}n\equiv 1(mod4),\hfill \\ ⌈\frac{n+1}{3}⌉,\hfill & \mathrm{otherwise}.\hfill \end{array}\right.\end{array}$$

A wheel $W_n$, $n\ge 3$, is a graph obtained by joining all vertices of a cycle $C_n$ to a further vertex c, called the center. Thus, $W_n$ contains $n+1$ vertices, say, $c,x_1,x_2,\dots ,x_n$, and $2n$ edges $c{x}_i$, $1\le i\le n$, $x_i{x}_{i+1}$, $1\le i\le n-1$, and $x_n{x}_1$.

In the present paper, we determine the exact value of the irregularity strength and the exact value of the modular irregularity strength of wheels. The paper is organized as follows. First, we investigate the existence of an irregular assignment of wheels. We improve the main idea of the construction of an irregular assignment for fan graphs used in [13] and we construct an edge labeling with the desired irregular properties. The existence of such labeling proves the exact value of the irregularity strength of wheels. Next, we modify this irregular mapping of wheels in six cases, and, for each case, we determine the exact value of the modular irregularity strength.

2. Irregular Assignment of Wheels

In this section, we discuss the irregularity strength for wheels. According to the lower bound given in (1), we have that $\mathrm{s}\left(W_n\right)\ge ⌈\frac{n+2}{3}⌉.$ To show that $⌈\frac{n+2}{3}⌉$ is also an upper bound of the irregularity strength of wheels, we construct an edge labeling and show that this labeling meets the required properties.

Now, for $n\ge 5$, we define the edge labeling $\psi$ as follows:

$$\begin{array}{cccc}\hfill \psi \left(x_i{x}_{i+1}\right)=& ⌈\frac{i-1}{3}⌉+⌈\frac{i}{3}⌉,\hfill & \hfill & \mathrm{for}1\le i\le ⌈\frac{n}{2}⌉,\hfill \\ \hfill \psi \left(x_n{x}_1\right)=& 1,\hfill & & \hfill \\ \hfill \psi \left(x_{n-i}{x}_{n-i+1}\right)=& ⌈\frac{i-1}{3}⌉+⌈\frac{i}{3}⌉+1,\hfill & & \left\{\begin{array}{c}\mathrm{for}1\le i\le \frac{n-3}{2}\mathrm{if}n\mathrm{is}\mathrm{odd},\hfill \\ \mathrm{for}1\le i\le \frac{n}{2}-1\mathrm{if}n\mathrm{is}\mathrm{even},\hfill \end{array}\right.\hfill \\ \hfill \psi \left(c{x}_i\right)=& \left\{\begin{array}{cc}1,\hfill & \mathrm{for}i=1,\hfill \\ 2,\hfill & \mathrm{for}i=n,\hfill \end{array}\right.\hfill \\ \hfill \psi \left(c{x}_i\right)=& ⌈\frac{i-2}{3}⌉+⌈\frac{i}{3}⌉,\hfill & & \left\{\begin{array}{c}\mathrm{for}2\le i\le \frac{n+1}{2}\mathrm{if}n\mathrm{is}\mathrm{odd},\hfill \\ \mathrm{for}2\le i\le \frac{n}{2}\mathrm{if}n\mathrm{is}\mathrm{even},\hfill \end{array}\right.\hfill \\ \hfill \psi \left(c{x}_{n-i}\right)=& ⌈\frac{i+1}{3}⌉+⌈\frac{i+2}{3}⌉,\hfill & & \left\{\begin{array}{c}\mathrm{for}1\le i\le \frac{n-1}{2}-2\mathrm{if}n\mathrm{is}\mathrm{odd},\hfill \\ \mathrm{for}1\le i\le \frac{n}{2}-1\mathrm{if}n\mathrm{is}\mathrm{even},\hfill \end{array}\right.\hfill \\ \hfill \psi \left(c{x}_{n-i}\right)=& ⌈\frac{i}{3}⌉+⌈\frac{i+1}{3}⌉+1,\hfill & \hfill & \mathrm{for}i=\frac{n-1}{2}-1\mathrm{if}n\mathrm{is}\mathrm{odd}.\hfill \end{array}$$

(3)

Lemma 1.

The edge labeling ψ defined in (3) is an $⌈\frac{n+2}{3}⌉$-labeling of wheels $W_n$, $n\ge 5$.

Proof. 

Consider the edge labeling $\psi$ of wheels $W_n$, $n\ge 5$, defined above. One can easily check that, for odd n,

$$\begin{array}{cc}\hfill & max\left\{\psi \left(x_i{x}_{i+1}\right):1\le i\le \frac{n+1}{2}\right\}=\psi (x_{\frac{n+1}{2}}{x}_{\frac{n+3}{2}})=⌈\frac{n-1}{6}⌉+⌈\frac{n+1}{6}⌉\le ⌈\frac{n+2}{3}⌉,\hfill \\ \hfill & max\left\{\psi (x_{n-i}{x}_{n-i+1}):1\le i\le \frac{n-3}{2}\right\}=\psi (x_{\frac{n+3}{2}}{x}_{\frac{n+5}{2}})=⌈\frac{n-5}{6}⌉+⌈\frac{n-3}{6}⌉+1\le ⌈\frac{n+2}{3}⌉,\hfill \\ \hfill & max\left\{\psi (c{x}_i):2\le i\le \frac{n+1}{2}\right\}=\psi (c{x}_{\frac{n+1}{2}})=⌈\frac{n-3}{6}⌉+⌈\frac{n+1}{6}⌉\le ⌈\frac{n+2}{3}⌉,\hfill \\ \hfill & max\left\{\psi \left(c{x}_{n-i}\right):1\le i\le \frac{n-1}{2}-2\right\}=\psi (c{x}_{\frac{n+5}{2}})=⌈\frac{n-3}{6}⌉+⌈\frac{n-1}{6}⌉<⌈\frac{n+2}{3}⌉,\hfill \\ \hfill & \psi (c{x}_{n-\frac{n-1}{2}+1})=\psi (c{x}_{\frac{n+3}{2}})=⌈\frac{n-3}{6}⌉+⌈\frac{n-1}{6}⌉+1=⌈\frac{n+2}{3}⌉.\hfill \end{array}$$

For even n, we verify that

$$\begin{array}{cc}\hfill & max\left\{\psi \left(x_i{x}_{i+1}\right):1\le i\le \frac{n}{2}\right\}=\psi (x_{\frac{n}{2}}{x}_{\frac{n+2}{2}})=⌈\frac{n-2}{6}⌉+⌈\frac{n}{6}⌉\le ⌈\frac{n+2}{3}⌉,\hfill \\ \hfill & max\left\{\psi \left(x_{n-i}{x}_{n-i+1}\right):1\le i\le \frac{n-2}{2}\right\}=\psi (x_{\frac{n+2}{2}}{x}_{\frac{n+4}{2}})=⌈\frac{n-4}{6}⌉+⌈\frac{n-2}{6}⌉+1\le ⌈\frac{n+2}{3}⌉,\hfill \\ \hfill & max\left\{\psi \left(c{x}_i\right):2\le i\le \frac{n}{2}\right\}=\psi (c{x}_{\frac{n}{2}})=⌈\frac{n-4}{6}⌉+⌈\frac{n}{6}⌉\le ⌈\frac{n+2}{3}⌉,\hfill \\ \hfill & max\left\{\psi \left(c{x}_{n-i}\right):1\le i\le \frac{n}{2}-1\right\}=\psi (c{x}_{\frac{n+2}{2}})=⌈\frac{n}{6}⌉+⌈\frac{n+2}{6}⌉=⌈\frac{n+2}{3}⌉.\hfill \end{array}$$

Observe that, under the edge labeling $\psi$, the edge labels of a wheel $W_n$, $n\ge 5$, are, at most, $⌈\frac{n+2}{3}⌉$. This implies that the edge labeling $\psi$ is an $⌈\frac{n+2}{3}⌉$-labeling.   ☐

The next lemma provides values of weights of the vertices of wheels produced by the edge labeling $\psi$.

Lemma 2.

The induced weights of the vertices of $W_n$, $n\ge 5$, under the edge labeling ψ defined in (3), are

$$\begin{array}{cc}\hfill w{t}_{\psi }\left(x_i\right)& =\left\{\begin{array}{cc}3,\hfill & \mathit{for}i=1,\hfill \\ 2i,\hfill & \mathit{for}2\le i\le ⌈\frac{n}{2}⌉,\hfill \\ n+2,\hfill & \mathit{for}i=⌈\frac{n}{2}⌉+1,\hfill \\ 5,\hfill & \mathit{for}i=n,\hfill \end{array}\right.\hfill \\ \hfill w{t}_{\psi }\left(x_{n-i}\right)& =2i+5,\mathit{for}1\le i\le ⌈\frac{n-1}{2}⌉-2,\hfill \\ \hfill w{t}_{\psi }\left(c\right)& =\left\{\begin{array}{cc}\frac{n(n+5)}{6},\hfill & \mathit{for}n\equiv 0,1,3,4(mod6),\hfill \\ \frac{(n+1)(n+4)}{6},\hfill & \mathit{for}n\equiv 2,5(mod6).\hfill \end{array}\right.\hfill \end{array}$$

Proof. 

Under the labeling $\psi$, the weights of vertices $x_i$, $1\le i\le n$, admit the following values:

$$\begin{array}{cc}\hfill w{t}_{\psi }\left(x_1\right)=& \psi \left(x_n{x}_1\right)+\psi \left(x_1{x}_2\right)+\psi \left(c{x}_1\right)=3,\hfill \\ \hfill w{t}_{\psi }\left(x_i\right)=& \psi \left(x_{i-1}{x}_i\right)+\psi \left(x_i{x}_{i+1}\right)+\psi \left(c{x}_i\right)=⌈\frac{i-2}{3}⌉+⌈\frac{i-1}{3}⌉+⌈\frac{i-1}{3}⌉+⌈\frac{i}{3}⌉+⌈\frac{i-2}{3}⌉\hfill \\ & +⌈\frac{i}{3}⌉=2i,\mathrm{for}2\le i\le ⌈\frac{n}{2}⌉,\hfill \\ \hfill w{t}_{\psi }(x_{\frac{n+3}{2}})=& \psi (x_{\frac{n+1}{2}}{x}_{\frac{n+3}{2}})+\psi (x_{\frac{n+3}{2}}{x}_{\frac{n+5}{2}})+\psi (c{x}_{n-\frac{n-1}{2}+1})=⌈\frac{n-1}{6}⌉+⌈\frac{n+1}{6}⌉\hfill \\ & +⌈\frac{n-5}{6}⌉+⌈\frac{n-3}{6}⌉+1+⌈\frac{n-3}{6}⌉+⌈\frac{n-1}{6}⌉+1=n+2,\hfill \\ \hfill w{t}_{\psi }(x_{\frac{n}{2}+1})=& \psi (x_{\frac{n}{2}}{x}_{\frac{n+2}{2}})+\psi (x_{\frac{n+2}{2}}{x}_{\frac{n+4}{2}})+\psi (c{x}_{\frac{n}{2}+1})=⌈\frac{n-2}{6}⌉+⌈\frac{n}{6}⌉+⌈\frac{n-4}{6}⌉\hfill \\ & +⌈\frac{n-2}{6}⌉+1+⌈\frac{n}{6}⌉+⌈\frac{n+2}{6}⌉=n+2,\hfill \\ \hfill w{t}_{\psi }\left(x_{n-i}\right)=& \psi \left(x_{n-i-1}{x}_{n-i}\right)+\psi \left(x_{n-i}{x}_{n-i+1}\right)+\psi \left(c{x}_{n-i}\right)=⌈\frac{i}{3}⌉+⌈\frac{i+1}{3}⌉+1+⌈\frac{i-1}{3}⌉\hfill \\ & +⌈\frac{i}{3}⌉+1+⌈\frac{i+1}{3}⌉+⌈\frac{i+2}{3}⌉=2i+5,\mathrm{for}1\le i\le ⌈\frac{n-1}{2}⌉-2,\hfill \\ \hfill w{t}_{\psi }\left(x_n\right)=& \psi \left(x_{n-1}{x}_n\right)+\psi \left(x_n{x}_1\right)+\psi \left(c{x}_n\right)=5.\hfill \end{array}$$

Now, the set of edges $c{x}_1,c{x}_2,\dots ,c{x}_{3p+3}$, $p=⌊\frac{n}{6}⌋$ when $n\equiv 4,5(mod6)$ and $p=⌊\frac{n}{6}⌋-1$; otherwise, we split them into mutually disjoint triplets ($c{x}_{3a+1}$, $c{x}_{3a+2}$, $c{x}_{3a+3}$) for $a=0,1,2,\dots ,p$. The sum of labels of edges for each such triplet is

$$\sum _{j=1}^3\psi \left(c{x}_{3a+j}\right)=⌈\frac{3a-1}{3}⌉+⌈\frac{3a+1}{3}⌉+⌈\frac{3a}{3}⌉+⌈\frac{3a+2}{3}⌉+⌈\frac{3a+1}{3}⌉+⌈\frac{3a+3}{3}⌉=6a+4.$$

The set of edges $c{x}_n,c{x}_{n-1},\dots ,c{x}_{n-3q-2}$, $q=⌊\frac{n}{6}⌋-1$, we split into mutually disjoint triplets ($c{x}_{n-3b}$, $c{x}_{n-3b-1}$, $c{x}_{n-3b-2}$) for $b=0,1,2,\dots ,q$. The sum of labels of edges for each such triplet is

$$\sum _{j=1}^3\psi \left(c{x}_{n-3b+1-j}\right)=⌈\frac{3b+1}{3}⌉+⌈\frac{3b+2}{3}⌉+⌈\frac{3b+2}{3}⌉+⌈\frac{3b+3}{3}⌉+⌈\frac{3b+3}{3}⌉+⌈\frac{3b+4}{3}⌉=6b+7.$$

Let us distinguish six cases according to the residue of n modulo 6 for the enumeration of the weight of the center vertex c.

Case 1.$n\equiv 0(mod6)$.

Split the edges $c{x}_1,c{x}_2,\dots ,c{x}_{\frac{n}{2}}$ into $\frac{n}{6}$ mutually disjoint triplets ($c{x}_{3a+1}$, $c{x}_{3a+2}$, $c{x}_{3a+3}$) for $a=0,1,2,\dots ,\frac{n}{6}-1$, and split the edges $c{x}_n,c{x}_{n-1},\dots ,c{x}_{\frac{n}{2}+1}$ into $\frac{n}{6}$ mutually disjoint triplets ($c{x}_{n-3b}$, $c{x}_{n-3b-1}$, $c{x}_{n-3b-2}$) for $b=0,1,2,\dots ,\frac{n}{6}-1$. Then, for the weight of the center vertex, we obtain

$$\begin{array}{cc}\hfill w{t}_{\psi }\left(c\right)& =\sum _{a=0}^{\frac{n}{6}-1}\sum _{j=1}^3\psi \left(c{x}_{3a+j}\right)+\sum _{b=0}^{\frac{n}{6}-1}\sum _{j=1}^3\psi \left(c{x}_{n-3b+1-j}\right)=\sum _{a=0}^{\frac{n}{6}-1}(6a+4)+\sum _{b=0}^{\frac{n}{6}-1}(6b+7)\hfill \\ & =\frac{n(n+5)}{6}.\hfill \end{array}$$

Case 2.$n\equiv 2(mod6)$.

Split the edges $c{x}_1,c{x}_2,\dots ,c{x}_{\frac{n}{2}-1}$ into $\frac{n-2}{6}$ mutually disjoint triplets ($c{x}_{3a+1}$, $c{x}_{3a+2}$, $c{x}_{3a+3}$) for $a=0,1,2,\dots ,\frac{n-2}{6}-1$, and split the edges $c{x}_n,c{x}_{n-1},\dots ,c{x}_{\frac{n}{2}+2}$ into $\frac{n-2}{6}$ mutually disjoint triplets ($c{x}_{n-3b}$, $c{x}_{n-3b-1}$, $c{x}_{n-3b-2}$) for $b=0,1,2,\dots ,\frac{n-2}{6}-1$. Then, the weight of the center vertex is

$$\begin{array}{cc}\hfill w{t}_{\psi }\left(c\right)=& \sum _{a=0}^{\frac{n-2}{6}-1}\sum _{j=1}^3\psi \left(c{x}_{3a+j}\right)+\psi (c{x}_{\frac{n}{2}})+\psi (c{x}_{n-\frac{n}{2}+1})+\sum _{b=0}^{\frac{n-2}{6}-1}\sum _{j=1}^3\psi \left(c{x}_{n-3b+1-j}\right)\hfill \\ \hfill =& \sum _{a=0}^{\frac{n-2}{6}-1}(6a+4)+⌈\frac{n-4}{6}⌉+⌈\frac{n}{6}⌉+⌈\frac{n}{6}⌉+⌈\frac{n+2}{6}⌉+\sum _{b=0}^{\frac{n-2}{6}-1}(6b+7)=\frac{(n+1)(n+4)}{6}.\hfill \end{array}$$

Case 3.$n\equiv 4(mod6)$.

Split the edges $c{x}_1,c{x}_2,\dots ,c{x}_{\frac{n}{2}+1}$ into $\frac{n-4}{6}+1$ mutually disjoint triplets ($c{x}_{3a+1}$, $c{x}_{3a+2}$, $c{x}_{3a+3}$) for $a=0,1,2,\dots ,\frac{n-4}{6}$, and split the edges $c{x}_n,c{x}_{n-1},\dots ,c{x}_{\frac{n}{2}+3}$ into $\frac{n-4}{6}$ mutually disjoint triplets ($c{x}_{n-3b}$, $c{x}_{n-3b-1}$, $c{x}_{n-3b-2}$) for $b=0,1,2,\dots ,\frac{n-4}{6}-1$. Then, the center vertex receives the following weight:

$$\begin{array}{cc}\hfill w{t}_{\psi }\left(c\right)=& \sum _{a=0}^{\frac{n-4}{6}}\sum _{j=1}^3\psi \left(c{x}_{3a+j}\right)+\psi (c{x}_{n-\frac{n}{2}+2})+\sum _{b=0}^{\frac{n-4}{6}-1}\sum _{j=1}^3\psi \left(c{x}_{n-3b+1-j}\right)\hfill \\ \hfill =& \sum _{a=0}^{\frac{n-4}{6}}(6a+4)+⌈\frac{n-2}{6}⌉+⌈\frac{n}{6}⌉+\sum _{b=0}^{\frac{n-4}{6}-1}(6b+7)=\frac{n(n+5)}{6}.\hfill \end{array}$$

Case 4.$n\equiv 1(mod6)$.

Split the edges $c{x}_1,c{x}_2,\dots ,c{x}_{\frac{n-1}{2}}$ into $\frac{n-1}{6}$ mutually disjoint triplets ($c{x}_{3a+1}$, $c{x}_{3a+2}$, $c{x}_{3a+3}$) for $a=0,1,2,\dots ,\frac{n-1}{6}-1$, and split the edges $c{x}_n,c{x}_{n-1},\dots ,c{x}_{\frac{n+3}{2}}$ into $\frac{n-1}{6}$ mutually disjoint triplets ($c{x}_{n-3b}$, $c{x}_{n-3b-1}$, $c{x}_{n-3b-2}$) for $b=0,1,2,\dots ,\frac{n-1}{6}-1$. Then, the center vertex admits the following weight:

$$\begin{array}{cc}\hfill w{t}_{\psi }\left(c\right)=& \sum _{a=0}^{\frac{n-1}{6}-1}\sum _{j=1}^3\psi \left(c{x}_{3a+j}\right)+\psi (c{x}_{\frac{n+1}{2}})+\sum _{b=0}^{\frac{n-1}{6}-1}\sum _{j=1}^3\psi \left(c{x}_{n-3b+1-j}\right)\hfill \\ \hfill =& \sum _{a=0}^{\frac{n-1}{6}-1}(6a+4)+⌈\frac{n-3}{6}⌉+⌈\frac{n+1}{6}⌉+\sum _{b=0}^{\frac{n-1}{6}-1}(6b+7)=\frac{n(n+5)}{6}.\hfill \end{array}$$

Case 5.$n\equiv 3(mod6)$.

Split the edges $c{x}_1,c{x}_2,\dots ,c{x}_{\frac{n-1}{2}-1}$ into $\frac{n-3}{6}$ mutually disjoint triplets ($c{x}_{3a+1}$, $c{x}_{3a+2}$, $c{x}_{3a+3}$) for $a=0,1,2,\dots ,\frac{n-3}{6}-1$, and split the edges $c{x}_n,c{x}_{n-1},\dots ,c{x}_{\frac{n+1}{2}+2}$ into $\frac{n-3}{6}$ mutually disjoint triplets ($c{x}_{n-3b}$, $c{x}_{n-3b-1}$, $c{x}_{n-3b-2}$) for $b=0,1,2,\dots ,\frac{n-3}{6}-1$. Then, for the weight of the center vertex, we obtain

$$\begin{array}{cc}\hfill w{t}_{\psi }\left(c\right)=& \sum _{a=0}^{\frac{n-3}{6}-1}\sum _{j=1}^3\psi \left(c{x}_{3a+j}\right)+\psi (c{x}_{\frac{n-1}{2}})+\psi (c{x}_{\frac{n+1}{2}})+\psi (c{x}_{n-\frac{n-1}{2}+1})\hfill \\ \hfill & +\sum _{b=0}^{\frac{n-3}{6}-1}\sum _{j=1}^3\psi \left(c{x}_{n-3b+1-j}\right)=\sum _{a=0}^{\frac{n-3}{6}-1}(6a+4)+⌈\frac{n-5}{6}⌉+⌈\frac{n-1}{6}⌉+⌈\frac{n-3}{6}⌉\hfill \\ & +⌈\frac{n+1}{6}⌉+⌈\frac{n-3}{6}⌉+⌈\frac{n-1}{6}⌉+1+\sum _{b=0}^{\frac{n-3}{6}-1}(6b+7)=\frac{n(n+5)}{6}.\hfill \end{array}$$

Case 6.$n\equiv 5(mod6)$.

Split the edges $c{x}_1,c{x}_2,\dots ,c{x}_{\frac{n+1}{2}}$ into $\frac{n-5}{6}+1$ mutually disjoint triplets ($c{x}_{3a+1}$, $c{x}_{3a+2}$, $c{x}_{3a+3}$) for $a=0,1,2,\dots ,\frac{n-5}{6}$, and split the edges $c{x}_n,c{x}_{n-1},\dots ,c{x}_{\frac{n+1}{2}+3}$ into $\frac{n-5}{6}$ mutually disjoint triplets ($c{x}_{n-3b}$, $c{x}_{n-3b-1}$, $c{x}_{n-3b-2}$) for $b=0,1,2,\dots ,\frac{n-5}{6}-1$. Then, for the center vertex weight, we have

$$\begin{array}{cc}\hfill w{t}_{\psi }\left(c\right)=& \sum _{a=0}^{\frac{n-5}{6}}\sum _{j=1}^3\psi \left(c{x}_{3a+j}\right)+\psi (c{x}_{n-\frac{n-1}{2}+1})+\psi (c{x}_{n-\frac{n-1}{2}+2})\hfill \\ & +\sum _{b=0}^{\frac{n-5}{6}-1}\sum _{j=1}^3\psi \left(c{x}_{n-3b+1-j}\right)=\sum _{a=0}^{\frac{n-5}{6}}(6a+4)+⌈\frac{n-3}{6}⌉+⌈\frac{n-1}{6}⌉+1+⌈\frac{n-3}{6}⌉\hfill \\ & +⌈\frac{n-1}{6}⌉+\sum _{b=0}^{\frac{n-5}{6}-1}(6b+7)=\frac{(n+1)(n+4)}{6}.\hfill \end{array}$$

This concludes the proof.   ☐

The next theorem gives the exact value of the irregularity strength of wheels.

Theorem 2.

Let $W_n$, $n\ge 3$, be a wheel on $n+1$ vertices. Then,

$$\begin{array}{c}\hfill \mathrm{s}\left(W_n\right)=\left\{\begin{array}{cc}3,\hfill & \mathit{if}n=3\mathit{and}n=4,\hfill \\ ⌈\frac{n+2}{3}⌉,\hfill & \mathit{if}n\ge 5.\hfill \end{array}\right.\end{array}$$

Proof. 

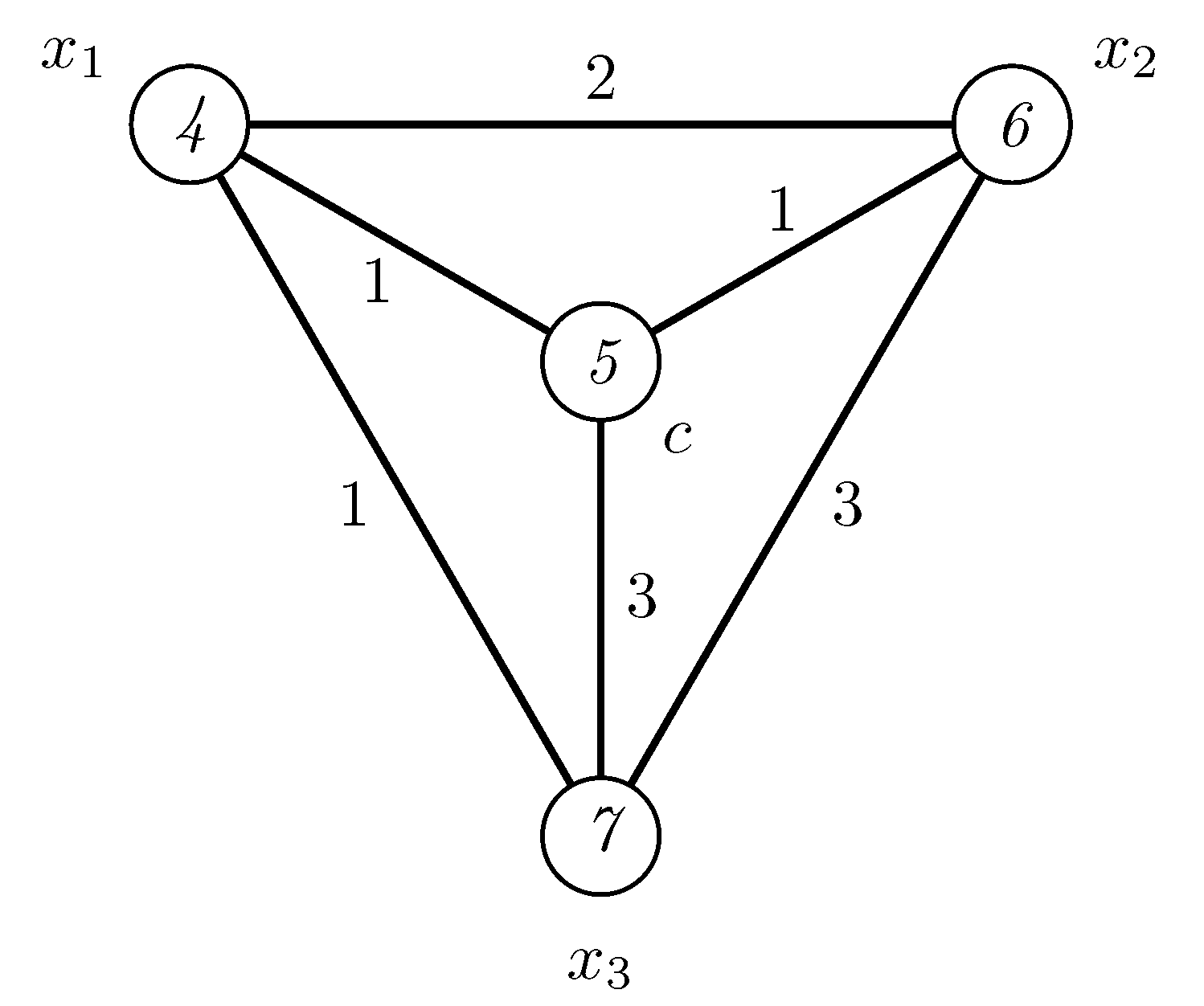
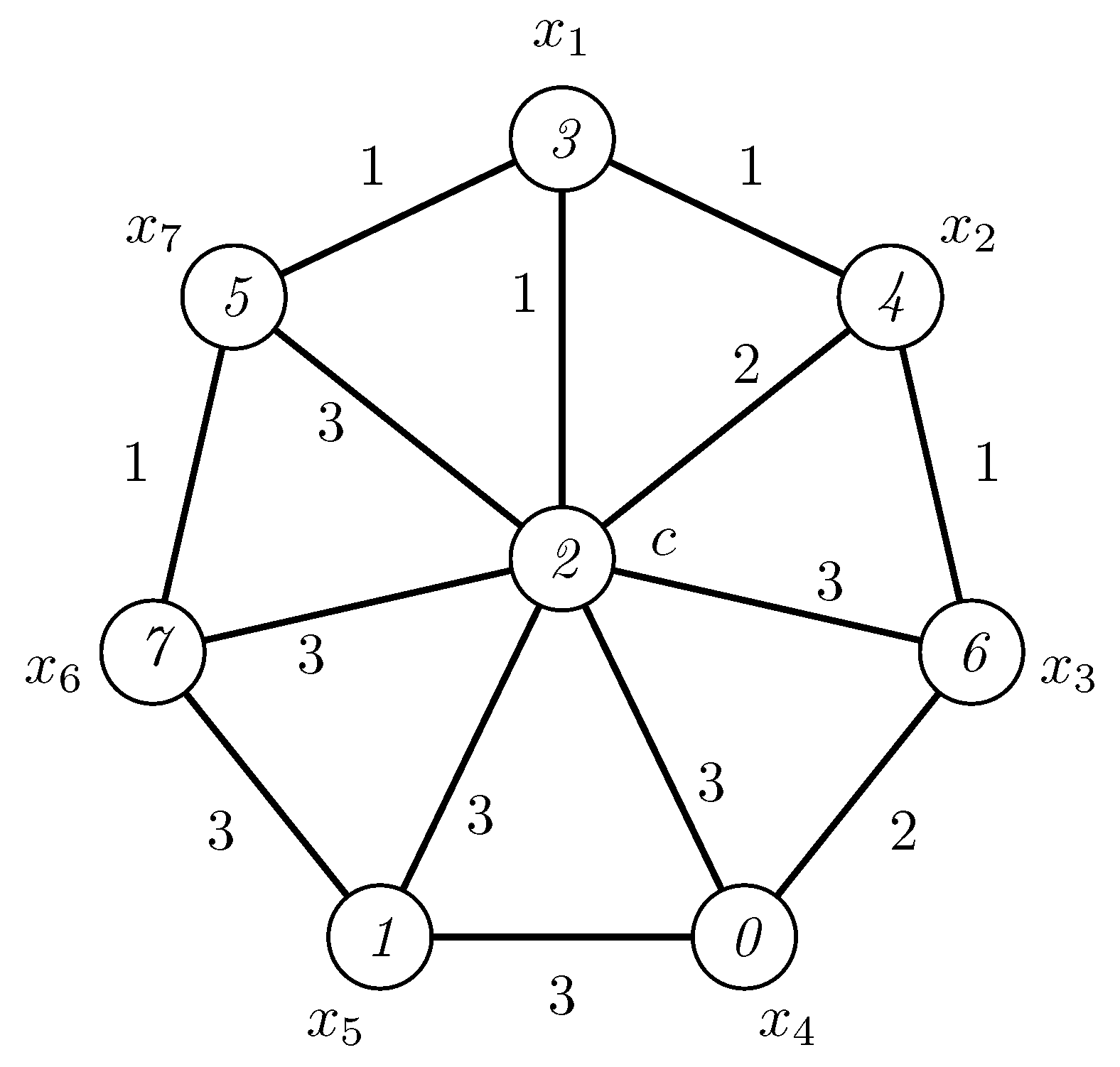
Chartrand et al. in [1] proved that $\mathrm{s}\left(K_n\right)=3$ for each $n\ge 3$. Since $W_3=K_4$, it follows that $\mathrm{s}\left(W_3\right)=3$. Figure 1 depicts an irregular 3-labeling of the wheel $W_3$.

Figure 1. An irregular 3-labeling of the wheel $W_3$.

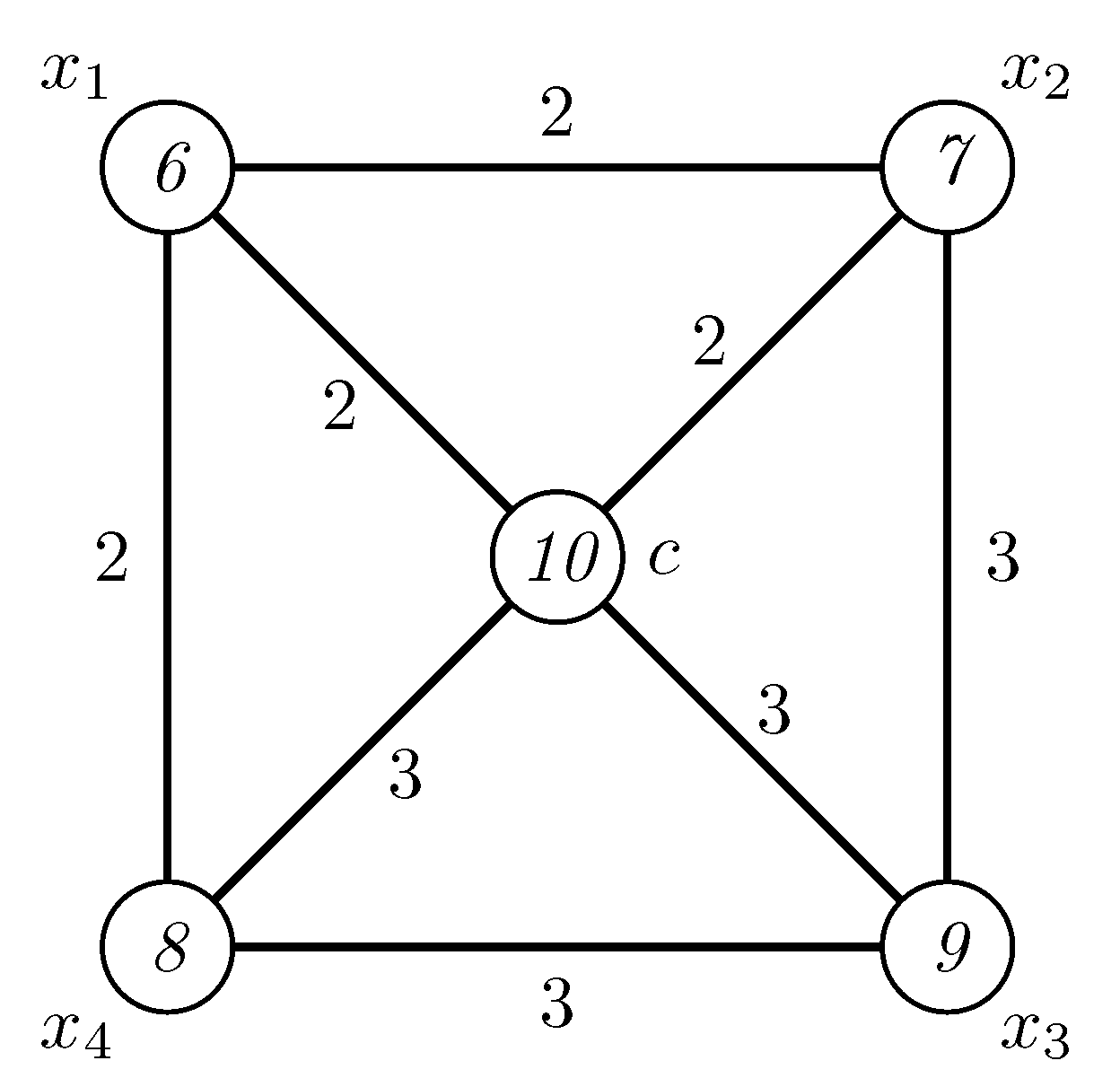
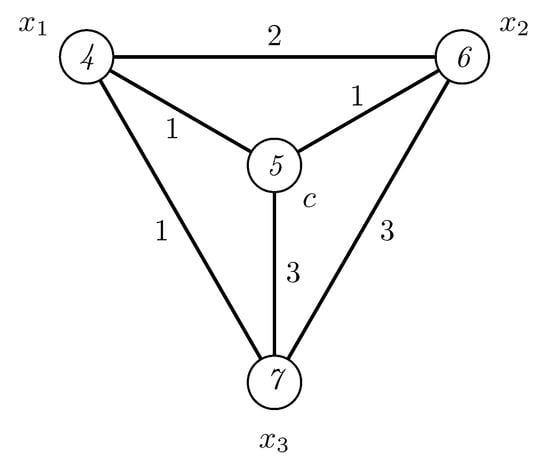
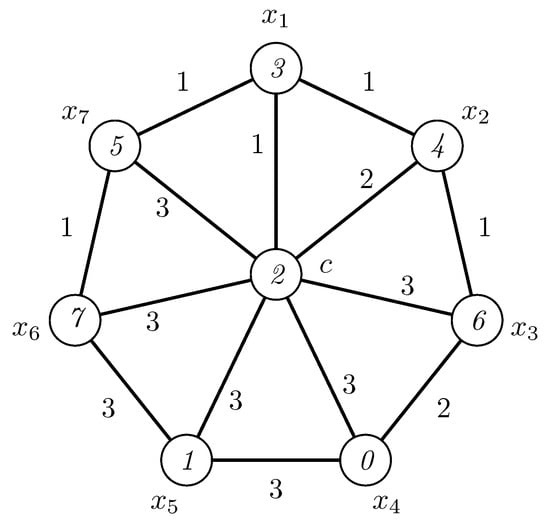
According to the lower bound given in (1), we have that $\mathrm{s}\left(W_n\right)\ge ⌈\frac{n+2}{3}⌉$. Hence, $\mathrm{s}\left(W_4\right)\ge 2$. Suppose that there exists an irregular 2-labeling of $W_4$. As the vertices $x_i$, $i=1,2,3,4$, are of degree 3, then, under any 2-labeling, the smallest weight of a vertex, say $x_1$, is at least 3 (this is realizable as the sum of edge labels 1 + 1 +1) and the largest weight of the vertex, which must be $x_3$, is, at most, 6 (this is realizable as the sum of edge labels 2 + 2 +2). Since all vertices $x_i$ must have distinct weights, it follows that the weight of the center vertex is 6 and we have a contradiction. It follows that there is no irregular 2-labeling of $W_4$. Figure 2 illustrates an irregular 3-labeling of the wheel $W_4$.

Figure 2. An irregular 3-labeling of the wheel $W_4$.

Now, for $n\ge 5$, we consider the edge labeling $\psi$ given in (3). Lemma 1 shows that, under the edge labeling $\psi$, the edge labels of wheels $W_n$, $n\ge 5$, are, at most, $⌈\frac{n+2}{3}⌉$. Lemma 2 proves that the weights of vertices $x_i$, $i=1,2,\dots ,n$, under the labeling $\psi$ successively attain values $3,4,\dots ,n+2$. Since

$$\frac{(n+1)(n+4)}{6}>\frac{n(n+5)}{6}>n+2$$

for any $n\ge 5$, we find that the center vertex weight $w{t}_{\psi }\left(c\right)>n+2$. It follows that the vertex weights are distinct for all pairs of distinct vertices and the labeling $\psi$ is a suitable edge-irregular $⌈\frac{n+2}{3}⌉$-labeling. This concludes the proof.   ☐

3. Modular Irregular Assignment of Wheels

For determining the exact value of the modular irregularity strength of wheels, we use a modular irregular assignment as a suitable modification of the irregular $⌈\frac{n+2}{3}⌉$-labeling $\psi$. From Lemma 2, it follows that the weights of vertices $x_i$, $i=1,2,\dots ,n$, $n\ge 5$, under the labeling $\psi$, gradually reach the values $3,4,\dots ,n,n+1,n+2$, i.e., the modular weights are $3,4,\dots ,n,0,1$$(modn+1)$. In order to obtain a modular irregular assignment of wheel $W_n$, the center vertex modular weight has to be congruent to $2(modn+1)$. To produce such a modular weight of the center vertex, we increase (decrease) the labels of edges of $W_n$ in such a way that these operations will have no impact on the weights of the vertices $x_i$, $i=1,2,\dots ,n$.

The following lemma gives the exact value of the modular irregularity strength of wheels $W_n$, for even $n\ge 4$.

Lemma 3.

Let $W_n$ be a wheel on $n+1$ vertices with $n\ge 4$ even. Then,

$$\begin{array}{c}\hfill \mathrm{ms}\left(W_n\right)=\left\{\begin{array}{cc}3,\hfill & \mathit{if}n=4,\hfill \\ 5,\hfill & \mathit{if}n=10,\hfill \\ ⌈\frac{n+2}{3}⌉,\hfill & \mathit{otherwise}.\hfill \end{array}\right.\end{array}$$

Proof. 

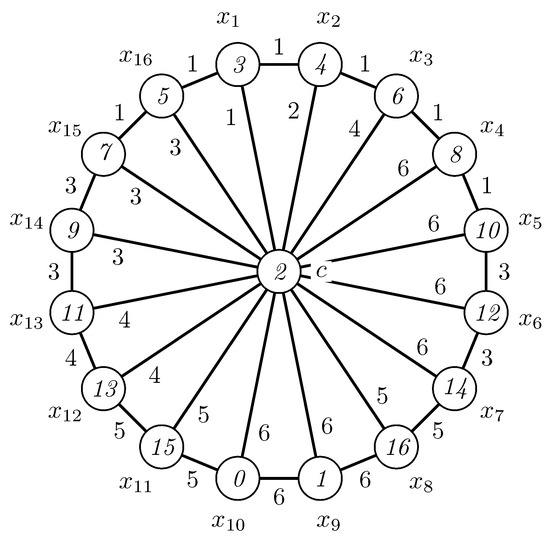
The existence of a modular irregular 3-labeling of the wheel $W_4$ follows from Figure 2, where the modular weights of vertices $x_i$, $i=1,2,3,4$, are $1,2,4,3(mod5)$ and the modular weight of the center vertex is $0(mod5)$.

Next, for even $n>4$, we will consider the following three cases.

Case 1.$n\equiv 0(mod6)$.

Define an edge labeling $f_0$ as modification of the labeling $\psi$ in the following way.

$$\begin{array}{cc}\hfill f_0\left(x_i{x}_{i+1}\right)=& \psi \left(x_i{x}_{i+1}\right),\mathrm{for}1\le i\le \frac{n}{2},\hfill \\ \hfill f_0\left(x_n{x}_1\right)=& \psi \left(x_n{x}_1\right),\hfill & & \\ \hfill f_0\left(x_{n-i}{x}_{n-i+1}\right)=& \left\{\begin{array}{cc}\psi \left(x_{n-i}{x}_{n-i+1}\right)+1,\hfill & \mathrm{for}i=1,\hfill \\ \psi \left(x_{n-i}{x}_{n-i+1}\right)+2,\hfill & \mathrm{for}i=3,5,7,\dots ,\frac{n}{3}-3,\frac{n}{3}-1,\hfill \\ \psi \left(x_{n-i}{x}_{n-i+1}\right),\hfill & \mathrm{otherwise},\hfill \end{array}\right.\hfill \\ \hfill f_0\left(c{x}_i\right)=& \left\{\begin{array}{cc}1,\hfill & \mathrm{for}i=1,n,\hfill \\ \psi \left(c{x}_i\right),\hfill & \mathrm{for}2\le i\le \frac{n}{2},\hfill \end{array}\right.\hfill \\ \hfill f_0\left(c{x}_{n-i}\right)=& \left\{\begin{array}{cc}\psi \left(c{x}_{n-i}\right)-1,\hfill & \mathrm{for}i=1,\hfill \\ \psi \left(c{x}_{n-i}\right)-2,\hfill & \mathrm{for}i=2,3,4,\dots ,\frac{n}{3}-2,\frac{n}{3}-1,\hfill \\ \psi \left(c{x}_{n-i}\right),\hfill & \mathrm{otherwise}.\hfill \end{array}\right.\hfill \end{array}$$

It is a matter of routine checking that, for $n=6$, the edge label $f_0\left(x_5{x}_6\right)=\psi \left(x_5{x}_6\right)+1=3=⌈\frac{n+2}{3}⌉$, and for $n>6$, we have

$$\begin{array}{cc}\hfill max& \left\{f_0\left(x_{n-i}{x}_{n-i+1}\right):i=1,3,5,7,\dots ,\frac{n}{3}-3,\frac{n}{3}-1\right\}=\psi (x_{n-\frac{n}{3}+1}{x}_{n-\frac{n}{3}+2})+2\hfill \\ & =⌈\frac{n-6}{9}⌉+⌈\frac{n-3}{9}⌉+3\le ⌈\frac{n+2}{3}⌉.\hfill \end{array}$$

Moreover, decreasing the labels of the edges $c{x}_n$, $c{x}_{n-1}$ by one and the labels of the edges $c{x}_{n-i}$, $i=2,3,4,\dots ,\frac{n}{3}-2,\frac{n}{3}-1$, by two, and increasing the label of the edge $x_{n-1}{x}_n$ by one and the labels of the edges $x_{n-i}{x}_{n-i+1}$, $i=3,5,7,\dots ,\frac{n}{3}-3,\frac{n}{3}-1$, by two has no effect on the weights of vertices $x_i$, $1\le i\le n$. They still successively attain values from 3 to $n+2$. On the other hand, decreasing the labels of the edges $c{x}_n$, $c{x}_{n-1}$ and $c{x}_{n-i}$, $i=2,3,4,\dots ,\frac{n}{3}-2,\frac{n}{3}-1$, decreases the center vertex weight and we obtain

$$w{t}_{f_0}\left(c\right)=w{t}_{\psi }\left(c\right)-2-2\left(\frac{n}{3}-2\right)=\frac{n(n+1)}{6}+2.$$

Since $\frac{n}{6}$ is an integer, it follows that $w{t}_{f_0}\left(c\right)\equiv 2(modn+1)$. This implies that the modified labeling $f_0$ is a required modular irregular $⌈\frac{n+2}{3}⌉$-labeling of $W_n$.

Case 2.$n\equiv 2(mod6)$. In light of Lemma 2, we can see that under the labeling $\psi$, the weight of the center vertex is $\frac{(n+1)(n+4)}{6}$ and it is not congruent to 2 $(modn+1)$. Therefore, we modify the edge labeling (3) as follows:

$$\begin{array}{cc}\hfill f_2\left(x_i{x}_{i+1}\right)=& \left\{\begin{array}{cc}1,\hfill & \mathrm{for}i=1,2,\hfill \\ \psi \left(x_i{x}_{i+1}\right),\hfill & 3\le i\le \frac{n}{2},\hfill \end{array}\right.\hfill \\ \hfill f_2\left(x_n{x}_1\right)=& \psi \left(x_n{x}_1\right),\hfill & & \\ \hfill f_2\left(x_{n-i}{x}_{n-i+1}\right)=& \psi \left(x_{n-i}{x}_{n-i+1}\right),\mathrm{for}1\le i\le \frac{n-2}{2},\hfill \\ \hfill f_2\left(c{x}_i\right)=& \psi \left(c{x}_i\right),\mathrm{for}i=1,n,\hfill \\ \hfill f_2\left(c{x}_i\right)=& \left\{\begin{array}{cc}2,\hfill & \mathrm{for}i=2,\hfill \\ 3,\hfill & \mathrm{for}i=3,\hfill \\ \psi \left(c{x}_i\right),\hfill & \mathrm{for}4\le i\le \frac{n}{2},\hfill \end{array}\right.\hfill \\ \hfill f_2\left(c{x}_{n-i}\right)=& \psi \left(c{x}_{n-i}\right),\mathrm{for}1\le i\le \frac{n}{2}-1.\hfill \end{array}$$

The new labeling $f_2$ reduces the value of the edge $x_2{x}_3$ by one and increases the values of edges $c{x}_2$ and $c{x}_3$ by one. This modification of the labeling $\psi$ has no impact on the weights of the vertices $x_2$ and $x_3$. However, increasing the values of the edges $c{x}_2$ and $c{x}_3$ results in an increase in the weight of the center vertex and we obtain

$$w{t}_{f_2}\left(c\right)=w{t}_{\psi }\left(c\right)+2=\frac{(n+1)(n+4)}{6}+2.$$

As $\frac{n+4}{6}$ is an integer, subsequently, $w{t}_{f_2}\left(c\right)\equiv 2(modn+1)$. This proves that the constructed edge labeling $f_2$ is a suitable modular irregular $⌈\frac{n+2}{3}⌉$-labeling of $W_n$.

Case 3.$n\equiv 4(mod6)$.

According to Lemma 2, we have that $w{t}_{\psi }\left(c\right)=\frac{n(n+5)}{6}\not\equiv 2(modn+1)$. This means that the edge labeling $\psi$ is not modular irregular.

Let $n=10$. From Theorem 2, it follows that $\mathrm{s}\left(W_{10}\right)=4$ and $w{t}_{\psi }\left(c\right)=25$. According to (2), we have that $\mathrm{ms}\left(W_{10}\right)\ge 4$. Suppose that there exists a modular irregular 4-labeling $\phi$ of $W_{10}$. Since the vertices $x_i$, $i=1,2,\dots ,10$, are of degree 3, then the smallest vertex weight is at least 3 and the largest one cannot be more than 12 (as the sum of edge labels 4+4+4). Clearly, the weights of vertices $x_i$ successively assume values from 3 to 12, which means the values $3,4,\dots ,10,0,1(mod11)$. Because $w{t}_{\psi }\left(c\right)=25\not\equiv 2(mod11)$, then the weight of the center under the labeling $\phi$ must be either $w{t}_{\phi }\left(c\right)=24\equiv 2(mod11)$ or $w{t}_{\phi }\left(c\right)=35\equiv 2(mod11)$.

Let us first assume that $w{t}_{\phi }\left(c\right)=24$. The sum of all the vertex weights of $W_{10}$ is

$$\begin{array}{c}\hfill \sum _{i=1}^{10}w{t}_{\phi }\left(x_i\right)+w{t}_{\phi }\left(c\right)=3+4+\cdots +12+24=99.\end{array}$$

(4)

In the computation of the vertex weights of $W_{10}$, each edge label is used twice. Then, the sum of all edge labels used to calculate the vertex weights is equal to the sum of all the vertex weights. With respect to (4), we obtain

$$\begin{array}{c}\hfill 2\sum _{i=1}^{10}\phi \left(c{x}_i\right)+2\sum _{i=1}^9\phi \left(x_i{x}_{i+1}\right)+2\phi \left(x_n{x}_1\right)=99.\end{array}$$

(5)

Using parity considerations for the left-hand and the right-hand sides of Equation (5), we obtain a contradiction. Thus, there is no modular irregular 4-labeling of $W_{10}$ with $w{t}_{\phi }\left(c\right)=24$.

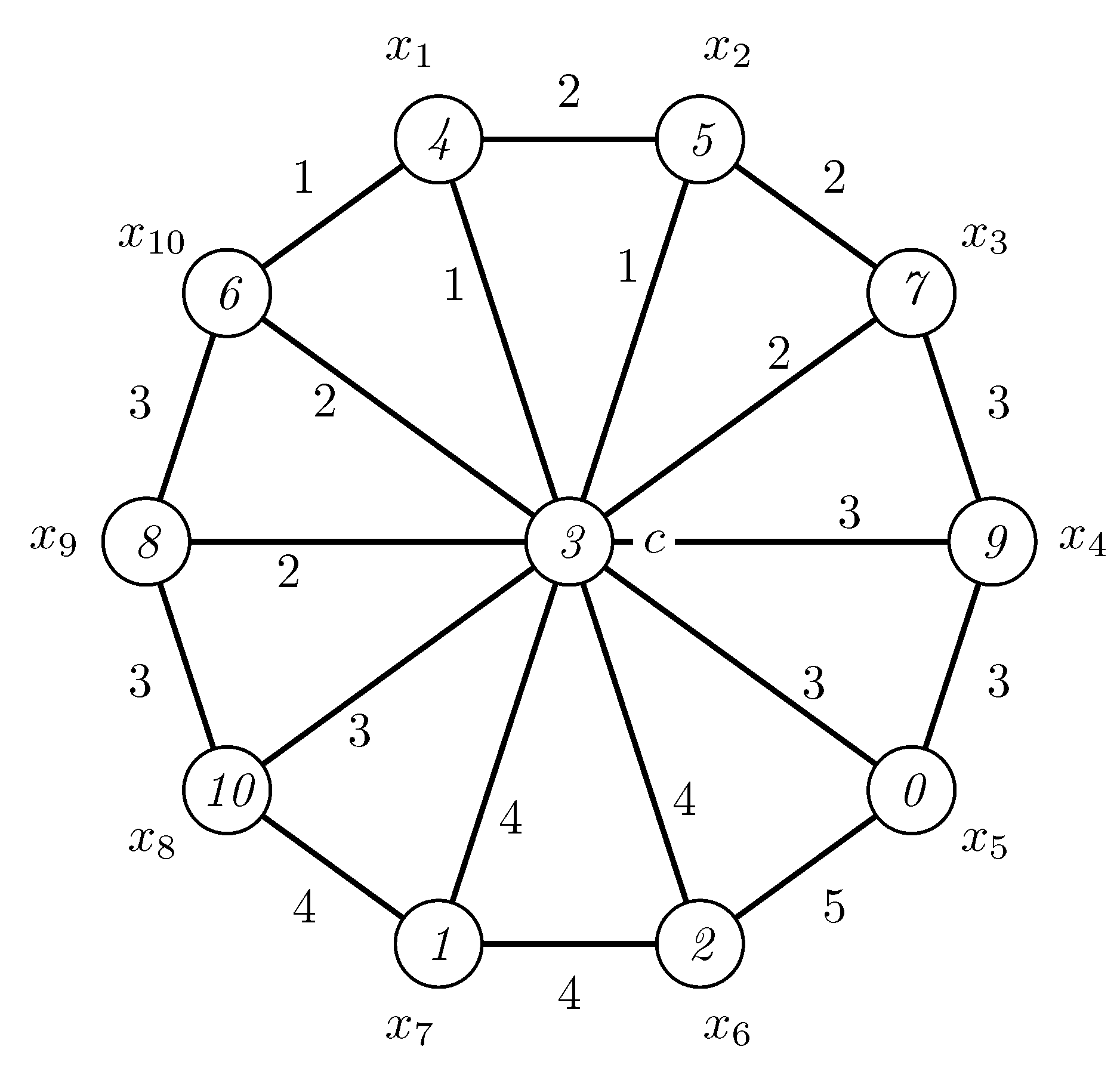
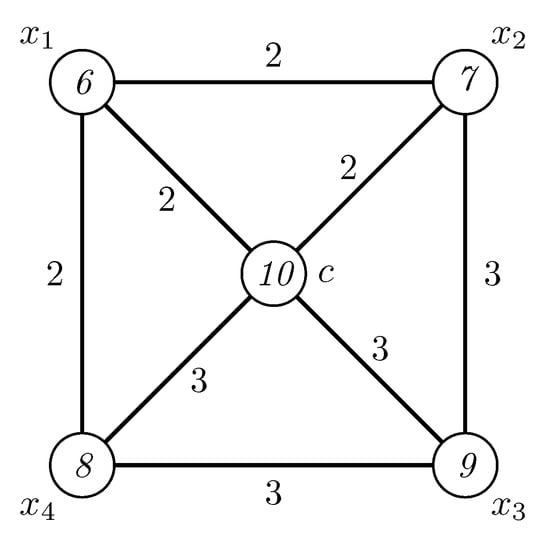
Now, let us assume that $w{t}_{\phi }\left(c\right)=35$. Under a modular irregular 4-labeling $\phi$ of $W_{10}$, if $w{t}_{\phi }\left(x_i\right)=3$, then $\phi \left(c{x}_i\right)=1$. If $w{t}_{\phi }\left(x_j\right)=4$, then $\phi \left(c{x}_j\right)$ is, at most, 2 and if $w{t}_{\phi }\left(x_k\right)=5$, then $\phi \left(c{x}_k\right)$ is, at most, 3. Values of the other seven edges incident with the center can be, at most, 4. Thus the weight of the center cannot be more than 34 and, again, we have a contradiction. This proves that there is no modular irregular 4-labeling of $W_{10}$. A modular irregular 5-labeling of $W_{10}$ is displayed in Figure 3.

Figure 3. A modular irregular 5-labeling of $W_{10}$.

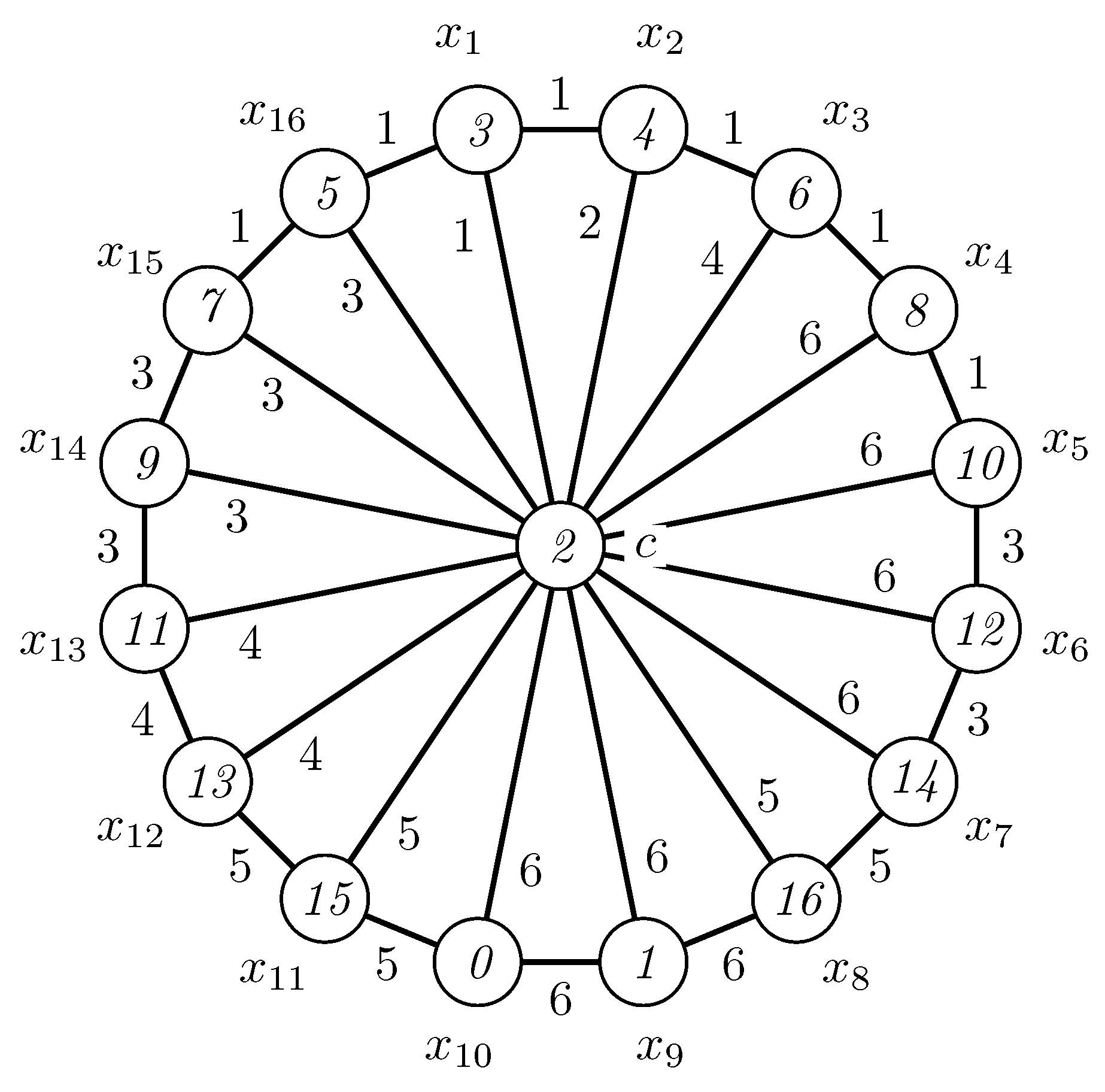
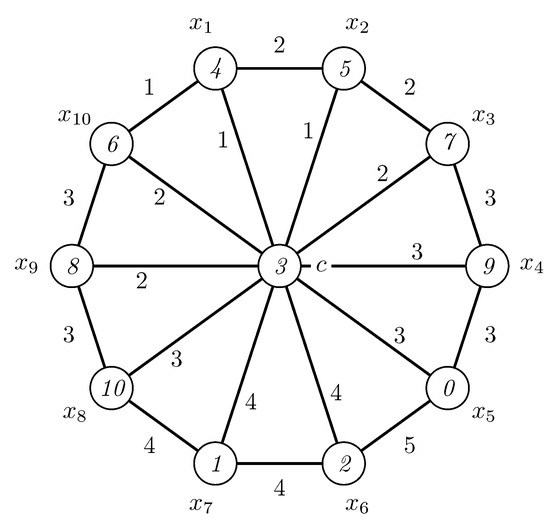
For the wheel $W_{16}$, we have a special modular irregular 6-labeling, given in Figure 4.

Figure 4. A modular irregular 6-labeling of $W_{16}$.

To obtain a required edge labeling with the property that the weights of vertices $x_i\in V\left(W_n\right)$ will not change and the weight of the center vertex will be congruent to two $(modn+1)$, we construct an edge labeling $f_4$ of $W_n$, $n\ge 22$, such that

$$\begin{array}{cc}\hfill f_4\left(x_i{x}_{i+1}\right)=& \left\{\begin{array}{cc}1,\hfill & \mathrm{for}1\le i\le 4,\hfill \\ \psi \left(x_i{x}_{i+1}\right),\hfill & \mathrm{for}5\le i\le \frac{n}{2}-1\mathrm{if}i\mathrm{is}\mathrm{odd},\hfill \\ \psi \left(x_i{x}_{i+1}\right)-2,\hfill & \mathrm{for}6\le i\le \frac{n+2}{3}\mathrm{if}i\mathrm{is}\mathrm{even},\hfill \\ \psi \left(x_i{x}_{i+1}\right)-1,\hfill & \mathrm{for}i=\frac{n+2}{3}+2,\hfill \\ \psi \left(x_i{x}_{i+1}\right),\hfill & \mathrm{for}\frac{n+2}{3}+4\le i\le \frac{n}{2}\mathrm{if}i\mathrm{is}\mathrm{even},\hfill \end{array}\right.\hfill \\ \hfill f_4\left(x_n{x}_1\right)=& \psi \left(x_n{x}_1\right),\hfill & & \\ \hfill f_4\left(x_{n-i}{x}_{n-i+1}\right)=& \psi (x_{n-i}{x}_{n-i+1}),\mathrm{for}1\le i\le \frac{n-2}{2},\hfill \\ \hfill f_4\left(c{x}_i\right)=& \left\{\begin{array}{cc}1,\hfill & \mathrm{for}i=1,\hfill \\ 2,\hfill & \mathrm{for}i=2,n,\hfill \\ 4,\hfill & \mathrm{for}i=3,\hfill \\ 6,\hfill & \mathrm{for}i=4,\hfill \\ \psi \left(c{x}_i\right)+2,\hfill & \mathrm{for}5\le i\le \frac{n+2}{3}+1,\hfill \\ \psi \left(c{x}_i\right)+1,\hfill & \mathrm{for}\frac{n+2}{3}+2\le i\le \frac{n+2}{3}+3,\hfill \\ \psi \left(c{x}_i\right),\hfill & \mathrm{for}\frac{n+2}{3}+4\le i\le \frac{n}{2},\hfill \end{array}\right.\hfill \\ \hfill f_4\left(c{x}_{n-i}\right)=& \psi \left(c{x}_{n-i}\right),\mathrm{for}1\le i\le \frac{n}{2}-1.\hfill \end{array}$$

It is not difficult to verify that increasing the labels of the edges $c{x}_2$, $c{x}_{\frac{n+2}{3}+2}$, $c{x}_{\frac{n+2}{3}+3}$ by one, the labels of the edges $c{x}_3$, $c{x}_i$, $5\le i\le \frac{n+2}{3}+1$, by two and the label of the edge $c{x}_4$ by three and decreasing the labels of the edges $x_2{x}_3$, $x_3{x}_4$, $x_{\frac{n+2}{3}+2}{x}_{\frac{n+2}{3}+3}$ by one and the labels of the edges $x_i{x}_{i+1}$, $4\le i\le \frac{n+2}{3}$ for even i has no impact on the weights of the vertices $x_i\in V\left(W_n\right)$, as they successively assume values from 3 to $n+2$. However, increasing the labels of the edges $c{x}_i$, $2\le i\le \frac{n+2}{3}+3$, results in an increase in the value of the center vertex and we obtain

$$w{t}_{f_4}\left(c\right)=w{t}_{\psi }\left(c\right)+\frac{2n+1}{3}+3=\frac{(n+1)(n+8)}{6}+2.$$

Because $\frac{n+8}{6}$ is an integer, $w{t}_{f_4}\left(c\right)\equiv 2(modn+1)$. Moreover, it is easy to check that $max\left\{f_4\left(c{x}_i\right):2\le i\le \frac{n+2}{3}+3\right\}=f_4(c{x}_{\frac{n+2}{3}+3})=\psi (c{x}_{\frac{n+2}{3}+3})+1=⌈\frac{n+5}{9}⌉+⌈\frac{n+2}{9}⌉+2<⌈\frac{n+2}{3}⌉$. In light of the previous discussion, it follows that for $n\ge 22$, the labeling $f_4$ is the desired modular irregular $⌈\frac{n+2}{3}⌉$-labeling of $W_n$.   ☐

Directly from Theorem 1, we achieve the following result.

Corollary 1.

If $n\equiv 1(mod4)$, then the wheel $W_n$ on $n+1$ vertices has no modular irregular labeling.

In the next lemma, we give the exact value of the modular irregularity strength of wheels $W_n$, for odd $n\ge 3$.

Lemma 4.

Let $W_n$ be a wheel on $n+1$ vertices with odd $n\ge 3$. Then,

$$\begin{array}{c}\hfill \mathrm{ms}\left(W_n\right)=\left\{\begin{array}{cc}3,\hfill & \mathit{if}n=3,\hfill \\ \infty ,\hfill & \mathit{if}n\equiv 1(mod4),\hfill \\ ⌈\frac{n+2}{3}⌉,\hfill & \mathit{otherwise}.\hfill \end{array}\right.\end{array}$$

Proof. 

Similarly to the proof of Lemma 3, the edge labeling $\psi$ described in (3) is not a modular irregular labeling of $W_n$, except for $n=15$, because, applying Lemma 2, we have that the weight of the center vertex is not congruent to two $(modn+1)$. For this reason, we will modify the edge labeling $\psi$ in the following three cases.

Case 1.$n\equiv 3(mod12)$.

The edge labeling of the wheel $W_3$ depicted in Figure 1 is an irregular 3-labeling that meets the properties of the modular irregular labeling. Consequently, $\mathrm{ms}\left(W_3\right)=3$.

It is an easy exercise to check that the edge labeling $\psi$ for $W_{15}$ is also a modular irregular 6-labeling. For $n\ge 27$, we modify the edge labeling $\psi$ in the following way:

$$\begin{array}{cc}\hfill f_3\left(x_i{x}_{i+1}\right)=& \left\{\begin{array}{cc}\psi \left(x_i{x}_{i+1}\right)+1,\hfill & \mathrm{for}3\le i\le \frac{n-3}{6}-1\mathrm{if}i\mathrm{is}\mathrm{odd},\hfill \\ \psi \left(x_i{x}_{i+1}\right),\hfill & \mathrm{otherwise},\hfill \end{array}\right.\hfill \\ \hfill f_3\left(x_n{x}_1\right)=& \psi \left(x_n{x}_1\right),\hfill & & \\ \hfill f_3\left(x_{n-i}{x}_{n-i+1}\right)=& \psi \left(x_{n-i}{x}_{n-i+1}\right),\mathrm{for}1\le i\le \frac{n-3}{2},\hfill \\ \hfill f_3\left(c{x}_i\right)=& \left\{\begin{array}{cc}1,\hfill & \mathrm{for}i=1,\hfill \\ 2,\hfill & \mathrm{for}i=n,\hfill \\ \psi \left(c{x}_i\right)-1,\hfill & \mathrm{for}3\le i\le \frac{n-3}{6},\hfill \\ \psi \left(c{x}_i\right),\hfill & \mathrm{otherwise},\hfill \end{array}\right.\hfill \\ \hfill f_3\left(c{x}_{n-i}\right)=& \psi \left(c{x}_{n-i}\right),\mathrm{for}1\le i\le \frac{n-1}{2}-1.\hfill \end{array}$$

One can see that increasing the labels of the edges $x_i{x}_{i+1}$ for $3\le i\le \frac{n-3}{6}-1$ if i is odd, and decreasing the labels of the edges $c{x}_i$ for $3\le i\le \frac{n-3}{6}$ does not change the weights of the vertices $x_i\in V\left(W_n\right)$, but it reduces the weight of the center by $\frac{n-3}{6}-2$ and we obtain

$$w{t}_{f_3}\left(c\right)=w{t}_{\psi }\left(c\right)-\left(\frac{n-3}{6}-2\right)=\frac{(n+1)(n+3)}{6}+2.$$

Indeed, $\frac{n+3}{6}$ is an integer and $w{t}_{f_3}\left(c\right)\equiv 2(modn+1)$.

Case 2.$n\equiv 7(mod12)$. For $n=7$, we have a suitable modular irregular 3-labeling, as illustrated in Figure 5.

Figure 5. A modular irregular 3-labeling of $W_7$.

For $n\ge 19$, we define the following edge labeling:

$$\begin{array}{cc}\hfill f_7\left(x_i{x}_{i+1}\right)=& \left\{\begin{array}{cc}\psi \left(x_i{x}_{i+1}\right)-1,\hfill & \mathrm{for}2\le i\le \frac{n+5}{6}+2\mathrm{if}i\mathrm{is}\mathrm{even},\hfill \\ \psi \left(x_i{x}_{i+1}\right),\hfill & \mathrm{otherwise},\hfill \end{array}\right.\hfill \\ \hfill f_7\left(x_n{x}_1\right)=& \psi \left(x_n{x}_1\right),\hfill & & \\ \hfill f_7\left(x_{n-i}{x}_{n-i+1}\right)=& \psi (x_{n-i}{x}_{n-i+1}),\mathrm{for}1\le i\le \frac{n-3}{2},\hfill \\ \hfill f_7\left(c{x}_i\right)=& \left\{\begin{array}{cc}1,\hfill & \mathrm{for}i=1,\hfill \\ 2,\hfill & \mathrm{for}i=n,\hfill \\ \psi \left(c{x}_i\right)+1,\hfill & \mathrm{for}2\le i\le \frac{n+5}{6}+3,\hfill \\ \psi \left(c{x}_i\right),\hfill & \mathrm{otherwise},\hfill \end{array}\right.\hfill \\ \hfill f_7\left(c{x}_{n-i}\right)=& \psi (c{x}_{n-i}),\mathrm{for}1\le i\le \frac{n-1}{2}-1.\hfill \end{array}$$

It is a routine procedure to verify that the edge labeling $f_7$ does not increase the largest values of the edges in $W_n$, has no effect on the weights of vertices $x_i\in V\left(W_n\right)$, but increases the weight of the center vertex by $\frac{n+5}{6}+2$. Thus, we obtain

$$w{t}_{f_7}\left(c\right)=w{t}_{\psi }\left(c\right)+(\frac{n+5}{6}+2)=\frac{(n+1)(n+5)}{6}+2.$$

Clearly, $\frac{n+5}{6}$ is an integer and then $w{t}_{f_7}\left(c\right)\equiv 2(modn+1)$.

Case 3.$n\equiv 11(mod12)$.

For $n\ge 11$, we construct an edge labeling $f_{11}$ as follows:

$$\begin{array}{cc}\hfill f_{11}\left(x_i{x}_{i+1}\right)=& \left\{\begin{array}{cc}\psi \left(x_i{x}_{i+1}\right)-1,\hfill & \mathrm{for}2\le i\le \frac{n-1}{2}-1\mathrm{if}i\mathrm{is}\mathrm{even},\hfill \\ \psi \left(x_i{x}_{i+1}\right),\hfill & \mathrm{otherwise},\hfill \end{array}\right.\hfill \\ \hfill f_{11}\left(x_n{x}_1\right)=& \psi \left(x_n{x}_1\right),\hfill & & \\ \hfill f_{11}\left(x_{n-i}{x}_{n-i+1}\right)=& \left\{\begin{array}{cc}\psi \left(x_{n-i}{x}_{n-i+1}\right)-1,\hfill & \mathrm{for}i=1,3,\hfill \\ \psi \left(x_{n-i}{x}_{n-i+1}\right),\hfill & \mathrm{otherwise},\hfill \end{array}\right.\hfill \\ \hfill f_{11}\left(c{x}_i\right)=& \left\{\begin{array}{cc}1,\hfill & \mathrm{for}i=1,\hfill \\ 3,\hfill & \mathrm{for}i=n,\hfill \\ \psi \left(c{x}_i\right)+1,\hfill & \mathrm{for}2\le i\le \frac{n-1}{2},\hfill \\ \psi \left(c{x}_i\right),\hfill & \mathrm{for}i=\frac{n+1}{2},\hfill \end{array}\right.\hfill \\ \hfill f_{11}\left(c{x}_{n-i}\right)=& \left\{\begin{array}{cc}\psi \left(c{x}_{n-i}\right)+1,\hfill & \mathrm{for}1\le i\le 3,\hfill \\ \psi \left(c{x}_{n-i}\right),\hfill & \mathrm{otherwise}.\hfill \end{array}\right.\hfill \end{array}$$

Again, it is a matter of routine checking to see that the labeling $f_{11}$ has no impact on the the weights of vertices $x_i\in V\left(W_n\right)$. However, by increasing the labels of the edges $c{x}_i$, $2\le i\le \frac{n-1}{2}$, and $c{x}_{n-i}$, $1\le i\le 3$, the weight of the center increases by $\frac{n-1}{2}+3$ and we have

$$w{t}_{f_{11}}\left(c\right)=w{t}_{\psi }\left(c\right)+\left(\frac{n-1}{2}+3\right)=\frac{(n+1)(n+7)}{6}+2.$$

Since, under the edge labeling $f_{11}$, $w{t}_{f_{11}}\left(c\right)\equiv 2(modn+1)$ and the edge labels of wheels $W_n$, $n\ge 11$, are, at most, $⌈\frac{n+2}{3}⌉$, it follows that $f_{11}$ is a required modular irregular $⌈\frac{n+2}{3}⌉$-labeling of $W_n$ and we are finished.   ☐

4. Conclusions

In the given paper, we investigated the existence of an irregular assignment of wheels and we determined the exact value of the irregularity strength of wheels $W_n$ of order $n+1$, $n\ge 3$, as follows:

$$\begin{array}{c}\hfill \mathrm{s}\left(W_n\right)=\left\{\begin{array}{cc}3,\hfill & \mathrm{if}n=3\mathrm{and}n=4,\hfill \\ ⌈\frac{n+2}{3}⌉,\hfill & \mathrm{if}n\ge 5.\hfill \end{array}\right.\end{array}$$

The constructed irregular assignments of wheels was modified in six cases according to the residue of n modulo 6 for obtaining the corresponding modular irregular assignments. These modular irregular assignments prove the following exact value of the modular irregularity strength of $W_n$.

Theorem 3.

Let $W_n$ be a wheel on $n+1$ vertices with $n\ge 3$. Then,

$$\begin{array}{c}\hfill \mathrm{ms}\left(W_n\right)=\left\{\begin{array}{cc}3,\hfill & \mathit{if}n=3\mathit{and}n=4,\hfill \\ 5,\hfill & \mathit{if}n=10,\hfill \\ \infty ,\hfill & \mathit{if}n\equiv 1(mod4),\hfill \\ ⌈\frac{n+2}{3}⌉,\hfill & \mathit{otherwise}.\hfill \end{array}\right.\end{array}$$

The results of the paper prove that the irregularity strength and the modular irregularity strength for wheels are the same, except for two cases, where the wheel $W_{10}$ is a special case and wheels $W_n$ for $n\equiv 1(mod4)$ are excluded according to Theorem 1. The same is true for the fan graphs; see [13]. For further investigation, we propose the following open problem.

Problem 1.

Is there another family of graphs, besides wheels and fan graphs, for which the irregularity strength and the modular irregularity strength are the same?