1. Introduction
The Olympic Games are one of the most significant sporting events around the world, and for two weeks, athletes from all over the world compete in different sports disciplines to achieve the long-sought-for gold medal. As reflected in the Olympic charter, “the Olympic Games are competitions between athletes in individual or team sports, not between countries.” However, as [
1] pointed out, despite this idealized statement and that the International Olympic Committee refuses to recognize rankings by countries and medals, it is a fact that the medal table plays a dominant role in media coverage and public interest.
Hosting the Olympic Games for a city means putting in the effort and substantial economic investment for a country to such an extent that it may result in many years of recovery for both cities and countries. Sometimes, the general population understands such recovery and effort when the sporting success overcomes national expectations concerning its athletes’ success. That was the case in Spain; hosting the XXV Olympiad Games in Barcelona meant a change in sports perception and investment. After the Seoul games in 1988, the Olympic Sports Association, ADO, was established. The ADO is a non-profit institution in which its purpose is to support, develop, and promote national athletes with high performance at the Olympic level. The objective was to provide elite Spanish athletes with the means and resources necessary to achieve a good result at the 1992 Barcelona Olympic Games. The program supported and still keeps supporting athletes with good results in international championships and those who can participate in the Olympic Games, providing funds such as athletic scholarships. (To obtain information about ADO program, see [
2]).
Nowadays, sports is part of our daily lives. It is present in many people’s routines, such as athletes, or as spectators. Sport activities directly or indirectly impact several social spheres such as education, health, leisure, and the production of goods and services.
Sport, culture, and society are concepts that are strongly intertwined today. Thus, sports is a fundamental element in training and improving our society’s quality of life. Likewise, as mass phenomena, major sporting events are part of the culture, and it is not possible to understand modern society without sports as an essential component. In this manner, sports is the engine of new technological advances, fosters values that constitute an attitude towards life, enhances self-esteem, and is the main protagonist of the new global communication media activity.
For all of these factors, many countries invest in their athletes to link their athletes’ success to the well-being of the society comprising them. Consequently, it is about facing an investment to obtain a return in the medium and long term. Hence, knowing the investment’s efficiency can help finance different sports modalities to a greater or lesser extent. The efficiency from the economic point of view has been approached from different perspectives and with varying analysis tools, including stochastic frontiers.
Much of the applications of stochastic production frontiers for assessing firm inefficiencies exist in agricultural and industrial settings, among others [
3,
4,
5].
In the field of sport, stochastic frontier models can be found in [
6,
7,
8,
9,
10,
11,
12,
13,
14,
15], and most of these works focus on applying stochastic frontier analysis to specific sport leagues or sports. Reference [
1] analyzed the Olympic games by using population and gross domestic product, and Reference [
16] analyzed the countries’ efficiencies in the Rio 2016 Summer Olympics with stochastic frontier models with the number of participants as the output. Furthermore, Reference [
17] measured the efficiency of the Spanish (Summer) Olympic sports federations and Reference [
18] analysed the performance of high-level Spanish athletes in the (Summer) Olympic Games according to gender.
The literature concerning the calculation of technical efficiency in Olympic sports is scarce. Reference [
1] deserves to be considered and is the closest to the work presented here and is based on [
19] regarding the variables considered, although this last one does not make use of stochastic frontier. Reference [
1] measures the efficiency of the participating countries (with and without distinguishing by gender) by using an extensive database that includes tens of years, using a translog production function instead of the Cobb–Douglas production function used here. Although the dependent variable is the same as the one considered in this work, their philosophy is different since they manage aspects such as income level, being or having been the host country of some Olympic games, training plans, etc. The work presented here focuses only on data concerning Spanish athletes and the budget’s impact on efficiency (from different standpoints), distinguishing and without distinguishing by gender. This fact, at least for Spain, is considered fundamental due to the Barcelona Olympics (1992) for which public authorities developed important financial support programs for numerous sports disciplines. To Spain, those games constituted a turning point concerning the success that Spaniard’s athletes reached then, which has continued to the extent that these aids have been maintained over time.
In this work, to analyze efficiency using stochastic frontier analysis, Olympic sports activity is considered a firm for which its output is the number of medals and Olympic diplomas achieved in several Olympic games by Spanish athletes. The idea of awarding Olympic diplomas is intended to recognize the effort of those athletes who obtained lower results than the first three (awarded with medals). In 1949, the IOC decided to award Olympic diplomas to the top six and chose to award Olympic diplomas to the top eight in 1981. Thus, the first three classifieds receive a medal and diploma, and the next six only received diplomas. However, this work will distinguish between medal winners (the top three) and Olympic diploma recipients (the next six ranked). The inputs required to achieve success can be from the budget for each sports discipline, the number of licenses, the sports scholarships and the number of scholarship-holding athletes who can carry out their training under certain special conditions in high-performance centres. Furthermore, we will determine how inputs linked to economic factors or sport factors are involved in the results. Once the inputs are chosen, we will evaluate each discipline’s efficiency throughout stochastic frontier analysis. To our knowledge, this approach to study the efficiency in Olympic Games has not been carried out before when disciplines and athletes are considered simultaneously.
The paper is organized in four sections, and this introduction constitutes the first section.
Section 2 introduces the main model used to provide the parameters used to obtain the technical efficiency of the different sport disciplines for the Spanish athletes in the Olympic games. The empirical application is shown in
Section 3. Finally, the main conclusions drawn from the paper are presented in
Section 4.
2. Theoretical Framework
The stochastic frontier production function was independently proposed by [
20,
21] and is generally used in the economic literature for estimating of technical efficiency of firms. Although the literature existent in this matter is extensive, we recommend [
22] in order to attain a broad vision about stochastic frontier analysis.
Taken in its entirety, the estimating methods of technical and cost efficiency can be considered either parametric or non-parametric. The first involves the estimation of a stochastic production frontier (SPF) (alternatively, a stochastic cost frontier (SCF)) by assuming an explicit functional form and distribution on the data ([
3,
20,
21,
23,
24,
25,
26], among others), where the output of a firm depends on a set of inputs in addition to inefficiency and random error. The second approach is a linear programming technique of data envelopment analysis (DEA); this is a non-parametric approach that does not impose any assumptions regarding functional form and that does not take into account random error (see for instance, [
27]). This second technique will not be considered in this work; therefore, no mention will be made of it in the remainder of this paper.
Our primary interest is on the stochastic frontier model in a cross-sectional framework between these two modeling alternatives. The model, in this scenario, can be written as , where the sign of the last term depends on whether the frontier describes costs (positive) or production (negative). For example, if we suppose that takes the form of a log-linear Cobb–Douglas, then the stochastic production frontier (SPF) model can be written as follows: , where is the natural logarithm of the production of the i-th firm; is a 1 vector of (natural log transformations) input quantities of the i-th firm; is a vector of unknown parameters; and the disturbance term (which is asymmetric) is considered to have two components, one with a strictly non-negative distribution (which is a non-negative component, usually denominated as the inefficiency term) and another with a symmetric distribution (which is referred to as the idiosyncratic error). This random variable attempts to measure the deviations produced in the final product and is not entirely the producer’s responsibility. For example, in the sports scenario, the weather and economic adversities can reduce the budget, and other circumstances, such as the current SARS-CoV-2 pandemic, can affect athletes’ training or pure chance can reduce performance and production. Note that measures technical inefficiency because it measures the shortfall of output from its stochastic frontier that provides the maximal possible value. The independence of and u makes it easy to obtain the density of , which is then used to calculate the model parameters’ maximum likelihood estimation. Additionally, it is possible to obtain the conditional density of and . These help as a basis for obtaining estimates for firm-specific inefficiency.
In this respect, distributional assumptions are required for
and
. With regard to
and in general, these random variables are expected to be independently and identically distributed (iid) normal distributions,
. Moreover, in terms of
, several assumptions may be made; for instance, [
21] assigned the exponential distribution to
, and reference [
3] assumed a half-normal distribution, while reference [
20] considered both distributions. However, since both the half-normal and the exponential distributions are single-parameter specifications with modes at zero, some scepticism has been expressed concerning their generality. Thus, reference [
28] suggested the truncated normal and gamma distribution for
. References [
23,
24] proposed gamma distribution, and reference [
26] suggested the two-parameter gamma density as a more general option.
Recently, other methods of modeling SPF and SCF are based on the dependence of errors terms such as what [
5,
29] performed with copulas and [
30,
31] with closed-form solutions by using bivariate distributions.
We assume here the classical stochastic frontier model with normal and half-normal distributions, which is described by the following stochastic representation:
The error term,
, is commonly assumed to be independently and identically distributed as
and pretends to capture the random variation at the output due to factors beyond the control of firms, such as weather, illness, etc. That is,
;
are half-normal distributions with parameter
; and
and
are distributed independently of each other and of the regressors. A few works dealing with breaking the independence hypothesis between the two random variables have appeared in the economic literature (see for instance [
29,
30,
31]). Thus, the probability density functions of
and
are described as follows:
where
,
,
and
.
In this case (see for example [
22]), we have, by using (
1) and (
2), the marginal distribution of
and the conditional distribution of
u given
are given by the following:
where
,
,
,
, and
and
are the standard normal cumulative distribution and density functions, respectively.
The marginal
possesses mean and variance given by the following.
However, to date, the absence of a sufficiently flexible multivariate distribution has made it impossible to obtain full information estimation of multivariate data models.
Specification of the Production Function and Variables
We will use the classical Cobb–Douglas ([
22,
32], among others) functional form of a production function, which has been widely used in economic literature to represent the relationship of output to inputs. Thus, we estimate a log-linear Cobb–Douglas production function for the
n pooled non-zero data in all cases without imposing linear homogeneity to the input factors considered. The estimated model is written as follows:
where the variable
is the unknown scalar intercept parameter,
and
are the unknown slope parameters (the output elasticities of the inputs which are considered constants determined by available technology),
is the natural log-transformed output, and
and
are the natural log-transformed inputs.
In our scenario, the output
is given by the following.
On the other hand, inputs associated with economic factors are considered: The total budget (measured in euros) is the sum of funds assigned by an institution linked to the national government, the Higher Sports Council, and regional federations. Moreover, the scholarships’ budget is associated with the ADO program (also measured in euros) and defined by prebeado. On the other hand, among the variables related to athletes, we consider high-level athletes (dan), athletes in high-performance centers (car), and athletes in the ADO program (dado). The number of athletes measures these last three variables. Therefore, we have the following:
is a vector of parameters to be estimated.
3. Empirical Results
In this section, we use the theoretical developments shown in
Section 2 to estimate the technical efficiency term and the idiosyncratic error of each sport discipline.
3.1. Data
The data for this paper were obtained from direct correspondence with the Spanish Olympic Committee, COE. They contained information from 2005 to 2016, including the results obtained in the Olympic years for all the Olympic disciplines in which Spanish athletes have participated. Unfortunately, the COVID-19 pandemic frustrated the possibility of having results for the Olympic games 2020. The data collected included the federative licenses by gender, national population of the country by gender, and budged assigned from different sources of funding. We highlight that financial support has been decreasing over the years because companies have reduced their economic aid to the Olympic project. Furthermore, data included information about the number per year and gender of high-level athletes, athletes using high-performance centers, and the number of athletes receiving the different modalities of the ADO program’s scholarships. Finally, data about the total number of athletes winning medals, diplomas, and those participating in finals are included. Once all the variables were analyzed for Olympic and non-Olympic years and in all the disciplines, only the budget and the sports scholarships were significant for explaining the output in terms of medals and diplomas. Since the length of the data in the two scenarios considered (all disciplines and Olympic years) do not coincide for all women and men, we show in
Table 1 a summary of them.
The descriptive statistics of the data are shown in
Table 2 and
Table 3 in which is observed a slight increase in the average of budget and scholarships for the Olympic years.
It should be observed that as some disciplines are not represented for a given year for women and the same applies to other disciplines for a given year for men, the means are different for all women and men.
3.2. Results Based in Ordinary Least Squares and SPF
The maximum likelihood estimates for the production frontier model assumed and for a sample of
n data can be obtained by maximizing the log-likelihood function derived from (
3) and restricted by (
5). After performing some algebra, it is given by the following.
Table 4 and
Table 5 show two estimation methods applied to the data: ordinary least squares (OLS) and maximum likelihood obtained by maximizing directly the expression given in (
6).
The model was estimated by using maximum likelihood in two stages. Firstly, we have used the simplex method, a search procedure that requires only function evaluations, not derivatives. To apply simplex, OLS initial values are used for parameters and then values for and are determined. The most important use of simplex is to refine initial estimates before applying one of the derivative-based methods, which are more sensitive to the choice of initial estimates. For all models, we used five iterations in this stage. In the second stage, the BFGS (Broyden, Fletcher, Goldfarb, and Shanno) algorithm was applied to obtain the final estimates of the parameters and the asymptotic variance-covariance matrix estimated by the final iteration of the approximation of the inverse Hessian. Finally, we computed regression standard errors and the covariance matrix, allowing for heteroscedasticity. These computations were performed using RATS software.
In
Table 3, the data for the different sports have been estimated by considering men and women together. The results show that for the stochastic frontier production model, SFP, all parameters are significant unlike the OLS model, which only detects the constant and the coefficient beta of the input associated with athletes and the elasticity production-sports factor. Furthermore, separately considered by gender, in the SFP, the constant, the elasticity production-economic, the elasticity production-sports,
, and
are significant for women; however, for men, none of them were significant in the models except for
and
in SFP. In
Table 5, in which only the Olympic years are included, for the results for men and men and women taken together, all the variables are significant in the SFP model; for women, the production-economic factor is not significant in the SFP nor the OLS model. In the OLS, only the constant and the budget were significant for men and women together; for the rest of the variables and models, none of the variables were significant.
In summary, the results in terms of the sign are the same for both models, OLS and SFP. Let us remember that the most interesting contribution of this last model compared to the first one is the possibility of calculating the efficiency, which is impossible from the OLS model. The signs of the SFP coefficients are as expected. The elasticity for
and
implies that the change in these contributors produce changes in the production-sport in the estimated value for
and
, respectively. These changes are greater for women than for men in all cases. Then, the model tells us that small input modifications will initially generate a greater output value in the female gender than in the male. The non-significance for the case of the estimated values of the parameters for men, in the case of considering the different sports disciplines (
Table 5), leads us to be especially cautious in the efficiency values that are obtained from them and which will be considered in the next subsection.
3.3. Efficiency
As stated earlier, technical efficiency (TE) of the
ith sport discipline is calculated from
,
, where the expectation is taken with respect to (
4) and results in the following.
Thus, it is calculated using the conditional expectation
, conditioned on the composed error (
), and evaluated using the estimated parameters presented in
Table 4 and
Table 5.
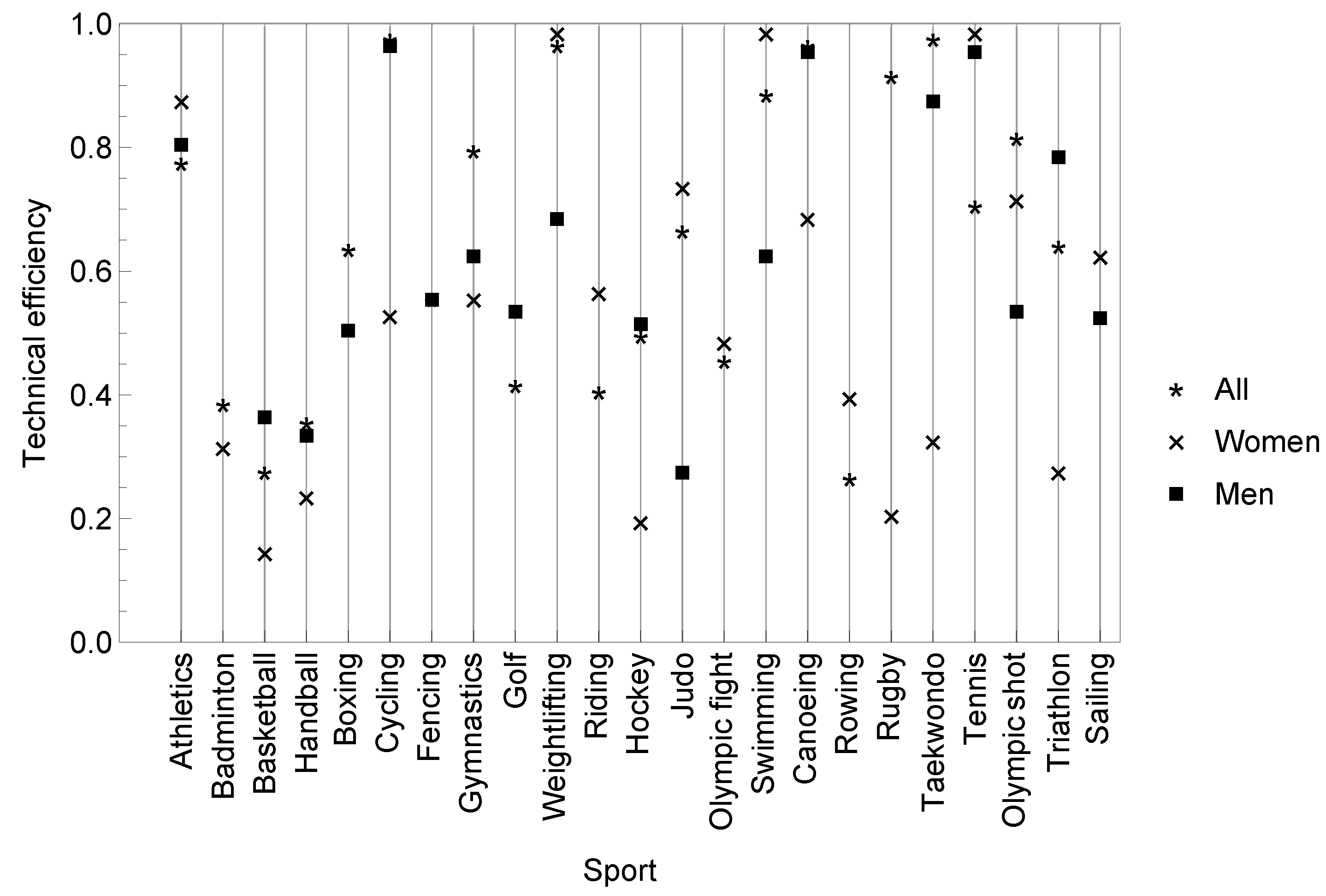
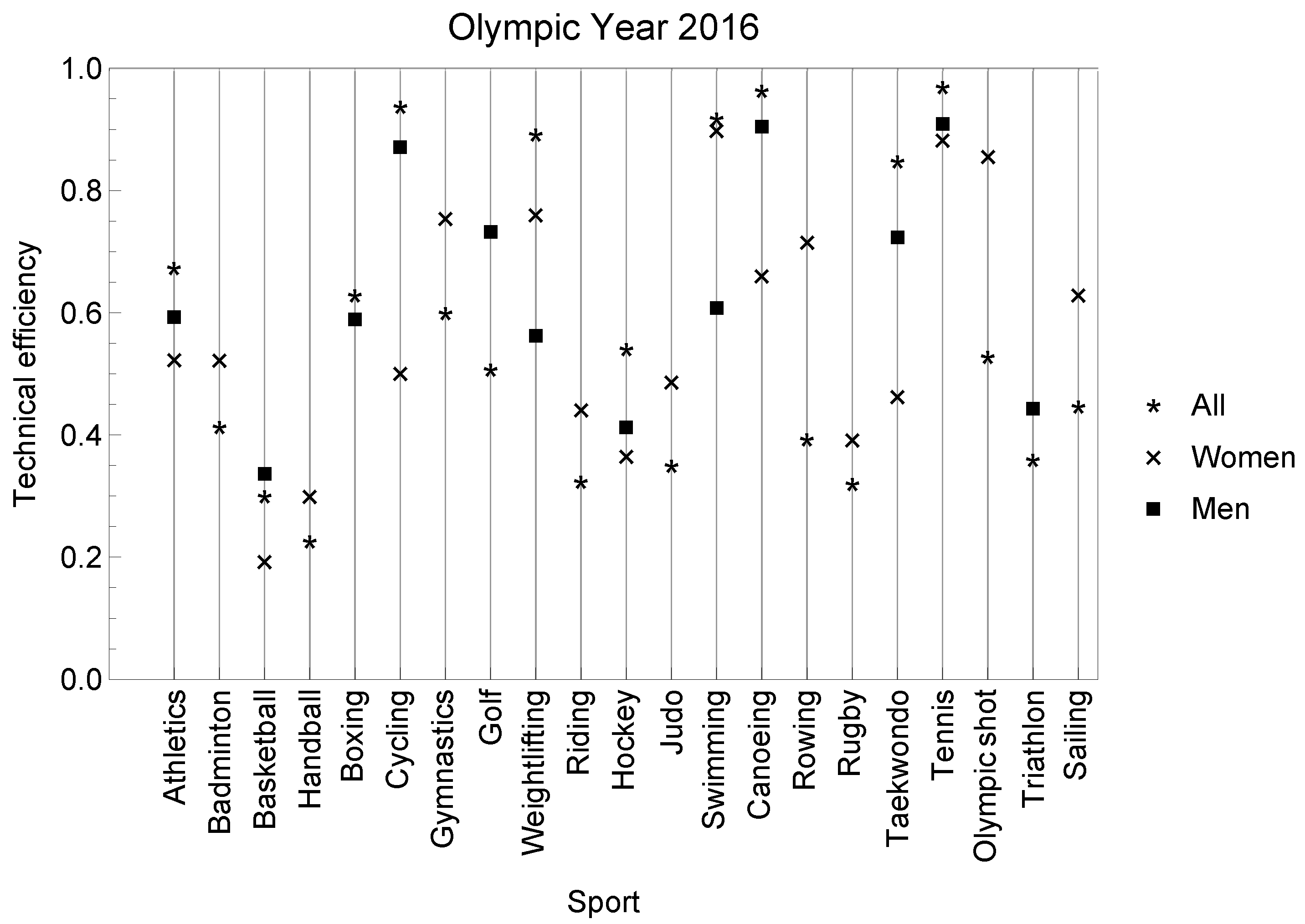
Regarding technical efficiencies, based on
Table 4 and
Table 5, they have been calculated for all sports over the period 2005–2016 and all sports in the Olympic years. The results are shown in
Table 6 (see also
Figure 1) and
Table 7 (see also
Figure 2,
Figure 3 and
Figure 4), respectively. It can be observed that when men and women are considered together, and all disciplines are analyzed; the most efficient sports are cycling, weightlifting, canoeing, Taekwondo, and tennis over the entire period. By gender, cycling, canoeing, and Taekwondo are more efficient in men, however, women show high efficiency in weightlifting. In tennis, both men and women show high technical efficiency concerning the inputs, although a slight difference in favour of women is observed. When considering the Olympic years, more sports are incorporated but not in all the Olympics Games, for example, athletics in 2008 for both men and women and cycling in 2008 and 2016 for men. Judo also appeared in 2008 and swimming in 2012 and 2016, and all three were for women. On the other hand, only canoeing shows high technical efficiency in all the Olympic years considered including 2008, 2012, and 2016 and only for men. Finally, tennis in 2016 appears when men and women are considered together and is closer to maximum efficiency level in men’s case. The fact that tennis is close to maximum efficiency coincides with what was stated by [
17], and it could be related to the greater participation of tennis players in international competitions and, therefore, related to the more extensive options to increase their performance. For a complete analysis of the performance by gender among high-level Spanish athletes in the Olympic Games, refer to [
18]. furthermore, it is remarkable that sports such as basketball, handball, hockey, and rugby show low efficiency over the peirod of 2005–2016 and also for the Olympic years. None of the team sports were close to the efficiency border. A possible explanation could be related to the more professional character of these sports, mainly basketball and handball. The inputs such as scholarships or the ADO program for these sports may have less weight. However, Spain has had a good performance in terms of results for these sports. Moreover, Spain traditionally has consistently performed better in individual sports than in team sports. Until 2016, of all the medals obtained by the Spanish Olympic team, only 13.33% corresponded to team sports (with a participation of 33%) [
33].
In all the cases, the signs of the coefficients of the stochastic frontier are as expected, and they are, in general, significant. The coefficient of the scholarships also indicates that the value of output has trended upwards more than it did for budget input, except for the case in which only the Olympic years are considered
(see
Table 4 and
Table 5). As it is well known, returns to scale are concerned with changes in the output due to a proportional change in the inputs.
4. Conclusions and Future Research
In this work, a stochastic frontier analysis has been carried out to study the technical efficiency of high-level sport in Spain by assuming a Cobb–Douglas function. We have taken as inputs the investment, via national and regional budgets, and the scholarships assigned to athletes in the different modalities through the ADO program, established before the celebration of the Olympic games held in Barcelona and which has been maintained subsequently for the other games. It has also been used as inputs in the number of athletes to whom the budgets and scholarships are intended for and is differentiated between high-level athletes, athletes who receive ADO scholarships, and athletes in high-performance centers. The results in terms of medals and diplomas obtained by the athletes show that, when the Cobb–Douglas function is used in the SPF, the parameters can be interpreted as both inputs’ elasticities. The elasticity coefficients are all positive, so the exogenous variables, economic allocation via budgets and scholarships, and sports factors associated with top athletes positively affect the output. Moreover, it is also appreciated that the factors linked to athletes positively impact sport results, medals, and diplomas and are larger than the economic factors.
When all activities are considered over the period 2005–2016, sporting factors have a more significant impact on output than when only the Olympic years are considered. They have a greater weight when athletes (men and women) are considered together or when women were considered separately. They have less impact on the output if the PRO-athletes are only men. In the Olympic years, the contribution to output between economic and sporting factors is slightly superior than the elasticity production-sports when athletes’ genders are separately considered. Concerning the stochastic frontier model, the parameters’ estimates had a relatively good fit. The likelihood ratio test for the and coefficients shows that it is significantly different from zero, thus increasing the credibility of the SFP model’s estimation. All coefficients are significant, with the expected signs, and the efficiency parameter remains significantly different from zero.
On the other hand, for all sports modalities in non-Olympic years, the sum of the parameters considering the set of athletes, men, and women is slightly higher than unity. In such a case, it would imply increasing returns to scale, i.e., the performance in the production of medals and diplomas will be more than proportional to the effort of capital endowments via budget. However, when the Olympic years are taken or activities separated by men and women are considered, the sum of the parameters is always less than unity. Such a case implies diminishing returns to scale, which means that for double budgetary efforts and athletes’ level, the returns in sports results would increase in a lower proportion than the inputs used.
In both cases, the individual practice sports show higher efficiency for all sports modalities from 2005 to 2016 and for the Olympic years 2008–2012 and 2016. Thus, cycling, canoeing, and tennis are the most efficient sports. However, athletics was closer to maximum efficiency only in the 2008 Olympic year; instead, the rest of the Olympic years is far from the border. What is noteworthy to highlight is that the national budget and scholarships were reduced relative to this sport by and , respectively, between 2008 and 2016.
Since 1992, Spanish sport has made significant progress, and this is mainly due to the support of business corporations financing athletes, ensuring their preparation in the different Olympic cycles, and ensuring that sports preparation had the highest possible efficiency during the Olympic Games. However, this financial support has decreased over the years mainly because companies have reduced their economic aid to the Olympic project. Consequently, Spanish sport must find resources in the future so that athletes can continue training and competing at the highest level and so that they can maintain the sporting level that they have achieved over the last decades.
Studies on stochastic frontiers in Olympic performance are not intended to explain by themselves the causes of sporting success in a country. Still, they are a tool available for lawmakers and sport managers in organizing national sports systems and optimizing resources for high-level sport. Reference [
34] stated that the analysis of sports success as a practical problem is so complex that it hardly can be explained solely with a mathematical model.
To conclude, considering the lack of efficiency analysis not at the country level but at the athlete level, it would be interesting to carry out future research focused on taking data for athletes worldwide by countries and Olympic specialties in order to compare results with those found here. Due to the fact that the Olympic movement is a global phenomenon involving thousands of athletes of all nationalities, more studies at the national level are needed to foster cross-country analysis and, thus, a better understanding of the factors that result in sporting success.