Generation of Two Correlated Stationary Gaussian Processes
Abstract
:1. Introduction
2. Method of Linear Filters
2.1. Two Correlated Gaussian White Noises
2.2. Two Correlated Gaussian Processes
3. Method of Series Expansion with Random Amplitudes
3.1. Simulation of a Single Stationary Gaussian Process
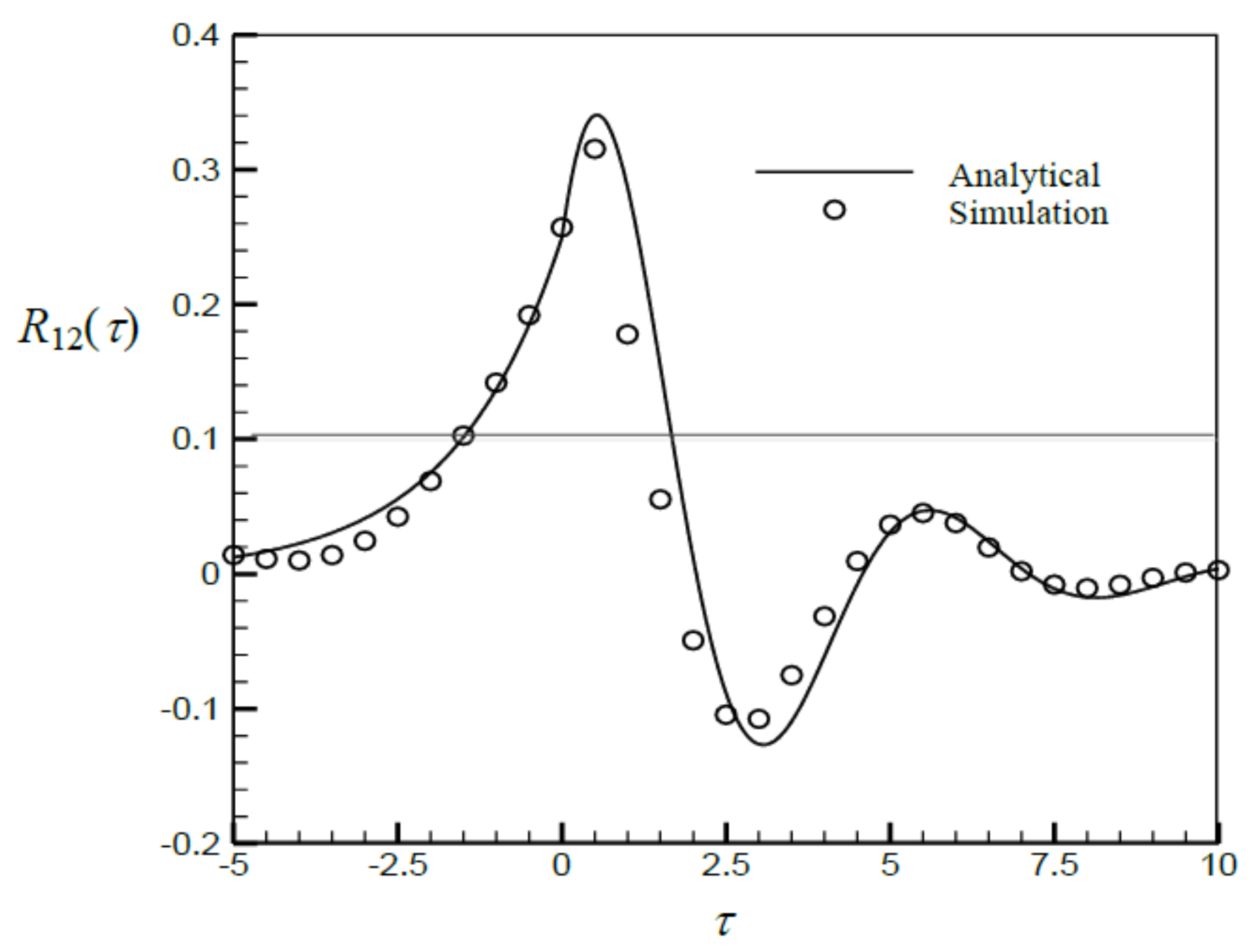
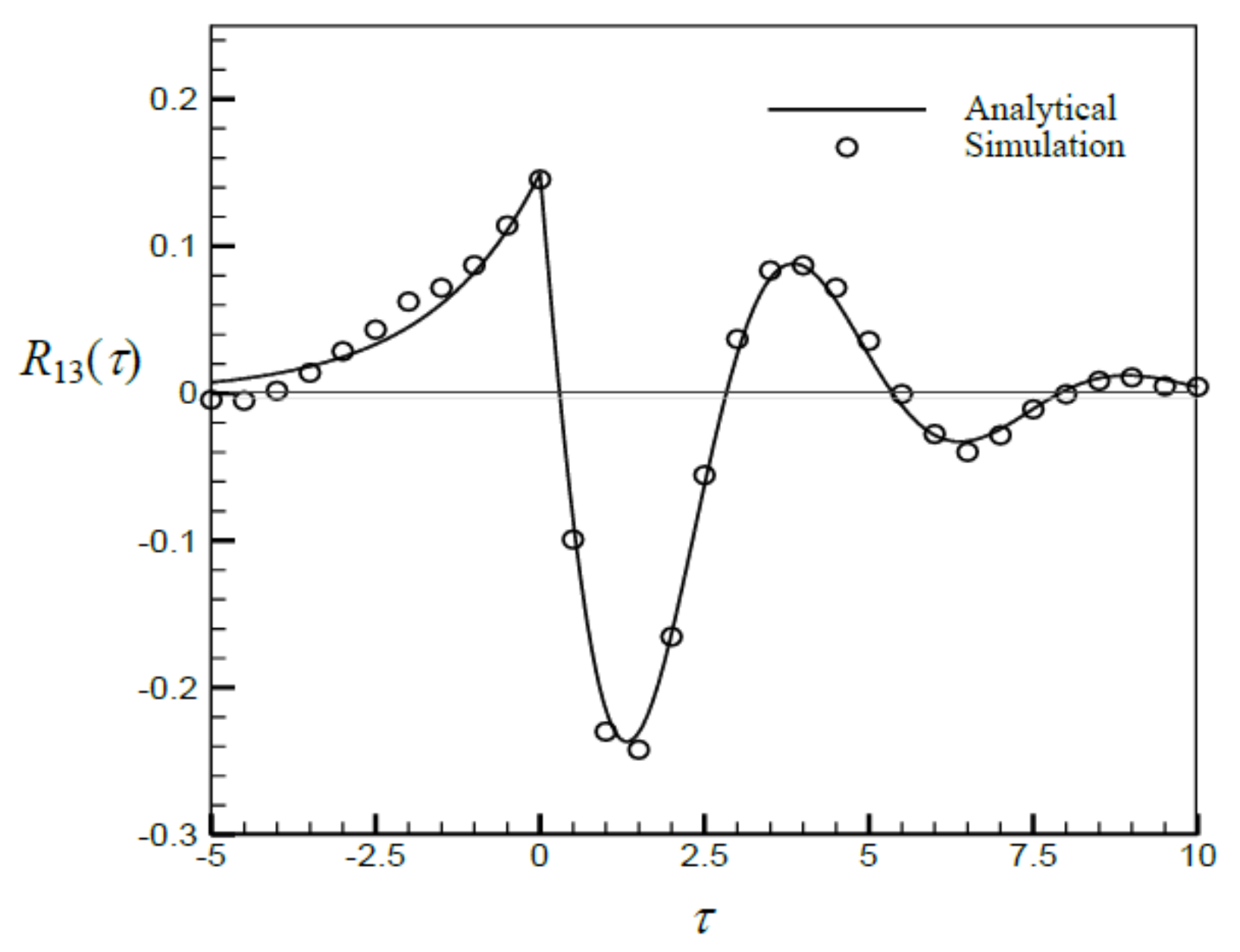
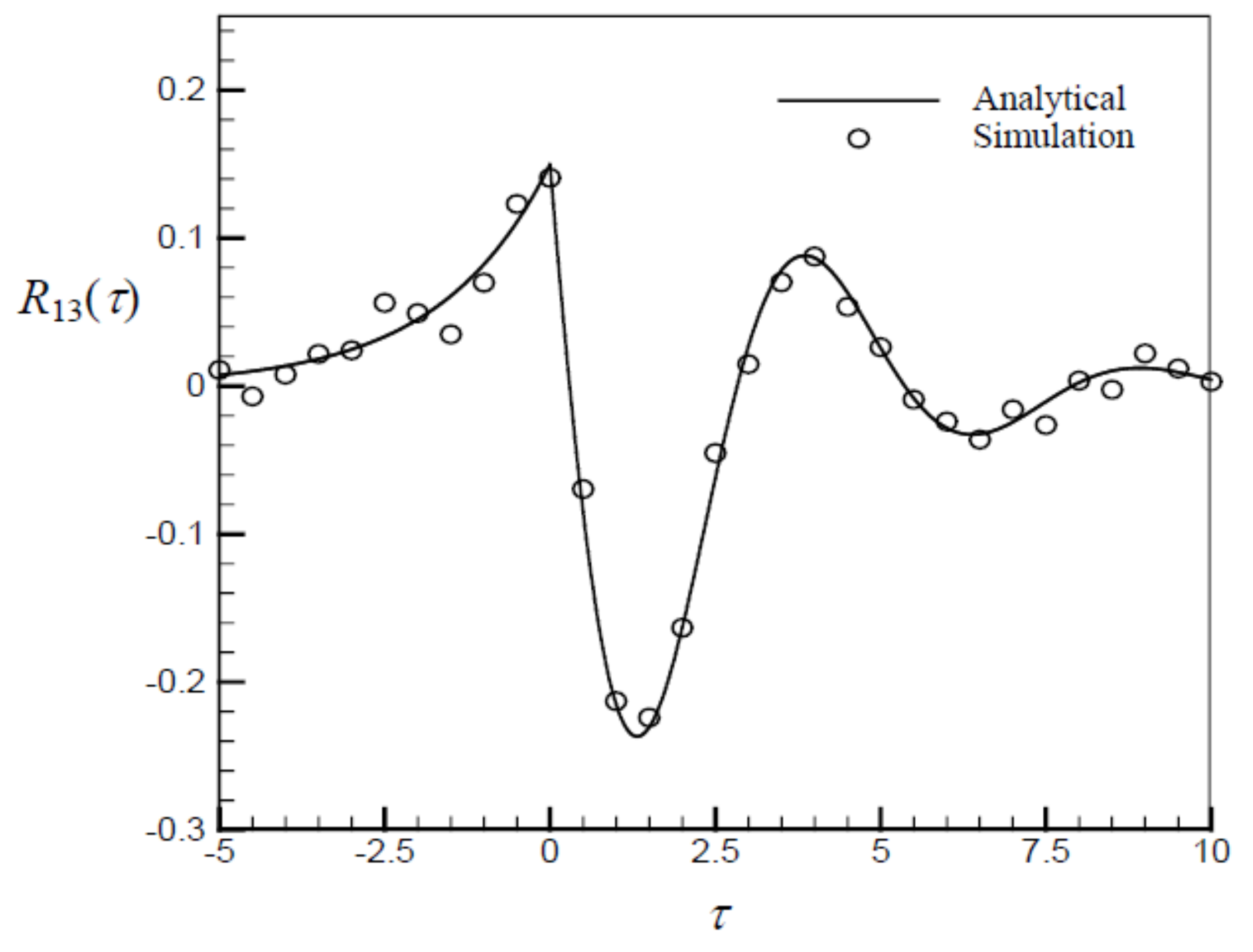
3.2. Generation of Two Correlated Stationary Gaussian Processes
4. Method of Series Expansion with Random Phases
4.1. Simulation of a Single Stationary Gaussian Process
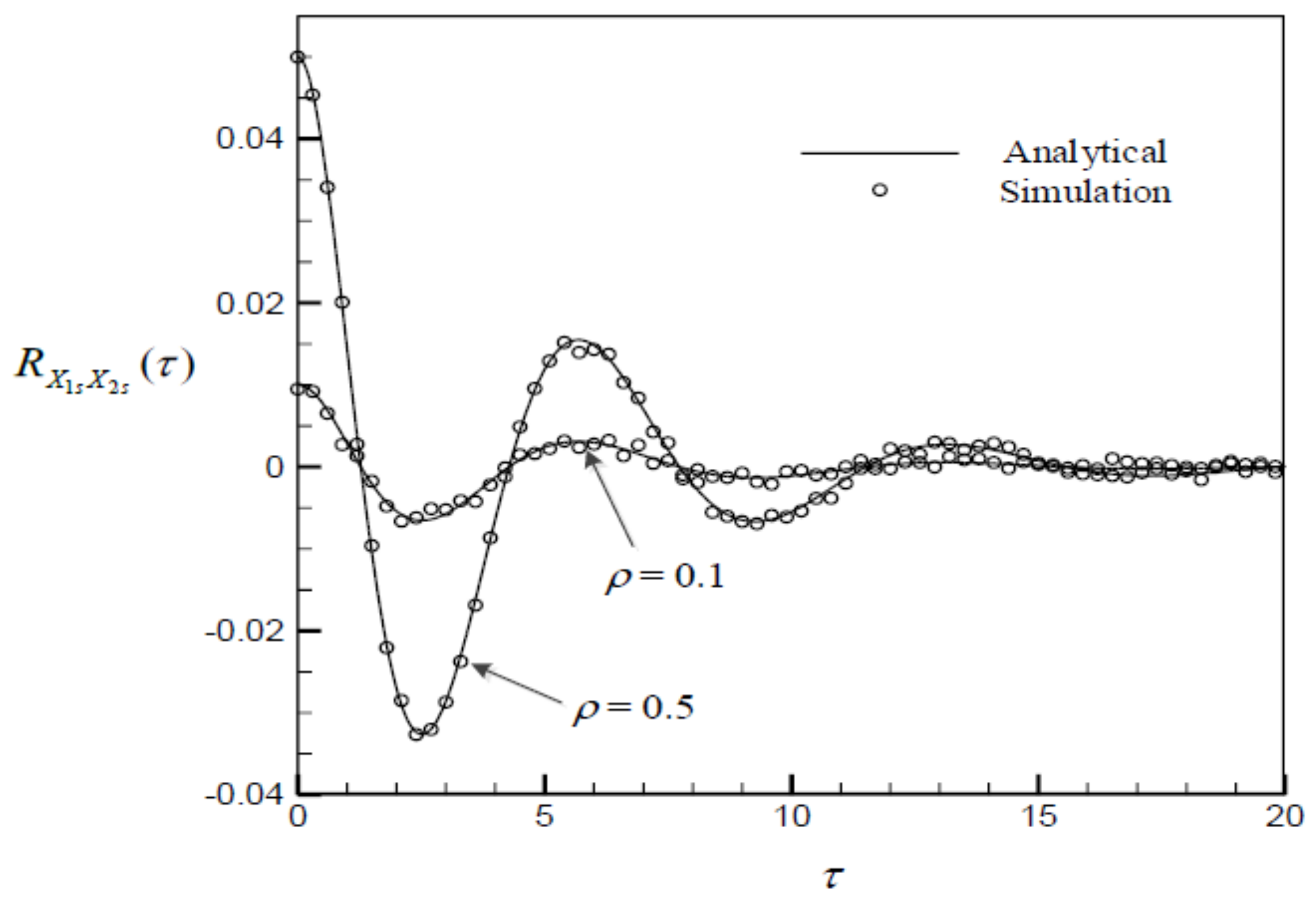
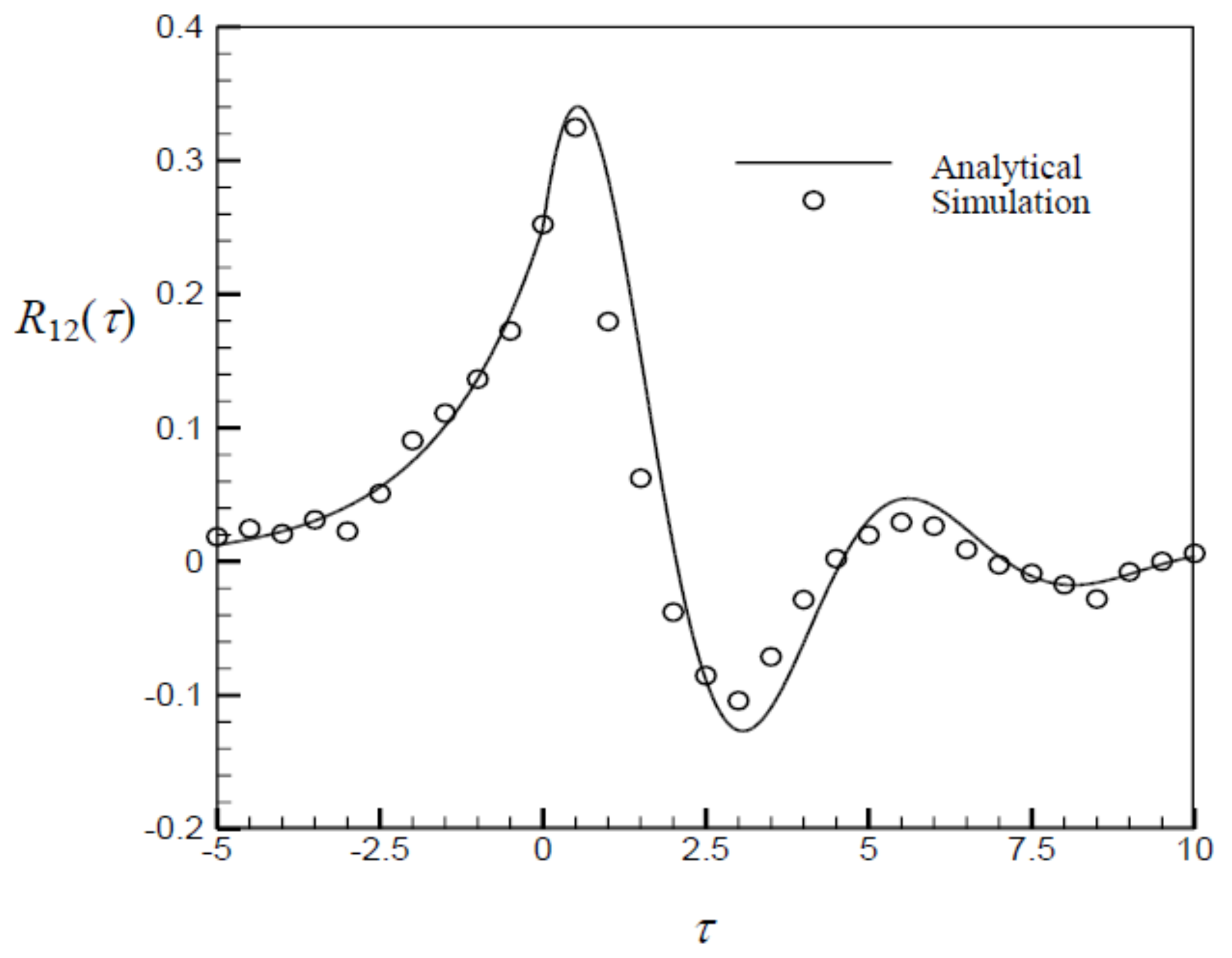
4.2. Generation of Two Correlated Stationary Gaussian Processes
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Shinozuka, M.; Deodatis, G. Simulation of stochastic processes by spectral representation. Appl. Mech. Rev. 1991, 44, 191–204. [Google Scholar] [CrossRef]
- Cai, G.Q.; Zhu, W.Q. Elements of Stochastic Dynamics; World Scientific Publisher: Singapore, 2016. [Google Scholar]
- Lin, Y.K.; Cai, G.Q. Probabilistic Structural Dynamics. In Advanced Theory and Applications; McGraw-Hill: New York, NY, USA, 1995, 2004. [Google Scholar]
- Muhuri, P.K. A study of the stability of the rolling motion of a ship in an irregular seaway. Int. Shipbuild. Prog. 1980, 27, 139–142. [Google Scholar] [CrossRef]
- Roberts, J.B. A stochastic theory for nonlinear ship rolling in irregular seas. J. Ship Res. 1982, 26, 229–245. [Google Scholar] [CrossRef]
- Ghaderpour, E.; Pagiatakis, S.D. Least-squares wavelet analysis of unequally spaced and non-stationary time series and its applications. Mathematical Geosci. 2017, 49, 819–844. [Google Scholar] [CrossRef]
- Winterstein, S.R. Nonlinear vibration models for extremes and fatigue. J. Eng. Mech. 1988, 114, 1772–1790. [Google Scholar] [CrossRef]
- Grigoriu, M. Simulation of stationary non-Gaussian translation processes. J. Eng. Mech. 1998, 124, 121–126. [Google Scholar] [CrossRef]
- Deodatis, G.; Micaletti, R.C. Simulation of highly skewed non-Gaussian stochastic processes. J. Eng. Mech. 2001, 127, 1284–1295. [Google Scholar] [CrossRef]
- Wu, C.; Cai, G.Q. Effects of excitation probability distribution on system responses. Int. J. Non-Linear Mech. 2004, 39, 1463–1472. [Google Scholar] [CrossRef]
- Shinozuka, M.; Jan, C.M. Digital simulation of random processes and its applications. J. Sound Vib. 1972, 25, 111–128. [Google Scholar] [CrossRef]
- Deodatis, G. Simulation of ergodic multivariate stochastic processes. J. Eng. Mech. 1996, 122, 778–787. [Google Scholar] [CrossRef]
- Cai, G.Q.; Zhu, W.Q. Generation of two correlated stationary Gaussian processes and application to ship rolling motion. Probabilistic Eng. Mech. 2019, 57, 26–31. [Google Scholar] [CrossRef]
- Mignolet, M.P.; Spanos, P.D. Recursive simulation of stationary multi-variate random processes, Part, I. J. Appl. Mech. 1987, 54, 674–680. [Google Scholar] [CrossRef]
- Mignolet, M.P.; Spanos, P.D. Recursive simulation of stationary multi-variate random processes, Part II. J. Appl. Mech. 1987, 54, 681–687. [Google Scholar] [CrossRef]
- Cai, G.Q. Generation of correlated random variables and stochastic processes. Probab. Eng. Mech. 2018, 52, 40–46. [Google Scholar] [CrossRef]
- Li, Y.; Kareem, Q. Simulation of multi-variate random processes, hybrid DFT and digital filtering approach. J. Eng. Mech. 1993, 119, 1078–1098. [Google Scholar] [CrossRef]
- Ramadan, O.; Novak, M. Simulation of spatially incoherent random ground motions. J. Eng. Mech. 1993, 119, 997–1016. [Google Scholar] [CrossRef]
- Chai, W.; Naess, A.; Leira, B.J. Filter models for prediction of stochastic ship roll response. Probab. Eng. Mech. 2015, 41, 104–114. [Google Scholar] [CrossRef]
- Chai, W.; Naess, A.; Leira, B.J. Stochastic nonlinear ship rolling in random beam seas by path integration method. Probabilistic Eng. Mech. 2016, 44, 43–52. [Google Scholar] [CrossRef]
- Pierson, W.J.; Moskowitz, L.A. A proposal spectral form for fully developed wind seas based on the similarity theory of S. A. Kitaigorodskii. J. Geophys. Res. 1964, 69, 5181–5190. [Google Scholar] [CrossRef]
- Dalzell, J.F. A Study of the Distribution of Maxima of Non-Linear Ship Rolling in a Seaway; Report DL-71-1562; Stevens Institute of Technology: Hoboken, NJ, USA, 1971. [Google Scholar]
- Dalzell, J.F. A Note on the distribution of maxima of ship rolling. J. Ship Res. 1973, 17, 217–226. [Google Scholar] [CrossRef]
- Faltinsen, O.M. Sea Loads on Ships and Offshore Structures; Cambridge University Press: Oxford, UK, 1993. [Google Scholar]
- Hsieh, S.R.; Troesch, A.W.; Shaw, S.W. A nonlinear probabilistic method for predicting vessel capsizing in random beam seas. Proc. R. Soc. Lond. A 1994, 446, 195–211. [Google Scholar]
- Paroka, D.; Ohkura, Y.; Umeda, N. Analytical prediction of capsizing probability of a ship in beam wind and waves. J. Ship Res. 2006, 50, 187–195. [Google Scholar] [CrossRef]
- Kougioumtzoglou, I.A.; Spanos, P.D. Stochastic response analysis of the softening Duffing oscillator and ship capsizing probability determination via a numerical path integral approach. Probab. Eng. Mech. 2014, 35, 67–74. [Google Scholar] [CrossRef]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cai, G.-Q.; Huan, R.; Zhu, W. Generation of Two Correlated Stationary Gaussian Processes. Mathematics 2021, 9, 2687. https://doi.org/10.3390/math9212687
Cai G-Q, Huan R, Zhu W. Generation of Two Correlated Stationary Gaussian Processes. Mathematics. 2021; 9(21):2687. https://doi.org/10.3390/math9212687
Chicago/Turabian StyleCai, Guo-Qiang, Ronghua Huan, and Weiqiu Zhu. 2021. "Generation of Two Correlated Stationary Gaussian Processes" Mathematics 9, no. 21: 2687. https://doi.org/10.3390/math9212687
APA StyleCai, G.-Q., Huan, R., & Zhu, W. (2021). Generation of Two Correlated Stationary Gaussian Processes. Mathematics, 9(21), 2687. https://doi.org/10.3390/math9212687




