Splitting Sequences for Coding and Hybrid Incremental ARQ with Fragment Retransmission

Abstract

This paper proposes a code defined on a finite ring ${\mathbb{Z}}_{p_M}$, where $p_M$ = $2^m-1$ is a Mersenne prime, and m is a binary size of ring elements. The code is based on a splitting sequence (splitting set) $\mathcal{S}$, defined for the given multiplier set $\mathcal{E}=\left\{\pm 2^0, \pm 2^1,\dots , \pm 2^{m-1}\right\}$. The elements of $\mathcal{E}$ correspond to the weights of binary error patterns that can be corrected, with the bidirectional single-bit error being the representative that occurs the most. The splitting set splits the code-word into sub-words, which inspired the name splitting code. Each sub-word, provided with auxiliary control symbols that are a byproduct of the coding procedure, corrects a single symbol error. The code can be defined, with some constraints, for general Mersenne numbers as well, while the multiplier set can be adjusted for adjacent binary errors correction. The application proposed for this code is a hybrid three-stage incremental ARQ procedure that transmits the code-word in the first stage, auxiliary control symbols in the second stage, and retransmits the sub-words detected as incorrect in the third stage. At each stage, error correction can be turned on or off, keeping both the retransmission rate and residual error rate at a low level.

1. Introduction

Splitting is a process in discrete algebra that applies to additive Abelian groups. Suppose that $\mathcal{E}$ is a finite set of integers, and $\mathcal{G}$ is an Abelian group. If it is possible to find a subset, $\mathcal{S}\subset \mathcal{G}$, such that every nonzero element, $ℊ\in \mathcal{G}$, can be uniquely represented in the form $\epsilon ·𝓈$, where $\epsilon \in \mathcal{E}$ and $𝓈\in \mathcal{S}$, then it is said that $\mathcal{E}$ splits $\mathcal{G}$ with splitting set $\mathcal{S},$ with a trivial case $\mathcal{S}=\mathcal{G}$ and $\mathcal{E}=\left\{1\right\}$. The set $\mathcal{E}$ is called a multiplier set, while the splitting set $\mathcal{S}$ is frequently referred to as a splitting sequence, ${𝓈}_1, {𝓈}_2, \dots$ [1].

A number of theoretical contributions justify the importance of the topic, to name just a few. The product of the groups was analyzed as early as 1942 in the works of G. Hajόs [2] (in German). Non-Abelian groups were elaborated upon in [3]. The factorizations of the semigroup of modular arithmetic integers into subsets $\mathcal{E}$ and $\mathcal{S}$, where $\mathcal{E}$ is equal to {1, 2, …, k} or { ±1, ±2, …, ±k}, was given in [4]. In the context of the geometry of numbers, the same multiplier sets are thoroughly analyzed in [5].

In addition to deep mathematical elaboration, some contributions also offer application examples, primarily in the domain of coding theory. The analysis of perfect run-length limited codes capable of correcting single peak shifts was performed in [6]. In [7], the author analyzed multiplier sets $\left\{1, a,\dots , a^r,b,\dots , b^s\right\}$ and $\left\{\pm 1, \pm a,\dots , \pm a^r,\pm b,\dots , \pm b^s\right\}$ and proved the existence of perfect three- and four-shift codes. Another paper [1] gives a general and completely proven theory for generalized splitting, applied to the design of codes that corrects asymmetric errors with limited magnitude and with possible implementation in write-once memory (WOM) codes. A comprehensive review of historical notes, relationships to other mathematical structures, and applications was recently given in [8].

There is no implementation of splitting for an error-control code that corrects errors that are the consequence of ordinary Gaussian noise.

This paper fills this gap, proposing an error-correcting code based on a multiplier set, $\mathcal{E}=\left\{\pm 2^0, \pm 2^1,\dots , \pm 2^{m-1}\right\}$, that splits a finite ring, ${\mathbb{Z}}_{p_M}$, where $p_M$ is a Mersenne prime [9]. If the elements (symbols) of ${\mathbb{Z}}_{p_M}$ are mapped into m binary digits (bits), then ${\epsilon }_j=\pm 2^j\in \mathcal{E}$ corresponds to the integer weight of a bidirectional single-bit error that occurs at the (j + 1)^st position of the erroneously received symbol, j = 0, …, m − 1. The sign of ${\epsilon }_j$ denotes the direction of the error: positive, 0→1, when zero is erroneously perceived as one, and negative, 1→0, when one is perceived as zero. The exponent ${ }^j$ shows the position of the corrupted bit. The code can be extended to ${\mathbb{Z}}_{n_M}$, where $n_M$ is a general Mersenne number [9]. The main feature of the code is that its code-word can be split into the sub-words that correspond to the splitting set $\mathcal{S}$, so we propose the name splitting code. If the error correction is excluded, the code’s detection capacities are equivalent to Fletcher’s checksum error detection code [10].

The application of the proposed code is envisaged in automatic repeat request procedures (ARQs). Increased power consumption inherent to forward error control (FEC) codes initiate a regain of ARQ popularity [11] via their improved versions, such as Chase Combining Hybrid ARQ (CC-HARQ) [12] and incremental redundancy (IR) HARQ [13]. Decreased consumption is paid by latency, resulting in engineering compromises [14]. Another approach is the selective retransmission of fragments of the entire message [15], which might also comprise aggregated packets [16,17]. Packet aggregation is a technique aiming for energy efficiency improvement and quality of service (QoS) enhancement, especially in low-power communications [16]. The procedure proposed in this paper is based on a hybrid ARQ with incremental redundancy and selective fragment retransmission that implements the splitting code.

The aims of our code are to work reliably, which is guaranteed by its theoretical foundation, to have a low-power consuming realization, and to reduce the retransmission rate. The code is based on the approved patents, listed in Section 6, that address these problems. The first patent proposes an integer code with energy consumption optimization, while the second one deals with a hybrid integer code ARQ optimization.

The difference between the proposed solution and already existing codes based on splitting is that the latter ones are designed for very specific types of errors that are not inherent in transmission systems. For this reason, these codes are not suitable for ARQ procedures. Besides, the focus of these contributions is based on a theoretical background, and no attention is devoted to power consumption optimization.

The paper is organized as follows: the methods are presented in Section 2, introducing a design of a forward error control (FEC) code based on splitting sequences and Mersenne primes. The code corrects errors in the binary field by implementing integer ring operations. Section 3 and Section 4 are devoted to the results. Section 3 presents some elaborations of the proposed splitting code regarding its embedded sub-word structures, general Mersenne numbers, correctable error patterns, adjacent error correction, and asymmetrical perfectness. Section 4 proposes an application of splitting codes for an incremental hybrid retransmission procedure. The discussion and the concluding remarks are given in Section 5, followed by a table that summarizes the notations and abbreviations.

2. Mersenne Primes and Splitting Sequences for Binary Errors Correction

A prime number is called a Mersenne prime if it can be written as $p_M$ = $2^m$− 1 [9]. The corresponding ring, ${\mathbb{Z}}_{p_M}$, is a field GF($p_M$) as well. The underlying additive Abelian group is cyclic: the additive order of each non-zero ring element is equal to $p_M$, so each non-zero element, $z_k\in {\mathbb{Z}}_{p_M}$, is a generator of ${\mathbb{Z}}_{p_M}$.

The cardinality of the multiplier set $\mathcal{E}=\left\{\pm 2^0, \pm 2^1,\dots , \pm 2^{m-1}\right\}$ that corresponds to a single-bit error weight is equal to $\left|\mathcal{E}\right|=2·m$. Since $\left|{\mathbb{Z}}_{p_M}\backslash \left\{0\right\}\right|$ $=2^m$ − 2, it follows that the cardinality of the splitting set is equal to $\left|\mathcal{S}\right|=\frac{\left|{\mathbb{Z}}_{p_M} \backslash \left\{0\right\}\right|}{\left|\mathcal{E}\right|}=\frac{2^{m-1}-1}{m}$. A list of the first few Mersenne primes with the corresponding cardinality $\left|\mathcal{S}\right|$ is given in Table 1, while a complete list of splitting elements ${𝓈}_i$, $i=1, \dots , \left|\mathcal{S}\right|$, can be found in a patent application [18].

Since ${\mathbb{Z}}_{p_M}$ is a finite-integer ring, $z_k=k\in {\mathbb{Z}}_{p_M}\backslash \left\{0\right\}, k=1, \dots ,2^m-2$. Further on, ${𝓈}_i\in \mathcal{S}, i=1, \dots , \left|\mathcal{S}\right|,$ and ${\epsilon }_j\in \mathcal{E}, j=1, \dots , 2·m.$ The indices k, i, and j are reserved for symbol, splitting sequence, and error, respectively. The multiplication of each $z_k\in {\mathbb{Z}}_{p_M}\backslash \left\{0\right\}$ by ${\epsilon }_j$ modulo $p_M$ yields a different permutation of integers $z_k$; integers at the same position within different permutations are mutually different. This is a straightforward consequence of the maximal additive order of the ring elements $z_k\in {\mathbb{Z}}_{p_M}\backslash \left\{0\right\}$.

Table 1. Mersenne primes and code-word lengths for RS, extended Hamming and splitting code.

Symbol Length m	Mersenne Prime pM = 2m − 1	Number of Elements in Splitting Set $\left|\mathcal{S}\right|$	Code-Word Lengths (in bits)
			Reed–Solomon	Extended Hamming	Splitting
2	3	-	6	8	-
3	7	1	21	32	24
5	31	3	155	512	460
7	127	9	889	8192	7952
13	8191	315	106,483	33,554,432	33,538,076

Table 1. Mersenne primes and code-word lengths for RS, extended Hamming and splitting code.

Symbol Length m	Mersenne Prime pM = 2m − 1	Number of Elements in Splitting Set $\left|\mathcal{S}\right|$	Code-Word Lengths (in bits)
			Reed–Solomon	Extended Hamming	Splitting
2	3	-	6	8	-
3	7	1	21	32	24
5	31	3	155	512	460
7	127	9	889	8192	7952
13	8191	315	106,483	33,554,432	33,538,076

To design a code, we first prove the following Lemma 1:

For every combination of i, j, and k, where $i=1, \dots , \left|\mathcal{S}\right|, j=1, \dots , 2·m \mathrm{and} k=1, \dots ,2^m-2,$ the pair $({𝓈}_i·{\epsilon }_j, z_k·{\mathcal{E}}_j$) is given a unique value. In other words, $({𝓈}_{i1}·{\epsilon }_{j1}, z_{k1}·{\epsilon }_{j1}$) $=({𝓈}_{i2}·{\epsilon }_{j2}, z_{k2}·{\epsilon }_{j2}$) iff $\left(\left({𝓈}_{i1}={𝓈}_{i2}\right) \wedge ({\epsilon }_{j1}={\epsilon }_{j2 }) \wedge (z_{k1}=z_{k2 })\right)$.

Proof. 

Each product $({𝓈}_i·{\epsilon }_j)$ is unique according to the definition of splitting. So, if ${\epsilon }_{j1} \ne {\epsilon }_{j2}$, or if ${𝓈}_{i1} \ne {𝓈}_{i2}$, or if both ${\epsilon }_{j1} \ne {\epsilon }_{j2}$ and ${𝓈}_{i1} \ne {𝓈}_{i2}$, then the products ${𝓈}_{i1}·{\epsilon }_{j1} \mathrm{and} {𝓈}_{i2}·{\epsilon }_{j12}$ must be different. It follows that $({𝓈}_{i1}·{\epsilon }_{j1}, z_{k1}·{\epsilon }_{j1}$) $\ne$ $({𝓈}_{i2}·{\epsilon }_{j2}, z_{k2}·{\epsilon }_{j2}$) as their first terms are different, regardless of $z_k$. □

If ${\epsilon }_{j1}={\epsilon }_{j2}={\epsilon }_j$, it should be recalled that the order of $z_k$ is maximal. Then, if $z_{k1} \ne z_{k2}$, results of their multiplication by the same number ${\epsilon }_j$ will be different. So, $({𝓈}_i·{\epsilon }_j, z_{k1}·{\epsilon }_j$) $\ne$ $({𝓈}_i·{\epsilon }_j, z_{k2}·{\epsilon }_j$) as their second terms $(z_{k1}·{\epsilon }_j) \mathrm{and} (z_{k2}·{\epsilon }_j)$ are different, regardless of ${𝓈}_i$.

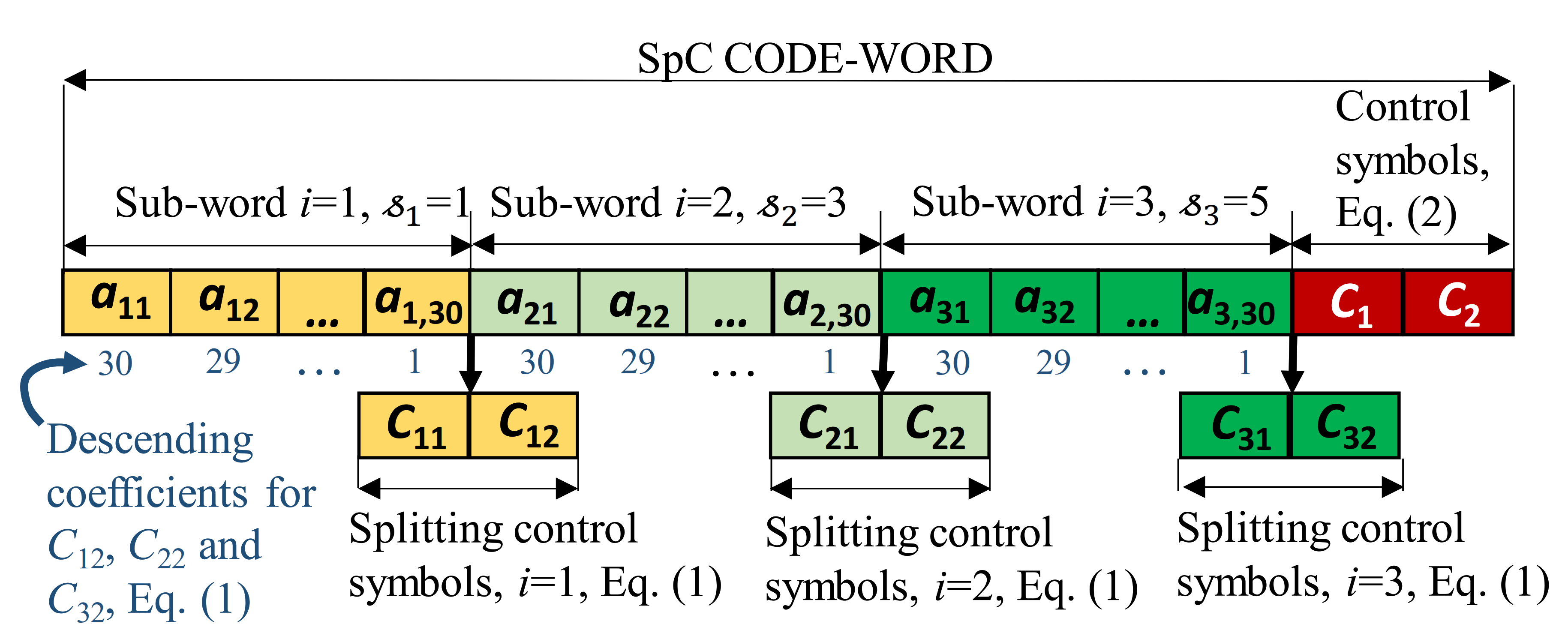
The impact of the splitting sequence is that each code-word of the proposed will be also “split”—it will comprise $\left|\mathcal{S}\right|$ splitting sub-words of length $\left|{\mathbb{Z}}_{p_M} \backslash \left\{0\right\}\right|$, as shown in the example in Figure 1. In this example, m = 5, $p_M$ = $2^5$− 1 = 31, and the stream of information symbols is split into $\left|\mathcal{S}\right|=\frac{2^{5-1}-1}{5}=3$ for sub-words with lengths of 30.

Each sub-word corresponds to one splitting element ${𝓈}_i$, i = 1, …, $\left|\mathcal{S}\right|$. If symbols in sub-words are labeled with the non-zero integer value $z_k=k$ then, according to Lemma 1, for each combination of i, j, and k, the pair $({𝓈}_i·{\epsilon }_j, z_k·{\epsilon }_j$) yields one out of $\left|\mathcal{E}\right|·\left|{\mathbb{Z}}_{p_M} \backslash \left\{0\right\}\right|·\left|\mathcal{S}\right|={\left(2^m-2\right)}^2$ unique values. In the pair $({𝓈}_i·{\epsilon }_j, z_k·{\epsilon }_j$), value ${\epsilon }_j$ corresponds to the error weight, ${𝓈}_i$ marks the sub-word, and $z_k=k$ is a marker of one out of $\left|{\mathbb{Z}}_{p_M} \backslash \left\{0\right\}\right|$ symbols within the sub-word. These three elements indicate the value and position of error and enable its correction.

To construct the code that corrects an error listed in the multiplier set $\mathcal{E}=\left\{\pm 2^0, \pm 2^1,\dots , \pm 2^{m-1}\right\}$, it is sufficient to find a coding procedure that adds two control symbols for which the pair $({𝓈}_i·{\epsilon }_j, z_k·{\epsilon }_j$) forms a unique syndrome. Such a syndrome would give information about the error weight (${\epsilon }_j$), its position within the sub-word ($z_k=k$), and the sub-word within which the error occurred (${𝓈}_i)$. The proposed code is referred to as “splitting code” as it is based on a splitting sequence, and the corresponding abbreviation is SpC.

The first part of the coding procedure is performed for each sub-word separately and involves forming auxiliary splitting control symbols.

From now on, all the operations are modulo $p_M$, except if stated otherwise.

The first auxiliary splitting control symbol, which is given by the first part of Equation (1), is the sum of information symbols in the sub-word, while the second one, which is given by the second part of Equation (1), is the sum of information symbols weighted by the descending non-zero ring elements $\left(2^m-1-k\right)$:

$$C_{i1}=-{{\displaystyle \sum }}_{k=1}^{2^m-2}{a}_{ik}, C_{i2}=-{{\displaystyle \sum }}_{k=1}^{2^m-2}\left(2^m-1-k\right)·a_{ik}, i=1,\dots , \left|\mathcal{S}\right|,$$

(1)

where $a_{ik}$ is the kth information symbol from the ith splitting sub-word (Figure 1).

The splitting control symbols $C_{i1}$ and $C_{i2}$ are auxiliary, and therefore not a part of the code-word. However, if coupled with the sub-words, they can form embedded FEC code-words (Figure 1). The property that the byproducts of the coding procedure, $C_{i1}$ and $C_{i2},$ form embedded sub-codes within the SpC is exploited in the following sections.

From Equation (1), it seems that the coding procedure requires two additions and one multiplication per information symbol. However, the coding procedure in Figure 2a follows the speed-up scheme from Fletcher’s error-detecting checksums [10] and eliminates the multiplications. This scheme also explains the descending order of the coefficients in $C_{i2}$.

The control symbols for the splitting code are formed as:

$$C_1={{\displaystyle \sum }}_{i=1}^{\left|\mathcal{S}\right|}{𝓈}_i·C_{i1}, C_2={{\displaystyle \sum }}_{i=1}^{\left|\mathcal{S}\right|}{C}_{i2}.$$

(2)

At the receiver, syndrome forming follows the same procedure (Figure 2b):

$$S_1={{\displaystyle \sum }}_{i=1}^{\left|\mathcal{S}\right|}{𝓈}_i· {{\displaystyle \sum }}_{k=1}^{2^m-2}{\widehat{a}}_{ik}+{\widehat{C}}_1, S_2={{\displaystyle \sum }}_{i=1}^{\left|\mathcal{S}\right|}{{\displaystyle \sum }}_{k=1}^{2^m-2}\left(2^m-1-k\right)·{\widehat{a}}_{ik}+{\widehat{C}}_2,$$

(3)

where “^” denotes the estimation of the received symbols. If a single error of weight, ${\epsilon }_j$, occurs at the kth symbol of the ith splitting sub-word, ${\widehat{a}}_{ik}=a_{ik}$+${\epsilon }_j$, the corresponding syndromes would be:

$$\left(S_1, S_2\right)=\left({𝓈}_{i }·{\epsilon }_j,\left(2^m-1-k\right)·{\epsilon }_j\right)=\left({𝓈}_{i }·{\epsilon }_j,-k·{\epsilon }_j\right)=\left({𝓈}_{i }·{\epsilon }_j,-z_k·{\epsilon }_j\right),$$

(4)

which, according to Lemma 1, uniquely represent the occurrence of a single-bit error.

If ${\epsilon }_j$ was known, it would be easy to find the splitting sub-word, $i$, and the position, $k$, of the erroneous symbol within the sub-word: ${𝓈}_{i }=S_1/{\epsilon }_j$ and $k=-S_2/{\epsilon }_j$ (modular division). However, ${\epsilon }_j$ is not known. Moreover, there are three pieces of information, ${\epsilon }_j, {𝓈}_{i }, \mathrm{and} z_k=k,$ required for error correction, and only two syndromes to provide them.

Figure 2. (a) Coding, (b) syndrome forming, and (c) error-correcting procedures. The coding procedure requires two additions per information symbol, and two additions, two negations, and one multiplication per sub-word. The splitting control symbols $C_{i1}$ and $C_{i2}$ are byproducts of coding procedure. Text in gray marks the changes due to the truncation and shortening described in Section 3.3 and Section 3.4. l_i—length of the ith sub-word; ss—number of sub-words.

Figure 2. (a) Coding, (b) syndrome forming, and (c) error-correcting procedures. The coding procedure requires two additions per information symbol, and two additions, two negations, and one multiplication per sub-word. The splitting control symbols $C_{i1}$ and $C_{i2}$ are byproducts of coding procedure. Text in gray marks the changes due to the truncation and shortening described in Section 3.3 and Section 3.4. l_i—length of the ith sub-word; ss—number of sub-words.

The third, hidden piece of information is the property of the Abelian additive group: each correctable error weight, ${\epsilon }_j$, is a closed cyclic permutation of the weight $\pm 2^0=\pm 1$. The n-fold multiplication of error weight ${\epsilon }_j$ by a factor of two, or, equivalently, n cyclic shifts of its binary value to the right eventually yields $\pm 1$. Once determined by consecutively doubling (or cyclic shifting) the first syndrome n times until its value becomes $\pm 1·{𝓈}_i$, the obtained n $\in$ {0, …, m − 1} straightforwardly gives the required error weight and the sub-word within which it occurs:

$$S_1·2^n={𝓈}_{i }·{\epsilon }_j·2^n={𝓈}_{i }·\left(\pm 2^j\right)·2^n=\pm 2^{j+n}·{𝓈}_i=\pm 2^m·{𝓈}_i=\pm {𝓈}_i.$$

(5)

The number of multiplications, n, shows that the absolute value of ${\epsilon }_j$ is equal to $abs({\epsilon }_j)=2^j=2^{m-n},$ while its sign is equivalent to the sign of the splitting element obtained after the n-fold multiplication of the first syndrome, i.e.,$sign({\epsilon }_j)=sign(S_1·2^n)$. The outcome of Equation (5), $\pm {𝓈}_i,$ points out that the error occurs within the i^th sub-word.

Multiplying the second syndrome by the same factor $2^n$, or cyclically shifting it n times, yields the position of the erroneous symbol:

$$\begin{gathered} S_2·2^n=-k·\left(\pm 2^j\right)·2^n=-k·\left(\pm 1\right)=-k·sign(S_1·2^n)\Rightarrow \\ \Rightarrow k=-1·\left(S_2·2^n\right)·sign(S_1·2^n) \end{gathered}$$

(6)

The error is corrected if the error weight ${\epsilon }_j$ is subtracted from the k^th received symbol ${\widehat{a}}_{ik}$, located in the splitting sub-stream i, as shown in Figure 2c.

Figure 2 points out that the procedures of coding and error correction are simple and suitable for applications where energy resources are scarce. The coding procedure requires two additions per information symbol, and two additions, one multiplication and two complements per splitting sub-word. Similar requirements hold for syndrome forming. Error correction requires n < m cyclic shifts and $2·n·\left|\mathcal{S}\right|$ comparisons, while the look-up table comprises the elements of the splitting set $\left|\mathcal{S}\right|$.

A case when only one syndrome is non-zero indicates an error at the control symbol, which is irrelevant as the control symbols are discarded anyway.

The basic idea of correcting a single error in the binary field using the algebraic structures defined on the non-binary alphabet appeared long ago [19], and, to our knowledge, it did not have a predecessor. It was briefly analyzed in [20], but in a constrained form, without variability in sub-words lengths, without any theoretical analysis, and without a connection to splitting sequences and Mersenne primes. Some additional explanations can be found in the last paragraph of [21].

3. Properties and Modifications of Splitting Code

This section lists some modifications of the splitting code: it can be adjusted to non-prime Mersenne numbers, and it can be adjusted to correct adjacent error pairs within an integer, including the circular adjacency.

The section also describes some properties of the splitting code: all its variants can correct some binary error patterns besides a single-bit error, its sub-code-word corrects a single-symbol error in the case of Mersenne prime, and a single-bit error (plus some additional patterns) in a case of Mersenne non-prime, it can be scaled by shortening sub-words, or by omitting sub-words, and, in a case of Mersenne primes, it can be considered as “asymmetrically perfect”.

3.1. Correctable Error Patterns

The error weights ${\epsilon }_j=\pm 2^j, j=0,\dots ,m-1$ correspond not only to the single-bit error but also to all bidirectional error patterns with this weight. The correctable error patterns are:

(1)

 m₁ positive errors (0→1) followed by a single negative error (1→0) and $m-m_1-1$ zeros, $m_1=0,\dots ,m-1$;

(2)

 A chain of $m-1$ adjacent positive errors (0→1) followed by zero;

(3)

 All inversions of patterns (1) and (2) when a positive error is substituted by negative and vice versa;

(4)

 All circular shifts of the previous patterns (1), (2), (3).

Obviously, error patterns are data-dependent, but most transmission systems use binary scramblers, so bias is excluded.

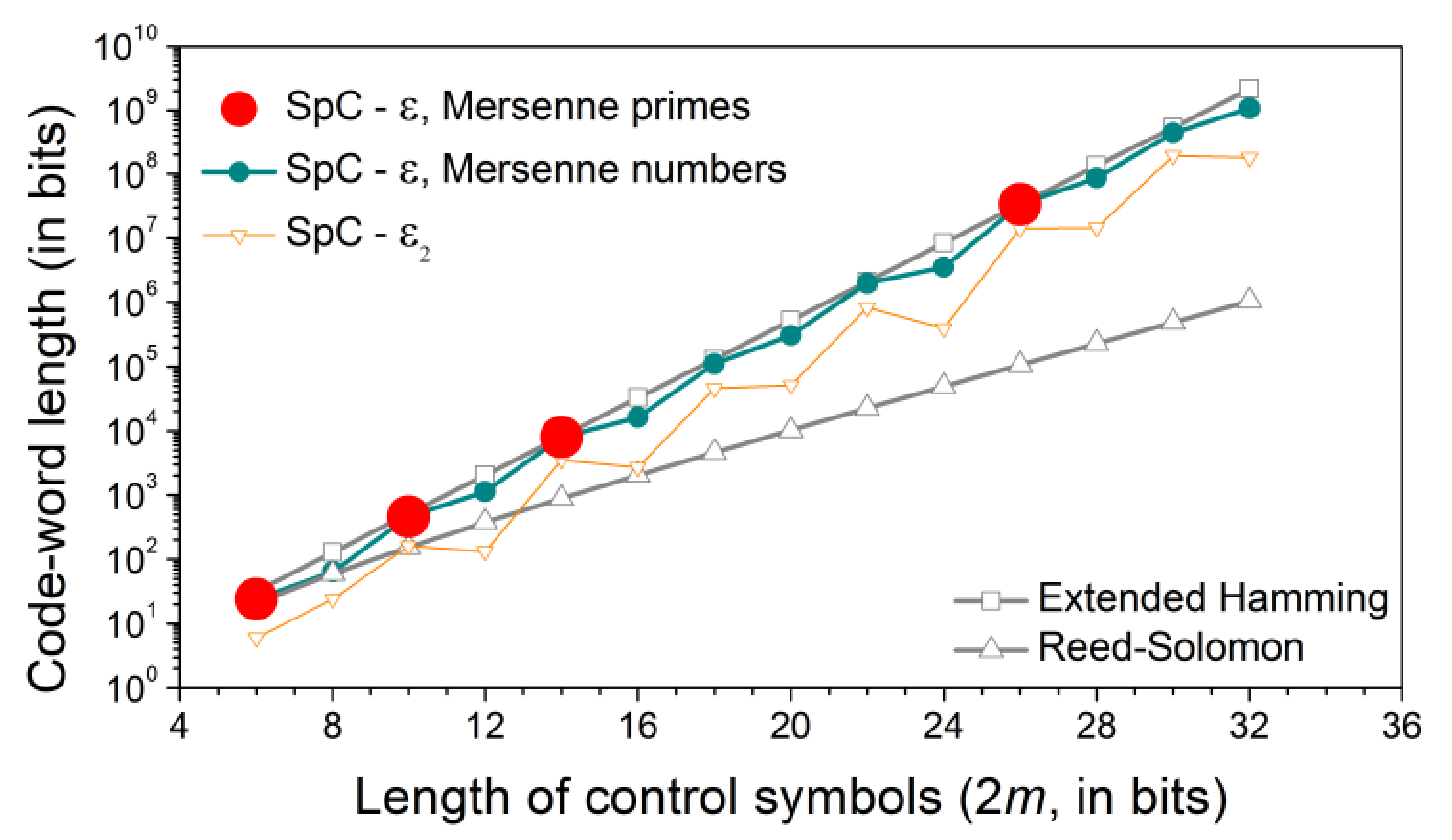
The maximal code-word lengths of splitting code, Reed–Solomon code, and extended Hamming code with equivalent redundancy are presented in Table 1. The code-word of SpC is slightly shorter than the one of the extended Hamming code, although both ones correct a single-bit error. The difference is due to their additional capabilities: the extended Hamming code detects an even number of errors, while the SpC corrects multiple bidirectional error patterns that correspond to the single-bit error weight.

3.2. Embedded Sub-Code of the Splitting Code

If compared to the single-symbol correcting the RS code (Table 1), the code length of SpC, for the same redundancy, is increased approximately $\left|\mathcal{S}\right|$ times. This increase is at the cost of reduced correction capability from a symbol error to a single-bit error.

However, if the individual SpC sub-words are coupled with the auxiliary splitting control symbols $C_{i1}$ and $C_{i2}$, they form embedded SpC sub-codes (Figure 1). Their respective syndromes are:

$$\begin{gathered} \left(S_{i1}, S_{i2}\right)=\left({{\displaystyle \sum }}_{k=1}^{2^m-2}{\widehat{a}}_{ik}+{\widehat{C}}_{i1}, {{\displaystyle \sum }}_{k=1}^{2^m-2}\left(2^m-1-k\right)·{\widehat{a}}_{ik}+{\widehat{C}}_{i2}\right)= \\ =\left({\epsilon }_{ij}, \left(2^m-1-k\right)·{\epsilon }_{ij} \right). \end{gathered}$$

(7)

The first syndrome directly shows the error weight, ${\epsilon }_{ij}=S_{i1}$, while the second one shows the error position within the sub-code, $k=-S_{i2}/{\epsilon }_{ij}=-S_{i2}/S_{i1},$ where the division is modular. Since the order of elements is maximal, the pair $\left(S_{i1}, S_{i2}\right)$ has a unique value for each non-zero element of ${\mathbb{Z}}_{p_M}$.

Therefore, each embedded sub-code can correct any single symbol error. It is comparable to the single-symbol correcting the Reed–Solomon code, except that the RS is a $\left(2^m-1, 2^m-3\right)$ code defined over GF(2^m), while the SpC sub-code is a $\left(2^m, 2^m-2\right)$ code defined over GF(2^m –1) = $\mathrm{GF}\left(p_M\right)$. So, the proposed SpC can be regarded as a “split” version of the single-symbol correcting code: its length is multiplied as many times as there are splitting symbols, but its error-correcting capabilities are reduced from a single symbol to a single bit (operations in this paragraph are decimal).

The splitting control symbols $C_{i1}$ and $C_{i2}$ and syndromes $S_{i1}$ and $S_{i2}$ are byproducts of coding procedure, so the formation of sub-codes requires no additional processes. The embedded sub-codes are a useful property of SpC, which is a core element of the procedure proposed in the following section.

3.3. Truncated Splitting Code for General Mersenne Numbers $n_M$

So far, we only considered the Mersenne primes $p_M$ = $2^m$ − 1, with the symbol length m also being a prime [22]. However, the information symbols with a prime number of bits have limited application value.

The splitting, though truncated (incomplete), can be applied for arbitrary m, i.e., to any Mersenne number n_M = $2^m$− 1. Then, some elements of the splitting set do not have maximal order, so the splitting ${𝓈}_i·{\epsilon }_j$ and/or products $z_k·{\epsilon }_j$ are not unique.

For example, the Mersenne number for m = 6 is n_M = 63. Its factors are 3, 7, 9, and 21, and their orders are 21, 9, 7, and 3, respectively. The splitting set is $\mathcal{S}=\left\{1, 3, 5, 7, 9, 11, 21\right\}$, but only the elements ${𝓈}_i$ ∈ {1, 5, 11} have maximal additive order. The splitting code can still be formed, but with the truncated splitting set ${\mathcal{S}}_{\mathrm{T}}=\left\{1, 5, 11\right\}$, with a lower number of the sub-words, and a lower code rate. The set of syndrome values will not be complete, raising the possibility for error detection (Figure 2c). The corresponding ring ${\mathbb{Z}}_{n_M}$ is not a field, so the sub-codes from Section 3.2. cannot correct all possible errors within a symbol, only the weights corresponding to a single-bit error. A list of Mersenne non-prime numbers, n_M, and the cardinality $\left|{\mathcal{S}}_{\mathrm{T}}\right|$ of the truncated splitting sets is given in Table 2, while the corresponding splitting elements with the maximal additive order, ${𝓈}_i$, $i=1, \dots , \left|{\mathcal{S}}_{\mathrm{T}}\right|$, can be found in the patent application [18].

From now on, the term “splitting code” and the abbreviation SpC is used for the truncated splitting codes as well.

Table 2. The cardinality of the truncated splitting sets ${\mathcal{S}}_{\mathrm{T}}$.

Symbol Length m	Mersenne Non-Prime Numbers nM = 2m − 1	Number and List of Non-Trivial Prime Factors of nM	Number of Elements in the Truncated Splitting Set $\left|{\mathcal{S}}_{\mathbf{T}}\right|$	Number of Elements $𝓈\in \mathcal{S}$ with Order below the Minimal
4	15	2 (3,5)	1	2
6	63	3 (3,3,7)	3	4
8	255	3 (3,5,17)	8	6
9	511	2 (7,73)	24	2
10	1023	3 (3,11,31)	30	6
11	2047	2 (23,89)	88	2
12	4095	5 (3,3,5,7,13)	72	22
14	16,383	3 (3,43,127)	378	6
15	32,767	3 (7,31,151)	900	6
16	65,535	4 (3,5,17,257)	1024	14

Table 2. The cardinality of the truncated splitting sets ${\mathcal{S}}_{\mathrm{T}}$.

Symbol Length m	Mersenne Non-Prime Numbers nM = 2m − 1	Number and List of Non-Trivial Prime Factors of nM	Number of Elements in the Truncated Splitting Set $\left|{\mathcal{S}}_{\mathbf{T}}\right|$	Number of Elements $𝓈\in \mathcal{S}$ with Order below the Minimal
4	15	2 (3,5)	1	2
6	63	3 (3,3,7)	3	4
8	255	3 (3,5,17)	8	6
9	511	2 (7,73)	24	2
10	1023	3 (3,11,31)	30	6
11	2047	2 (23,89)	88	2
12	4095	5 (3,3,5,7,13)	72	22
14	16,383	3 (3,43,127)	378	6
15	32,767	3 (7,31,151)	900	6
16	65,535	4 (3,5,17,257)	1024	14

3.4. Shortened Splitting Codes and Error Detection

The splitting code can be shortened by either omitting the sub-words or shortening them. The shortening need not be uniform: each shortened sub-word can be of a different length, l_i. It implies the changes in Equations (1), (3), (4), and (7), where the term $2^m-1$ should be substituted by $l_i+1$, and $\left|\mathcal{S}\right|$ in summations of Equations (2) and (3) should be substituted by the number of sub-words, denoted as ss. The position of the erroneous byte within the sub-word is then equal to:

$$k=l_i+1-\left(S_2·2^n\right)·sign(S_1·2^n).$$

(8)

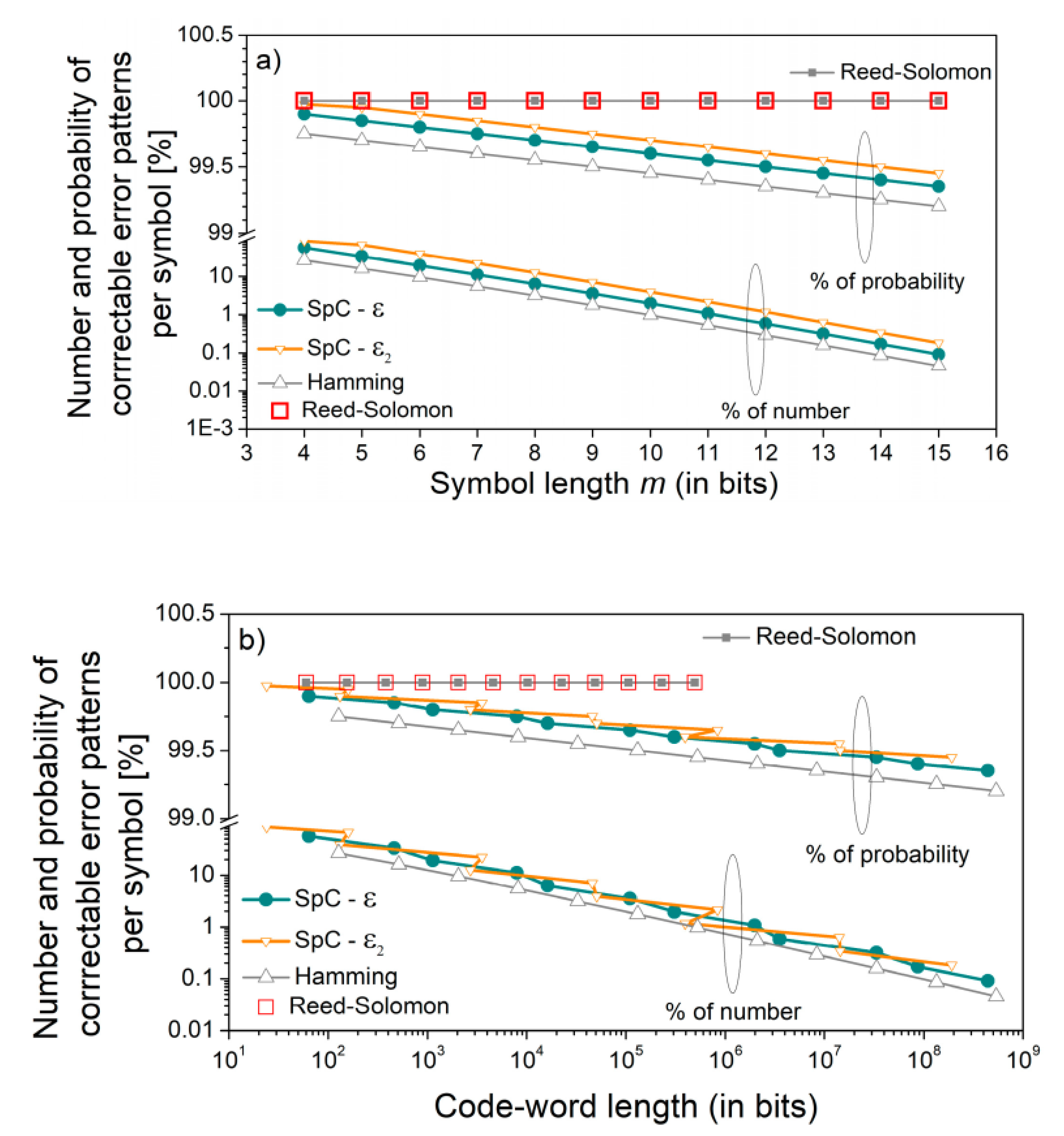
Shortening or omitting the sub-words reduces the number of syndrome values that correspond to the correctable errors, offering the possibility for error detection. This is another issue important for the application proposed in the following section. This reduction is shown in Figure 3, for two SpCs, one corresponding to Mersenne number (m = 12), and the other to Mersenne prime (m = 13). In Figure 3a, the sub-word lengths are shortened, keeping the number of sub-words as the parameter. In Figure 3b, the number of sub-words is reduced, keeping the length as the parameter. The percentage of syndromes that indicate correctable error patterns reaches 100% for Mersenne primes only.

3.5. Splitting Code for Adjacent Error Correction

The error patterns from Section 3.1. include adjacent and circularly adjacent error pairs of different polarities, 01→10 and 10→01. Error pairs are inherent to systems with differential coding, and it would be useful to correct the remaining patterns, 00→11 and 11→00. To accomplish this, it is sufficient to create a multiplier set, ${\mathcal{E}}_2$, that includes the corresponding weights: ${\mathcal{E}}_2=\left\{\pm 2^0, \dots , \pm 2^{m-1},\pm 3·2^0,\dots ,\pm 3·2^{m-1} \right\}$. Since the full splitting set for ${\mathcal{E}}_2$ could not be found (its non-existence is not proven), a truncated splitting set that comprises the elements with maximal order can be used, similar to Section 3.3.

Unfortunately, if exponent m is even, $m=2·r$, the error weight $\epsilon =3·2^0=3$ is a factor of Mersenne number: $n_M=2^m-1=2^{2·r}-1=4^r-1=\left(4-1\right)·\left(1+4+\cdots +4^{r-1}\right)=3·\left(1+4+\cdots +4^{r-1}\right)$ (decimal). Then, the maximal order of elements is not 2^m − 1, but (2^m—1)/3. The code can be formed, but the maximal length of sub-words is reduced and equal to (2^m −1)/3 −1.

Besides the error patterns (1), (2), (3), and (4) from Section 3.1, the correctable error patterns also include:

(5)

Two zeros, followed by (m—2) negative errors;

(6)

A positive error, followed by m₂ negative errors, then positive error and (m—m₂—2) zeros, m₂ = 0, …, m − 2;

(7)

Negative error followed by zero and by m₃ negative errors, then positive error followed by (m—m₃—3) zeros, m₃ = 0, …, m—3;

(8)

All inversions of patterns (5), (6), and (7) when a positive error is substituted by a negative and vice versa;

(9)

All circular shifts of the previous patterns (5), (6), (7) and (8).

The cardinality $\left|{\mathcal{S}}_{\mathrm{T}2}\right|$ of the truncated splitting sets for ${\mathcal{E}}_2$ is given in

Table 3. The cardinality of the truncated splitting sets ${\mathcal{S}}_{\mathrm{T}2} \mathrm{for} {\mathcal{E}}_2$.

Symbol Length m	Number of Elements in the Truncated Splitting Set $\left|{\mathcal{S}}_{\mathbf{T}2}\right|$ for ${\mathcal{E}}_2$
4	1
5	1
6	1
7	4
8	4
9	10
10	15
11	37
12	24
13	133
14	189
15	389
16	512

, while the elements of the splitting set with the maximal possible additive order, ${𝓈}_i$, $i=1, \dots , {\mathcal{S}}_{\mathrm{T}2}$, are listed in the patent application [18]. The comparison of code-word lengths for extended Hamming code, RS code, and splitting codes for multiplication sets $\mathcal{E} \mathrm{with} \left|\mathcal{S}\right| \mathrm{or} \left|{\mathcal{S}}_{\mathrm{T}}\right|,$ and ${\mathcal{E}}_2$ is shown in Figure 4. Even with the reduced number of sub-words with truncated splitting sets $\left|{\mathcal{S}}_{\mathrm{T}}\right|$, the length of SpC does not considerably decrease with respect to extended Hamming code. The increase in code lengths of SpC with ${\mathcal{E}}_2$ as a function of m is not monotonous. It is due to the decrease in sub-word length for even values of m. For lower values of m, the SpC with ${\mathcal{E}}_2$ is not justified as its length is below the RS code that corrects all symbol errors.

Figure 5 shows the ratio of correctable error patterns with respect to all error patterns and the ratio of the probability of correctable errors with respect to the total probability of errors. These features are given as a function of symbol length, m (Figure 5a), and as a function of maximal code-word length (Figure 5b).

3.6. Asymmetrically Perfect Splitting Codes

As stated in the introduction, each $z_k\in {\mathbb{Z}}_{p_M}$ can be uniquely represented in the form ${\epsilon }_j·{𝓈}_i$, where ${\epsilon }_j\in \mathcal{E}$ and ${𝓈}_i\in \mathcal{S}$, with every ${𝓈}_i \mathrm{and} z_k$ having a maximal order. Such splitting can be considered “perfect”, in contrast to splitting over ${\mathbb{Z}}_{n_M}$, where splitting elements do not have maximal order. In spite of perfect splitting, the splitting code for correcting a single-bit error weight defined over ${\mathbb{Z}}_{p_M}$ is not perfect. Perfect codes imply that the code-words and their correctable counterparts symmetrically fill the complete code-word space without overlapping and without free space left [23]. However, the following analysis, implementing decimal operations, shows the existence of surpluses:

The maximal code-word length is equal to $\frac{{\left(2^m-2\right)}^2}{2·m}$ + 2 symbols. Each symbol can obtain one out of $2^m-1$ possible values, so the entire code-word space comprises $C_S={\left(2^m-1\right)}^{\left(\frac{{\left(2^m-2\right)}^2}{2·m}+2\right)}$ code-words:

$$C_S={\left(2^m-1\right)}^{\left(\frac{{\left(2^m-2\right)}^2}{2·m}+2\right)}={\left(2^m-1\right)}^{\left(\frac{{\left(2^m-2\right)}^2}{2·m}\right)}·{\left(2^m-1\right)}^2=C_{EF}·{\left(2^m-1\right)}^2,$$

(9)

where $C_{EF}$ = ${\left(2^m-1\right)}^{\left(\frac{{\left(2^m-2\right)}^2}{2·m}\right)}$ is the number of error-free code-words.

The code-word can be either error-free or with an error at one of its $\frac{{\left(2^m-2\right)}^2}{2·m}$ +2 symbols. There are $2·m$ possible error values, so the total number of allowed code-words is equal to:

$$C_C={\left(2^m-1\right)}^{\left(\frac{{\left(2^m-2\right)}^2}{2·m}\right)}·\left(\left(\frac{{\left(2^m-2\right)}^2}{2·m}+2\right)·2·m+1\right)=C_{EF}·\left({\left(2^m-2\right)}^2+4·m+1\right)$$

(10)

In perfect codes, $C_S-C_C=0$.

In the proposed splitting code:

$$C_S-C_C=C_{EF}·\left({\left(2^m-1\right)}^2-{\left(2^m-2\right)}^2-4·m-1\right)=C_{EF}·2·\left(2^m-2-2·m\right).$$

(11)

The difference can be interpreted as follows: each of $C_{EF}$ code-words can be additionally corrupted at one of its two control symbols by $\left(2^m-2-2·m\right)$ different error values. The total number of error values is equal to $2^m-2$. The number of allowed ones is equal to $2·m$, but they are already included in $C_C$, shown in Equation (10). So, the number of error values that can be corrected in control symbols is equal to $2^m-2$.

The difference between the cardinality of the entire code-word space and the number of correctable code-words shows that, if an error of any weight corrupts a control symbol, it can be corrected. This is intuitively clear from the explanation given at the end of Section 3.1.—the code corrects a single-bit error if it occurs at the information symbol and a single-symbol error if it occurs at the control symbol.

The correctable errors that occur at control symbols encircle different spheres around the code-word than the errors that corrupt the information symbols. Nevertheless, all the points in the code-word space are covered without overlapping. As the term “quasi-perfect” code is used in a different context [24], we call the splitting codes over ${\mathbb{Z}}_{p_M}$ “asymmetrically perfect”. Formally, there are 51 asymmetrically perfect splitting codes, as 51 Mersenne primes have been discovered so far [25]. The ones that may have applicative value are defined with m = {5, 7, 13, 17, 19, 31, 61}.

4. Application Example: An ARQ Procedure for Selective Fragment Retransmission of Aggregated Data

The application of the proposed splitting code is suited for the procedures that use packet aggregation with fragment retransmission. In packet aggregation, instead of a separate header for each packet, all packets are grouped into a single frame and share a joint header [26]. The overhead reduction decreases its impact on energy per transmitted bit, simultaneously increasing the throughput and efficiency [27,28]. The applications of packet aggregation are, among others, in the domain of VoIP [29] and wireless networks [30].

Aggregation with fragment retransmission (AFR) [17] opposes the idea of a single header for all packets, as it excludes joint error control and forms a separate check sequence for each packet (or fragment). If an error occurs, only the corrupted packets/fragments are retransmitted. Such a technique has already been used to improve communication performance in low data rate networks [31], to reduce delay, as well as in high data rate networks [17], to preserve delay and throughput efficiency in a case of the data rate change. The retransmission of packets/fragments of unequal and variable length was considered in [32,33], but transmitting the length of each particular packet is an additional overhead burden.

As an application of the splitting code, we propose a hybrid ARQ procedure with incremental redundancy for fragment retransmission. Each splitting sub-word is allocated to a single fragment, while incremental redundancy is formed as auxiliary splitting control symbols, two per each sub-word. To avoid ambiguities, in this context the splitting code-word provided with overhead is regarded as a “frame”, and the corresponding splitting sub-words are regarded as “fragments”.

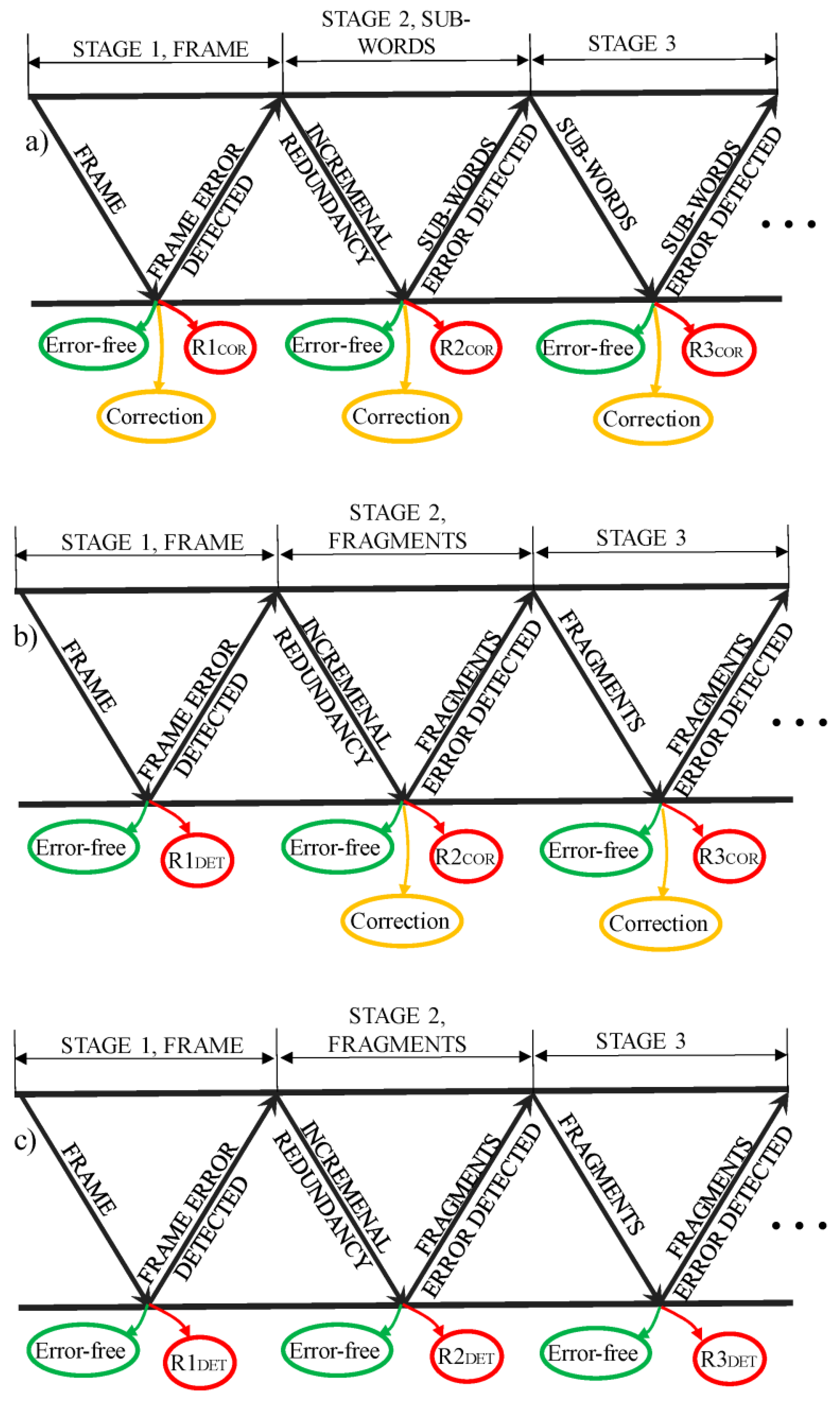
The proposed procedure comprises three-stage retransmission that can be followed by a standard automatic repeat request (ARQ). In the first stage, the auxiliary splitting control symbols, $C_{i1}$ and $C_{i2}$, formed during the coding procedure, are stored, while the control symbols, $C_1$ and $C_2$, are transmitted alongside the frame. In the case of a negative response (NAK), in the second stage, the stored auxiliary splitting control symbols are transmitted. The fragments and splitting controls are coupled and checked for errors. In the third stage, only the unacknowledged fragments are retransmitted. If the failure of the same fragment persists, subsequent fragment retransmissions follow a standard ARQ, according to the scheduled maximal number of retransmissions.

The splitting code offers easy switching between error correction and error detection, so there are several possible scenarios. Scenario (a) includes error correction both in the first and in the second stage, as shown in Figure 6a. If multiple frame errors occur, some of them can be falsely perceived as correctable—the residual frame errors, R1_COR, in Figure 6a. The remaining multiple errors are detected, and for these frames, the auxiliary check symbols (incremental redundancy) are sent within the second stage. At the receiver, the check symbols are coupled with already received fragments. The third stage is initiated for fragments with multiple errors. Such errors can be either missed (residual fragment errors, R2_COR and R3_COR in Figure 6) or detected. The fragments with detected errors are retransmitted in the third stage, and, if their erroneous status persists, retransmitted again following the standard ARQ procedure.

In scenario (b), in the first stage, error detection is performed, and the incremental redundancy is sent for all the frames with the non-zero syndrome(s), while the correction is performed in the second stage (Figure 6b). In scenario (c), no error correction is performed (Figure 6c) at any stage. The last scenario (d) includes error correction in the first stage, and detection at the subsequent stages.

Regarding residual errors if only error detection is performed, R1_DET, R2_DET, R3_DET in Figure 6 correspond to the residual errors of the Fletchers error-detection checksums with detection capabilities comparable to the cyclic redundancy check (CRC) codes [10]. As already stated, the splitting FEC code is based on the Fletchers checksums, so if the error correction is turned off, the code is reverted to its detection origins, and the only residual frames/fragments errors are the ones when the code falsely declares a no-error event.

Figure 6. Different scenarios of the proposed hybrid incremental ARQ based on splitting code: (a) error correction performed at frame and at fragment stages; (b) error correction performed at fragment stages only; (c) no error correction performed. Frame, its incremental redundancy and its erroneous fragments are sent in stages 1, 2 and 3, respectively. The frames/fragments that are error-free, corrected or with residual errors require no further transmissions.

Figure 6. Different scenarios of the proposed hybrid incremental ARQ based on splitting code: (a) error correction performed at frame and at fragment stages; (b) error correction performed at fragment stages only; (c) no error correction performed. Frame, its incremental redundancy and its erroneous fragments are sent in stages 1, 2 and 3, respectively. The frames/fragments that are error-free, corrected or with residual errors require no further transmissions.

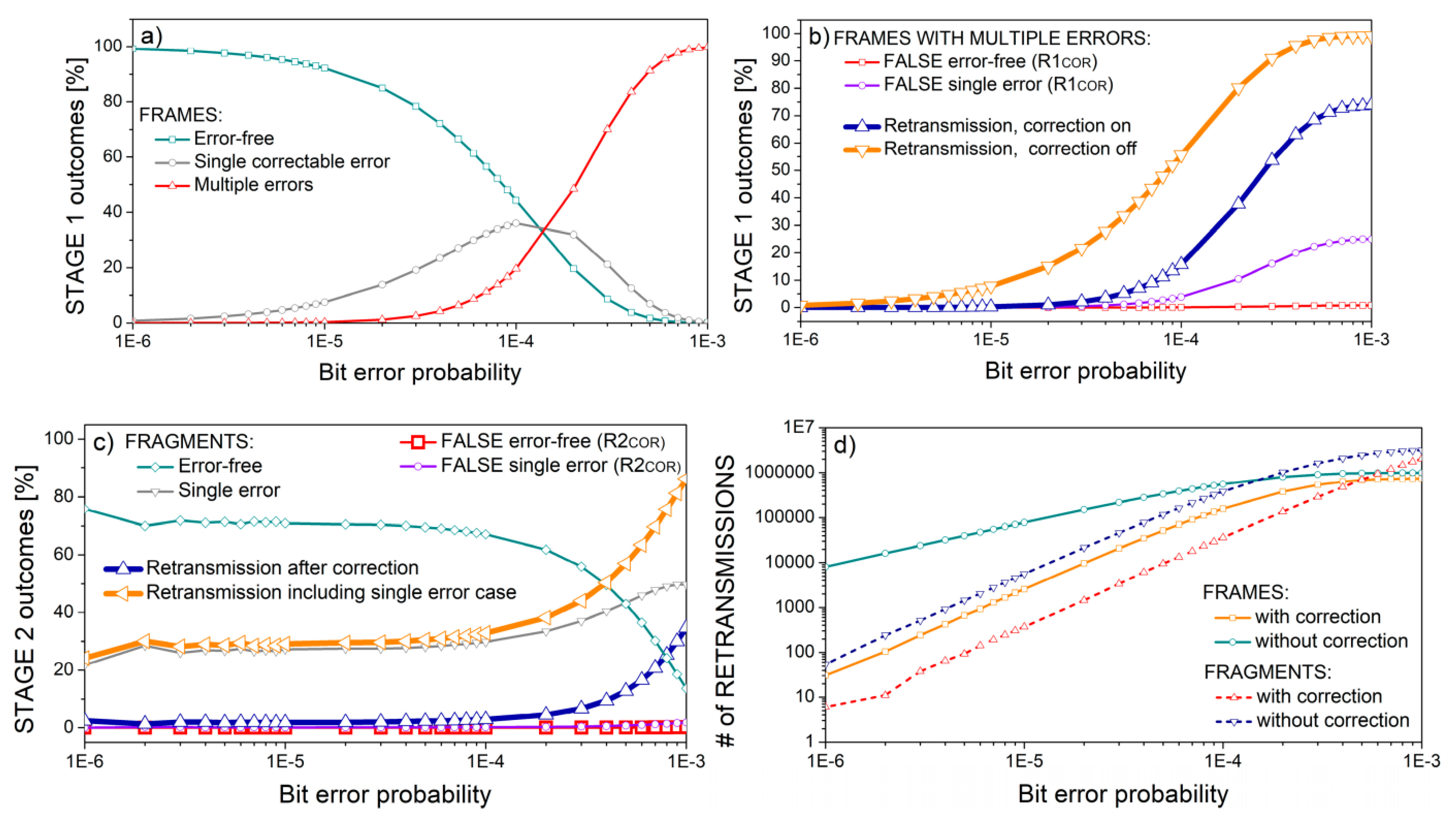
Figure 7 shows the stage outcomes for the frames comprising m = 8 symbols, with fragment length equal to 2^m−1 − 1 = 127 symbols, half of its theoretical maximum. The number of fragments per frame is set to the theoretical maximum (eight fragments, Table 2). The simulation is performed in the Gaussian noise environment. The distribution of frames according to errors is shown in Figure 7a. Figure 7b shows the cases of multiple error frames when errors can be either detected or missed. Fragment distribution in the case of frames with multiple errors is shown in Figure 7c. To gain a better insight into the decrease in retransmissions if error correction is turned on, the absolute number of both frame and fragment retransmissions is presented in Figure 7d. Retransmission decrease is at the cost of increased residual errors that comprise both “FALSE single error” and “FALSE error-free” cases from Figure 7b,c.

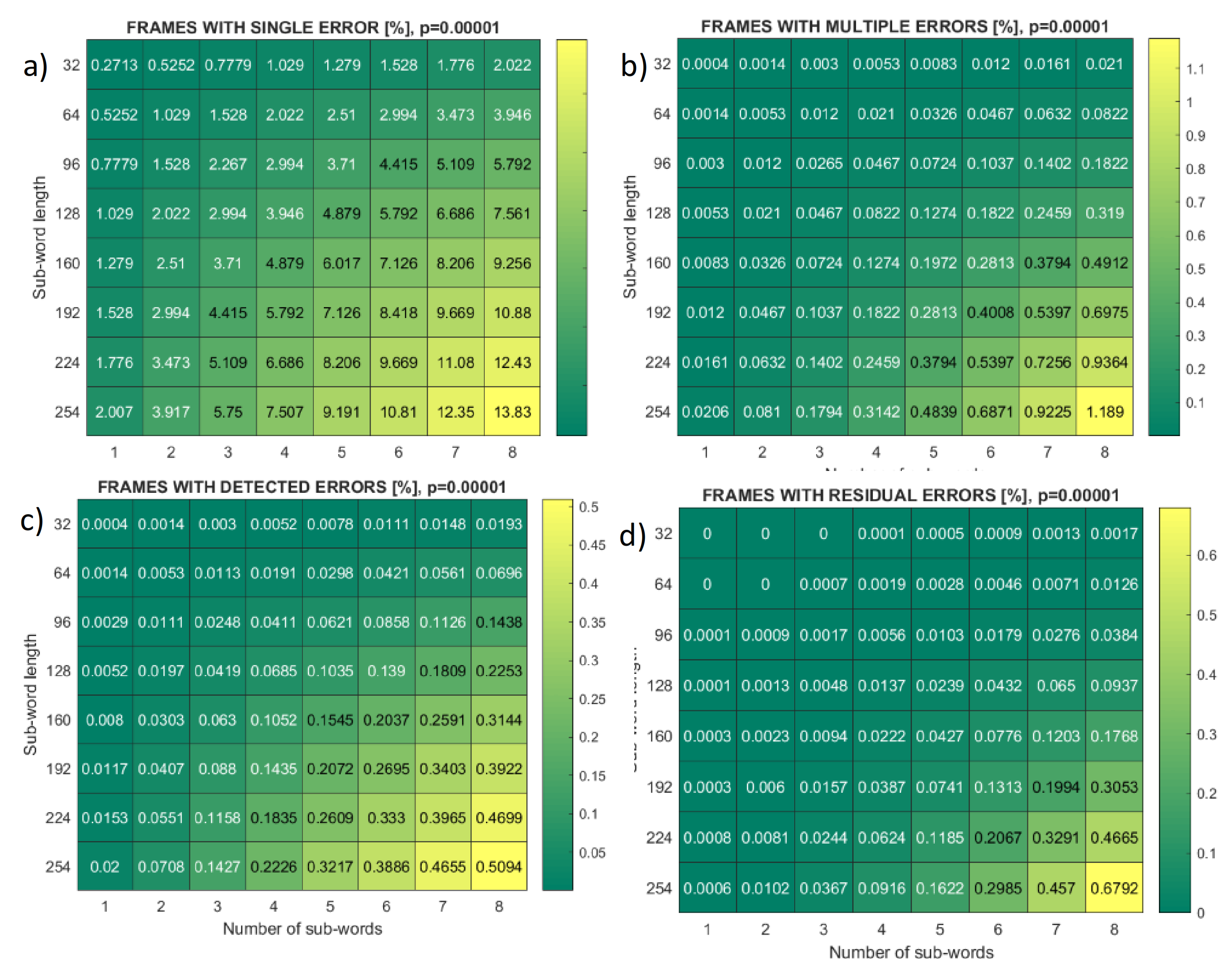
Figure 8 presents m = 8 frame statistics for bit error rate p = 10⁻⁵ and different pairs of fragment length and number. Heat maps cover the statistics of single-error frames, multiple-error frames, frames with detected errors (retransmitted incremental redundancy), and frames with residual errors. It can be seen that the percentage of frames with residual errors is below the percentage of frames with multiple errors detected, except when both the length and number of fragments are at their maximal values.

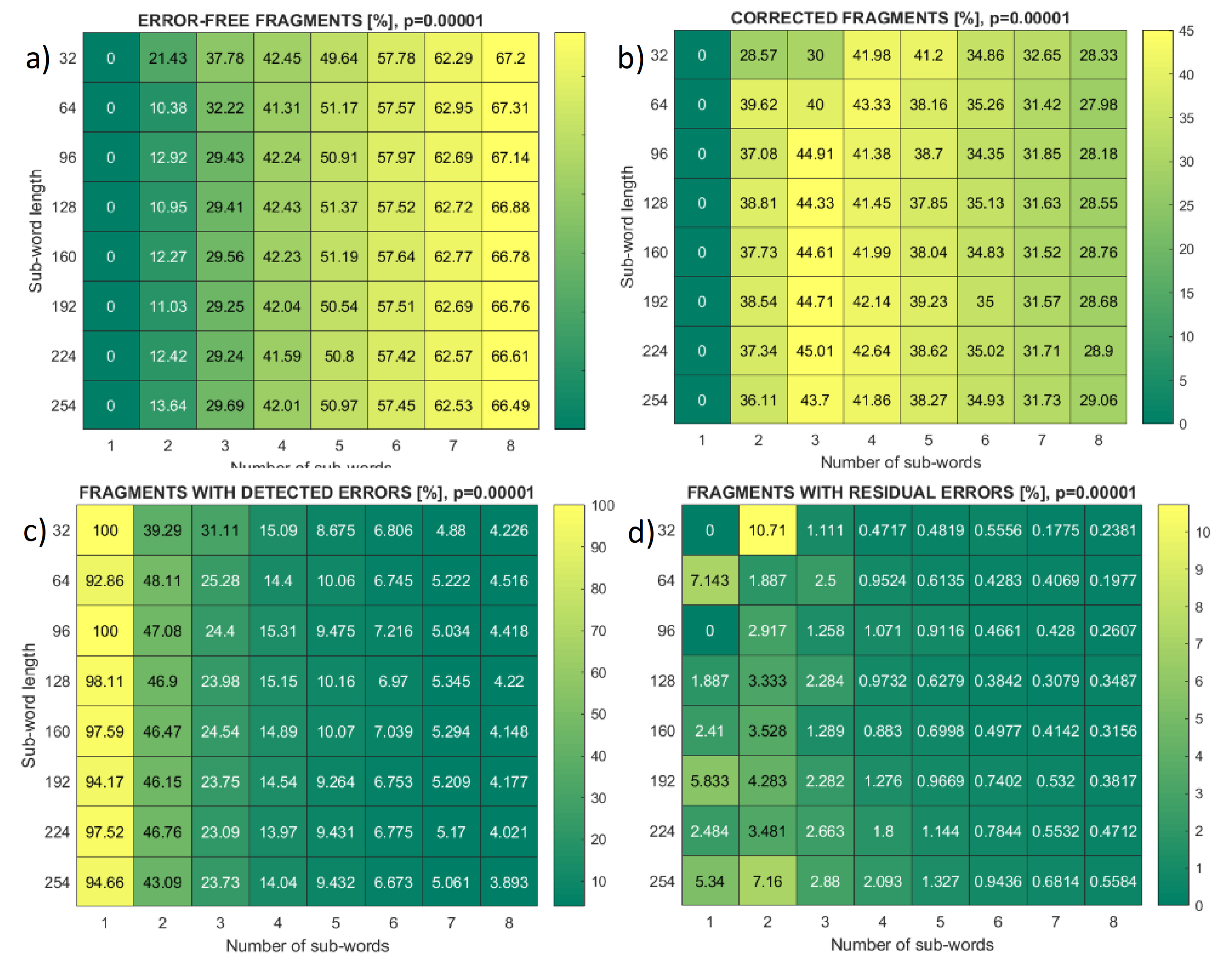
Figure 9 presents similar heat maps, but for fragments of frames that contain multiple errors. If a frame with multiple errors comprises only one fragment, then this fragment also contains multiple errors and cannot be corrected, as shown in the leftmost columns of Figure 9a,b. Figure 9c,d show that the percentage of fragments with detected errors in all cases exceeds the percentage of fragments with residual error.

Figure 8. Heat maps of frame error events, symbol length m = 8, bit error rate p = 10⁻⁵, for different fragments (sub-words) number and length. (a) Single error; (b) multiple errors; (c) detected errors; (d) missed (residual) errors.

Figure 8. Heat maps of frame error events, symbol length m = 8, bit error rate p = 10⁻⁵, for different fragments (sub-words) number and length. (a) Single error; (b) multiple errors; (c) detected errors; (d) missed (residual) errors.

Figure 9. Heat maps of fragment error events, symbol length m = 8, bit error rate p = 10⁻⁵, for different fragments (sub-words) number and length within a frame. (a) Error-free fragments; (b) single error; (c) detected errors; (d) missed (residual) errors.

Figure 9. Heat maps of fragment error events, symbol length m = 8, bit error rate p = 10⁻⁵, for different fragments (sub-words) number and length within a frame. (a) Error-free fragments; (b) single error; (c) detected errors; (d) missed (residual) errors.

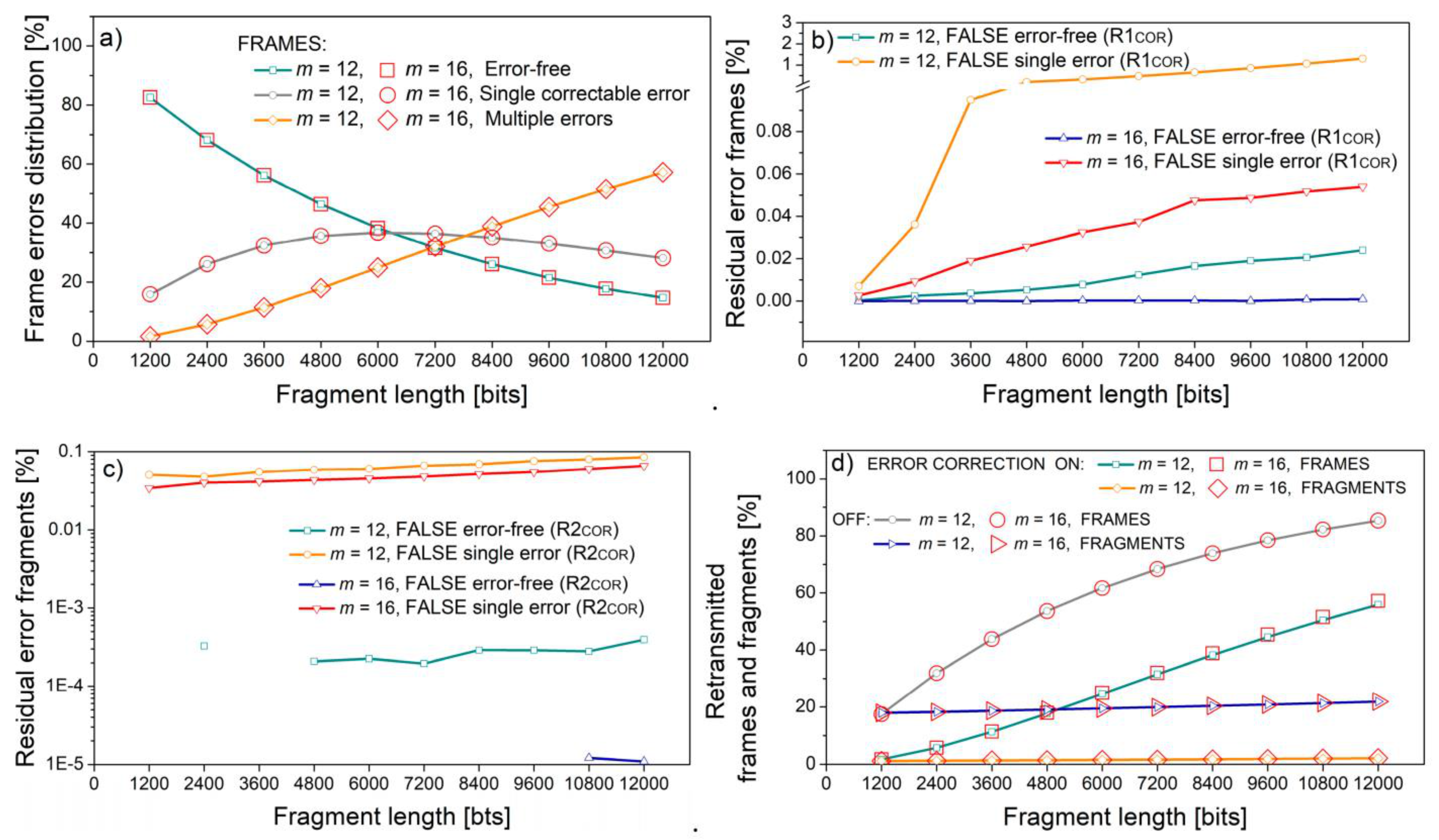
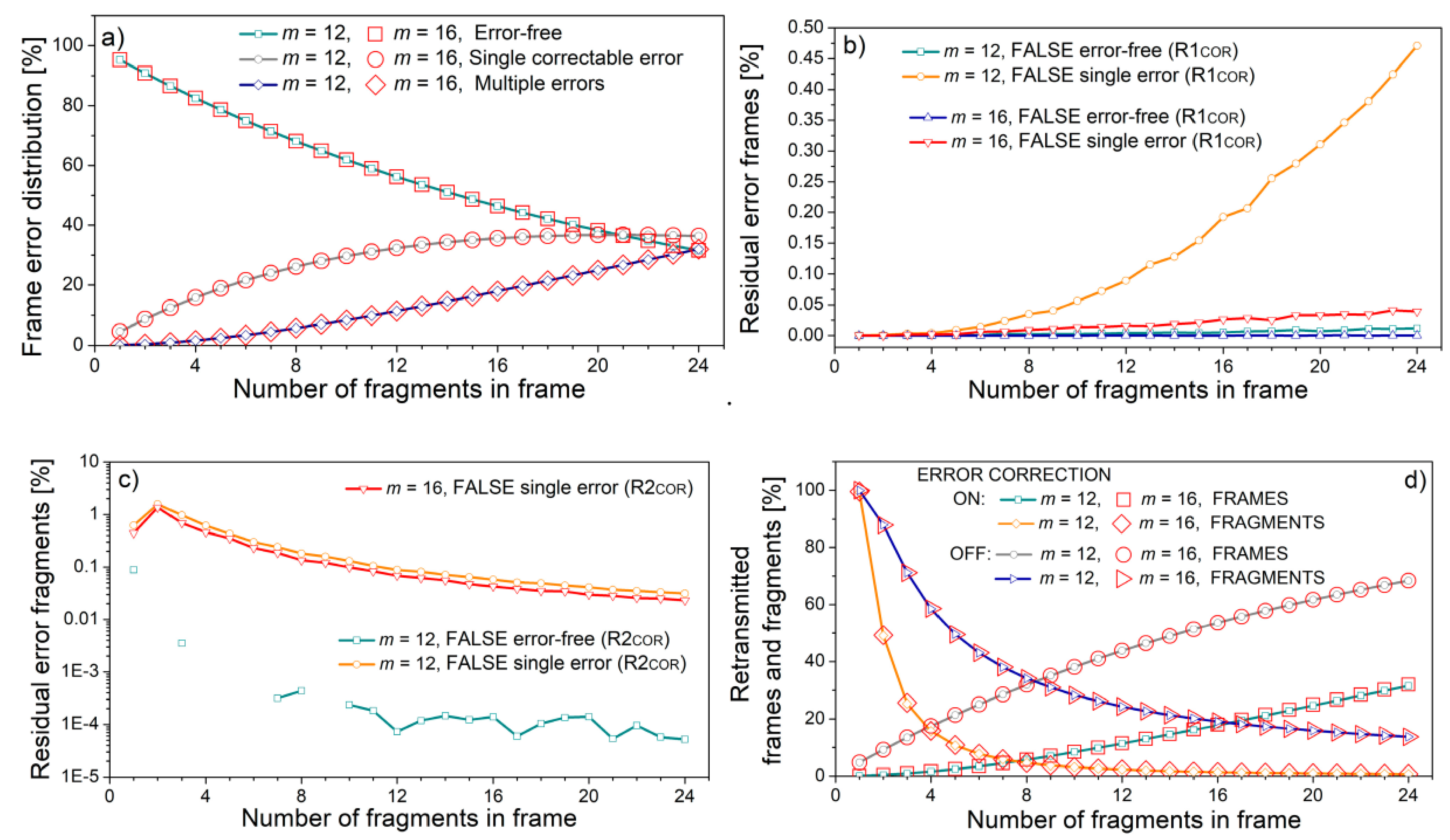
The influence of the fragment (sub-word) length is presented in Figure 10, for bit error rate p = 10⁻⁵, with frames consisting of sixteen fragments, and two types of symbols, m = 12 and m = 16. The respective fragment lengths in bits are equal, as the length of 100 symbols with m = 12 is equivalent to 75 symbols with m = 16, providing the same frame error distribution in both cases (Figure 10a). The difference between m = 12 and m = 16 cases is observed in residual errors, both for frames (Figure 10b) and fragments (Figure 10c). The residual errors for m = 16 are well below the m = 12 case, due to the increased control redundancy per the same information content. However, although the difference in absolute values exists, it is by several orders of magnitude lower than the retransmission rate and does not alter it significantly (Figure 10d).

The influence of the number of fragments within a frame is presented in Figure 11 for bit error rate p = 10⁻⁵, and a fragment length equal to 400 symbols if m = 12, and 300 symbols if m = 16. In both cases, the fragment length is equal to 4800 bits. Again, the difference between two symbol types is only reflected in residual errors (Figure 11b,c). Again, these changes do not affect the retransmission rate.

5. Discussion and Conclusions

The proposed splitting code corrects a single-bit error operating the m bit integer ring. It corrects also corrects multiple bit errors within the symbol, provided that their integer weight corresponds to a single bit error weight (Figure 5). The coding, syndrome forming, and error correction procedures are simple (Figure 2). The code rate for codes of maximal length is almost equivalent to the extended Hamming code, especially if SpC is defined using the Mersenne primes (Figure 4). The slight difference is because the extended Hamming code additionally detects an even number of errors, while SpC corrects additional error patterns, and can additionally detect some other errors, especially in its shortened versions (Figure 3).

Error correction can be easily turned off; then, splitting code becomes equivalent to Fletcher’s checksums for error detection.

The code-word of splitting code is partitioned in sub-words that correspond to the splitting set S (Figure 1). This partitioning is suitable for mapping the individual packets into sub-words to form an aggregated frame—code-words with joint control symbols and joint headers. The byproducts of the coding procedure for each particular sub-word form auxiliary splitting control symbols that can be stored and transmitted if necessary. Thus, formed sub-code-words can also correct single-bit errors, except when defined using Mersenne primes when they correct single-symbol errors. Based on this feature, we proposed a hybrid incremental ARQ procedure as an application of SpC code. The procedure comprises three stages, with several implementation scenarios, based on turning the error correction on and off (Figure 6). In the first stage, a frame is transmitted, in a second, auxiliary control symbols are transmitted, and in the third, the sub-words (fragments) with detected errors are re-transmitted. Figure 7, Figure 8 and Figure 9 show the frame and fragment event distribution for m = 8 symbols. The results are presented as a percentage of all transmitted frames (Figure 7a,b,d and Figure 8), and as a percentage of all fragments from frames with multiple errors (Figure 7c,d and Figure 9). The figures show that the retransmission rate considerably decreases if the error correction is turned on (Figure 7b–d), but at the cost of increased residual frame and fragment rate. Residual errors are partitioned into falsely perceived error-free cases that persist if error correction is turned off, and into falsely perceived single-bit error cases, which are inherent in error-correcting scenarios. Both cases are equivalent and constant considering the fragments (Figure 7c), but the percentage of false single error frames increases with bit error probability.

Heat maps in Figure 8, for bit-error-rate p = 10⁻⁵, varies sub-words (fragments) length and number up to their maximal values which are, for m = 8, equal to 30 symbols and 8 sub-words, respectively. The frame statistic reveals that the portion of multiple-error frames that correspond to residual errors (sum of false error-free and false single-error events) is well below the portion of multiple error frames that correspond to detected errors that initiate the second stage of transmission. The exception is maximal-length frames for which most, or in the case of Mersenne primes, all syndrome values are reserved for correctable errors and very little remains for detection (Figure 8c,d). On the other hand, heat maps in Figure 9c,d reveal that the percentage of fragments with detected errors exceeds the number of fragments with residual errors for all sets of parameters.

The two leftmost columns in fragment heat maps in Figure 9 present the case of short frames, where the errors are less likely to appear. A small number of multiple error frames was hardly sufficient for reliable statistics in the case of such rare events as residual errors. For this reason, the colors in these columns of Figure 9d are not ordered. Considering the first column, it corresponds to the frames with only one sub-word. If the frame contains multiple errors, the sub-word also contains multiple errors, and the number of error-free or single-error cases is set to zero (Figure 9a,b).

Figure 10 and Figure 11 present the results for m = 12 and m = 16. These symbol lengths are chosen as they correspond to 150% and 200% of a classical eight-bit byte. In both figures, the abscissa shows the frame length in increasing order: in Figure 10, due to the increase in the fragment length, and in Figure 11, due to the increase in the number of fragments. For this reason, the graphs showing the percentage of residual error frames in Figure 10b and Figure 11b, and the percentage of residual error fragments in Figure 10c and Figure 11c follow a similar trend both for frames and fragments.

However, the trends of frame and fragment retransmission rates differ (Figure 11d). Frame retransmission increases with frame size as multiple errors are more likely to occur in long frames, but fragment retransmission decreases. The reason lies in the fact that fragment retransmission is only possible if the frame contains multiple errors. Only in this case does the ARQ procedure enter stage two. If there is just a single fragment within the frame, all the errors are located within this fragment and the retransmission will surely occur. If the number of fragments is greater than one but still small, the multiple errors from the frame are divided among the small number of fragments. Consequently, the probability that some fragments will contain more than one error is high, resulting in retransmission. This is the reason for the increased retransmission rate for a small number of fragments in Figure 11d, also observable in Figure 9c.

In Figure 10, the number of fragments is set to 16, which is 22.22% of the maximum for m = 12, and only 1.5626% of the maximum for m = 16. Similarly, in Figure 11, fragment (sub-word) length is set to 4800 bits, which is 400 symbols—9.77% of maximal length for m = 12, and 300 symbols—0.46% of maximal length for m = 16. In other words, for the same code-word (frame) and sub-word (fragment) parameters, the m = 16 case occupies a lower portion of the code-word space than the m = 12 case. This difference, coupled with the increased protective redundancy, is reflected in a considerably lower number of false single-error frames and false error-free fragments. The number of false error-free frames and false single-error fragments is also lower, but only slightly. These values are of the order of a fraction of percent, so their influence on the total retransmission rate is very low. However, in a trade-off between the retransmissions, latency, power requirements, and residual errors when error corrections are turned on and off, these differences give the platform for optimization study, also considering different scenarios with error correction on and off, and in errors in more realistic surroundings than Gaussian. This will be the subject of our further research.

6. Patents

Some segments of this work are based on the following patent applications:

• D. Bajić, National patent no. 54806, “Low power error control code for aggregated packets of unequal length”, pp 8–14 (for Table 1 and Table 2) and pp 14–17 (for Table 3). http://pub.zis.gov.rs/rs-pubserver/document?iDocId=90253&iepatch=.pdf, 1 August 2016.
• D. Bajić, National patent no. 54807, “Hybrid error-control procedure with selective retransmission for aggregated unequal length packet transmission using low power integer code“, 1 August 2016.