A Fast Fixed-Point Algorithm for Convex Minimization Problems and Its Application in Image Restoration Problems

Abstract

In this paper, we introduce a new iterative method using an inertial technique for approximating a common fixed point of an infinite family of nonexpansive mappings in a Hilbert space. The proposed method’s weak convergence theorem was established under some suitable conditions. Furthermore, we applied our main results to solve convex minimization problems and image restoration problems.

1. Introduction

Let us first mention a mathematical scheme for an image restoration problem, as well as some algorithms that will be employed to solve it. The following linear pattern is a simple pattern of an image restoration problem, that is,

$$Ax=b+y,$$

(1)

where $A\in {\mathbb{R}}^{m\times n}$ is the blurring operation, $x\in {\mathbb{R}}^{n\times 1}$ is an image, $b\in {\mathbb{R}}^{m\times 1}$ is the observed image, and y is an additive noise. The image restoration problem is finding the original image $x^{\star }\in {\mathbb{R}}^{n\times 1}$ that satisfies (1). It is well known that the image restoration problem is a dominant topic in image processing.

In order to find the solution of the problem (1), we minimize the additive noise to approximate the original image by using the method known as the least squares (LS) problem:

$$\underset{x}{min}\left\{{\parallel Ax-b\parallel }_2^2\right\},$$

(2)

where $\parallel ·\parallel$ is an ${\ell }_2$-norm defined by ${\parallel x\parallel }_2=\sqrt{{\sum }_{k=1}^n{\left|x_k\right|}^2}.$ There are many iterations that can solve the problem (2) such as the Richardson iteration; see [1] for the details. However, the number of unknown variables is much more than the observations that cause (2) to be an ill-posed problem because of a huge norm result, which is thus meaningless; see [2,3]. Therefore, in order to improve the ill conditioned least squares problem, several regularization methods were introduced. One of the most popular regularization methods is the Tikhonov regularization suggested by Tikhonov; see [4]. It is defined to solve the following minimization problem:

$$\underset{x}{min}\left\{{\parallel Ax-b\parallel }_2^2+\beta {\parallel Lx\parallel }_2^2\right\},$$

(3)

where $\beta$ is called a positive regularization parameter and $L\in {\mathbb{R}}^{m\times n}$ is called the Tikhonov matrix. In the standard form, L is set to be the identity. In statistics, (3) is known as a ridge regression. To improve the original LS (2) and classical regularization such as subset selection and ridge regression (3) for solving (1), Tibshirani [5] defined a new method, called the least absolute shrinkage and selection operator (LASSO) model, as the following form:

$$\underset{x}{min}\left\{{\parallel Ax-b\parallel }_2^2+\beta {\parallel x\parallel }_1\right\},$$

(4)

where $\beta$ is a positive regularization parameter, ${\parallel x\parallel }_1={\sum }_{k=1}^n\left|x_k\right|$, and ${\parallel x\parallel }_2=\sqrt{{\sum }_{k=1}^n{\left|x_k\right|}^2}.$ This model can be used to solve the problem (1) utilizing optimization methods; see [5,6] for instances. The problem presented in (4) can be extended to the general natural formulation as follows:

$$\underset{x}{min}\left\{\varphi \left(x\right)+\psi \left(x\right)\right\}.$$

(5)

The solution of Problem (5) is usually established under the following assumptions:

(i)

$\psi$ is a lower semicontinuous function and proper convex from a Hilbert space H into $\mathbb{R}\cup \{+\infty \}$;

(ii)

$\varphi$ is a convex differentiable function from H into $\mathbb{R}$ with $\nabla \varphi$ being ℓ-Lipschitz constant for some $\ell >0,$ that is, $\parallel \nabla \varphi \left(x\right)-\nabla \varphi \left(y\right)\parallel \le \ell \parallel x-y\parallel$ for all $x,y\in {\mathbb{R}}^n.$

The set of all solutions of the problem (5) will is denoted by argmin$(\varphi +\psi )$.

It is well known that if $x^{\star }\in$ argmin$(\varphi +\psi )$, then the solution of (5) can be reformulated as the problem of finding a zero-solution $x^{\star }$ such that:

$$0\in \partial \psi \left(x^{\star }\right)+\nabla \varphi \left(x^{\star }\right),$$

(6)

where $\nabla \varphi$ is the gradient operator of function $\varphi$ and $\partial \psi$ is the subdifferential of function $\psi$; see [7] for more details. Furthermore, Parikh and Boyd [8] solved the problem (6) by using the proximal gradient technique, that is if $x^{\star }$ solves (6), then:

$$x^{\star }={\mathrm{prox}}_{\kappa \psi }(I-\kappa \nabla \varphi )\left(x^{\star }\right),$$

where $\kappa$ is a positive parameter, ${\mathrm{prox}}_{\kappa \psi }={(I+\kappa \partial \psi )}^{-1}$, and I is the identity operator. This means that $x^{\star }$ is a fixed point of the proximal operator. In [9,10,11], the authors guaranteed many important properties of proximal operators, for instance prox${}_{\kappa \psi }$ is well defined with a full domain, single-valued, and even nonexpansive.

In addition, the classical forward–backward splitting algorithm (FBS) [12] is generated by $x_1\in {\mathbb{R}}^n$ and:

$$x_{n+1}={\mathrm{prox}}_{{\kappa }_n\psi }(I-{\kappa }_n\nabla \varphi )\left(x_n\right),$$

(7)

where ${\kappa }_n\in (0,\frac{2}{\ell })$ is the step size and I is the identity operator with prox${}_{\psi }$ the proximity operator of $\psi$ defined by prox${\displaystyle {}_{\psi }\left(x\right):=\arg \underset{y\in {\mathbb{R}}^n}{min}\left\{\varphi \left(y\right)+\frac{1}{2}{\parallel x-y\parallel }_2^2\right\};}$ see [13] for more details. Because of its simplicity, the method (7) has been widely utilized to solve the problem (5), and as a result, it has been enhanced by many works, as seen in [11,14,15,16].

From the work [8], it is worth noting that the fixed-point theory can be applied to solve the problem (5). The fixed-point theory plays a very important role for solving many problems in science, data science, economics, medicine, and engineering; see [11,17,18,19,20,21,22,23] for more details. There are several methods for finding the approximate solutions of fixed-point problems; see [24,25,26,27,28,29,30]. Shoaib [31] proved a result of Al Mazrooei et al. [32] by using new contractive conditions on a closed set in b-multiplicative metric space. They obtained a unique common solution of Fredholm multiplicative integral equations. Recently, Kim [33] introduced the coupled Mann pair iterative scheme for a common coupled fixed point in Hilbert spaces.

In order to accelerate the convergence rate of the studied methods, Polyak [34] introduced the technique for improving the rate of convergence and giving a better convergence behavior of those methods by adding an inertial step. The following iterative methods with an inertial step can be used for improving the performance of (7).

The inertial forward–backward splitting (IFBS) was presented by Moudafi and Oliny in [35] as follows:

$$\left\{\begin{array}{c}{z}_n=x_n+{\rho }_n(x_n-x_{n-1}),\hfill \\ x_{n+1}={\mathrm{prox}}_{{\kappa }_n\psi }(z_n-{\kappa }_n\nabla \varphi \left(x_n\right)),\hfill \end{array}\right.$$

where $x_0,x_1\in {\mathbb{R}}^n,{\kappa }_n\in (0,\frac{2}{\ell })$, and ${\rho }_n$ is the inertial parameter that controls the momentum $x_n-x_{n-1}$. The convergence of the IFBS can be guaranteed by proper choices of ${\kappa }_n$ and ${\rho }_n$.

The fast iterative shrinkage-thresholding algorithm (FISTA) is defined by:

$$\left\{\begin{array}{c}{z}_n={\mathrm{prox}}_{\frac{1}{\ell }\psi }(x_n-\frac{1}{\ell }\nabla \varphi \left(x_n\right)),\hfill \\ t_{n+1}=\frac{1+\sqrt{1+4t_n^2}}{2},{\rho }_n=\frac{t_n-1}{t_{n+1}},\hfill \\ x_{n+1}=z_n+{\rho }_n(z_n-z_{n-1}),\hfill \end{array}\right.$$

where $n\in \mathbb{N},x_1=z_0\in {\mathbb{R}}^n$, and $t_1=1.$ This notion was suggested by Beck and Teboulle [6]. They also proved the FISTA’s convergence rate and applied it to solve image restoration problems.

Recently, Verma and Shukla [16] proposed the new accelerated proximal gradient algorithm (NAGA) as follows:

$$\left\{\begin{array}{c}{z}_n=x_n+{\rho }_n(x_n-x_{n-1}),\hfill \\ y_n=(1-{\tau }_n)z_n+{\tau }_n{\mathrm{prox}}_{{\kappa }_n\psi }(z_n-{\kappa }_n\nabla \varphi \left(z_n\right)),\hfill \\ x_{n+1}={\mathrm{prox}}_{{\kappa }_n\psi }(y_n-{\kappa }_n\nabla \varphi \left(y_n\right)),\hfill \end{array}\right.$$

where $n\in \mathbb{N},x_0,x_1\in {\mathbb{R}}^n,{\tau }_n\in (0,1),{\kappa }_n\in (0,\frac{2}{\ell }),$ and ${\rho }_n\in (0,1)$ is the inertial parameter, which controls the momentum $x_n-x_{n-1}$. The authors proved NAGA’s convergence theorem under the condition $\frac{\parallel x_n-x_{n-1}{\parallel }_2}{{\rho }_n}\to 0$ and applied it to solve the convex minimization problem for a multitask learning framework using sparsity-inducing regularizes.

Motivated and inspired by all the works mentioned above, in this article, we introduced a new iterative method for the approximation of a common fixed point of an infinite family of nonexpansive mappings in Hilbert spaces. We also proved weak convergence theorems of the introduced method under some suitable conditions. Furthermore, we applied our main results for solving a convex minimization problem and image restoration problems.

This paper is organized as follows: The next section proposes some preliminary results that will be utilized throughout the paper. In Section 3, we introduce a new accelerated algorithm using the inertial techniques and analyze its weak convergence to the solution (5). After that, we apply our main results to solving image restoration problems, and some numerical experiments of the proposed methods are given in Section 4. In the last section, we present the brief conclusion of our work.

2. Preliminaries

Throughout this article, let $\mathbb{N}$ and $\mathbb{R}$ be the set of positive integers and real numbers, respectively. Let H be a real Hilbert space with the inner product $\langle ·,·\rangle$ and the norm $\parallel ·\parallel$ induced by the inner product. The weak and strong convergences of $\left\{x_n\right\}$ in H are denoted by $x_n\rightharpoonup x$ and $x_n\to x$, respectively, for each sequence $\left\{x_n\right\}$ in H.

Let C be a nonempty closed convex subset of a real Hilbert space H. A mapping T from C into itself is said to be an ℓ-Lipschitz operator if there exists $\ell >0$ such that:

$$\parallel Tx-Ty\parallel \le \ell \parallel x-y\parallel ,\forall x,y\in C.$$

If $\ell =1$, then T is called a nonexpansive operator. The set of all fixed points of T is denoted by $F\left(T\right)$, that is $F\left(T\right)=\{x\in C:Tx=x\}.$ Let $\left\{T_n\right\}$ and $\Omega$ be families of nonexpansive mappings of C into itself such that $\varnothing \ne F(\Omega )\subset F:={\cap }_{n=1}^{\infty }F\left(T_n\right)$, where $F(\Omega )$ is the set of all common fixed points of $\Omega .$

A sequence $\left\{T_n\right\}$ is said to satisfy the NST condition $\left(I\right)$ with $\Omega$ [36], if for every bounded sequence $\left\{x_n\right\}$ in C,

$$\underset{n\to +\infty }{lim}\parallel x_n-T_n{x}_n\parallel =0⟹\underset{n\to +\infty }{lim}\parallel x_n-T{x}_n\parallel =0,\forall T\in \Omega .$$

Note that $\left\{T_n\right\}$ is said to satisfy the NST condition $\left(I\right)$ with T when $\Omega$ is a singleton, that is $\Omega =\left\{T\right\}.$ After that, the concept of the NST${}^{\star }$ condition was introduced by Nakajo et al. [37], and the examples of mappings that satisfy the NST${}^{\star }$ condition were given.

A sequence $\left\{T_n\right\}$ is said to satisfy the NST${}^{\star }$ condition if for every bounded sequence $\left\{x_n\right\}$ in $C,$

$$\underset{n\to \infty }{lim}\parallel x_n-T_n{x}_n\parallel =0=\underset{n\to \infty }{lim}\parallel x_n-x_{n+1}\parallel ⟹{\omega }_w\left(x_n\right)\subset \Omega ,$$

where ${\omega }_w\left(x_n\right)$ is the set of all weak cluster points of $\left\{x_n\right\}$.

Note that the NST${}^{\star }$ condition is more general than the NST condition $\left(I\right)$. It can be directly obtained from the definition given above that if $\left\{T_n\right\}$ satisfies the NST condition $\left(I\right)$, then $\left\{T_n\right\}$ satisfies the NST${}^{\star }$ condition.

Lemma 1

([38,39]). Let H be a real Hilbert space. For any $u,v\in H$ and $r\in [0,1]$, the following results hold:

(i) 

${\parallel u-v\parallel }^2={\parallel x\parallel }^2-2\langle u,v\rangle +{\parallel v\parallel }^2;$

(ii) 

${\parallel ru+(1-r)v\parallel }^2={r\parallel u\parallel }^2+{(1-r)\parallel v\parallel }^2-r(1-r){\parallel u-v\parallel }^2.$

The identity in Lemma 1 (ii) implies that the following equality holds:

$${\parallel ru+sv+tw\parallel }^2={r\parallel u\parallel }^2+{s\parallel v\parallel }^2+{t\parallel w\parallel }^2{-rs\parallel u-v\parallel }^2{-st\parallel v-w\parallel }^2-rt{\parallel u-w\parallel }^2$$

(8)

for all $u,v,w\in H$ and $r,s,t\in [0,1]$ with $r+s+t=1.$

In proving our main theorem, we need the following lemmas.

Lemma 2

([40]). Let $\left\{u_n\right\},\left\{v_n\right\}$, and $\left\{w_n\right\}$ be sequences of nonnegative real numbers such that $u_{n+1}\le (1+w_n)u_n+v_n$ for all $n\in \mathbb{N}.$ If ${\sum }_{n=1}^{\infty }{w}_n<+\infty$ and ${\sum }_{n=1}^{\infty }{v}_n<+\infty ,$ then ${lim}_{n\to +\infty }{u}_n$ exists.

Lemma 3

([35]). Let H be a Hilbert space, and let $\left\{u_n\right\}$ be a sequence in H such that there exists a nonempty set $F\subset H$ satisfying: for every $p\in F,{lim}_{n\to +\infty }\parallel u_n-p\parallel$ exists. Any weak cluster point of $\left\{u_n\right\}$ is in $F.$ Then, there exists u in F with $\left\{u_n\right\}$ converging weakly to $u.$

We end this section with the following lemmas, which will be used to prove our main results in the next section.

Lemma 4

([41]). Let $\left\{u_n\right\}$ and $\left\{{\rho }_n\right\}$ be sequences of nonnegative real numbers such that $u_{n+1}\le (1+{\rho }_n)u_n+{\rho }_n{u}_{n-1}$ for all $n\in \mathbb{N}.$ Then, the following holds

$$u_{n+1}\le M·\prod _{j=1}^n(1+2{\rho }_j),$$

where $M=max\{u_1,u_2\}.$ Moreover, if ${\sum }_{n=1}^{\infty }{\rho }_n<+\infty ,$ then $\left\{u_n\right\}$ is bounded.

Recall the definition of the forward–backward operator of lower semicontinuous and convex functions $\varphi ,\psi :{\mathbb{R}}^n\to (-\infty ,+\infty )$ as follows: A forward–backward operator T is defined by $T:={\mathrm{prox}}_{\kappa \psi }(I-\kappa \nabla \varphi )$ for $\kappa >0,$ where $\nabla \varphi$ is the gradient operator of function $\varphi$ and ${\mathrm{prox}}_{\kappa \psi }(I-\kappa \nabla \varphi )x:=\arg {min}_{y\in H}\{\psi \left(y\right)+\frac{1}{2\kappa }{\parallel y-x\parallel }^2\}$ (see [7,11]). The operator prox${}_{\kappa \psi }$ was defined by Moreak in 1962 [42] and called the proximity operator with respect to $\kappa$ and $\psi$. We know that T is a nonexpansive mapping whenever $\kappa \in (0,\frac{2}{\ell })$.

Lemma 5

([14]). Let ψ be a lower semicontinuous function and proper convex from a Hilbert space H into $\mathbb{R}\cup \{+\infty \}$, and let ϕ be a convex differentiable function from H into $\mathbb{R}$ with $\nabla \varphi$ being ℓ-Lipschitz constant for some $\ell >0.$ Let T be the forward–backward operator of ϕ and ψ. A sequence $\left\{T_n\right\}$ satisfies the NST condition (I) with T if $\left\{T_n\right\}$ is the forward–backward operator of ϕ and ψ such that ${\kappa }_n\to \kappa$ with ${\kappa }_n,\kappa \in \left(0,\frac{2}{\ell }\right).$

3. Main Results

In this section, we begin by formally introducing a new algorithm for finding a common fixed point of a countable family of nonexpansive mappings in a real Hilbert space H. Let $\{T_n:H\to H\}$ be a family of nonexpansive mappings with $\left\{{\tau }_n\right\},\left\{{ϵ}_n\right\},\left\{{\mu }_n\right\}$, and $\left\{{\zeta }_n\right\}$ being sequences in $(0,1)$.

Next, we prove a weak convergence theorem of Algorithm 1 for a family of nonexpansive mappings in a real Hilbert space.

Algorithm 1: (MSA): A modified S-algorithm.

Initial. Take $x_0,x_1\in H$ arbitrarily and $n=1$. Choose ${\rho }_n\ge 0$ and ${\sum }_{n=1}^{\infty }{\rho }_n<+\infty$.  Step 1. Compute $z_n,y_n$, and $x_{n+1}$ using: $$\left\{\begin{array}{c}{z}_n=x_n+{\rho }_n(x_n-x_{n-1}),\hfill \\ y_n=(1-{\tau }_n-{ϵ}_n)z_n+{\tau }_n{T}_n{z}_n+{ϵ}_n{T}_n{x}_n,\hfill \\ x_{n+1}=(1-{\mu }_n-{\zeta }_n)y_n+{\mu }_n{T}_n{z}_n+{\zeta }_n{T}_n{y}_n.\hfill \end{array}\right.$$  Then, update $n:=n+1$, and go to Step 1.

Theorem 1.

Let H be a real Hilbert space, and let $\{T_n:H\to H\}$ be a family of nonexpansive mappings such that $F:={\cap }_{n=1}^{\infty }F\left(T_n\right)\ne \varnothing$. Let $\left\{x_n\right\}$ be a sequence generated by Algorithm 1 and $\left\{{\tau }_n\right\},\left\{{ϵ}_n\right\}\left\{{\mu }_n\right\}$, and $\left\{{\zeta }_n\right\}$ be sequences in $(0,1)$ satisfying the following conditions:

(i) 

${\displaystyle 0<\underset{n\to \infty }{lim\; inf}({\tau }_n+{ϵ}_n)\le \underset{n\to \infty }{lim\; sup}({\tau }_n+{ϵ}_n)<1}$;

(ii) 

${\displaystyle 0<\underset{n\to \infty }{lim\; inf}{\tau }_n}$;

(iii) 

${\displaystyle 0<\underset{n\to \infty }{lim\; sup}{\mu }_n}$.

If $\left\{T_n\right\}$ satisfies the NST${}^{\star }$ condition, then $\left\{x_n\right\}$ converges weakly to an element in $F.$

Proof. 

Let $p\in F.$ Then, by Algorithm 1 and $T_n$ being nonexpansive, we have:

$$\parallel z_n-p\parallel =\parallel x_n+{\rho }_n(x_n-x_{n-1})-p\parallel \le \parallel x_n-p\parallel +{\rho }_n\parallel x_n-x_{n-1}\parallel ,$$

and:

$$\begin{array}{cc}\hfill \parallel y_n-p\parallel & =\parallel (1-{\tau }_n-{ϵ}_n)z_n+{\tau }_n{T}_n{z}_n+{ϵ}_n{T}_n{x}_n-p\parallel \hfill \\ \hfill & \le (1-{\tau }_n-{ϵ}_n)\parallel z_n-p\parallel +{\tau }_n\parallel T_n{z}_n-p\parallel +{ϵ}_n\parallel T_n{x}_n-p\parallel \hfill \\ \hfill & \le (1-{\tau }_n-{ϵ}_n)\parallel z_n-p\parallel +{\tau }_n\parallel z_n-p\parallel +{ϵ}_n\parallel x_n-p\parallel \hfill \\ \hfill & =(1-{ϵ}_n)\parallel z_n-p\parallel +{ϵ}_n\parallel x_n-p\parallel .\hfill \end{array}$$

It follows that:

$$\begin{array}{cc}\hfill \parallel y_n-p\parallel & \le (1-{ϵ}_n)[\parallel x_n-p\parallel +{\rho }_n\parallel x_n-x_{n-1}\parallel ]+{ϵ}_n\parallel x_n-p\parallel \hfill \\ \hfill & \le \parallel x_n-p\parallel +{\rho }_n\parallel x_n-x_{n-1}\parallel .\hfill \end{array}$$

The above inequality implies:

$$\begin{array}{cc}\hfill \parallel x_{n+1}-p\parallel & =\parallel (1-{\mu }_n-{\zeta }_n)y_n+{\mu }_n{T}_n{z}_n+{\zeta }_n{T}_n{y}_n-p\parallel \hfill \\ \hfill & \le (1-{\mu }_n-{\zeta }_n)\parallel y_n-p\parallel +{\mu }_n\parallel T_n{z}_n-p\parallel +{\zeta }_n\parallel T_n{y}_n-p\parallel \hfill \\ \hfill & \le (1-{\mu }_n-{\zeta }_n)\parallel y_n-p\parallel +{\mu }_n\parallel z_n-p\parallel +{\zeta }_n\parallel y_n-p\parallel \hfill \\ \hfill & =(1-{\mu }_n)\parallel y_n-p\parallel +{\mu }_n\parallel z_n-p\parallel \hfill \\ \hfill & \le (1-{\mu }_n)[\parallel x_n-p\parallel +{\rho }_n\parallel x_n-x_{n-1}\parallel ]+{\mu }_n[\parallel x_n-p\parallel +{\rho }_n\parallel x_n-x_{n-1}\parallel ]\hfill \\ \hfill & =\parallel x_n-p\parallel +{\rho }_n\parallel x_n-x_{n-1}\parallel \hfill \\ \hfill & \le \parallel x_n-p\parallel +{\rho }_n(\parallel x_n-p\parallel +\parallel p-x_{n-1}\parallel )\hfill \\ \hfill & =(1+{\rho }_n)\parallel x_n-p\parallel +{\rho }_n\parallel x_{n-1}-p\parallel .\hfill \end{array}$$

(9)

By Lemma 4, we obtain that $\parallel x_{n+1}-p\parallel \le M·{\prod }_{j=1}^n(1+2{\rho }_j),$ where $M=max\{\parallel x_1-p\parallel ,\parallel x_2-p\parallel \}.$ Since ${\sum }_{n=1}^{\infty }{\rho }_n<+\infty ,$ we obtain that $\left\{x_n\right\}$ is bounded. This together with ${\sum }_{n=1}^{\infty }{\rho }_n<+\infty$ give ${\sum }_{n=1}^{\infty }{\rho }_n\parallel x_n-x_{n-1}\parallel <+\infty .$ Using (9) and Lemma 2, we obtain that ${lim}_{n\to \infty }\parallel x_n-p\parallel$ exists for all $p\in F.$ Coming back to the definition of $y_n,$ from (8), one has that:

$$\begin{array}{cc}\hfill \parallel y_n{-p\parallel }^2& =\parallel (1-{\tau }_n-{ϵ}_n)(z_n-p)+{\tau }_n(T_n{z}_n-p)+{ϵ}_n(T_n{x}_n-p){\parallel }^2\hfill \\ \hfill & =(1-{\tau }_n-{ϵ}_n)\parallel z_n{-p\parallel }^2+{\tau }_n\parallel T_n{z}_n{-p\parallel }^2+{ϵ}_n{\parallel T_n{x}_n-p\parallel }^2\hfill \\ \hfill & -{\tau }_n(1-{\tau }_n-{ϵ}_n)\parallel z_n-T_n{z}_n{\parallel }^2-{\tau }_n{ϵ}_n{\parallel T_n{z}_n-T_n{x}_n\parallel }^2\hfill \\ \hfill & -{ϵ}_n(1-{\tau }_n-{ϵ}_n){\parallel z_n-T_n{x}_n\parallel }^2\hfill \\ \hfill & \le (1-{ϵ}_n)\parallel z_n{-p\parallel }^2+{ϵ}_n\parallel x_n{-p\parallel }^2-{\tau }_n(1-{\tau }_n-{ϵ}_n){\parallel z_n-T_n{z}_n\parallel }^2.\hfill \end{array}$$

(10)

By (8), (10), together with Lemma 1 and the nonexpansiveness of $T_n$, we have:

$$\begin{array}{cc}\hfill \parallel x_{n+1}{-p\parallel }^2& \le (1-{\mu }_n-{\zeta }_n)\parallel y_n{-p\parallel }^2+{\mu }_n\parallel T_n{z}_n{-p\parallel }^2+{\zeta }_n{\parallel T_n{y}_n-p\parallel }^2\hfill \\ \hfill & \le (1-{\mu }_n-{\zeta }_n)\parallel y_n{-p\parallel }^2+{\mu }_n\parallel z_n{-p\parallel }^2+{\zeta }_n{\parallel y_n-p\parallel }^2\hfill \\ \hfill & =(1-{\mu }_n)\parallel y_n{-p\parallel }^2+{\mu }_n{\parallel z_n-p\parallel }^2\hfill \\ \hfill & =(1-{\mu }_n)[(1-{ϵ}_n)\parallel z_n{-p\parallel }^2+{ϵ}_n\parallel x_n-p{\parallel }^2]\hfill \\ \hfill & -(1-{\mu }_n){\tau }_n(1-{\tau }_n-{ϵ}_n)\parallel z_n-T_n{z}_n{\parallel }^2+{\mu }_n{\parallel z_n-p\parallel }^2\hfill \\ \hfill & =(1-{ϵ}_n+{\mu }_n{ϵ}_n)\parallel z_n{-p\parallel }^2+{ϵ}_n(1-{\mu }_n){\parallel x_n-p\parallel }^2\hfill \\ \hfill & -(1-{\mu }_n){\tau }_n(1-{\tau }_n-{ϵ}_n){\parallel z_n-T_n{z}_n\parallel }^2\hfill \\ \hfill & \le (1-{ϵ}_n+{\mu }_n{ϵ}_n)[\parallel x_n{-p\parallel }^2+2{\rho }_n\parallel x_n-p\parallel \parallel x_n-x_{n-1}\parallel ]\hfill \\ \hfill & +(1-{ϵ}_n+{\mu }_n{ϵ}_n){\rho }_n^2\parallel x_n-x_{n-1}{\parallel }^2+{ϵ}_n(1-{\mu }_n){\parallel x_n-p\parallel }^2\hfill \\ \hfill & -(1-{\mu }_n){\tau }_n(1-{\tau }_n-{ϵ}_n){\parallel z_n-T_n{z}_n\parallel }^2\hfill \\ \hfill & =\parallel x_n{-p\parallel }^2+2{\rho }_n(1-{ϵ}_n+{\mu }_n{ϵ}_n)\parallel x_n-p\parallel \parallel x_n-x_{n-1}\parallel \hfill \\ \hfill & +(1-{ϵ}_n+{\mu }_n{\beta }_n){\rho }_n^2{\parallel x_n-x_{n-1}\parallel }^2\hfill \\ \hfill & -(1-{\mu }_n){\tau }_n(1-{\tau }_n-{ϵ}_n){\parallel z_n-T_n{z}_n\parallel }^2.\hfill \end{array}$$

Since ${\displaystyle \underset{n\to \infty }{lim}\parallel x_n-p\parallel }$ exists for all $p\in F$ and ${\displaystyle \sum _{n=1}^{\infty }{\rho }_n\parallel x_n-x_{n-1}\parallel <+\infty ,}$ we have from the above inequality that:

$$\underset{n\to \infty }{lim}(1-{\mu }_n){\tau }_n(1-{\tau }_n-{ϵ}_n){\parallel z_n-T_n{z}_n\parallel }^2=0.$$

By the conditions (i) and (iii), we conclude that:

$$\underset{n\to \infty }{lim}\parallel z_n-T_n{z}_n\parallel =0.$$

(11)

This implies by the nonexpansiveness of $T_n$ that:

$$\begin{array}{cc}\hfill \parallel x_n-T_n{x}_n\parallel & \le \parallel x_n-z_n\parallel +\parallel z_n-T_n{z}_n\parallel +\parallel T_n{z}_n-T_n{x}_n\parallel \hfill \\ \hfill & \le \parallel x_n-z_n\parallel +\parallel z_n-T_n{z}_n\parallel +\parallel z_n-x_n\parallel \hfill \\ \hfill & =2\parallel x_n-z_n\parallel +\parallel z_n-T_n{z}_n\parallel .\hfill \end{array}$$

Thus:

$$\parallel x_n-T_n{x}_n\parallel \le 2\parallel x_n-z_n\parallel +\parallel z_n-T_n{z}_n\parallel .$$

(12)

By the definition of $z_n$, we obtain:

$$\parallel z_n-x_n\parallel =\parallel x_n+{\rho }_n(x_n-x_{n-1})-x_n\parallel =|{\rho }_n|\parallel x_n-x_{n-1}\parallel ={\rho }_n\parallel x_n-x_{n-1}\parallel .$$

(13)

From (12) and (13), we obtain:

$$\begin{array}{cc}\hfill \parallel x_n-T_n{x}_n\parallel & \le 2{\rho }_n\parallel x_n-x_{n-1}\parallel +\parallel z_n-T_n{z}_n\parallel .\hfill \end{array}$$

(14)

By (11), (14), and ${\sum }_{n=1}^{\infty }{\rho }_n\parallel x_n-x_{n-1}\parallel <+\infty ,$ we obtain:

$$\underset{n\to \infty }{lim}\parallel x_n-T_n{x}_n\parallel =0.$$

(15)

From (13) and ${\sum }_{n=1}^{\infty }{\rho }_n\parallel x_n-x_{n-1}\parallel <+\infty ,$ we obtain:

$$\underset{n\to \infty }{lim}\parallel z_n-x_n\parallel =0.$$

(16)

Since:

$$\begin{array}{cc}\hfill \parallel y_n-z_n\parallel & \le {\tau }_n\parallel T_n{z}_n-z_n\parallel +{ϵ}_n\parallel T_n{x}_n-z_n\parallel \hfill \\ \hfill & \le {\tau }_n\parallel T_n{z}_n-z_n\parallel +{ϵ}_n(\parallel T_n{x}_n-x_n\parallel +\parallel x_n-z_n\parallel ),\hfill \end{array}$$

by (11), (15), and (16), we obtain:

$$\begin{array}{cc}\hfill \underset{n\to \infty }{lim}\parallel y_n-z_n\parallel & =0.\hfill \end{array}$$

(17)

From $\parallel y_n-x_n\parallel \le \parallel y_n-z_n\parallel +\parallel z_n-x_n\parallel ,$ (16) and (17), we obtain:

$$\underset{n\to \infty }{lim}\parallel y_n-x_n\parallel =0.$$

(18)

Since:

$$\begin{array}{cc}\hfill \parallel x_{n+1}-x_n\parallel & \le (1-{\mu }_n-{\zeta }_n)\parallel y_n-x_n\parallel +{\mu }_n\parallel T_n{z}_n-x_n\parallel +{\zeta }_n\parallel T_n{y}_n-x_n\parallel \hfill \\ \hfill & \le (1-{\mu }_n-{\zeta }_n)\parallel y_n-x_n\parallel +{\mu }_n[\parallel T_n{z}_n-T_n{x}_n\parallel +\parallel T_n{x}_n-x_n\parallel ]\hfill \\ \hfill & +{\zeta }_n[\parallel T_n{y}_n-T_n{x}_n\parallel +\parallel T_n{x}_n-x_n\parallel ]\hfill \\ \hfill & \le (1-{\mu }_n-{\zeta }_n)\parallel y_n-x_n\parallel +{\mu }_n[\parallel z_n-x_n\parallel +\parallel T_n{x}_n-x_n\parallel ]\hfill \\ \hfill & +{\zeta }_n[\parallel y_n-x_n\parallel +\parallel T_n{x}_n-x_n\parallel ],\hfill \end{array}$$

it follows by (15)–(18) that ${lim}_{n\to \infty }\parallel x_{n+1}-x_n\parallel =0.$ Since $\left\{T_n\right\}$ satisfies the NST${}^{\star }$ condition, we obtain that the set of all weak cluster points of the sequence $\left\{x_n\right\}$ is a subset of $F.$ Applying Lemma 3, we obtain that there exists $x\in F$ such that $x_n\rightharpoonup x.$ □

Now, we move on to the application of our introduced algorithm for solving a convex minimization problem (5) by setting $T_n:=$ prox${}_{{\kappa }_n\psi }(I-{\kappa }_n\nabla \varphi )$ in Algorithm 1.

Next, we prove that a sequence $\left\{x_n\right\}$ generated by Algorithm 2 converges weakly to the solution of the convex minimization problem (5).

Algorithm 2: (FBMSA): A forward-backward modified S-algorithm.

Initial. Take $x_0,x_1\in H$ arbitrarily and $n=1$. Choose ${\rho }_n\ge 0$ and ${\sum }_{n=1}^{\infty }{\rho }_n<+\infty .$  Step 1. Compute $z_n,y_n$ and $x_{n+1}$ using: $$\left\{\begin{array}{c}{z}_n=x_n+{\rho }_n(x_n-x_{n-1}),\hfill \\ y_n=(1-{\tau }_n-{ϵ}_n)z_n+{\tau }_n{\mathrm{prox}}_{{\kappa }_n\psi }(I-{\kappa }_n\nabla \varphi )z_n+{ϵ}_n{\mathrm{prox}}_{{\kappa }_n\psi }(I-{\kappa }_n\nabla \varphi )x_n,\hfill \\ x_{n+1}=(1-{\mu }_n-{\zeta }_n)y_n+{\mu }_n{\mathrm{prox}}_{{\kappa }_n\psi }(I-{\kappa }_n\nabla \varphi )z_n+{\zeta }_n{\mathrm{prox}}_{{\kappa }_n\psi }(I-{\kappa }_n\nabla \varphi )y_n.\hfill \end{array}\right.$$  Then, update $n:=n+1$, and go to Step 1.

Theorem 2.

Let g be a lower semicontinuous function and proper convex from a real Hilbert space H into $\mathbb{R}\cup \{+\infty \}$, and let ϕ be a convex differentiable function from H into $\mathbb{R}$ with $\nabla \varphi$ being ℓ-Lipschitz constant for some $\ell >0.$ Let $\left\{x_n\right\}$ be a sequence generated by Algorithm 2 such that ${\kappa }_n\to \kappa$ with ${\kappa }_n,\kappa \in \left(0,\frac{2}{\ell }\right)$. Suppose $\left\{{\tau }_n\right\},\left\{{ϵ}_n\right\},\left\{{\mu }_n\right\}$ and $\left\{{\zeta }_n\right\}$ are sequences in $(0,1)$ satisfying the assumptions as in Theorem 1. Then, $\left\{x_n\right\}$ converges weakly to an element in argmin$(\varphi +\psi )$.

Proof. 

Let T and $T_n$ be the forward–backward operators of $\varphi$ and $\psi$ with respect to $\kappa$ and ${\kappa }_n$, respectively. Then, $T:=$prox${}_{\kappa \psi }(I-\kappa \nabla \varphi )$ and $T_n:=$prox${}_{{\kappa }_n\psi }(I-{\kappa }_n\nabla \varphi )$. Then, T and $\left\{T_n\right\}$ are nonexpansive operators for all n. By Proposition 26.1 in [7], $F:={\cap }_{n=1}^{\infty }F\left(T_n\right)=\mathrm{argmin}(\varphi +\psi )$. It follows from Lemma 5 that $\left\{T_n\right\}$ satisfies the NST${}^{\star }$ condition. Using Theorem 1, we obtain the required result. □

4. Applications

The image restoration problem is solved using Algorithm 2 in this part. We also compared the deburring efficiency of Algorithm 2 with NAGA [16], FISTA [6], IFBS [35], and FBS [12]. As the mentioned in the literature, the image restoration problems can be related to the LASSO problem, that is ${\displaystyle \underset{x}{min}{\{\parallel Ax-b\parallel }_2^2+{\beta \parallel x\parallel }_1\},}$ where A represents the blurring operator, $x\in {\mathbb{R}}^n$ is the original image, b is the observed image, and $\beta$ is a positive regularization parameter.

To solve image restoration problem, especially the true RGB images, this model is highly costly to compute for the multiplication of $Ax$ and ${\parallel x\parallel }_1$ because of the size of matrix A and x, as well as their members. In order to overcome this problem, most of researchers in this area employ the 2D fast Fourier transform for the transformation of the true RGB images, and the above model is slightly reformulated by using the 2D fast Fourier transform as the following form:

$$\underset{x}{min}{\{\parallel \mathcal{A}x-b\parallel }_2^2+{\beta \parallel \mathcal{W}x\parallel }_1\},$$

(19)

where $\mathcal{A}$ is the blurring operator, which is often chosen as $\mathcal{A}=\mathcal{B}\mathcal{W},\mathcal{B}$ is the blurring matrix, $\mathcal{W}$ is the 2D fast Fourier transform, $b\in {\mathbb{R}}^{m\times n}$ is the observed image of size $m\times n$, and $\beta$ is a positive regularization parameter. Hence, it can be viewed as the summation of two convex minimization problem, that is, ${\displaystyle \underset{x}{min}\{\varphi \left(x\right)+\psi \left(x\right)\}.}$ Therefore, Algorithm 2, FBS [12], IFBS [35], FISTA [6], and NAGA [16] can be applied to solve an image restoration problem by setting $\varphi \left(x\right)={\parallel \mathcal{A}x-b\parallel }_2^2,\psi \left(x\right)=\beta {\parallel \mathcal{W}x\parallel }_1.$

In our experiment, we selected the regularization parameter $\beta =5\times {10}^{-5}$ and considered the original image size of $256\times 256$ px. The Gaussian blur of size $9\times 9$ and standard deviation $\xi =4$ were used to rate the blurred and noisy image. Figure 1 shows the original and observed images.

We used the peak signal-to-noise ratio (PSNR) as a measure of the performance of our algorithm, which is defined as follows:

$$\mathrm{PSNR}\left(x_n\right)=10{log}_{10}\left(\frac{{255}^2}{MSE}\right),$$

where MSE$=\frac{1}{{256}^2}{\parallel x_n-x\parallel }^2,$ the mean-squared error for original image x. The concept of the PSNR was proposed by Thung and Raveendran [43] in 2009. It is worth noting that a higher PSNR demonstrates a higher quality for deblurring the image. Then, we computed the Lipschitz constant ℓ by using the maximum eigenvalues of the matrix $A^{T}A$.

Table 1. Algorithms and their setting controls.

Methods	Setting
Algorithm 2	${\tau }_n={\zeta }_n=0.950,{ϵ}_n={\mu }_n=0.005,{\kappa }_n=\frac{n}{\ell (n+1)}$ and
	${\rho }_n=\left\{\begin{array}{c}\frac{n}{n+1}\mathrm{if}1\le n<N\hfill \\ \frac{1}{2^n}\mathrm{otherwise},\mathrm{where}N\mathrm{is}\mathrm{astop}\mathrm{number}\mathrm{of}\mathrm{iteration}.\hfill \end{array}\right.$
FISTA	$\kappa =\frac{1}{\ell },{\rho }_n=\frac{t_n-1}{t_{n+1}},$ where $t_{n+1}=\frac{1+\sqrt{1+4t_n^2}}{2}.$
NAGA	${\tau }_n=0.500,{\kappa }_n=\frac{n}{\ell (n+1)}$ and ${\rho }_n=\frac{t_n-1}{t_{n+1}},$ where $t_{n+1}=\frac{1+\sqrt{1+4t_n^2}}{2}.$
IFBS	${\kappa }_n=\frac{n}{\ell (n+1)}$ and ${\rho }_n=\left\{\begin{array}{c}\frac{1}{n^2{\parallel x_n-x_{n-1}\parallel }_2^2}\mathrm{if}{x}_n\ne x_{n-1}\hfill \\ 0\mathrm{otherwise}\hfill \end{array}\right.$
FBS	${\kappa }_n=\frac{n}{\ell (n+1)}$

shows the parameters for Algorithm 2, FISTA, NAGA, IFBS, and FBS.

As seen in Table 1, all parameters were created to satisfy all conditions of those convergence theorems for each algorithm. By Theorem 2, the sequence $\left\{x_n\right\}$ generated by Algorithm 2 converges to the original image.

For this experiment, our programs were run on an Intel(R) core(TM) i7-9700CPU with 32.00 GB RAM, Windows 10, in the MATLAB computing environment. From the controllers, which were set as above, we obtained the results of deblurring the image of Wat Phra Singh Woramahaviharn with 1000 iterations as in

Table 2. The values of the PSNR at $x_{200},x_{300},x_{400},x_{500},x_{1000}$.

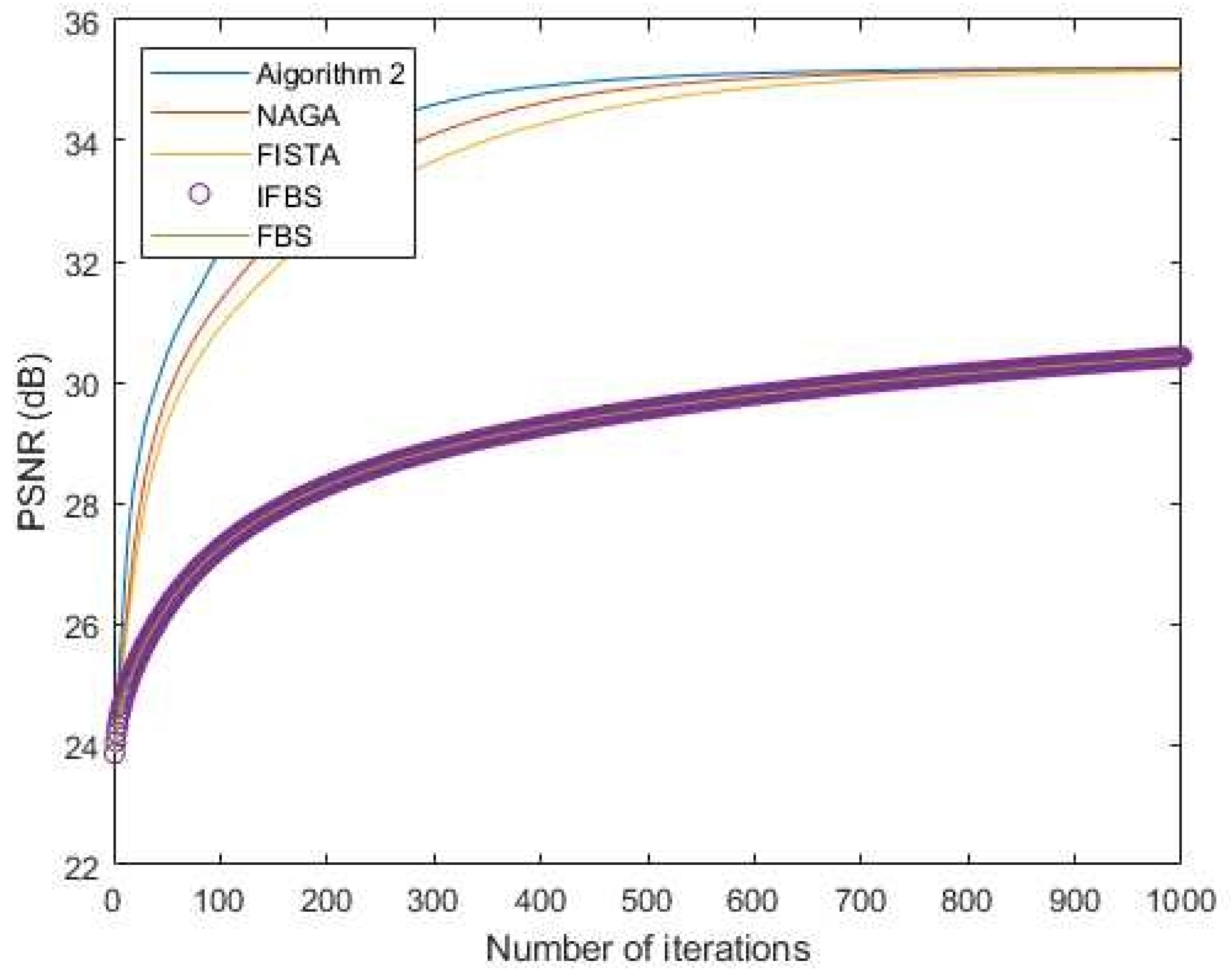
Iteration No.	Peak Signal-to-Noise Ratio (PSNR)
	Algorithm 2	NAGA	FISTA	IFBS	FBS
200	33.8764	33.1457	32.6173	28.2840	28.2840
300	34.5951	34.1018	33.6556	28.8650	28.8650
400	34.8902	34.6174	34.2689	29.2593	29.2593
500	35.0391	34.8766	34.6409	29.5532	29.5532
1000	35.2068	35.1961	35.1562	30.4187	30.4186

.

Table 2 shows the images’ recovery efficiency compared to other methods under different numbers of iterations. It is seen from Table 2 that Algorithm 2 has a higher PSNR than the other algorithms. Therefore, the convergence behavior of our algorithm is better than those of NAGA, FISTA, IFBS, and FBS.

Moreover, the results of deblurring the image of Wat Phra Singh Woramahaviharn at the 1000th iteration of all the studied algorithms are presented in Figure 2.

It was derived from the graph of PSNR in Figure 2 that Algorithm 2 gives a higher value of the PSNR than the other algorithms. This demonstrates that Algorithm 2’s image restoration performance is better than those of NAGA, FISTA, IFBS, and FBS.

We observed from Figure 3 that Algorithm 2 gives a better result of deblurring for Wat Phra Singh Woramahaviharn in all the numbers of iterations.

5. Conclusions

This paper introduced a new accelerated algorithm for solving a common fixed-point problem of a family of nonexpansive operators. The weak convergence theorem for this method was proven by setting some conditions. Our main results can be applied to solve a minimization problem involving two proper lower semicontinuous and convex functions. The proposed method was also used to solve the image restoration problems. To compare the performance of the studied algorithm, we conducted certain numerical experiments and obtained that the PSNR of our proposed algorithm is higher than those of FBS [12], IFBS [35], FISTA [6], and NAGA [16].