Abstract
In this paper, we propose a family of indistinguishability operators, that we have called Yager Possibilitic Response Functions (YPRFs for short), as an appropriate tool for allocating tasks to a collective of agents. In order to select the best agent to carry out each task, we have used the so-called response threshold method, where each agent decides the next task to perform following a probabilistic Markov process and, in addition, involves a response function which models how appropriate the task is for the agent. In previous works, we developed a new response threshold method which incorporates the use of indistinguishability operators as response functions and possibility theory instead of probability, for task allocation from a very general perspective without taking into account the specific characteristics of the agents except their limitations to carry out a task. Such an allocation is modelled by means of possibilistic, instead of probabilisitic, Markov chains. We show that possibilistic Markov chains outperform its probabilistic counterparts for the aforementioned propose. All the indistinguishability operators considered in previous papers were not able to take into account the agents’ restrictions for moving from a task to another one, or equivalently to carry out a task instead of another one. In order to avoid this handicap, we introduce a new kind of response functions, YPRFs, which are modelled by means of indistinguishability operators obtained via Yager t-norms. This new type of response functions drops to zero when an agent, due to its limitations, is not able to execute a task and, therefore, is able to model a generic multi-agent system with restrictions. The performed simulation, under Matlab, allows us to compare the results obtained using the new YPRFs with those obtained applying celebrated response functions also generated via indistinguishability operators (that we call Original Possibilitic Response Functions, OPRFs for short). Moreover, the results confirm that the YPRFs are able to take into account agent’s restrictions while the OPRFs are not able. Finally, in the light of the experimental results, we can confirm that those systems modelled.
1. Introduction
It is well known that the use of a group formed by two or more agents, which work all together in order to carry out a common objective, provides several advantages compared to those cases in which only a single agent is under consideration. Thus, systems with two or more agents (from now on termed as multi-agent systems) can perform tasks or missions either faster or in a more flexible way than systems with a single agent. Moreover, they are more robust. Making a profit of these systems implies that several issues must be faced up, such as task decomposition, task assignment or movement coordination. This paper focuses on the “Multi-agent Task Allocation” (MATA for short) problem which is selecting the best agent, as for instance robots or any intelligence entity, to execute each of the tasks that must be performed. In order to make this decision, the system must take into account several factors or movement restrictions. Thus, the agents have a series of characteristics that limit which tasks can be reached and carried out. When we deal with real physical agents, an example of these restrictions is given by the energy limitation. Since we focus on treating the system from an abstract approach this paper could be useful to describe many kinds of agents with movement restrictions such as robots, airplanes, tourists, insects and so on.
Nowadays, several methods have been proposed for addressing the MATA problem [1,2]. The so-called Swarm Intelligence methods are one of the most widely used in the literature (see, for instance, [3]). These are inspired by the behaviour of colonies of insects, like for example colonies of ants or bees, where a cooperative and intelligence pattern emerges from the interaction of very simple behaviours [4]. Scalability, simplicity or robustness are some of the main advantages that swarm intelligence provides compared to other paradigms. Response-threshold methods (RTM for short), introduced by G. Theraulaz et al. in [5], are the most commonly used swarm-like methods [6,7]. The classical RTM assigns a value to each agent and to each task. Such a value is called stimulus and it can be interpreted as an adequacy level of the task under consideration from the point of view of the agent. For example, the stimulus can be the inverse of the distance between the task and the agent. An agent decides to perform a task according to a probability function, called response function, that depends on the stimulus and on a parameter of the system known as threshold. When the task decision making only depends on the current task being performed, the evolution of the system can be modelled as memoryless process, i.e., as a probabilistic Markov chain.
The Markovian probabilistic approach has several well known disadvantages. Concretely, the response functions (transition probabilities) must meet the axioms of probability, i.e., the probability of moving from one task to the others must be a probability distribution. However, in real missions this constraint is not satisfied in general. Besides, when the system admits an equilibrium (stationary distribution of probability), the convergence is asymptotic. Of course, such a characteristic is not too much useful when a working decision must be made on-line in real missions. These facts make that the probability approach and, thus, the probabilistic response functions, could not be appropriate as a theoretical foundation for the task allocation problem. From a practical point of view, the convergence of the Markov chain must make possible to predict the behaviour of the system over time and, therefore, allows to make suitable decisions.
In [8], a new theoretical formalism for a RTM was proposed based on possibility theory in the sense of [9]. Hence the RTM was implemented considering transition possibilities instead of transition probabilities and, therefore, both possibilistic transition functions and possibilistic Markov chains (also known as fuzzy Markov chains) instead of the classical probabilistic ones. We refer the reader to [10] for the basics about fuzzy Markov chains. Furthermore, in [11], it was proved the suitability of indistinguishability operators as mathematical toolto model possibilistic response functions (see [12] for a detailed treatment of indistinguishability operators). Thanks to indistinguishability operators, a formal method to generate possibilistic response functions was introduced in the same reference. Moreover, those response functions known in the literature were retrieved as a particular case of such a methodology. The aforesaid method was applied to generate possibilistic response functions as indistinguishability operators obtained from, on the one hand, the family of t-norms due to Dombi and, on the other hand, from the family of t-norms due to Aczél and Alsina. A large number of experiments validated the utility of the generated response functions and, thus, the use of indistinguishability operators to simulate the allocation of a set of tasks in a multi-agent system.
All indistinguishability operators considered in [11] present a common characteristic, which is that they always take values strictly greater than zero. Since an indistinguishability operator is identified with a response function which, at the same time, provides the possibility transition, the fact that it takes values strictly greater than zero can be interpreted as follows: an agent is always able to transit from its current state (or task) to any other one. Nevertheless, there are cases in which this assumption is not fulfilled and, therefore, the transition possibility between two tasks may be null. For example, in multi-robot systems, each robot has a limited amount of energy (batteries capacity) for executing the mission which limits its movements. Of course, when the energy level is below the energy necessary for a robot to move from one task to another one, then the transition possibility should be zero.
In the light of the exposed inconvenient, this paper proposes a new type of response function that takes the zero value when, due to its restrictions, an agent is not able to carry out a specific task. It will be proved that the new response functions, from now on called Yager Possibilitic Response Functions (YPRFs for short), are an indistinguishability operator obtained from the family of t-norms due to Yager. These new indistinguishability operators will be applied, as possibility transition functions, to allocate tasks in a RTM multi-agent system with fuzzy Markov chains. In order to validate our approach several simulations will be performed using Matlab in such a way that the agents must carry out an inspection-like mission, where the agents must visit a set of points located in the space. These points are randomly placed in the environment or arranged in clusters or groups. Once an agent has reached a task it must decide the next one to visit following a fuzzy Markov chain. Due to their restrictions, as for instance energy limitations, some agents will not be able to execute tasks placed far away from its initial location. As will be explained later (see Section 4.1), there are several real situations that fit this generic task description. The results about the system’s behaviour that will be obtained using YPRFs will be compared with the system’s behaviour that can be obtained when the Original Possibilitic Response Functions (OPRFs for short) are applied. The experimental results will be used to show that the systems which involve the classical response functions (OPRFs) exhibit a very unnatural behavior, from the restrictions viewpoint, specially when the tasks are clustered in groups. In contrast, the YPRFs, proposed in this paper, are an excellent candidate to model the transitions when agent’s restrictions are under consideration in the aforementioned scenarios. Moreover, in all cases, we will show that fuzzy Markov chains outperform their probabilistic counterparts in the spirit of [11]. Thus, to our best knowledge, this paper states for the first time that indistinguishability operators are an appropriate mathematical tool to deal with the agents restrictions in task allocation problems, and shows how the modelling based on their use and fuzzy Markov chains outperform the classical swarm-like approaches. It must be stressed that the objective of this paper is to show that YPRFs are useful to model a generic multi-agent system with restrictions, without taking into account the specific characteristics of the agents except their limitations. Notice that we have included in the description of our system neither any model of a concrete agent nor of its limitations (see Section 2). Observe that the information about the aforementioned limitations are included, in a generic sense, in agent’s stimulus. So our general approach should be adapted appropriately when specific agents are taken under consideration.
The remainder of the paper is organized as follows: Section 2 reviews the main concepts on Swarm Intelligence, Response Threshold Methods and Fuzzy Markov Chains. Moreover, we recall the main aspects on indistinguishability operators that are necessary in our study. In Section 3, we introduce Yager Possibilitic Response Functions and we prove that these new response functions are exactly indistinguishability operators obtained from the family of Yager t-norms. Then, in Section 4, we explain a description of generic tasks that could fit with several real missions where the agents must visit a set of points located in the space. Moreover, the experimental framework and our simulation results are exposed. Finally, Section 5 summarizes the conclusions of our work and our future work.
2. Preliminaries on Response Threshold Methods and Indistinguishability Operators
In this section we introduce the main concepts which will be crucial in our subsequent discussion. Concretely, we recall notions about both probabilistic (classical) and possibilistic RTMs, indistinguishability operators and fuzzy Markov chains. Moreover, a short review of our previous work related to this field will be also exposed.
2.1. Response Threshold Methods
As mentioned in Section 1, response threshold methods are one of the most widely used methods for allocating tasks in a decentralized way. Let denote the set of positive integer numbers and let . Denote by R and T the set of agents and the set of tasks to carry out, where and . According to [13] (see also [6]) the classical response threshold method assigns to each agent and to each task , a stimulus , where stands for the positive real numbers set, which represents how appropriate is for . In this paper we consider the stimulus equals the inverse of the distance between the task and the agent. The agent starts the execution of following a given probability , which also depends on a parameter called threshold . When exceds the given threshold , the agent starts to execute the task . Following [7], one of the most widely used expression for is given as follows:
where . In the literature, the preceding expression is known as probability response function (see, for instance, [5]).
In the particular case in which the stimulus only depends on the inverse of the Euclidean distance among tasks, the probability response function (1) can be transformed into the following one
It must be stressed that in , by means of we express the Euclidean distance between the positions where the agent and the task are located. From now on, we assume that the agent is always located at any task and, thus, the distance is computed as the distance between the position of the tasks where the agent is located and the position of the task . A very usual assumption is to consider that all agents share the same threshold and, therefore, no reference to the agent is made in . Since the agent is always assumed to be located at any task we will denote, from now on, by . Observe that, in this way, can be interpreted as the probability with which an agent leaves the task in order to perform the task . Thus, initially each agent would be allocated to a random task and then the system would evolve from this initial situation through Equation (2). An agent cannot make any decision (change the task) while going from one task to another.
In this approach the decision about what is the next task to be performed is modelled separately for each agent in such a way that each agent makes such a decision individually without exchanging information with the rest of agents. Hence the agent decision making sequence is modelled as a probabilistic Markov chain which involves the transition probabilities .
In [8], as exposed in Section 1, it was highlighted several inconveniences of this kind of probabilistic process: problems about the selection of the probability response function when more than two tasks are under consideration and asymptotic converge to a probability distribution. Motivated by these handicaps, a new possibilistic theoretical formalism for implementing the RTM algorithms based on possibilistic response functions and the use of fuzzy Markov chains was proposed in [8]. Later on, the relationship between the possibilistic response functions and indistinguishability operators was explored in [11].
2.2. Fuzzy Markov Chains
In this subsection we recall the basics about fuzzy Markov chains and how they have been used in task allocation problems via RTMs.
According to [10,14], a possibilistic Markov (memoryless) process can be defined in the following way. Denote by () a finite set of states. If the system is in the system states at time (), then the system will move to the state with possibility at time . Let be the fuzzy state set, that is, the possibility distribution of the systems at time . Thus denotes the possibility that the state occurs at time for all . It must be noted that , where ∨ stands for the maximum operator on . According to the preceding facts, the evolution of the possibilistic Markov chain is given, for all , by
where ∧ stands for the minimum operator on . The preceding expression admits a matrix formulation as follows:
where is the fuzzy transition matrix (the matrix that involves the possibility that the system moves from a state to the others), ∘ is the matrix product in the max–min algebra .
On account of [10], a possibility distribution of the system states at time is said to be stationary, or stable, whenever .
One of the main advantages of possibilistic Markov chains with respect to their probabilistic counterpart is given by the fact that, under certain conditions, provided by Duan in [15], the system converges to a stationary distribution in at most steps, where m is the number of possible states. Contrarily, the convergence of probabilistic Markov chains is, in general, only guaranteed asymptotically. Let us recall the aforesaid conditions. To this end, we denote by the set of square matrices of order n over endowed with the matrix product ∘ in the max–min algebra.
Following [15], a matrix is said to be power-convergent if there exists such that , where denotes the max–min composition of A and itself k times. Moreover, the least such that A is power-convergent is denoted by and called the index of A. Furthermore, given , we denote by the fact that for all , where ≤ stands for the usual order on . Finally, a matrix will said to be column diagonally dominant provided that for all .
Taking into account the above introduced concepts, Duan stated the next result which warranties the finite convergence character of fuzzy Markov chains.
Theorem 1.
Let . Assume that A is column diagonally dominant and that . Then A is power-convergent and .
Regarding to RTMs, in [8], it was showed that the transition probabilities, given by (2) (which do not satisfy in general the probability distributions requirements), fulfil all assumptions of possibility theory and, thus, they were treated as possibilities in such a way that the allocation problem was addressed as a fuzzy (posisibilistic) Markov chain under the matrix operation ∘ based on the max–min algebra. In this direction, it was showed that fuzzy Markov chains predicts in a better way, than the probabilistic ones, the future behaviour of the system because they are more robust with respect to errors or vagueness inherent in the task position information and, according to Theorem 1, they converge to a stationary possibility distribution in finite time.
2.3. RTM via Indistinguishability Operators
In the light of the advantages provided by the use of possibility theory in RTMs applied to task allocation problems, the relationship between transition possibilities given by and indistinguishability operators was studied in [11]. Concretely, it was showed that indistinguishability operators can be an appropriate mathematical tool to model transition possibilities (possibilistic response functions) and, in addition, a formal method to generate possibilistic response functions was stated in the same reference. With the aim of recalling the aforementioned relationship, we recall a few basic aspects of operators.
According to [12], given a non-empty set X and a t-norm T (for the basics of t-norms we refer the reader to [16]), a T-indistinguishability operator is a fuzzy set satisfying for each the following:
- (i)
- ; (Reflexivity)
- (ii)
- ; (Symmetry)
- (iii)
- . (Transitivity)
The notion of indistinguishability operator is understood as a measure of similarity. Hence can be interpreted as the degree of indistinguishability between the objects x and y. The greater the most similar are x and y.
On account of [11], the probability response function given by matches up with the next indistinguishability operator:
where x and y denotes the coordinates of the allocations and , respectively. Of course, in this case the numerical value provided by the indistinguishability operator given by (4) must be interpreted as a possibility instead of a probability. It must be stressed that the operator given by (4) is an indistinguishability operator when the t-norm T under consideration is the Dombi . Besides, in the same reference, a new indistinguishability operator was induced from the Aczél and Alsina t-norm which is given by
where, again, x and y denotes the coordinates of the allocation and , respectively. A large number of experiments validated the utility of both generated response functions, and , and thus, the use of indistinguishability operators to simulate the allocation of a set of tasks in a multi-agent system. It must be pointed out that the systems behaviour was very similar when both indistinguishability operators were implemented in the experiments.
Observe that and take values larger than 0 and, therefore, they are not able to take into account those tasks that an agent cannot carry out due to its restrictions (as, for instance, battery energy).
Inspired by this fact we propose a new indistinguishability operator which will allow us to overcome this inconvenience. In the following, motivated by the similarity of experimental results obtained when and were implemented we will only compare the results obtained from the indistinguishability operator with those that provides the use of . Thus, as was pointed out in Section 1, we will refer to the indistinguishability operator as Original Response Function (OPRF for short).
3. Yager Possibilitic Response Function as an Indistinguishability Operator
In the light of the aforesaid drawbacks of the OPRFs, in this section we will introduce the new aforementioned response function, referenced to as Yager Possibilitic Response Function (YPRF for short) and we will prove that it can be modelled as an indistinguishability operator. To this end, given two tasks and , denote the Euclidean distance by . Taking this into account, consider the transition between the current task and the next one provided by:
where is the response threshold associated to the an agent . It must be stressed that, fixed i, the values fulfil the axiomatics of a possibility distribution in the sense of [9]. Clearly, such values do not satisfy the axiomatics of a probability distribution. Moreover, notice that when the distance between the tasks is greater than the value is exactly 0. Thus, allows us to model agent restrictions that cannot be considered when indistinguishability operators and are considered. For example, for a multi-robot system, the parameter can model the robots’ energy levels, that restricts the targets that a robot is able to reach. Furthermore, the value increases when the distance decreases. In this sense, the values can be understood as a transition possibility function. Therefore, fixed a threshold and given two tasks and , we define the Yager Possibilitic Response Function as follows:
where x and y denotes the coordinates of the allocations and , respectively.
Next we prove that the YPRF is exactly an indistinguishability operator. To this end, let us recall the Yager family of t-norms (see [16]).
Let . The function given by:
is called the Yager t-norm for the parameter .
Now we are able to prove the result below which provides that the new response function is a -indistinguishability operator.
Theorem 2.
Set and . If is a metric space, then the fuzzy set is a -indistinguisahbility operator for , where
for all .
Proof.
Obviously, we have that and that for all . Next we show that is satisfied for all .
Let . We distinguish two cases:
Case 1. Suppose that . Then,
If , then . Thus,
Otherwise and . Then,
and
So, since
we obtain that
Case 2. Suppose that . Then we have that .
As before, if , then . It follows that
Otherwise and . Then, on the one hand,
and
On the other hand, observe that
Therefore, and so
Thus, is a -indistinguishability operator. □
In the light of the preceding result we obtain the next one.
Corollary 3.
Set and . Then the fuzzy set is a -indistinguishability operator, where
for all .
Notice that if we implement a fuzzy Markov process according to the RTM algorithm as described in Section 2.2 and involving the YPRF given by (7), then the possibilistic transition matrix fulfils all conditions in the statement of Theorem 1 and, hence, the convergence of the chain to a stationary possibilistic distribution is guaranteed in at most steps, where m is the number of tasks to be performed.
4. Experimental Results
In this section we will analyse the results of experiments carried out to test and validate the new YPRFs as transition possibility functions into a fuzzy Markov chain, which implements a response threshold method. We will study the number of steps needed to converge to a stationary possibilistic distribution. Moreover, we will study the adequacy of the YPRFs, given by (7), to model the evolution of the system when agents’ limitations are taken into account. All the results are compared with those obtained through the use of OPRFs, that is when we use the indistinguishability operators given by (4). Besides all results are compared with those obtained via its probabilistic Markov chain counterpart. In order to make such a comparison we have applied the conversion possibilistic-to-probabilistic introduced in [17]. A comparison of the results obtained when we use the YPRF indistinguishabilities with those obtained through the use of the indistinguishability operators has not been made because, as we have exposed in Section 3, the indistinguishability operators and provide very similar results.
4.1. Task Description
In order to validate our approach the agents must carry out an inspection-like mission where the agents must visit a set of points located in the space. These points are randomly placed in the environment or arranged in clusters or groups. Once an agent has reached a task, it must decide the next one to visit following a possibility/probability value provided by the YPRFs or ORPFs. Each agent has a set of constraints, such as the maximum displacement distance which is modelled by the threshold value.
There are several real situations that fit the aforementioned task description. An instance is given by those missions that can be considered as an inspection task that must be performed by a swarm of autonomous aerial or terrestrial robots, as was suggested in [18]. Each cluster of points could be a neighborhood of a city and each of the cluster points belonging to the neighborhood can be considered as a building that must be inspected by the robots. In [19], a set of aerial robots must perform a reconnaissance mission where the targets appear in form of clusters. It is not hard to see how this mission have a great interest to assist military missions [20]. In [21], the authors highlight how a set of robots can address the so-called “fog of war”. This is a very well known military term which describes the uncertainty in the battle such as positions of the enemies troops. For example, in an urban scenario, a set of robots could escort a convoy to inspect surrounding buildings for enemies. In this case each building would be one of the points and the aforementioned clusters of points would be the neighbourhoods of the city. It must be pointed out that, in order to address these kind of problems with a swarm of robots, the US Defence Advanced Research Projects Agency (DARPA) launched in 2016 the OFFSET-program (OFFensive Swarm-Enabled Tactics).
More examples of inspection and reconnaissance missions that could be addressed by our methods can be found in [22,23]. In these cases, a multi-robot system of autonomous surface and underwater vehicles must mitigate a flood disaster using auction-like methods and Petri Nets. The vehicles should, among other tasks, cover a certain environment collecting information. As in the previous military-task, in this case the tasks could be grouped in clusters or areas of interest that the robots must inspect. Moreover, there are a set of constraints that describes the validity of allocations of vehicles to tasks. Despite these systems make use of auction algorithms, instead of an swarm-like approach (see for example [24,25,26]), the set of constraints is equivalent to the constraints provided by the threshold of YPRFs.
4.2. Experimental Framework
During the aforementioned inspection task each place to visit must be identified with the states of the system. When an agent arrives at a task, it must decide on the next task to be performed by following a Markov chain. We have considered both cases, i.e., the case in which the transition matrix is induced by the OPRF, and that in which such a matrix is induced by the YPRF. Moreover, their probabilist counterparts Markov chains have been simulated too.
The OPRF and YPRF have been considered, always with the power value n equals 2. Several synthetic environments with different positions of the objects in the environment (placements of the tasks) have been considered and tested with MatlabThe source code is available at the following repository: https://github.com/joseGuerreroUIB/MDPIMathematics2021.git. Figure 1 represents these environments, where each blue dot is a task. As can be seen, the task are placed randomly (see Figure 1a) or arranged into 2, 3, 6, 8 and 10 clusters. All the environments have the same dimensions: width = 600 units and high = 600 units. The threshold parameter, , has the same value for each agent and it depends on the maximum distance between tasks as follows:
where is the maximum distance between two points and is a parameter of the system which allows us to modulate the tendency of the agent to leave a task. In our case is equal to units of distance and . Recall that parameter is the maximum distance that an agent is able to reach (see Equation (6)). In Equation (8), value is divided by in order to obtain the threshold, thus the parameter nTH can be considered as the portion of the space reachable by an agent. For example, when nTH = 1, the agents can reach all the tasks and they have no restrictions. When, for example, nTH = 2 the agents only can reach half of the whole space.
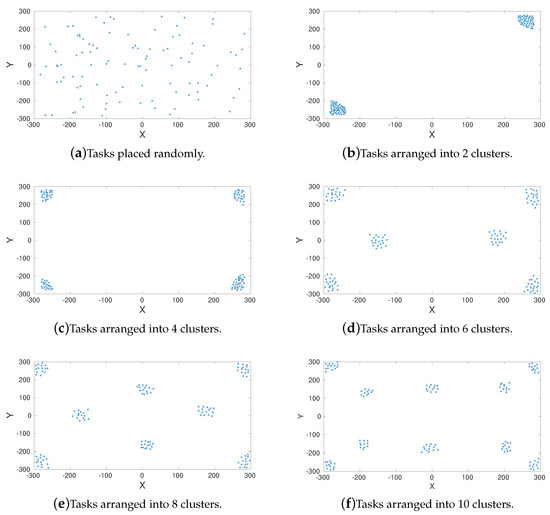
Figure 1.
Environments with 120 tasks used for the experiments. Blue dots represent the position of the tasks or objects.
4.3. Experiments with Randomly Placed Tasks
Firstly, we analyse the number of steps needed to converge to a stationary distribution using the OPRF and YPRF with both possibilistic and probabilistic Markov chains. Recall that, as was mentioned in Section 2.2, the convergence to stationary distribution in a finite number of steps is not guaranteed for probabilistic Markov chains. Along the experiments we assume that if the convergence is not reached after 500 steps, then either the system does not converge or the required convergence time is long much with respect to the possibilistic case.
Table 1 shows the mean number of steps required to converge when the objects are placed randomly in the environment (see Figure 1a). The probabilistic/possibilistic Markov chains for different values of the parameter and for the OPRFs and YPRFs have been considered. Each experiment has been performed over 500 different randomly generated environments. The first column of the table shows the values of the parameter . The second column shows the percentage of experiments that has converged when the probabilsitic Markov chain is considered. The number of steps required to converge, when the system converges, are shown in the third column. As can be seen, the percentage of convergence with an ORPF and a probabilistic Markov chain are very similar for all values. In contrast, when a YPRF is considered the percentage of convergent experiments decreases and the number of steps to converge increases as the increases. The 4th column shows the standard deviation of the number of steps for the probabilistic case. The 5th and the 6th columns of Table 1 show, respectively, the percentage of simulations that converge and the number of steps need to converge to a stationary distribution in the possibilistic case. Finally, the last column shows the standard deviation for the number of steps needed to converge when the fuzzy Markov chains are under consideration. Obviously, the convergence of these chains is always guaranteed and, therefore, in all cases this percentage is . The number of steps to converge depends on neither the parameter nor the indistinguishability operator under consideration and, in addition, it is always equal to steps. Note that this value is much lower than the number of steps needed by its probabilistic counterpart. Furthermore, as Duan’s theorem conditions (see Theorem 1) do not depend on the system parameter, the number of steps required to converge depends on the parameter either. Finally, it must be point that the probabilistic Markov chains induced by a YRPF require a great number of steps to converge compared with its ORPF counterparts. The theoretical reason of this behaviour is still under research. It seems that a probabilistic matrix with many values equal zero increases the number of steps required to converge. In any case, Fuzzy Markov chains show a more robust behaviour and do not require a greater number of steps required to converge to a stable distribution.

Table 1.
Steps required to converge for probabilistic/possibilistic Markov chains with random environments.
4.4. Experiments with Tasks Arranged in Clusters
In this section we will discuss the experiments made when the tasks are distributed in clusters.
4.4.1. Convergence Analysis
First of all we discuss the number of iterations needed to converge to a stable distribution. Figure 2 shows the number of steps needed to converge to a stable possibility distribution. Such a number of steps depends on neither the parameter nor the indistinguishability operator (ORPF or YRPF). Moreover, as can be seen, the greater number of cluster, the lower number of iterations to converge. The results for its probabilistic counterpart have not been collected in a table or figure because there is not convergence in general. When the YRPF is used and , the induced Markov chain does not converge for any number of clusters (it requires more than 500 iterations). The experimental results show that after 500 iterations the convergence is never reachable. When the ORPF is under consideration and , the resulting probabilistic Markov chain only converges for 4 and 10 clusters and requires 99 and 110 iterations respectively for all simulations. Similar results are obtained for other values of .
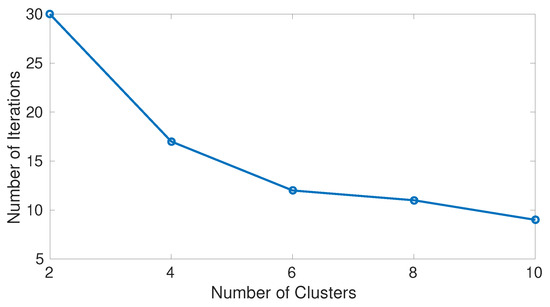
Figure 2.
Number of iterations to converge to a stable possibility distribution with 120 tasks and clustered environments.
In the following we study the impact of the threshold value () and the response function on the values of the resulting matrix obtained after iterating multiple times the transition matrix P of the Markov chain for tasks arranged into clusters (see Figure 1b–f). In order to simplify the visualization, each element of the transition matrix is encoded with a color. Thus the whole matrix can be showed as an image where the lower the possibility, or probability, the darker the color. Moreover, the tasks in the matrix are grouped by clusters, so that, all the tasks of a cluster are placed in consecutive position of the matrix.
4.4.2. Probabilistic vs. Possibilistic
Figure 3a shows the transition matrix of the possibility Markov chain induced by the OPRF with 120 tasks clustered into 8 groups (see Figure 1e) and . The yellow colors represent possibilities close to 1, in contrast, dark blue ones are possibilities with zero value or close to zero. Figure 3b shows the matrix after reaching a stationary possibilistic distribution, as was defined in Section 2.2. Thus, this figure shows the values of the such that , and therefore if is a stationary possibilistic distribution, then , where ∘ stands for the matrix product in the max–min algebra. The value stands for the number of iterations required to converge to a possibilistic stationary distribution. Figure 2 shows the aforementioned value depending on the number of clusters. As can be seen, both figures clearly show the 8 clusters of tasks (yellow rectangles), very specially after reaching the stationary state (Figure 3b). This means that, on the one hand, an agent which initially is assigned to a task in a given cluster has a very great possibility (equal or close to 1) of staying in the same cluster in the future. On the other hand, this agent has possibility close to 0, but greater than 0, of leaving its initial cluster. Figure 4 shows the corresponding matrices for the same environment (8 clusters of tasks) and threshold value () but now using the YPRF. As can be seen, the results are very similar to those obtained with the OPRF. So with a low value of , agent’s behaviour does not depend on the response function, OPRF or YPRF, used to induce the transition matrix.
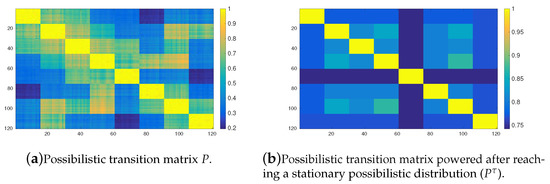
Figure 3.
Possibilistic transition matrix induced by the OPRF with for the 120 tasks arranged into 8 clusters.
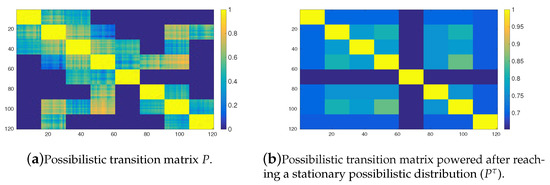
Figure 4.
Possibilistic transition matrix induced by the YPRF with for the 120 tasks arranged into 8 clusters.
Moreover, as can be seen in Figure 3a and subsequent, the tasks in the same cluster are colored in yellow tones, which means possibilistic values near to one. For example, the tasks near to the first cluster (top-right yellow square) have yellow-like colors which means high transition possibilities. From these light colors we can conclude that the tasks are very near. In contrast, the farther away the groups are from each other, the darker the colours of the figure (dark blue colours) are. Thus, if the tasks were far away from the first cluster, the colors would be darker.
Figure 5 shows the probabilistic transition matrix induced from the OPRF with and tasks arranged into 8 clusters. That is, this matrix is obtained after applying the possibilistic-to-probabilistic transformation (see Section 4.3), to the possibilistic transition matrix shown in Figure 3. Although the scale of the colors is different from the one used in the aforementioned possibilistic figure, the obtained conclusions are still valid. The transition matrix also has high values (yellow like colors) for tasks in the same cluster, similar to the probabilistic case. Figure 5b shows the values of the matrix after 500 iterations computed with the matrix product in the the sum-product algebra. It must be stressed that the probabilistic Markov chain does not converge to a stable probability distribution. Recall that we assume that if the system does not converge after 500 iterations, then the time taken exceeds too much, with respect to the possibilistic case, the required convergence time. Moreover, the general shape of the probabilistic transition matrix does not change after 500 iterations. So if the system has not converged after 500 iterations, then it will not converge in general. The differences with respect to its possibilistic counterpart (see Figure 3b) are very remarkable. In the probabilistic case the agents has a very high possibility to leave its initial cluster and very low probobability to stay in it and, therefore, they cannot discriminate the groups of tasks. This behaviour seems very unnatural, specially when the agents have energy restrictions and keeping in mind the type of real missions exposed in Section 4.1. These results using the YPRF are shown in Figure 6. Furthermore, the values of transition probabilities between tasks belonging to the same cluster in the transition matrix are reduced if we compare them with those given in the case in which the OPRF is used (see Figure 6a and compare Figure 5a). The obtained matrix after 500 iterations (see Figure 6b) shows that a very similar pattern to that obtained in the case of the OPRF arises when we use the YRPF. Similar results are obtained when different number of clusters are considered. So, in the light of these results, we can conclude that the probabilistic Markov chains induced from the OPRF and the YPRF with a low value of the parameter exhibit unnatural behaviour and, therefore the probabilistic framework is not appropriate for allocating tasks when these type of environments are considered. Similar results has been obtained with higher values of the parameter, as can be seen in Figure 7. This figure shows the same results as Figure 5 with .
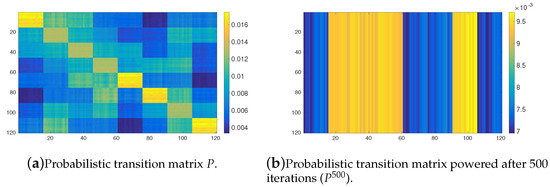
Figure 5.
Probabilistic transition matrix induced by the OPRF with for the 120 tasks arranged into 8 clusters.
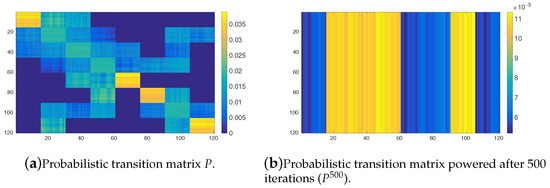
Figure 6.
Probabilistic transition matrix induced by the YPRF with for the 120 tasks arranged into 8 clusters.
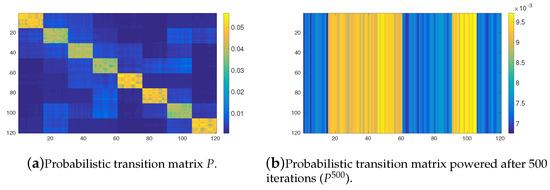
Figure 7.
Probabilistic transition matrix induced by the OPRF with for the 120 tasks arranged into 8 clusters.
4.4.3. Impact of the Parameter
Next we analyse the impact of the parameter on the behaviour of the system. On the one hand, Figure 8 shows the possibilistic transition matrix powered after reaching a stationary possibilistic distribution when the transitions are induced by means of the OPRF with 120 tasks arranged into 8 clusters for . On the other hand, Figure 9 shows the same set of matrices but now induced by means of the YPRF. If both set of figures are compared, then it can be observed that the YPRF function is able to make a better discrimination of the 8 clusters than the OPRF. For example if , then the aforementioned matrix induced by means of the YPRF remains unchanged and, hence, it is able to identify the 8 clusters of tasks (see Figure 9b,c). In contrast, the grater the the value of parameter , the grater the difference between possibilistic transitions induced through the OPRF and the YRPF. (see Figure 8b,c. Moreover, it can be observed that this response function cannot discriminate totally the clusters and, therefore, it cannot guarantee that an agent with mobility restrictions does not move to an unreachable cluster of tasks.
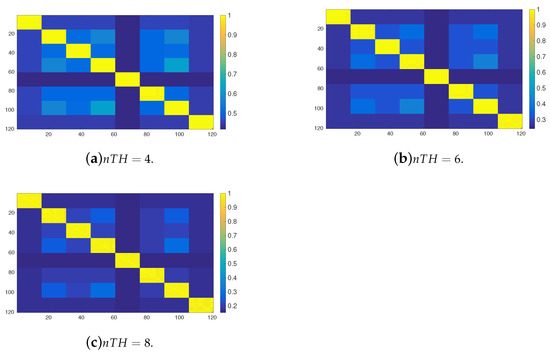
Figure 8.
Possibilistic transition matrix, induced by the OPRF, powered after reaching a stationary possibilistic distribution () for the 120 tasks arranged into 8 clusters and different values of .
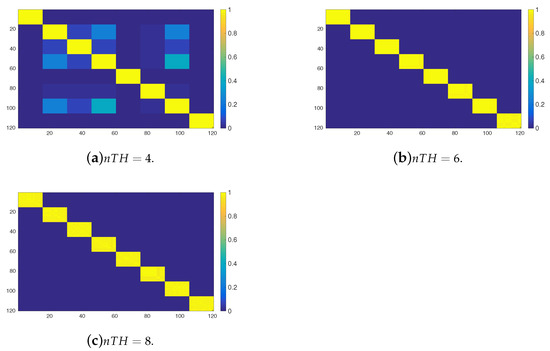
Figure 9.
Possibilistic transition matrix, induced by the YPRF, powered after reaching a stationary possibilistic distribution () for the 120 tasks arranged into 8 clusters and different values of .
Figure 10 shows the probabilistic transition matrices powered 500 times obtained after applying the possibilistic-to-probabilistic transformation to the possibilistic transition matrices induced using the OPRF for 120 tasks clustered into 8 groups with (see Figure 8). As can be observed, the results are similar to those explained for , and therefore we can conclude that the probabilistic Markov chains are not suitable for task allocation for such environments. Nevertheless, Figure 11 shows the same powered probabilistic matrix when the probabilistic transitions are induced by the YPRF with 20 tasks clustered into 8 groups and . In this case, the system shows a consistent behaviour and the results are very similar to those obtained with fuzzy Markov chains (see Figure 9), specially when has a high value. Although only the environment with 8 clusters of tasks has been showed for all the experiments, similar results have been obtained with a different number of clusters.
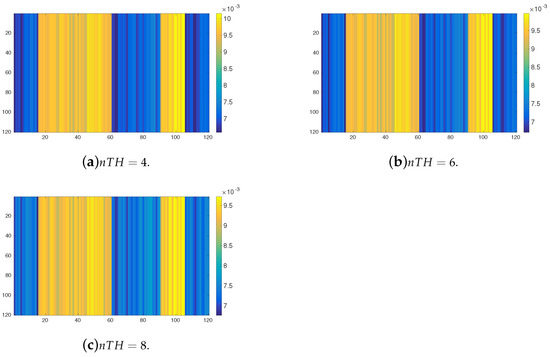
Figure 10.
Probabilistic transition matrix, induced by the OPRF, powered after 500 iterations () for the 120 tasks arranged into 8 clusters and different values of .
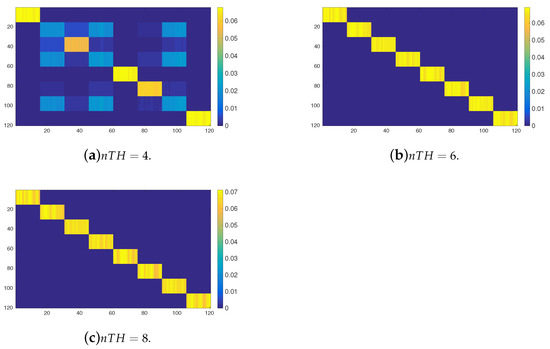
Figure 11.
Probabilistic transition matrix, induced by the YPRF, powered after 500 iterations () for the 120 tasks arranged into 8 clusters and different values of .
4.4.4. Impact of the Number of Clusters
The impact of the number of clusters of tasks on the transition matrix after reaching a stationary possibilistic distribution can be observed in Figure 12 and Figure 13 for the OPRF and for the YPRF, respectively. The value of parameter is in both equal to 4. In the light of these experiments, the meaning of the value , given in Section 4.2, seems properly interpreted. Recall that the parameter can be viewed as the portion of the space available from a given place when transition matrix is induced by the YRPF operator. In this case and, therefore, when the YRPF operator is used the agents can reach of the whole space. As can be seen, when the number of cluster is not equal the value, in this case 4, and the transition matrix is induced by ORPF, the transition possibility from one cluster to another one could be greater than zero, and therefore the agents are able to “jump” from one cluster to another one. This behaviour could be undesirable in some situations. For example, Figure 12b shows the results for ORPF when the number of clusters is equal to the parameter. In this case, when an agent stays in a cluster it has a very high possiblitity to remain in the same cluster (see the yellow squares) but has a low possibility to visit the neighbouring groups (soft blue or green squares). In contrast, when the number of cluster is 10, much greater than , (see Figure 12d) the possibility of one agent to scape from its original group is higher. As can be seen, the soft blue or green squares, that stand for low possibility values but greater than zero, are more common in the figure. In contrast, when the transition matrix is induced by the YPRF, the fuzzy Markov chain is able to identify in a more precise way the clusters of tasks of the environment (see Figure 13a–d). For example, with tasks arranged into 6 clusters and considering the YRPF,the possibility of an agent to transit from one cluster to another one is very low if it is compared with its ORPF counterpart.
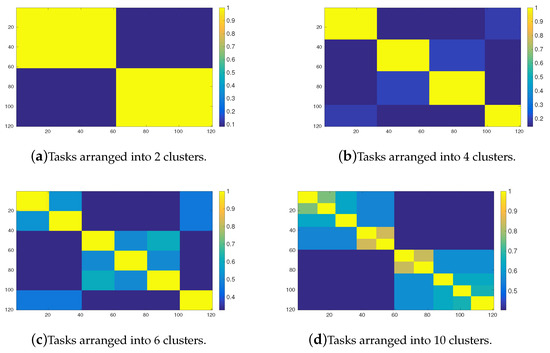
Figure 12.
Possibilistic transition matrix, induced by the OPRF, powered after reaching a stationary possibilistic distribution () for the 120 tasks, and different number of clusters of tasks.
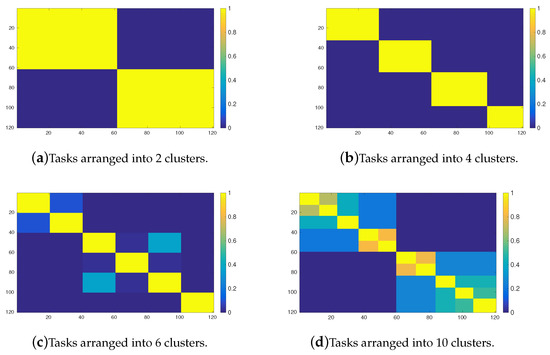
Figure 13.
Possibilistic transition matrix, induced by the YPRF, powered after reaching a stationary possibilistic distribution () for the 120 tasks, and different number of clusters of tasks.
4.5. Summary and Discussion of the Experimental Results
In the light of the experimental results we can draw some conclusions that are summarized in this section. Maybe the most interesting conclusion from the experiments has been to note that, even if the probabilistic Markov chain converges, the probabilistic transition matrix induced with the OPRF, after a great number of iterations (500 during the experiments), exhibits a very unnatural behaviour that makes them not suitable for modelling task allocation problems in the considered environments and the possible real situations exhibited in Section 4.1. Moreover, a very few number of probabilistic Markov chains converge, in contrast the convergence is guaranteed for all their possibilistic counterparts induced by OPRFs or YRPFs. Finally, it must be stressed that the possibilistic Markov chains whose transition matrix is induced through YPRFs show an appropriate a very good behaviour for environments with tasks clustered into groups and, thus, they would be a suitable mathematical tool for modelling real missions as those mentioned in Section 4.1, unlike the possibilsitic Markov chains whose transition matrix is induced through the OPRF.
5. Conclusions and Future Work
In this paper we have studied a new indistinguishability operator, that we have called YPRF and which is induced via Yager t-norms, as a response function for Swarm Multi-Agent Task Allocation problems. YPRFs take the zero value when the distance between the agent and the next task to perform or place to visit is greater than a threshold and, thus, they are able to take into account, from a generic perspective, the restrictions of the agent to perform a task. We have made a large number of experiments and we have compared the results obtained when the YPRFs are used with those provided by response functions induced by the family of t-norms due to Dombi, which we have called OPRFs. Unlike YPRFs, OPRFs always provide transition possibilities greater than zero. Both response functions have been tested using possibilistic and probabilsitic Markov chains in order to allocate the tasks to the agents. The possibilistic Markov chains outperform their probabilistic counterparts, requiring a lower number of steps to converge. We have showed that the possibistic Markov chains whose transition matrix is induced by YPRFs allow us to model in an appropriate way the behaviour of the system in those environments with tasks clustered into groups. Possible real missions in which this kind of multi-agent systems could play a central role have been also described. However, we have seen that the probabilistic Markov chains whose transition matrix is induced by means of OPRFs are not suitable for such a target.
In the light of these first results a deeper study of the impact of the parameter on the system must be made. Moreover, further analysis on the construction of new YPRFs that depends on more factors than the distance between tasks must be done in such a way that the description of the system, a model of concrete agents and their limitations can be developed. Furthermore, we expect to implement these systems in a colony of real robots.
Author Contributions
M.-d.-M.B.-F.: Data curation; Formal analysis; Investigation; Methodology; Resources; Software; Validation; Visualization; Roles/Writing and original draft. J.G.: Data curation; Investigation; Methodology; Resources; Software; Visualization; Roles-Writing and original draft; Project administration; Writing, review and editing. J.-J.M.: Conceptualization; Formal analysis; Investigation; Methodology; Project administration; Supervision; Visualization; Writing, review and editing. O.V.: Conceptualization; Formal analysis; Funding acquisition; Investigation; Methodology; Project administration; Supervision;Visualization;Writing—review and editing. All authors have read and agreed to the published version of the manuscript.
Funding
The authors acknowledge financial support from FEDER/Ministerio de Ciencia, Innovación y Universidades-Agencia Estatal de Investigación/−Proyecto PGC2018-095709-B-C21. This work is also partially supported by Programa Operatiu FEDER 2014-2020 de les Illes Balears, by project PROCOE/4/2017 (Direcció General d’Innovació i Recerca, Govern de les Illes Balears) and by projects ROBINS and BUGWRIGHT2. These two latest projects have received funding from the European Union’s Horizon 2020 research and innovation programme under grant agreements No 779776 and No 871260, respectively. This publication reflects only the authors views and the European Union is not liable for any use that may be made of the information contained therein.
Data Availability Statement
Data supporting reported results and source codes are available at: https://github.com/joseGuerreroUIB/MDPIMathematics2021.git.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Gerkey, B.P. On Multi-Robot Task Allocation. Ph.D. Thesis, Center of Robotics and Embedded Systems, University of Southern California, Los Angeles, CA, USA, 2003. [Google Scholar]
- Guerrero, J.; Oliver, G.; Valero, O. Multi-Robot Coalitions Formation with Deadlines: Complexity Analysis and Solutions. PLoS ONE 2017, 12, 1–26. [Google Scholar] [CrossRef] [PubMed]
- Yang, X.S. Recent Advances in Swarm Intelligence and Evolutionary Computation; Springer: Berlin/Heidelberg, Germany, 2015. [Google Scholar]
- Hamann, H. Introduction to Swarm Robotics. In Swarm Robotics: A Formal Approach; Springer International Publishing: Cham, Switzerland, 2018; pp. 1–32. [Google Scholar]
- Theraulaz, G.; Bonabeau, E.; Denuebourg, J. Response threshold reinforcements and division of labour in insect societies. Proc. R. Soc. Lond. B Biol. Sci. 1998, 265, 327–332. [Google Scholar] [CrossRef]
- Agassounon, W.; Martinoli, A. Efficiency and Robustness of Threshold-Based Distributed Allocation Algorithms in Multi-Agent Systems. In Proceedings of the First International Joint Conference on Autonomous Agents and Multiagent Systems: Part 3, Bologna, Italy, July 2002; pp. 1090–1097. [Google Scholar] [CrossRef]
- Castello, E.; Yamamoto, T.; Libera, F.D.; Liu, W.; Winfield, A.F.T.; Nakamura, Y.; Ishiguro, H. Adaptive foraging for simulated and real robotic swarms: The dynamical response threshold approach. Swarm Intell. 2016, 10, 1–31. [Google Scholar] [CrossRef]
- Guerrero, J.; Valero, O.; Oliver, G. Toward a Possibilistic Swarm Multi-Robot Task Allocation: Theoretical and Experimental Results. Neural Process. Lett. 2017, 46, 881–897. [Google Scholar] [CrossRef]
- Dubois, H.P. Fuzzy Sets and Systems: Theory and Applications; Academic Press: Warsaw, Poland, 1980. [Google Scholar]
- Avrachenkov, K.; Sanchez, E. Fuzzy Markov chains and decision making. Fuzzy Optim. Decis. Mak. 2002, 1, 143–159. [Google Scholar] [CrossRef]
- Guerrero, J.; Miñana, J.J.; Valero, O.; Oliver, G. Indistinguishability Operators Applied to Task Allocation Problems in Multi-Agent Systems. Appl. Sci. 2017, 7, 963. [Google Scholar] [CrossRef]
- Recasens, J. Indistinguishability Operators: Modelling Fuzzy Equalities and Fuzzy Equivalence Relations; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar] [CrossRef]
- Bonabeau, E.; Theraulaz, G.; Deneubourg, J. Fixed response threshold threshold and the regulation of division labour in insect societes. Bull Math Biol. 1998, 4, 753–807. [Google Scholar] [CrossRef]
- Zadeh, L. Fuzzy sets as a basis for a theory of possibility. Fuzzy Sets Syst. 1971, 3, 177–200. [Google Scholar] [CrossRef]
- Duan, J. The transitive clousure, convegence of powers and adjoint of generalized fuzzy matrices. Fuzzy Sets Syst. 2004, 145, 301–311. [Google Scholar] [CrossRef]
- Klement, R.; Mesiar, R.; Pap, E. Triangular Norms; Kluwer Academic Publishers: Dordrecht, The Netherlands, 2000. [Google Scholar] [CrossRef]
- Vajargah, B.F.; Gharehdaghi, M. Ergodicity of Fuzzy Markov Chains Based on Simulation Using Sequences. Int. J. Math. Comput. Sci. 2014, 11, 159–165. [Google Scholar] [CrossRef][Green Version]
- Schranz, M.; Umlauft, M.; Sende, M.; Elmenreich, W. Swarm Robotic Behaviors and Current Applications. Front. Robot. AI 2020, 7, 36. [Google Scholar] [CrossRef]
- Wang, Y.; Bai, P.; Liang, X.; Wang, W.; Zhang, J.; Fu, Q. Reconnaissance Mission Conducted by UAV Swarms Based on Distributed PSO Path Planning Algorithms. IEEE Access 2019, 7, 105086–105099. [Google Scholar] [CrossRef]
- Lehto, M.; Hutchinson, B. Mini-drones swarms and their potential in conflict situations. In Proceedings of the ICCWS 2020 15th International Conference on Cyber Warfare and Security, Norfolk, VA, USA, 12–13 March 2020. [Google Scholar] [CrossRef]
- Weiss, L.G. Autonomous robots in the fog of war. IEEE Spectr. 2011, 48, 30–57. [Google Scholar] [CrossRef]
- Scerri, P.; Kannan, B.; Velagapudi, P.; Macarthur, K.; Stone, P.; Taylor, M.; Dolan, J.; Farinelli, A.; Chapman, A.; Dias, B.; et al. Flood Disaster Mitigation: A Real-world Challenge Problem for Multi-Agent Unmanned Surface Vehicles. In Proceedings of the International Conference on Autonomous Agents and Multiagent Systems, Taipei, Taiwan, 2–6 May 2011; Volume 7068, pp. 252–269. [Google Scholar] [CrossRef]
- Farinelli, A.; Raeissi, M.M.; Marchi, N.; Brooks, N.; Scerri, P. Interacting with team oriented plans in multi-robot systems. Auton. Agents -Multi-Agent Syst. 2016. [Google Scholar] [CrossRef]
- Mitiche, H.; Boughaci, D.; Gini, M. Iterated Local Search for Time-extended Multi-robot Task Allocation with Spatio-temporal and Capacity Constraints. J. Intell. Syst. 2019, 28, 347–360. [Google Scholar] [CrossRef]
- Guerrero, J.; Oliver, G. Multi-robot coalition formation in real-time scenarios. Robot. Auton. Syst. 2012, 60, 1295–1307. [Google Scholar] [CrossRef]
- Jones, G.; Dias, B.; Stentz, A. Time-extended multi-robot coordination for domains with intra-path constraints. Auton. Robot. 2011, 30, 41–56. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).