Abstract
Broadly speaking, an adversarial example against a classification model occurs when a small perturbation on an input data point produces a change on the output label assigned by the model. Such adversarial examples represent a weakness for the safety of neural network applications, and many different solutions have been proposed for minimizing their effects. In this paper, we propose a new approach by means of a family of neural networks called simplicial-map neural networks constructed from an Algebraic Topology perspective. Our proposal is based on three main ideas. Firstly, given a classification problem, both the input dataset and its set of one-hot labels will be endowed with simplicial complex structures, and a simplicial map between such complexes will be defined. Secondly, a neural network characterizing the classification problem will be built from such a simplicial map. Finally, by considering barycentric subdivisions of the simplicial complexes, a decision boundary will be computed to make the neural network robust to adversarial attacks of a given size.
1. Introduction
Adversarial examples are currently one of the main problems for the robustness of neural networks applications [1]. Broadly speaking, an adversarial example against a classification model occurs when a small perturbation on an input data point produces a change on its classification. Adversarial examples are usually associated with computer vision tasks [2]. In this context, small generally refers to changes that are not appreciable by human perception. Recently, several studies have shown that adversarial examples also appear in other contexts such as natural language processing [3], multivariate time series [4] or recommendation systems [5]. Therefore, the study of adversarial examples is of an undoubted importance for building reliable models, and also leads us to wonder about the mechanisms of our brain and the differences between artificial and natural classification processes.
Since the discovery of adversarial examples as a weakness for the safety of neural network models in real-world problems, many attacks and defenses have been proposed [6], each of which builds on the other. One of the most popular approaches to study models’ robustness and adversarial examples is based on the concept of margin. From a geometrical point of view, data are points in an d-dimensional metric space and a classifier splits such a metric space into regions. In a classification problem, each region is associated with a label and all the points in such a region are classified with the corresponding label. Roughly speaking, the margin of the model is the minimum distance between the training data and the decision boundary (i.e., the set of regions’ boundaries). In the literature, there are many approaches that try to maximize such a margin (see, for instance, [7]). The concept of margin in Neural Network is strongly influenced by its use in Support Vector Machines (SVMs) [8]. In such way, in [9], the final softmax layer of the neural network is replaced with a linear SVM. In [10], a way of reducing empirical margin errors was proposed, and in [11], the discriminability of Deep Neural Networks (DNNs) features is enhanced via an ensemble strategy.
In this paper, we explore this idea of margin between regions associated with labels from a novel point of view. To the best of our knowledge, this is the first time where adversarial examples are studied with techniques from Algebraic Topology. Our approach can be summarized as follows. The starting point is a classification problem where the data are d-dimensional vectors which are mapped onto a set of k labels with a one-hot representation. From a topological point of view, such set of instances can be seen as the vertices of a simplicial complex embedded in a bounded polytope in (details are given below), and the set of k one-hot labels can be endowed with the structure of a k-dimensional simplex (in fact, labels are considered since we add an unknown label to the set of one-hot labels). In this way, a simplicial map between both topological structures arises in a natural manner, since each vertex in the simplicial complex corresponds to an instance of the dataset, and it is mapped onto the vertex of the simplex that represents the corresponding label. The second step is to apply the extended Simplicial Approximation Theorem [12] that allows us to provide a constructive proof of the Universal Approximation Theorem obtaining a a neural network that classifies correctly all the instances of the dataset. As shown in [12], all the weights of such a neural network can be computed directly from the simplicial complexes without any kind of training processes. Finally, by considering these ideas together with a subdivision process of the simplices, a decision boundary for the classification problem will be computed to make the neural network robust to adversarial attacks of a given size, since the mesh of a simplicial complex can be bounded by the number of subdivisions and the neural network obtained is based on the simplices used in the simplicial map.
Regarding other approaches to these ideas found in the literature, in [13], the authors proved the existence of a two-hidden-layer neural network which can approximate any continuous multivariable function with arbitrary precision, and, in [14], they provided a constructive method through a numerical analysis approach. Therefore, such papers can be seen as alternative constructive proofs to the Universal Approximation Theorem where no adversarial examples on classification problems were considered. A related approach that uses simplicial complexes to feed a neural network, is the concept of Simplicial Neural Network (SNN), provided in [15], that consists of a generalization of Graph Neural Networks (GNNs) with the property that compared to GNNs, SNNs exploit higher order relationships between the input data due to representing the data using simplicial complexes. Let us observe that, although having a similar name, our approach has a totally different goal.
The paper is organized as follows. In Section 2, all the basic concepts needed to understand the rest of the paper are presented. In Section 3, we introduce the concept of simplicial-map neural networks. Their use to build neural networks for classification tasks robust to adversarial attacks of a given size is presented in Section 4. The paper ends with conclusions and future works listed in Section 5.
2. Background
In this section, some of the preliminary concepts from Algebraic Topology and Neural Networks are recalled. Several useful references for this section are [16,17,18,19]. Let us notice that, in order to provide a bridge between Algebraic Topology and Neural Network, some concepts need to be reinterpreted.
Firstly, let us state some basic notation. Given two integers , let . Hereafter, let be an integer and let be the origin of the Euclidean space . Let a one-hot vector of length k be denoted as with . Let be the set of all the one-hot vectors of length k. Let us observe that where for and .
Now, we recall different fundamental structures such as polytopes and simplicial complexes. Convex polytopes can be seen as a generalization in any dimension of the notion of polygons.
Definition 1.
The convex hull of a set , denoted by , is the smallest convex set containing S. A convex polytope in is the convex hull of a finite set of points. Besides, the set of vertices of a convex polytope is the minimum set of points in such that .
Accordingly, a convex polytope is a closed bounded subset of , and the set of vertices of a convex polytope always exists and it is unique. A particular case of convex polytopes are simplices. Geometrically, a simplex is a generalization of a triangle to any dimension. For example, a 0-simplex is a point, a 1-simplex is a line segment, a 2-simplex is a triangle, a 3-simplex is a tetrahedron, and so on. In this paper, all the considered simplicial complexes have their vertices in the Euclidean space . Nevertheless, simplicial complexes can be defined abstractly.
Definition 2.
Let us consider a finite set V whose elements will be called vertices. A simplicial complex K consists of a finite collection of nonempty subsets (called simplices) of V such that:
- 1.
- Any subset of V with exactly one point of V is a simplex of K called 0-simplex or vertex.
- 2.
- Any nonempty subset of a simplex σ is a simplex, called a face of σ.
A simplex σ with exactly points is called a k-simplex. We also say that the dimension of σ is k and write . A maximal simplex of K is a simplex that is not face of any other simplex in K. The dimension of K is denoted by and it is the maximum dimension of its maximal simplices. The set of vertices of a simplicial complex K will be denoted by . For a vertex v of V, the star of v is the set of simplices having v as a face and it is denoted by . A simplicial complex K is pure if all its maximal simplices have the same dimension.
Let us consider a simplicial complex K whose vertices are in . If a k-simplex of K satisfies that it is a set of affinely independent points, then its realization is the convex polytope , which is the convex hull of its vertices. If all the simplices of K have a realization in satisfying that the intersection of two realizations is the realization of a simplex of K, then the union of their realizations is a subspace of denoted by and called the embedding of K in .
Next, the definition of triangulation of a convex polytope is recalled.
Definition 3.
A triangulation of a convex polytope is a simplicial complex K such that .
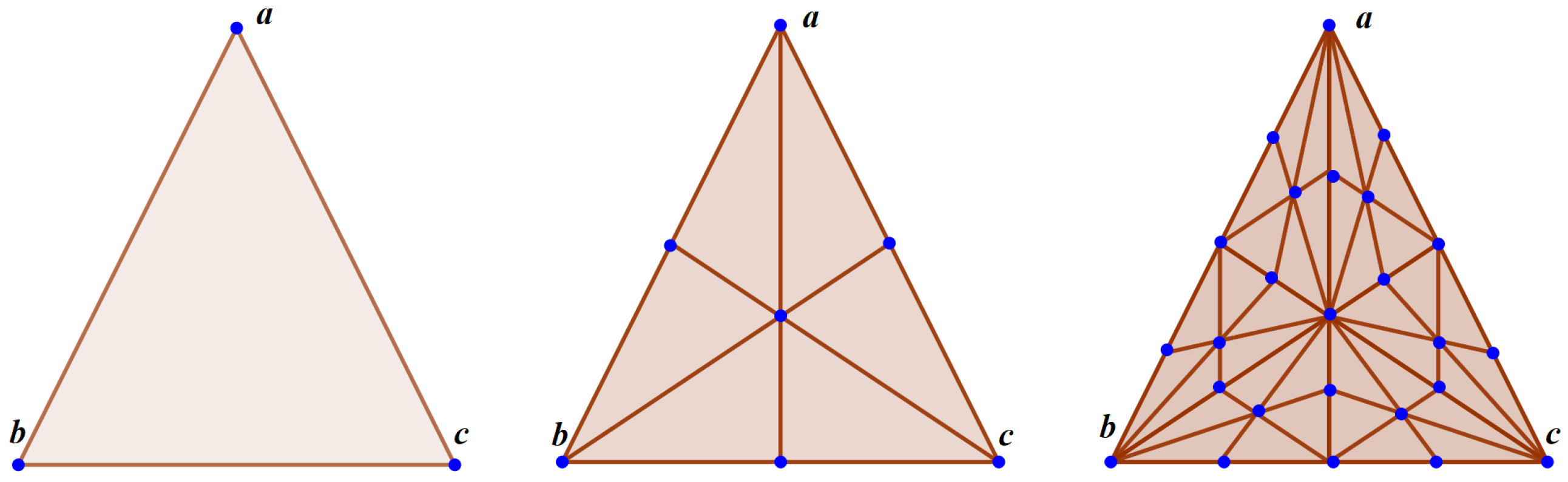
Let us recall that given a set of points in , its barycenter, denoted by , is . In particular, for . The barycentric subdivision of a simplicial complex will be the main tool to refine the neural network in the next sections and consists of getting a new simplicial complex by splitting the simplices in a standard way (see Figure 1). The t-th iteration of the barycentric subdivision of a simplicial complex K will be denoted by being . Next definition provides a formalization of this idea.
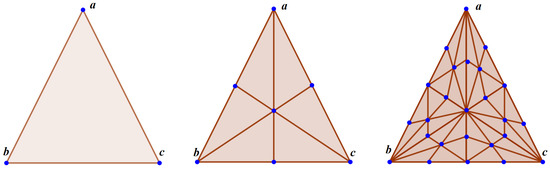
Figure 1.
Example of a barycentric subdivision. Let be the set of the three vertices (in blue) of the triangle depicted on the left. Let . From left to right: , , and are shown.
Definition 4.
Let K be a simplicial complex with vertices in . The barycentric subdivision is the simplicial complex defined as follows. The set of vertices of is the set of barycenters of all the simplices of K. The simplices of are the finite nonempty collections of which are totally ordered by the face relation in K. That is, any k-simplex σ of can be written as an ordered set such that being a face of for and . In particular, if σ is maximal then there exists a k-simplex satisfying that for .
Let us recall the definition of the Voronoi diagram of a set of points.
Definition 5.
Let be a set of points in . The Voronoi cell is defined as:
Then, the Voronoi diagram of S, denoted as , is the set of Voronoi cells:
From the Voronoi diagram , a particular simplicial complex, called the Delaunay complex of S and denoted as , can be constructed. Both structured can be computed in time (see [17], Chapter 4).
Definition 6.
Given a finite set of points in and its Voronoi diagram , the Delaunay complex of S can be defined as:
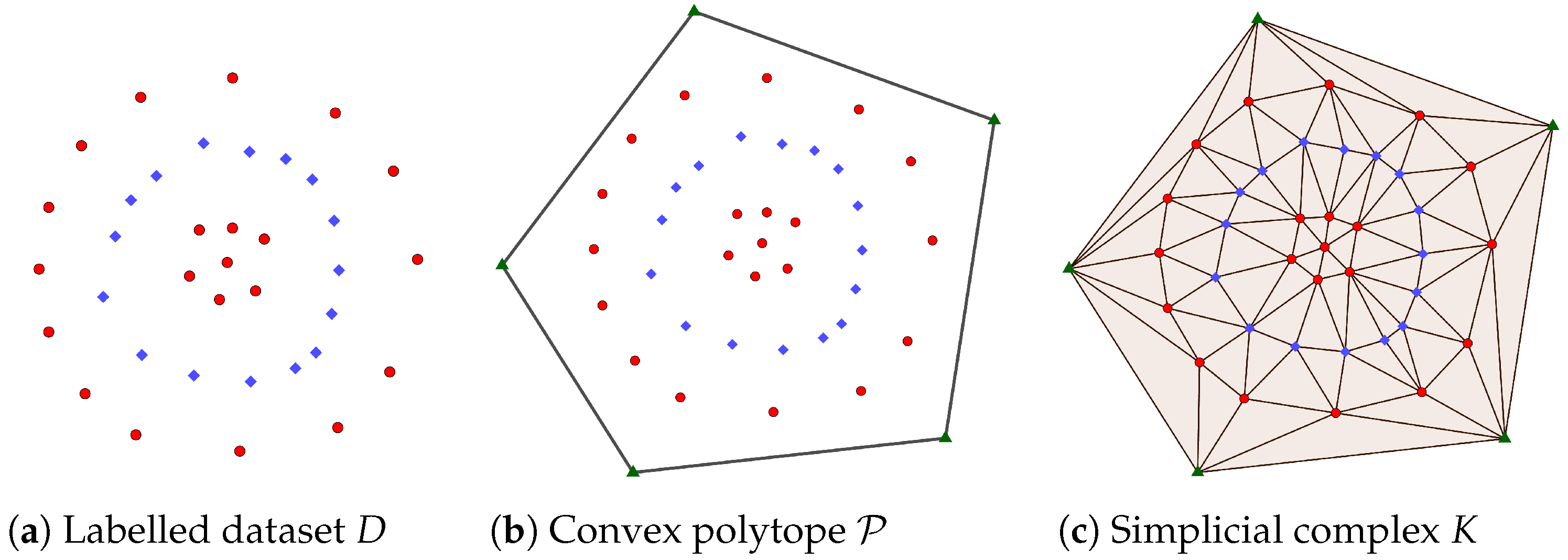
The Delaunay complex is a well-defined concept in the sense that is always a simplicial complex [17]. Usually, a finite set of points is said to be in general position when any subset of S with size at most is a set of affinely independent points. When the set of points is in general position, then the embedding of the Delaunay complex in is a triangulation of . In Figure 2, an example of the computation of a triangulation of a convex polytope , being the Delaunay complex of the set of vertices of together with a labelled dataset lying in the interior of , is provided.
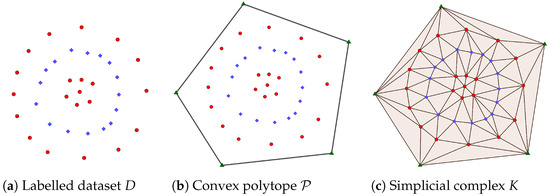
Figure 2.
Given a labelled dataset D, a convex polytope containing D can be computed. Then, the simplicial complex K can be obtained using the Delaunay triangulation of all the points of D and the vertices of .
Let us see now how to define maps between simplicial complexes.
Definition 7.
Given two simplicial complexes K and L, a vertex map is a function from the vertices of K to the vertices of L such that for any simplex , the set
is a simplex of L.
Let us observe that if and the composition of vertex maps is a vertex map. Let us see now that a vertex map can always be extended to a continuous function satisfying that if then .
Definition 8.
The simplicial map induced by the vertex map is a continuous function defined as follows. Let . Then,
being , for all , such that
where is a simplex of K such that .
Next, we recall one of the key ideas in this paper. Simplicial maps can be used to approximate continuous functions as closed as desired.
Definition 9.
Let K and L be simplicial complexes and a continuous function. A simplicial map induced by a vertex map is a simplicial approximation of g if
for each vertex v of K.
Let us notice that is thought here as an open set of points. That is, .
Theorem 1.
Simplicial Approximation Theorem ([20], p. 56) If is a continuous function between the underlying spaces of two simplicial complexes K and L, then there is a sufficiently large integer such that is a simplicial approximation of g.
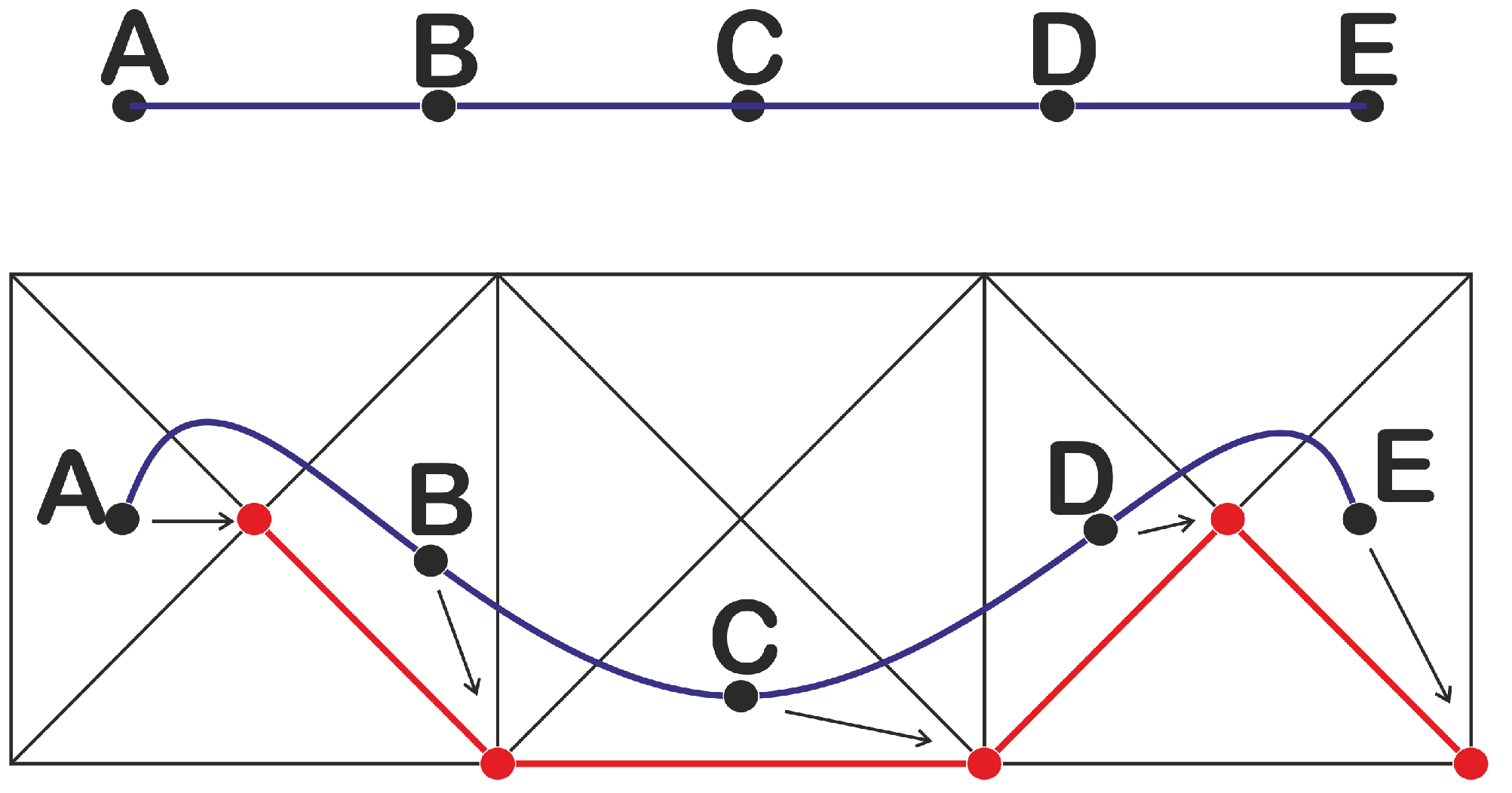
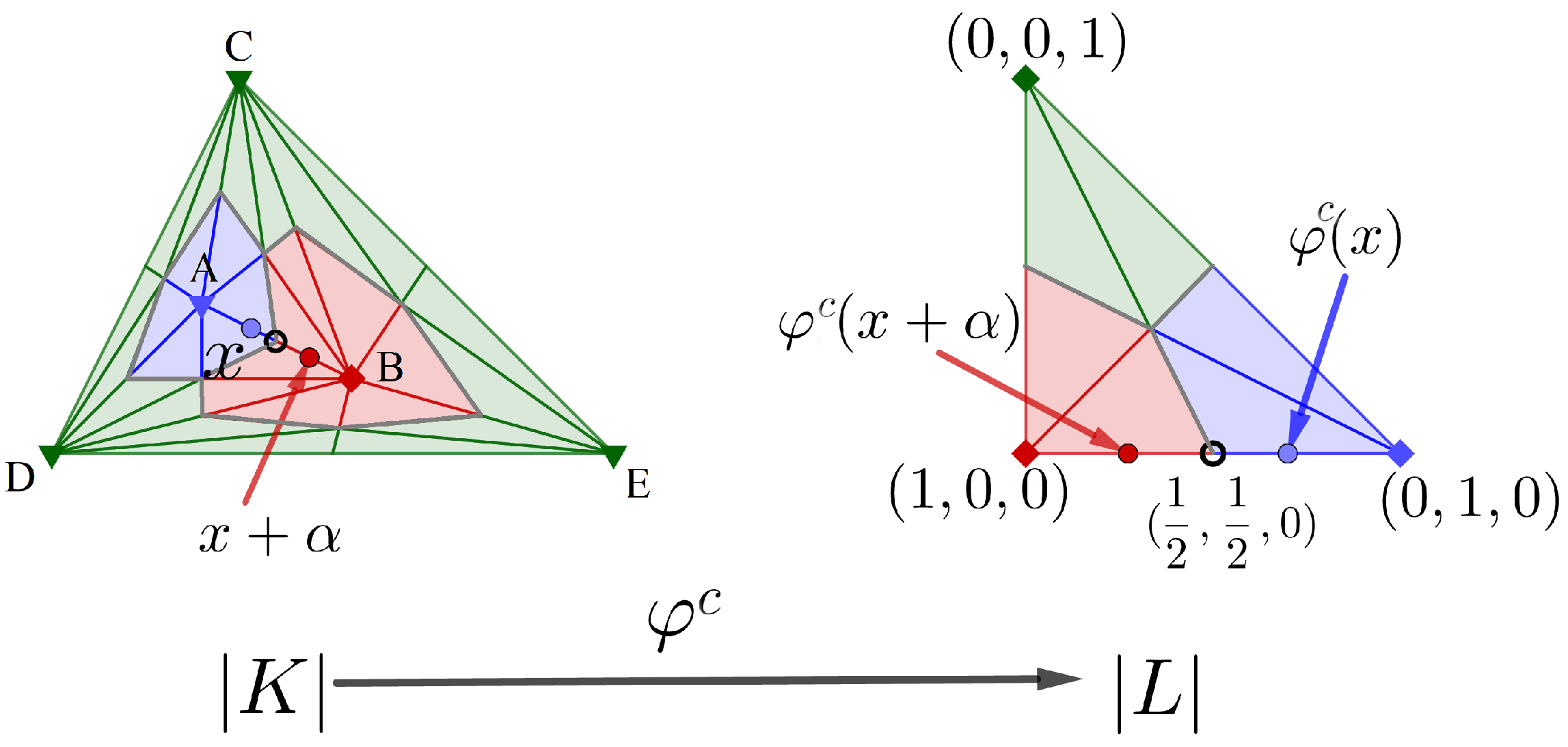
In Figure 3, an example of a simplicial approximation is provided. Theorem 1 was extended in [12] by introducing a bound to the distance between the continuous function and its simplicial approximation.
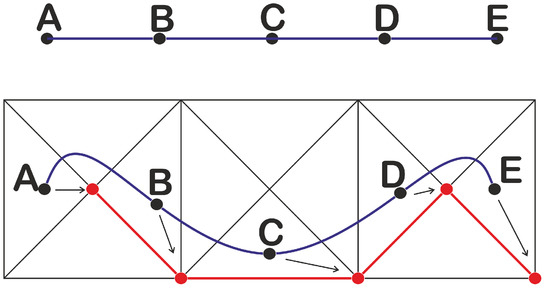
Figure 3.
On the top, we can see a 1-simplex with two iterated applications of the barycentric subdivision. On the bottom, a continuous function was applied to the straight line and a simplicial approximation (in red) is provided. The star condition is satisfied and no more barycentric subdivisions are needed.
Proposition 1
(Simplicial Approximation Theorem Extension [12]).Given and a continuous function between the underlying spaces of two simplicial complexes K and L, there exists such that is a simplicial approximation of g and .
Once concepts from Algebraic Topology have been stated, let us provide the definition of neural network, and a connection between these two fields using results from [12].
Definition 10
(adapted from [19]).Given , a multi-layer feed-forward network defined between spaces and is a function composed by functions:
where the integer is the number of hidden layers and, for , the function is defined as
where , , and for ; , , and being an integer for (called the width of the i-th hidden layer); being a real-valued matrix (called the matrix of weights of ); being a point in (called the bias term); and being a function (called the activation function).
In the literature, many other definitions of neural networks are available. The field is continuously adding new ideas and there is not a general definition which covers all the possible approaches, but many of the problems where neural networks are applied are based on the idea of finding a set of weights and bias where the remaining features of the neural network (number of hidden layers, their dimension, and activation functions) are settled at the beginning of the problem. As usual, such set of features of the neural network beyond the weights and the bias, will be called the architecture of the neural network. A constructive method for approximating multidimensional functions with neural networks was provided in [12]. Such networks have two hidden layers and the weights are not obtained by a training method, but they are determined by a given simplicial map.
Theorem 2
(Theorem 4 of [12]).Let us consider a simplicial map between the embedding of two finite pure simplicial complexes K and L of dimension d and k, respectively. Then a two-hidden-layer feed-forward network such that for all can be explicitly defined.
The construction of the neural network given in [12] to prove Theorem 2 gives rise to the concept of simplicial-map neural network introduced in the next section.
3. Simplicial-Map Neural Networks
The explicit construction of the neural network given in [12] is the main tool used in this paper for computing neural networks robust to adversarial attacks. Such a concrete construction is called simplicial-map neural network.
Definition 11.
Let K and L be two finite pure simplicial complexes of dimension d and k, respectively. Let us consider the simplicial map induced by a vertex map . Let be the maximal simplices of K, where and for and . Let be the maximal simplices of L, where and for and . The simplicial-map neural network induced by is a two-hidden-layer feed-forward neural network denoted by with the following architecture:
- an input layer composed of neurons;
- a first hidden layer composed of neurons;
- a second hidden layer composed of neurons; and
- an output layer with neurons.
Then, being
Firstly, being
where and . The bias term is and the function is then defined as:
Secondly, where
being and for ; ; ; and . The bias term is null and the function is defined as:
Thirdly, being
the bias term is null, and is defined as:
being for and
In [12], it is proven that and coincide for all .
Proposition 2
([12]). Let K and L be two finite pure simplicial complexes of dimension and , respectively. Let us consider the simplicial map induced by a vertex map . Then, the simplicial-map neural network induced by the simplicial map satisfies that for all .
4. Classification with Simplicial-Map Neural Networks
In this section, simplicial-map neural networks are considered as tools for classification tasks and for the study of adversarial examples. As usual, the classification problem will consist of finding a set of weights adapted to a labelled dataset given a fixed architecture.
Definition 12.
Let be integers. A labelled dataset D is a finite set of pairs
where, for , if , and represents a one-hot vector. We say that is the label of or, equivalently, that belongs to the class . Besides, we will denote by the ordered set of points .
The concept of supervised classification problem for neural networks can be defined as follows.
Definition 13.
Given a labelled dataset , an integer , and activation functions for , a supervised classification problem consists of looking for the weights and bias terms for , such that the associated neural network , with , and , satisfies:
- for all .
- maps to a vector of scores such that for and .
If such a neural network exists, we will say that characterizes D, or, equivalently, that correctly classifies D.
Let us remark that the success of a classification model as a neural network is not usually measured on the correct classification on the input dataset, but on the correct classification of unseen examples, (that is, pairs not in D), collected in a test set. In this paper, we chose such a restrictive definition since we are more interested in dealing with the problem of the robustness of neural networks against adversarial attacks than in the problem of overfitting. Besides, let us observe that, as usual, the scores can be interpreted as a probability distribution over the labels.
Remark 1.
It is known that some functions like the logistic sigmoid, the softmax or the softplus satisfy the properties of a probability distribution and they are broadly applied in deep learning models. Our function also behaves like a probability distribution which is adequate for multiclassification tasks.
Next, we provide the definition of some of the main concepts in this paper, the confidence set , the classified set , and the decision boundary of . The intuition behind these concepts is that x belongs to the confidence set of if the output is one of the possible one-hot vectors. If the output is a vector where the maximum is reached in exactly one coordinate, we say that x belongs to the classified set of . Otherwise, the output is a vector where the maximum is reached in two or more coordinates, i.e., the instance has equal probability to belong to two or more output classes, then we say that x belongs to the decision boundary of . Let us observe that and .
Definition 14.
Let be integers. Let be a labelled dataset and a neural network that characterizes D. Let , with . If there exists such that , then we say that x belongs to the set and it has label (with probability ). Moreover, we define to be the union of the sets for . Besides, when , we say that x belong to the confidence set . Finally, we say that x belongs to the decision boundary if there exists such that .
The following is a key result to define a simplicial-map neural network that characterizes a given labelled dataset.
Proposition 3.
Let be integers. Let L be the simplicial complex with only one maximal k-simplex with for and . Let be a labelled dataset and let be the vertices of a convex polytope such that . Let us assume that is in general position. Let . Then, the map defined as follows is a vertex map:
Proof.
L is composedof a maximal simplex. Any subset of vertices of a simplex is a simplex by definition. Then, any map between vertices of to is a vertex map. Specifically, is a vertex map. □
By abuse of notation, we will say that a point with barycentric coordinates has label if . Let us notice that an unknown label has been assigned to the vertex of L.
Proposition 4.
Let be the vertex map defined in Proposition 3. Then, the simplicial-map neural network induced by the simplicial map characterizes D.
Proof.
By Proposition 2, the neural network satisfies that for all . Besides, let us observe that the Cartesian coordinates of coincide with its barycentric coordinates. Moreover, for all , and, by definition, when . Then, we can conclude that characterizes D. □
Again, by abuse of notation, when is a simplicial-map neural network, we will denote by , , and , its confidence set, classified set and decision boundary, respectively.
Remark 2.
Firstly, let us observe that, with the assumptions of Proposition 3, if belongs to the decision boundary then for some satisfying that there are at least two vertices in σ having different labels. Moreover, for some with all its vertices in . Secondly, if σ is a d-simplex in , then either all its vertices belong to the confidence set or with satisfying that and . Finally, if σ is a d-simplex in for then either all its vertices belong to the classified subset for some , or with satisfying that and .
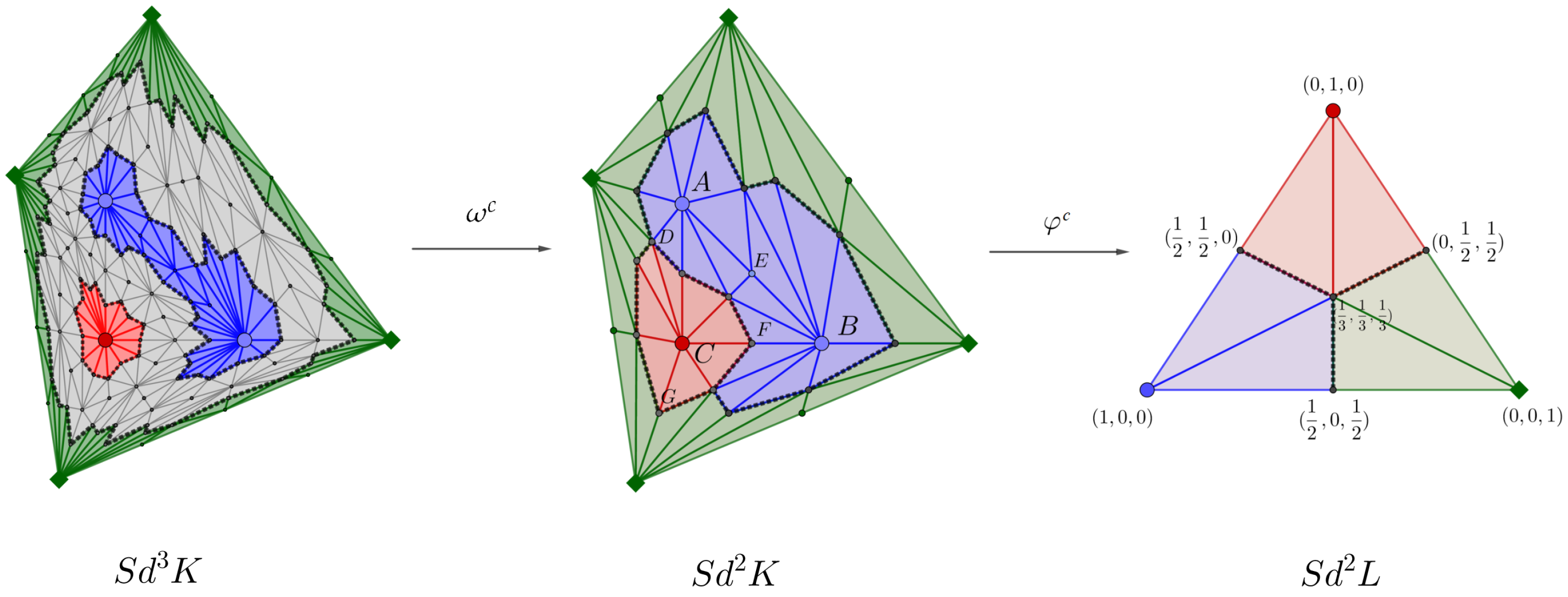
As the following result states, when , we can obtain a vertex map from to applying the barycentric subdivision, inducing a neural network that coincides with for any integer . Figure 4 illustrates these concepts.
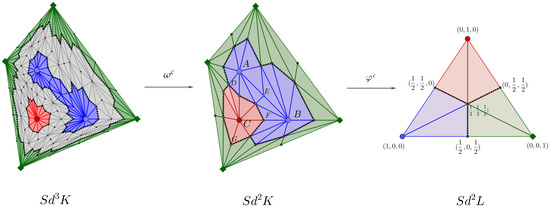
Figure 4.
Let be the Delaunay complex of where is the set of red and blue points, and are the green vertices (depicted in the center). Let L be the simplicial complex with one maximal simplex (pictured on the right). Let us consider the vertex map that sends the blue points to , the red point C to , and the green points (labelled as unknown) to . Then, gives rise to the simplicial map and the simplicial-map neural network . The decision boundary of is pictured on the center as the set of points in the boundary of the red, blue or green region. For example, , and . Let us consider now the barycenter subdivision of K shown on the left and the simplicial map which relates both simplicial complexes. The decision boundary of is the gray zone on the left picture.
Lemma 1.
Let be the vertex map defined in Proposition 3. For an integer and any , there exists such that . Then, the map defined as:
is a vertex map inducing a neural network that coincides with for any integer .
Proof.
Let be an integer. Let us observe that is a vertex map. By induction, let us assume that is a vertex map. Let . By definition of barycentric subdivision, we can assume that
Then,
Since is a vertex map, then is a simplex of and is a face of for all with , by definition of . Then, : is a simplex of .
Now, let us see that . By induction, let us prove that . Let . Then, there exist a d-simplex and a d-simplex such that and for all .
Then,
being for all and . Therefore,
being . Let us observe that
Now, let us observe that
for all . Then, for all ,
with for all and , concluding the proof. □
Computing Simplicial-Map Neural Networks Robust to Adversarial Attacks
In this subsection, the main result of the paper is provided. It states that we can always compute a neural network characterizing a given labelled dataset, and being robust to adversarial attacks of a given size. Firstly, let us define the concepts of adversarial example and robustness of neural networks against adversarial attacks. Some interesting references on these concepts are [21,22].
Definition 15.
Let be integers. Let be a labelled dataset and a neural network that characterizes D. Let : being a norm on . Let us suppose that has label ℓ. Then, an adversarial example of size r is defined as with such that has label with . A neural network is called robust to adversarial attacks of size r if no labelled point has an adversarial example of size r.
Proposition 5.
With the assumptions of Proposition 4, we have that is not robust to adversarial attacks of size r for .
Proof.
By Remark 2, consider such that there exist v and w being two vertices of with different labels. Let . Then z is in the decision boundary of and , are edges of . Let where . Then x has the same label as v and . Let where . Then has the same label as w and . Then, concluding that is an adversarial example of size r and . □
Example 1.
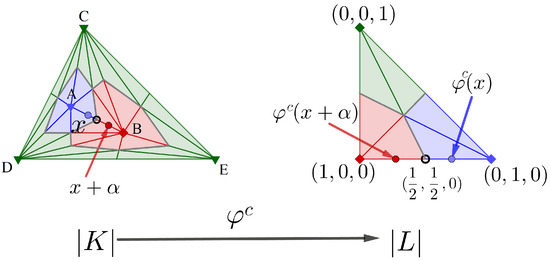
Let . Let us consider the labelled dataset , and the convex polytope with vertices , , . Then, is composed by five maximal 2-simplices and L by just one maximal 2-simplex. This way, and are composed by the maximal 2-simplices showed in Figure 5. Let , with , be in the geometric realization of the segment with endpoints . Then, with and . Therefore, x is classified as with probability d. Take . Then, z belongs to the decision boundary since . Take . Then, with and . Therefore, is classified as with probability .

Figure 5.
An adversarial example x for the simplicial-map neural network .
Since and , then is not robust to adversarial attacks of any size r with . See Figure 5.
Let us now introduce the main result of this paper stating that there exists a two-hidden-layer neural network characterizing a given labelled dataset and being robust to adversarial attacks of size for r being small enough. In order to define such a neural network robust to adversarial examples, we will construct a continuous function from to with the idea of later applying the Simplicial Approximation Theorem and the composition of simplicial maps to obtain a simplicial map from to that will give rise to a neural network robust to adversarial attacks of a given size . Let us observe that, to be able to compute such a robust neural network, the size r should be smaller than the distance between the decision boundary and the confidence set.
Theorem 3.
Let be integers. Let : , , be a labelled dataset. Then, there exists a two-hidden-layer neural network characterizing D and robust to adversarial attacks of size , for r being small enough.
Proof.
Let us consider a convex polytope such that the points of are inside . Then, we can compute the Delaunay complex that will be denoted simply by K (see Figure 4), and a simplicial complex L composed of just one maximal k-simplex. As claimed in Proposition 4, a simplicial map can be defined between and giving rise to a neural network that characterizes D (see Proposition 2). However, is not robust to adversarial attacks (see Proposition 5). Our goal is to define a new simplicial map such that its associated simplicial-map neural network is robust to adversarial attacks. To reach that aim, we need r to be small enough, that is, , where , , so adversarial attacks will be placed between the confidence set and the decision boundary . Then, a continuous function will be defined depending on such r, to later apply the Simplicial Approximation Theorem Extension (Proposition 1), obtaining a simplicial approximation of g as close to g as desired. Then, will be a simplicial map giving rise to a simplicial-map neural network robust to adversarial attacks of size r.
Let us define now the continuous function . Let be a d-simplex of . Let us observe that, by Remark 2, the vertices of satisfy the following property:
- All the vertices of are in . Then, .
- Otherwise, being and .
In the latter case, let us define the continuous function as follows. Without loss of generality, let us assume that with .
Let us compute the set of points of at distance less than r to and let us send, by g, such points to points in .
Let x be a point of with barycentric coordinates with respect to .
Let .
Let be the projection of x in whose barycentric coordinates with respect to are:
Let be the point in with barycentric coordinates with respect to , aligned with x and . Then,
So, for .
Now, for .
Then, .
Let . Then, if . Then,
Let us observe that and for , we have that so .
Besides, for , we have that so .
Let us prove that g is continuous at any point .
Let us observe that, by construction, g is continuous in the interior of of every d-simplex .
Let x be a point in for some d-simplices .
Let and with and . Let be the simplex with lower dimension such that . Then, by definition of simplicial complex, and the barycentric coordinates of x with respect to and coincide.
By Remark 2, we have to consider two cases:
- (1)
- All the vertices of belong to . Then and .
- (2)
- with and . Then and so the definition of with respect to and coincides.
Now, by Proposition 1, given , there exist and a simplicial map such that . By Lemma 1, is a vertex map. Since the composition of simplicial maps is a simplicial map, then is a simplicial map, concluding that is a simplicial-map neural network.
Let us prove now that is robust to adversarial attacks of size r. First of all, the following properties holds:
- (1)
- If then , being .
- (2)
- Let and . If then , being .Since then for a d-simplex with . Then, by Remark 2, , with and . Besides, since then , therefore .
- (3)
- If then , being .If then there exists such that . Then, by (0). Now, since , then by (1).
- (4)
- Let . If then .By contradiction, let us assume that and for some . Then, by (2), leading to a contradiction.
- (5)
- Let . If with probability and then and . This last statement is a consequence of (2) and that .
Now, let being . Let with and let . Let us prove that or .
On one hand, if then by (4). On the other hand, if then or by (3), concluding the proof. □
Example 2.
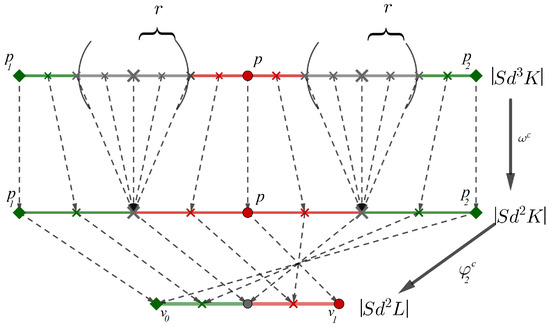
Let us consider a labelled dataset with composed of just one point. Let be a segment with endpoints and in such that . Let such that . Let K be the Delaunay complex of that consists of just the two maximal simplices and . Let L be a simplicial complex composed by a maximal 1-simplex with endpoints and . Then, a simplicial map can be defined as in Proposition 3 together with a neural network as in Proposition 4. However, is not robust to attacks of size r as it has been proved in Proposition 5. Then, following the proof of Theorem 3, in Figure 6, we have computed barycentric subdivisions on K until we approximate g by the simplicial map . Finally, the neural network induced by the composition is robust to adversarial attacks of size r.

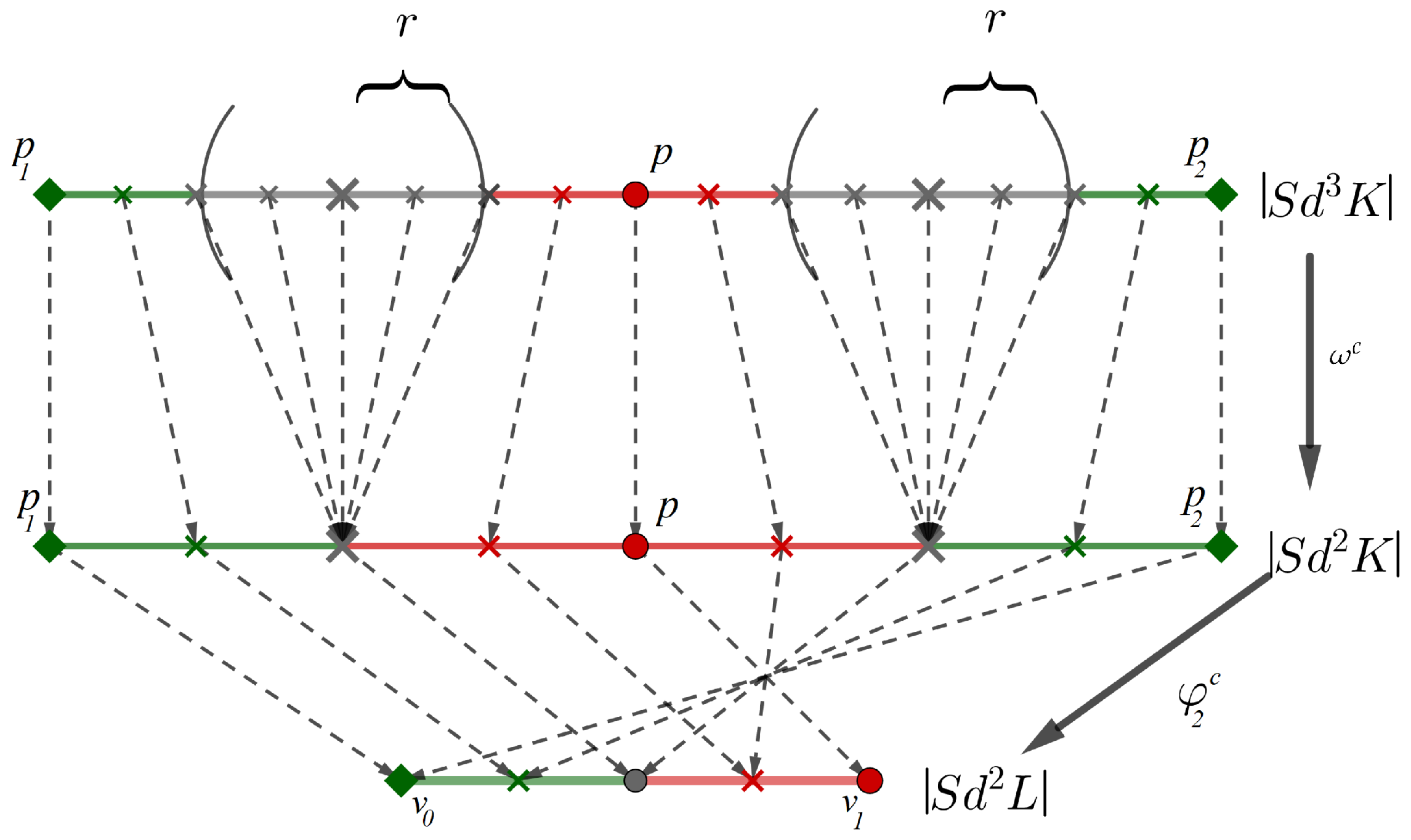
Figure 6.
Three simplicial complexes with simplicial maps and between them are shown illustrating a neural network robust to adversarial attacks of size r.
5. Conclusions and Future Work
Neural networks are one of the most promising tools in artificial intelligence and, currently, with the big success on real-world problem of Deep Learning architectures, it has become one of the most widely used. From a mathematical point of view, neural network can be seen as the composition of a big amount of simple functions, mainly from linear algebra, and the so-called activation functions. Since the efficiency of such neural networks depends of the choice of an appropriate set of parameters, most of the efforts in the study of such networks has been focused on optimization techniques. After a first wave of research based on these optimization techniques, many researchers are considering the study of neural networks by using different mathematical techniques as analysis, geometry or, as in this paper, algebraic topology.
Specifically, in this paper, we have presented a family of neural networks, called simplicial-map neural networks, that are robust to adversarial examples. The main contribution of the paper is a constructive proof that shows how to define a neural network robust to adversarial attacks of a given size. This result is proven thanks to the connection of neural networks with concepts from Algebraic Topology. By endowing the set of instances of a classification problem with the structure of simplicial complex and considering the set of one-hot labels as a simplex, provides a new point of view that allows to find the exact values of the weights of the associated network without any kind of training or optimization process.
Finally, we plan to provide an implementation of our methods that takes into account the efficiency issues that arise in creating neural networks following our approach. We believe that this point of view opens a new bridge between Neural Network and Algebraic Topology which can lead to a fruitful flow of concepts, problems and solutions in both directions.
Author Contributions
Conceptualization, R.G.-D., M.A.G.-N., J.H. and E.P.-H.; methodology, R.G.-D., M.A.G.-N., J.H. and E.P.-H.; formal analysis, R.G.-D., M.A.G.-N., J.H. and E.P.-H.; investigation, R.G.-D., M.A.G.-N., J.H. and E.P.-H.; writing—original draft preparation, R.G.-D., M.A.G.-N., J.H. and E.P.-H.; writing—review and editing, R.G.-D., M.A.G.-N., J.H. and E.P.-H. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by MICINN, FEDER/UE under grant PID2019-107339GB-100.
Institutional Review Board Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Szegedy, C.; Zaremba, W.; Sutskever, I.; Bruna, J.; Erhan, D.; Goodfellow, I.; Fergus, R. Intriguing properties of neural networks. arXiv 2013, arXiv:cs.CV/1312.6199. [Google Scholar]
- Fezza, S.A.; Bakhti, Y.; Hamidouche, W.; Déforges, O. Perceptual Evaluation of Adversarial Attacks for CNN-based Image Classification. In Proceedings of the Eleventh International Conference on Quality of Multimedia Experience (QoMEX), Berlin, Germany, 5–7 June 2019; pp. 1–6. [Google Scholar] [CrossRef]
- Garg, S.; Ramakrishnan, G. BAE: BERT-based Adversarial Examples for Text Classification. arXiv 2020, arXiv:cs.CL/2004.01970. [Google Scholar]
- Karim, F.; Majumdar, S.; Darabi, H. Adversarial Attacks on Time Series. IEEE Trans. Pattern Anal. Mach. Intell. 2020, 1. [Google Scholar] [CrossRef] [PubMed]
- Christakopoulou, K.; Banerjee, A. Adversarial Attacks on an Oblivious Recommender. In Proceedings of the 13th ACM Conference on Recommender Systems, Association for Computing Machinery, Copenhagen, Denmark, 20 September 2019; pp. 322–330. [Google Scholar] [CrossRef]
- Xu, H.; Ma, Y.; Liu, H.; Deb, D.; Liu, H.; Tang, J.; Jain, A.K. Adversarial Attacks and Defenses in Images, Graphs and Text: A Review. Int. J. Autom. Comput. 2020, 17, 151–178. [Google Scholar] [CrossRef]
- Yan, Z.; Guo, Y.; Zhang, C. Adversarial Margin Maximization Networks. IEEE Trans. Pattern Anal. Mach. Intell. 2019, 1. [Google Scholar] [CrossRef] [PubMed]
- Cortes, C.; Vapnik, V. Support Vector Networks. Mach. Learn. 1995, 20, 273–297. [Google Scholar] [CrossRef]
- Tang, Y. Deep Learning using Linear Support Vector Machines. arXiv 2013, arXiv:cs.LG/1306.0239. [Google Scholar]
- Sun, S.; Chen, W.; Wang, L.; Liu, X.; Liu, T. On the Depth of Deep Neural Networks: A Theoretical View. In Proceedings of the Thirtieth AAAI Conference on Artificial Intelligence, Phoenix, AZ, USA, 12–17 February 2016; Schuurmans, D., Wellman, M.P., Eds.; AAAI Press: Palo Alto, CA, USA, 2016; pp. 2066–2072. [Google Scholar]
- Wang, X.; Zhang, S.; Lei, Z.; Liu, S.; Guo, X.; Li, S.Z. Ensemble Soft-Margin Softmax Loss for Image Classification. In Proceedings of the 27th International Joint Conference on Artificial Intelligence, IJCAI’18, Stockholm, Sweden, 13–19 July 2018; AAAI Press: Palo Alto, CA, USA, 2018; pp. 992–998. [Google Scholar]
- Paluzo-Hidalgo, E.; Gonzalez-Diaz, R.; Gutiérrez-Naranjo, M.A. Two-hidden-layer feed-forward networks are universal approximators: A constructive approach. Neural Netw. 2020, 131, 29–36. [Google Scholar] [CrossRef] [PubMed]
- Ismailov, V.E. On the approximation by neural networks with bounded number of neurons in hidden layers. J. Math. Anal. Appl. 2014, 417, 963–969. [Google Scholar] [CrossRef]
- Guliyev, N.J.; Ismailov, V.E. Approximation capability of two hidden layer feedforward neural networks with fixed weights. Neurocomputing 2018, 316, 262–269. [Google Scholar] [CrossRef]
- Ebli, S.; Defferrard, M.; Spreemann, G. Simplicial Neural Networks. arXiv 2020, arXiv:cs.LG/2010.03633. [Google Scholar]
- Spanier, E.H. Algebraic Topology; Springer: New York, NY, USA, 1995. [Google Scholar]
- Boissonnat, J.D.; Chazal, F.; Yvinec, M. Geometric and Topological Inference; Cambridge Texts in Applied Mathematics; Cambridge University Press: Cambridge, UK, 2018. [Google Scholar] [CrossRef]
- Okabe, A.; Boots, B.; Sugihara, K.; Chiu, S.N.; Kendall, D.G. Definitions and Basic Properties of Voronoi Diagrams. In Spatial Tessellations: Concepts and Applications of Voronoi Diagrams, 2nd ed.; John Wiley & Sons: Chichester, UK, 2000; pp. 43–112. [Google Scholar] [CrossRef]
- Hornik, K. Approximation Capabilities of Multilayer Feedforward Networks. Neural Netw. 1991, 4, 251–257. [Google Scholar] [CrossRef]
- Edelsbrunner, H.; Harer, J. Computational Topology—An Introduction; American Mathematical Society: Providence, RI, USA, 2010; pp. 1–241. [Google Scholar]
- Lecuyer, M.; Atlidakis, V.; Geambasu, R.; Hsu, D.; Jana, S. Certified Robustness to Adversarial Examples with Differential Privacy. In Proceedings of the IEEE Symposium on Security and Privacy (SP), San Francisco, CA, USA, 18–19 May 2019; pp. 656–672. [Google Scholar] [CrossRef]
- Yuan, X.; He, P.; Zhu, Q.; Li, X. Adversarial Examples: Attacks and Defenses for Deep Learning. IEEE Trans. Neural Netw. Learn. Syst. 2019, 30, 2805–2824. [Google Scholar] [CrossRef] [PubMed]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).